基于对数域加性信号分解的时序SAR图像相干斑抑制方法

康健; 童风雨; 白雨松; 丁翔; 冀腾宇; 张柘

doi:10.12000/JR22242

基于对数域加性信号分解的时序SAR图像相干斑抑制方法

DOI: 10.12000/JR22242

康健^1, ,,
童风雨¹,
白雨松¹,
丁翔¹,
冀腾宇²,
张柘^{3, 4, 5, ,}

1.
苏州大学电子信息学院苏州 215006
2.
西北工业大学数学与统计学院西安 710072
3.
苏州市微波成像处理与应用技术重点实验室苏州 215123
4.
苏州空天信息研究院苏州 215123
5.
中国科学院空天信息创新研究院北京 100190

基金项目: 国家自然科学基金(62101371)，江苏省青年基金(BK20210707)

详细信息

作者简介:
康　健，副教授，硕士生导师，主要研究方向为SAR/InSAR信号处理、遥感图像解译等

童风雨，硕士生，主要研究方向为目标检测技术

白雨松，硕士生，主要研究方向为SAR干涉技术

丁　翔，硕士生，主要研究方向为SAR图像去噪

冀腾宇，讲师，硕士生导师，主要研究方向为张量分解等

张　柘，研究员，博士生导师，主要研究方向为稀疏信号处理、稀疏微波成像等

通讯作者:
康健 jiankang@suda.edu.cn

张柘 zhangzhe01@aircas.ac.cn

责任主编：陈溅来 Corresponding Editor: CHEN Jianlai
中图分类号: TP753
计量
- 文章访问数: 1021
- HTML全文浏览量: 373
- PDF下载量: 164
- 被引次数: 0
出版历程
- 收稿日期: 2022-12-25
- 修回日期: 2023-02-28
- 网络出版日期: 2023-03-14
- 刊出日期: 2023-10-28

SAR Time Series Despeckling Based on Additive Signal Component Decomposition in Logarithm Domain

KANG Jian^{1
, ,},
TONG Fengyu¹,
BAI Yusong¹,
DING Xiang¹,
JI Tengyu²,
ZHANG Zhe^{3, 4, 5
, ,}

1.
School of Electronic and Information Engineering, Soochow University, Suzhou 215006, China
2.
School of Mathematical and Statistics, Northwestern Polytechnical University, Xi’an 710072, China
3.
Suzhou Key Laboratory of Microwave Imaging, Processing and Application Technology, Suzhou 215123, China
4.
Suzhou Aerospace Information Research Institute, Suzhou 215123, China
5.
Aerospace Information Research Institute, Chinese Academy of Sciences, Beijing 100190, China

Funds: The National Natural Science Foundation of China (62101371), Jiangsu Province Science Foundation for Youths (BK20210707)

More Information

Corresponding author: KANG Jian, jiankang@suda.edu.cn; ZHANG Zhe, zhangzhe01@aircas.ac.cn

摘要

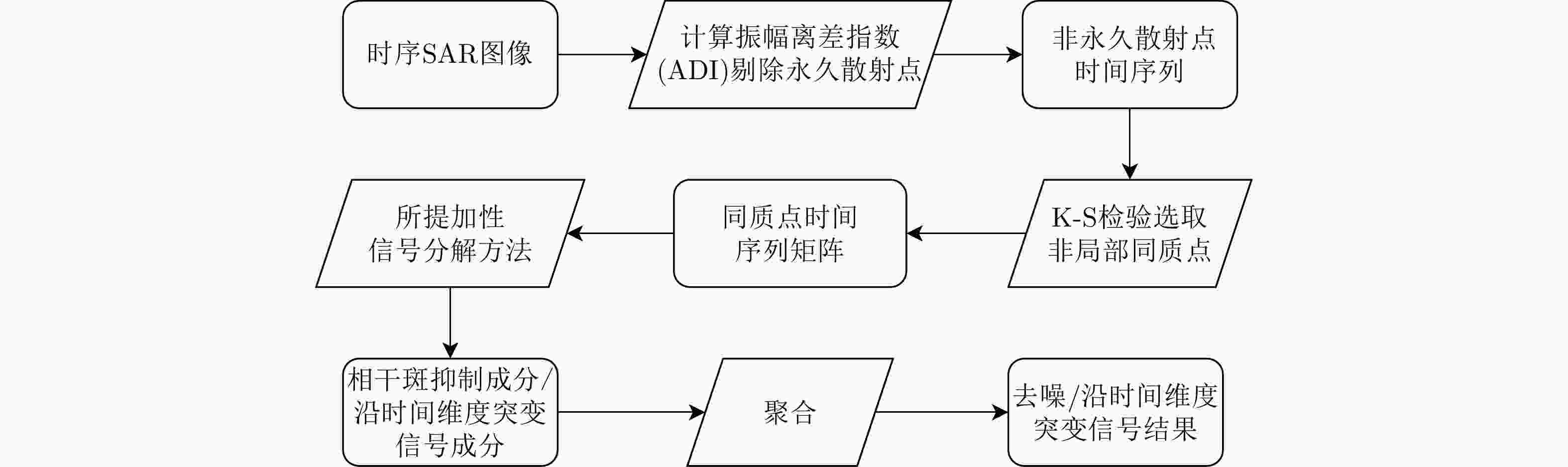
摘要: 随着合成孔径雷达(SAR)在测绘带宽度、空间以及时间分辨率上的大幅提升，由不同时间获取的SAR图像配准得到的时间序列能更加精确地提供观测区域的动态变化信息。然而，相干斑噪声以及沿时间维度突变信号为后续的解译工作带来了严重挑战。尽管现有的主流方法可以对时序SAR图像的相干斑进行有效抑制，但沿时间维度突变信号会对去噪结果产生干扰。为更好地解决此问题，该文提出了一种基于对数域加性信号分解的方法，能同时抑制相干斑噪声并且对时序图像中的稳定信号和沿时间维度突变信号进行分离，从而消除突变信号对于去噪结果的影响。在仿真数据受到突变信号干扰的情况下，所提方法与其他主流方法相比，其去噪结果在峰值信噪比(PSNR)指标上取得了大约3 dB的提升。在哨兵1号数据上，所提方法能鲁棒地对时序图像中的相干斑噪声进行抑制，并且得到的突变信号成分也为后续的解译工作提供了参考数据。
- 相干斑噪声抑制 /
- 非局部滤波 /
- SAR图像去噪 /
- 时序SAR图像
Abstract: With the substantial improvement of Synthetic Aperture Radar (SAR) regarding swath width and spatial and temporal resolutions, a time series obtained by registering SAR images acquired at different times can provide more accurate information on the dynamic changes in the observed areas. However, inherent speckle noise and outliers along the temporal dimension in the time series pose serious challenges for subsequent interpretation tasks. Although existing state-of-the-art methods can effectively suppress the speckle noise in a SAR time series, outliers along the temporal dimension will interfere with the denoising results. To better solve this problem, this paper proposes an additive signal decomposition method in the logarithm domain that can suppress the speckle noise and separate stable data and outliers along the temporal dimension in a time series, thus eliminating the impact of outliers on the denoising results. When the simulated data are disturbed by outliers, the proposed method can achieve an approximately 3 dB improvement in the Peak Signal-to-Noise Ratio (PSNR) compared to the other state-of-the-art methods. On Sentinel-1 data, the proposed method robustly suppresses the speckle noise in a time series, and the obtained outliers along the temporal dimension provide reference data for subsequent interpretation tasks.
- Speckle noise suppression /
- Nonlocal filtering /
- SAR image denoising /
- SAR image time series

HTML全文

图 1 含有沿时间维度突变信号的SAR幅度时间序列

Figure 1. SAR amplitude time series with outliers along the temporal dimension

下载: 全尺寸图片幻灯片

图 2 本文所提方法流程图

Figure 2. Flow chart of the proposed method

下载: 全尺寸图片幻灯片

图 3 本文采用的仿真数据

Figure 3. Simulation data used in this paper

下载: 全尺寸图片幻灯片

图 4 仿真数据相干斑抑制结果

Figure 4. Speckle suppression results of the simulated data

下载: 全尺寸图片幻灯片

图 5 本文方法的参数敏感性分析

Figure 5. Parameter sensitivity analyses of the proposed method

下载: 全尺寸图片幻灯片

图 6 所提方法对于图像数目的敏感性分析

Figure 6. Sensitivity analysis of the proposed method with respect to the number of images

下载: 全尺寸图片幻灯片

图 7 上海近海区域哨兵1号数据的相干斑抑制结果

Figure 7. Speckle suppression results for Sentinel-1 data in the Shanghai offshore region

下载: 全尺寸图片幻灯片

图 8 上海浦东机场区域哨兵1号数据的相干斑抑制结果

Figure 8. Speckle suppression results for Sentinel-1 data in Shanghai pudong airport region

下载: 全尺寸图片幻灯片

图 9 近海区域图像边缘提取结果对比

Figure 9. Comparison of image edge extraction results in offshore areas

下载: 全尺寸图片幻灯片

图 10 海上舰船区域图像边缘提取结果对比

Figure 10. Comparison of image edge extraction results of ship region

下载: 全尺寸图片幻灯片

表 1 仿真数据相干斑抑制结果的定量分析

Table 1. Quantitative analysis of speckle suppression results in simulation data

方法	PSNR (dB)			MSSIM (dB)			MCC
方法	–	0.5%	1.0%	–	0.5%	1.0%	–	0.5%	1.0%
SqueeSAR	30.95	29.81	28.42	0.51	0.43	0.38	0.87	0.80	0.75
MSAR-BM3D	35.01	18.02	15.12	0.56	0.26	0.18	0.93	0.35	0.26
RABASAR	35.07	32.97	30.51	0.63	0.49	0.39	0.96	0.91	0.82
DespecKS-NLLRTV	29.53	28.70	28.41	0.54	0.31	0.28	0.90	0.88	0.88
本文方法	32.07	32.82	33.15	0.57	0.56	0.55	0.92	0.92	0.91

下载: 导出CSV

表 2 4块同质区域计算得到的等效视数

Table 2. The equivalent apparent number calculated by four homogeneous regions

方法	ENL
方法	A1	A2	A3	A4
原始图像	0.872	0.794	0.907	0.936
SqueeSAR	325.30	3.25	64.33	72.55
MSAR-BM3D	176.40	15.48	65.22	117.07
RABASAR	26.33	24.40	24.13	17.07
DespecKS-NLLRTV	54.86	59.32	110.70	85.61
本文方法	107.30	74.68	80.11	139.50

下载: 导出CSV

表 3 沿时间维度突变信号的熵值分析

Table 3. Entropy analysis of the outliers along the temporal dimension

地点	测试日期	DespecKS-NLLRTV	本文方法
近海	2020-09-15	14.618	0.306
近海	2021-02-06	15.791	0.144
机场	2019-12-02	18.623	0.643
机场	2020-09-27	16.032	0.736

下载: 导出CSV

参考文献(28)

[1]	MOREIRA A, PRATS-IRAOLA P, YOUNIS M, et al. A tutorial on synthetic aperture radar[J]. IEEE Geoscience and Remote Sensing Magazine, 2013, 1(1): 6–43. doi: 10.1109/MGRS.2013.2248301
[2]	邓云凯, 赵凤军, 王宇. 星载SAR技术的发展趋势及应用浅析[J]. 雷达学报, 2012, 1(1): 1–10. doi: 10.3724/SP.J.1300.2012.20015 DENG Yunkai, ZHAO Fengjun, and WANG Yu. Brief analysis on the development and application of spaceborne SAR[J]. Journal of Radars, 2012, 1(1): 1–10. doi: 10.3724/SP.J.1300.2012.20015
[3]	陈杰, 杨威, 王亚敏, 等. 高时相星载序贯SAR图像运动目标检测方法[J]. 雷达学报, 2022, 11(6): 1048–1060. doi: 10.12000/JR22184 CHEN Jie, YANG Wei, WANG Yamin, et al. Moving target monitoring algorithm based on high-frame-rate SAR images[J]. Journal of Radars, 2022, 11(6): 1048–1060. doi: 10.12000/JR22184
[4]	XUE Feiyang, LV Xiaolei, DOU Fangjia, et al. A review of time-series interferometric SAR techniques: A tutorial for surface deformation analysis[J]. IEEE Geoscience and Remote Sensing Magazine, 2020, 8(1): 22–42. doi: 10.1109/MGRS.2019.2956165
[5]	徐丰, 王海鹏, 金亚秋. 深度学习在SAR目标识别与地物分类中的应用[J]. 雷达学报, 2017, 6(2): 136–148. doi: 10.12000/JR16130 XU Feng, WANG Haipeng, and JIN Yaqiu. Deep learning as applied in SAR target recognition and terrain classification[J]. Journal of Radars, 2017, 6(2): 136–148. doi: 10.12000/JR16130
[6]	ARGENTI F, LAPINI A, BIANCHI T, et al. A tutorial on speckle reduction in synthetic aperture radar images[J]. IEEE Geoscience and Remote Sensing Magazine, 2013, 1(3): 6–35. doi: 10.1109/MGRS.2013.2277512
[7]	VASILE G, TROUVE E, LEE J S, et al. Intensity-driven adaptive-neighborhood technique for polarimetric and interferometric SAR parameters estimation[J]. IEEE Transactions on Geoscience and Remote Sensing, 2006, 44(6): 1609–1621. doi: 10.1109/TGRS.2005.864142
[8]	LEE J S, GRUNES M R, and GRANDI G D. Polarimetric SAR speckle filtering and its implication for classification[J]. IEEE Transactions on Geoscience and Remote Sensing, 1999, 37(5): 2363–2373. doi: 10.1109/36.789635
[9]	BIOUCAS-DIAS J M and FIGUEIREDO M A T. Multiplicative noise removal using variable splitting and constrained optimization[J]. IEEE Transactions on Image Processing, 2010, 19(7): 1720–1730. doi: 10.1109/TIP.2010.2045029
[10]	DALSASSO E, YANG Xiangli, DENIS L, et al. SAR image despeckling by deep neural networks: From a pre-trained model to an end-to-end training strategy[J]. Remote Sensing, 2020, 12(16): 2636. doi: 10.3390/rs12162636
[11]	XIONG Kai, ZHAO Guanghui, WANG Yingbin, et al. SPB-Net: A deep network for SAR imaging and despeckling with downsampled data[J]. IEEE Transactions on Geoscience and Remote Sensing, 2021, 59(11): 9238–9256. doi: 10.1109/TGRS.2020.3034102
[12]	MOLINI A B, VALSESIA D, FRACASTORO G, et al. Speckle2Void: Deep self-supervised SAR despeckling with blind-spot convolutional neural networks[J]. IEEE Transactions on Geoscience and Remote Sensing, 2022, 60: 5204017. doi: 10.1109/TGRS.2021.3065461
[13]	DELEDALLE C A, DENIS L, POGGI G, et al. Exploiting patch similarity for SAR image processing: The nonlocal paradigm[J]. IEEE Signal Processing Magazine, 2014, 31(4): 69–78. doi: 10.1109/MSP.2014.2311305
[14]	XU Gang, GAO Yandong, LI Jinwei, et al. InSAR phase denoising: A review of current technologies and future directions[J]. IEEE Geoscience and Remote Sensing Magazine, 2020, 8(2): 64–82. doi: 10.1109/MGRS.2019.2955120
[15]	QUEGAN S, LE TOAN T, YU Jiongjiong, et al. Multitemporal ERS SAR analysis applied to forest mapping[J]. IEEE Transactions on Geoscience and Remote Sensing, 2000, 38(2): 741–753. doi: 10.1109/36.842003
[16]	TROUVE E, CHAMBENOIT Y, CLASSEAU N, et al. Statistical and operational performance assessment of multitemporal SAR image filtering[J]. IEEE Transactions on Geoscience and Remote Sensing, 2003, 41(11): 2519–2530. doi: 10.1109/TGRS.2003.817270
[17]	SU Xin, DELEDALLE C A, TUPIN F, et al. Two-step multitemporal nonlocal means for synthetic aperture radar images[J]. IEEE Transactions on Geoscience and Remote Sensing, 2014, 52(10): 6181–6196. doi: 10.1109/TGRS.2013.2295431
[18]	FERRETTI A, FUMAGALLI A, NOVALI F, et al. A new algorithm for processing interferometric data-stacks: SqueeSAR[J]. IEEE Transactions on Geoscience and Remote Sensing, 2011, 49(9): 3460–3470. doi: 10.1109/TGRS.2011.2124465
[19]	CHIERCHIA G, EL GHECHE M, SCARPA G, et al. Multitemporal SAR image despeckling based on block-matching and collaborative filtering[J]. IEEE Transactions on Geoscience and Remote Sensing, 2017, 55(10): 5467–5480. doi: 10.1109/TGRS.2017.2707806
[20]	PARRILLI S, PODERICO M, ANGELINO C V, et al. A nonlocal SAR image denoising algorithm based on LLMMSE wavelet shrinkage[J]. IEEE Transactions on Geoscience and Remote Sensing, 2012, 50(2): 606–616. doi: 10.1109/TGRS.2011.2161586
[21]	ZHAO Weiying, DELEDALLE C A, DENIS L, et al. Ratio-based multitemporal SAR images denoising: RABASAR[J]. IEEE Transactions on Geoscience and Remote Sensing, 2019, 57(6): 3552–3565. doi: 10.1109/TGRS.2018.2885683
[22]	BAIER G, HE Wei, and YOKOYA N. Robust nonlocal low-rank SAR time series despeckling considering speckle correlation by total variation regularization[J]. IEEE Transactions on Geoscience and Remote Sensing, 2020, 58(11): 7942–7954. doi: 10.1109/TGRS.2020.2985400
[23]	CHAMBOLLE A and POCK T. A first-order primal-dual algorithm for convex problems with applications to imaging[J]. Journal of Mathematical Imaging and Vision, 2011, 40(1/2): 120–145. doi: 10.1007/s10851-010-0251-1
[24]	BOYD S, PARIKH N, CHU E, et al. Distributed optimization and statistical learning via the alternating direction method of multipliers[J]. Foundations and Trends ^® in Machine Learning, 2011, 3(1): 1–122. doi: 10.1561/2200000016
[25]	FERRETTI A, PRATI C, and ROCCA F. Permanent scatterers in SAR interferometry[J]. IEEE Transactions on Geoscience and Remote Sensing, 2001, 39(1): 8–20. doi: 10.1109/36.898661
[26]	DELEDALLE C A, DENIS L, TABTI S, et al. MuLoG, or how to apply Gaussian denoisers to multi-channel SAR speckle reduction?[J]. IEEE Transactions on Image Processing, 2017, 26(9): 4389–4403. doi: 10.1109/TIP.2017.2713946
[27]	WANG Yilun, YANG Junfeng, YIN Wotao, et al. A new alternating minimization algorithm for total variation image reconstruction[J]. SIAM Journal on Imaging Sciences, 2008, 1(3): 248–272. doi: 10.1137/080724265
[28]	PARIKH N and BOYD S. Proximal algorithms[J]. Foundations and Trends ^® in Optimization, 2014, 1(3): 127–239. doi: 10.1561/2400000003