作者中心
专家审稿
责编办公
编辑办公
-
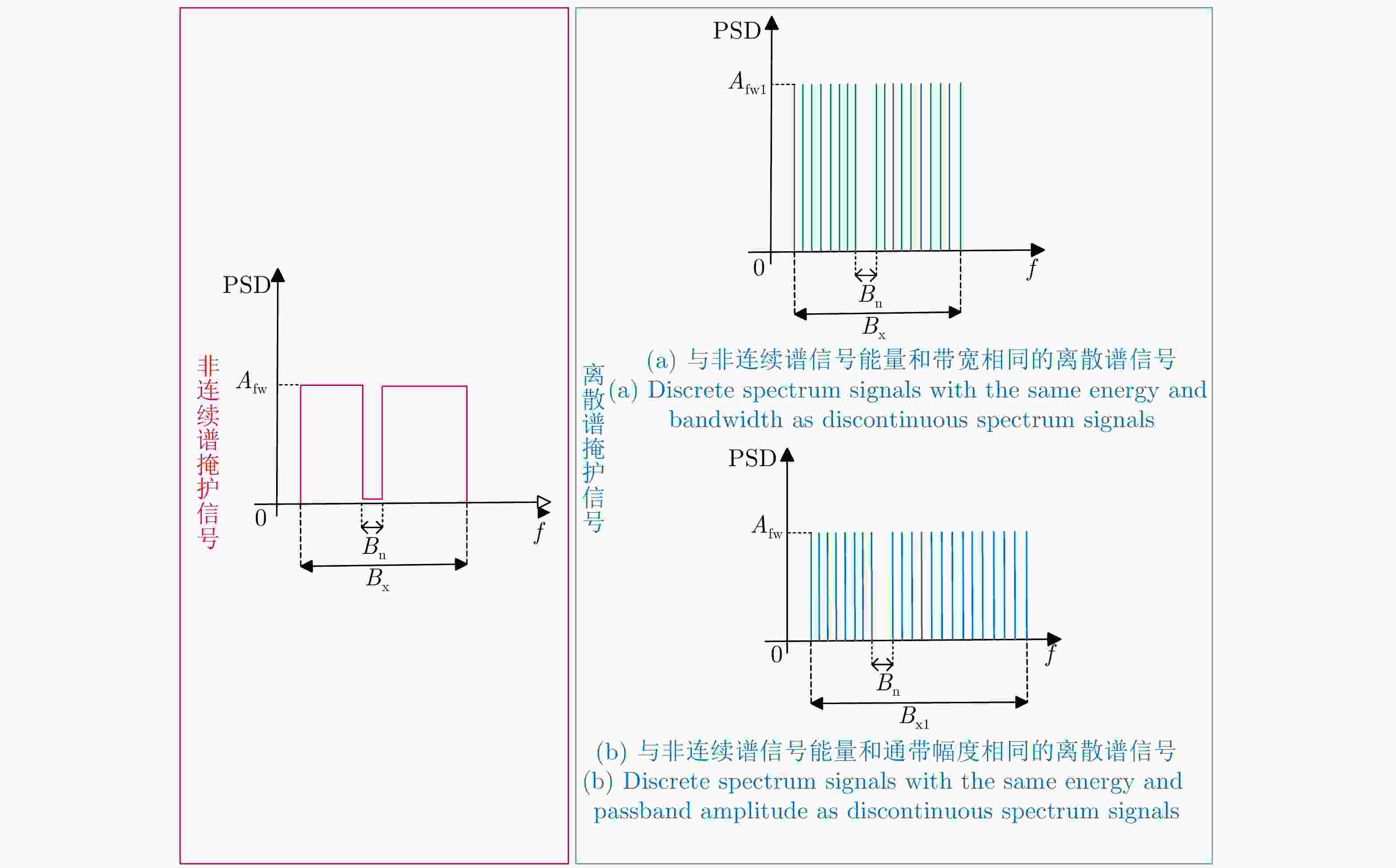
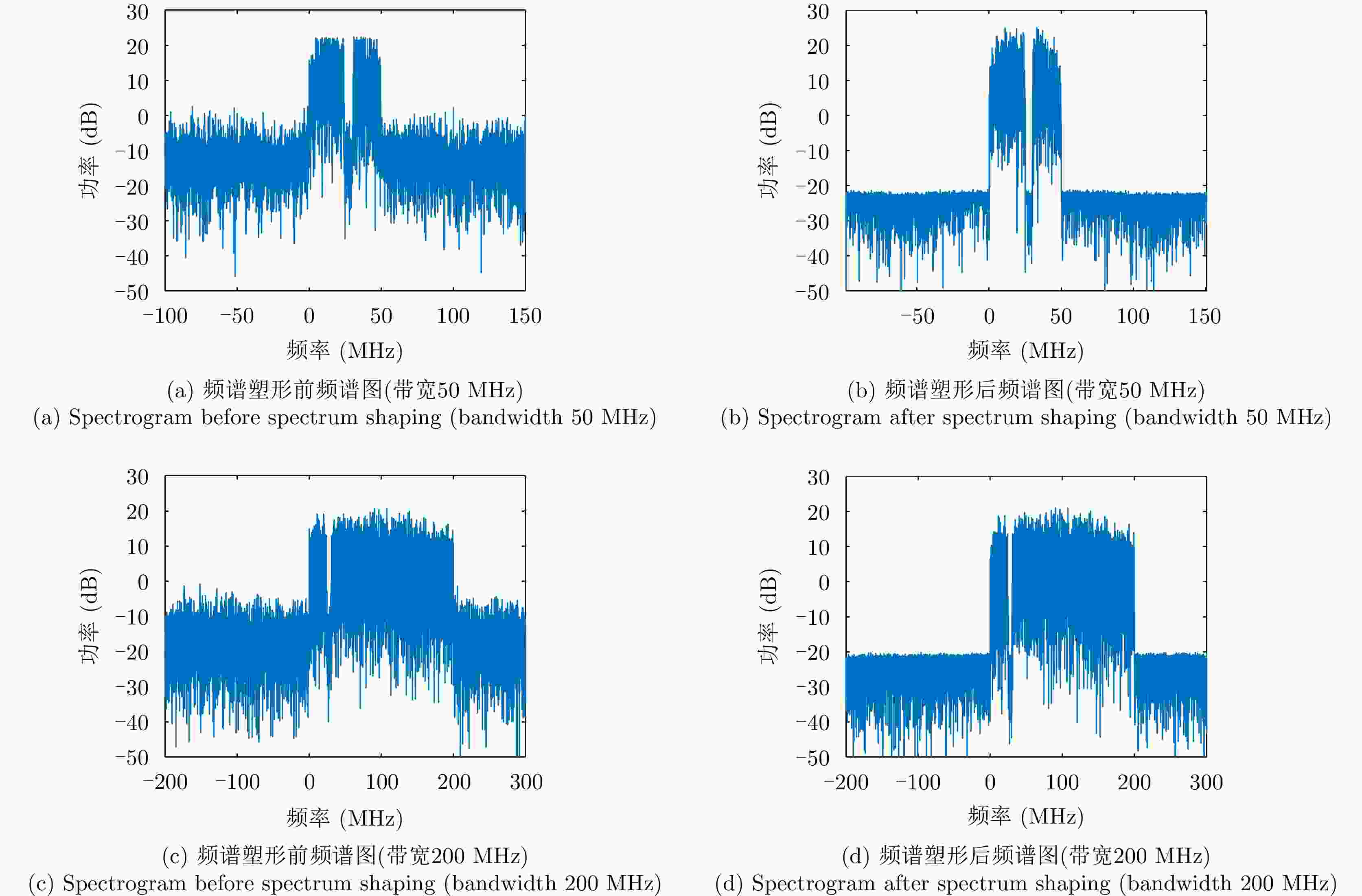
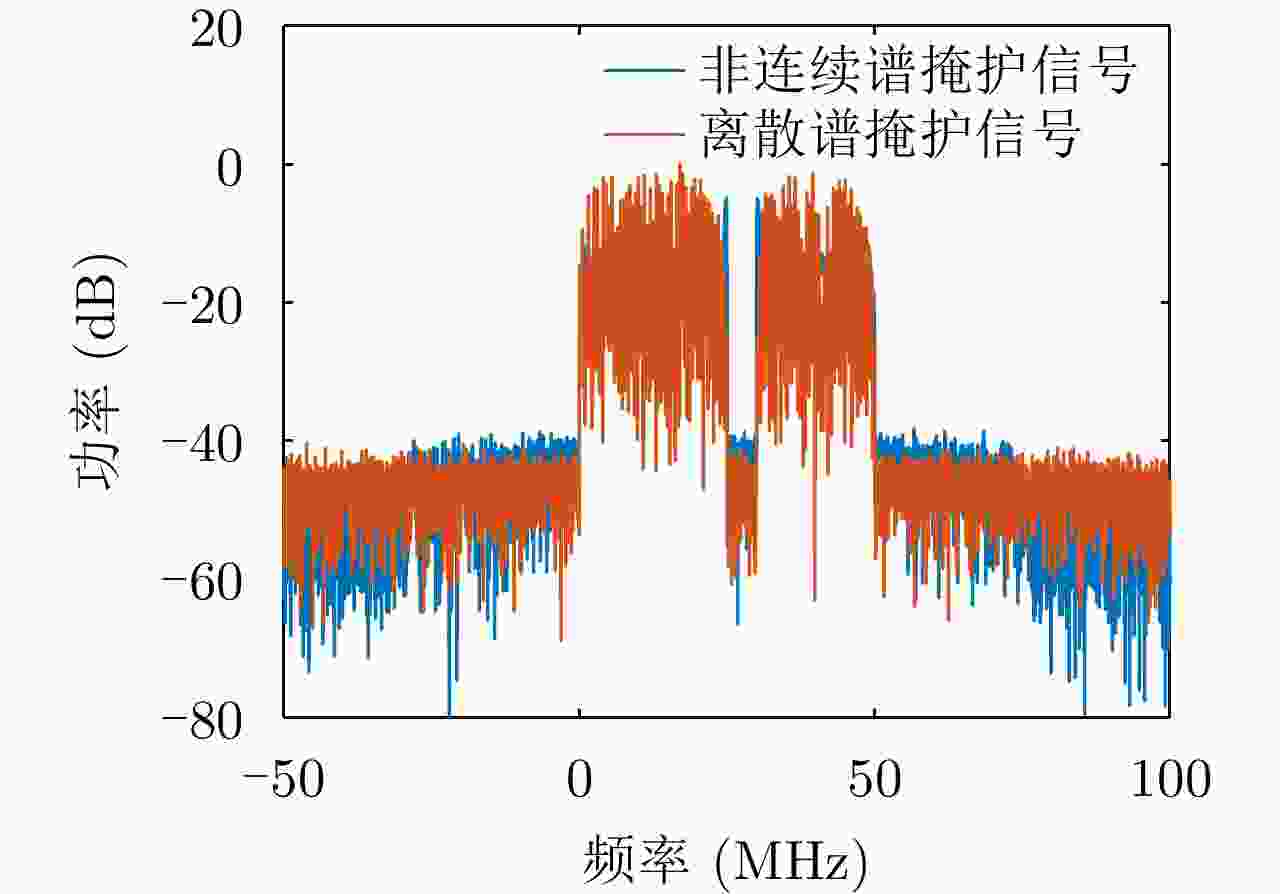
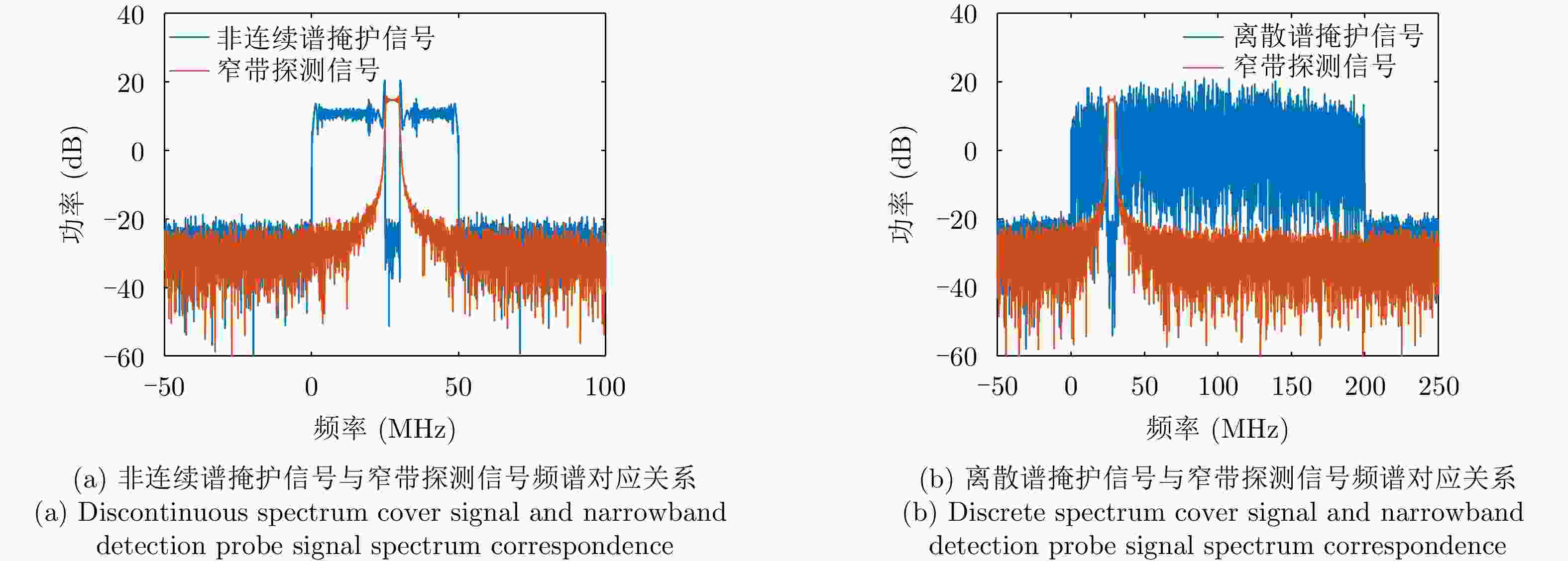
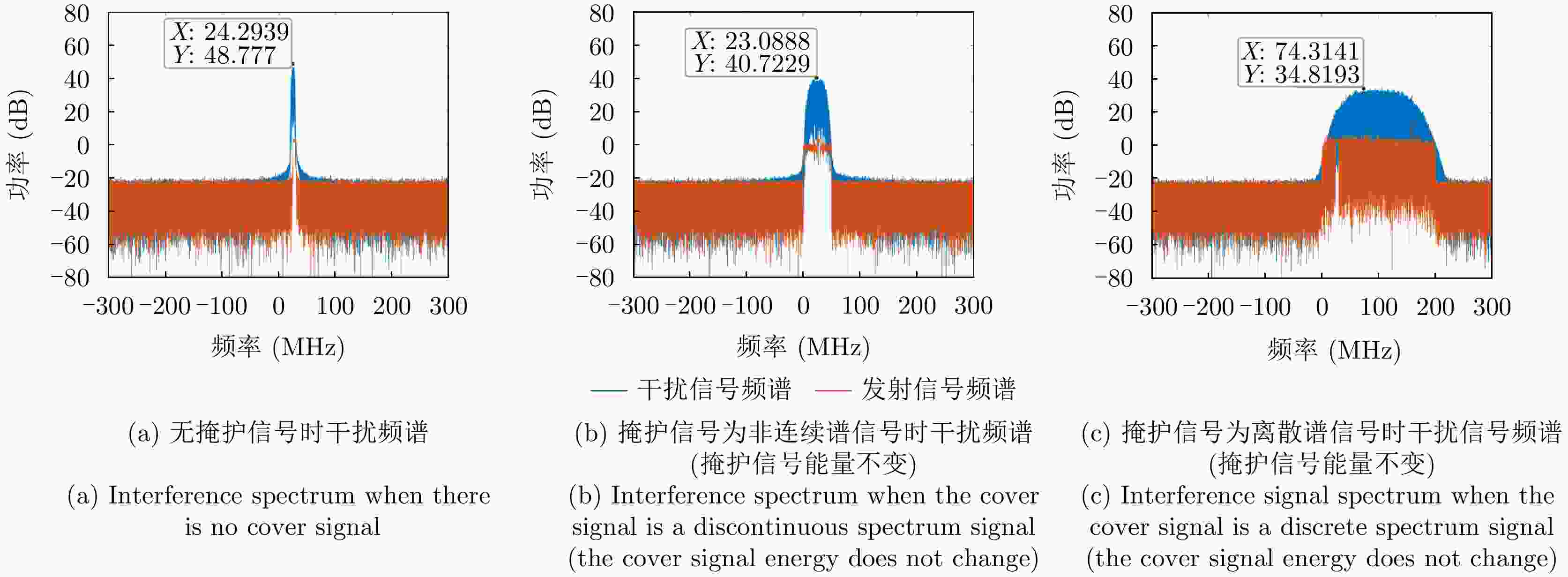
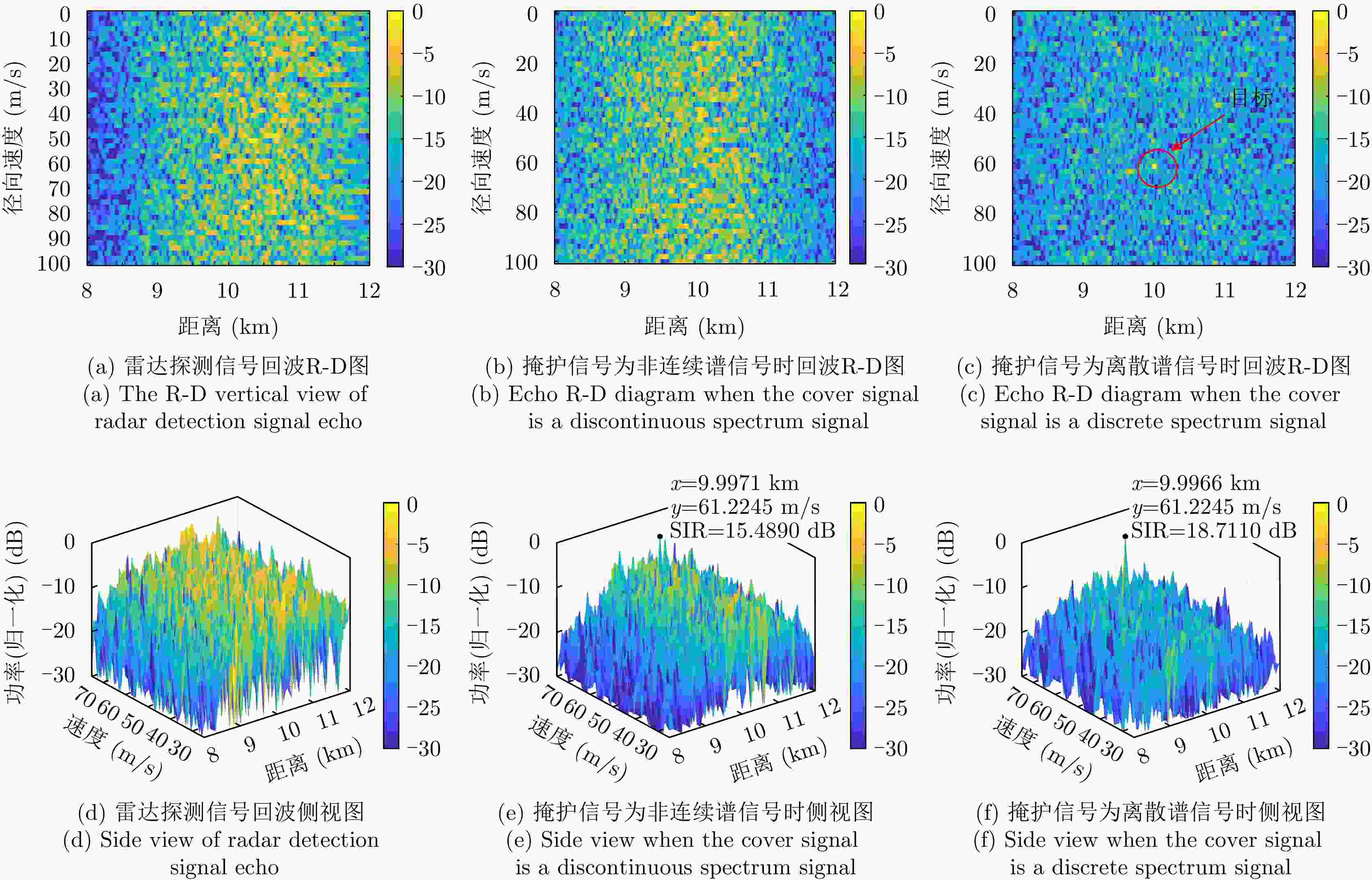
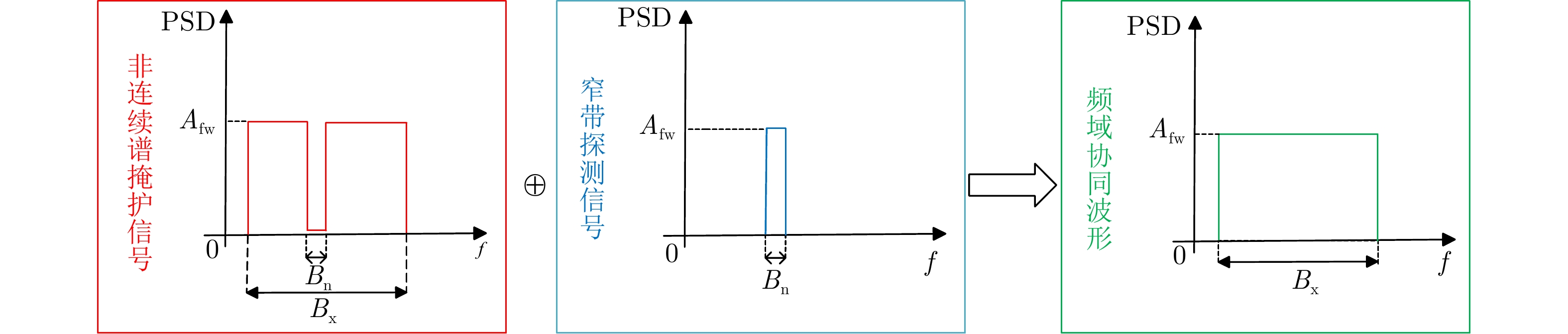
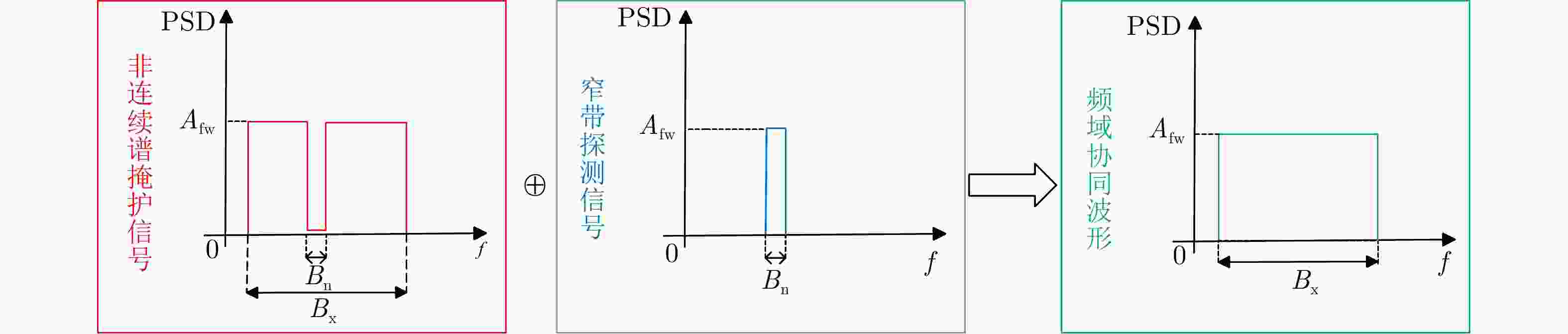
摘要: 射频掩护是最早的雷达主动抗干扰措施之一，其通过在雷达脉冲信号之前发射不同频率的掩护脉冲来诱导敌方干扰机，实现抗干扰。近年来，随着抗干扰需求更加迫切，射频掩护技术进一步发展，最具代表性的是采用非连续谱信号作为掩护信号，但掩护信号的能量利用率仍存在提升空间。针对此问题，该文在非连续谱掩护信号基础上提出了一种离散谱掩护信号，建立了恒模和频谱幅度联合约束下的波形设计优化问题，通过交替向量乘子法以及频谱塑形算法求解，生成频谱离散、能量聚集的掩护信号。仿真结果表明，在能量和带宽相同的情况下，离散谱掩护信号相比于非连续谱掩护信号具有更高的频谱幅度，提升5～12 dB；在能量相同，频谱幅度接近的情况下，离散谱掩护信号能覆盖更大的频谱范围，实现了更好的抗干扰掩护效果。
-
关键词:
- 射频掩护 /
- 非连续谱信号 /
- 抗干扰 /
- 波形设计 /
- 交替向量乘子法(ADMM)
Abstract: Radio Frequency-screen is one of the earliest radar active antijamming measures. It achieves antijamming by transmitting cover pulses of different frequencies before the radar pulse signal to induce enemy jammers. As the demand for antijamming measures has become increasingly urgent in recent years, Radio Frequency-screen technology has been further developed. The most representative is the use of discontinuous spectrum signals as a cover signal. However, energy utilization for sending the cover signal can be improved further. To address this problem, this paper proposes a discrete spectrum cover signal based on the discontinuous spectrum cover signal and establishes the waveform design function under the joint constraint of constant modulus and spectral amplitude. The cover signal with discrete spectrum and energy aggregation is generated using the Alternating Direction Method of Multipliers (ADMM) and spectrum shaping algorithm solution. The simulation results show that the discrete spectrum cover signal has a higher spectral amplitude of approximately 5～12 dB than the discontinuous-spectrum cover signal for the same energy and bandwidth. Moreover, the discrete spectrum cover signal can cover a larger spectral range with the same energy and close spectral amplitude, realizing a better antijamming cover effect. -
图 1 频域协同波形功率配置原理示意图
Figure 1. Schematic of frequency domain cooperative waveform power configuration principle
图 2 非连续谱掩护信号与离散谱掩护信号对比图
Figure 2. Comparison of discontinuous spectrum cover signal and discrete spectrum cover signal
图 3 离散谱掩护波形频谱示意图
Figure 3. Schematic diagram of the discrete spectrum cover waveform spectrum
图 8 通带内频谱功率差值随谱线间隔占带宽百分比的变化趋势
Figure 8. Trend of spectral power difference in the passband with the percentage of spectral line spacing over the bandwidth
图 9 离散谱掩护信号通带起伏方差随波纹控制项变化趋势
Figure 9. Trend of discrete spectrum cover signal passband undulation with ripple control term
图 10 离散谱掩护信号通带平均幅度随波纹控制项变化趋势
Figure 10. Trend of discrete spectrum cover signal passband average amplitude with ripple control term
图 11 窄带探测信号和宽带掩护信号的频谱对应关系(探测信号与掩护信号有效辐射功率之比为1:4)
Figure 11. Spectral correspondence of narrowband detection signal and broadband cover signal (the ratio of detection signal to cover signal power is 1:4)
图 12 窄带探测信号和宽带掩护信号的频谱对应关系(探测信号与掩护信号有效辐射功率之比为1:1)
Figure 12. Spectral correspondence of narrowband detection signal and broadband cover signal (the ratio of detection signal to cover signal power is 1:1)
图 14 噪声调频干扰场景下R-D图对比
Figure 14. Comparison of R-D diagram under noise FM jamming scenarios
图 16 组合干扰场景下R-D图对比
Figure 16. Comparison of R-D diagram under combined interference scenarios
1 恒模约束下离散谱波形设计算法
1. Discrete spectrum waveform design algorithm under constant modulus constraint
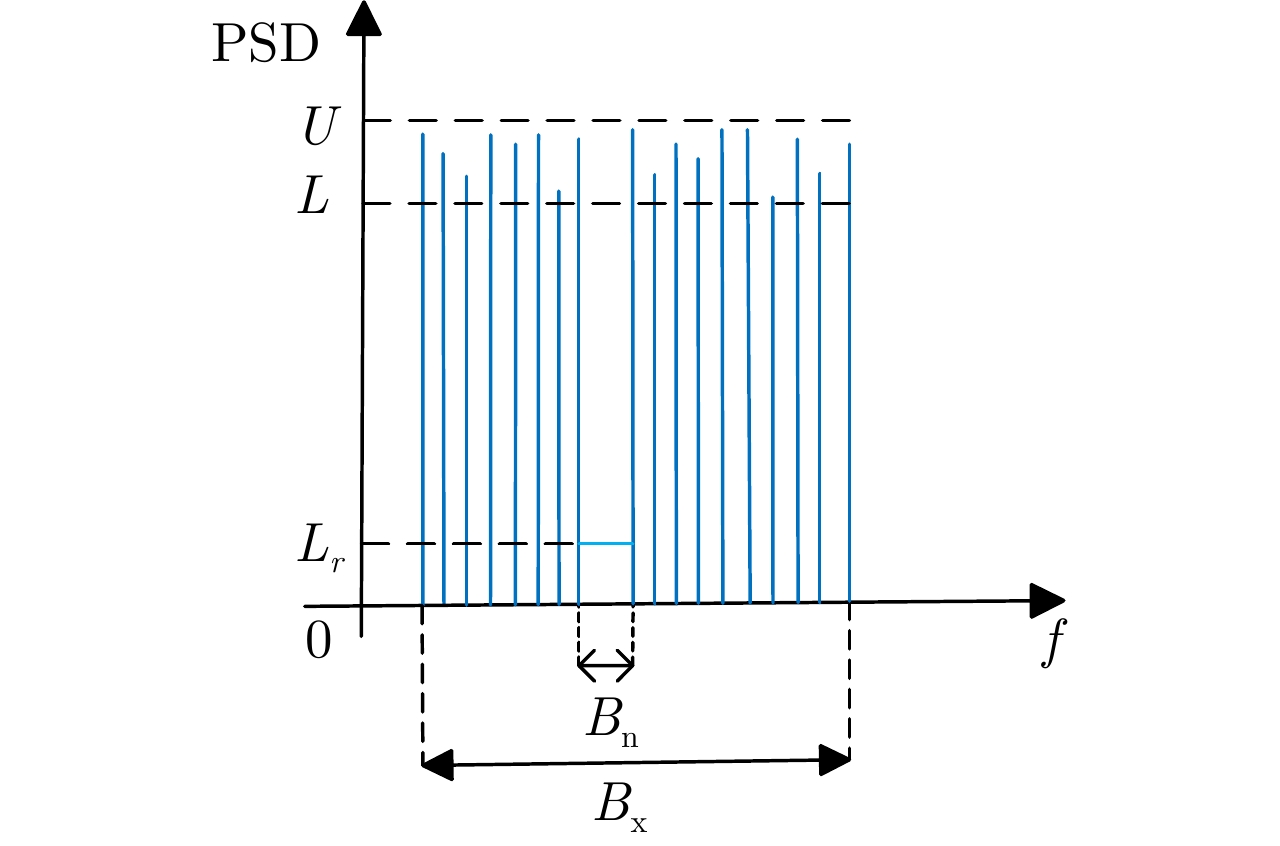
输入：R, y 初始化： $ {{\bar {\boldsymbol{a}}}}(0),{\boldsymbol{\bar x}}(0),{{\boldsymbol{\bar f}}_p}(0),{{\boldsymbol{\lambda}} _1}(0),{{\boldsymbol{\lambda}} _{2,p}}(0) $ 1：for $t = 0,1, \cdots ,{N_{{\text{iter}}}}$，其中 ${N_{{\text{iter}}}}$为预先设定的最大迭代次数。 2： 更新 ${\boldsymbol{\bar a}}(t + 1)$： $ {\boldsymbol{\bar a}}(t + 1) = - \dfrac{1}{2}{\boldsymbol{R}}_1^{ - 1}{{\boldsymbol{d}}_1}(t + 1) $ 3： 更新 ${\boldsymbol{\bar x}}(t + 1)$： $ \left[ {\begin{array}{*{20}{c}} {{{\bar x}_k}} \\ {{{\bar x}_{k + K}}} \end{array}} \right] = - \dfrac{{\left[ {\begin{array}{*{20}{c}} {{d_{2,k}}(t + 1)} \\ {{d_{2,k + K}}(t + 1)} \end{array}} \right]}}{{\left\| {\left[ {\begin{array}{*{20}{c}} {{d_{2,k}}(t + 1)} \\ {{d_{2,k + K}}(t + 1)} \end{array}} \right]} \right\|}},\;k = 0,1, \cdots, K - 1 $ 4： 更新 ${{\boldsymbol{\bar f}}_p}(t + 1)$： $ {\bar {\boldsymbol{f}}_p}(t + 1) = \left\{ \begin{aligned} & {\dfrac{{\sqrt {(U + L)/2 + r} }}{{\left\| {{{{{\stackrel \frown{\boldsymbol f} }}}_p}(t + 1)} \right\|}}{{{{\stackrel \frown{\boldsymbol f} }}}_p}(t + 1),{\text{ }}\left\| {{{{{\stackrel \frown{\boldsymbol f} }}}_p}(t + 1)} \right\| \ge \sqrt {(U + L)/2 + r} } \\ & {\dfrac{{\sqrt {(U + L)/2 - r} }}{{\left\| {{{{{\stackrel \frown{\boldsymbol f} }}}_p}(t + 1)} \right\|}}{{{{\stackrel \frown{\boldsymbol f} }}}_p}(t + 1),{\text{ }}\left\| {{{{{\stackrel \frown{\boldsymbol f} }}}_p}(t + 1)} \right\| \le \sqrt {(U + L)/2 - r} } \\ & {{{{{\stackrel \frown{\boldsymbol f} }}}_p}(t + 1),{\text{ }}\sqrt {(U + L)/2 - r} < \left\| {{{{{\stackrel \frown{\boldsymbol f} }}}_p}(t + 1)} \right\| < \sqrt {(U + L)/2 + r} } \end{aligned} \right. $ 5： 更新 $ {{\boldsymbol{\lambda}} _1}(t + 1) $, $ {{\boldsymbol{\lambda}} _{2,p}}(t + 1) $： $ {{\boldsymbol{\lambda}} _1}(t + 1) = {{\boldsymbol{\lambda}} _1}(t) + \rho ({\boldsymbol{\bar x}} - {\boldsymbol{\bar V\bar a}}) $
$ {{\boldsymbol{\lambda}} _{2,p}}(t + 1) = {{\boldsymbol{\lambda}} _{2,p}}(t) + \rho ({{\boldsymbol{\bar f}}_p} - {{\boldsymbol{\bar v}}_p}{\boldsymbol{\bar a}}),p = 1,2, \cdots ,P $6：end 当 $t = {N_{{\text{iter}}}}$或同时满足 $\left\| {{\boldsymbol{\bar x}}(t + 1) - {\boldsymbol{\bar V\bar a}}(t + 1)} \right\| < {\delta _1}$, $ \left\| {{{{\boldsymbol{\bar f}}}_p}(t + 1) - {{{\boldsymbol{\bar v}}}_p}{\boldsymbol{\bar a}}(t + 1)} \right\| < {\delta _2} $ 7：对得到的时域序列 ${\boldsymbol{\bar x}}$进行频谱塑形 8：for $t = 0,1, \cdots ,{N_{{\text{iter}}}}$，其中 ${N_{{\text{iter}}}}$为预先设定的最大迭代次数 9： 更新 $ {\boldsymbol{\theta}} (t + 1) $： $ {\boldsymbol{\theta}} (t + 1) = \arg \{ {{\boldsymbol{F}}^{\text{H}}}{\boldsymbol{x}}\} $ 10： 更新 ${\boldsymbol{x}}(t + 1)$： $ {\boldsymbol{x}}(t + 1) = {{\text{e}}^{{\text{j}}\arg ({\boldsymbol{F}}({\boldsymbol{y}}{{\text{e}}^{{\text{j}}{\boldsymbol{\theta}} }}))}} $ 11：end 当 $t = {N_{{\text{iter}}}}$或 $ \left\| {{{\boldsymbol{F}}^{\text{H}}}{\boldsymbol{x}} - {\boldsymbol{y}}{{\text{e}}^{{\text{j}}{\boldsymbol{\theta}} }}} \right\|_2^2 < {\delta _3} $时，获得波形序列x 
下载: 导出CSV
表 1 评价指标
Table 1. Evaluation Indicators
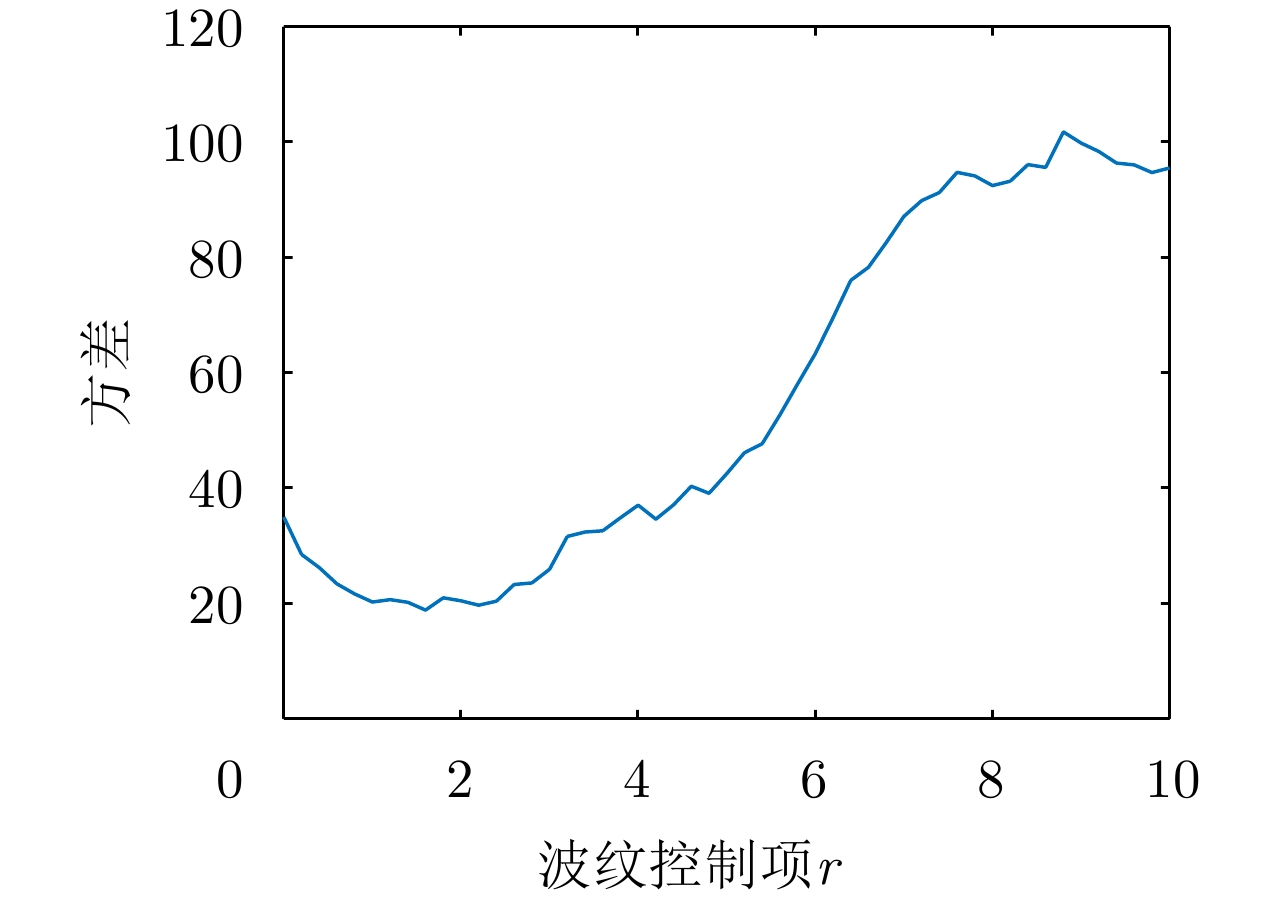
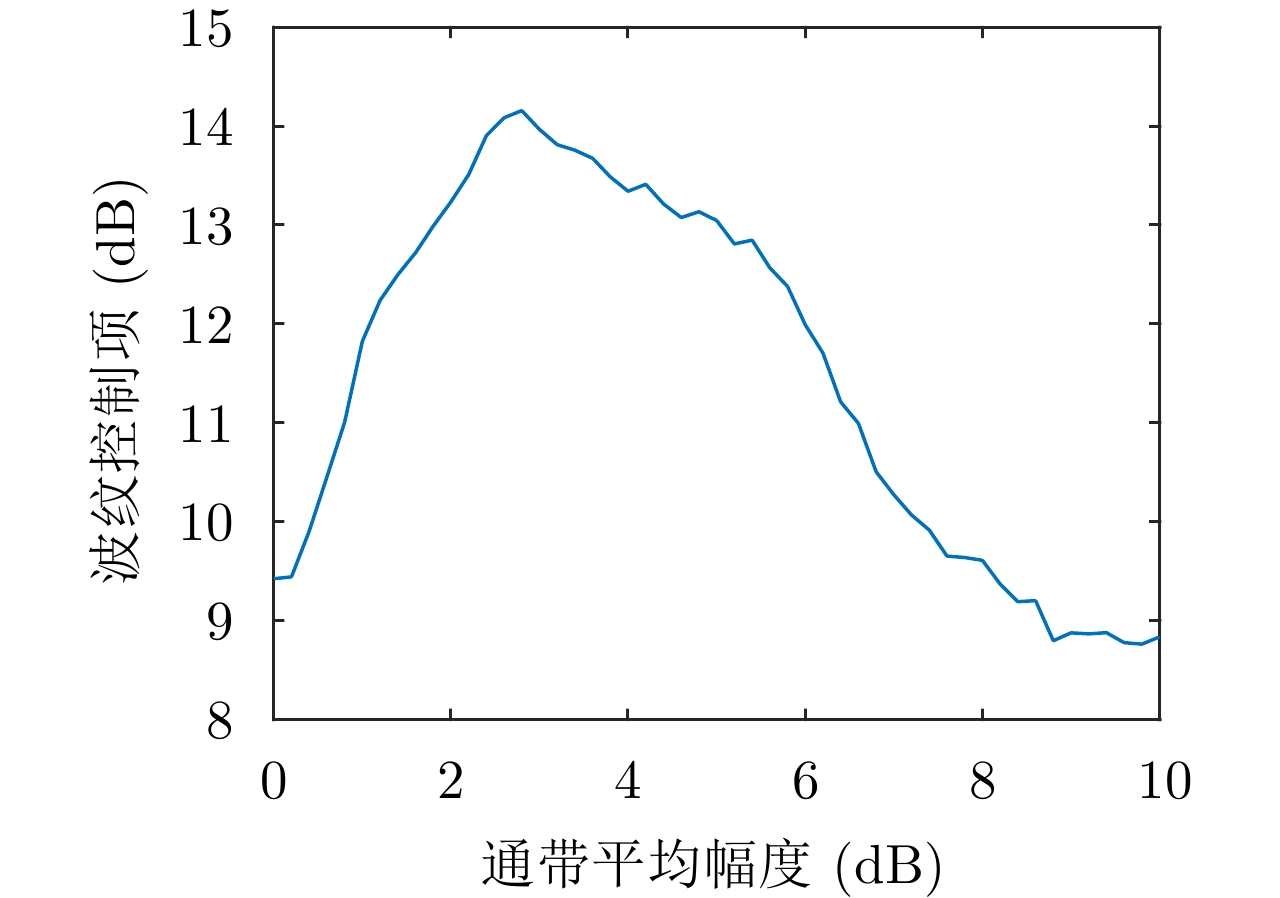
指标 符号 计算公式 通带平均幅度 $ {A_{{\rm{fw}}}} $ $ {A_{{\rm{fw}}}} = \displaystyle\sum\nolimits_{p = 1}^P {\left\| {{{\boldsymbol{f}}_p}} \right\|/P} $ 阻带最大幅度 $ {\epsilon}_{1} $ $ {\epsilon}_{1}=\underset{s}{\mathrm{max}}\Vert {f}_{s}\Vert $ 通带起伏度 ${\sigma ^2}$ ${\sigma ^2} = {\displaystyle\sum\nolimits_{p = 1}^P {(\left\| {{{\boldsymbol{f}}_p}} \right\| - {A_{{\rm{fw}}}})} ^2}/P$ 消耗干扰资源比例 $\eta $ $\eta = {W_{{\text{waste}}}}/{W_{{\text{all}}}}$
下载: 导出CSV
表 2 掩护信号参数
Table 2. Cover signal parameters
参数 数值 离散谱掩护信号带宽( ${\text{MHz}}$) $ [50{\text{ 200}}] $ 离散谱掩护信号时宽( ${\text{μs}}$) $ 25 $ 离散谱掩护信号阻带区域( ${\text{MHz}}$) 25～30 离散谱掩护信号谱线间隔(MHz) 0.5 非连续谱掩护信号带宽(MHz) 50 非连续谱掩护信号时宽(μs) 25 非连续谱掩护信号阻带区域(MHz) 25～30 采样率(MHz) 600
下载: 导出CSV
表 3 发射信号参数
Table 3. Transmit signal parameters
参数 数值 载频( ${\text{GHz}}$) 1 时宽( $ {\text{μs}} $) $ 25 $ 脉冲重复间隔( $ {\text{μs}} $) $ 100 $ 采样率( ${\text{MHz}}$) ${\text{600}}$ 脉冲个数 $50$ 离散谱掩护信号带宽( ${\text{MHz}}$) ${\text{200}}$ 非连续谱掩护信号带宽( ${\text{MHz}}$) ${\text{50}}$ 窄带信号带宽( ${\text{MHz}}$) ${\text{5}}$ 探测信号与掩护信号有效辐射功率之比 1:4
下载: 导出CSV
表 4 抗干扰场景参数
Table 4. Anti-interference scene parameters
参数 数值 目标距离( ${\text{km}}$) $10$ 目标速度( ${\text{m/s}}$) $60$ 干信比( ${\text{dB}}$) $45$
下载: 导出CSV
表 5 抗干扰场景参数
Table 5. Anti-interference scene parameters
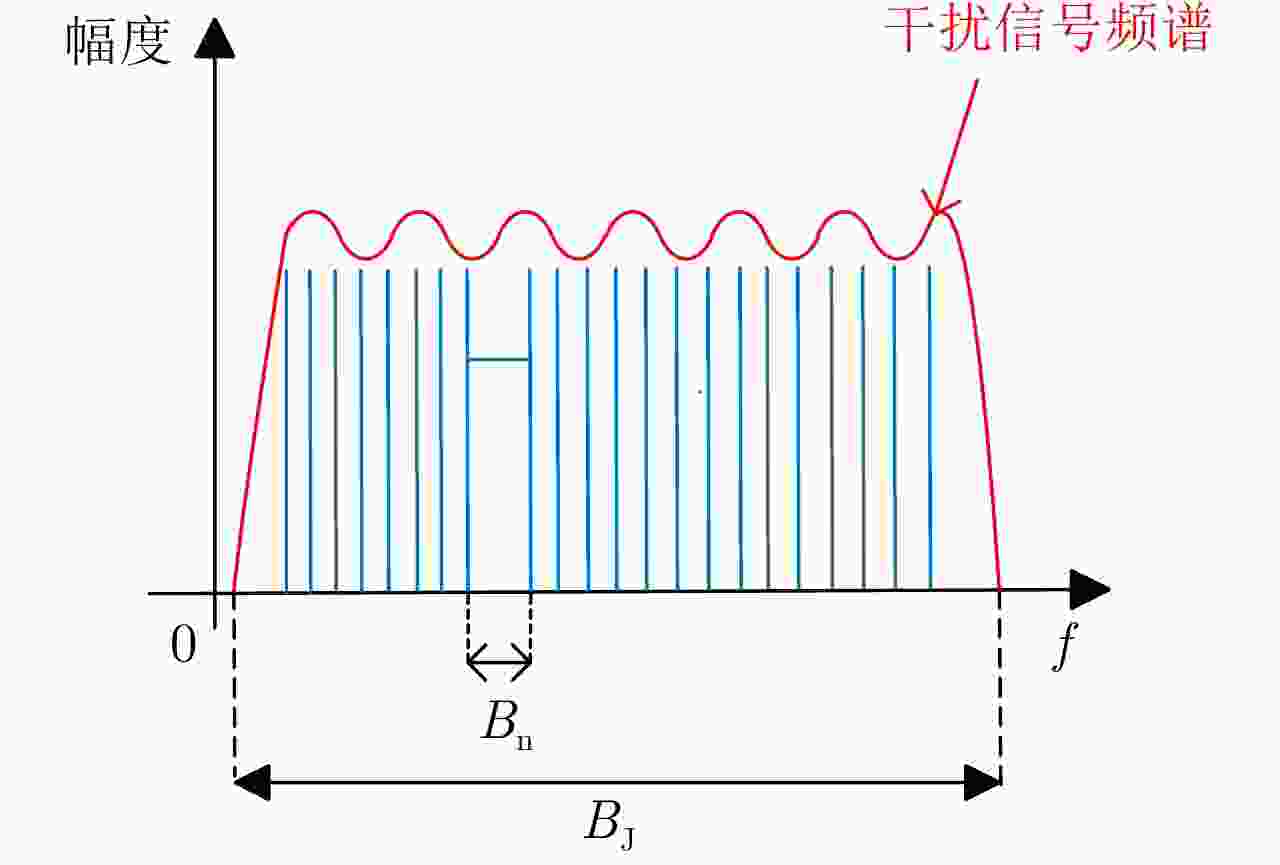
参数 数值 目标距离( ${\text{km}}$) $10$ 目标速度( ${\text{m/s}}$) $60$ 干扰假目标距离( ${\text{km}}$) ${\text{9}}{\text{.8}}$ 干扰假目标速度( ${\text{m/s}}$) $62$ 切片时长( $ {\text{μs}} $) 1 转发次数 5 干信比( ${\text{dB}}$) ${\text{30}}$ 灵巧干扰中噪声信号带宽( ${\text{MHz}}$) $10$
下载: 导出CSV
-
[1] 金珊珊, 王春阳, 邱程, 等. 对抗应答式干扰的射频掩护脉冲设计[J]. 中国电子科学研究院学报, 2014, 9(4): 377–381. doi: 10.3969/j.issn.1673-5692.2014.04.010JIN Shanshan, WANG Chunyang, QIU Cheng, et al. Design of RF protecting signal for transponder jamming suppression[J]. Journal of CAEIT, 2014, 9(4): 377–381. doi: 10.3969/j.issn.1673-5692.2014.04.010 [2] 张昭建, 谢军伟, 杨春晓, 等. 掩护脉冲信号抗转发式欺骗干扰性能分析[J]. 弹箭与制导学报, 2016, 36(4): 149–152, 156. doi: 10.15892/j.cnki.djzdxb.2016.04.039.ZHANG Zhaojian, XIE Junwei, YANG Chunxiao, et al. Performance analysis of screening pulse signal confronts to deception jamming[J]. Journal of Projectiles, Rockets, Missiles and Guidance, 2016, 36(4): 149–152, 156. doi: 10.15892/j.cnki.djzdxb.2016.04.039. [3] 丁爽, 尚朝轩, 韩壮志, 等. 连续波掩护信号技术研究[J]. 现代防御技术, 2018, 46(1): 190–194. doi: 10.3969/j.issn.1009-086x.2018.01.030DING Shuang, SHANG Chaoxuan, HAN Zhuangzhi, et al. Continuous wave radio frequency-screen signal[J]. Modern Defense Technology, 2018, 46(1): 190–194. doi: 10.3969/j.issn.1009-086x.2018.01.030 [4] 杨娟. 雷达射频掩护的认知抗干扰技术研究[D]. [硕士论文], 西安电子科技大学, 2018.YANG Juan. Research on the cognitive anti-jamming technology of radar radio frequency-screen[D]. [Master dissertation], Xidian University, 2018. [5] 李尔康. 基于干扰认知的雷达反干扰波形设计与实现[D]. [硕士论文], 电子科技大学, 2022.LI Erkang. Design and implementation of radar anti-jamming waveform based on jamming cognition[D]. [Master dissertation], University of Electronic Science and Technology of China, 2022. [6] 杨超, 蒋卫锋. 雷达有源诱饵设计考虑因素[J]. 舰船电子工程, 2016, 36(5): 81–82, 95.YANG Chao and JIANG Weifeng. Considerations for radar active decoy design[J]. Ship Electronic Engineering, 2016, 36(5): 81–82, 95. [7] 陈新竹. 多功能数字阵列雷达空域抗有源干扰方法研究[D]. [博士论文], 上海交通大学, 2020.CHEN Xinzhu. Research on spatial jamming cancellation in mutifunction digital array radar[D]. [Ph.D. dissertation], Shanghai Jiao Tong University, 2020. [8] BUTT F A, NAQVI I H, and NAJAM A I. Radar ECCM against deception jamming: A novel approach using bi-static and mono-static radars[C]. 2012 15th International Multitopic Conference (INMIC), Islamabad, Pakistan, 2012: 137–141. doi: 10.1109/INMIC.2012.6511482. [9] ZHAO Dehua, WEI Yinsheng, and LIU Yongtan. Hopped-frequency waveform design for range sidelobe suppression in spectral congestion[J]. IET Radar, Sonar & Navigation,2018, 12(1): 87–94. doi: 10.1049/iet-rsn.2017.0232 [10] 赵德华. 频谱拥堵环境下的自适应雷达波形设计研究[D]. [博士论文], 哈尔滨工业大学, 2018.ZHAO Dehua. Research on waveform design for adaptive radar in spectrum congested environment[D]. [Ph.D. dissertation], Harbin Institute of Technology, 2018. [11] 余显祥, 路晴辉, 杨婧, 等. 短基线收发分置频域协同波形设计方法[J]. 雷达学报, 2022, 11(2): 227–239. doi: 10.12000/JR22014YU Xianxiang, LU Qinghui, YANG Jing, et al. Frequency domain cooperative waveform design method for short baseline transceiver[J]. Journal of Radars, 2022, 11(2):227–239. doi: 10.12000/JR22014 [12] TERRY Guo and ROBERT Qiu. OFDM waveform design compromising spectral nulling, side-lobe suppression and range resolution[C]. 2014 IEEE Radar Conference, Cincinnati, USA, 2014: 1424–1429. [13] 位寅生, 徐朝阳. 非连续谱雷达信号设计综述[J]. 雷达学报, 2022, 11(2): 183–197. doi: 10.12000/JR22023WEI Yinsheng and XU Zhaoyang. Review of signal design for discontinuous spectrum radar[J]. Journal of Radars, 2022, 11(2): 183–197. doi: 10.12000/JR22023 [14] LI Xiaodong and CIMINI L J. Effects of clipping and filtering on the performance of OFDM[C]. 1997 IEEE 47th Vehicular Technology Conference. Technology in Motion, Phoenix, USA, 1997: 1634–1638. [15] BOYD S, PARIKH N, CHU E, et al. Distributed optimization and statistical learning via the alternating direction method of multipliers[J]. Foundations and Trends® in Machine Learning , 2010, 3(1): 1–122. doi: 10.1561/2200000016 [16] TANG Bo, LI Jian, and LIANG Junli. Alternating direction method of multipliers for radar waveform design in spectrally crowded environments[J]. Signal Processing, 2018, 142: 398–402. doi: 10.1016/j.sigpro.2017.08.003 [17] TANG Bo, LI Jun, ZHANG Yu, et al. Design of MIMO radar waveform covariance matrix for Clutter and Jamming suppression based on space time adaptive processing[J]. Signal Processing, 2016, 121: 60–69. doi: 10.1016/j.sigpro.2015.10.033 [18] LIANG Junli, SO H C, LI Jian, et al. Unimodular sequence design based on alternating direction method of multipliers[J]. IEEE Transactions on Signal Processing, 2016, 64(20): 5367–5381. doi: 10.1109/TSP.2016.2597123 [19] LIANG Junli, SO H C, LI Jian, et al. On optimizations with magnitude constraints on frequency or angular responses[J]. Signal Processing, 2018, 145: 214–224. doi: 10.1016/j.sigpro.2017.12.009 [20] ROWE W, STOICA P, and LI Jian. Spectrally constrained waveform design [sp Tips&Tricks][J].IEEE Signal Processing Magazine, 2014, 31(3): 157–162. doi: 10.1109/MSP.2014.2301792 [21] 彭德强. 线性调频信号和噪声调频信号性能对比分析[J]. 舰船电子对抗, 2021, 44(1): 22–26. doi: 10.16426/j.cnki.jcdzdk.2021.01.005PENG Deqiang. Analysis of the performance comparison between LFM signal and noise FM signal[J]. Shipboard Electronic Countermeasure, 2021, 44(1): 22–26. doi: 10.16426/j.cnki.jcdzdk.2021.01.005 [22] 金珊珊, 王春阳, 李欣. 灵巧干扰及其对抗技术综述[J]. 现代防御技术, 2014, 42(4): 131–135, 142.JIN Shanshan, WANG Chunyang, and LI Xin. Overview on smart noise jamming and countermeasures[J]. Modern Defense Technology, 2014, 42(4): 131–135, 142. -
计量
- 文章访问数: 693
- HTML全文浏览量: 423
- PDF下载量: 201
- 被引次数: 0
