作者中心
专家审稿
责编办公
编辑办公
-
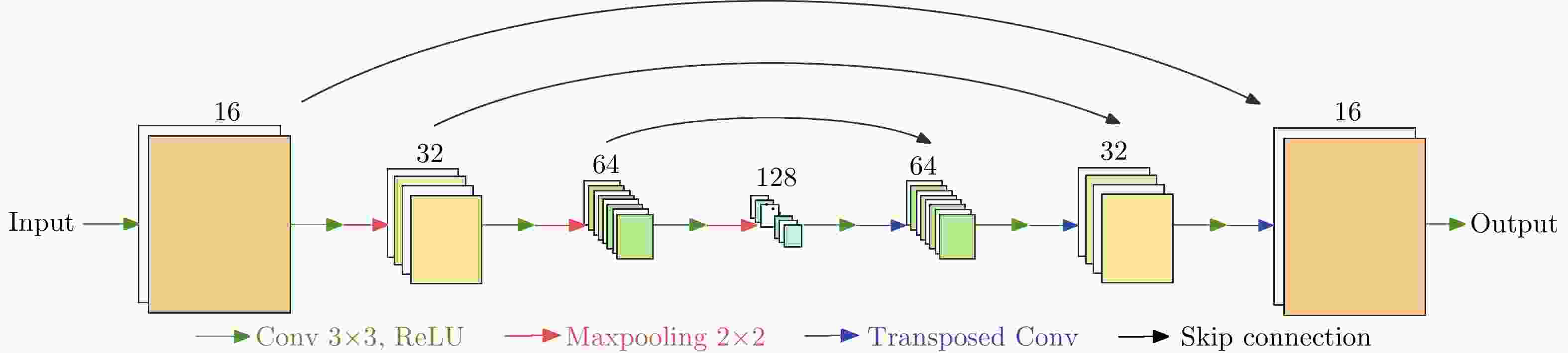
摘要: 稀疏孔径逆合成孔径雷达(ISAR)成像的目标是从不完整的回波中恢复和重建高质量ISAR图像，现有方法主要可以分为基于模型的方法和基于深度学习的方法两大类：一方面，基于模型的稀疏孔径ISAR成像方法往往具备显性的数学模型，对雷达回波的成像过程有清晰的物理建模，但算法有效性上不如基于学习的方法。另一方面，基于深度学习的方法通常高度依赖训练数据，难以适配空间目标ISAR成像任务中高实时、高动态的现实应用需求。针对上述问题，该文提出了一种基于元学习的高效、自适应稀疏孔径ISAR成像算法。所提方法主要包含基于学习辅助的交替迭代优化和元学习优化两部分。基于学习辅助的交替迭代优化继承了ISAR成像机理的回波成像模型，保证了方法数学物理可解释性的同时避免了方法对数据的依赖性；基于元学习的优化策略通过引入非贪婪优化策略，提高了算法跳出局部最优解的能力，保证了病态非凸条件下的算法收敛性能。最后，实验结果表明：该文方法可以在不依赖训练数据、不进行预训练的情况下实现高效、自适应的稀疏孔径ISAR成像，并取得优于其他常规ISAR成像算法的性能。
-
关键词:
- 逆合成孔径雷达 /
- 稀疏孔径ISAR成像 /
- 学习辅助 /
- 非凸优化 /
- 元学习
Abstract: Sparse Aperture-Inverse Synthetic Aperture Radar (SA-ISAR) imaging methods aim to reconstruct high-quality ISAR images from the corresponding incomplete ISAR echoes. The existing SA-ISAR imaging methods can be roughly divided into two categories: model-based and deep learning-based methods. Model-based SA-ISAR methods comprise physical ISAR imaging models based on explicit mathematical formulations. However, due to the high nonconvexity and ill-posedness of the SA-ISAR problem, model-based methods are often ineffective compared with deep learning-based methods. Meanwhile, the performance of the existing deep learning-based methods depends on the quality and quantity of the training data, which are neither sufficient nor precisely labeled in space target SA-ISAR imaging tasks. To address these issues, we propose a metalearning-based SA-ISAR imaging method for space target ISAR imaging tasks. The proposed method comprises two primary modules: the learning-aided alternating minimization module and the metalearning-based optimization module. The learning-aided alternating minimization module retains the explicit ISAR imaging formulations, guaranteeing physical interpretability without data dependency. The metalearning-based optimization module incorporates a non-greedy strategy to enhance convergence performance, ensuring the ability to escape from poor local modes during optimization. Extensive experiments validate that the proposed algorithm demonstrates superior performance, excellent generalization capability, and high efficiency, despite the lack of prior training or access to labeled training samples, compared to existing methods. -
图 3 不同ISAR成像方法在仿真数据上的可视化对比结果
Figure 3. The visual imaging results on the of the simulated ISAR data
图 4 不同ISAR成像方法在实测数据上的可视化对比结果(稀疏率为0.25)
Figure 4. The visual imaging results on the of the real ISAR data (sparsity rate 0.25)
图 5 不同ISAR成像方法在实测数据上的可视化对比结果(稀疏率为0.125)
Figure 5. The visual imaging results on the of the real ISAR data (sparsity rate 0.125)
图 6 消融实验成像结果
Figure 6. The visual results of the ablation studies of the proposed method
1 一种基于元学习的稀疏孔径ISAR成像算法
1. A meta-learning based sparse aperture ISAR imaging method
1 给定：稀疏孔径一维距离像S 2 初始化：网络输入$ {\boldsymbol{Z}}_{\boldsymbol{X}}^{\mathrm{0,0}} $，网络参数$ {\boldsymbol{\theta }}_{\boldsymbol{X}}^{\mathrm{0,0}} $。 3 for $ k\leftarrow \mathrm{0,1},\cdots ,K $ do 4 for $ t\leftarrow \mathrm{0,1},\cdots ,T $ do 5 ${\boldsymbol{X} }^{(k,t)}={ {{G} } }_{\boldsymbol{X} }\left({\boldsymbol{Z} }_{\boldsymbol{X} }^{(k,t)},{\boldsymbol{\theta } }_{\boldsymbol{X} }^{\left(k\right)}\right)$ 6 ${\mathcal{L} }_{ {\boldsymbol{Z} }_{\boldsymbol{X} } }^{(k,t)}={\left\|\boldsymbol{S}-\boldsymbol{D}\boldsymbol{F}{\boldsymbol{X} }^{(k,t)}\right\|}_{{\rm{F}}}^{2}+\beta {\left\|{\boldsymbol{X} }^{(k,t)}\right\|}_{1}$ 7 ${\boldsymbol{Z} }_{\boldsymbol{X} }^{(k,t+1)}={\boldsymbol{Z} }_{\boldsymbol{X} }^{(k,t)}-{\gamma }_{\boldsymbol{X} }^{(k,t)}\cdot {\rm{Adam}}\left({\nabla }_{ {\boldsymbol{Z} }_{\boldsymbol{X} }^{(k,t)} }{\mathcal{L} }_{ {\boldsymbol{Z} }_{\boldsymbol{X} } }^{(k,t)}\right)$ 8 end
9 ${\mathcal{L} }_{ {\rm{meta} } }^{\left(k\right)}=\displaystyle\sum _{t=1}^{T}\left\{ {\left\|\boldsymbol{S}-\boldsymbol{D}\boldsymbol{F}\cdot { { {G} } }_{\boldsymbol{X} }\left({\boldsymbol{Z} }_{\boldsymbol{X} }^{(k,t)},{\boldsymbol{\theta } }_{\boldsymbol{X} }^{\left(k\right)}\right)\right\|}_{{\rm{F}}}^{2}\right.$
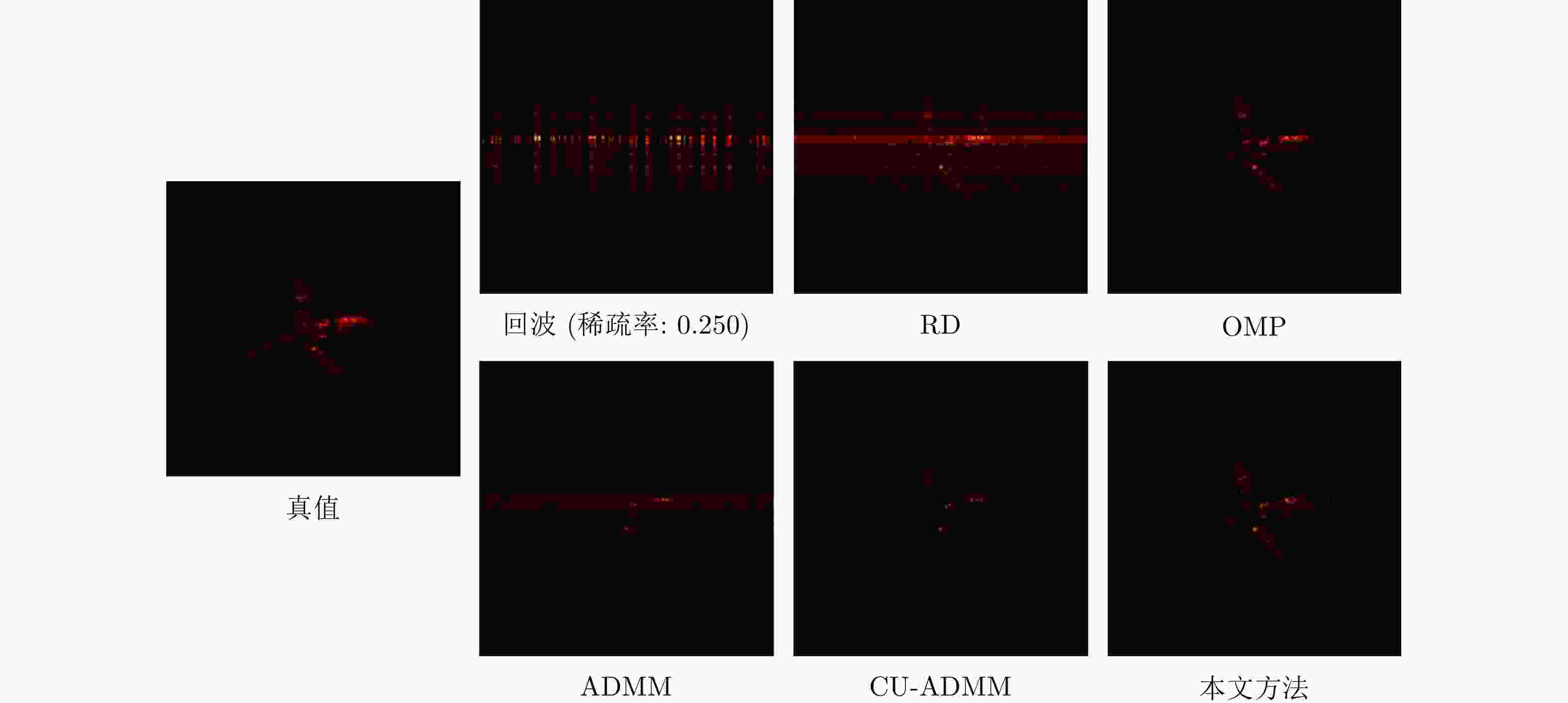
$\left. +\beta {\left\|{ {{G} } }_{\boldsymbol{X} }\left({\boldsymbol{Z} }_{\boldsymbol{X} }^{(k,t)},{\boldsymbol{\theta } }_{\boldsymbol{X} }^{\left(k\right)}\right)\right\|}_{1}\right\}$10 ${\boldsymbol{\theta } }_{\boldsymbol{X} }^{(k+1)}={\boldsymbol{\theta } }_{\boldsymbol{X} }^{\left(k\right)}-{\gamma }_{{\rm{meta}}}^{\left(k\right)}\cdot {\rm{Adam}}\left({\nabla }_{ {\boldsymbol{\theta } }_{\boldsymbol{X} }^{\left(k\right)} }{\mathcal{L} }_{{\rm{meta}}}^{\left(k\right)}\right)$ 11 $ {\boldsymbol{Z}}_{\boldsymbol{X}}^{(k+1, 0)}={\boldsymbol{Z}}_{\boldsymbol{X}}^{(k,T)} $ 12 end 13 输出：${\boldsymbol{X} }^{(K,T)}={ {{G} } }_{\boldsymbol{X} }\left({\boldsymbol{Z} }_{\boldsymbol{X} }^{(K,T)},{\boldsymbol{\theta } }_{\boldsymbol{X} }^{\left(K\right)}\right)$ 
下载: 导出CSV
表 1 不同方法在仿真ISAR数据集上的平均成像性能对比(稀疏率为0.250)
Table 1. The average imaging results on the of the simulated ISAR data (sparsity rate 0.250)
下载: 导出CSV
表 2 不同方法在仿真ISAR数据集上的平均成像性能对比(稀疏率为0.125)
Table 2. The average imaging results on the of the simulated ISAR data (sparsity rate 0.125)
下载: 导出CSV
表 3 不同方法在实测ISAR数据集上的平均成像性能对比(稀疏率为0.250)
Table 3. The average imaging results on the of the real ISAR data (sparsity rate 0.250)
下载: 导出CSV
表 4 不同方法在实测ISAR数据集上的平均成像性能对比(稀疏率为0.125)
Table 4. The average imaging results on the of the real ISAR data (sparsity rate 0.125)
下载: 导出CSV
表 5 本文方法中元学习优化的消融实验
Table 5. The ablation studies of the proposed method
稀疏率 方法 图像熵 PSNR (dB) RMSE 0.250 本文方法 5.1500 52.9602 0.0143 无元学习模块 5.5986 51.2857 0.0191 0.125 本文方法 5.1143 51.2460 0.0174 无元学习模块 5.2697 50.3675 0.0206
下载: 导出CSV
表 6 5种方法的计算复杂度对比
Table 6. The computational complexity comparison of five methods
方法 计算复杂度 训练
时间(h)测试
时间(s)RD ${\mathcal{O} }\left({ {{M} } }^{2}\right)$ 无 $ < $1.0 OMP[4] ${\mathcal{O} }\left({{K} }{ {{M} } }^{2}\right)$ 无 4.4 ADMM[5] ${\mathcal{O} }\left({{K} }{ {{M} } }^{3}\right)$ 无 1.6 CU-ADMM[19] ${\mathcal{O} }\left({{K} }{ {{M} } }^{3}\right)$ 2 $ < $1.0 本文方法 ${\mathcal{O} }\left({{K} }{ {{M} } }^{2}{{N} }{\displaystyle\sum }_{l=1}^{L}{ {{C} } }_{l}{ {{C} } }_{l+1}\right)$ 无 18.4
下载: 导出CSV
-
[1] 丁鹭飞, 耿富录, 陈建春. 雷达原理[M]. 5版. 北京: 电子工业出版社, 2014.DING Lufei, GENG Fulu, and CHEN Jianchun. Principle of Radar[M]. 5th ed. Beijing: Publishing House of Electronics Industry, 2014. [2] 张双辉. 基于贝叶斯框架的稀疏孔径ISAR成像技术研究[D]. [博士论文], 国防科学技术大学, 2016.ZHANG Shanghui. Research on sparse aperture inverse synthetic aperture radar imaging withing Bayesian framework[D]. [Ph.D. dissertation], National University of Defense Technology, 2016. [3] MALLAT S G and ZHANG Zhifeng. Matching pursuits with time-frequency dictionaries[J]. IEEE Transactions on Signal Processing, 1993, 41(12): 3397–3415. doi: 10.1109/78.258082 [4] TROPP J A and GILBERT A C. Signal recovery from random measurements via orthogonal matching pursuit[J]. IEEE Transactions on Information Theory, 2007, 53(12): 4655–4666. doi: 10.1109/TIT.2007.909108 [5] BOYD S, PARIKH N, CHU E, et al. Distributed optimization and statistical learning via the alternating direction method of multipliers[J]. Foundations and Trends® in Machine Learning, 2011, 3(1): 1–122. doi: 10.1561/2200000016 [6] DONOHO D L. Compressed sensing[J]. IEEE Transactions on Information Theory, 2006, 52(4): 1289–1306. doi: 10.1109/TIT.2006.871582 [7] ZHANG Lei, QIAO Zhijun, XING Mengdao, et al. High-resolution ISAR imaging by exploiting sparse apertures[J]. IEEE Transactions on Antennas and Propagation, 2012, 60(2): 997–1008. doi: 10.1109/TAP.2011.2173130 [8] PENG Shaowen, LI Shangyuan, XUE Xiaoxiao, et al. High-resolution W-band ISAR imaging system utilizing a logic-operation-based photonic digital-to-analog converter[J]. Optics Express, 2018, 26(2): 1978–1987. doi: 10.1364/OE.26.001978 [9] 陈阿磊, 王党卫, 马晓岩, 等. 一种基于估计理论的ISAR超分辨成像方法[J]. 系统工程与电子技术, 2010, 32(4): 740–744.CHEN Alei, WANG Dangwei, MA Xiaoyan, et al. Method of super resolution imaging for ISAR based on estimation theory[J]. Systems Engineering and Electronics, 2010, 32(4): 740–744. [10] ZHANG Lei, WANG Hongxian, and QIAO Zhijun. Resolution enhancement for ISAR imaging via improved statistical compressive sensing[J]. EURASIP Journal on Advances in Signal Processing, 2016, 2016(1): 80. doi: 10.1186/s13634-016-0379-2 [11] XU Gang, XING Mengdao, XIA Xianggen, et al. High-resolution inverse synthetic aperture radar imaging and scaling with sparse aperture[J]. IEEE Journal of Selected Topics in Applied Earth Observations and Remote Sensing, 2015, 8(8): 4010–4027. doi: 10.1109/JSTARS.2015.2439266 [12] WEI Shunjun, ZHANG Xiaoling, SHI Jun, et al. Sparse reconstruction for SAR imaging based on compressed sensing[J]. Progress in Electromagnetics Research, 2010, 109: 63–81. doi: 10.2528/PIER10080805 [13] RONNEBERGER O, FISCHER P, and BROX T. U-Net: Convolutional networks for biomedical image segmentation[C]. 18th International Conference on Medical Image Computing and Computer-Assisted Intervention, Munich, Germany, 2015: 234–241. [14] GOODFELLOW I, POUGET-ABADIE J, MIRZA M, et al. Generative adversarial networks[J]. Communications of the ACM, 2020, 63(11): 139–144. doi: 10.1145/3422622 [15] YANG Ting, SHI Hongyin, LANG Manyun, et al. ISAR imaging enhancement: Exploiting deep convolutional neural network for signal reconstruction[J]. International Journal of Remote Sensing, 2020, 41(24): 9447–9468. doi: 10.1080/01431161.2020.1799449 [16] QIN Dan, LIU Diyang, GAO Xunzhang, et al. ISAR resolution enhancement using residual network[C]. 2019 IEEE 4th International Conference on Signal and Image Processing (ICSIP), Wuxi, China, 2019: 788–792. [17] QIN Dan and GAO Xunzhang. Enhancing ISAR resolution by a generative adversarial network[J]. IEEE Geoscience and Remote Sensing Letters, 2021, 18(1): 127–131. doi: 10.1109/LGRS.2020.2965743 [18] WANG Haobo, LI Kaiming, LU Xiaofei, et al. ISAR resolution enhancement method exploiting generative adversarial network[J]. Remote Sensing, 2022, 14(5): 1291. doi: 10.3390/rs14051291 [19] LI Ruize, ZHANG Shuanghui, ZHANG Chi, et al. Deep learning approach for sparse aperture ISAR imaging and autofocusing based on complex-valued ADMM-Net[J]. IEEE Sensors Journal, 2021, 21(3): 3437–3451. doi: 10.1109/JSEN.2020.3025053 [20] LI Ruize, ZHANG Shuanghui, ZHANG Chi, et al. A computational efficient 2-D block-sparse ISAR imaging method based on PCSBL-GAMP-Net[J]. IEEE Transactions on Geoscience and Remote Sensing, 2021, 60: 5214814. doi: 10.1109/TGRS.2021.3111901 [21] LEMPITSKY V, VEDALDI A, and ULYANOV D. Deep image prior[C]. The IEEE/CVF Conference on Computer Vision and Pattern Recognition, Salt Lake City, USA, 2018: 9446–9454. [22] LIANG Jingyun, ZHANG Kai, GU Shuhang, et al. Flow-based kernel prior with application to blind super-resolution[C]. The 2021 IEEE/CVF Conference on Computer Vision and Pattern Recognition, Nashville, USA, 2021: 10596–10605. [23] YUE Zongsheng, ZHAO Qian, XIE Jianwen, et al. Blind image super-resolution with elaborate degradation modeling on noise and kernel[C]. The 2022 IEEE/CVF Conference on Computer Vision and Pattern Recognition, New Orleans, USA, 2022: 2118–2128, [24] XIA Jingyuan, LI Shengxi, HUANG Junjie, et al. Metalearning-based alternating minimization algorithm for nonconvex optimization[J]. IEEE Transactions on Neural Networks and Learning Systems, 2022: 1–15. [25] YANG Zhixiong, XIA Jingyuan, LUO Junshan, et al. A Learning-aided flexible gradient descent approach to MISO beamforming[J]. IEEE Wireless Communications Letters, 2022, 11(9): 1895–1899. doi: 10.1109/LWC.2022.3186160 [26] KINGMA D P and BA J. Adam: A method for stochastic optimization[C]. 3rd International Conference on Learning Representations, San Diego, USA, 2015. -
计量
- 文章访问数: 917
- HTML全文浏览量: 613
- PDF下载量: 180
- 被引次数: 0
