作者中心
专家审稿
责编办公
编辑办公
An Intelligent Frequency Decision Method for a Frequency Agile Radar Based on Deep Reinforcement Learning
-
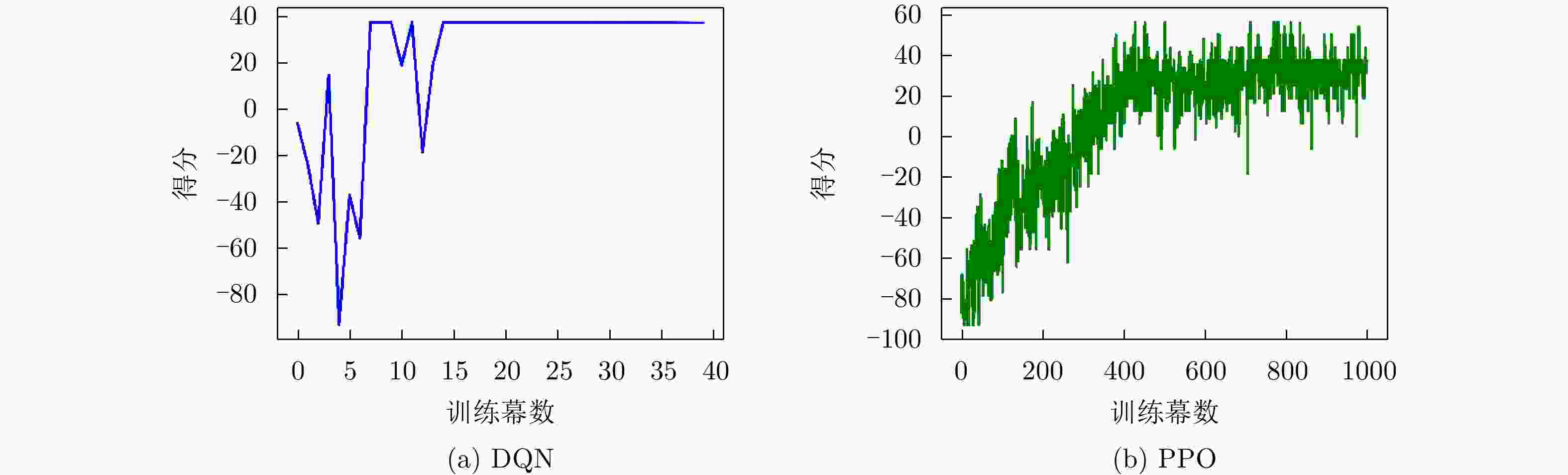
摘要: 自卫式干扰机发射的瞄准干扰使多种基于信号处理的被动干扰抑制方法失效，对现代雷达产生了严重威胁，频率捷变作为一种主动对抗方式为对抗瞄准干扰提供了可能。针对传统随机跳频抗干扰性能不稳定、频点选取自由度有限、策略学习所需时间长等问题，该文面向频率捷变雷达，提出了一种快速自适应跳频策略学习方法。首先设计了一种频点可重复选取的频率捷变波形，为最优解提供了更多选择。在此基础上，通过利用雷达与干扰机持续对抗收集到的数据，基于深度强化学习的探索与反馈机制，不断优化频点选取策略。具体来说，通过将上一时刻雷达频点及当前时刻感知到的干扰频点作为强化学习输入，神经网络智能选取当前时刻各子脉冲频点，并根据目标检测结果以及信干噪比两方面评价抗干扰效能，从而优化策略直至最优。从提高最优策略收敛速度出发，设计的输入状态不依赖历史时间步、引入贪婪策略平衡搜索-利用机制、配合信干噪比提高奖励差异。多组仿真实验结果表明，所提方法能够收敛到最优策略且具备较高的收敛效率。Abstract: The aiming jamming emitted by self-defense jammers renders various passive anti-jamming measures based on signal processing ineffective, posing severe threats to modern radars. Frequency agility, as an active countermeasure, enables the resistance of aiming jamming. In response to issues such as the unstable anti-jamming performance of traditional random frequency hopping, limited freedom in frequency selection, and the long time required for strategic learning, the paper proposes a fast-adaptive frequency-hopping strategy for a frequency agile radar. First, a frequency agile waveform with repeatable frequency selection is designed, providing more choices for an optimal solution. Accordingly, using the data collected through continuous confrontation between a radar and a jammer, and the exploration and feedback mechanism of deep reinforcement learning, a frequency-selection strategy is continuously optimized. Specifically, considering radar frequency from the previous time and jamming frequency perceived at the current time as reinforcement learning inputs, the neural network intelligently selects each subpulse frequency at the current time and optimizes the strategy until it is optimal based on the anti-jamming effectiveness evaluated by the target detection result and Signal-to-Jamming-plus-Noise Ratio (SJNR). To improve the convergence speed of the optimal strategy, the designed input state is independent of the historical time step, the introduced greedy strategy balances the search-utilization mechanism, and the SJNR differentiates rewards more. Multiple sets of simulations show that the proposed method can converge to the optimal strategy and has high convergence efficiency.
-
Key words:
- Frequency agile radar /
- Anti-jamming /
- Waveform design /
- Aiming jamming /
- Deep Q-Network (DQN)
-
图 2 MDP的随机独立性与强化学习的优化目标
Figure 2. The random independence of MDP and the optimization objectives of reinforcement learning
图 4 全连接神经网络结构示意图
Figure 4. The schematic diagram of fully connected neural network structure
图 7 脉内侦干策略的子脉冲频点决策训练结果
Figure 7. The training results of sub-pulse frequency decision for the intra-pulse interception-jamming strategy
图 8 训练用CPI数量对脉内侦干策略下对抗成功率的影响
Figure 8. The impact of the number of CPI used for training on the success rate of confrontation for the intra-pulse interception-jamming strategy
图 9 雷达与干扰对抗4个PRT的策略及对抗奖励
Figure 9. The strategies and rewards for radar anti-jamming during four PRT periods
图 10 雷达执行最优策略的时频图及一维距离像
Figure 10. The time-frequency map and the one-dimensional High-Resolution Range Profile (HRRP) for radar executing optimal strategy
图 11 脉间侦干策略的子脉冲频点决策训练结果
Figure 11. The training results of sub-pulse frequency decision for the pulse-to-pulse interception-jamming strategy
图 12 训练用CPI数量对脉间侦干策略对抗成功率的影响
Figure 12. The impact of the number of CPI used for training on the success rate of confrontation for the pulse-to-pulse interception-jamming strategy
图 13 对抗3个侦干周期的雷达策略及对抗奖励
Figure 13. The strategies and rewards for radar anti-jamming during three interception-jamming periods
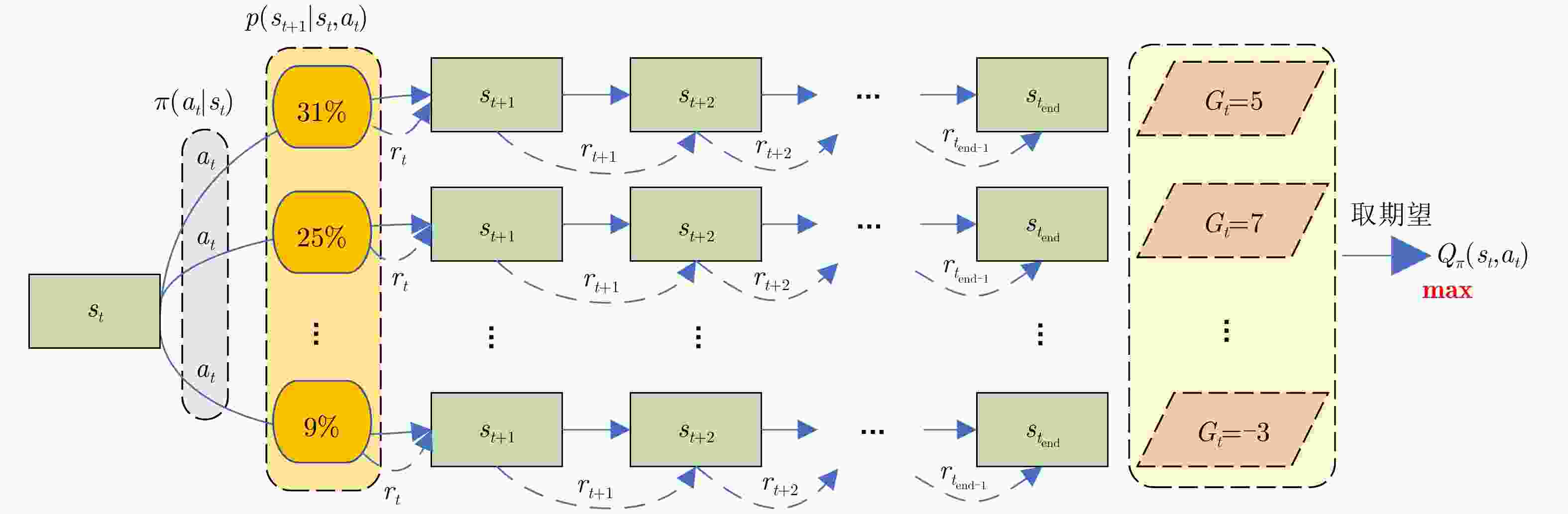
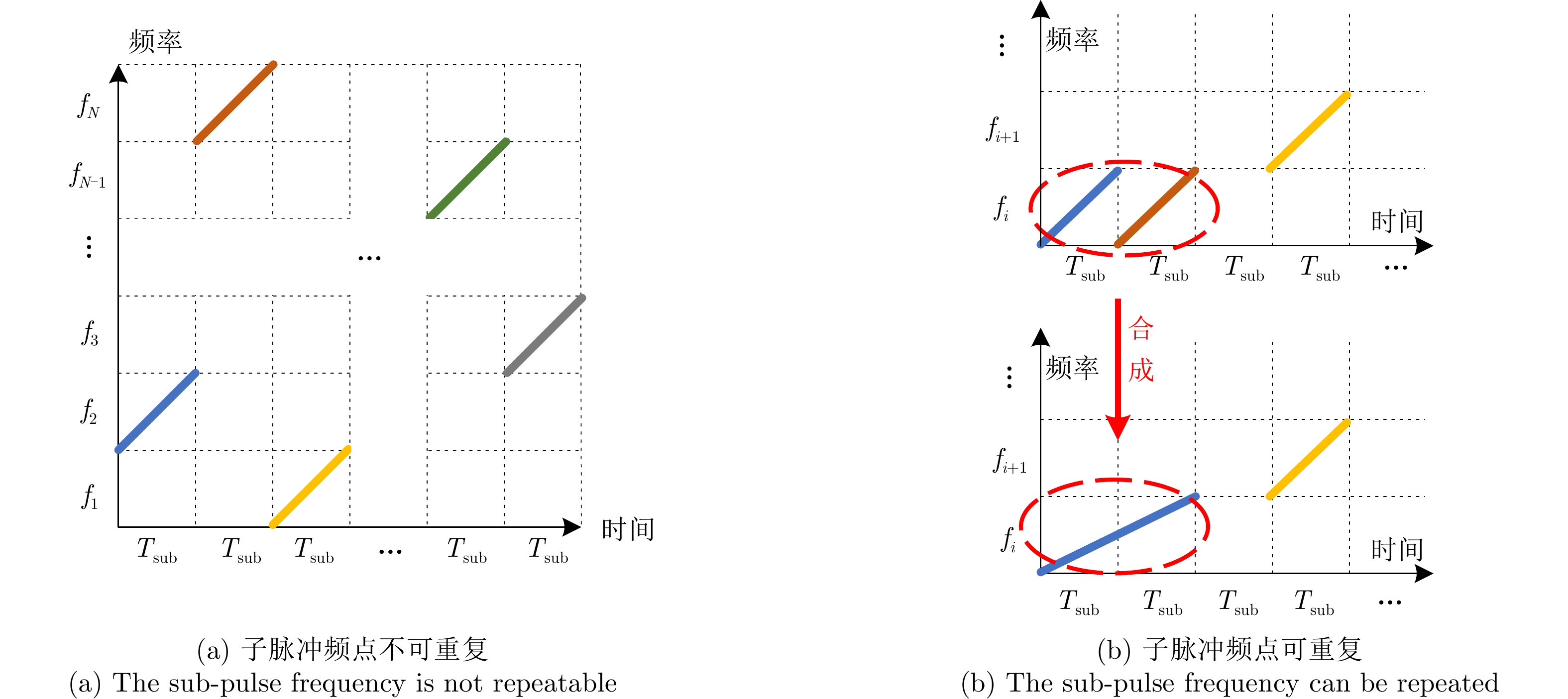
1 基于深度Q网络的雷达子脉冲频点决策
1. Radar sub-pulse frequency decision based on Deep Q-Network (DQN)
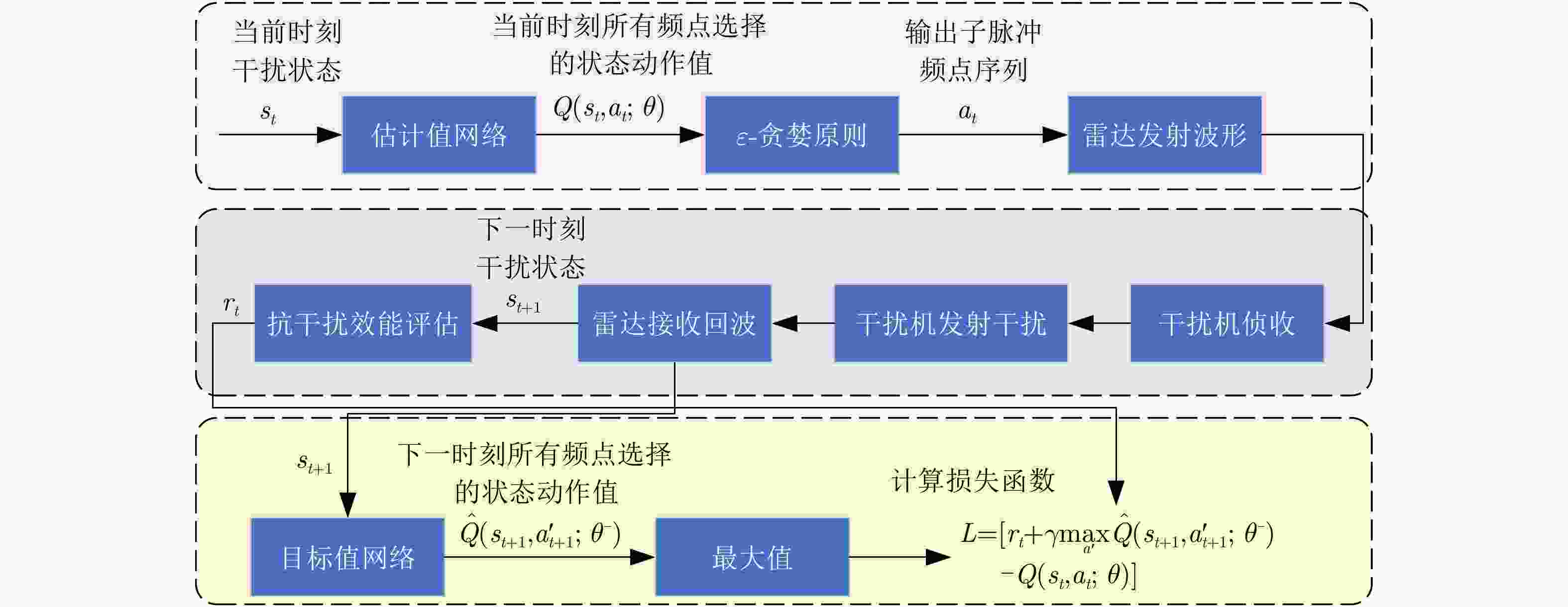
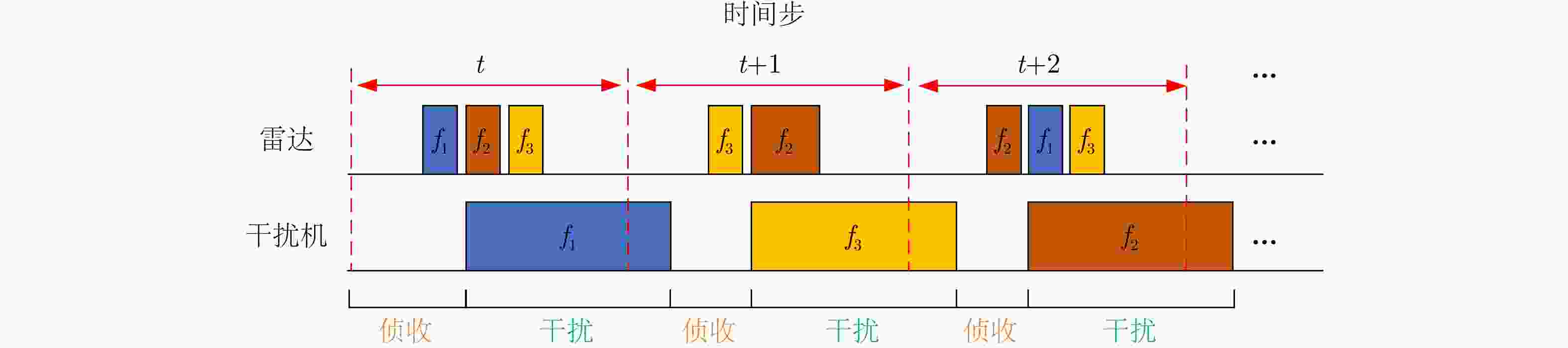
Step 1：初始化： Step 1-1：使用随机参数$\theta $初始化估计值${\text{Q}}$网络 Step 1-2：使用参数${\theta ^ - }{\text{=}}\theta $初始化目标值$ {{\hat {\rm Q}}} $网络 Step 1-3：初始化经验池D Step 1-4：初始化干扰策略，雷达子脉冲数量及频点，折扣因
子$\gamma $，学习率$\alpha $，贪婪因子$\varepsilon $，软间隔更新系数$\tau $等参数Step 2：每幕： Step 2-1：设置初始状态$ {s_1} = \left[ {{f_{{\mathrm{R}},0}},{f_{{\mathrm{J}},1}}} \right] $ Step 2-2：每个时间步： Step 2-2-1：使用$\varepsilon $-贪婪原则依据估计值网络的输出结果选择
各子脉冲频点$ {a_t} = {f_{{\mathrm{R}},t}} = \left[ {{f_{{\mathrm{sub}}1,t}},{f_{{\mathrm{sub}}2,t}}, \cdots ,{f_{{\mathrm{sub}}N,t}}} \right] $，即以
$1 - \varepsilon $概率选择估计值网络输出的最佳的频点或者以$\varepsilon $概率随
机选择频点Step 2-2-2：雷达发射子脉冲频率捷变波形，接收到回波后，感
知得到下一时刻状态$ {s_{t + 1}} $并根据目标检测结果和脉压后的信
干噪比评估当前时刻奖励${r_t}$Step 2-2-3：将$\left( {{s_t},{a_t},{r_t},s{}_{t + 1}} \right)$存储到经验池D中，如果经验池
中的样本数超出预定数量，则删除早期训练样本数据，以便存
储并使用最新样本数据Step 2-2-4：如果经验池D中保存数量超过起始值，则从D中选
择批大小(batchsize)个样本作为训练集输入到估计值和目标值
网络中，分别计算得到$ Q\left( {{s_t},{a_t};\theta } \right) $和$ y = {r_t} + \gamma \max \hat Q ( {s_{t + 1}},$
$a_{t + 1}';{\theta ^ - } ) $，并反向梯度求导使误差函数$L\left( \theta \right) = \left[ y - Q\left( {s_t},{a_t}; \right.\right. $
$ \left. \left.\theta \right) \right]^2 $趋近0，更新估计值网络参数$\theta $Step 2-2-5：每隔一定的时间步软更新目标值网络参数${\theta ^ - }$ Step 2-3：结束该时间步 Step 2-4：降低贪婪概率$\varepsilon $ Step 3：结束该幕 
下载: 导出CSV
表 1 频率捷变信号参数设置
Table 1. The parameter settings of frequency agile signal
参数 数值 子脉冲调制类型 LFM 子脉冲个数 3 子脉冲频点 [10 MHz, 30 MHz, 50 MHz] 子脉冲脉宽 5 μs 子脉冲带宽 5 MHz 信噪比 0 dB
下载: 导出CSV
表 2 干扰参数设置
Table 2. The parameter settings of jamming
干扰类型 参数 数值 窄带瞄频 瞄准频点 [10 MHz, 30 MHz, 50 MHz] 带宽 10 MHz 干噪比 35 dB 宽带阻塞 带宽 120 MHz 干噪比 30 dB
下载: 导出CSV
表 3 DQN参数设置
Table 3. The parameter settings of DQN
参数 数值 批大小 64 学习率 0.001 折扣因子 0.99 缓冲区大小 10000 起始训练样本量 64 贪婪因子衰减系数 0.2 幕 32个时间步 目标值网络更新周期 4个时间步 目标值网络软间隔更新系数 0.01 隐藏层数量 2 隐藏层神经元个数 64 归一化系数 80
下载: 导出CSV
表 4 脉内侦干策略的对抗成功率(%)
Table 4. The success rate of confrontation for the intra-pulse interception-jamming strategy (%)
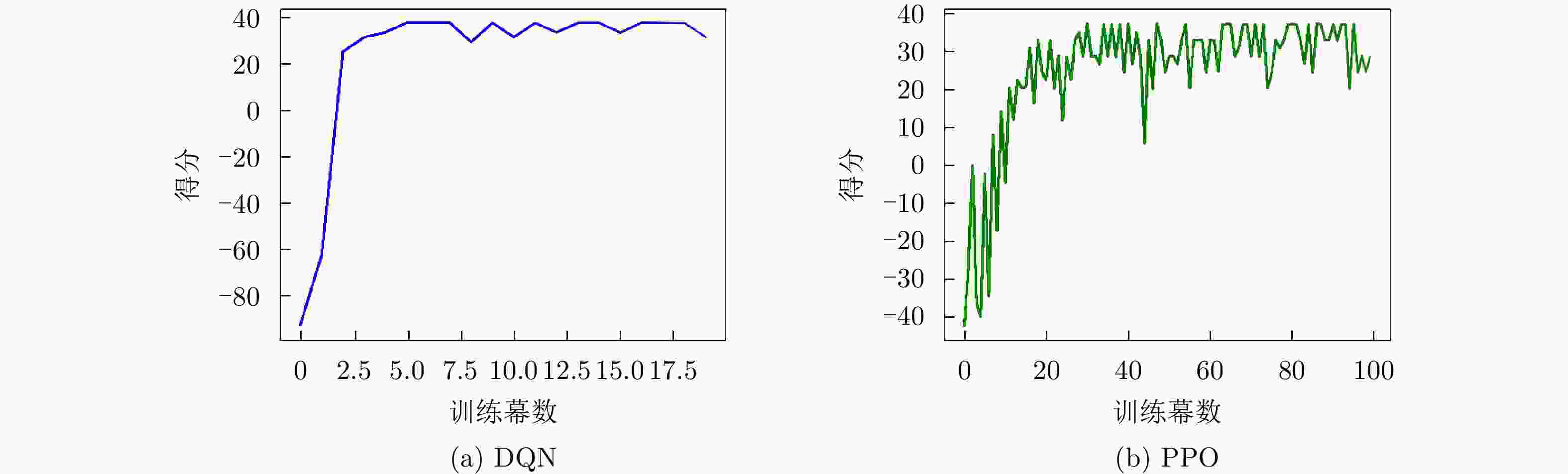
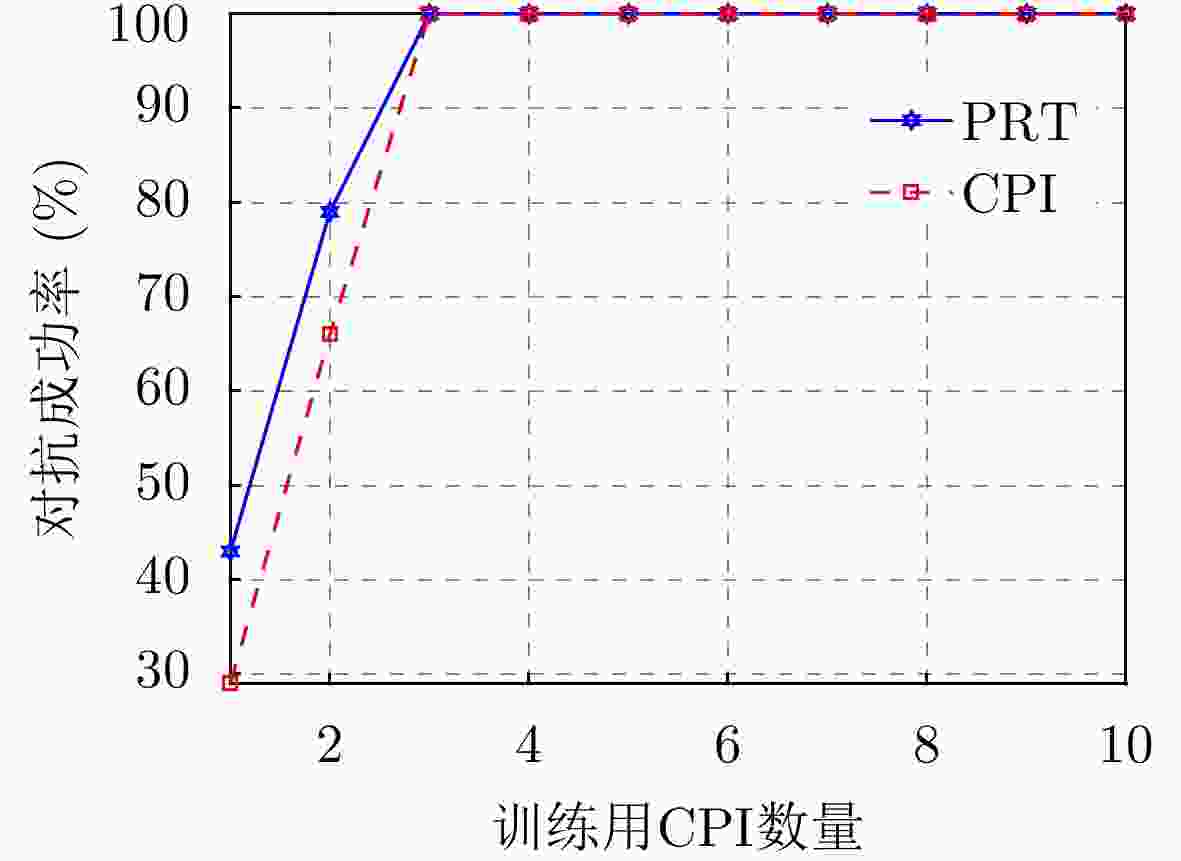
策略 PRT对抗成功率 CPI对抗成功率 随机频点 9.7 0 PPO 94 9 DQN 100 100
下载: 导出CSV
表 5 脉内侦干策略下各种雷达策略对抗1000次结果(fJ=fsub1)
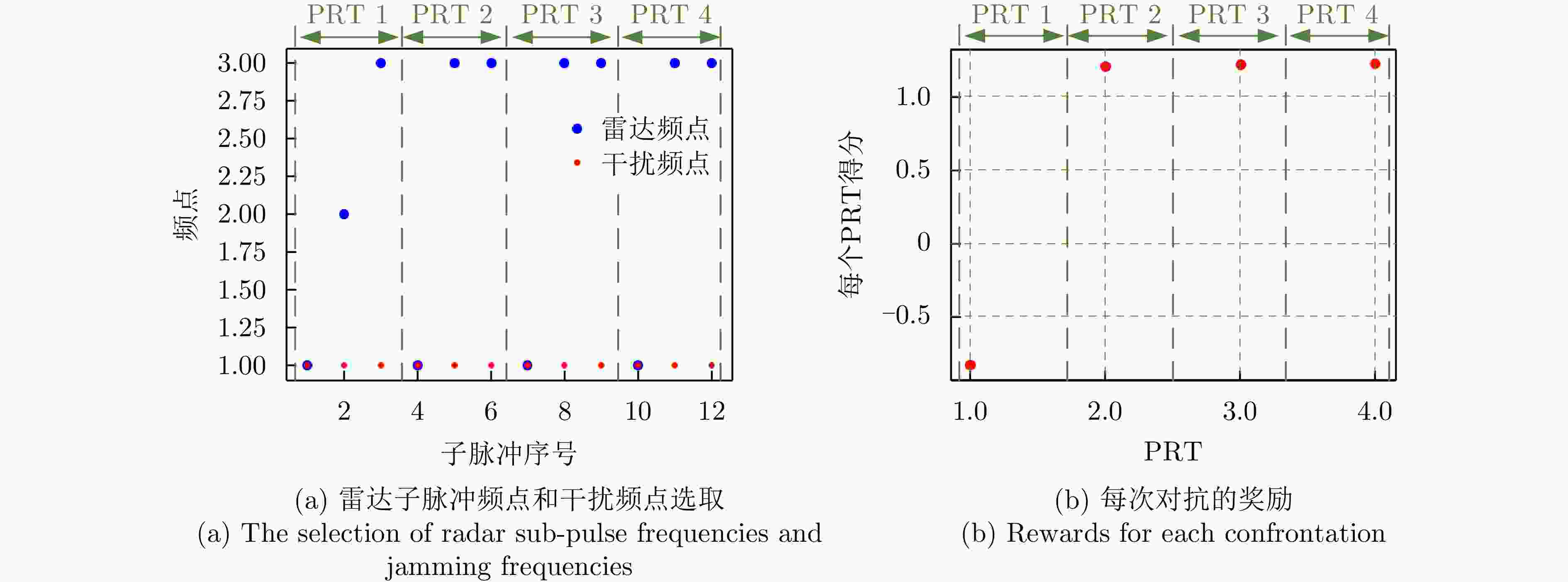
Table 5. The results of 1000 confrontations with various radar strategies for the intra-pulse interception-jamming strategy (fJ=fsub1)
雷达频点选择 目标检测率(%) 信干噪比(dB) 平均得分 [1,1,1] 0 — –3.00 [1,1,2] 0 11.09 –1.12 [1,1,3] 0 12.25 –0.96 [1,2,2] 97.6 15.20 1.09 [1,2,3] 81.7 12.78 0.78 [1,3,3] 99.7 16.06 1.19 [2,1,1] 98.3 15.35 1.12 [2,1,3] 75.6 12.47 0.64 [2,3,3] 97.7 15.19 1.10 [3,1,1] 99.6 16.07 1.18 注：综合考虑噪声随机性引起的得分波动情况，加粗项为最优策略
下载: 导出CSV
表 6 脉间侦干策略的对抗成功率(%)
Table 6. The success rate of confrontation for the pulse-to-pulse interception-jamming strategy (%)
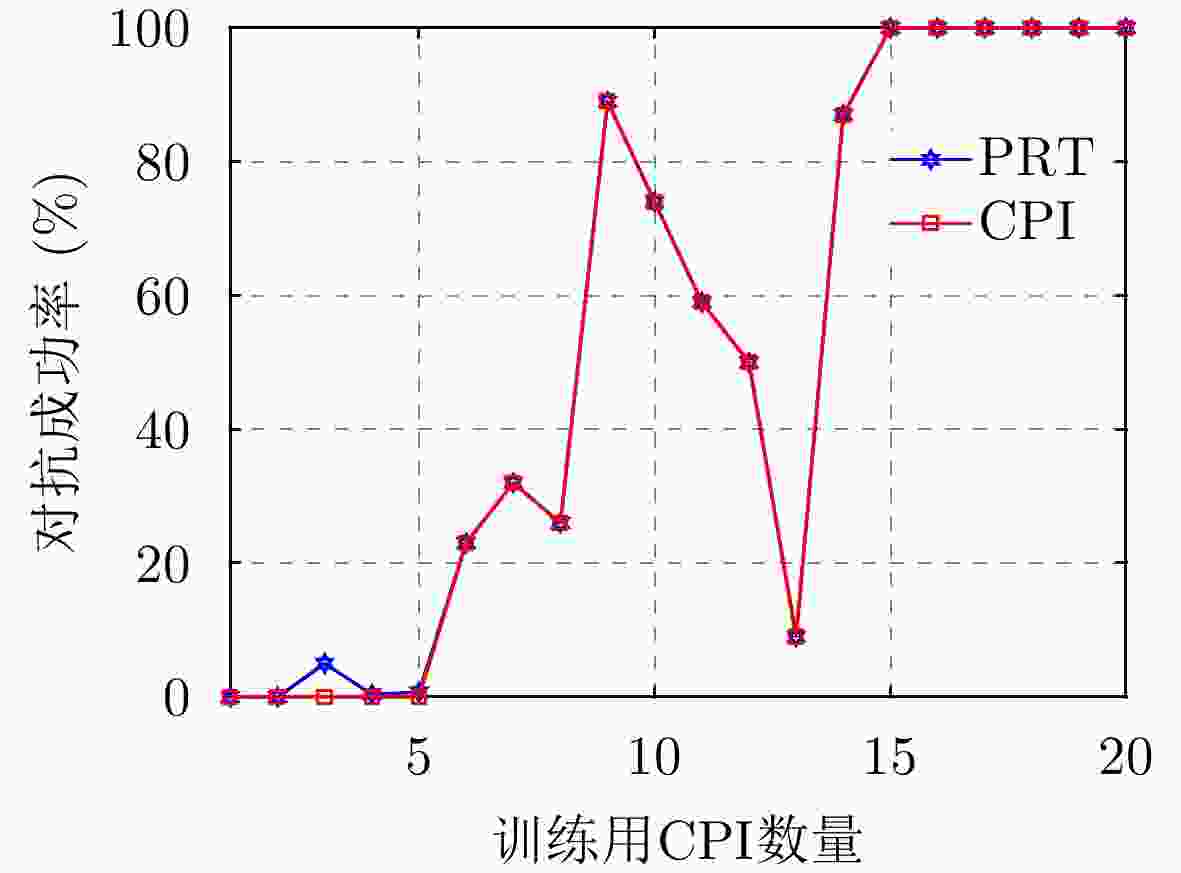
策略 PRT对抗成功率 CPI对抗成功率 随机频点 0.7 0 PPO 93.6 31 DQN 100 100
下载: 导出CSV
表 7 脉间侦干策略下各种雷达策略对抗1000次的结果(fJ=1)
Table 7. The results of 1000 confrontations with various radar strategies for the pulse-to-pulse interception-jamming strategy (fJ=1)
雷达频点选择 目标检测率(%) 信干噪比(dB) 平均得分 [1,1,1] 0 — –3.00 [1,2,3] 81.3 12.74 0.76 [2,2,2] 99.7 17.08 3.17 [3,3,3] 100 17.58 3.22 注：加粗项表示最优策略
下载: 导出CSV
-
[1] 李永祯, 黄大通, 邢世其, 等. 合成孔径雷达干扰技术研究综述[J]. 雷达学报, 2020, 9(5): 753–764. doi: 10.12000/JR20087.LI Yongzhen, HUANG Datong, XING Shiqi, et al. A review of synthetic aperture radar jamming technique[J]. Journal of Radars, 2020, 9(5): 753–764. doi: 10.12000/JR20087. [2] 崔国龙, 余显祥, 魏文强, 等. 认知智能雷达抗干扰技术综述与展望[J]. 雷达学报, 2022, 11(6): 974–1002. doi: 10.12000/JR22191.CUI Guolong, YU Xianxiang, WEI Wenqiang, et al. An overview of antijamming methods and future works on cognitive intelligent radar[J]. Journal of Radars, 2022, 11(6): 974–1002. doi: 10.12000/JR22191. [3] 李康. 雷达智能抗干扰策略学习方法研究[D]. [博士论文], 西安电子科技大学, 2021. doi: 10.27389/d.cnki.gxadu.2021.003098.LI Kang. Research on radar intelligent antijamming strategy learning method[D]. [Ph.D. dissertation], Xidian University, 2021. doi: 10.27389/d.cnki.gxadu.2021.003098. [4] JIANG Wangkui, LI Yan, LIAO Mengmeng, et al. An improved LPI radar waveform recognition framework with LDC-Unet and SSR-Loss[J]. IEEE Signal Processing Letters, 2022, 29: 149–153. doi: 10.1109/LSP.2021.3130797. [5] GARMATYUK D S and NARAYANAN R M. ECCM capabilities of an ultrawideband bandlimited random noise imaging radar[J]. IEEE Transactions on Aerospace and Electronic Systems, 2002, 38(4): 1243–1255. doi: 10.1109/TAES.2002.1145747. [6] GOVONI M A, LI Hongbin, and KOSINSKI J A. Low probability of interception of an advanced noise radar waveform with linear-FM[J]. IEEE Transactions on Aerospace and Electronic Systems, 2013, 49(2): 1351–1356. doi: 10.1109/TAES.2013.6494419. [7] CUI Guolong, JI Hongmin, CAROTENUTO V, et al. An adaptive sequential estimation algorithm for velocity jamming suppression[J]. Signal Processing, 2017, 134: 70–75. doi: 10.1016/j.sigpro.2016.11.012. [8] YU K B and MURROW D J. Adaptive digital beamforming for angle estimation in jamming[J]. IEEE Transactions on Aerospace and Electronic Systems, 2001, 37(2): 508–523. doi: 10.1109/7.937465. [9] DAI Huanyao, WANG Xuesong, LI Yongzhen, et al. Main-lobe jamming suppression method of using spatial polarization characteristics of antennas[J]. IEEE Transactions on Aerospace and Electronic Systems, 2012, 48(3): 2167–2179. doi: 10.1109/TAES.2012.6237586. [10] 鲍秋香. 频率随机捷变雷达抗扫频干扰性能仿真[J]. 舰船电子对抗, 2021, 44(5): 78–81. doi: 10.16426/j.cnki.jcdzdk.2021.05.017.BAO Qiuxiang. Simulation of anti-sweep jamming performance of frequency random agility radar[J]. Shipboard Electronic Countermeasure, 2021, 44(5): 78–81. doi: 10.16426/j.cnki.jcdzdk.2021.05.017. [11] 全英汇, 方文, 沙明辉, 等. 频率捷变雷达波形对抗技术现状与展望[J]. 系统工程与电子技术, 2021, 43(11): 3126–3136. doi: 10.12305/j.issn.1001-506X.2021.11.11.QUAN Yinghui, FANG Wen, SHA Minghui, et al. Present situation and prospects of frequency agility radar wave form countermeasures[J]. Systems Engineering and Electronics, 2021, 43(11): 3126–3136. doi: 10.12305/j.issn.1001-506X.2021.11.11. [12] MINSKY M. Steps toward artificial intelligence[J]. Proceedings of the IRE, 1961, 49(1): 8–30. doi: 10.1109/JRPROC.1961.287775. [13] ARULKUMARAN K, DEISENROTH M P, BRUNDAGE M, et al. Deep reinforcement learning: A brief survey[J]. IEEE Signal Processing Magazine, 2017, 34(6): 26–38. doi: 10.1109/MSP.2017.2743240. [14] JIANG Wen, REN Yihui, and WANG Yanping. Improving anti-jamming decision-making strategies for cognitive radar via multi-agent deep reinforcement learning[J]. Digital Signal Processing, 2023, 135: 103952. doi: 10.1016/j.dsp.2023.103952. [15] JIANG Wen, WANG Yanping, LI Yang, et al. An intelligent anti-jamming decision-making method based on deep reinforcement learning for cognitive radar[C]. 2023 26th International Conference on Computer Supported Cooperative Work in Design (CSCWD), Rio de Janeiro, Brazil, 2023: 1662–1666. doi: 10.1109/CSCWD57460.2023.10152833. [16] WEI Jingjing, WEI Yinsheng, YU Lei, et al. Radar anti-jamming decision-making method based on DDPG-MADDPG algorithm[J]. Remote Sensing, 2023, 15(16): 4046. doi: 10.3390/rs15164046. [17] AZIZ M M, MAUD A, and HABIB A. Reinforcement learning based techniques for radar anti-jamming[C]. 2021 International Bhurban Conference on Applied Sciences and Technologies (IBCAST), Islamabad, Pakistan, 2021: 1021–1025. doi: 10.1109/IBCAST51254.2021.9393209. [18] LI Kang, JIU Bo, LIU Hongwei, et al. Reinforcement learning based anti-jamming frequency hopping strategies design for cognitive radar[C]. 2018 IEEE International Conference on Signal Processing, Communications and Computing (ICSPCC), Qingdao, China, 2018: 1–5. doi: 10.1109/ICSPCC.2018.8567751. [19] LI Kang, JIU Bo, and LIU Hongwei. Deep Q-network based anti-jamming strategy design for frequency agile radar[C]. 2019 International Radar Conference (RADAR), Toulon, France, 2019: 1–5. doi: 10.1109/RADAR41533.2019.171227. [20] LI Kang, JIU Bo, WANG Penghui, et al. Radar active antagonism through deep reinforcement learning: A way to address the challenge of mainlobe jamming[J]. Signal Processing, 2021, 186: 108130. doi: 10.1016/j.sigpro.2021.108130. [21] WU Qinhao, WANG Hongqiang, LI Xiang, et al. Reinforcement learning-based anti-jamming in networked UAV radar systems[J]. Applied Sciences, 2019, 9(23): 5173. doi: 10.3390/app9235173. [22] AK S and BRÜGGENWIRTH S. Avoiding jammers: A reinforcement learning approach[C]. 2020 IEEE International Radar Conference (RADAR), Washington, USA, 2020: 321–326. doi: 10.1109/RADAR42522.2020.9114797. [23] AILIYA, YI Wei, and YUAN Ye. Reinforcement learning-based joint adaptive frequency hopping and pulse-width allocation for radar anti-jamming[C]. 2020 IEEE Radar Conference (RadarConf20), Florence, Italy, 2020: 1–6. doi: 10.1109/RadarConf2043947.2020.9266402. [24] ZHANG Jiaxiang and ZHOU Chao. Interrupted sampling repeater jamming suppression method based on hybrid modulated radar signal[C]. 2019 IEEE International Conference on Signal, Information and Data Processing (ICSIDP), Chongqing, China, 2019: 1–4. doi: 10.1109/ICSIDP47821.2019.9173093. -
计量
- 文章访问数: 1034
- HTML全文浏览量: 366
- PDF下载量: 203
- 被引次数: 0
