作者中心
专家审稿
责编办公
编辑办公
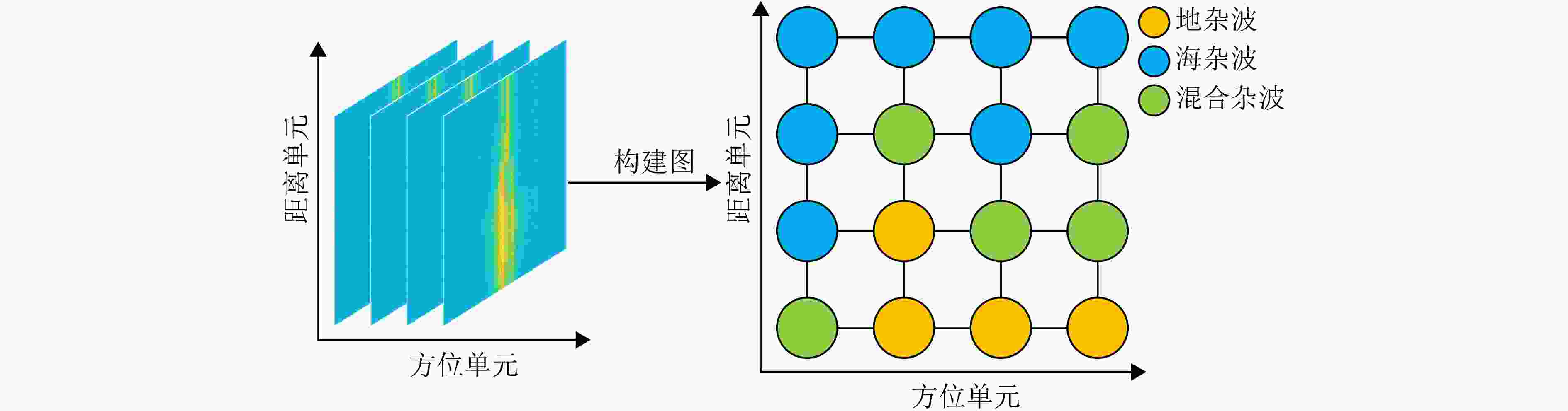
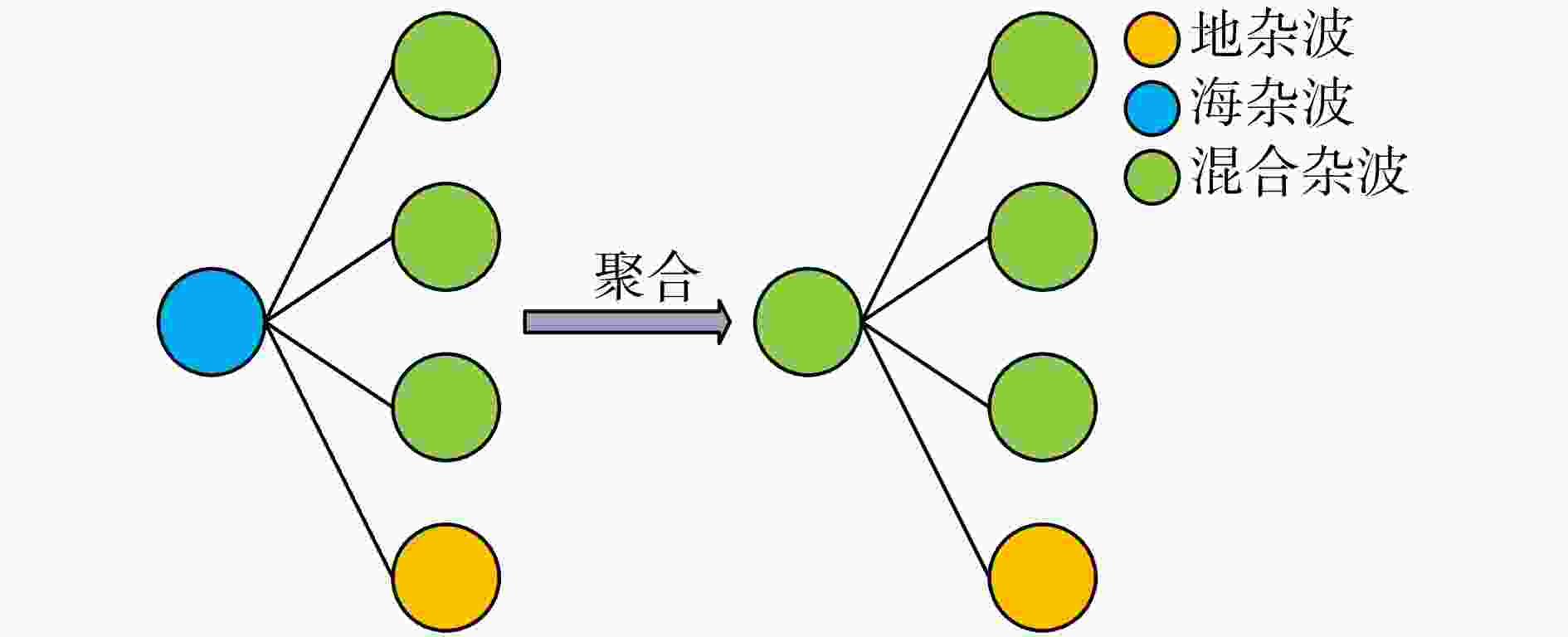
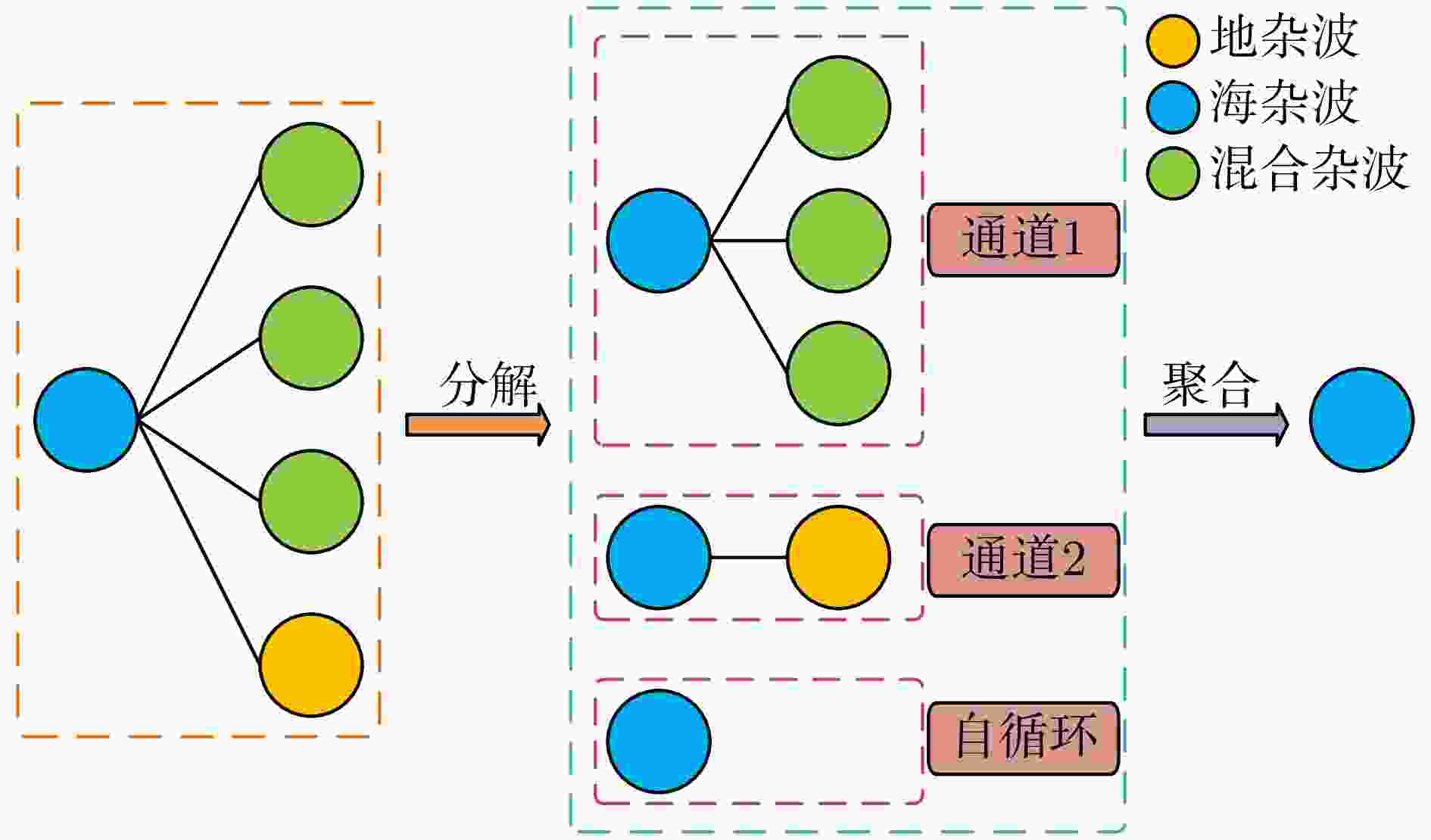
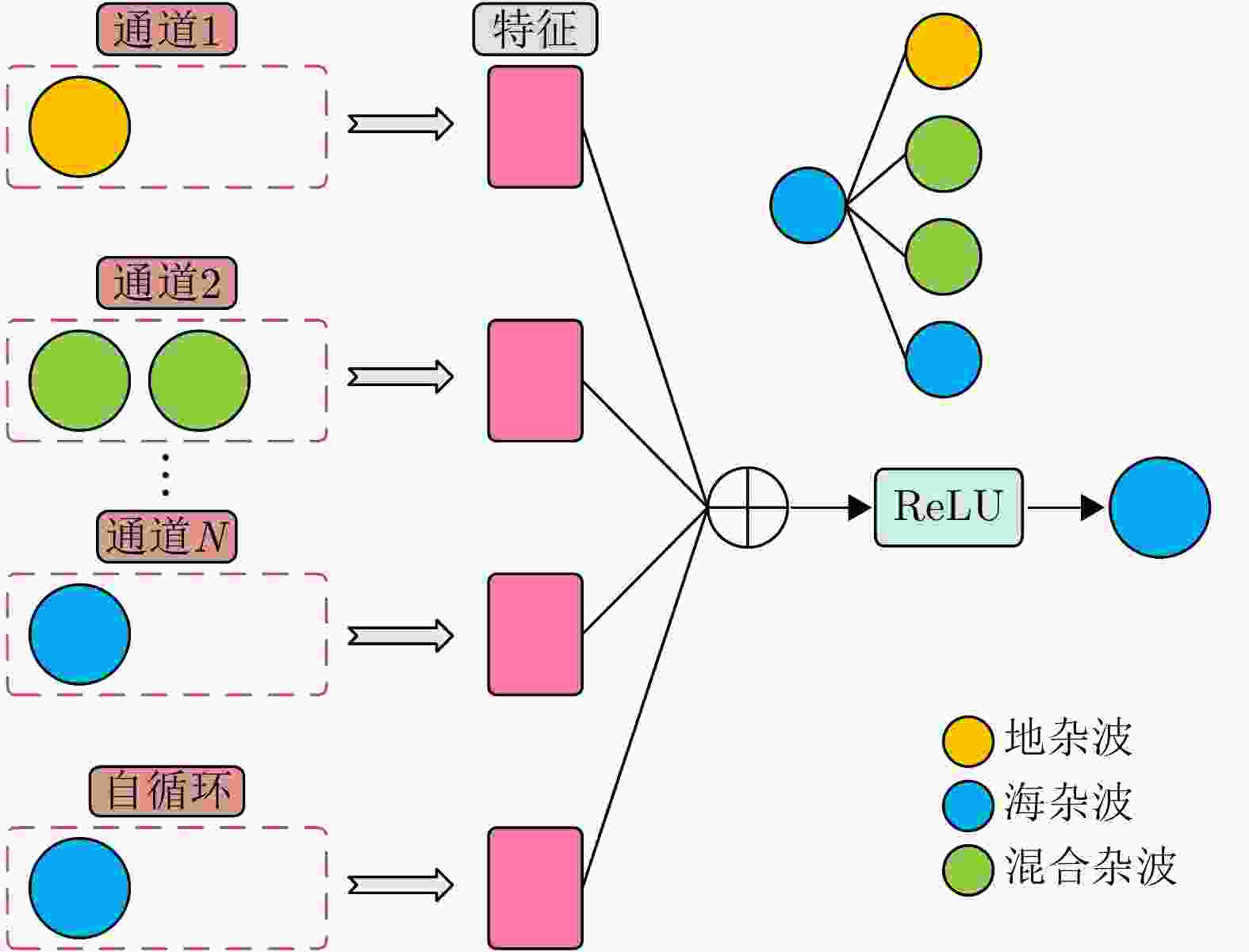
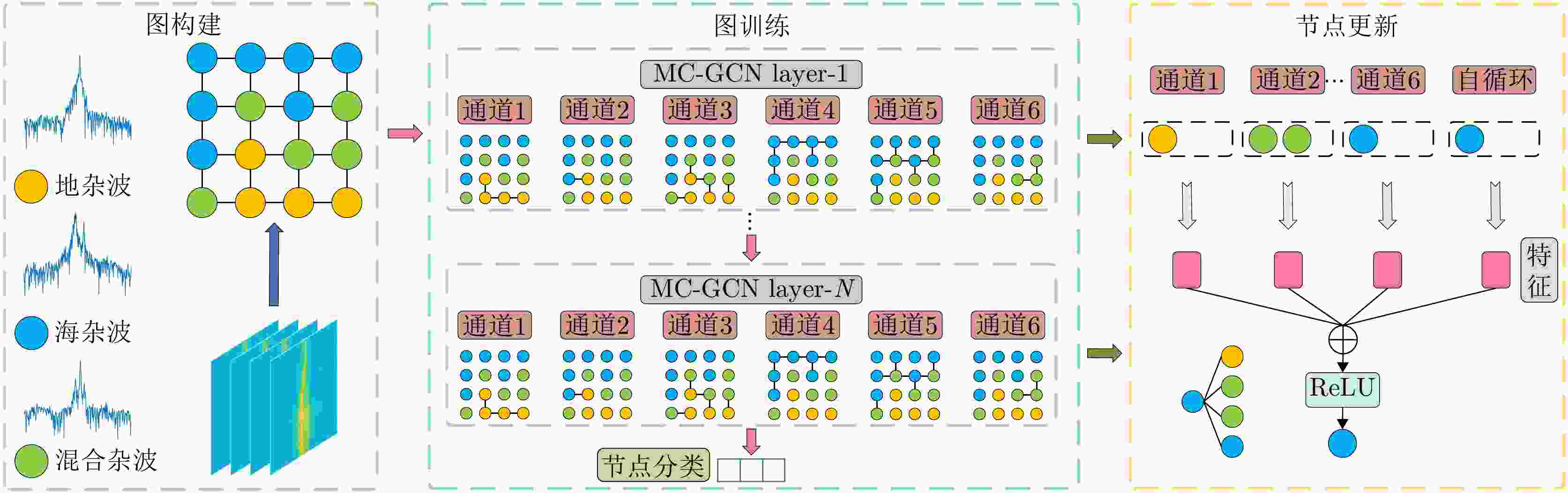
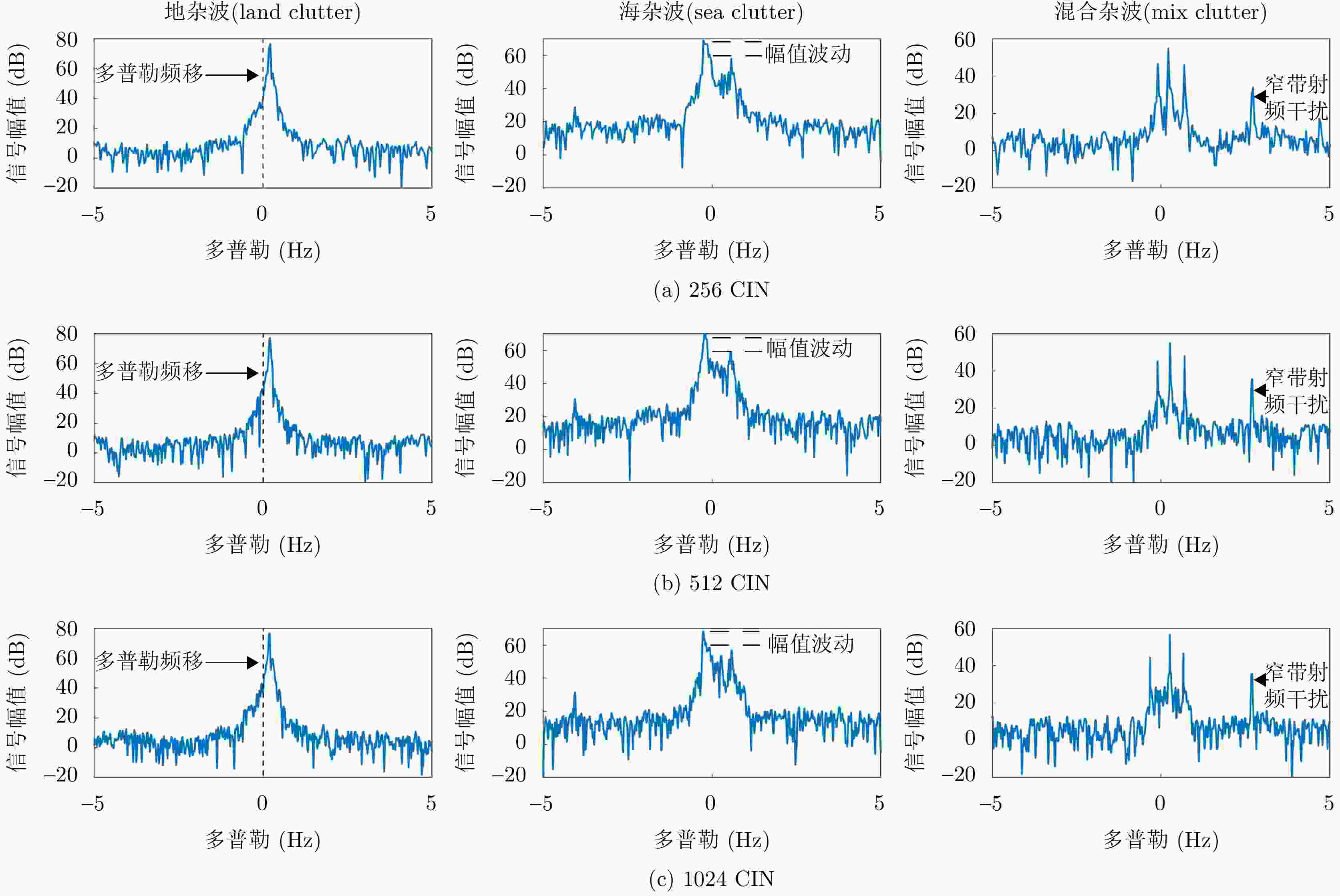
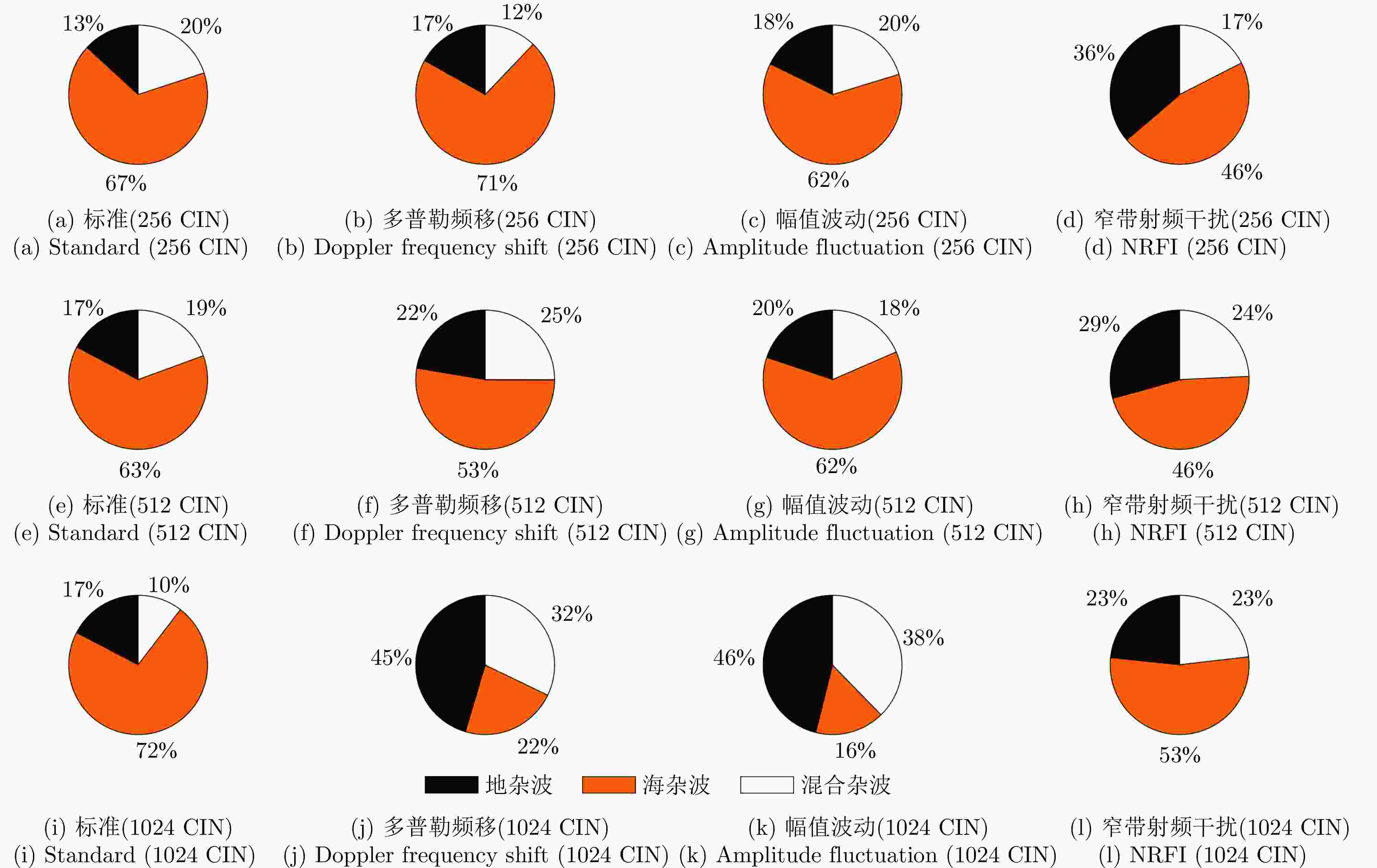
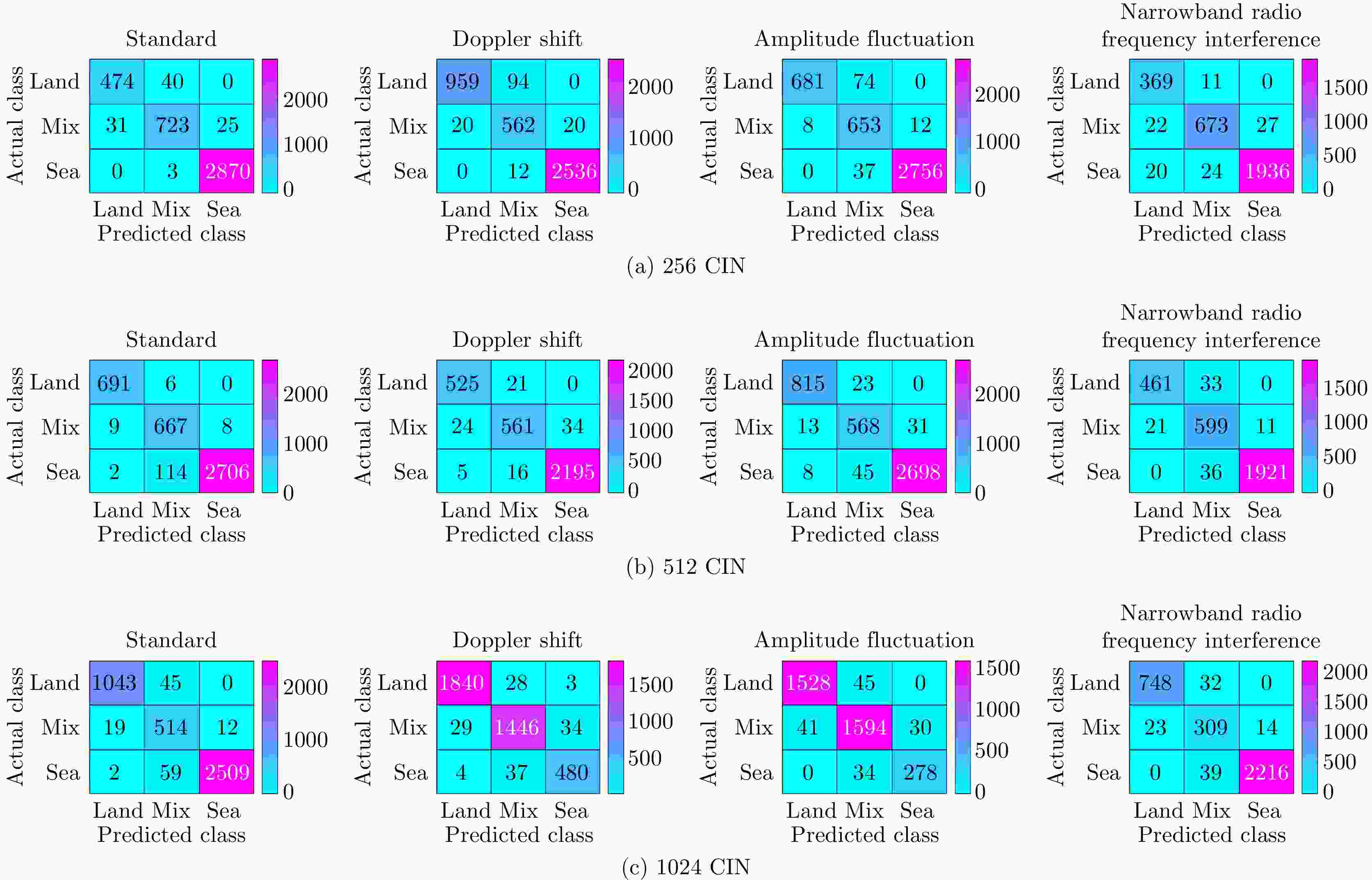
Land-sea Clutter Classification Method Based on Multi-channel Graph Convolutional Networks
-
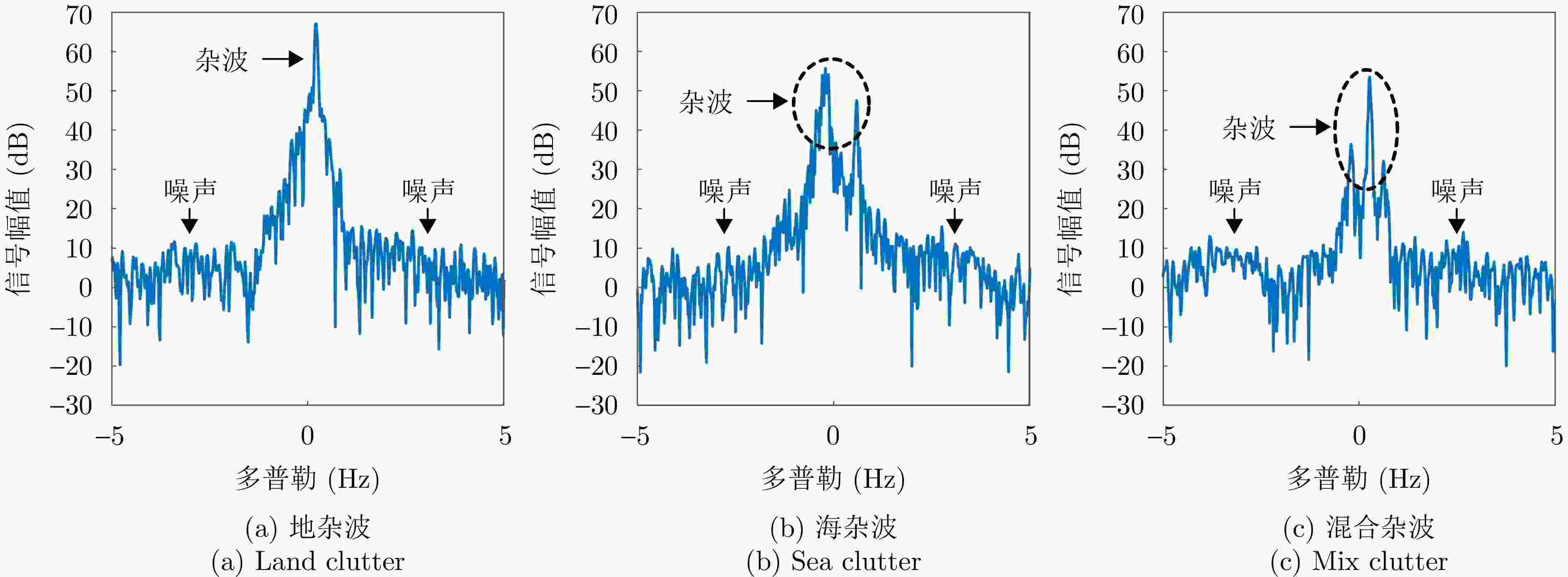
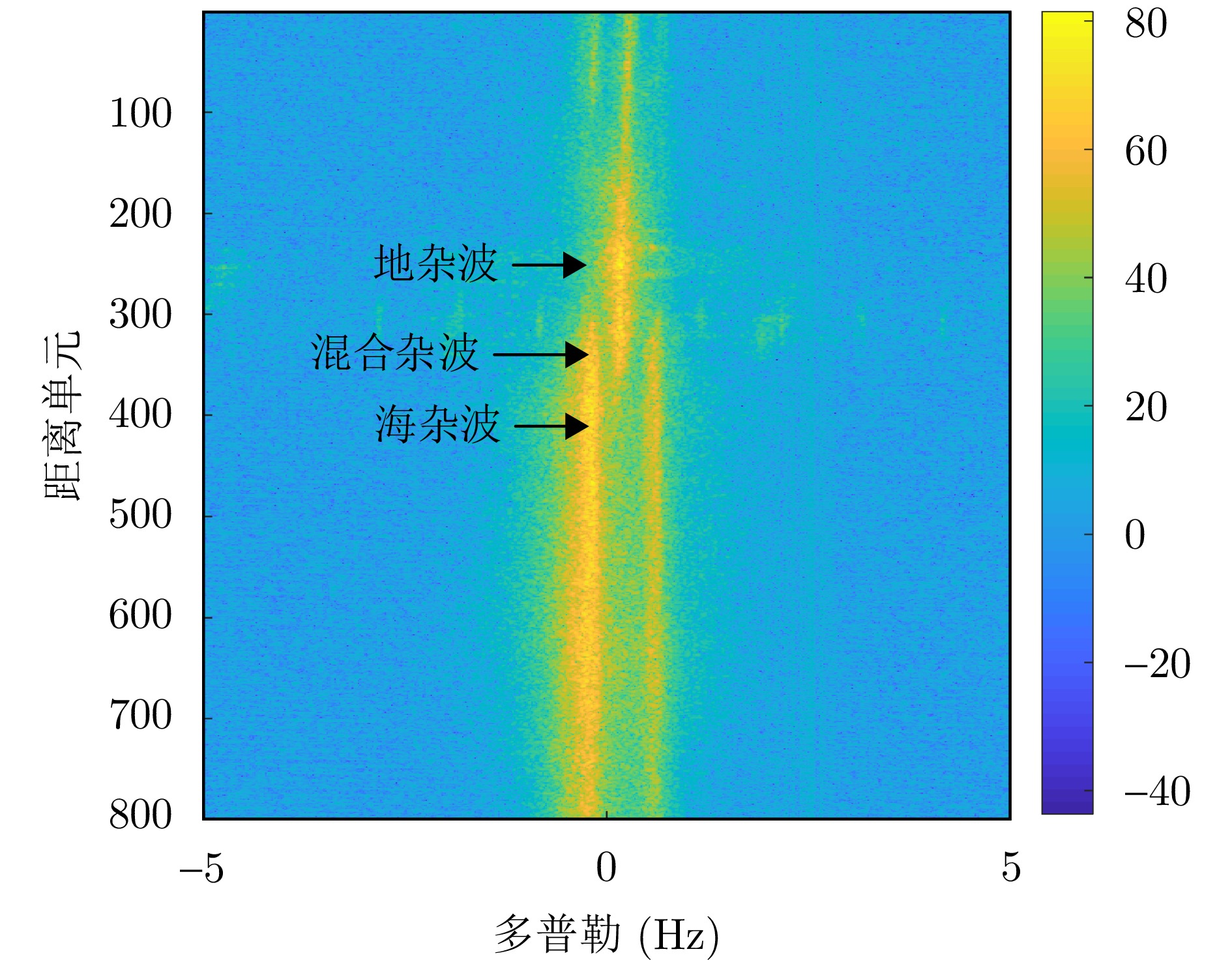
摘要: 地海杂波分类是提升天波超视距雷达目标定位精度的关键技术，其核心是判别距离多普勒(RD)图中每个方位-距离单元背景源自陆地或海洋的过程。基于传统深度学习的地海杂波分类方法需海量高质量且类别均衡的有标签样本，训练时间长，费效比高；此外，其输入为单个方位-距离单元杂波，未考虑样本的类内和类间信息，导致模型性能不佳。针对上述问题，该文通过分析相邻方位-距离单元之间的相关性，将地海杂波数据由欧氏空间转换为非欧氏空间中的图数据，引入样本之间的关系，并提出一种基于多通道图卷积神经网络(MC-GCN)的地海杂波分类方法。MC-GCN将图数据由单通道分解为多通道，每个通道只包含一种类型的边和一个权重矩阵，通过约束节点信息聚合的过程，能够有效缓解由异质性造成的节点属性误判。该文选取不同季节、不同时刻、不同探测区域RD图，依据雷达参数、数据特性和样本比例，构建包含12种不同场景的地海杂波原始数据集和36种不同配置的地海杂波稀缺数据集，并对MC-GCN的有效性进行验证。通过与最先进的地海杂波分类方法进行比较，该文所提出的MC-GCN在上述数据集中均表现最优，其分类准确率不低于92%。Abstract: Land-sea clutter classification is essential for boosting the target positioning accuracy of skywave over-the-horizon radar. This classification process involves discriminating whether each azimuth-range cell in the Range-Doppler (RD) map is overland or sea. Traditional deep learning methods for this task require extensive, high-quality, and class-balanced labeled samples, leading to long training periods and high costs. In addition, these methods typically use a single azimuth-range cell clutter without considering intra-class and inter-class relationships, resulting in poor model performance. To address these challenges, this study analyzes the correlation between adjacent azimuth-range cells, and converts land-sea clutter data from Euclidean space into graph data in non-Euclidean space, thereby incorporating sample relationships. We propose a Multi-Channel Graph Convolutional Networks (MC-GCN) for land-sea clutter classification. MC-GCN decomposes graph data from a single channel into multiple channels, each containing a single type of edge and a weight matrix. This approach restricts node information aggregation, effectively reducing node attribute misjudgment caused by data heterogeneity. For validation, RD maps from various seasons, times, and detection areas were selected. Based on radar parameters, data characteristics, and sample proportions, we construct a land-sea clutter original dataset containing 12 different scenes and a land-sea clutter scarce dataset containing 36 different configurations. The effectiveness of MC-GCN is confirmed, with the approach outperforming state-of-the-art classification methods with a classification accuracy of at least 92%.
-
图 3 相邻方位-距离单元绝对距离
Figure 3. The absolute distance between adjacent azimuth-range cells
图 4 相邻方位-距离单元余弦相似度
Figure 4. The cosine similarity between adjacent azimuth-range cells
图 5 相邻方位-距离单元皮尔逊相关系数
Figure 5. The pearson correlation coefficient between adjacent azimuth-range cells
图 10 基于MC-GCN的地海杂波分类流程图
Figure 10. Flowchart of the land-sea clutter classification based on MC-GCN
图 12 原始数据集中不同类别杂波比例
Figure 12. Proportion of different categories of clutter in the original dataset
图 14 MC-GCN在原始数据集上的PE, RE和F1值
Figure 14. PE, RE and F1 values of MC-GCN on the original dataset
图 15 MC-GCN在原始数据集上的正确率与损失曲线
Figure 15. Accuracy and loss curve of MC-GCN on the original dataset
图 16 MC-GCN的地海杂波分类结果图
Figure 16. Figure of the land-sea clutter classification results by MC-GCN
表 1 地海杂波数据集设置(%)
Table 1. The setting of land-sea clutter dataset (%)
分组 样本特性 原始数据集 稀缺数据集 测试集 训练集 训练集 训练集 训练集 A组 标准 70 50 30 10 30 多普勒频移 70 50 30 10 30 幅值波动 70 50 30 10 30 窄带射频干扰 70 50 30 10 30 B组 标准 70 50 30 10 30 多普勒频移 70 50 30 10 30 幅值波动 70 50 30 10 30 窄带射频干扰 70 50 30 10 30 C组 标准 70 50 30 10 30 多普勒频移 70 50 30 10 30 幅值波动 70 50 30 10 30 窄带射频干扰 70 50 30 10 30 
下载: 导出CSV
表 2 实验环境
Table 2. Experimental environment
环境 版本 System Windows10(64-bit) GPU NVIDIA GeForce RTX 3090 CUDA 11.3.1 python 3.8.0 torch 1.11.0 torchvison 0.12.0 Numpy 1.24.3 matplotlib 3.5.1 dgl 1.1.0
下载: 导出CSV
表 3 实验参数
Table 3. Experimental parameters
参数 数值 Epoch 500 Learning rate 0.001 Hidden units 16 Layers 2 Input size $ \left[ {{N_{\mathrm{R}}} \times {N_{\mathrm{A}}},{N_{\mathrm{D}}}} \right] $ Output size $ \left[ {{N_{\mathrm{R}}} \times {N_{\mathrm{A}}},3} \right] $ Beta1 0.5 Beta2 0.999
下载: 导出CSV
表 4 原始数据集相关性分析
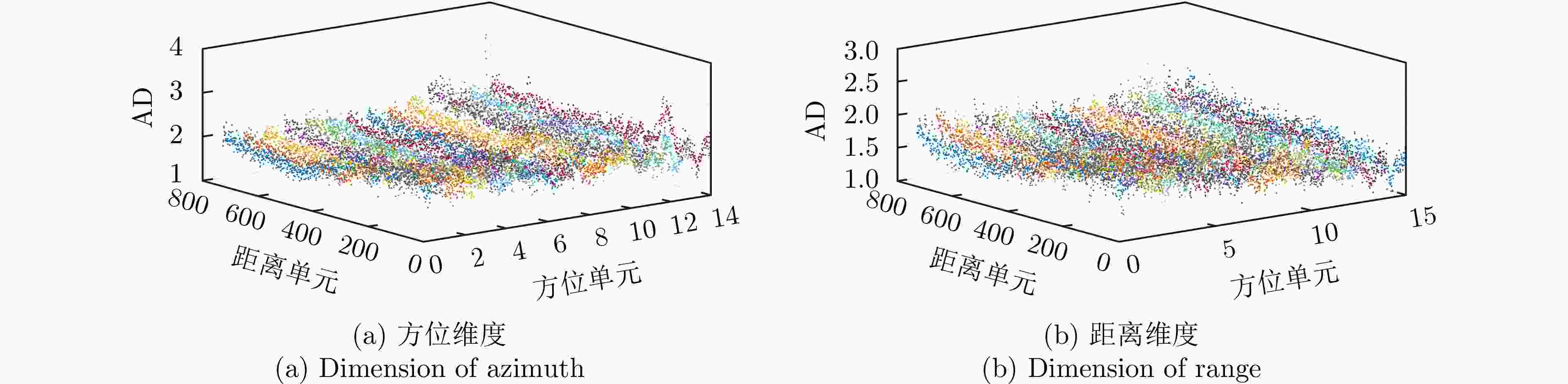
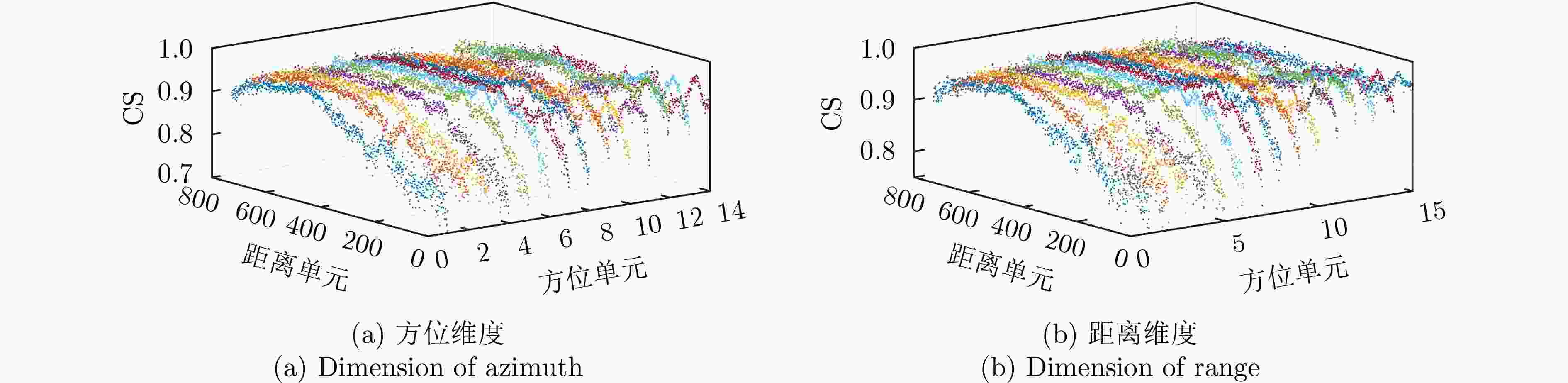
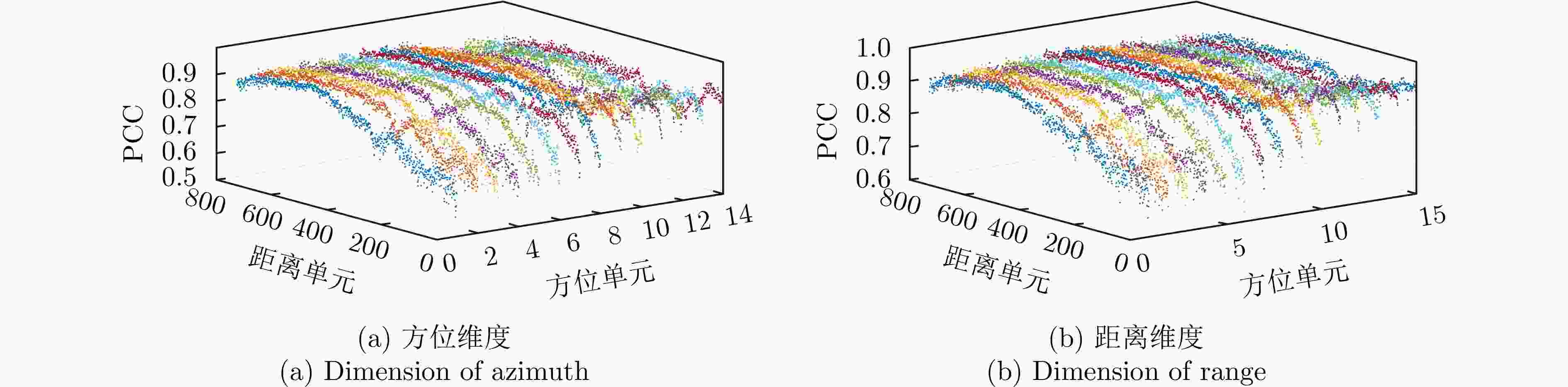
Table 4. Correlation analysis on the original dataset
分组 标准 多普勒频移 幅值波动 窄带射频干扰 AD CS PCC AD CS PCC AD CS PCC AD CS PCC A组 2.21, 1.79 0.76, 0.84 0.73, 0.82 1.97, 1.87 0.95, 0.95 0.81, 0.82 1.97, 1.59 0.88, 0.92 0.84, 0.89 2.04, 1.60 0.92, 0.95 0.81, 0.88 B组 1.96, 1.71 0.89, 0.92 0.83, 0.87 1.90, 1.47 0.93, 0.95 0.86, 0.90 1.88, 1.59 0.90, 0.93 0.86, 0.89 2.10, 1.83 0.85, 0.89 0.72, 0.79 C组 1.95, 1.52 0.91, 0.94 0.84, 0.89 2.11, 1.71 0.90, 0.93 0.76, 0.82 2.13, 1.69 0.97, 0.98 0.71, 0.81 1.99, 1.63 0.91, 0.94 0.83, 0.88
下载: 导出CSV
表 5 原始数据集与稀缺数据集上分类准确率(%)
Table 5. Classification accuracy on the original dataset and the scarce dataset (%)
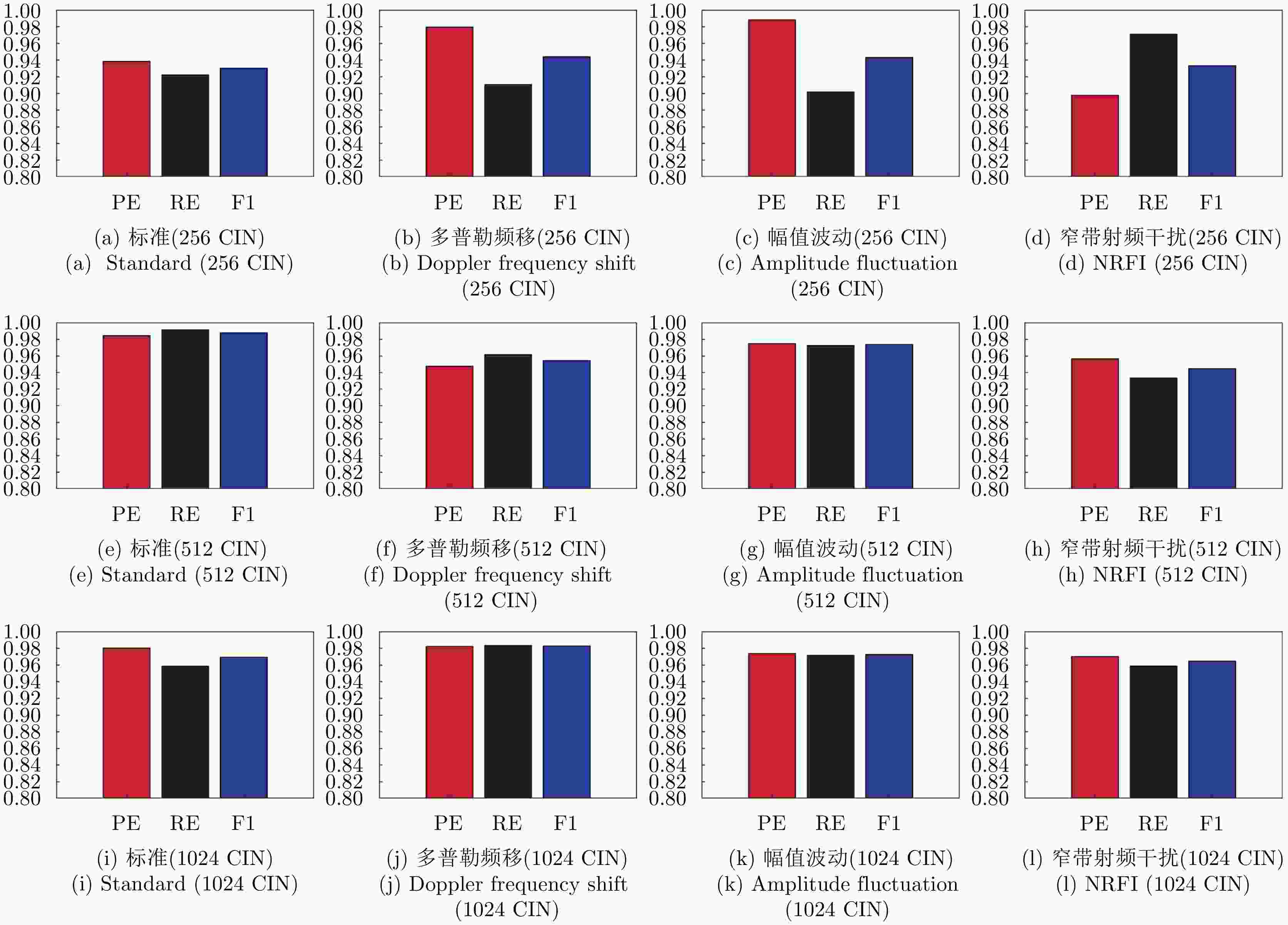
分组 方法 标准(AC) 多普勒频移(AC) 幅值波动(AC) 窄带射频干扰(AC) 70% 50% 30% 10% 70% 50% 30% 10% 70% 50% 30% 10% 70% 50% 30% 10% A组 MC-GCN 97.62 96.78 95.93 95.09 96.52 96.33 96.05 96.19 96.90 96.73 96.76 96.40 96.63 96.28 96.24 93.32 GCN 94.88 94.50 92.53 90.03 90.98 90.48 89.82 89.08 96.29 95.19 96.12 91.51 92.72 91.28 89.52 89.13 GAT 94.91 92.74 93.15 92.89 90.89 89.63 89.18 86.01 95.05 95.98 94.81 92.86 91.67 91.21 89.82 88.87 TA-GAN 94.21 92.59 90.61 90.37 92.36 91.16 88.69 86.27 94.12 93.94 92.95 91.99 92.37 91.69 90.11 88.52 ResNet18 95.40 90.20 84.84 78.63 94.48 90.75 83.65 75.44 96.57 89.83 84.43 75.02 95.49 91.56 85.45 77.48 DCNN 94.29 90.75 82.81 74.53 93.46 89.75 81.83 72.94 95.97 90.68 82.74 69.52 95.05 91.12 83.27 70.64 B组 MC-GCN 96.69 96.28 95.04 95.88 97.04 97.08 95.22 95.75 97.14 95.52 95.04 93.47 96.72 96.53 96.34 95.30 GCN 93.58 93.10 92.81 92.27 93.82 93.70 92.90 90.78 91.08 91.22 90.34 88.97 92.19 90.18 90.77 89.51 GAT 94.08 93.72 93.62 92.96 92.40 92.04 91.57 90.64 92.86 91.46 89.87 88.83 92.72 91.77 91.34 89.90 TA-GAN 94.29 92.74 91.79 90.37 94.37 92.72 91.49 91.66 92.28 91.38 89.05 87.96 93.43 91.98 90.80 88.96 ResNet18 96.11 90.39 83.42 75.18 95.36 89.72 81.19 74.74 94.14 90.66 81.79 74.38 93.33 89.90 83.28 75.84 DCNN 95.68 89.57 81.35 74.96 94.92 88.43 79.76 71.48 93.15 88.51 78.24 71.39 92.74 85.80 78.56 72.94 C组 MC-GCN 96.74 96.62 95.57 94.71 96.53 96.51 95.97 95.94 95.78 95.95 94.80 92.88 96.81 96.49 96.37 95.92 GCN 92.43 91.03 88.96 87.29 90.10 91.38 89.06 88.85 91.09 91.50 90.41 87.39 92.61 91.53 90.09 89.45 GAT 92.44 90.84 89.94 89.36 91.26 90.54 90.06 89.42 92.07 91.45 91.12 90.50 91.60 91.78 90.45 88.50 TA-GAN 92.36 91.61 89.47 86.64 91.79 90.96 89.52 88.33 92.47 91.99 90.89 89.87 92.41 91.46 90.51 89.73 ResNet18 94.90 90.41 85.19 77.49 95.19 90.00 80.01 74.62 95.44 91.30 81.21 73.71 93.67 89.47 86.42 77.47 DCNN 94.66 89.36 81.59 76.97 94.75 88.97 79.58 72.38 93.45 87.16 79.44 71.21 91.95 87.27 82.86 75.64 注：加粗数值表示最优分类准确率。
下载: 导出CSV
表 6 MC-GCN在原始数据集在不同通道组合下分类准确率(%)
Table 6. Classification accuracy of the original dataset under different channel combinations (%)
通道数 标准(AC) 多普勒频移(AC) 幅值波动(AC) 窄带射频干扰(AC) 1 2 3 4 5 6 A组 B组 C组 A组 B组 C组 A组 B组 C组 A组 B组 C组 √ √ √ √ √ √ 97.62 96.69 97.74 96.52 97.04 96.53 96.90 97.14 95.78 96.63 96.72 96.81 × √ √ √ √ √ 90.41 91.93 87.62 85.29 89.14 91.28 79.27 84.53 93.49 92.05 85.98 91.68 √ × √ √ √ √ 96.09 95.33 94.19 95.21 94.29 95.18 95.85 95.54 94.02 96.05 95.92 95.48 √ √ × √ √ √ 95.24 94.93 91.72 93.38 92.46 89.41 95.40 94.41 90.94 89.00 95.40 95.83 √ √ √ × √ √ 94.43 93.59 94.24 91.14 93.30 88.31 93.12 91.74 91.06 93.52 92.06 93.01 √ √ √ √ × √ 92.26 93.50 93.45 92.81 93.38 91.72 91.63 93.97 92.01 92.78 91.88 93.85 √ √ √ √ √ × 91.98 91.31 84.08 90.41 88.19 89.69 94.07 87.74 88.61 93.47 92.84 86.98 注：√表示选用当前通道，×表示没有选用当前通道，加粗数值表示最优分类准确率。
下载: 导出CSV
表 7 不同方法在标准场景下跨域分类准确率(%)
Table 7. Cross-domain classification accuracy of different methods in standard scenarios (%)
训练集 方法 A→B B→A A→C C→A B→C C→B 70% MC-GCN 90.91 86.15 80.51 89.41 79.21 86.51 ResNet18 81.28 84.57 79.25 85.37 83.52 84.94 50% MC-GCN 87.75 86.96 89.27 89.56 66.60 85.84 ResNet18 74.39 76.82 68.74 74.58 75.73 77.48 30% MC-GCN 87.10 87.91 79.32 80.75 55.29 79.56 ResNet18 62.54 67.49 63.46 66.57 69.49 68.37 10% MC-GCN 88.94 78.23 74.99 80.56 85.27 84.58 ResNet18 55.97 58.36 52.18 57.43 61.72 60.15
下载: 导出CSV
表 8 计算复杂度
Table 8. Computation complexity
模型 空间复杂度(MB) 时间复杂度(s) MC-GCN 0.157 23 GCN 0.016 10 DCNN 10.535 805
下载: 导出CSV
-
[1] GUO Zhen, WANG Zengfu, LAN Hua, et al. OTHR multitarget tracking with a GMRF model of ionospheric parameters[J]. Signal Processing, 2021, 182: 107940. doi: 10.1016/j.sigpro.2020.107940. [2] LAN Hua, WANG Zengfu, BAI Xianglong, et al. Measurement-level target tracking fusion for over-the-horizon radar network using message passing[J]. IEEE Transactions on Aerospace and Electronic Systems, 2021, 57(3): 1600–1623. doi: 10.1109/TAES.2020.3044109. [3] GUO Zhen, WANG Zengfu, HAO Yuhang, et al. An improved coordinate registration for over-the-horizon radar using reference sources[J]. Electronics, 2021, 10(24): 3086. doi: 10.3390/electronics10243086. [4] WHEADON N S, WHITEHOUSE J C, MILSOM J D, et al. Ionospheric modelling and target coordinate registration for HF sky-wave radars[C]. 1994 Sixth International Conference on HF Radio Systems and Techniques, York, UK, 1994: 258–266. doi: 10.1049/cp:19940504. [5] BARNUM J R and SIMPSON E E. Over-the-horizon radar target registration improvement by terrain feature localization[J]. Radio Science, 1998, 33(4): 1077–1093. doi: 10.1029/98RS00831. [6] TURLEY M D E, GARDINER-GARDEN R S, and HOLDSWORTH D A. High-resolution wide area remote sensing for HF radar track registration[C]. 2013 International Conference on Radar, Adelaide, SA, Australia, 2013: 128–133. doi: 10.1109/RADAR.2013.6651973. [7] JIN Zhenlu, PAN Quan, ZHAO Chunhui, et al. SVM based land/sea clutter classification algorithm[J]. Applied Mechanics and Materials, 2012, 236/237: 1156–1162. doi: 10.4028/www.scientific.net/AMM.236-237.1156. [8] 王俊, 郑彤, 雷鹏, 等. 深度学习在雷达中的研究综述[J]. 雷达学报, 2018, 7(4): 395–411. doi: 10.12000/JR18040.WANG Jun, ZHENG Tong, LEI Peng, et al. Study on deep learning in radar[J]. Journal of Radars, 2018, 7(4): 395–411. doi: 10.12000/JR18040. [9] 何密, 平钦文, 戴然. 深度学习融合超宽带雷达图谱的跌倒检测研究[J]. 雷达学报, 2023, 12(2): 343–355. doi: 10.12000/JR22169.HE Mi, PING Qinwen, and DAI Ran. Fall detection based on deep learning fusing ultrawideband radar spectrograms[J]. Journal of Radars, 2023, 12(2): 343–355. doi: 10.12000/JR22169. [10] CHEN Xiaolong, SU Ningyuan, HUANG Yong, et al. False-alarm-controllable radar detection for marine target based on multi features fusion via CNNs[J]. IEEE Sensors Journal, 2021, 21(7): 9099–9111. doi: 10.1109/JSEN.2021.3054744. [11] LI Can, WANG Zengfu, ZHANG Zhishan, et al. Sea/land clutter recognition for over-the-horizon radar via deep CNN[C]. 2019 International Conference on Control, Automation and Information Sciences, Chengdu, China, 2019: 1–5. doi: 10.1109/ICCAIS46528.2019.9074545. [12] 李灿, 张钰, 王增福, 等. 基于代数多重网格的天波超视距雷达跨尺度地海杂波识别方法[J]. 电子学报, 2022, 50(12): 3021–3029. doi: 10.12263/DZXB.20220389.LI Can, ZHANG Yu, WANG Zengfu, et al. Cross-scale land/sea clutter classification method for over-the-horizon radar based on algebraic multigrid[J]. Acta Electronica Sinica, 2022, 50(12): 3021–3029. doi: 10.12263/DZXB.20220389. [13] ZHANG Xiaoxuan, WANG Zengfu, LU Kun, et al. Data augmentation and classification of sea-land clutter for over-the-horizon radar using AC-VAEGAN[J]. IEEE Transactions on Geoscience and Remote Sensing, 2023, 61: 5104416. doi: 10.1109/TGRS.2023.3274296. [14] ZHANG Xiaoxuan, LI Yang, PAN Quan, et al. Triple loss adversarial domain adaptation network for cross-domain sea-land clutter classification[J]. IEEE Transactions on Geoscience and Remote Sensing, 2023, 61: 5110718. doi: 10.1109/TGRS.2023.3328302. [15] ZHANG Xiaoxuan, WANG Zengfu, JI Mingyue, et al. A sea-land clutter classification framework for over-the-horizon radar based on weighted loss semi-supervised generative adversarial network[J]. Engineering Applications of Artificial Intelligence, 2024, 133: 108526. doi: 10.1016/j.engappai.2024.108526. [16] ZHOU Jie, CUI Ganqu, HU Shengding, et al. Graph neural networks: A review of methods and applications[J]. AI Open, 2020, 1: 57–81. doi: 10.1016/j.aiopen.2021.01.001. [17] WU Zonghan, PAN Shirui, CHEN Fengwen, et al. A comprehensive survey on graph neural networks[J]. IEEE Transactions on Neural Networks and Learning Systems, 2021, 32(1): 4–24. doi: 10.1109/TNNLS.2020.2978386. [18] WU Lingfei, CHEN Yu, SHEN Kai, et al. Graph neural networks for natural language processing: A survey[J]. Foundations and Trends® in Machine Learning, 2023, 16(2): 119–328. doi: 10.1561/2200000096. [19] YUAN Hao, YU Haiyang, GUI Shurui, et al. Explainability in graph neural networks: A taxonomic survey[J]. IEEE Transactions on Pattern Analysis and Machine Intelligence, 2023, 45(5): 5782–5799. doi: 10.1109/TPAMI.2022.3204236. [20] SU Ningyuan, CHEN Xiaolong, GUAN Jian, et al. Maritime target detection based on radar graph data and graph convolutional network[J]. IEEE Geoscience and Remote Sensing Letters, 2022, 19: 4019705. doi: 10.1109/LGRS.2021.3133473. [21] SU Ningyuan, CHEN Xiaolong, GUAN Jian, et al. Radar maritime target detection via spatial-temporal feature attention graph convolutional network[J]. IEEE Transactions on Geoscience and Remote Sensing, 2024, 62: 5102615. doi: 10.1109/TGRS.2024.3358862. [22] LANG Ping, FU Xiongjun, DONG Jian, et al. A novel radar signals sorting method via residual graph convolutional network[J]. IEEE Signal Processing Letters, 2023, 30: 753–757. doi: 10.1109/LSP.2023.3287404. [23] FENT F, BAUERSCHMIDT P, and LIENKAMP M. RadarGNN: Transformation invariant graph neural network for radar-based perception[C]. The IEEE/CVF Conference on Computer Vision and Pattern Recognition Workshops, Vancouver, BC, Canada, 2023: 182–191. doi: 10.1109/CVPRW59228.2023.00023. [24] VELIČKOVIĆ P. Everything is connected: Graph neural networks[J]. Current Opinion in Structural Biology, 2023, 79: 102538. doi: 10.1016/j.sbi.2023.102538. [25] XIAO Shunxin, WANG Shiping, DAI Yuanfei, et al. Graph neural networks in node classification: Survey and evaluation[J]. Machine Vision and Applications, 2022, 33(1): 4. doi: 10.1007/s00138-021-01251-0. [26] NIVEN E B and DEUTSCH C V. Calculating a robust correlation coefficient and quantifying its uncertainty[J]. Computers & Geosciences, 2012, 40: 1–9. doi: 10.1016/j.cageo.2011.06.021. [27] KIPF T N and WELLING M. Semi-supervised classification with graph convolutional networks[EB/OL]. https://arxiv.org/abs/1609.02907, 2017. [28] CAI Lei, LI Jundong, WANG Jie, et al. Line graph neural networks for link prediction[J]. IEEE Transactions on Pattern Analysis and Machine Intelligence, 2022, 44(9): 5103–5113. doi: 10.1109/TPAMI.2021.3080635. [29] XIE Yu, LIANG Yanfeng, GONG Maoguo, et al. Semisupervised graph neural networks for graph classification[J]. IEEE Transactions on Cybernetics, 2023, 53(10): 6222–6235. doi: 10.1109/TCYB.2022.3164696. [30] LIAO Wenlong, BAK-JENSEN B, PILLAI J R, et al. A review of graph neural networks and their applications in power systems[J]. Journal of Modern Power Systems and Clean Energy, 2022, 10(2): 345–360. doi: 10.35833/MPCE.2021.000058. [31] MCPHERSON M, SMITH-LOVIN L, and COOK J M. Birds of a feather: Homophily in social networks[J]. Annual Review of Sociology, 2001, 27: 415–444. doi: 10.1146/annurev.soc.27.1.415. [32] VELIČKOVIĆ P, CUCURULL G, CASANOVA A, et al. Graph attention networks[EB/OL]. https://doi.org/10.48550/arXiv.1710.10903, 2017. [33] DU Jian, ZHANG Shanghang, WU Guanhang, et al. Topology adaptive graph convolutional networks[EB/OL]. https://doi.org/10.48550/arXiv.1710.10370, 2018. -
计量
- 文章访问数: 214
- HTML全文浏览量: 86
- PDF下载量: 181
- 被引次数: 0
