机载雷达脉间波形参数伪随机跳变技术

崔国龙; 樊涛; 孔昱凯; 余显祥; 沙明辉; 孔令讲

doi:10.12000/JR21189

机载雷达脉间波形参数伪随机跳变技术

DOI: 10.12000/JR21189

1.
电子科技大学信息与通信工程学院成都 611731
2.
北京无线电测量研究所北京 100854

基金项目: 国家自然科学基金(61771109, U19B2017, 62101097)，长江学者奖励计划，中国博士后科学基金(2020M680147, 2021T140096)

详细信息

作者简介:
崔国龙(1982–)，男，安徽人，电子科技大学教授，博士生导师，《雷达学报》编委。研究方向为最优化理论和算法、雷达目标检测理论、波形多样性以及阵列信号处理等

樊　涛(1997–)，男，江西人，电子科技大学在读博士生。研究方向为雷达波形设计与处理、最优化理论和算法以及雷达杂波抑制等

孔昱凯(1996–)，男，河南人，电子科技大学在读博士生。研究方向为雷达杂波抑制、干扰智能认知以及雷达抗干扰波形设计等

余显祥(1991–)，男，四川人，电子科技大学博士后。研究方向为雷达波形设计与处理、最优化理论算法以及阵列信号处理等

沙明辉(1986–)，男，研究员。研究方向为雷达抗干扰和信号处理等

孔令讲(1974–)，男，河南人，电子科技大学教授，博士生导师，《雷达学报》编委。研究方向为新体制雷达、统计信号处理、优化理论和算法、雷达信号处理、非合作信号处理技术和自适应阵列信号处理等

通讯作者:
崔国龙 cuiguolong@uestc.edu.cn

责任主编：廖桂生 Corresponding Editor: LIAO Guisheng
中图分类号: TN958
计量
- 文章访问数: 2051
- HTML全文浏览量: 939
- PDF下载量: 302
- 被引次数: 0
出版历程
- 收稿日期: 2021-11-26
- 修回日期: 2022-03-10
- 网络出版日期: 2022-04-11
- 刊出日期: 2022-04-28

Pseudo-random Agility Technology for Interpulse Waveform Parameters in Airborne Radar

1.
School of Information and Communication Engineering, University of Electronic Science and Technology of China, Chengdu 611731, China
2.
Beijing Institute of Radio Measurement, Beijing 100854, China

Funds: The National Natural Science Foundation of China (61771109, U19B2017, 62101097), The Chang Jiang Scholars Program, China Postdoctoral Science Foundation (2020M680147, 2021T140096)

More Information

Corresponding author: CUI Guolong, cuiguolong@uestc.edu.cn

摘要

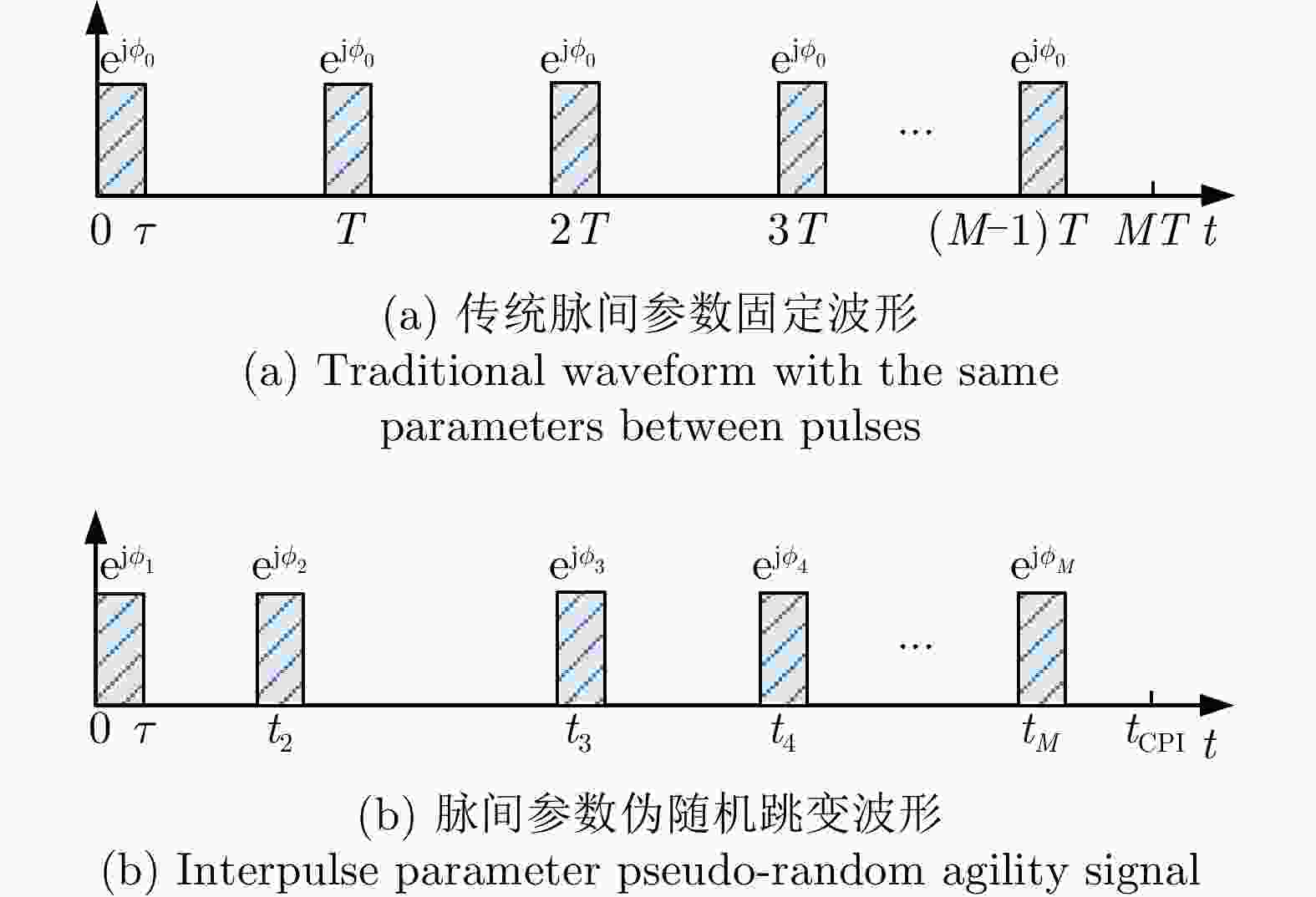
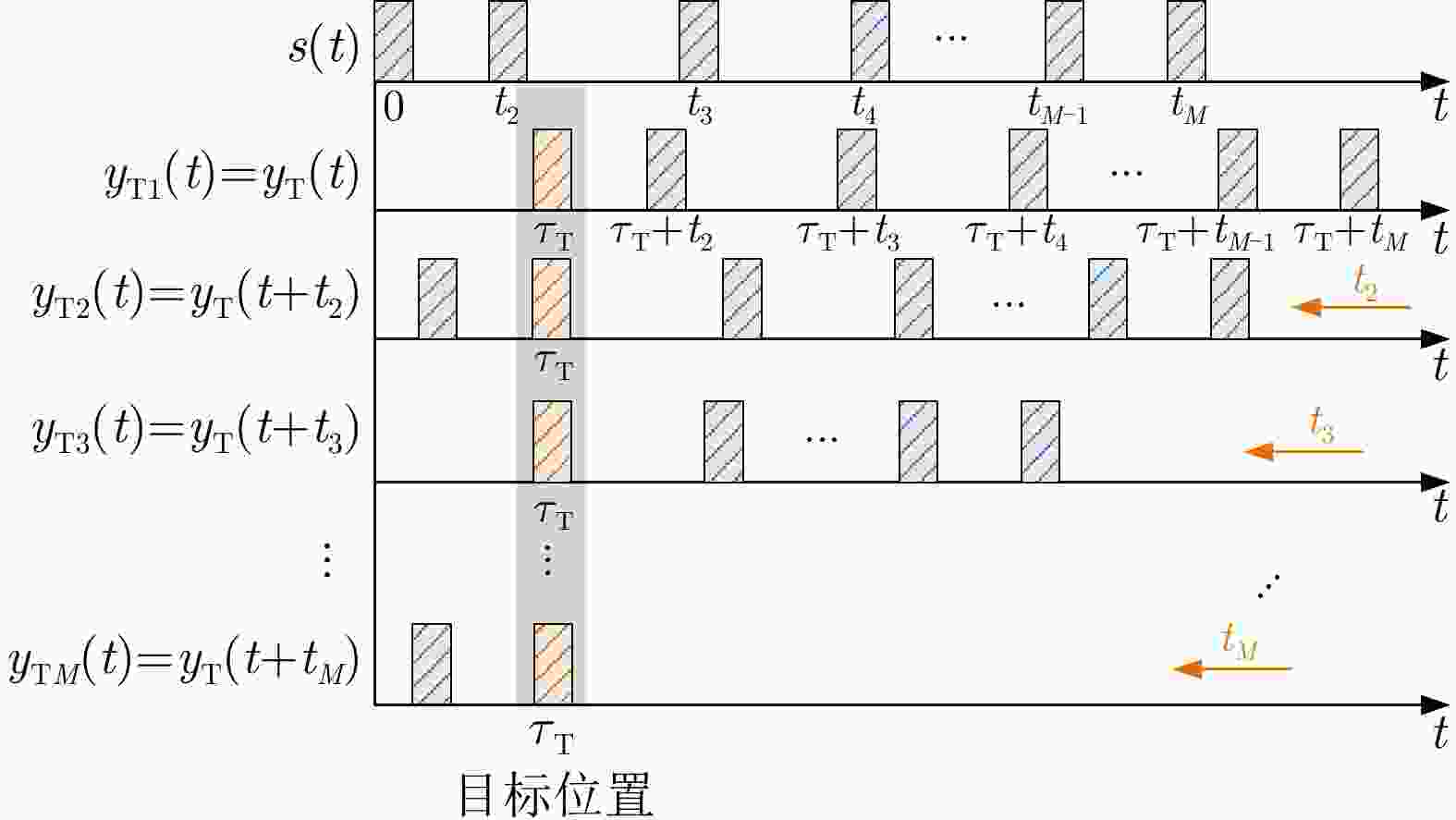
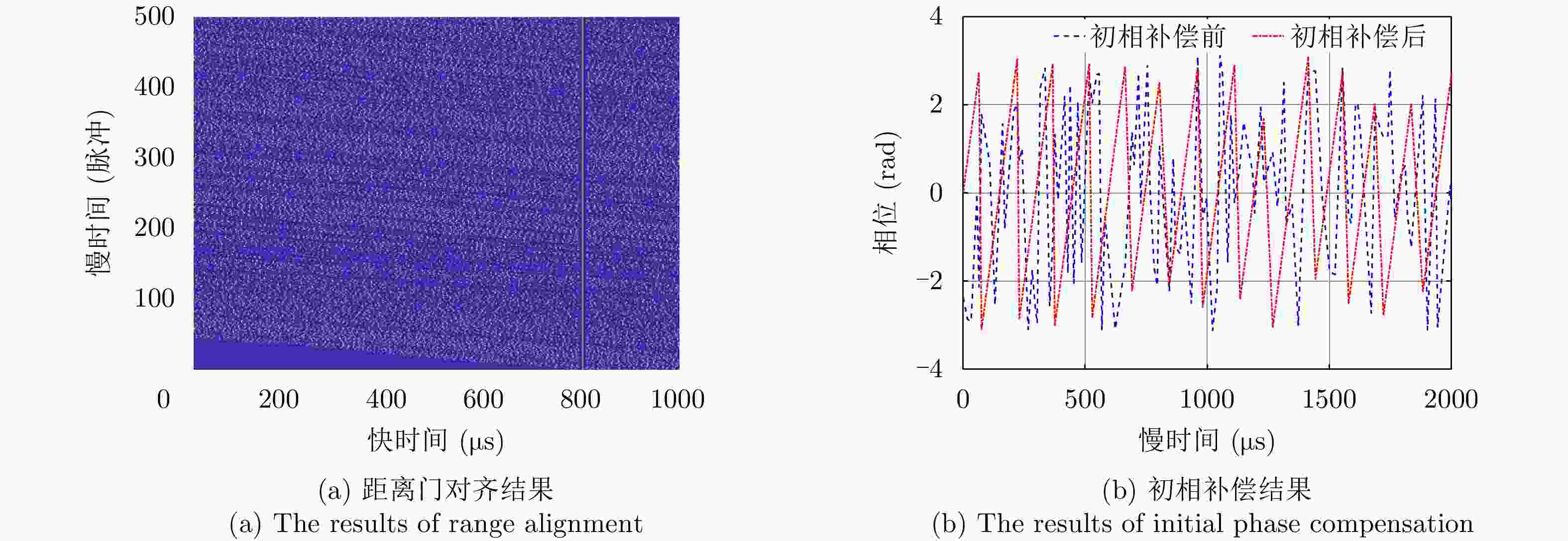
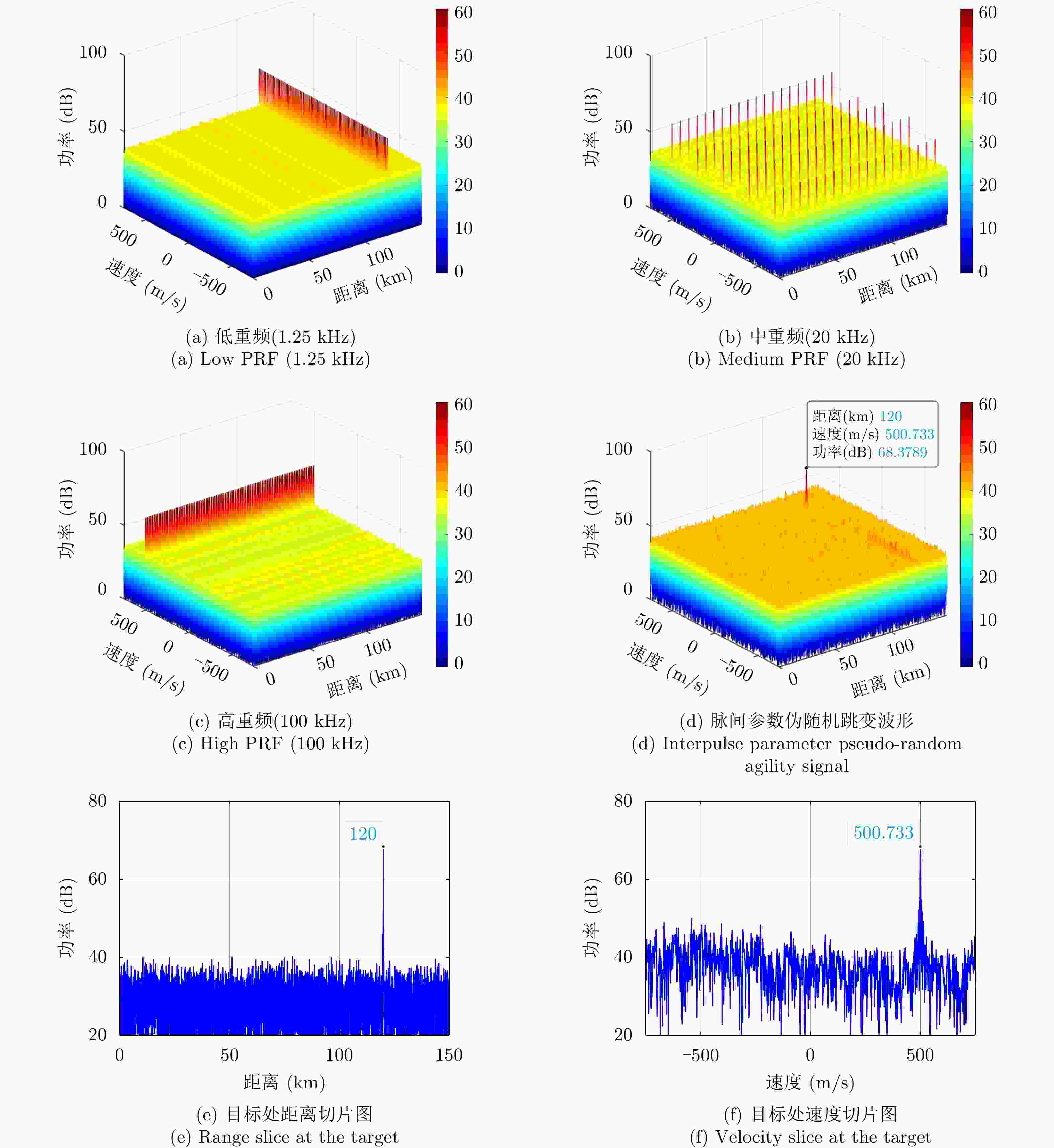
摘要: 机载雷达脉间波形参数伪随机跳变主要是通过优化设计脉冲重复间隔、初相、频率和幅度等参数，增加雷达波形的复杂度与不确定性，提升机载雷达反杂波和抗干扰能力，是机载雷达技术的主要发展方向之一。脉间参数的伪随机跳变给多脉冲相参积累、杂波谱特性建模等带来困难。该文建立了脉间参数伪随机跳变信号模型，提出了非均匀参数捷变脉间相参处理方法，并分析了抗干扰性能。在此基础上，研究了脉冲重复间隔捷变下的机载雷达杂波回波模型，提出了发射-接收滤波器联合优化设计的强杂波处理方法，并进行了仿真验证。
- 机载雷达 /
- 脉间波形 /
- 伪随机跳变 /
- 相参处理 /
- 杂波抑制
Abstract: The pseudo-random agility technology for interpulse waveform parameters in airborne radar increases the complexity and uncertainty of radar waveform and improves its anti-clutter and anti-interference ability by optimizing the pulse repetition interval, initial phase, frequency, and amplitude, which is one of the main developmental directions of airborne radar technology. The pseudo-random agility of interpulse parameters makes multi-pulse coherent accumulation and modeling of clutter spectrum characteristics difficult. In this paper, a pseudo-random agility signal model of interpulse parameters is established. Furthermore, a non-uniform parameter coherent processing method is proposed, and the anti-interference performance is analyzed. Based on the analysis, the clutter echo model of airborne radar with random pulse repetition interval is studied, and a joint transmitter-receiver filter design is proposed for strong clutter processing. Finally, numerical simulation is conducted to verify the results.
- Airborne radar /
- Interpulse waveform /
- Pseudo-random agility /
- Coherent processing /
- Clutter suppression

HTML全文

图 1 机载雷达探测场景示意图

Figure 1. Schematic diagram of airborne radar detection scene

下载: 全尺寸图片幻灯片

图 2 发射波形示意图

Figure 2. Diagrams of the transmitted waveforms

下载: 全尺寸图片幻灯片

图 3 脉间波形参数伪随机跳变信号相参处理流程

Figure 3. Coherent processing flow of interpulse parameter pseudo-random agility signal

下载: 全尺寸图片幻灯片

图 4 点目标距离门对齐示意图

Figure 4. Schematic diagram of point target range alignment

下载: 全尺寸图片幻灯片

图 5 距离门对齐和初相补偿处理结果

Figure 5. The results of range alignment and initial phase compensation

下载: 全尺寸图片幻灯片

图 6 相参积累结果

Figure 6. The results of coherent processing

下载: 全尺寸图片幻灯片

图 7 目标速度维结果

Figure 7. Target velocity dimension results

下载: 全尺寸图片幻灯片

图 8 欺骗干扰白化示意图

Figure 8. Schematic diagram of deception interference with whitening

下载: 全尺寸图片幻灯片

图 9 抗干扰效果

Figure 9. Anti-interference effect

下载: 全尺寸图片幻灯片

图 10 机载雷达杂波单元划分示意图

Figure 10. Schematic diagram of airborne radar clutter unit division

下载: 全尺寸图片幻灯片

图 11 机载雷达杂波谱

Figure 11. Clutter spectrum of airborne radar

下载: 全尺寸图片幻灯片

图 12 SGO算法收敛曲线

Figure 12. Convergence curve of SGO algorithm

下载: 全尺寸图片幻灯片

图 13 模糊函数比较

Figure 13. Contrast of ambiguity function

下载: 全尺寸图片幻灯片

图 14 机载雷达杂波抑制结果

Figure 14. The results of airborne radar clutter suppression

下载: 全尺寸图片幻灯片

表 1 杂波仿真参数

Table 1. Clutter simulation parameters

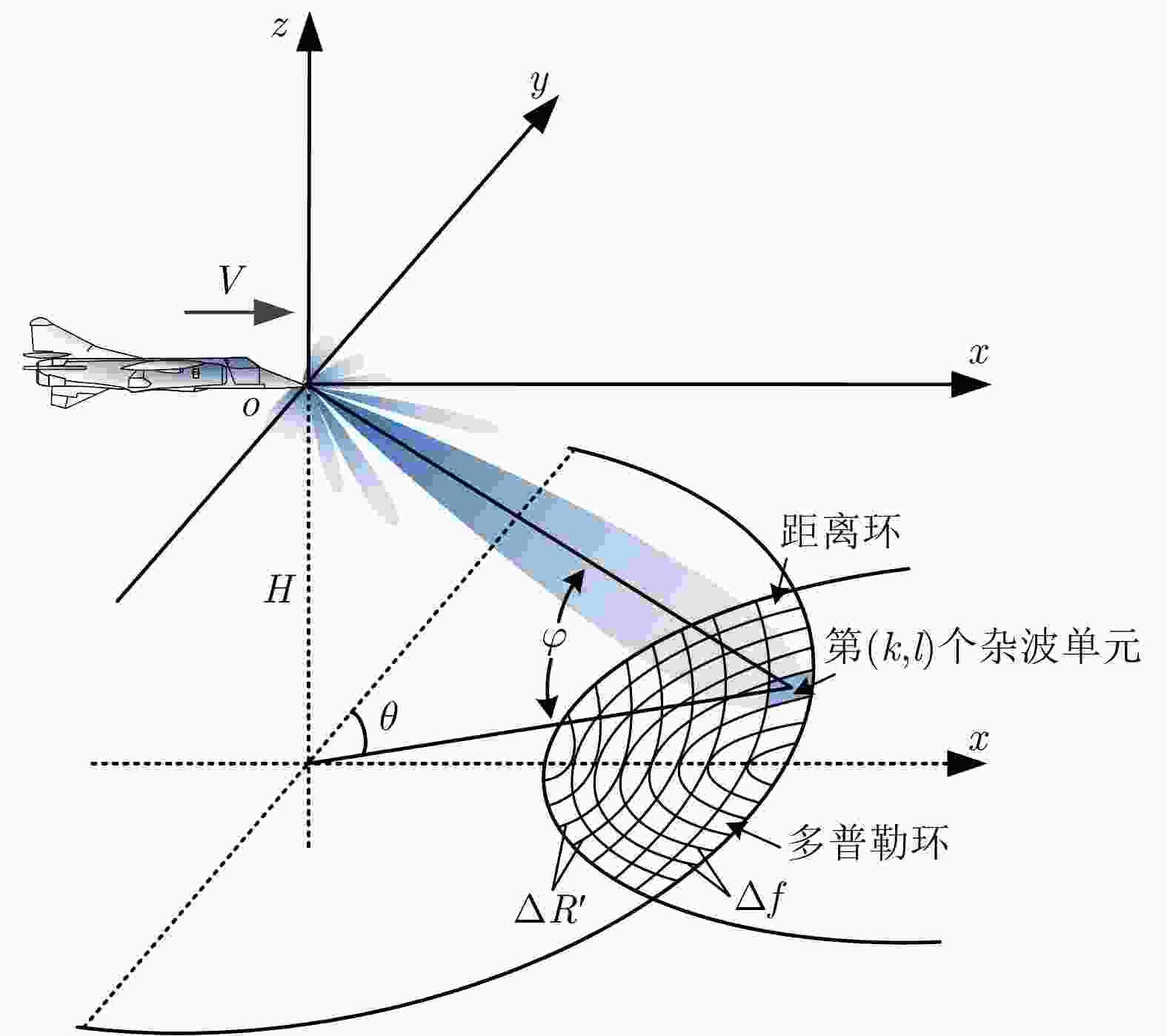
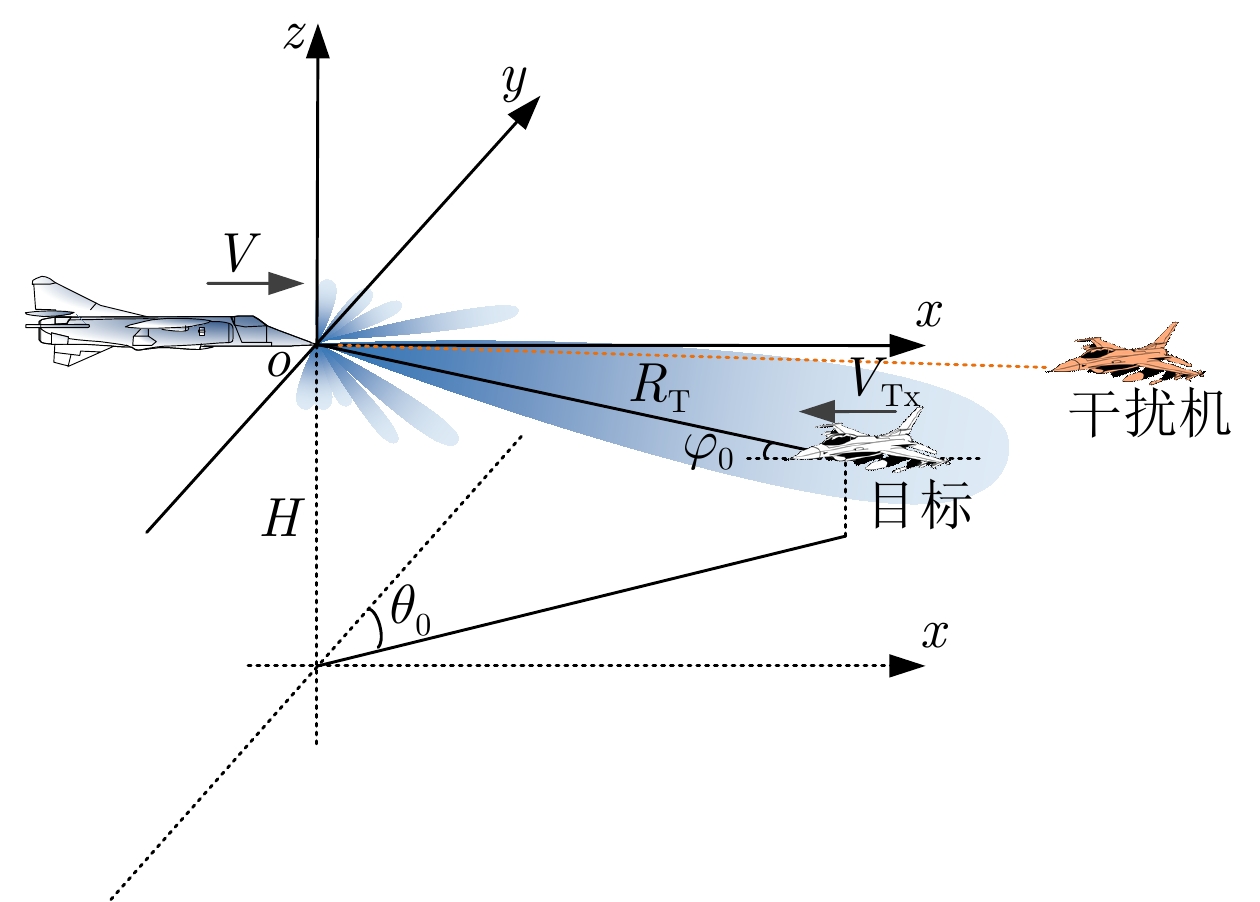
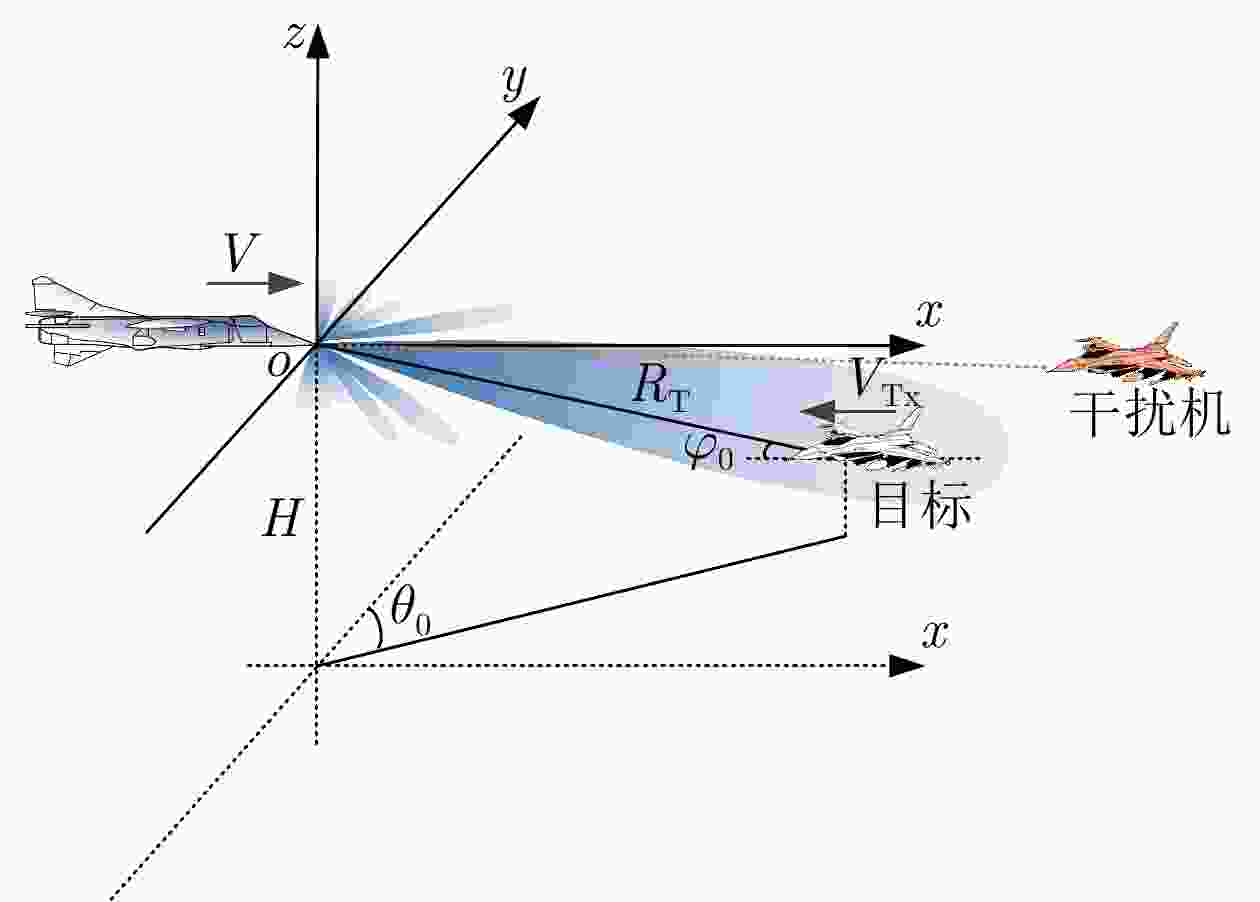
参数	数值	参数	数值
波长$\lambda $	0.03 m	载机高度$H$	8 km
相控阵规模$N \times N$	40×40	载机速度$V$	140 m/s
阵元间隔$d$	${\lambda \mathord{\left/ {\vphantom {\lambda 2}} \right. } 2}$	距离环间隔$\Delta R$	15 m
波束指向$\left({\theta }_{0},\,{\varphi }_{0}\right)$	(2°, –10°)	多普勒环间隔$\Delta f$	100 Hz
阵元加权类型	泰勒加权	最大多普勒频率${f_m}$	${{4V} \mathord{\left/ {\vphantom {{4V} \lambda }} \right. } \lambda }$
波束最大增益$G$	30 dB	杂波后向散射率模型	Morchin模型^[38]
雷达发射功率${P_{\text{T}}}$	10 kW	噪声功率$\sigma _{\text{w}}^2$	–130 dBW

下载: 导出CSV

参考文献(39)

[1]	SKOLNIK M I. Radar Handbook[M]. 3rd ed. New York: McGraw-Hill, 2008.
[2]	STIMSON G W. Introduction to Airborne Radar[M]. 2nd ed. Mendham: SciTech Publishing, Inc. , 1998.
[3]	AUBRY A, DE MAIO A, JIANG Bo, et al. Ambiguity function shaping for cognitive radar via complex quartic optimization[J]. IEEE Transactions on Signal Processing, 2013, 61(22): 5603–5619. doi: 10.1109/TSP.2013.2273885
[4]	ALHUJAILI K, MONGA V, and RANGASWAMY M. Quartic gradient descent for tractable radar slow-time ambiguity function shaping[J]. IEEE Transactions on Aerospace and Electronic Systems, 2020, 56(2): 1474–1489. doi: 10.1109/TAES.2019.2934336
[5]	NAGHSH M M, SOLTANALIAN M, STOICA P, et al. A doppler robust design of transmit sequence and receive filter in the presence of signal-dependent interference[J]. IEEE Transactions on Signal Processing, 2014, 62(4): 772–785. doi: 10.1109/TSP.2013.2288082
[6]	全英汇, 方文, 沙明辉, 等. 频率捷变雷达波形对抗技术现状与展望[J]. 系统工程与电子技术, 2021, 43(11): 3126–3136. doi: 10.12305/j.issn.1001-506X.2021.11.11 QUAN Yinghui, FANG Wen, SHA Minghui, et al. Present situation and prospects of frequency agility radar waveform countermeasures[J]. Systems Engineering and Electronics, 2021, 43(11): 3126–3136. doi: 10.12305/j.issn.1001-506X.2021.11.11
[7]	LONG Xingwang, LI Kun, TIAN Jing, et al. Ambiguity function analysis of random frequency and PRI agile signals[J]. IEEE Transactions on Aerospace and Electronic Systems, 2021, 57(1): 382–396. doi: 10.1109/TAES.2020.3016851
[8]	吴耀君. 脉间频率捷变雷达抗干扰研究[D]. [硕士论文], 西安电子科技大学, 2018. WU Yaojun. Research on anti-jamming performance of frequency agility radar[D]. [Master dissertation], Xidian University, 2018.
[9]	HUANG Tianyao, LIU Yimin, MENG Huadong, et al. Cognitive random stepped frequency radar with sparse recovery[J]. IEEE Transactions on Aerospace and Electronic Systems, 2014, 50(2): 858–870. doi: 10.1109/TAES.2013.120443
[10]	DE MAIO A, DE NICOLA S, HUANG Yongwei, et al. Design of phase codes for radar performance optimization with a similarity constraint[J]. IEEE Transactions on Signal Processing, 2009, 57(2): 610–621. doi: 10.1109/TSP.2008.2008247
[11]	崔国龙, 余显祥, 杨婧, 等. 认知雷达波形优化设计方法综述[J]. 雷达学报, 2019, 8(5): 537–557. doi: 10.12000/JR19072 CUI Guolong, YU Xianxiang, YANG Jing, et al. An overview of waveform optimization methods for cognitive radar[J]. Journal of Radars, 2019, 8(5): 537–557. doi: 10.12000/JR19072
[12]	LIN K. Anti-jamming MTI radar using variable pulse-codes[D]. [Master dissertation], Massachusetts Institute of Technology, 2002.
[13]	苏峰, 高梅国, 田黎育, 等. 基于脉间码型捷变的相位编码旁瓣抑制方法[J]. 北京理工大学学报, 2009, 29(5): 441–445. SU Feng, GAO Meiguo, TIAN Liyu, et al. Sidelobe suppression of phase-coded radar signal based on interpulse code agility[J]. Transactions of Beijing Institute of Technology, 2009, 29(5): 441–445.
[14]	ZHANG Jindong, ZHU Daiyin, and ZHANG Gong. New antivelocity deception jamming technique using pulses with adaptive initial phases[J]. IEEE Transactions on Aerospace and Electronic Systems, 2013, 49(2): 1290–1330. doi: 10.1109/TAES.2013.6494414
[15]	XIONG Wei, WANG Xinhai, and ZHANG Gong. Cognitive waveform design for anti-velocity deception jamming with adaptive initial phases[C]. 2016 IEEE Radar Conference, Philadelphia, USA, 2016: 1–5.
[16]	吴健. 基于波形分集的雷达抗有源欺骗干扰技术研究[D]. [硕士学位], 电子科技大学, 2015: 48–64. WU Jian. Research of technology against radar active deception jamming based on waveform diversity[D]. [Master dissertation], University of Electronic Science and Technology of China, 2015: 48–64.
[17]	YANG Ya, WU Jian, CUI Guolong, et al. Optimized phase-coded waveform design against velocity deception[C]. 2015 IEEE Radar Conference, Arlington, USA, 2015: 400–404.
[18]	葛鹏. 基于知识辅助的雷达波形设计算法研究[D]. [博士论文], 电子科技大学, 2017: 60–97. GE Peng. Research on methods of knowledge-aided radar waveform design[D]. [Ph. D. dissertation], University of Electronic Science and Technology of China, 2017: 60–97.
[19]	张洋, 位寅生. 基于认知的抗折叠扩展杂波波形设计方法[J]. 系统工程与电子技术, 2018, 40(10): 2216–2222. doi: 10.3969/j.issn.1001-506X.2018.10.09 ZHANG Yang and WEI Yinsheng. Waveform design of range-folded spread clutter mitigation based on cognition[J]. Systems Engineering and Electronics, 2018, 40(10): 2216–2222. doi: 10.3969/j.issn.1001-506X.2018.10.09
[20]	葛萌萌, 余显祥, 严正欣, 等. 脉间波形幅相联合设计抗欺骗干扰方法[J]. 电子科技大学学报, 2021, 50(4): 481–487. doi: 10.12178/1001-0548.2021075 GE Mengmeng, YU Xianxiang, YAN Zhengxin, et al. Optimized amplitude-phase waveform against deceptive jamming[J]. Journal of University of Electronic Science and Technology of China, 2021, 50(4): 481–487. doi: 10.12178/1001-0548.2021075
[21]	AUBRY A, DEMAIO A, FARINA A, et al. Knowledge-aided (potentially cognitive) transmit signal and receive filter design in signal-dependent clutter[J]. IEEE Transactions on Aerospace and Electronic Systems, 2013, 49(1): 93–117. doi: 10.1109/TAES.2013.6404093
[22]	黄琼丹, 李勇, 卢光跃. 脉间Costas跳频脉内多载波混沌相位编码雷达信号设计与分析[J]. 电子与信息学报, 2015, 37(6): 1483–1489. doi: 10.11999/JEIT140653 HUANG Qiongdan, LI Yong, and LU Guangyue. Design and analysis of inter-pulse costas frequency hopping and intra-pulse multi-carrier chaotic phase coded radar signal[J]. Journal of Electronics &Information Technology, 2015, 37(6): 1483–1489. doi: 10.11999/JEIT140653
[23]	TANG Bo and TANG Jun. Joint design of transmit waveforms and receive filters for MIMO radar space-time adaptive processing[J]. IEEE Transactions on Signal Processing, 2016, 64(18): 4707–4722. doi: 10.1109/TSP.2016.2569431
[24]	GE Mengmeng, YU Xianxiang, YAN Zhengxin, et al. Joint cognitive optimization of transmit waveform and receive filter against deceptive interference[J]. Signal Processing, 2021, 185: 108084. doi: 10.1016/j.sigpro.2021.108084
[25]	TANG Bo, LI Jun, ZHANG Yu, et al. Design of MIMO radar waveform covariance matrix for clutter and jamming suppression based on space time adaptive processing[J]. Signal Processing, 2016, 121: 60–69. doi: 10.1016/j.sigpro.2015.10.033
[26]	TANG Bo, TUCK J, and STOICA P. Polyphase waveform design for MIMO radar space time adaptive processing[J]. IEEE Transactions on Signal Processing, 2020, 68: 2143–2154. doi: 10.1109/TSP.2020.2983833
[27]	CUI Guolong, FU Yue, YU Xianxiang, et al. Robust transmitter-receiver design in the presence of signal-dependent clutter[J]. IEEE Transactions on Aerospace and Electronic Systems, 2018, 54(4): 1871–1882. doi: 10.1109/TAES.2018.2805147
[28]	YU Xianxiang, CUI Guolong, YANG Jing, et al. MIMO radar transmit-receive design for moving target detection in signal-dependent clutter[J]. IEEE Transactions on Vehicular Technology, 2020, 69(1): 522–536. doi: 10.1109/TVT.2019.2951399
[29]	FAN Tao, GE Mengmeng, GAN Na, et al. Transmit-receive design for non-uniform pulse repetition interval airborne radar in the presence of signal-dependent clutter[C]. 2020 IEEE Radar Conference, Florence, Italy, 2020: 1–6.
[30]	MAIER M W. Non-uniform PRI pulse-Doppler radar[C]. The 1993 (25th) Southeastern Symposium on System Theory, Tuscaloosa, USA, 1993: 164–168.
[31]	FAN Tao, KONG Yukai, WANG Mingxing, et al. Doppler filter bank design for non-uniform PRI radar in signal-dependent clutter[C]. 2021 IEEE Radar Conference, Atlanta, USA, 2021: 1–5.
[32]	KAVEH M and COOPER G R. Average ambiguity function for a randomly staggered pulse sequence[J]. IEEE Transactions on Aerospace and Electronic Systems, 1976, AES-12(3): 410–413. doi: 10.1109/TAES.1976.308245
[33]	LIU Zhen, WEI Xizhang, and LI Xiang. Aliasing-free moving target detection in random pulse repetition interval radar based on compressed sensing[J]. IEEE Sensors Journal, 2013, 13(7): 2523–2534. doi: 10.1109/JSEN.2013.2249762
[34]	刘振, 魏玺章, 黎湘. 一种新的随机PRI脉冲多普勒雷达无模糊MTD算法[J]. 雷达学报, 2012, 1(1): 28–35. doi: 10.3724/SP.J.1300.2012.10063 LIU Zhen, WEI Xizhang, and LI Xiang. Novel method of unambiguous moving target detection in pulse-Doppler radar with random pulse repetition interval[J]. Journal of Radars, 2012, 1(1): 28–35. doi: 10.3724/SP.J.1300.2012.10063
[35]	KONG Yukai, CUI Guolong, GUO Shisheng, et al. Coherent radar detection framework with non-uniform pulse repetition intervals[J]. IEEE Access, 2020, 8: 18645–18657. doi: 10.1109/ACCESS.2019.2963374
[36]	LU Yuxiang, TANG Ziyue, ZHANG Yuanpeng, et al. Maximum unambiguous frequency of random PRI radar[C]. 2016 CIE International Conference on Radar, Guangzhou, China, 2016: 1–5.
[37]	JAO J K and GOGGINS W B. Efficient, closed-form computation of airborne pulse-Doppler radar clutter[C]. Proceedings of IEEE International Radar Conference, Arlington, USA, 1985: 17–22.
[38]	MORCHIN W C. Airborne Early Warning Radar[M]. Boston: Artech House, 1990.
[39]	FAN Tao, YU Xianxiang, GAN Na, et al. Transmit-receive design for airborne radar with nonuniform pulse repetition intervals[J]. IEEE Transactions on Aerospace and Electronic Systems, 2021, 57(6): 4067–4084. doi: 10.1109/TAES.2021.3090915