一种基于多维交替方向乘子法的多输入多输出逆合成孔径雷达成像方法

邓理康; 张双辉; 张弛; 刘永祥

doi:10.12000/JR20132

一种基于多维交替方向乘子法的多输入多输出逆合成孔径雷达成像方法

DOI: 10.12000/JR20132

国防科技大学电子科学学院长沙 410073

基金项目: 国家自然科学基金(61801484, 61921001)

详细信息

作者简介:
邓理康(1991–)，男，福建建阳人，国防科技大学电子科学学院在读研究生，研究方向为双站雷达成像、MIMO雷达成像

张双辉(1989–)，男，湖南长沙人，博士，国防科技大学电子科学学院副研究员，研究方向为雷达成像、压缩感知、贝叶斯推断

张　弛(1994–)，男，湖北孝感人，国防科技大学电子科学学院在读博士生，研究方向为雷达成像、压缩感知、贝叶斯学习

刘永祥(1976–)，男，河北唐山人，博士，国防科技大学电子科学学院教授，博士生导师，研究方向为目标微动特性分析与识别

通讯作者:
张双辉 shzhang3@126.com

责任主编：张弓 Corresponding Editor: ZHANG Gong
中图分类号: TN957.51
计量
- 文章访问数: 1401
- HTML全文浏览量: 712
- PDF下载量: 171
- 被引次数: 0
出版历程
- 收稿日期: 2020-10-19
- 修回日期: 2021-01-27
- 网络出版日期: 2021-02-08
- 刊出日期: 2021-06-28

A Multiple-Input Multiple-Output Inverse Synthetic Aperture Radar Imaging Method Based on Multidimensional Alternating Direction Method of Multipliers

College of Electronic Science and Technology, National University of Defense Technology, Changsha 410073, China

Funds: The National Natural Science Foundation of China (61801484, 61921001)

More Information

Corresponding author: ZHANG Shuanghui, shzhang3@126.com

摘要

摘要: 基于傅里叶变换的传统逆合成孔径雷达(ISAR)成像方法存在数据存储量大、数据采集时间长的问题。压缩感知(CS)理论利用图像的稀疏性，可以利用有限的数据恢复图像，这极大降低了数据采集成本。但对于多维数据，传统压缩感知方法要将多维数据转化成一维向量，这造成了很大存储和计算负担。因此，该文提出一种基于多维度-交替方向乘子法(MD-ADMM)的多输入多输出-逆合成孔径雷达(MIMO-ISAR)成像快速稀疏重建方法。首先建立基于张量信号的压缩感知模型，然后用ADMM算法对模型进行优化，将测量矩阵分解为张量模态积，用张量元素除法替代矩阵求逆，显著减少所需的内存和计算负担。该方法只需少量的数据采样，就能实现快速成像。与其他基于张量的压缩感知方法相比，该方法具有鲁棒性强、图像质量好、计算效率高的优点。仿真和实测数据验证了该方法的有效性。
- 多维度-交替方向乘子法 /
- 压缩感知 /
- 多输入多输出-逆合成孔径雷达
Abstract: The disadvantages of the traditional Inverse Synthetic Aperture Radar (ISAR) imaging method based on Fourier transform include large data storage and long collection time. The Compressive Sensing (CS) theory can use limited data to restore an image with the sparsity of the image, reducing the cost of data collection. However for multidimensional data, the traditional compressive sensing methods need to convert three-dimensional data into a one-dimensional vector, causing the storage and calculation burden. Therefore, this study proposes a fast MultiDimensional Alternating Direction Method of Multipliers ((MD-ADMM)) sparse reconstruction method for Multiple-Input Multiple-Output ISAR (MIMO-ISAR) imaging. The CS model based on the tensor signal was established, and the model with the ADMM algorithm was optimized. The measured matrix is decomposed into a tensor modal product, and matrix inversion is replaced by tensor element division, significantly reducing memory consumption and computational burden. Fast ISAR imaging can be achieved by a small amount of data sampling by the proposed method. Compared with other tensor compressed sensing methods, this method has the advantages of stronger robustness, higher image quality, and computational efficiency. The effectiveness of the proposed method can be invalidated by simulated and measured data.

HTML全文

图 1 成像场景图

Figure 1. Geometry of imaging

下载: 全尺寸图片幻灯片

图 2 线性收发阵元的等效收发阵元示意图

Figure 2. The equivalent transceiver array element for linear receiving and transmitting array elements

下载: 全尺寸图片幻灯片

图 3 目标移动示意图

Figure 3. Motion of the target

下载: 全尺寸图片幻灯片

图 4 仿真目标三维散点图

Figure 4. 3D scatter of simulation target

下载: 全尺寸图片幻灯片

图 5 完整回波数据图像三视图

Figure 5. Three views of image with the complete echo

下载: 全尺寸图片幻灯片

图 6 回波采样形式

Figure 6. Undersampling masks of random sampling and block sampling

下载: 全尺寸图片幻灯片

图 7 稀疏度为50.0%时图像

Figure 7. Image when sparsity is 50.0%

下载: 全尺寸图片幻灯片

图 8 稀疏度为33.3%时的图像

Figure 8. Image when sparsity is 33.3%

下载: 全尺寸图片幻灯片

图 9 稀疏度为25.0%时的图像

Figure 9. Image when sparsity is 25.0%

下载: 全尺寸图片幻灯片

图 10 稀疏度为50.0%的块稀疏采样图像

Figure 10. The image of a sparsity of 50.0% by block sampling

下载: 全尺寸图片幻灯片

图 11 稀疏度为25.0%信噪比为–5 dB的图像

Figure 11. The image when sparsity is 25.0% and SNR=–5 dB

下载: 全尺寸图片幻灯片

图 12 稀疏度为25.0%信噪比为0 dB图像

Figure 12. The image when sparsity is 25.0% and SNR=0 dB

下载: 全尺寸图片幻灯片

图 13 稀疏度为25.0%信噪比为10 dB的图像

Figure 13. The image when sparsity is 25.0% and SNR=10 dB

下载: 全尺寸图片幻灯片

图 14 实测数据结果

Figure 14. Measured ISAR data results

下载: 全尺寸图片幻灯片

图 15 信噪比为0 dB实测数据结果

Figure 15. Measured ISAR data results under SNR=0 dB

下载: 全尺寸图片幻灯片

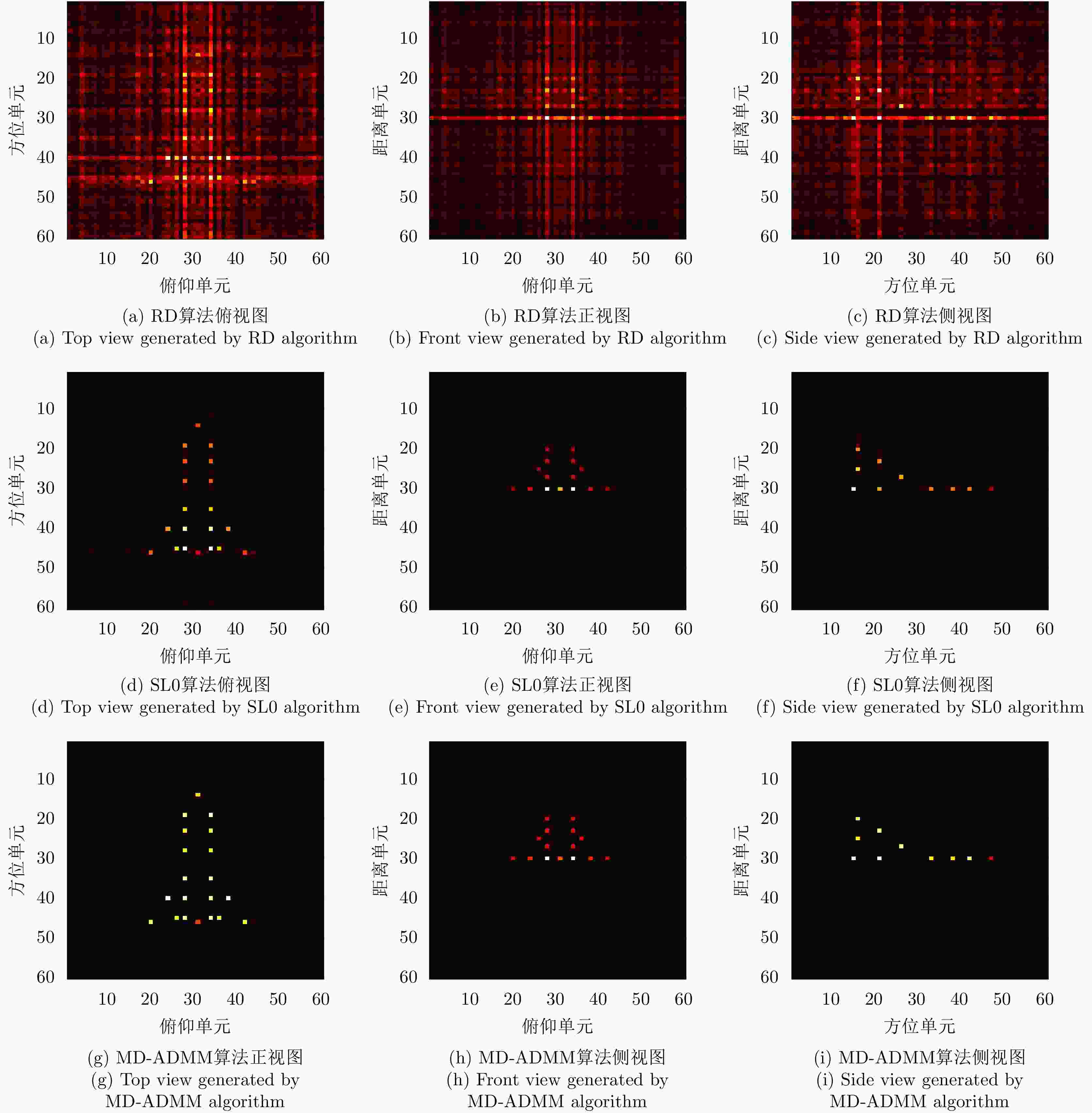
表 1 随机稀疏采样条件下数值结果

Table 1. Numerical results under random sparse sampling condition

稀疏度	算法	图像熵	PSNR	计算时间
50.0%	RD	9.490	34.075	0.012
	DR-2D-SL0	3.138	57.714	35.053
	MD-SL0	3.138	57.714	6.954
	MD-ADMM	3.006	61.678	3.518
33.3%	RD	10.505	28.430	0.010
	DR-2D-SL0	3.200	52.702	29.091
	MD-SL0	3.200	52.702	12.546
	MD-ADMM	2.959	53.888	6.088
25.0%	RD	10.965	26.003	0.0131
	DR-2D-SL0	3.373	48.755	54.008
	MD-SL0	3.373	48.755	28.509
	MD-ADMM	3.023	49.386	11.996

下载: 导出CSV

表 2 块稀疏采样条件下数值结果

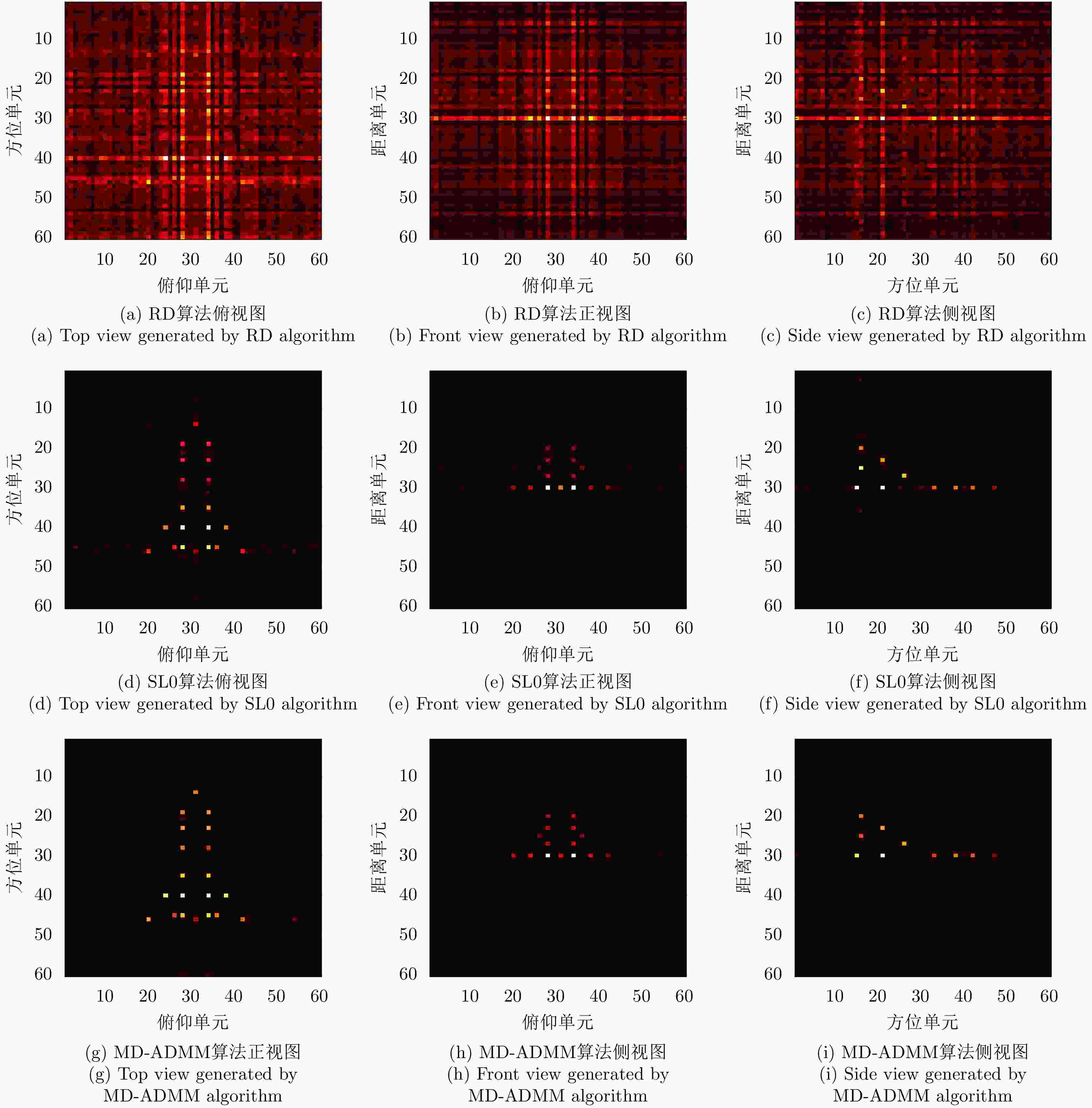
Table 2. Numerical results under block sparse sampling condition

稀疏度	算法	图像熵	PSNR	计算时间
50.0%	RD	8.336	32.885	0.012
	DR-2D-SL0	3.246	51.232	41.907
	MD-SL0	3.246	51.232	8.029
	MD-ADMM	3.037	53.274	3.660
33.3%	RD	8.553	27.495	0.0098
	DR-2D-SL0	3.700	42.188	42.518
	MD-SL0	3.700	42.188	17.954
	MD-ADMM	3.233	42.336	5.758
25.0%	RD	9.500	26.906	0.0092
	DR-2D-SL0	3.894	45.196	51.463
	MD-SL0	3.894	45.196	25.702
	MD-ADMM	3.337	47.201	11.536

下载: 导出CSV

表 3 不同信噪比条件下数值结果

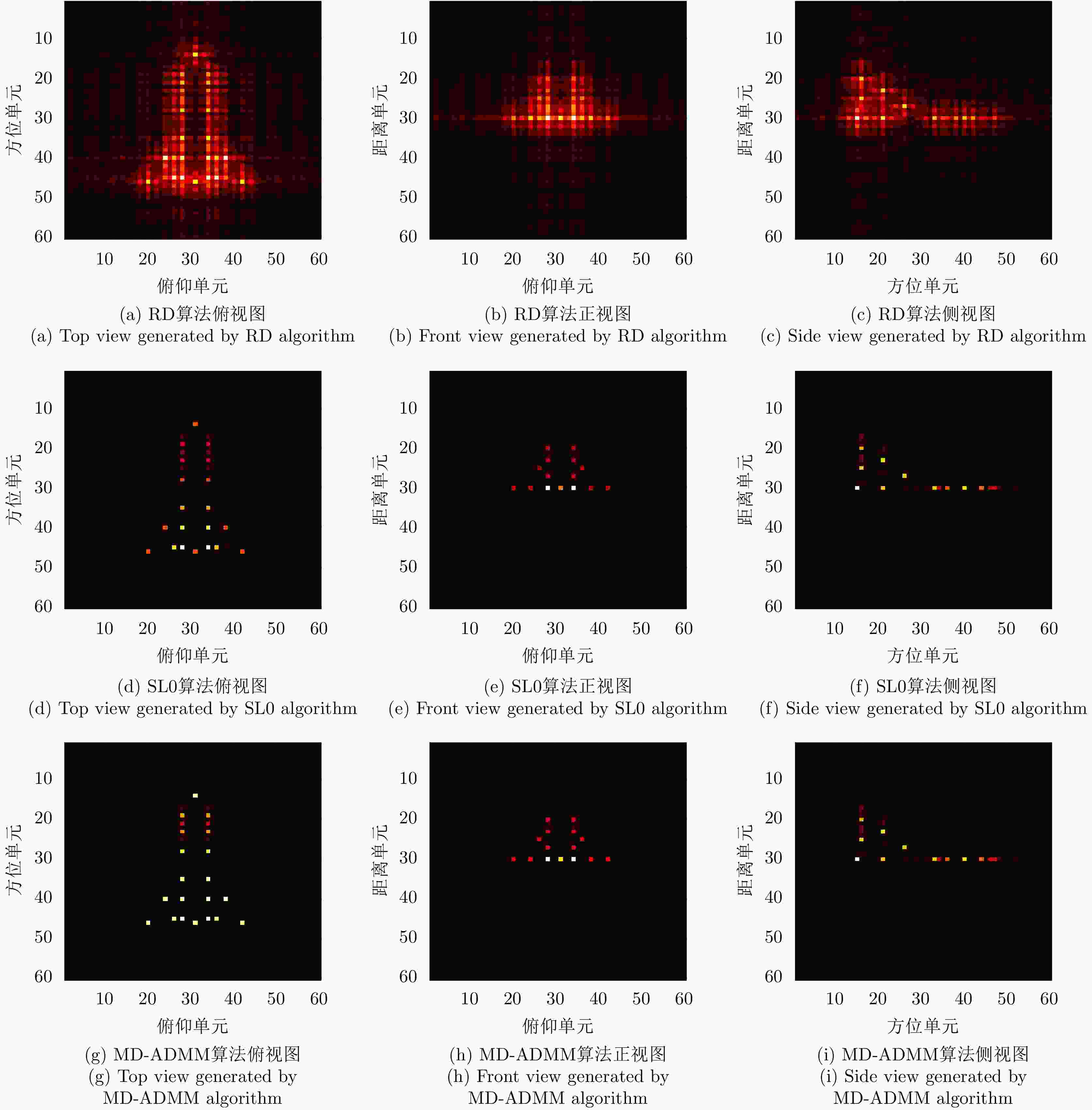
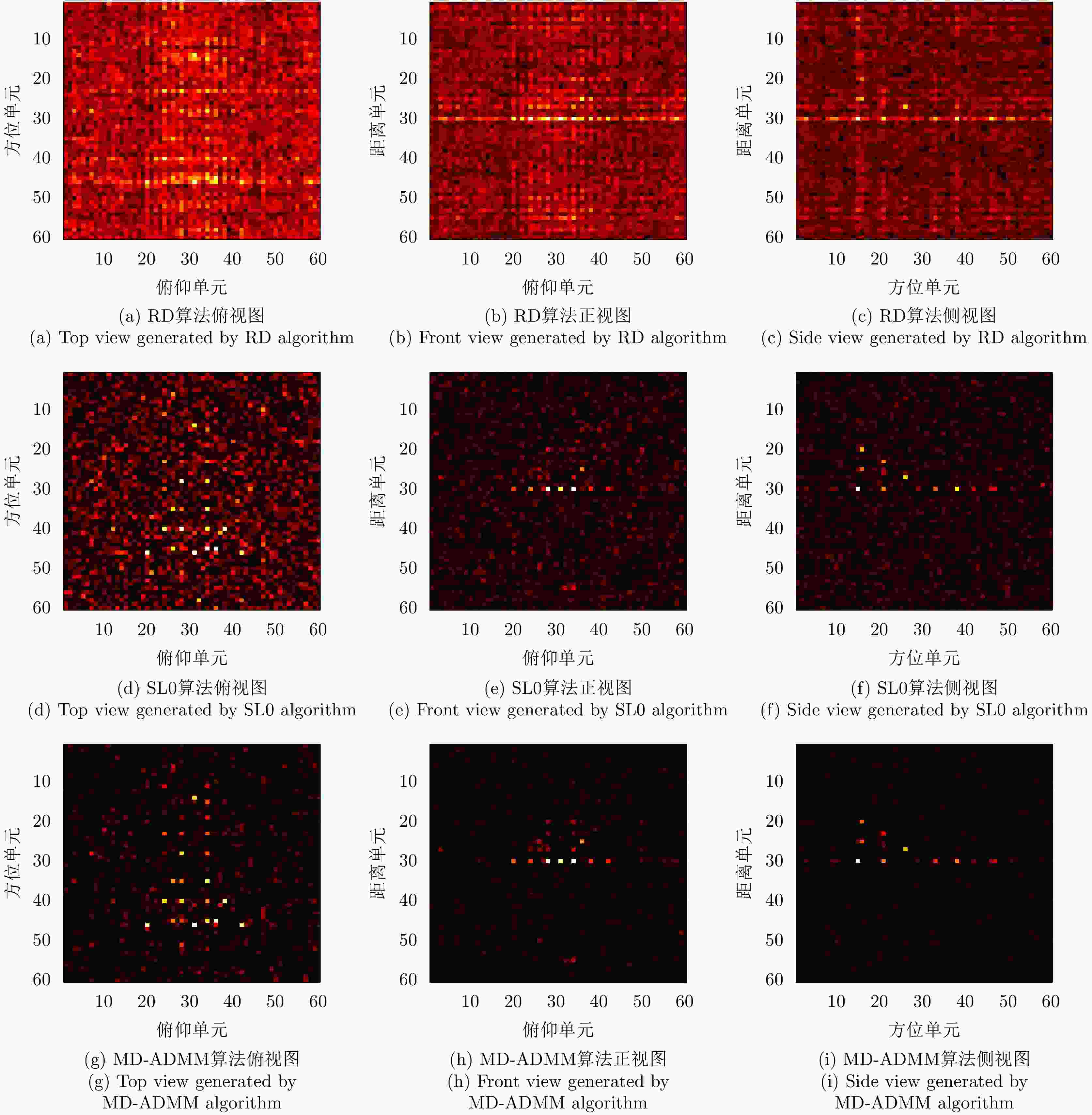
Table 3. Numerical results under different SNR conditions

信噪比	算法	图像熵	PSNR	计算时间
–5 dB	RD	11.8042	18.320	0.0177
	DR-2D-SL0	7.3218	37.639	49.998
	MD-SL0	7.3218	37.639	23.540
	MD-ADMM	4.779	43.352	10.775
0 dB	RD	11.535	23.452	0.013
	DR-2D-SL0	5.4086	43.285	48.776
	MD-SL0	5.4086	43.285	23.303
	MD-ADMM	2.977	47.449	10.715
10 dB	RD	11.116	27.145	0.0124
	DR-2D-SL0	3.948	45.619	48.754
	MD-SL0	3.948	45.619	23.484
	MD-ADMM	3.066	47.561	10.521

下载: 导出CSV

表 4 实测数据不同信噪比条件下的数值结果

Table 4. Numerical results of measured data for different signal-to-noise ratio conditions

信噪比	算法	图像熵	PSNR	计算时间
原始数据	RD	9.639	29.816	0.010
	MD-SL0	6.459	40.378	10.553
	MD-ADMM	5.296	41.364	3.743
0 dB	RD	10.242	26.909	0.0131
	MD-SL0	7.571	35.241	12.064
	MD-ADMM	6.183	39.090	4.274

下载: 导出CSV

参考文献(15)

[1]	MUSMAN S, KERR D, and BACHMANN C. Automatic recognition of ISAR ship images[J]. IEEE Transactions on Aerospace and Electronic Systems, 1996, 32(4): 1392–1404. doi: 10.1109/7.543860
[2]	MARTORELLA M, GIUSTI E, DEMI L, et al. Target recognition by means of polarimetric ISAR images[J]. IEEE Transactions on Aerospace and Electronic Systems, 2011, 47(1): 225–239. doi: 10.1109/TAES.2011.5705672
[3]	BARANIUK R and STEEGHS P. Compressive radar imaging[C]. 2007 IEEE Radar Conference, Waltham, USA, 2007: 128–133.
[4]	DUAN Guangqing, WANG Dangwei, MA Xiaoyan, et al. Three-dimensional imaging via wideband MIMO radar system[J]. IEEE Geoscience and Remote Sensing Letters, 2010, 7(3): 445–449. doi: 10.1109/LGRS.2009.2038728
[5]	HU Xiaowei, TONG Ningning, WANG Heming, et al. Multiple-input-multiple-output radar superresolution three-dimensional imaging based on multidimensional smoothed L0[J]. Journal of Applied Remote Sensing, 2016, 10(3): 035017. doi: 10.1117/1.JRS.10.035017
[6]	WANG Yong and LI Xuelu. 3-D imaging based on combination of the ISAR technique and a MIMO radar system[J]. IEEE Transactions on Geoscience and Remote Sensing, 2018, 56(10): 6033–6054. doi: 0.1109/TGRS.2018.2829912
[7]	CANDES E J and WAKIN M B. An introduction to compressive sampling[J]. IEEE Signal Processing Magazine, 2008, 25(2): 21–30. doi: 10.1109/MSP.2007.914731
[8]	DONOHO D L. Compressed sensing[J]. IEEE Transactions on Information Theory, 2006, 52(4): 1289–1306. doi: 10.1109/TIT.2006.871582
[9]	DUARTE M F and BARANIUK R G. Kronecker compressive sensing[J]. IEEE Transactions on Image Processing, 2012, 21(2): 494–504. doi: 10.1109/TIP.2011.2165289
[10]	QIU Wei, MARTORELLA M, ZHOU Jianxiong, et al. Three-dimensional inverse synthetic aperture radar imaging based on compressive sensing[J]. IET Radar, Sonar & Navigation, 2015, 9(4): 411–420.
[11]	HU Xiaowei, TONG Ningning, GUO Yiduo, et al. MIMO radar 3-D imaging based on multi-dimensional sparse recovery and signal support prior information[J]. IEEE Sensors Journal, 2018, 18(8): 3152–3162. doi: 10.1109/JSEN.2018.2810705
[12]	QIU Wei, ZHOU Jianxiong, ZHAO Hongzhong, et al. Three-dimensional sparse turntable microwave imaging based on compressive sensing[J]. IEEE Geoscience and Remote Sensing Letters, 2015, 12(4): 826–830. doi: 10.1109/LGRS.2014.2363238
[13]	ZHANG Shuanghui, LIU Yongxiang, and LI Xiang. Computationally efficient sparse aperture ISAR autofocusing and imaging based on fast ADMM[J]. IEEE Transactions on Geoscience and Remote Sensing, 2020, 58(12): 8751–8765. doi: 10.1109/TGRS.2020.2990445
[14]	ZHU Yutao, SU Yi, and YU Wenxian. An ISAR imaging method based on MIMO technique[J]. IEEE Transactions on Geoscience and Remote Sensing, 2010, 48(8): 3290–3299. doi: 10.1109/TGRS.2010.2045230
[15]	BOYD S, PARIKH N, CHU E, et al. Distributed optimization and statistical learning via the alternating direction method of multipliers[J]. Foundations and Trends® in Machine Learning, 2011, 3(1): 1–122.