作者中心
专家审稿
责编办公
编辑办公
-
摘要:
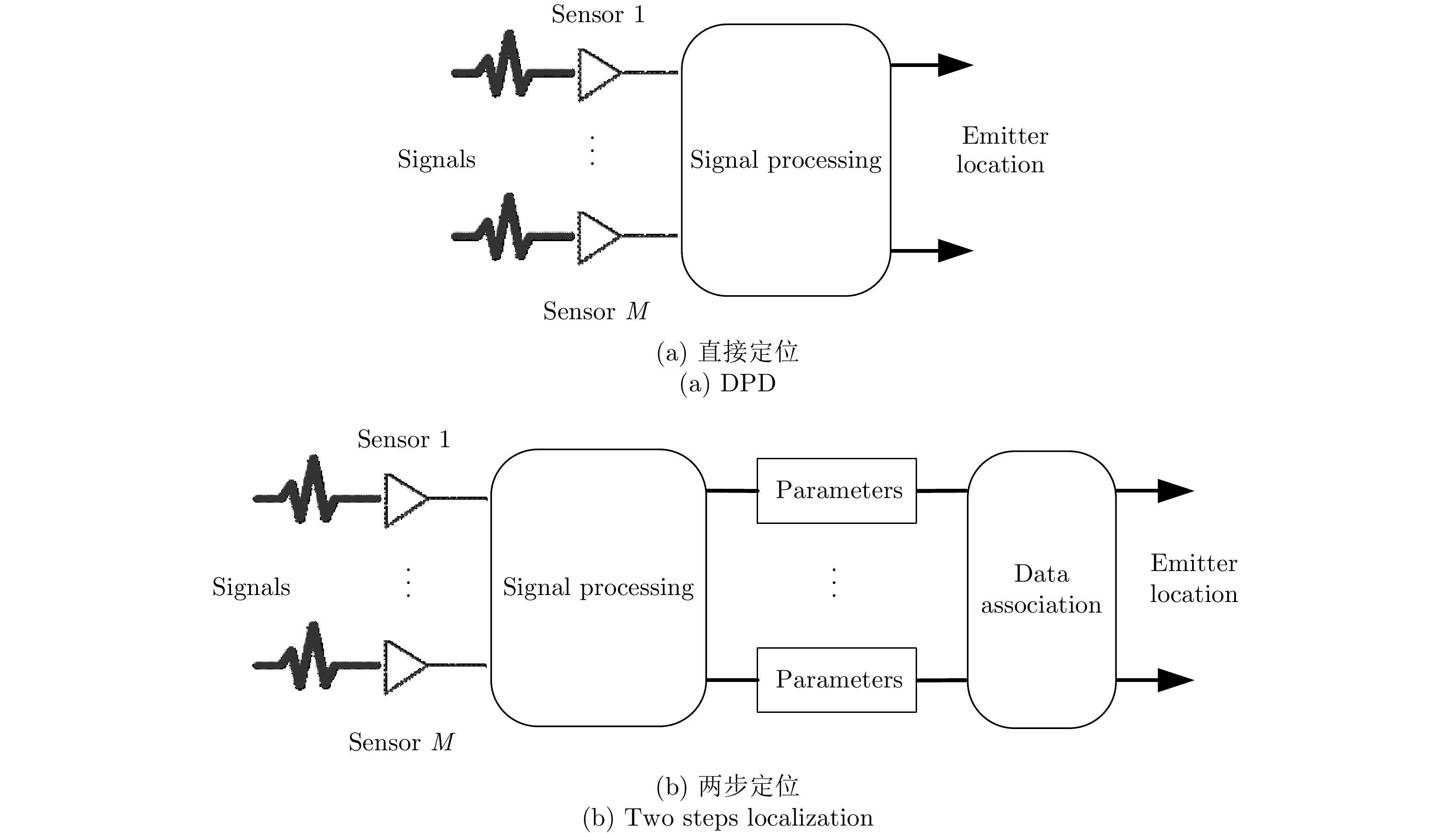
通过被动接收辐射源信号并确定其位置的无源定位技术，在电子侦察、搜索救援等领域具有重要价值。传统测向交叉、时差、频差等无源定位技术通常需要两步实现辐射源的定位，第1步通过截获的信号采样估计与辐射源位置有关的定位参数，第2步利用这些定位参数求解辐射源的位置，这种处理方式带来了信息量损失、定位参数关联困难、系统灵敏度需求高等问题。近十几年来，兴起了一种无需估计定位参数，而是直接处理原始采样信号获得辐射源位置估计的直接定位(DPD)技术，其具有适应低信噪比、无需参数关联、鲁棒性强等优势。在对已有直接定位技术进行全面总结基础上，该文归纳了基于不同信息类型的典型直接定位技术、特殊信号直接定位技术、高分辨率高精度直接定位技术、直接定位快速算法以及直接定位模型误差校正技术等已有成果，并对直接定位未来发展方向进行展望。
Abstract:Passive localization technology, which intercepts emitter signals and passively determines their positions, has important value in fields such as electronic reconnaissance and search and rescue. The traditional passive localization technology approach, i.e., cross-bearing, time difference of arrival, and frequency difference of arrival, requires two steps to estimate the emitter position—estimating the parameters related to the positions and then solving the emitter positions based on the previously estimated parameters. This process results in loss of information and difficulty with data association, and requires high system sensitivity. In recent years, a Direct Position Determination (DPD) method was developed that obtains the emitter positions directly by processing the original sampled signals and requires no estimation of intermediate parameters. This method is robust, achieves high performance with a low signal-to-noise ratio, and requires no parameter association. In this paper, we present a comprehensive summary of existing research on DPD and an overall introduction of DPD, including typical DPD methods based on different information types, DPD of special signals, high-resolution high-accuracy DPD, fast DPD algorithms, and the calibration technology used to address DPD model errors. We also consider the future outlook for DPD.
-
图 1 直接定位系统与传统两步定位系统示意图
Figure 1. Diagrammatic drawings of DPD and two steps localization systems
图 2 ES, ML, MUSIC, MVDR代价函数单位等高线图(星为辐射源真实位置)
Figure 2. The unitized contours of the cost functions based on ES, ML, MUSIC and MVDR (The stars stand for the real positions of the emitters)
图 3 相参直接定位信号处理和非相参直接定位信号处理示意图
Figure 3. Diagrammatic drawings of coherent processing and noncoherent processing of DPD
图 5 固定线阵和旋转线阵直接定位GDOP
Figure 5. The GDOP of DPD using stationary array and rotating array
图 6 基于小生境粒子群优化和BFGS的直接定位代价函数优化过程示意图
Figure 6. The optimized process of DPD cost function based on RNTPSO and BFGS
图 2 The unitized contours of the cost functions based on ES, ML, MUSIC and MVDR (The stars stand for the real positions of the emitters)
表 1 直接定位技术总结表
Table 1. Conclusive table of DPD
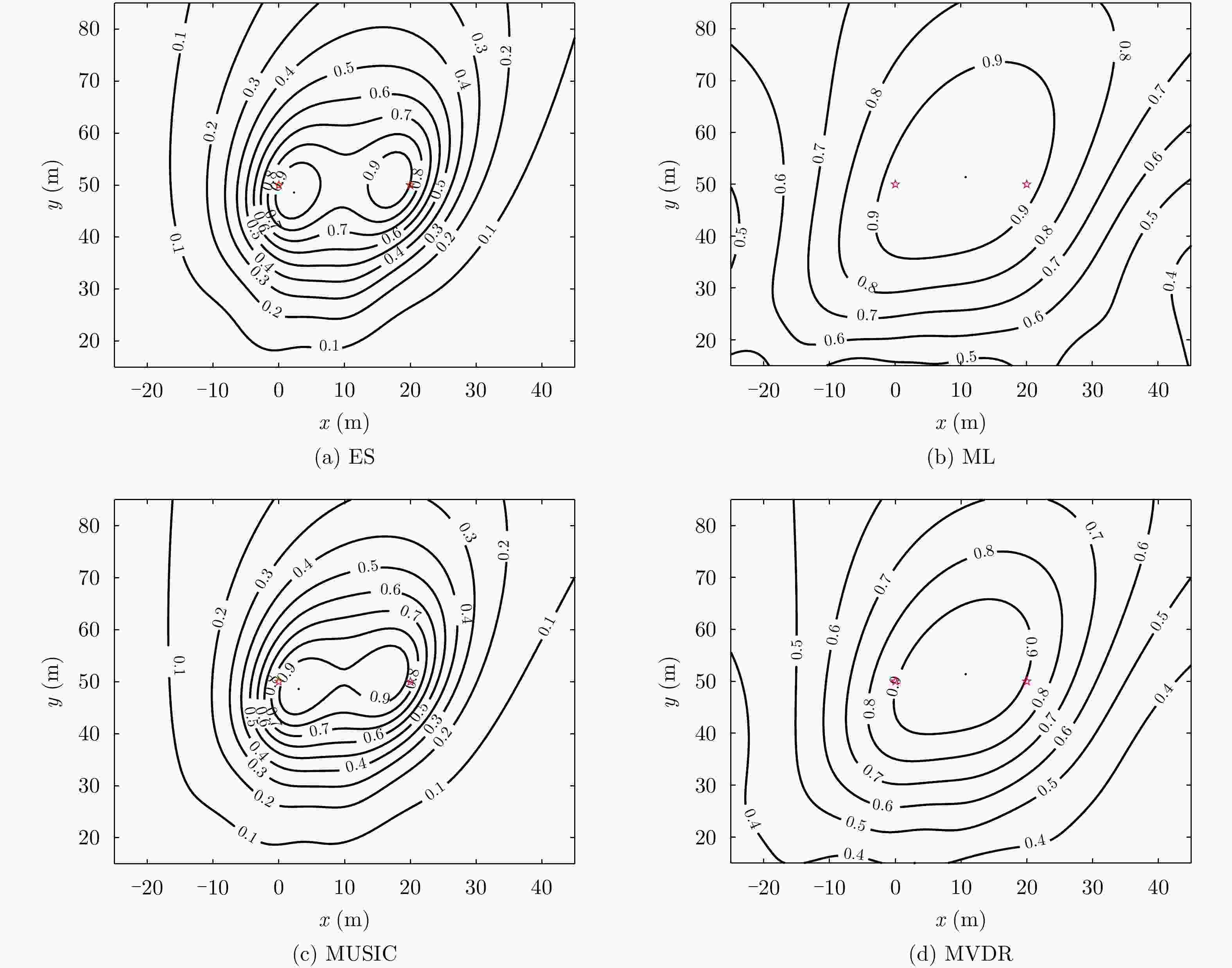
信息类型 阵列 代价函数 优化方法 文献 精度 分辨率 自由度 计算复杂度 DOA/TDOA ULA ML ExS 文献[33] 中 低 低 高 FDOA ULA MUSIC ExS 文献[46,47] 中 中 低 中 TDOA/FDOA ULA ML ExS 文献[50—52] 中 低 低 高 DOA/ FDOA ULA ML ExS 文献[53] 中 低 低 高 DOA/TDOA ULA MVDR ExS 文献[89—93] 中 中 低 中 DOA ULA ES RNTPSO 文献[48] 中 高 低 低 DOA/TDOA MIMO ML ExS 文献[101,102] 高 高 低 高 FDOA MIMO ML ExS 文献[103] 高 高 低 高 TDOA/FDOA ULA ML(Coherent) ExS 文献[58] 高 中 低 高 TDOA/DOA ULA MUSIC(Coherent) ExS 文献[49] 高 高 高 高 Doppler Shift/Rate Antenna ML ExS 文献[87] 中 – – 高 DOA SA MUSIC ExS 文献[98—100] 低 中 高 高 DOA RLA MUSIC ExS 文献[88] 高 高 低 中 DOA ULA MUSIC AP 文献[106] 中 中 低 低 DOA/TDOA ULA ML EM 文献[45] 中 低 低 中 DOA/TDOA ULA ML DA 文献[52] 中 低 低 中 
下载: 导出CSV
表 1 Conclusive table of DPD
Info type Array Cost function Optimization Reference Precision Resolution DoF Complexity DOA/TDOA ULA ML ExS [33] Mid Low Low High FDOA ULA MUSIC ExS [46,47] Mid Mid Low Mid TDOA/FDOA ULA ML ExS [50–52] Mid Low Low High DOA/FDOA ULA ML Exs [53] Mid Low Low High DOA/TDOA ULA MVDR ExS [89–93] Mid Mid Low Mid DOA ULA ES RNTPSO [48] Mid High Low Low DOA/TDOA MIMO ML ExS [101,102] High High Low High FDOA MIMO ML ExS [103] High High Low High TDOA/FDOA ULA ML(Coherent) ExS [58] High Mid Low High TDOA/DOA ULA MUSIC(Coherent) ExS [49] High High High High Doppler Shift/Rate Antenna ML ExS [87] Mid – – High DOA SA MUSIC ExS [98–100] Low Mid High High DOA RLA MUSIC ExS [88] High High Low Mid DOA ULA MUSIC AP [106] Mid Mid Low Low DOA/TDOA ULA ML EM [45] Mid Low Low Mid DOA/TDOA ULA ML DA [52] Mid Low Low Mid
下载: 导出CSV
-
[1] SCHMIDT R. Multiple emitter location and signal parameter estimation[J]. IEEE Transactions on Antennas and Propagation, 1986, 34(3): 276–280. doi: 10.1109/TAP.1986.1143830 [2] MCCLOUD M L and SCHARF L L. A new subspace identification algorithm for high resolution DOA estimation[J]. IEEE Transactions on Antennas and Propagation, 2002, 50(10): 1382–1390. doi: 10.1109/TAP.2002.805244 [3] RAJ A G and MCCLELLAN J H. Single snapshot super-resolution DOA estimation for arbitrary array geometries[J]. IEEE Signal Processing Letters, 2019, 26(1): 119–123. doi: 10.1109/LSP.2018.2881927 [4] SELVA J. Efficient wideband DOA estimation through function evaluation techniques[J]. IEEE Transactions on Signal Processing, 2018, 66(12): 3112–3123. doi: 10.1109/TSP.2018.2824256 [5] YANG J R. Measurement of amplitude and phase differences between two RF signals by using signal power detection[J]. IEEE Microwave and Wireless Components Letters, 2014, 24(3): 206–208. doi: 10.1109/LMWC.2013.2293665 [6] BALLAL T and BLEAKLEY C J. Phase-difference ambiguity resolution for a single-frequency signal in the near-field using a receiver triplet[J]. IEEE Transactions on Signal Processing, 2010, 58(11): 5920–5926. doi: 10.1109/TSP.2010.2062180 [7] BALLAL T and BLEAKLEY C J. Phase-difference ambiguity resolution for a single-frequency signal[J]. IEEE Signal Processing Letters, 2008, 15: 853–856. doi: 10.1109/LSP.2008.2005439 [8] CARTER G C. Coherence and Time Delay Estimation[M]. New York, NY: IEEE Press, 1993. [9] CHAN Y T and HO K C. A simple and efficient estimator for hyperbolic location[J]. IEEE Transactions on Signal Processing, 1994, 42(8): 1905–1915. doi: 10.1109/78.301830 [10] HO K C. Bias reduction for an explicit solution of source localization using TDOA[J]. IEEE Transactions on Signal Processing, 2012, 60(5): 2101–2114. doi: 10.1109/TSP.2012.2187283 [11] HO K C and CHAN Y T. Solution and performance analysis of geolocation by TDOA[J]. IEEE Transactions on Aerospace and Electronic Systems, 1993, 29(4): 1311–1322. doi: 10.1109/7.259534 [12] ULMAN R and GERANIOTIS E. Wideband TDOA/FDOA processing using summation of short-time CAF’s[J]. IEEE Transactions on Signal Processing, 1999, 47(12): 3193–3200. doi: 10.1109/78.806065 [13] HO K C, LU Xiaoning, and KOVAVISARUCH L. Source localization using TDOA and FDOA measurements in the presence of receiver location errors: Analysis and solution[J]. IEEE Transactions on Signal Processing, 2007, 55(2): 684–696. doi: 10.1109/TSP.2006.885744 [14] BELLO P. Joint estimation of delay, Doppler, and Doppler rate[J]. IRE Transactions on Information Theory, 1960, 6(3): 330–341. doi: 10.1109/TIT.1960.1057562 [15] ABATZOGLOU T. Fast maximum likelihood joint estimation of frequency and frequency rate[C]. IEEE International Conference on Acoustics, Speech, and Signal Processing, Tokyo, Japan, 1986: 1409–1412. [16] ZHANG Shuangxi and XING Mengdao. A novel Doppler chirp rate and baseline estimation approach in the time domain based on weighted local Maximum-Likelihood for an MC-HRWS SAR system[J]. IEEE Geoscience and Remote Sensing Letters, 2017, 14(3): 299–303. doi: 10.1109/LGRS.2016.2633359 [17] ZHANG Weiqiang. Fast Doppler rate estimation based on fourth-order moment spectrum[J]. Electronics Letters, 2015, 51(23): 1926–1928. doi: 10.1049/el.2015.2182 [18] TRINH-HOANG M, VIBERG M, and PESAVENTO M. Partial relaxation approach: An eigenvalue-based DOA estimator framework[J]. IEEE Transactions on Signal Processing, 2018, 66(23): 6190–6203. doi: 10.1109/TSP.2018.2875853 [19] WU Xiaohuan, ZHU Weiping, and YAN Jun. A high-resolution DOA estimation method with a family of nonconvex penalties[J]. IEEE Transactions on Vehicular Technology, 2018, 67(6): 4925–4938. doi: 10.1109/TVT.2018.2817638 [20] XU Xu, YE Zhongfu, and ZHANG Yufeng. DOA estimation for mixed signals in the presence of mutual coupling[J]. IEEE Transactions on Signal Processing, 2009, 57(9): 3523–3532. doi: 10.1109/TSP.2009.2021919 [21] CATOVIC A and SAHINOGLU Z. The Cramer-Rao bounds of hybrid TOA/RSS and TDOA/RSS location estimation schemes[J]. IEEE Communications Letters, 2004, 8(10): 626–628. doi: 10.1109/LCOMM.2004.835319 [22] LI Xinrong. RSS-Based location estimation with unknown pathloss model[J]. IEEE Transactions on Wireless Communications, 2006, 5(12): 3626–3633. doi: 10.1109/TWC.2006.256985 [23] PATWARI N, HERO A O, PERKINS M, et al. Relative location estimation in wireless sensor networks[J]. IEEE Transactions on Signal Processing, 2003, 51(8): 2137–2148. doi: 10.1109/TSP.2003.814469 [24] WANG Gang and YANG Kehu. A new approach to sensor node localization using RSS measurements in wireless sensor networks[J]. IEEE Transactions on Wireless Communications, 2011, 10(5): 1389–1395. doi: 10.1109/TWC.2011.031611.101585 [25] WEISS A J. On the accuracy of a cellular location system based on RSS measurements[J]. IEEE Transactions on Vehicular Technology, 2003, 52(6): 1508–1518. doi: 10.1109/TVT.2003.819613 [26] 郭福成, 樊昀, 周一宇, 等. 空间电子侦察定位原理[M]. 北京: 国防工业出版社, 2012: 44–47.GUO Fucheng, FAN Yun, ZHOU Yiyu, et al. Localization Principles in Space Electronic Reconnaissance[M]. Beijing: National Defense Industry Press, 2012: 44–47. [27] CHAN Y T and JARDINE F L. Target localization and tracking from Doppler-shift measurements[J]. IEEE Journal of Oceanic Engineering, 1990, 15(3): 251–257. doi: 10.1109/48.107154 [28] CHAN Y T and TOWERS J J. Passive localization from Doppler-shifted frequency measurements[J]. IEEE Transactions on Signal Processing, 1992, 40(10): 2594–2598. doi: 10.1109/78.157301 [29] TORRIERI D J. Statistical theory of passive location systems[J]. IEEE Transactions on Aerospace and Electronic Systems, 1984, AES–20(2): 183–198. [30] HO K C and CHAN Y T. Geolocation of a known altitude object from TDOA and FDOA measurements[J]. IEEE Transactions on Aerospace and Electronic Systems, 1997, 33(3): 770–783. doi: 10.1109/7.599239 [31] HU Dexiu, HUANG Zhen, CHEN Xi, et al. A moving source localization method using TDOA, FDOA and Doppler rate measurements[J]. IEICE Transactions on Communications, 2016, E99. B(3): 758–766. doi: 10.1587/transcom.2015EBP3355 [32] 张敏, 郭福成, 周一宇. 基于单个长基线干涉仪的运动单站直接定位[J]. 航空学报, 2013, 34(2): 378–386.ZHANG Min, GUO Fucheng, and ZHOU Yiyu. A single moving observer direct position determination method using a long baseline interferometer[J]. Acta Aeronautica et Astronautica Sinica, 2013, 34(2): 378–386. [33] WEISS A J. Direct position determination of narrowband radio frequency transmitters[J]. IEEE Signal Processing Letters, 2004, 11(5): 513–516. doi: 10.1109/LSP.2004.826501 [34] DEMISSIE B, OISPUU M, and RUTHOTTO E. Localization of multiple sources with a moving array using subspace data fusion[C]. The 2008 11th International Conference on Information Fusion, Cologne, Germany, 2008: 1–7. [35] OISPUU M. Direct state determination of multiple sources with intermittent emission[C]. 2009 17th European Signal Processing Conference, Glasgow, UK, 2009: 1948–1952. [36] YIN Jiexin, WANG Ding, WU Ying, et al. Direct localization of multiple stationary narrowband sources based on angle and Doppler[J]. IEEE Communications Letters, 2017, 21(12): 2630–2633. doi: 10.1109/LCOMM.2017.2755656 [37] HAO Kegang and WAN Qun. An efficiency-improved Tdoa-based direct position determination method for multiple sources[C]. IEEE International Conference on Acoustics, Speech, and Signal Processing, Brighton, United Kingdom, 2019: 4425–4429. [38] WAX M and KAILATH T. Decentralized processing in sensor arrays[J]. IEEE Transactions on Acoustics,Speech,and Signal Processing, 1985, 33(5): 1123–1129. doi: 10.1109/TASSP.1985.1164706 [39] AMAR A and WEISS A J. Advances in direct position determination[C]. Workshop Proceedings, 2004 Sensor Array and Multichannel Signal, Barcelona, Spain, 2004: 584–588. [40] AMAR A and WEISS A J. Direct position determination in the presence of model errors-known waveforms[J]. Digital Signal Processing, 2006, 16(1): 52–83. doi: 10.1016/j.dsp.2005.03.003 [41] AMAR A and WEISS A J. Analysis of direct position determination approach in the presence of model errors[C]. The IEEE/SP 13th Workshop on Statistical Signal Processing, Bordeaux, France, 2005: 521–524. [42] WANG Ding and WU Ying. Statistical performance analysis of direct position determination method based on Doppler shifts in presence of model errors[J].Multidimensional Systems and Signal Processing, 2017, 28(1): 149–182. doi: 10.1007/s11045-015-0338-3 [43] 陈芳香, 易伟, 周涛, 等. 应用膨胀算法提取目标的直接定位算法[J]. 雷达科学与技术, 2019, 17(2): 161–167. doi: 10.3969/j.issn.1672-2337.2019.02.008CHEN Fangxiang, YI Wei, ZHOU Tao, et al. A direct position determination method using the image expansion algorithm to extract targets[J]. Radar Science and Technology, 2019, 17(2): 161–167. doi: 10.3969/j.issn.1672-2337.2019.02.008 [44] 宋科康, 冯文涛. 采用DIRECT算法的外辐射源雷达高效直接定位方法[J]. 信号处理, 2020, 36(1): 149–154. doi: 10.16798/j.issn.1003-0530.2020.01.018SONG Kekang and FENG Wentao. An efficient method of direct position determination of passive radar with direct algorithm[J]. Journal of Signal Processing, 2020, 36(1): 149–154. doi: 10.16798/j.issn.1003-0530.2020.01.018 [45] TZORE E and WEISS A J. Expectation-maximization algorithm for direct position determination[J]. Signal Processing, 2017, 133: 32–39. doi: 10.1016/j.sigpro.2016.10.015 [46] AMAR A and WEISS A J. Direct Position Determination (DPD) of multiple known and unknown radio-frequency signals[C]. 2004 12th European Signal Processing Conference, Vienna, Austria, 2004: 1115–1118. [47] WEISS A J and AMAR A. Direct position determination of multiple radio signals[J]. EURASIP Journal on Advances in Signal Processing, 2005, 2005(1): 653549. doi: 10.1155/ASP.2005.37 [48] WU Guizhou, ZHANG Min, and GUO Fucheng. High-resolution direct position determination based on eigenspace using a single moving ULA[J]. Signal,Image and Video Processing, 2019, 13(5): 887–894. doi: 10.1007/s11760-019-01425-4 [49] OISPUU M and NICKEL U. 3D passive source localization by a multi-array network: Noncoherent vs. coherent processing[C]. International ITG Workshop on Smart Antennas (WSA), Bremen, Germany, 2010: 300–305. [50] LU Zhiyu, BA Bin, WANG Jianhui, et al. A direct position determination method with combined TDOA and FDOA based on particle filter[J]. Chinese Journal of Aeronautics, 2018, 31(1): 161–168. doi: 10.1016/j.cja.2017.11.007 [51] ZHOU Longjian, ZHU Weiqiang, LUO Jingqing, et al. Direct positioning maximum likelihood estimator using TDOA and FDOA for coherent short-pulse radar[J]. IET Radar,Sonar&Navigation, 2017, 11(10): 1505–1511. [52] 王云龙, 吴瑛. 联合时延与多普勒频率的直接定位改进算法[J]. 西安交通大学学报, 2015, 49(4): 123–129. doi: 10.7652/xjtuxb201504020WANG Yunlong and WU Ying. An improved direct position determination algorithm with combined time delay and Doppler[J]. Journal of Xi’an Jiaotong University, 2015, 49(4): 123–129. doi: 10.7652/xjtuxb201504020 [53] MA Fuhe, GUO Fucheng, and YANG Le. Direct position determination of moving sources based on delay and Doppler[J]. IEEE Sensors Journal, 2020, 20(14): 7859–7869. doi: 10.1109/JSEN.2020.2980012 [54] ZHANG Shangyu, HUANG Zhen, FENG Xuefeng, et al. Multi-sensor passive localization using direct position determination with time-varying delay[J]. Sensors, 2019, 19(7): 1541. doi: 10.3390/s19071541 [55] 王鼎, 吴志东, 尹洁昕. 信号波形已知条件下多目标直接定位性能分析及其改进算法[J]. 电子学报, 2017, 45(12): 2881–2889. doi: 10.3969/j.issn.0372-2112.2017.12.008WANG Ding, WU Zhidong, and YIN Jiexin. A performance analysis and improvement algorithm for multiple-source direct localization with known signal waveforms[J]. Acta Electronica Sinica, 2017, 45(12): 2881–2889. doi: 10.3969/j.issn.0372-2112.2017.12.008 [56] 王鼎, 张刚. 一种基于窄带信号多普勒频率测量的运动目标直接定位方法[J]. 电子学报, 2017, 45(3): 591–598. doi: 10.3969/j.issn.0372-2112.2017.03.013WANG Ding and ZHANG Gang. A direct localization method for moving narrowband source based on Doppler frequency shifts[J]. Acta Electronica Sinica, 2017, 45(3): 591–598. doi: 10.3969/j.issn.0372-2112.2017.03.013 [57] WEISS A J. Direct geolocation of wideband emitters based on delay and Doppler[J]. IEEE Transactions on Signal Processing, 2011, 59(6): 2513–2521. doi: 10.1109/TSP.2011.2128311 [58] LI Jinzhou, YANG Le, GUO Fucheng, et al. Coherent summation of multiple short-time signals for direct positioning of a wideband source based on delay and Doppler[J]. Digital Signal Processing, 2016, 48: 58–70. doi: 10.1016/j.dsp.2015.09.008 [59] BOSSE J, FERRÉOL A, and LARZABAL P. A spatio-temporal array processing for passive localization of radio transmitters[J]. IEEE Transactions on Signal Processing, 2013, 61(22): 5485–5494. doi: 10.1109/TSP.2013.2278515 [60] DELESTRE C, FERRÉOL A, and LARZABAL P. Lost-find: A spectral-space-time direct blind geolocalization algorithm[C]. IEEE International Conference on Acoustics, Speech and Signal Processing (ICASSP), Brisbane, Australia, 2015: 2619–2623. [61] CHEN Minqiu, MAO Xingpeng, LONG Xiaozhuan, et al. Underdetermined direct localization of emitters based on spatio-temporal processing[J]. IEEE Signal Processing Letters, 2018, 25(3): 452–456. doi: 10.1109/LSP.2018.2799224 [62] MA Fuhe, LIU Zhangmeng, and GUO Fucheng. Direct position determination for wideband sources using fast approximation[J]. IEEE Transactions on Vehicular Technology, 2019, 68(8): 8216–8221. doi: 10.1109/TVT.2019.2921981 [63] 欧阳鑫信, 万群, 曹景敏, 等. 跳频信号的时差直接定位[J]. 电子学报, 2017, 45(4): 820–825. doi: 10.3969/j.issn.0372-2112.2017.04.008OUYANG Xinxin, WAN Qun, CAO Jingmin, et al. TDOA-based direct geolocation of frequency-hopping signals[J]. Acta Electronica Sinica, 2017, 45(4): 820–825. doi: 10.3969/j.issn.0372-2112.2017.04.008 [64] MASAAKI I, KAZUNORI H, HIROKI M, et al. A DOA estimation method with Kronecker subspace for coherent signals[J]. IEEE Communications Letters, 2018, 22(11): 2306–2309. doi: 10.1109/LCOMM.2018.2870824 [65] SHAN Tiejun and KAILATH T. Adaptive beamforming for coherent signals and interference[J]. IEEE Transactions on Acoustics,Speech,and Signal Processing, 1985, 33(3): 527–236. doi: 10.1109/TASSP.1985.1164583 [66] LINEBARGER D A and JOHNSON D H. The effect of spatial averaging on spatial correlation matrices in the presence of coherent signals[J]. IEEE Transactions on Acoustics,Speech,and Signal Processing, 1990, 38(5): 880–884. doi: 10.1109/29.56037 [67] LINEBARGER D A, DEGROAT R D, and DOWLING E M. Efficient direction-finding methods employing forward/backward averaging[J]. IEEE Transactions on Signal Processing, 1994, 42(8): 2136–2145. doi: 10.1109/78.301848 [68] PHAM G T, LOUBATON P, and VALLET P. Performance analysis of spatial smoothing schemes in the context of large arrays[J]. IEEE Transactions on Signal Processing, 2016, 64(1): 160–172. doi: 10.1109/TSP.2015.2480044 [69] STEINWANDT J, ROEMER F, HAARDT M, et al. Performance analysis of multi-dimensional ESPRIT-type algorithms for arbitrary and strictly non-circular sources with spatial smoothing[J]. IEEE Transactions on Signal Processing, 2017, 65(9): 2262–2276. doi: 10.1109/TSP.2017.2652388 [70] 郭林朋, 曲长文, 冯奇, 等. 基于解相干MUSIC的相干信源直接定位法研究[J]. 舰船电子工程, 2019, 39(2): 52–55, 65. doi: 10.3969/j.issn.1672-9730.2019.02.014GUO Linpeng, QU Changwen, FENG Qi, et al. Research of direct position determination in coherent signal base on improved MUSIC algorithm[J]. Ship Electronic Engineering, 2019, 39(2): 52–55, 65. doi: 10.3969/j.issn.1672-9730.2019.02.014 [71] ZHOU Tao, YI Wei, and KONG Lingjiang. Direct position determination of multiple coherent sources using an iterative adaptive approach[J]. Signal Processing, 2019, 161: 203–213. doi: 10.1016/j.sigpro.2019.03.023 [72] SHAN Tiejun, WAX M, and KAILATH T. On spatial smoothing for direction-of- arrival estimation of coherent signals[J]. IEEE Transactions on Acoustics,Speech,and Signal Processing, 1985, 33(4): 806–811. doi: 10.1109/TASSP.1985.1164649 [73] LI Jian. Improved angular resolution for spatial smoothing techniques[J]. IEEE Transactions on Signal Processing, 1992, 40(12): 3078–3081. doi: 10.1109/78.175754 [74] MA C W and TENG C C. Detection of coherent signals using weighted subspace smoothing[J]. IEEE Transactions on Antennas and Propagation, 1996, 44(2): 179–187. doi: 10.1109/8.481645 [75] BAR-SHALOM O and WEISS A J. Direct position determination of OFDM signals[C]. The IEEE 8th Workshop on Signal Processing Advances in Wireless Communications, Helsinki, Finland, 2007: 1–5. [76] BAR-SHALOM O and WEISS A J. Efficient direct position determination of orthogonal frequency division multiplexing signals[J]. IET Radar,Sonar&Navigation, 2009, 3(2): 101–111. [77] LU Zhiyu, WANG Jianhui, BA Bin, et al. A novel direct position determination algorithm for orthogonal frequency division multiplexing signals based on the time and angle of arrival[J]. IEEE Access, 2017, 5: 25312–25321. doi: 10.1109/ACCESS.2017.2766632 [78] DELMAS J P and ABEIDA H. Stochastic Cramér-Rao bound for noncircular signals with application to DOA estimation[J]. IEEE Transactions on Signal Processing, 2004, 52(11): 3192–3199. doi: 10.1109/TSP.2004.836462 [79] ABEIDA H and DELMAS J P. Gaussian Cramer-Rao bound for direction estimation of noncircular signals in unknown noise fields[J]. IEEE Transactions on Signal Processing, 2005, 53(12): 4610–4618. doi: 10.1109/TSP.2005.859226 [80] STEINWANDT J, ROEMER F, HAARDT M, et al. Deterministic Cramér-Rao bound for strictly non-circular sources and analytical analysis of the achievable gains[J]. IEEE Transactions on Signal Processing, 2016, 64(17): 4417–4431. doi: 10.1109/TSP.2016.2566603 [81] XIA Yili, JELFS B, VAN HULLE M M, et al. An augmented echo state network for nonlinear adaptive filtering of complex noncircular signals[J]. IEEE Transactions on Neural Networks, 2011, 22(1): 74–83. doi: 10.1109/TNN.2010.2085444 [82] YIN Jiexin, WANG Ding, WU Ying, et al. ML-based single-step estimation of the locations of strictly noncircular sources[J]. Digital Signal Processing, 2017, 69: 224–236. doi: 10.1016/j.dsp.2017.06.024 [83] YIN Jiexin, WANG Ding, and WU Ying. An efficient direct position determination method for multiple strictly noncircular sources[J]. Sensors, 2018, 18(2): 324. doi: 10.3390/s18020324 [84] QIN Tianzhu, LU Zhiyu, BA Bin, et al. A decoupled direct positioning algorithm for strictly noncircular sources based on Doppler shifts and angle of arrival[J]. IEEE Access, 2018, 6: 34449–34461. doi: 10.1109/ACCESS.2018.2849574 [85] 王鼎, 张刚, 沈彩耀, 等. 一种针对恒模信号的运动单站直接定位算法[J]. 航空学报, 2016, 37(5): 1622–1633. doi: 10.7527/S1000-6893.2015.0347WANG Ding, ZHANG Gang, SHEN Caiyao, et al. A direct position determination algorithm for constant modulus signals with single moving observer[J]. Acta Aeronautica et Astronautica Sinica, 2016, 37(5): 1622–1633. doi: 10.7527/S1000-6893.2015.0347 [86] REUVEN A M and WEISS A J. Direct position determination of cyclostationary signals[J]. Signal Processing, 2009, 89(12): 2448–2464. doi: 10.1016/j.sigpro.2009.04.009 [87] WU Guizhou, ZHANG Min, GUO Fucheng, et al. Direct position determination of coherent pulse trains based on Doppler and Doppler rate[J]. Electronics, 2018, 7(10): 262. doi: 10.3390/electronics7100262 [88] WU Guizhou, ZHANG Min, HE Chaoxin, et al. Direct position determination using single moving rotating linear array: Noncoherent and coherent processing[J]. Chinese Journal of Aeronautics, 2020, 33(2): 688–700. doi: 10.1016/j.cja.2019.07.027 [89] TIRER T and WEISS A J. High resolution localization of narrowband radio emitters based on Doppler frequency shifts[J]. Signal Processing, 2017, 141: 288–298. doi: 10.1016/j.sigpro.2017.06.019 [90] TIRER T and WEISS A J. High resolution direct position determination of radio frequency sources[J]. IEEE Signal Processing Letters, 2016, 23(2): 192–196. doi: 10.1109/LSP.2015.2503921 [91] TZAFRI L and WEISS A J. High-resolution direct position determination using MVDR[J]. IEEE Transactions on Wireless Communication, 2016, 15(9): 6449–6461. doi: 10.1109/TWC.2016.2585116 [92] TZAFRI L and WEISS A J. Application of capon method to direct position determination[J]. ICT Express, 2016, 2(1): 5–9. doi: 10.1016/j.icte.2016.02.010 [93] HAO Kegang and WAN Qun. High resolution direct detection and position determination of sources with intermittent emission[J]. IEEE Access, 2019, 7: 43428–43437. doi: 10.1109/ACCESS.2019.2907136 [94] TIRER T and WEISS A J. Performance analysis of a high-resolution direct position determination method[J]. IEEE Transactions on Signal Processing, 2017, 65(3): 544–554. doi: 10.1109/TSP.2016.2621729 [95] HAWKES M and NEHORAI A. Acoustic vector-sensor beamforming and Capon direction estimation[J]. IEEE Transactions on Signal Processing, 1998, 46(9): 2291–2304. doi: 10.1109/78.709509 [96] STOICA P, HÄNDEL P, and SÖDERSTRÖM T. Study of Capon method for array signal processing[J]. Circuits,Systems and Signal Processing, 1995, 14(6): 749–770. doi: 10.1007/BF01204683 [97] VAIDYANATHAN C and BUCKLEY K M. Performance analysis of the MVDR spatial spectrum estimator[J]. IEEE Transactions on Signal Processing, 1995, 43(6): 1427–1437. doi: 10.1109/78.388855 [98] ZHANG Yankui, XU Haiyun, BA Bin, et al. Direct position determination of Non-circular sources based on Doppler-extended aperture with a moving coprime array[J]. IEEE Access, 2018, 6: 61014–61021. doi: 10.1109/ACCESS.2018.2875822 [99] ZHANG Yankui, BA Bin, WANG Daming, et al. Direct position determination of multiple non-circular sources with a moving coprime Array[J]. Sensors, 2018, 18(5): 1479. doi: 10.3390/s18051479 [100] KUMAR G, PONNUSAMY P, and AMIRI I S. Direct localization of multiple noncircular sources with a moving nested array[J]. IEEE Access, 2019, 7: 101106–101116. doi: 10.1109/ACCESS.2019.2929805 [101] BAR-SHALOM O and WEISS A J. Direct positioning of stationary targets using MIMO radar[J]. Signal Processing, 2011, 91(10): 2345–2358. doi: 10.1016/j.sigpro.2011.04.019 [102] GARCIA N, WYMEERSCH H, LARSSON E G, et al. Direct localization for massive MIMO[J]. IEEE Transactions on Signal Processing, 2017, 65(10): 2475–2487. doi: 10.1109/TSP.2017.2666779 [103] 邓丽娟, 张展, 魏平, 等. 分布式MIMO雷达中仅使用多普勒频移的直接定位技术[J]. 信号处理, 2018, 34(11): 1377–1384. doi: 10.16798/j.issn.1003-0530.2018.11.014DENG Lijuan, ZHANG Zhan, WEI Ping, et al. Direct position determination using merely Doppler frequency shifts in distributed MIMO radar[J]. Journal of Signal Processing, 2018, 34(11): 1377–1384. doi: 10.16798/j.issn.1003-0530.2018.11.014 [104] GOGINENI S and NEHORAI A. Target estimation using sparse modeling for distributed MIMO radar[J]. IEEE Transactions on Signal Processing, 2011, 59(11): 5315–5325. doi: 10.1109/TSP.2011.2164070 [105] CHEN Zhuohao, YU kai, LUO Jian, et al. An improved joint sparse representation of array covariance matrices approach in multi-source direct position[C]. The IEEE 11th International Conference on Mobile Ad Hoc and Sensor Systems, Philadelphia, USA, 2014: 696–701. [106] ZISKIND I and WAX M. Maximum likelihood localization of multiple sources by alternating projection[J]. IEEE Transactions on Acoustics,Speech,and Signal Processing, 1988, 36(10): 1553–1560. doi: 10.1109/29.7543 [107] YIN Jiexin, WANG Ding, WU Ying, et al. Single-step localization using multiple moving arrays in the presence of observer location errors[J]. Signal Processing, 2018, 152: 392–410. doi: 10.1016/j.sigpro.2018.06.009 [108] OISPUU M and NICKEL U. Direct detection and position determination of multiple sources with intermittent emission[J]. Signal Processing, 2010, 90(12): 3056–3064. doi: 10.1016/j.sigpro.2010.05.010 [109] SARENI B and KRAHENBUHL L. Fitness sharing and niching methods revisited[J]. IEEE Transactions on Evolutionary Computation, 1998, 2(3): 97–106. doi: 10.1109/4235.735432 [110] LI Xiaodong. Niching without niching parameters: Particle swarm optimization using a ring topology[J]. IEEE Transactions on Evolutionary Computation, 2010, 14(1): 150–169. doi: 10.1109/TEVC.2009.2026270 [111] LI Xiaodong. Erratum to "niching without niching parameters: Particle swarm optimization using a ring topology"[J]. IEEE Transactions on Evolutionary Computation, 2010, 14(4): 665–665. doi: 10.1109/TEVC.2010.2050024 [112] WANG Ding, YIN Jiexin, LIU Ruirui, et al. Robust direct position determination methods in the presence of array model errors[J]. EURASIP Journal on Advances in Signal Processing, 2018, 2018(1): 38. doi: 10.1186/s13634-018-0555-7 [113] BIALER O, RAPHAELI D, and WEISS A J. Maximum-likelihood direct position estimation in dense multipath[J]. IEEE Transactions on Vehicular Technology, 2013, 62(5): 2069–2079. doi: 10.1109/TVT.2012.2236895 [114] BAR-SHALOM O and WEISS A J. Direct emitter geolocation under local scattering[J]. Signal Processing, 2015, 117: 102–114. doi: 10.1016/j.sigpro.2015.05.003 [115] PICARD J S and WEISS A J. Direct position determination sensitivity to NLOS propagation effects on Doppler-shift[J]. IEEE Transactions on Signal Processing, 2019, 67(14): 3870–3881. doi: 10.1109/TSP.2019.2923152 [116] WU Guizhou, ZHANG Min, and GUO Fucheng. Self-Calibration direct position determination using a single moving array with sensor gain and phase errors[J]. Signal Processing, 2020, 173: 107587. doi: 10.1016/j.sigpro.2020.107587 [117] MA Fuhe, LIU Zhangmeng, and GUO Fucheng. Direct position determination in asynchronous sensor networks[J]. IEEE Transactions on Vehicular Technology, 2019, 68(9): 8790–8803. doi: 10.1109/TVT.2019.2928638 [118] WU Guizhou, ZHANG Min, and GUO Fucheng. On the use of a calibration emitter for direct position determination with single moving array in the presence of sensor gain and phase errors[J]. Digital Signal Processing, 2020, 102: 102734. doi: 10.1016/j.dsp.2020.102734 [119] BAR-SHALOM O and WEISS A J. Emitter geolocation using single moving receiver[J]. Signal Processing, 2014, 105: 70–83. doi: 10.1016/j.sigpro.2014.05.006 [120] WANG Hui, YI Jianxin, and WAN Xianrong. A fast direct cartesian localization in single frequency networks-based MIMO passive radar[C]. 2016 CIE International Conference on Radar (RADAR), Guangzhou, China, 2016: 1–4. [121] 余婉婷, 于宏毅, 杜剑平, 等. 辐射源信号波形已知的超视距目标直接定位方法[J]. 电子学报, 2019, 47(11): 2368–2377. doi: 10.3969/j.issn.0372-2112.2019.11.019YU Wanting, YU Hongyi, DU Jianping, et al. A direct position determination method for over-the-Horizon target on known radiation source waveforms[J].Acta Electronica Sinica, 2019, 47(11): 2368–2377. doi: 10.3969/j.issn.0372-2112.2019.11.019 [122] YI Wei, ZHOU Tao, AI Yue, et al. Suboptimal low complexity joint multi-target detection and localization for non-coherent MIMO radar with widely separated antennas[J]. IEEE Transactions on Signal Processing, 2020, 68: 901–916. doi: 10.1109/TSP.2020.2968282 [123] ZHANG Siwei, STAUDINGER E, JOST T, et al. Distributed direct localization suitable for dense networks[J]. IEEE Transactions on Aerospace and Electronic System, 2020, 56(2): 1209–1227. doi: 10.1109/TAES.2019.2928606 [124] 王裕旗, 孙光才, 杨军, 等. 基于长合成孔径的辐射源成像定位算法[J]. 雷达学报, 2020, 9(1): 185–194. doi: 10.12000/JR19080WANG Yuqi, SUN Guangcai, YANG Jun, et al. Passive localization algorithm for radiation source based on long synthetic aperture[J]. Journal of Radars, 2020, 9(1): 185–194. doi: 10.12000/JR19080 [125] XIA Wei and LIU Wei. Distributed adaptive direct position determination of emitters in sensor networks[J]. Signal Processing, 2016, 123: 100–111. doi: 10.1016/j.sigpro.2016.01.002 [126] XIA Wei, XIA Xinglong, LI Hongbin, et al. A noise-constrained distributed adaptive direct position determination algorithm[J]. Signal Processing, 2017, 135: 9–16. doi: 10.1016/j.sigpro.2016.12.028 [127] 朱颖童, 董春曦, 董阳阳, 等. 去中心化时差频差直接定位方法[J]. 航空学报, 2017, 38(5): 233–245.ZHU Yingtong, DONG Chunxi, DONG Yangyang, et al. Decentralized direct position determination method based on TDOA and FDOA[J]. Acta Aeronautica et Astronautica Sinica, 2017, 38(5): 233–245. [128] XIN Chen, DING Wang, YIN Jiexin, et al. A direct position-determination approach for multiple sources based on neural network computation[J]. Sensors, 2018, 18(6): 1925. doi: 10.3390/s18061925 [129] 陈鑫, 王鼎, 唐涛, 等. 阵列模型误差条件下直接定位性能分析及偏差修正方法[J]. 电子学报, 2019, 47(8): 1633–1642. doi: 10.3969/j.issn.0372-2112.2019.08.005CHEN Xin, WANG Ding, TANG Tao, et al. Performance analysis and deviation correction method of direct position determination in the presence of array modeling errors[J]. Acta Electronica Sinica, 2019, 47(8): 1633–1642. doi: 10.3969/j.issn.0372-2112.2019.08.005 -
图(12) / 表(2)
计量
- 文章访问数: 7503
- HTML全文浏览量: 2827
- PDF下载量: 824
- 被引次数: 0
