作者中心
专家审稿
责编办公
编辑办公
Distributed Radar Main-lobe Interference Suppression Method Via Joint Optimization of Array Configuration and Subarray Element Number
-
摘要: 针对单基雷达无法有效抑制伴随式主瓣压制干扰的问题，可通过部署稀疏辅助阵形成等效大孔径阵列，从空域上将主瓣干扰与目标进行分离，但该方法易形成空域栅瓣。针对以上问题，该文提出了一种基于阵列构型与阵元数量双参数迭代优化框架，该框架由阵列构型优化与子阵阵元数量优化两部分组成，其中阵列构型优化固定子阵阵元数量，基于最小方差无失真响应准则在主瓣干扰方向形成零陷，利用改进自适应遗传粒子群算法在孔径尺寸、子阵最小间距和主瓣干扰方向零陷深度等约束条件下优化阵列构型，抑制波束栅瓣；子阵阵元数量优化通过改进自适应遗传粒子群算法在有限子阵阵元数量、主瓣干扰方向零陷深度等约束条件下优化子阵阵元数量，进一步抑制波束栅瓣。此外，通过数值仿真验证了相同参数条件下阵列构型与阵元数量双参数迭代优化框架的有效性。最后，针对典型分布式机动平台协同探测场景，探索了主瓣干扰抑制和栅瓣抑制性能边界。
-
关键词:
- 分布式雷达 /
- 主瓣干扰抑制 /
- 栅瓣抑制 /
- 双参数迭代优化框架 /
- 改进自适应遗传粒子群算法
Abstract: To address the ineffectiveness of single-base radar in suppressing adjoint main-lobe interference, an equivalent large-aperture array can be designed by deploying sparse auxiliary arrays to separate main-lobe interference from targets in the spatial domain. However, this method is prone to generating spatial grating lobes. To overcome this problem, this study proposes a dual-parameter iterative optimization framework comprising two parts: array configuration optimization and subarray element number optimization. Array configuration optimization caters to the number of subarray elements and creates nulls in the main-lobe interference direction on the basis of the minimum variance distortionless response criterion. To suppress grating lobes of the beam an improved adaptive genetic particle swarm algorithm is used to optimize the array configuration under constraints, such as aperture size, minimum subarray spacing, and null depth in the main-lobe interference direction. Subarray element number optimization uses the above-mentioned algorithm to optimize the number of subarray elements under constraints, such as a limited number of subarray elements and null depth in the main-lobe interference direction, further suppressing beam grating lobes. Finally, numerical simulations confirmed the effectiveness of the dual-parameter iterative optimization framework for array configuration and element number under the same parameter conditions. Additionally, this study explores the performance boundaries of main-lobe interference suppression and grating lobe suppression for typical distributed mobile platform cooperative detection scenarios. -
1. 引言
目标的振动、转动等微动产生的微多普勒效应包含了目标的结构和运动信息，常用于目标的分类和识别[1–3]。目前，基于外辐射源雷达微多普勒效应目标分类和识别的研究还处于起步状态。外辐射源雷达是一种利用非合作照射源进行目标探测和分类识别的新体制雷达系统，其自身不辐射电磁能量，具有节约频谱资源，隐蔽性好，设备规模小，易于部署和组网等特点[4–6]。在微多普勒效应目标分类和识别方面，外辐射源雷达表现出得天独厚的优势：(1)收发分置可实现空间分集，有效避免探测盲区。(2)第三方辐射源多为连续波，长时间相干积累可记录多个连续的回波闪烁，同时有利于提高对低雷达散射截面积(Radar Cross-Section, RCS)微动目标的探测与分类识别能力。(3)对微多普勒特征的提取不要求高距离分辨率，参数估计不受第三方辐射源带宽的限制[7,8]。
针对微多普勒效应参数估计问题。文献[9,10]中依据微动目标正弦特征曲线，利用 Hough变换，在参数域中进行多维搜索提取出微动曲线进行参数估计。文献[11,12]通过正交匹配追踪(Orthogonal Matching Pursuit, OMP)算法进行稀疏逼近实现了微动目标参量的估计。上述方法均具有较好的鲁棒性，但由于估计参量维数较高导致计算量巨大。文献[13]利用微动目标在时频域的周期性，采用循环相关系数方法，实现了目标微动周期的估计，但信号周期较长时计算量急剧增加。文献[14]计算了信号的高阶矩函数，通过检测在不同时延下，高阶虚函数部分傅里叶变换累计结果的峰值位置，快速获得目标的旋转速率，相比于图像处理方法和OMP分解方法，计算复杂度较小，但抗噪性能差。而外辐射源雷达所利用的第三方辐射源多为连续波信号，其发射波形不可控，信号能量主要覆盖地面，杂波环境复杂且对空中目标增益低，利用长时间相干积累来提高处理增益会带来数据量巨大的挑战。上述因素决定了外辐射源雷达参数估计方法需要有良好的抗噪性能且计算量要小。
直升机旋翼旋转时对雷达信号产生周期性调制，当叶片发生镜面反射时，旋翼回波出现峰值，即回波闪烁。闪烁信号在时频图像中表现为一定宽度的频率带，且闪烁时间、闪烁间隔与直升机旋翼微动参数密切相关。针对外辐射源雷达参数估计问题，本文结合上述时频域中闪烁信号的特点，通过时频分析和正交匹配追踪算法实现了直升机旋翼微动参数的估计。本文首先给出了外辐射源雷达直升机旋翼微动信号模型，其次介绍了如何在时频图中提取出闪烁信号参数及正交匹配追踪算法对直升机旋翼微动参数的估计，最后仿真和实测证明了本文方法的有效性。
2. 外辐射源雷达直升机旋翼回波模型的建立
直升机旋转叶片与外辐射源雷达的位置关系如图1所示。以直升机旋转叶片的中心点为原点
o ，旋转叶片平面为xy 面，x 轴平行于发射站与接收站所在直线，建立空间坐标系(x,y,z) 。直升机相对于发射站和接收站距离为rT, rR ，方位角为γ, α ，仰角为βT, βR (cosβT≈cosβR=cosβ) 。叶片上某一散射点p 到原点o 距离为lP ，方位角为φt 。假设直升机平动得到补偿。在
t 时刻，从发射站经散射点p 到接收站的距离为：rP(t)=||RT −RP(t)||+||RR−RP(t)|| (1) 其中
RT, RR, RP(t) 分别为发射站、接收站、散射点p 在坐标系xyz 中的位置矢量。参考文献[1]中单基地直升机建模，将叶片看作线模型，外辐射源雷达直升机旋翼回波可表示为：
s(t)=Lexp{−j2πλ(rR+rT)}N∑k=1sinc{−ϕk(t)}⋅exp{jϕk(t)} (2) 其中，
ϕk(t)=−4πλL2cosβcos(α−γ2)cos(φk(t)) (3) φk(t)=2πfrt+φ0+(k−1)2π/N−α+γ2 (4) fr 为叶片转速，L 为叶片长度，N 为叶片数量，整数k (0<k≤N) 表示第k 个叶片，φ0 为叶片初相，λ 为照射源信号波长。由式(3)得第
k 个叶片引起的瞬时多普勒频移为：fk(t)=2πfrLλcosβcos(α−γ2)sin(φk(t)) (5) 由式(2)可知时域信号幅值受
sinc 函数调制，结合式(3)知当φk(t) 满足式(6)时，ϕk(t)=0 ，时域信号幅值最大，此刻即时域闪烁。φk(t)=±π2+2πn (6) 由式(2)知连续两个闪烁之间的时间间隔为：
Δt={12N⋅fr,N为奇数1N⋅fr, N为偶数 (7) 3. 直升机旋翼参数估计
3.1 时频分析提取闪烁信号参数
直升机旋翼回波的微多普勒呈非线性变化，通过对目标回波信号进行时频分析能够揭示信号频率的时变特性。短时傅里叶变化(Short-Time Fourier Transform, STFT)计算简单，且不产生交叉项。对直升机旋翼回波信号
s(t) 进行STFT到时频域TF(t,f)=∫s(τ)w(τ−t)e−j2πfτdτ (8) 其中，
w(t) 为窗函数。旋翼微多普勒效应特征曲线为正弦曲线，对应时域闪烁出现的时刻出现垂直于时间横轴的频率带，即时频域“闪烁”[15]。图2为直升机旋翼回波的时频图。当直升机旋翼的叶片数为奇数时(图2(a))，时频域中正负多普勒“闪烁”交替出现；若旋翼叶片数为偶数(图2(b))，则是同时出现。
设时频域中正频率“闪烁”发生的时间为
t0 ，由式(5)和式(6)知t0 满足：φk(t0)=π2+2πn(n为整数) (9) 由式(4)和式(9)得第
k 个叶片初相与叶片数量的关系：φ0={−πt0Δt1N−2π(k−1)1N+φ1, N为奇数−2πt0Δt1N−2π(k−1)1N+φ1,N为偶数 (10) 其中
φ1=α+γ2+2πn+π2(0≤φ0<2π) (11) 由于时频图像中闪烁信号频率带垂直于时间横轴，对正频率轴数据幅值进行累加计算，并判断累加后数据局部峰值点，可得到时频域中正频率“闪烁”发生的时间。同样，对负频率轴数据幅值进行累加计算得到时频域中负频率“闪烁”发生的时间。相应的也可得到闪烁间隔。
由式(7)知，闪烁间隔与旋翼转速、叶片数量密切相关。由式(10)知，闪烁发生的时间与叶片初相、叶片数量、整数
k 密切相关。因此，可根据得到的闪烁间隔，用叶片数量表示出旋翼转速。根据得到的闪烁时间，用叶片数量、整数k 表示出第k 个叶片初相。3.2 OMP估计直升机旋翼参数
由式(2)知时域回波信号可分解为：
s(t)=M∑m=1cmgm(t;Λ)=Dα (12) 其中，
gm 为第m 个原子，D 为以原子为列张成的字典矩阵D=[g1 g2 g3···gM] ∈CNt×M, M 为原子个数，Nt 为时间t 离散后的取值个数，Λ 为要估计的参量，cm 为原子系数，α∈CM 为系数矢量，是稀疏的。可转化最优l0 范数问题进行稀疏向量求解。OMP常用于求解此类问题，通过构建字典矩阵，不断选定与信号最匹配的原子进行稀疏逼近[16]。OMP将字典矩阵中原子正交化保证了迭代的最优性。由式(2)知直升机旋翼回波信号由参数
(fr,L,φ0,N,k) 确定。利用叶片数量N 、整数k (0<k≤N) 与旋翼转速和叶片初相的关系式(7)和式(10)，时域回波可转化为参数(L,N,k) 来表示。设时间采样点数Nt ，目标回波为Nt×1 的矩阵。确定待估参数的取值范围并离散化，叶片长度取值：L∈(L1,···,Lr,···,LNL) ，叶片数量N 的可能取值为：N∈(N1,···,Np,···,NNN) ，整数k 的取值为k∈(1,···,kq,···,kNq) (kNq≤NNN) 。由OMP算法原理可知，字典中的原子可按照待分解信号的内在特性来构造[16]。根据微动目标的时域回波表达式(2)，第
m 个原子可表示为：a(m)=sinc(ϕ(Lr,Np,kq))⋅exp{−jϕ(Lr,Np,kq)} (13) 其中
m=rpq (14) 并对原子集里的每个原子进行能量归一化：
a(m)←a(m)/‖a(m)‖F (15) 其中，
‖⋅‖F 表示矩阵的F范数。将5参量
(fr,L,φ0,N,k) 的估计转换为3参量(L,N,k) 估计，NL, NN, Nk 分别为L, N, k 的取值个数，由于常见直升机主旋翼叶片数量为：3片、5片、7片(奇数)，2片、4片、8片(偶数)，NN, Nk 较小，降低字典维数为：NL×Nk×NN ，可达到降低计算量的目的。3.3 直升机旋翼参数估计流程
直升机旋翼参数估计具体步骤如下：
步骤1 对直升机旋翼信号进行短时傅里叶变换，得到时频图像
TF(t,f) 。步骤2 对时频图中正频率轴数据幅值进行累加计算，并判断累加后数据局部峰值点，对应时频域正频率“闪烁”发生的时间。同样，对负频率轴数据幅值进行累加计算得到时频域中负频率“闪烁”发生的时间。
步骤3 根据步骤2中正负频率“闪烁”发生的时间，判别时频域中正负多普勒“闪烁”是否交替出现。若是，则旋翼叶片数为奇数，否则，旋翼叶片数为偶数。
步骤4 读取某一正频率闪烁发生的时间
t0 及闪烁间隔Δt 。依据式(7)用叶片数量N 表示出旋翼转速，依据式(10)和式(11)用叶片数量N 及整数k 表示出第k 个叶片初相。步骤5 确定
(L,N,k) 的取值范围并离散化：L∈(L1,···,Lr,···,LNL) ,N∈(N1,···,Np,···,NNN) ,k∈(1,···,kq,···,kNq) (kNq≤NNN) 。利用步骤4中表示出的旋翼转速及初相，依据式(13)和式(15)构建字典矩阵。步骤6 利用OMP算法寻找叶片数量，叶片长度的最优值，代入式(7)计算出旋翼转速，代入式(10)和式(11)计算出叶片初相。
4. 仿真验证
4.1 仿真结果分析
结合上述模型对直升机旋翼回波信号进行仿真，仿真参数设置如表1所示。
表 1 外辐射源雷达直升机旋翼回波模型仿真参数Table 1. Simulation parameters of helicopter rotor echo model for passive radar信号载频 叶片数 叶片长度 旋转速率 发射站方位角 接收站方位角 发射站仰角 接收站仰角 SNR 658 MHz 3 5 m 200 rpm 33° 76° 23° 23° –5 dB 图3(a)显示了信号的联合时频域特征，可看出闪烁信号及噪声严重影响直升机旋翼微多普勒特征曲线的检测，使微多普勒特征曲线提取困难。
分别对时频图像中正负频率轴数据幅值进行累加计算，得到时频域中正负多普勒“闪烁”时间，如图3(b)所示，图中正负多普勒“闪烁”等间隔交替出现，则旋翼叶片数为奇数。读取闪烁信号时间间隔为0.05 s，根据式(7)表示出旋翼转速为：
fr=10/N (16) 读取某一正频率闪烁信号对应时刻为0.066 s(此处选择了图3(b)中的第1个正频率闪烁信号)，根据式(10)和式(11)表示出第
k 个叶片初相为：φ0=−4.14/N−6.28×(k−1)/N+2.52 (17) 图3(c)为利用OMP方法对
(L,N,k) 的估计结果，得到叶片数为3片，图中给出了其对应的切面图，3叶片长度分别4.99 m, 5.00 m, 4.98 m，均值4.99 m，与理论基本一致，代入式(17)得3叶片初相分别为1.14 rad, 3.24 rad, 5.34 rad，代入式(16)得旋翼转速为200 rpm，与理论值一致，本文方法准确实现了直升机旋翼参数估计。图4为利用常规Hough变换，通过微多普勒曲线
f=fmax 检测对参数({f\!_r},{\varphi _0},L) 的估计结果。其中{f_{\max }} 为最大频移。{f_{\max }} = \frac{{4{{π}} {f\!_r}L}}{\lambda }\cos\beta \cos\left( \frac{{\alpha - \gamma }}{2}\right) (18) 图4中给出了参数空间中局部峰值点中心位置。可得到直升机旋翼转速为200 rpm。3叶片最大频移分别为385.6 Hz, 393.9 Hz, 389.8 Hz，平均值为390.0 Hz，由式(18)计算得叶片长度为4.96 m，与理论值基本一致。3叶片初相分别为0.91 rad, 3.16 rad, 5.24 rad，利用式(4)对初相进行修正，得到3叶片初相位为1.86 rad, 4.11 rad, 6.19 rad，存在较大的误差，是由于STFT受不确定原理的限制，时频图像中时频分辨率受限使参数空间中的局部峰值点扩展范围较大，只能大致估计局部峰值点的位置，估计结果精度较低。
4.2 计算复杂度分析
设待处理的时频图像大小为
{N_t} \times {N_f} 像素，{N_f} \approx {N_t} ，利用常规的Hough变换对微多普勒曲线f = {f_{\max }}\sin(2{{π}} {f\!_r}t{\rm{ + }}{\varphi _0}) 进行检测，参数({f\!_r},{\varphi _0},L) 分别量化为{N_{f_{r}}} ,{N_{{\varphi _0}}} ,{N_L} 份。乘法次数可近似表示为：2{N_{f_{r}}}{N_{{\varphi _0}}}{N_L}{N_t}^{\!2} 。直接使用OMP进行参数
({f\!_r},{\varphi _0},L) 估计时，设迭代次数为K，乘法次数近似表示为：K{N_{f\!_{r}}}{N_{{\varphi _0}}} {N_L}{N_t}^{\!2} 。本文方法计算量集中在OMP阶段，根据提取的时频域中的闪烁时间，依据式(7)和式(10)，最终转化为对参数
(L,N,k) 的估计，常见直升机的叶片数只有若干个取值，且由3.1节方法可判断出叶片数量的奇偶性，{N_N}{N_k} 远小于{N_{f_{r}}}{N_{{\varphi _0}}} 。本文方法乘法次数近似表示为：K{N_N}{N_k}{N_L}{N_t}^{\!2} 。在对直升机旋翼微动参数估计时，一般
{N_N}{N_k} 取值量级为101～102，迭代次数K的取值量级为{10^0} {\text ～} {10^1} ，当初相{\varphi _0} 的估计精度为7°时，2{N_{{\varphi _0}}} 取值量级为102，当转速{f_r} 的估计精度为10 rpm时，{N_{f_{r}}} 的取值量级为{10^1} ，在乘法次数上，常规 Hough变换参数估计方法为本文方法{10^0}{\text ～} {10^2} 倍，当进一步提高{f_r}, {\varphi _0} 的估计精度时，算法之间的计算量差距将进一步变大。本文在相同的配置环境下，利用Matlab仿真平台，常规Hough变换方法运行时长13006 s，而本文方法运行总时长只有145 s。5. 实验结果
5.1 实验场景
武汉大学电波传播实验室对EC_120B直升机进行了微多普勒效应探究外场实验，EC_120B直升机主旋翼3叶片，叶片长度5 m，额定转速406 rpm，实验中以武汉龟山电视塔数字电视信号为照射源，信号中心频率为658 MHz，带宽8 MHz，接收站位于武汉大学电波传播实验室楼顶，距离发射站7.56 km，实验场景如图5所示。本组实测数据相干积累时间0.8 s，可近似认为目标在这段时间位置不变，直升机旋翼转速为常量。
5.2 实验结果分析
图6(a)为去除目标主体影响后，对直升机旋翼回波信号进行短时傅里叶变换后的时频图像。可以观察到闪烁信号，但微多普勒特征曲线已观察不到。分别对时频图像中正负频率轴数据幅值进行累加计算，得到时频域中正负多普勒“闪烁”时间，如图6(b)所示，图中正负多普勒“闪烁”等间隔交替出现，则旋翼叶片数为奇数。
读取闪烁信号时间间隔为26.2 ms，根据式(7)用
N 表示出旋翼转速。读取某一正频率闪烁时间对应时间为0.25 s，利用式(10)和式(11)表示出第k 个叶片初相，图6(c)为利用OMP方法对(L,N,k) 的估计结果，得到叶片数量为3片，3叶片长度分别为4.93 m, 5.00 m, 4.66 m，均值4.86 m，存在较小的误差，与仰角，方位角估计不精确有关，由式(7)知旋翼转速均为382 rpm，符合实际情况。6. 结束语
本文根据外辐射源雷达直升机旋翼微动信号模型，充分利用时频域中闪烁信号特征和微动信号内在特性进行了参数估计。通过时频分析和正交匹配追踪算法，估计出了旋翼转速、叶片长度、叶片数量和初相。同时开展了外场实验。仿真数据和实测数据处理都表明本文方法对外辐射源雷达直升机旋翼参数估计的可行性。
-
图 5 3种算法 \gamma 与迭代次数k变化
Figure 5. \gamma versus iteration number k for three algorithms
图 7 不同 {d_{\min }} 下 \gamma 与迭代次数t关系
Figure 7. \gamma versus iteration number t for different {d_{\min }}
图 8 不同 {P_{\text{m}}} 下 \eta 与优化次数t关系
Figure 8. \eta versus iteration number t for different {P_{\text{m}}}
图 9 不同优化方式 \eta 与迭代次数t关系
Figure 9. \eta versus iteration number t for different optimization methods
图 10 不同优化方式归一化方向图
Figure 10. Normalized beampattern for different optimization methods
图 12 主雷达回波信号脉压结果与分布式雷达回波信号处理后的脉压结果
Figure 12. Main radar echo signal pulse compression result and distributed radar echo signal processed pulse compression result
图 13 主雷达不同位置 \eta 与迭代次数t关系
Figure 13. \eta versus iteration number t for different main radar position
图 14 方向图增益与试验次数n关系
Figure 14. Relationship between pattern gain and number of trials n
1 DPIOF算法流程
1. DPIOF algorithm flow
输入： {{\tilde {\boldsymbol{l}}}^{\left( 0 \right)}} , {{{\boldsymbol{m}}}^{\left( 0 \right)}} , T, P, {P_{\text{m}}} , H； 输出： {{\tilde {\boldsymbol{l}}}_{{\text{opt}}}} , {{{\boldsymbol{m}}}_{{\text{opt}}}} , {\eta _{{\text{opt}}}} ； 1： t = 0 ； 2： t = t + 1 ， h = 0 ； 3： h = h + 1 ； 4： 固定 {{\boldsymbol{m}}}_{{\text{opt}}}^{\left( {t - 1,H} \right)} ，利用IAG-PSO算法更新 {{\tilde {\boldsymbol{l}}}^{\left( {t,h} \right)}} ，得到目标
函数值 {\gamma ^{\left( {t,h} \right)}} ；5： 如果 {\gamma ^{\left( {t,h} \right)}} < {\gamma ^{\left( {t - 1,H} \right)}} ，令 {\tilde {\boldsymbol{l}}}_{{\text{opt}}}^{\left( {t,h} \right)} = {{\tilde {\boldsymbol{l}}}^{\left( {t,h} \right)}} , \gamma _{{\text{opt}}}^{\left( {t,h} \right)} = {\gamma ^{\left( {t,h} \right)}} ；
否则， {\tilde {\boldsymbol{l}}}_{{\text{opt}}}^{\left( {t,h} \right)} = {{\tilde {\boldsymbol{l}}}^{\left( {t - 1,H} \right)}} , \gamma _{{\text{opt}}}^{\left( {t,h} \right)} = {\gamma ^{\left( {t - 1,H} \right)}} ；6： 固定 {\tilde {\boldsymbol{l}}}_{{\text{opt}}}^{\left( {t,h} \right)} ，利用IAG-PSO算法更新 {{{\boldsymbol{m}}}^{\left( {t,h} \right)}} ，得到目标函数
值 {\eta ^{\left( {t,h} \right)}} ；7： 如果 {\eta ^{\left( {t,h} \right)}} < {\eta ^{\left( {t - 1,H} \right)}} ，令 {{\boldsymbol{m}}}_{{\text{opt}}}^{\left( {t,h} \right)} = {{{\boldsymbol{m}}}^{\left( {t,h} \right)}} , \eta _{{\text{opt}}}^{\left( {t,h} \right)} = {\eta ^{\left( {t,h} \right)}} ；
否则， {{\boldsymbol{m}}}_{{\text{opt}}}^{\left( {t,h} \right)} = {{{\boldsymbol{m}}}^{\left( {t - 1,H} \right)}} , \eta _{{\text{opt}}}^{\left( {t,h} \right)} = {\eta ^{\left( {t - 1,H} \right)}} ；8： 如果 h < H ，继续步骤3； 9： 如果 t = T ，结束；否则， {\text{Initial}}\left( {{\tilde {\boldsymbol{l}}}_{{\text{opt}}}^{\left( {t,h} \right)}} \right) ，令 {{\boldsymbol{m}}}_{{\text{opt}}}^{\left( {t,H} \right)} = {{{\boldsymbol{m}}}^{\left( 0 \right)}} ，
继续步骤2。
下载: 导出CSV
2 基于IAG-PSO算法求解流程
2. IAG-PSO algorithm solution flow
输入： {\text{Initial}}( {{\tilde {\boldsymbol{l}}}_{{\text{opt}}}^{\left( t \right)}} ) , P, {\text{NP}} , {w_{\max }} , {w_{\min }} , {p_{\text{c}}} , {p_{\text{m}}} , K，速度和位置边界条件； 输出： {{\tilde {\boldsymbol{l}}}^{\left( {t + 1} \right)}} , {\gamma ^{\left( {t + 1} \right)}} ； 1： k = 0 ，得到初始化后的新种群，计算种群中所有个体适应度 {\gamma ^{\left( 0 \right)}}\left( j \right) ， j = 1,2, \cdots ,{\text{NP}} ，得到 \gamma _{\min }^{\left( 0 \right)} , \gamma _{\text{u}}^{\left( 0 \right)} , {{\boldsymbol{p}}}_{{\text{best}}}^{\left( 0 \right)} , {{\boldsymbol{g}}}_{{\text{best}}}^{\left( 0 \right)} ； 2： k = k + 1 ； 3： 计算 c_1^{\left( k \right)} 和 c_2^{\left( k \right)} ，计算种群中个体j权值 w_{j}^{\left( k \right)} ，更新其速度和位置信息，越界处理，保留更新后适应度更小的个体，输出更新后种群中
个体j速度 {{\boldsymbol{v}}}_{j}^{\left( k \right)} 和位置 {\tilde {\boldsymbol{l}}}_{j}^{\left( k \right)} ， j = 1,2, \cdots ,{\text{NP}} ；4： 交叉操作，更新交叉池中个体速度 {{\boldsymbol{v}}}_i^{\prime\left( k \right)} 和位置 {\tilde {\boldsymbol{l}}}_i^{\prime\left( k \right)} ，越界处理，保留更新后适应度更小个体， i\left( {i = 1,2, \cdots ,{\text{cp}}} \right) ； 5： 变异操作，更新变异池中个体速度 {{\boldsymbol{v}}}_i^{\prime\prime\left( k \right)} 和位置 {\tilde {\boldsymbol{l}}}_i^{\prime\prime\left( k \right)} ，越界处理，保留更新后适应度更小个体， i\left( {i = 1,2, \cdots ,{\text{mp}}} \right) ； 6： 更新种群个体适应度 {\gamma ^{\left( k \right)}}\left( j \right) ，得到 \gamma _{\min }^{\left( k \right)} , \gamma _{\text{u}}^{\left( k \right)} , {{\boldsymbol{p}}}_{{\text{best}}}^{\left( k \right)} , {{\boldsymbol{g}}}_{{\text{best}}}^{\left( k \right)} ； 7： 如果 k = K ，令 {{\tilde {\boldsymbol{l}}}^{\left( {t + 1} \right)}} = {{\boldsymbol{g}}}_{{\text{best}}}^{\left( K \right)} , {\gamma ^{\left( {t + 1} \right)}} = \gamma _{\min }^{\left( K \right)} ，结束；否则，继续步骤2。
下载: 导出CSV
表 1 仿真参数
Table 1. Simulation parameters
参数 数值 参数 数值 信号载频 {f_0} 10 GHz 主雷达孔径 5 m 目标角度 {\theta _0} 0° 信噪比SNR 20 dB 干扰角度 {\theta _{\rm j}} 0.05° 干噪比INR 20 dB
下载: 导出CSV
表 2 IAG-PSO算法仿真参数
Table 2. IAG-PSO algorithm simulation parameters
参数 数值 参数 数值 种群数量 {\text{NP}} 100 交叉概率 {p_{\text{c}}} 0.8 最大迭代次数K 30 变异概率 {p_{\text{m}}} 0.3 权重最大值 {w_{\max }} 1 基因数量 6 权重最小值 {w_{\min }} 0.4 速度取值范围 [–2,2]
下载: 导出CSV
表 3 辅助雷达阵元数量与 {\boldsymbol{\eta}}
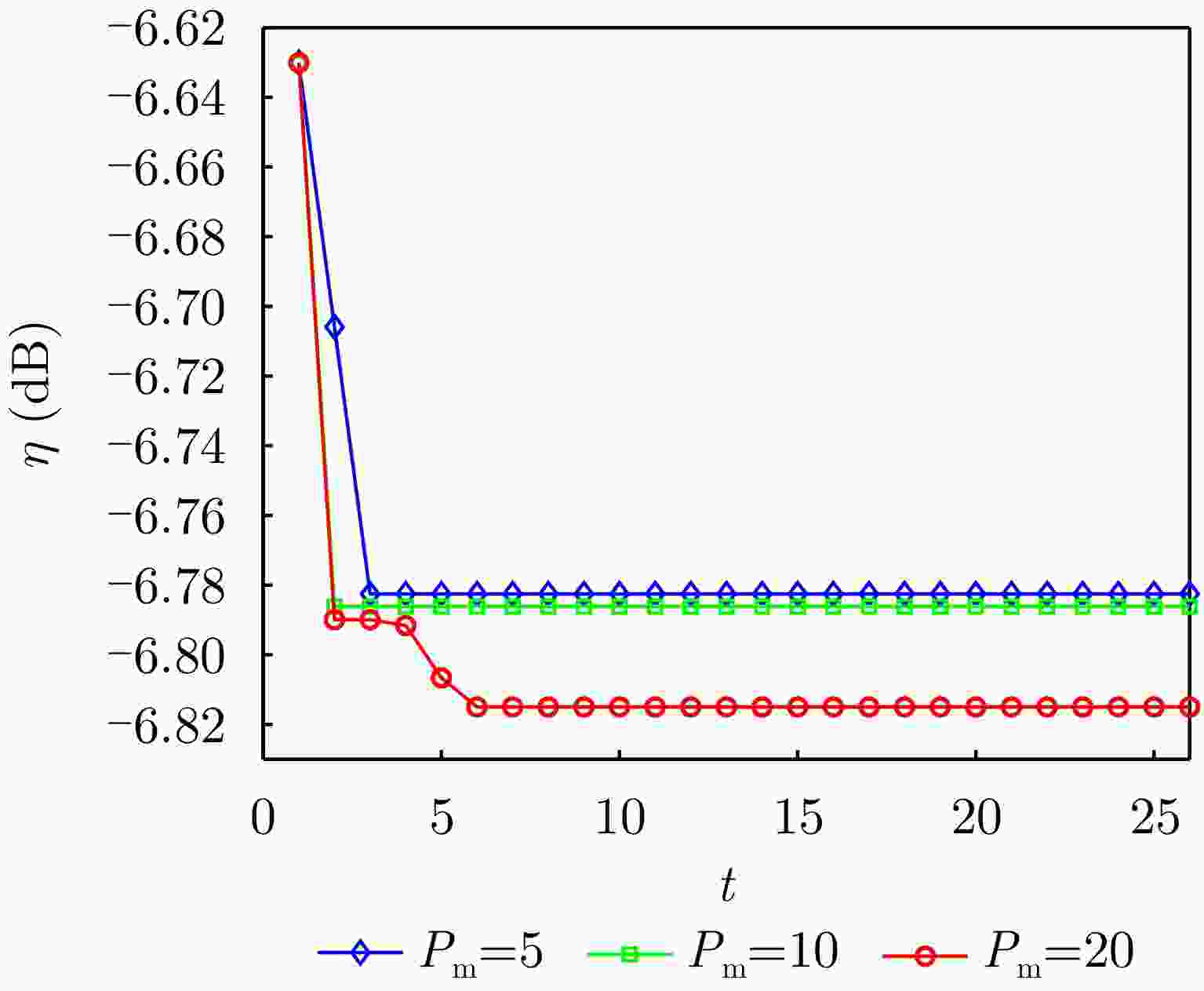
Table 3. The number of auxiliary subarray elements and {\boldsymbol{ \eta}}
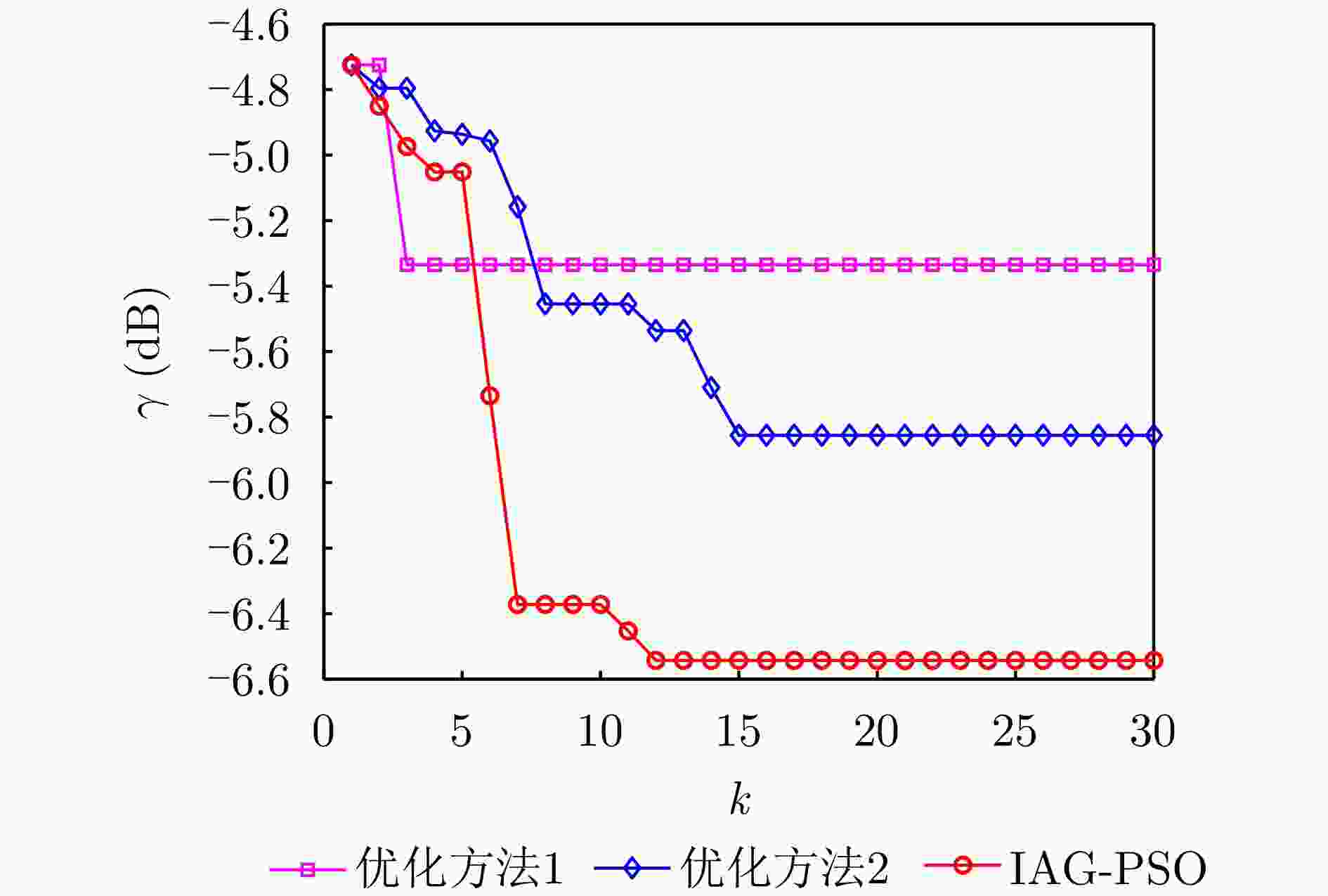
子阵 优化前 优化后 子阵2 61 61 子阵3 61 55 子阵4 61 61 子阵5 61 59 子阵6 61 47 子阵7 61 57 子阵8 61 41 \eta –6.630 dB –6.815 dB
下载: 导出CSV
表 4 不同优化方式的优化结果(dB)
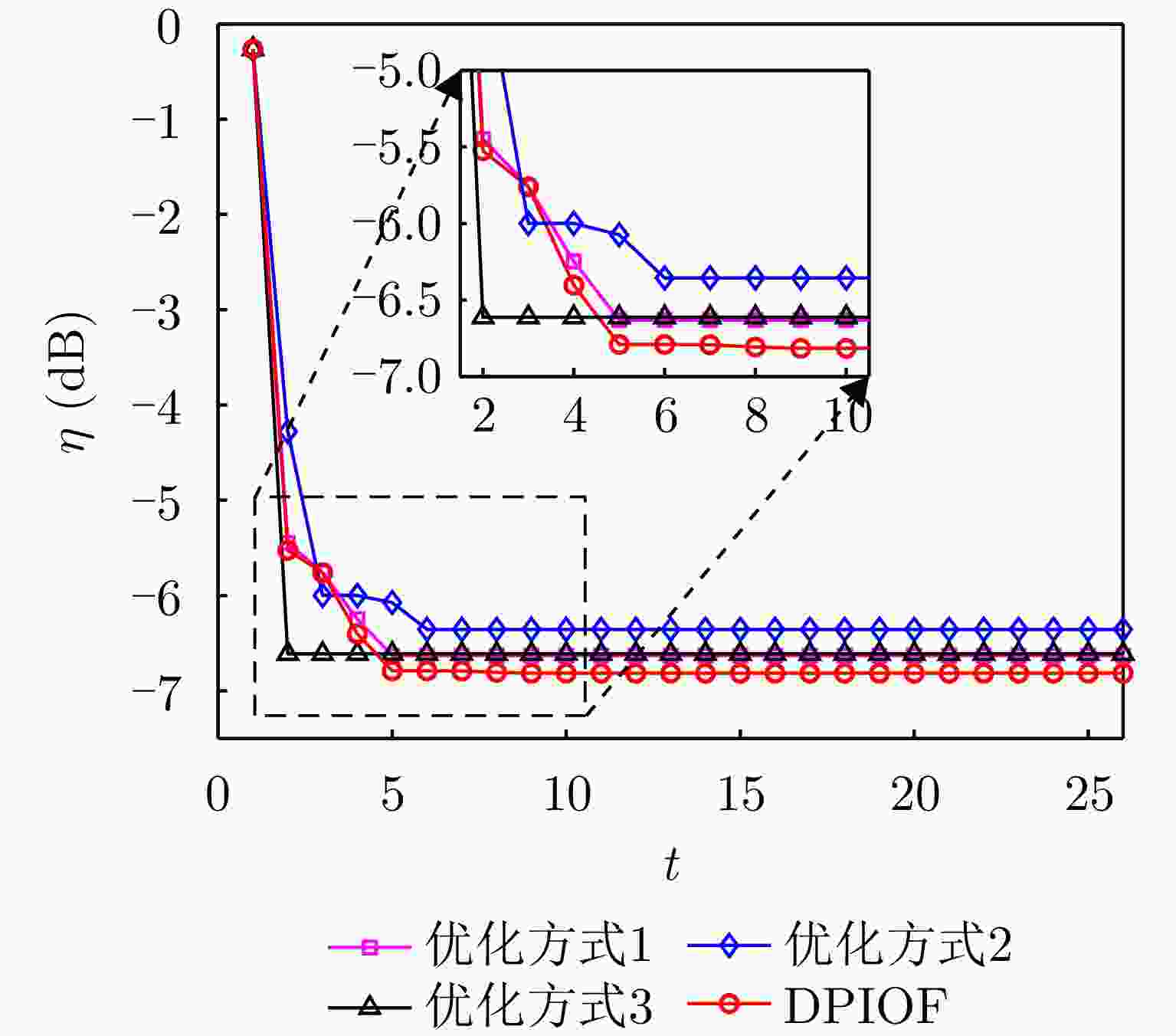
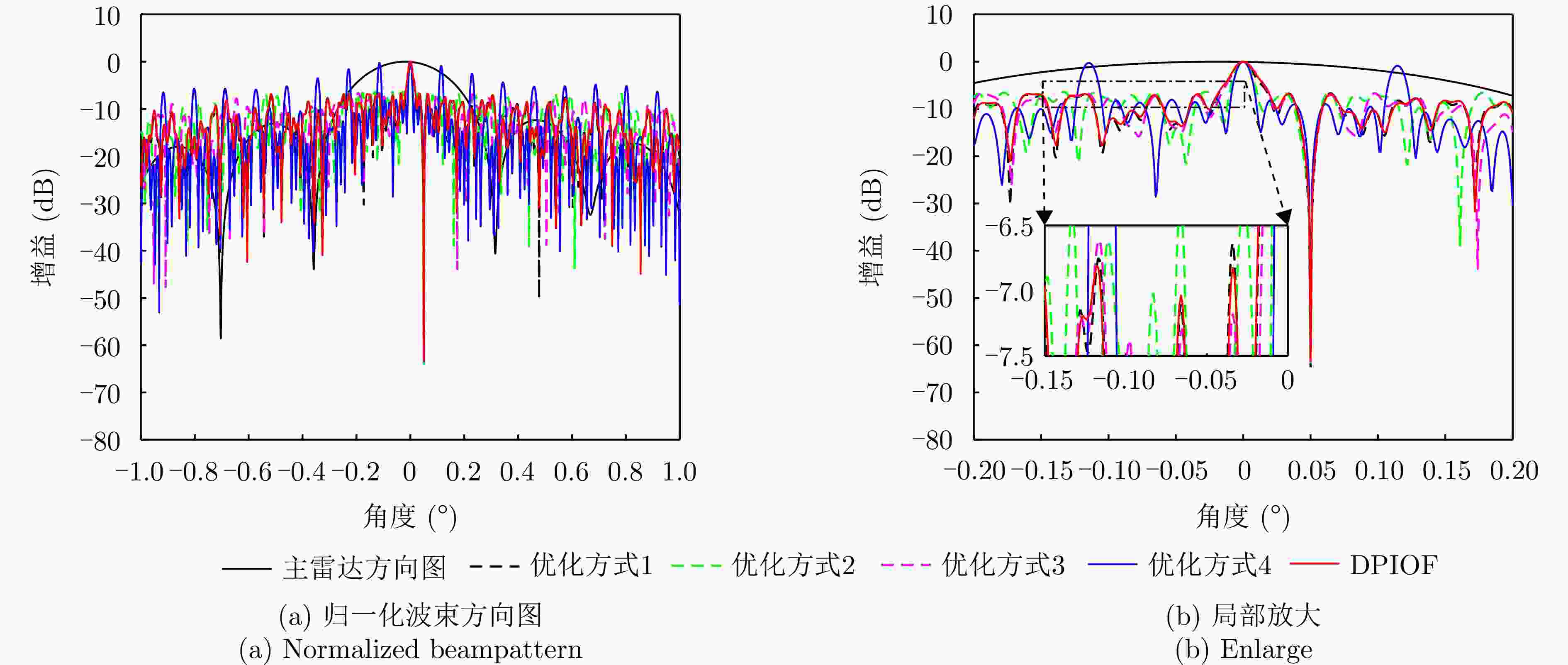
Table 4. Optimization results of different approaches (dB)
优化方式 \eta 优化方式1 –6.630 优化方式2 –6.355 优化方式3 –6.611 优化方式4 –0.265 DPIOF –6.815
下载: 导出CSV
表 5 回波数据的仿真参数
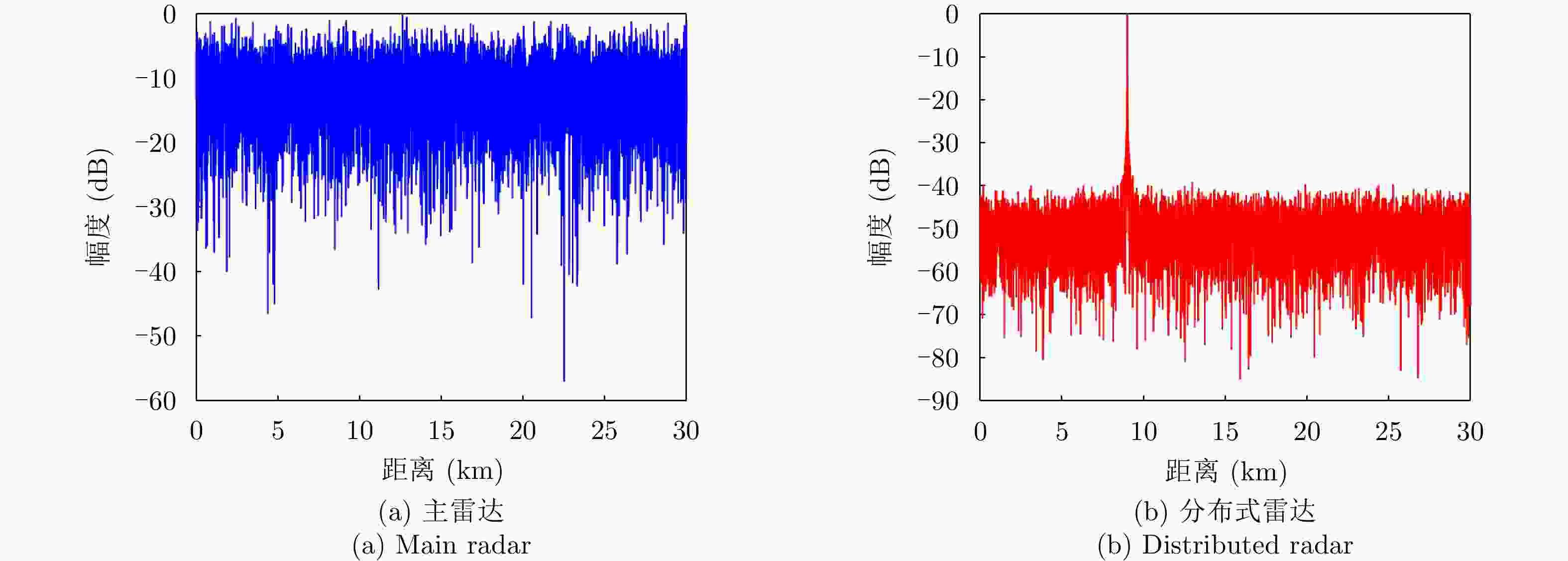
Table 5. Simulation parameters of echo data
参数 数值 参数 数值 信号载频 {f_0} 10 GHz 目标距离 9 km 信号带宽 20 MHz 采样率 50 MHz 信号脉宽 10 μs 干扰类型 噪声干扰 目标角度 {\theta _0} 0° 信噪比SNR –20 dB 干扰角度 {\theta _{\rm j}} 0.05° 干噪比INR 30 dB
下载: 导出CSV
表 6 主雷达不同位置优化结果(dB)
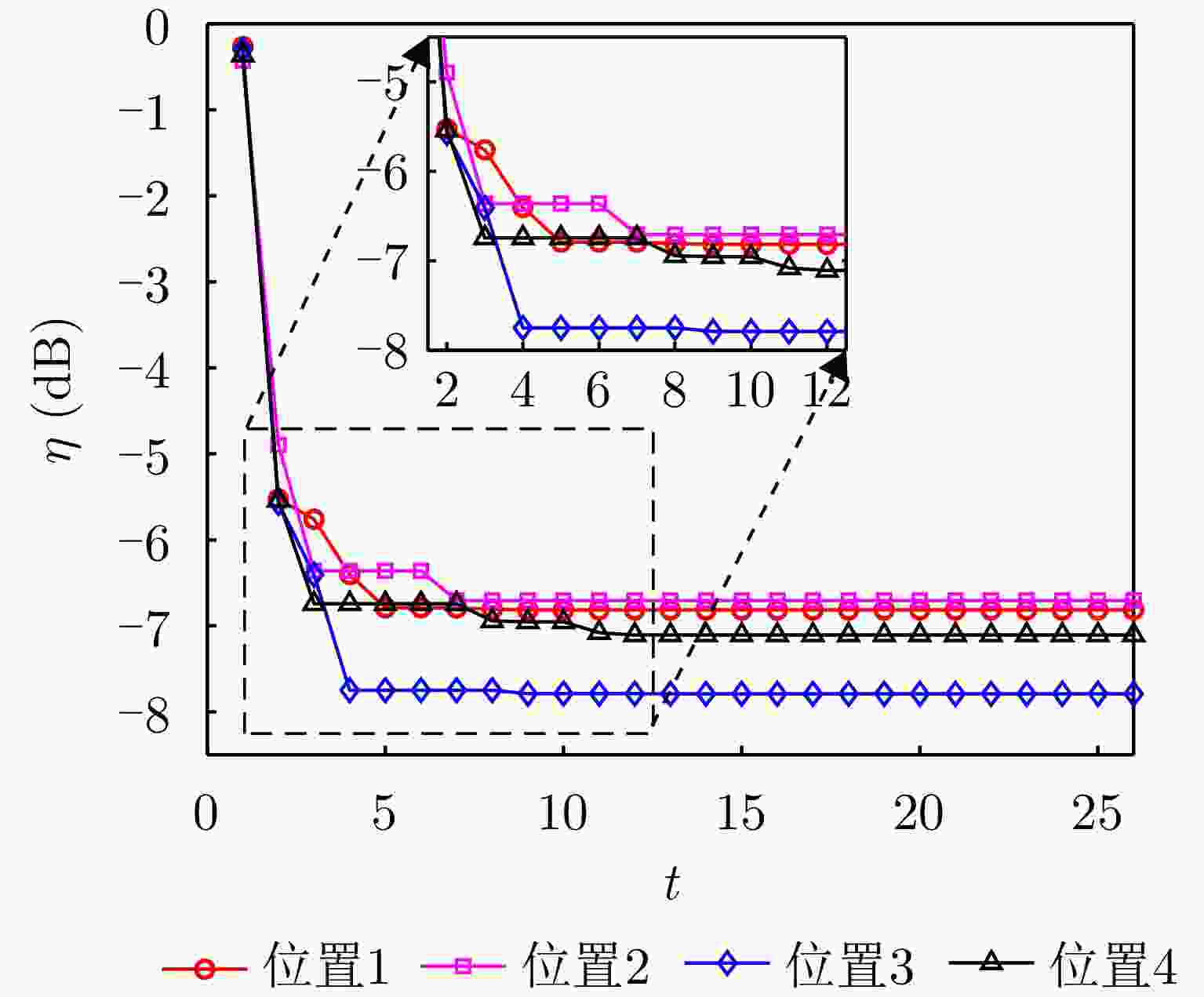
Table 6. Optimization results of different positions of the main radar (dB)
主雷达位置 \eta 位置1 –6.815 位置2 –6.705 位置3 –7.790 位置4 –7.107
下载: 导出CSV
-
[1] 赵国庆. 雷达对抗原理[M]. 2版. 西安: 西安电子科技大学出版社, 2012: 1–4.ZHAO Guoqing. Principle of Radar Countermeasure[M]. 2nd ed. Xi’an: Xidian University Press, 2012: 1–4. [2] KWAK C M. Application of DRFM in ECM for pulse type radar[C]. 2009 34th International Conference on Infrared, Millimeter, and Terahertz Waves, Busan, Korea (South), 2009. doi: 10.1109/ICIMW.2009.5324673. [3] 于恒力. 多站雷达系统协同抗有源干扰方法研究[D]. [博士论文], 西安电子科技大学, 2020: 27–28. doi: 10.27389/d.cnki.gxadu.2020.000015.YU Hengli. Study on active ECCM in multiple-radar systems[D]. [Ph.D. dissertation], Xidian University, 2020: 27–28. doi: 10.27389/d.cnki.gxadu.2020.000015. [4] 方愚渊, 魏嵩, 何超, 等. 雷达对抗技术研究综述与智能反干扰展望[J]. 信息对抗技术, 2024, 3(2): 5–26. doi: 10.12399/j.issn.2097-163x.2024.02.002.FANG Yuyuan, WEI Song, HE Chao, et al. An overview of radar anti-jamming technology and prospect on intelligent jamming-countermeasure game[J]. Information Countermeasure Technology, 2024, 3(2): 5–26. doi: 10.12399/j.issn.2097-163x.2024.02.002. [5] 王永良, 丁前军, 李荣锋. 自适应阵列处理[M]. 北京: 清华大学出版社, 2009: 66–73.WANG Yongliang, DING Qianjun, and LI Rongfeng. Adaptive Array Processing[M]. Beijing: Tsinghua University Press, 2009: 66–73. [6] 张小飞, 李建峰, 徐大专, 等. 阵列信号处理及MATLAB实现[M]. 2版 北京: 电子工业出版社, 2020: 55–60.ZHANG Xiaofei, LI Jianfeng, XU Dazhuan, et al. Array Signal Processing and MATLAB Implementation[M]. 2nd ed. Beijing: Publishing House of Electronic Industry, 2020: 55–60. [7] 李消霞. 动平台分布式雷达干扰抑制方法研究[D]. [硕士论文], 西安电子科技大学, 2021: 1–4. doi: 10.27389/d.cnki.gxadu.2021.003285.LI Xiaoxia. Research on interference suppression method of distributed radar on moving platform[D]. [Master dissertation], Xidian University, 2021: 1–4. doi: 10.27389/d.cnki.gxadu.2021.003285. [8] 韩博文, 兰天, 杨小鹏. 分布式阵列雷达波束-极化域联合主瓣干扰抑制方法[J]. 现代雷达, 2021, 43(10): 21–26. doi: 10.16592/j.cnki.1004-7859.2021.10.004.HAN Bowen, LAN Tian, and YANG Xiaopeng. Beamspace-polarization domain main-lobe jamming suppression method for distributed array radar[J]. Modern Radar, 2021, 43(10): 21–26. doi: 10.16592/j.cnki.1004-7859.2021.10.004. [9] 宋虎, 顾红, 王建, 等. 主瓣干扰下的自适应旁瓣对消算法设计[J]. 系统工程与电子技术, 2015, 37(8): 1723–1728. doi: 10.3969/j.issn.1001-506X.2015.08.02.SONG Hu, GU Hong, WANG Jian, et al. Adaptive multiple side-lobe canceller design for main-lobe jammer[J]. Systems Engineering and Electronics, 2015, 37(8): 1723–1728. doi: 10.3969/j.issn.1001-506X.2015.08.02. [10] 于芳. 分布式雷达干扰抑制算法与仿真实现研究[D]. [硕士论文], 电子科技大学, 2023: 71–74. doi: 10.27005/d.cnki.gdzku.2023.003667.YU Fang. Research on distributed radar jamming suppression algorithm and simulation implementation[D]. [Master dissertation], Xidian University, 2023: 71–74. doi: 10.27005/d.cnki.gdzku.2023.003667. [11] 蒲伟铭, 梁振楠, 陈新亮, 等. 一种鲁棒的分布式雷达主瓣干扰抑制方法[J]. 信号处理, 2022, 38(2): 250–257. doi: 10.16798/j.issn.1003-0530.2022.02.004.PU Weiming, LIANG Zhennan, CHEN Xinliang, et al. A robust method for mainlobe interference suppression based on distributed array radar[J]. Journal of Signal Processing, 2022, 38(2): 250–257. doi: 10.16798/j.issn.1003-0530.2022.02.004. [12] HEIMILLER R C, BELYEA J E, and TOMLINSON P G. Distributed array radar[J]. IEEE Transactions on Aerospace and Electronic Systems, 1983, AES-19(60): 831–839. doi: 10.1109/TAES.1983.309395. [13] 刘泉华, 张凯翔, 梁振楠, 等. 地基分布式相参雷达技术研究综述[J]. 信号处理, 2022, 38(12): 2443–2459. doi: 10.16798/j.issn.1003-0530.2022.12.001.LIU Quanhua, ZHANG Kaixiang, LIANG Zhennan, et al. Research overview of ground-based distributed coherent aperture radar[J]. Journal of Signal Processing, 2022, 38(12): 2443–2459. doi: 10.16798/j.issn.1003-0530.2022.12.001. [14] 刘兴华, 王国玉, 徐振海, 等. 分布式孔径相参合成原理、发展与技术实现综述[J]. 雷达学报, 2023, 12(6): 1229–1248. doi: 10.12000/JR23195.LIU Xinghua, WANG Guoyu, XU Zhenhai, et al. Review of principles, development and technical implementation of coherently combining distributed apertures[J]. Journal of Radars, 2023, 12(6): 1229–1248. doi: 10.12000/JR23195. [15] 易伟, 袁野, 刘光宏, 等. 多雷达协同探测技术研究进展: 认知跟踪与资源调度算法[J]. 雷达学报, 2023, 12(3): 471–499. doi: 10.12000/JR23036.YI Wei, YUAN Ye, LIU Guanghong, et al. Recent advances in multi-radar collaborative surveillance: Cognitive tracking and resource scheduling algorithms[J]. Journal of Radars, 2023, 12(3): 471–499. doi: 10.12000/JR23036. [16] ZHANG Honggang, LUO Jian, CHEN Xinliang, et al. Fresnel based frequency domain adaptive beamforming for large aperture distributed array radar[C]. 2016 IEEE International Conference on Signal Processing, Communications and Computing (ICSPCC), Hong Kong, China, 2016. doi: 10.1109/ICSPCC.2016.7753658. [17] 殷丕磊. 地基宽带分布式全相参雷达技术研究[D]. [博士论文], 北京理工大学, 2016: 112–116.YIN Pilei. Research on ground-based wideband distributed coherent aperture radar[D]. [Ph.D. dissertation], Beijing Institute of Technology, 2016: 112–116. [18] 张宗傲. 阵列雷达自适应主瓣干扰抑制算法研究[D]. [硕士论文], 北京理工大学, 2015: 23–33.ZHANG Zongao. Research on adaptive mainlobe interference suppression algorithm of array radar[D]. [Master dissertation], Beijing Institute of Technology, 2015: 23–33. [19] YANG Xiaopeng, ZHANG Zongao, ZENG Tao, et al. Mainlobe interference suppression based on Eigen-projection processing and covariance matrix reconstruction[J]. IEEE Antennas and Wireless Propagation Letters, 2014, 13: 1369–1372. doi: 10.1109/LAWP.2014.2339224. [20] ZHANG Honggang, LUO Jian, CHEN Xinliang, et al. Whitening filter for main-lobe interference suppression in distributed array radar[C]. 2016 CIE International Conference on Radar (RADAR), Guangzhou, China, 2016. doi: 10.1109/RADAR.2016.8059238. [21] LONG Teng, ZHANG Honggang, ZENG Tao, et al. High accuracy unambiguous angle estimation using multi-scale combination in distributed coherent aperture radar[J]. IET Radar, Sonar & Navigation, 2017, 11(7): 1090–1098. doi: 10.1049/iet-rsn.2016.0450. [22] LIU Ruitao, ZHANG Wei, YU Xianxiang, et al. Transmit-receive beamforming for distributed phased-MIMO radar system[J]. IEEE Transactions on Vehicular Technology, 2022, 71(2): 1439–1453. doi: 10.1109/TVT.2021.3133596. [23] 王铮, 孙雨泽, 杨小鹏, 等. 分布式雷达节点位置优化的多约束遗传算法研究[J]. 信号处理, 2019, 35(6): 979–985. doi: 10.16798/j.issn.1003-0530.2019.06.007.WANG Zheng, SUN Yuze, YANG Xiaopeng, et al. Research on multi-constrained genetic algorithm for distributed radar elements position optimization[J]. Journal of Signal Processing, 2019, 35(6): 979–985. doi: 10.16798/j.issn.1003-0530.2019.06.007. [24] LIU Ruitao, WANG Bing, WEI Wenqiang, et al. A general efficient design method for optimum nonuniform array pattern synthesis[C]. 2023 IEEE Radar Conference (RadarConf23), San Antonio, USA, 2023. doi: 10.1109/RadarConf2351548.2023.10149597. [25] YANG Xiaopeng, YIN Pilei, ZENG Tao, et al. Applying auxiliary array to suppress mainlobe interference for ground-based radar[J]. IEEE Antennas and Wireless Propagation Letters, 2013, 12: 433–436. doi: 10.1109/LAWP.2013.2254698. [26] 席昕, 刘高高, 刘强, 等. 对旁瓣相消的分布式干扰优化布阵方法[J]. 系统工程与电子技术, 2024, 46(8): 2623–2628. doi: 10.12305/j.issn.1001-506X.2024.08.10.XI Xin, LIU Gaogao, LIU Qiang, et al. Distributed interference optimal array method for sidelobe cancellation[J]. Systems Engineering and Electronics, 2024, 46(8): 2623–2628. doi: 10.12305/j.issn.1001-506X.2024.08.10. [27] 陈炽雄, 景小荣, 刘友永, 等. 基于改进粒子群算法的分布式频率分集阵栅瓣抑制方法[J]. 电讯技术, 2022, 62(12): 1813–1821. doi: 10.3969/j.issn.1001-893x.2022.12.015.CHEN Chixiong, JING Xiaorong, LIU Youyong, et al. A grid lobe suppression method of distributed frequency diverse array based on improved particle swarm optimization algorithm[J]. Telecommunication Engineering, 2022, 62(12): 1813–1821. doi: 10.3969/j.issn.1001-893x.2022.12.015. 期刊类型引用(3)
1. 张佳辉，苗洪利，杨忠昊，刘昆池. 基于SAR子孔径分解的海表面二维流场反演. 海洋学报. 2023(08): 24-30 . 
百度学术2. 李志远，郭嘉逸，张月婷，黄丽佳，李洁，吴一戎. 基于自适应动量估计优化器与空变最小熵准则的SAR图像船舶目标自聚焦算法. 雷达学报. 2022(01): 83-94 . 
本站查看3. 雷禹，冷祥光，孙忠镇，计科峰. 宽幅SAR海上大型运动舰船目标数据集构建及识别性能分析. 雷达学报. 2022(03): 347-362 . 本站查看其他类型引用(2)
-
下载:
百度学术
计量
- 文章访问数: 289
- HTML全文浏览量: 264
- PDF下载量: 124
- 被引次数: 5
