作者中心
专家审稿
责编办公
编辑办公
-
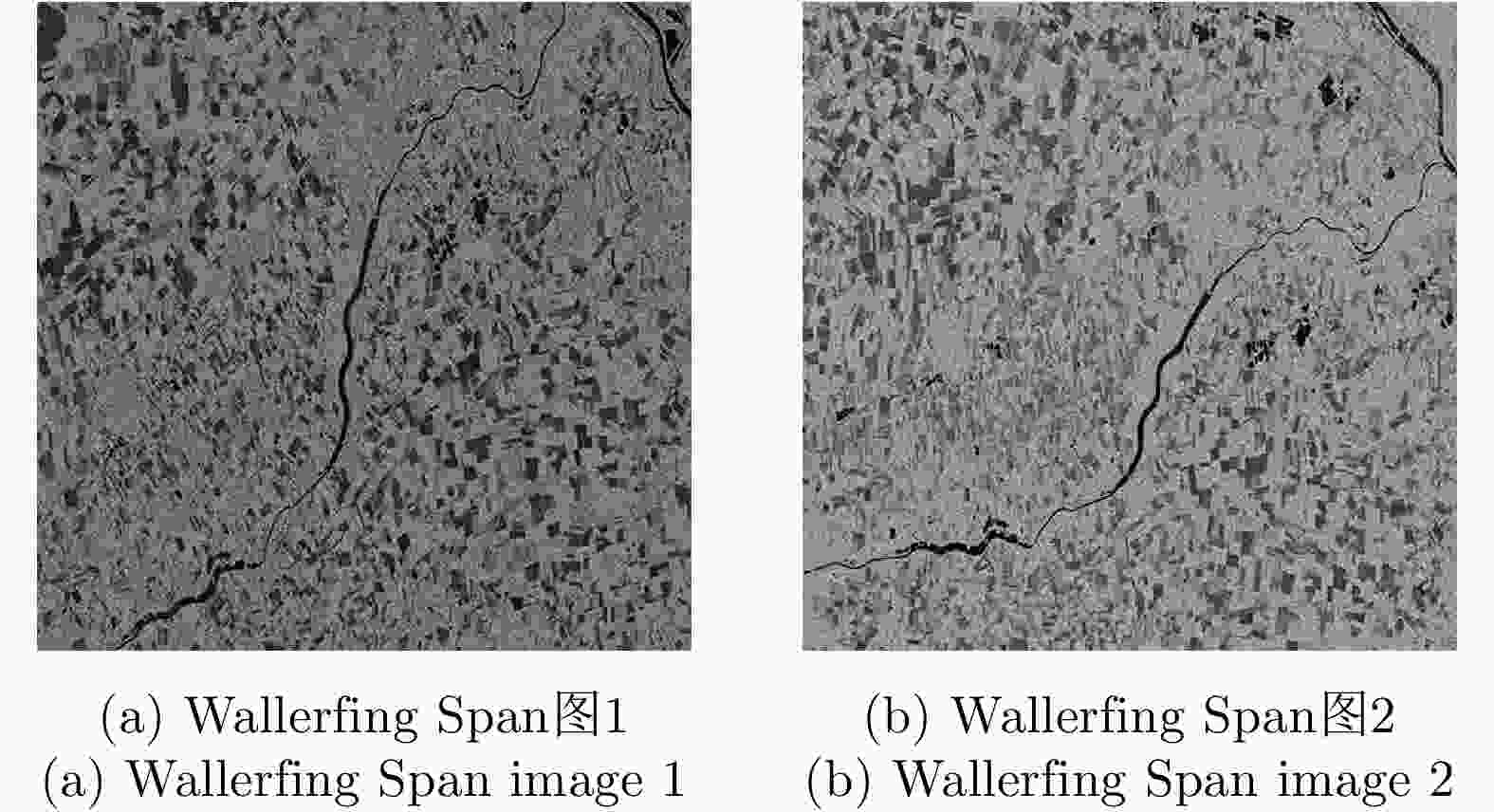
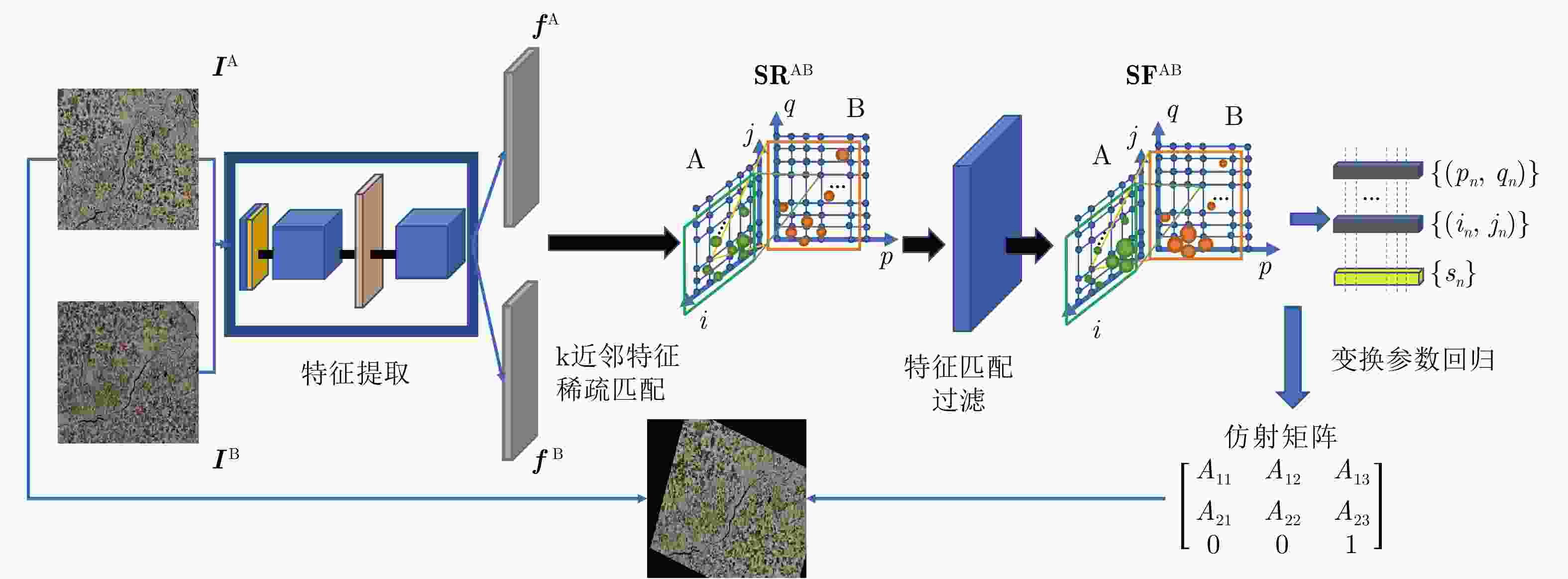
摘要: 极化SAR图像的配准是极化SAR图像处理的基础，需要具备较高的精度与速度。基于深度学习的极化SAR图像配准大多数是结合图像块特征的匹配与基于随机抽样一致性的参数迭代估计来实现的。目前尚未实现端到端的基于深度卷积神经网络的一步仿射配准。该文提出了一种基于弱监督学习的端到端极化SAR图像配准框架，无需图像切块处理或迭代参数估计。首先，对输入图像对进行特征提取，得到密集的特征图。在此基础上，针对每个特征点保留k对相关度最高的特征点对。之后，将该4D稀疏特征匹配图输入4D稀疏卷积网络，基于邻域一致性进行特征匹配的过滤。最后，结合输出的匹配点对置信度，利用带权最小二乘法进行仿射参数回归，实现图像对的配准。该文采用RADARSAT-2卫星获取的德国Wallerfing地区农田数据以及PAZ卫星获取的中国舟山港口地区数据作为测试图像对。通过对升降轨、不同成像模式、不同极化方式、不同分辨率的极化SAR图像对的配准测试，并与4种现有方法进行对比，验证了该方法具有较高的配准精度与较快的速度。Abstract: As the base of Synthetic Aperture Radar (SAR) image processing, the registration of polarimetric SAR images requires high accuracy and a fast speed. Most methods used to register polarimetric SAR images based on deep learning are combined with patch matching and iterative estimation, e.g. the random sample consensus algorithm. However, end-to-end deep convolutional neural networks have not been used in the non-iterative affine registration of polarimetric SAR images. This paper proposes a framework for end-to-end polarimetric SAR image registration that is based on weakly-supervised learning and uses no image patch processing or iterative parameter estimation. First, feature extraction is performed on input image pairs to obtain dense feature maps with the most relevant k matches kept for each feature point. To filter the matched feature pairs, the 4D sparse feature matching maps are then fed into a 4D sparse convolutional network based on neighborhood consensus. Lastly, the affine parameters are solved by the weighted least square method according to the degree of confidence of the matches, which enables the affine registration of the input image pair. As test image pairs, we use farmland data from Wallerfing, Germany obtained by the RADARSAT-2 satellite and Zhoushan port data from China obtained by the PAZ satellite. Comprehensive experiments were conducted on polarimetric SAR image pairs using different orbit directions, imaging modes, polarization types and resolutions. Compared with four existing methods, the proposed method was found to have high accuracy and a fast speed.
-
1. 引言
基于导航卫星的双基地SAR(Bistatic Synthetic Aperture Radar based on Global Navigation Satellite System, GNSS-BSAR)是空-地双基地SAR中一种典型的应用[1]，使用在轨的导航卫星作为发射源，地面部署接收机(地基、车载、机载)构成双基地SAR系统[2]。由于导航星座的日趋完善，其全球覆盖性以及重轨特性所带来的优势是其他照射源暂时所不能替代的，其中以地基接收机为主的导航卫星干涉合成孔径雷达(Interference Synthetic Aperture Radar based on the Global Navigation Satellite System, GNSS-InSAR)在场景形变监测领域有着广阔的应用前景[3]，成为了近年来研究热点。
在GNSS-BSAR系统成像方面，已有研究者分别使用不同的导航卫星星座进行了成像验证，包括了北斗[4,5]、GPS[6]、格洛纳斯[7]、伽利略[8]。除此以外文献[9]还提出了多角度融合方法以增强图像信噪比。在形变监测方面，来自伯明翰大学的学者们[10]使用直达波天线，配合长约50 m的线缆构建了理想点目标，并使用格洛纳斯作为发射源，首次实现了精度约为1 cm的1维形变反演结果。该实验初步验证了GNSS-InSAR应用于形变监测的可行性。为了进一步验证场景形变监测的可能，2017年文献[11]通过对接收机进行高精度移位来模拟场景建筑形变，成功反演出了形变，精度约为1 cm。在3维形变方面，2018年北京理工大学的技术团队[12]通过人为构建转发器，进行了精度可控的强点目标形变模拟，使用我国的北斗IGSO卫星，成功实现了精度优于5 mm的3维形变反演，这些验证性实验充分表明了GNSS-InSAR应用于场景形变检测的可能。
若要实现GNSS-InSAR场景的3维形变反演，需要同时至少3颗卫星从不同角度照射场景。由于GNSS-InSAR系统的拓扑高度非对称性以及导航信号的窄带特性[13]，加上导航卫星的重轨并非是严格意义上的重轨，除了不可避免的空间基线外，重轨时间也并非严格一致，因此在实际数据采集中，需要对系统构型以及数据采集时间进行严格的优化设计。文献[14]提出了一种联合优化方法，解决了面向大场景下的多星多角度构型优化问题，配合多个接收机实现综合分辨性能优异的大场景成像。文献[15]提出了空间去相干的理论描述框架，表明了空间去相干在GNSS-InSAR中的必要性，但未对数据采集时间进行说明。从当前实际情况出发，不精确的数据采集时间可能会造成存储资源浪费，空间去相干导致的数据截取进一步降低了数据有效性。具体如图1所示：
针对上述问题，本文提出了一种GNSS-InSAR场景连续数据采集优化方法，通过结合当前数据的卫星轨迹和两行星历数据文件(STK Two-Line Element sets, TLE)预测轨迹，基于相干系数轨迹对齐，获取卫星重轨时间间隔，得到最优的数据采集策略，从源头上降低数据的空间去相干性，提升所采集数据有效性，节约存储资源。在第2部分对GNSS-InSAR场景数据采集优化方法进行了详细介绍。第3部分针对提出的方法进行了实验设计，开展了实测数据采集，并针对采集的数据进行了初步分析。第4部分对全文进行总结。
2. GNSS-InSAR场景数据采集优化模型
2.1 GNSS-InSAR相干系数理论模型
对于GNSS-InSAR图像而言，经过保相成像处理后，场景中任意一点
(x0,y0) 的像素信息分别对应分辨单元内所有散射体回波的相参叠加，可建模为s(x0,y0)=∬f(x,y;t)exp[−j2πλr(x,y;P)]⋅W(x−x0,y−y0;P)dxdy+n(x0,y0;t) (1) 其中，
f(x,y;t) 为时间t 下的地表散射系数，P 为对应的合成孔径中心位置矢量，W(x,y;P) 表示系统的点扩散函数(PSF),n(x,y;t) 为图像的加性噪声。对于SAR图像的同名点像素，其相干系数可表示为[16]ρ=∬sm(x0,y0)s∗s(x0,y0)dxdy√∬sm(x0,y0)s∗m(x0,y0)dxdy∬ss(x0,y0)s∗s(x0,y0)dxdy (2) 其中，下标m表示主图像，
s 表示辅图像。根据柯西不等式可以判断：0≤ρ≤1 ，当ρ=0 时表示同名点完全不相干，当ρ=1 时，同名点完全相干。将点目标像素模型式(1)带入到式(2)并化简得到
ρ=∬sav(x,y)exp[−j2πλ(r(x,y;Pm)−r(x,y;Ps))]|W(x−x0,y−y0;Pm)|2dxdy√(∬sm(x,y)exp[−j2πλr(x,y;Pm)]|W(x−x0,y−y0;Pm)|2dxdy+nm)×(∬ss(x,y)exp[+j2πλr(x,y;Ps)]|W(x−x0,y−y0;Pm)|2dxdy+ns) (3) 式(3)的推导使用了如下近似：
(1) 由于导航卫星的高轨道特性，使得
W(x−x0, y−y0;Pm)≈W(x−x0,y−y0;Ps) 成立；(2) 相邻两天的噪声相干系数为0，即
n(x0,y0;tm)×n(x0,y0;ts)=0 (4) (3) 相邻两天的目标散射系数为
sav(x,y) ，即sav(x,y)≈f(x,y;tm)f∗(x,y;ts) (5) 对式(3)中的相干系数
ρ 进一步分解得到ρ=ρth×ρti×ρsp (6) 其中，热噪声相干系数
ρth 与时间相干系数ρti 分别由系统与实际目标决定。对于PS点[17]而言，地表散射系数相对稳定，不随时间变化，同时为了便于后续分析，假定散射系数为1得到空间相干系数
ρsp 的简化式为ρsp=∬exp[−j2πλ(r(x,y;Pm)−r(x,y;Ps))]|W(x−x0,y−y0;Pm)|2dxdy√(∬|W(x−x0,y−y0;Pm)|2dxdy)(∬|W(x−x0,y−y0;Pm)|2dxdy) (7) 从式(7)推导结果可以知道，空间基线主要是影响
r(x,y;P) 从而导致空间去相干。2.2 数据采集优化模型
导航卫星的重轨时间并非稳定不变，因此需要对数据采集时间进行有效预测，从源头上降低空间去相干，提高数据有效性。
假定主图像数据采集时间为
tm ，该采集时间可以通过文献[14]中的广义优化模型进行求解，辅图像数据采集时间为ts=tm+Δt ,Δt 为时间间隔，那么最优化数据采集模型可通过式(7)推导而来Δt=argmax{∬|˜W(x,y;Pm)|2exp[−j2πλ(r(x,y;Pm)−r(x,y;P(tm+Δt)))]dxdy} (8) 其中，
˜W(x,y;Pm) 为tm 下等效归一化PSF,P(tm+ Δt) 为Δt 时间偏置下得合成孔径中心位置矢量。第1天数据采集需要进行实验设计以确定最优数据采集时刻，往后的重轨天数据采集可以根据数据采集优化模型，同时结合星历文件进行预测。整体的预测流程如图2所示，
n 为任意一天采集的数据，k 为重轨天数间隔。
图 2 GNSS-InSAR数据采集时间优化流程Figure 2. Time optimization process of GNSS-InSAR data acquisition实际卫星位置对应的实际时间设为
tn ，经过模型优化得到的时间偏差为Δt ，那么第n+k 天对应的实际数据采集时间可表示为tn+k=tn+Δt (9) 3. 实验验证
3.1 GNSS-InSAR场景3维形变反演实验设计
对于固定场景的形变监测，首次数据采集的时候需要严格设计系统构型，使分辨率达到最优化。本次实验接收机部署在北京理工大学信息科学试验楼楼顶西北角，实施监测场景位于西偏北30°。使用理论分辨率计算公式[18]对该场景进行分辨率设计。仿真参数具体参见表1。
表 1 数据采集试验仿真参数Table 1. Data acquisition test simulation parameters参数 值 照射源 北斗 IGSO1～5 PRF 1000 Hz 带宽 10.23 MHz 合成孔径时间 600 s TLE文件更新日期 2019年4月29日 预定数据采集日期 2019年4月30日 以分辨单元面积作为判定依据，得到预定采集日期当天全时段下各个卫星在预定场景下所能得到的分辨单元面积如图3所示。
为了实现3维形变反演，需要同一时间下有3颗卫星对场景进行照射。图3中10点前后与17点前后满足当前场景上空有3颗IGSO卫星可见的条件。更进一步，为了使分辨单元面积达到最优，可以得到具体的数据采集时间。具体如图4红框标注，分别是9点30分前后与17点30分前后。
为了配合实验，在场景布置转发器，整体的系统构型如图5所示。
图 5 GNSS-InSAR场景3维形变反演实验拓扑构型设计结果Figure 5. GNSS-InSAR topological configuration design results of 3D deformation retrieval experiment3.2 重轨数据采集时间优化
以2019年4月30日采集的实测数据作为第
n 天数据，对于北斗的IGSO而言，重轨时间约为1天，即m =1，同时下载当天最新的TLE文件。以IGSO1为例，结合图2进行详细说明：(1) 使用实测数据的直达波进行卫星位置解算，同时根据TLE文件推算当天和相邻天的卫星轨迹。经过相干系数轨迹匹配之后，得到的轨迹如图6所示。
图 6 对齐后的TLE卫星轨迹与实测数据卫星轨迹Figure 6. Aligned TLE satellite trajectory and measured data satellite trajectory(2) 以匹配得到的TLE卫星轨迹作为参考，对重轨天的TLE卫星轨迹进行数据采集优化模型求解，系统的PSF与优化模型仿真结果分别如图7与图8所示。
图 7 场景[–147, 20, 0]处理论PSFFigure 7. Theoretical PSF in scene at position of [–147, 20, 0]对图8的结果分析可知，第1个峰值点为其本身，由于空间基线为0，相干系数为1。第2个峰值点相干系数为0.999644，满足除了第1个峰值点外相邻天相干系数最大值条件，因此第2个峰值点就是最佳重轨时的空间相干系数。此时经过模型优化得到的时间间隔为：
Δt=86163s=23h56min3s ，结合第1天的实测数据轨迹对应的时间t1=9h26min0s ，第2天准确的数据采集时间为：t2=9h22min3s 。3.3 结果分析
为了说明优化结果的正确性，在实验场景中放置转发器模拟理想点目标(图5)，同时按照优化后的时间进行5月1日数据采集。实际采集时间为
9h21min53s ，总采集时间约650 s。相邻两天的空间相干系数轨迹匹配结果如图9所示。从图9中峰值点位置来看，重轨数据采集优化模型得到的结果和实际结果相吻合。为了进一步说明，图10给出了IGSO1卫星实测数据成像结果。
对相邻两天的图像相干系数进行求解，得到图11所示结果。在同一坐标系下，仿真目标位于[–147, 20, 0]，空间相干系数为0.999644；转发器位于[–147, 20, 0]，相干系数为0.9996；两者的相干系数基本保持一致。
图9与图10的结果表明经过数据采集优化模型后得到的时间间隔与实际卫星轨迹的重轨时间相互吻合，在保证600 s预期合成孔径时间下，可以最大限度减少数据采集时间，节约存储资源。同时避免后期由于数据对齐带来的数据有效性降低问题。
4. 结论
在GNSS-InSAR场景1维/3维形变反演应用中，针对由于导航卫星重轨时间的非严格一致性与有效数据截取带来的数据冗余，数据有效性低等问题，本文提出了一种面向GNSS-InSAR场景数据采集的优化模型，采用实测数据与TLE文件相结合，根据当天数据采集时间，预测相邻天重轨时间，从而实现精确的数据采集。实测数据验证结果表明了数据采集时间优化模型的正确性。该方法的提出有利于GNSS-InSAR场景1维/3维形变反演实验的开展，在降低原始数据冗余度基础上，保证了有效数据时间长度大于预期合成孔径时间。
-
图 1 基于邻域一致性的SAR图像配准算法框图
Figure 1. Flowchart of image registration based on neighborhood consensus
图 5 DenseNet+SNCNet算法下，Wallerfing和舟山数据配准叠加图
Figure 5. Overlay map of Wallerfing and Zhou Shan data by DenseNet+SNCNet
图 6 SAR-SIFT+RANSAC算法下，Wallerfing和舟山数据配准叠加图
Figure 6. Overlay map of Wallerfing and Zhou Shan data by SAR-SIFT+RANSAC
图 7 不同算法下，Wallerfing和舟山数据配准的PCK曲线
Figure 7. PCK of Wallerfing and Zhou Shan image registration with different algorithms
图 9 600×600分辨率下，DenseNet-SNCNet和ResNet-SNCNet的配准结果
Figure 9. Registration result of DenseNet-SNCNet and ResNet-SNCNet at 600×600 resolution
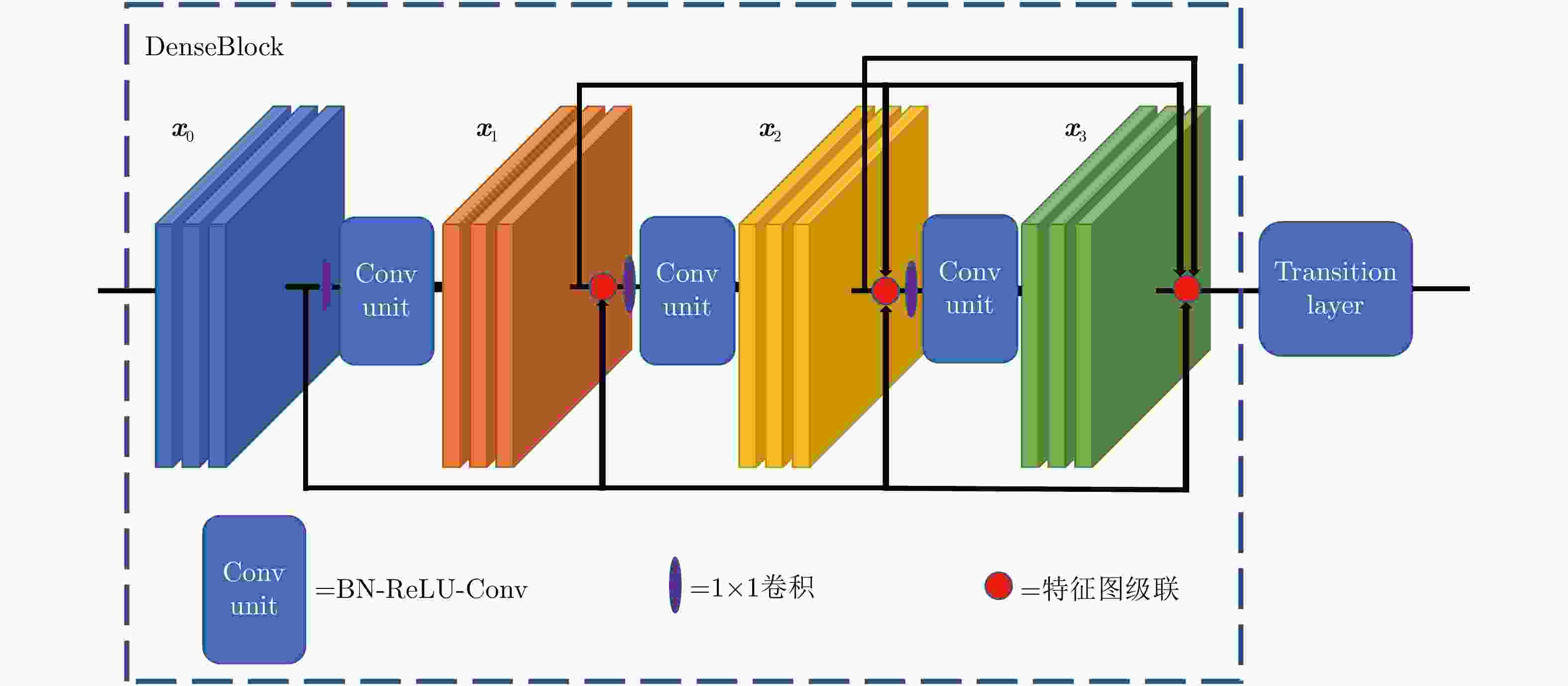
表 1 特征提取模块的结构
Table 1. Structure of the feature extraction module
网络的层 该层输出的尺寸 特征提取模块 Convolution
Pooling600×600×64
300×300×647×7 conv, stride 2
3×3 Max Pooling, stride 2DenseBlock(1) 300×300×256 [1×1conv3×3conv]×6 Transition layer(1) 300×300×128
150×150×1281×1 conv
2×2 Average Pooling, stride 2DenseBlock(2) 150×150×512 [1×1conv3×3conv]×12 Transition layer(2) 150×150×256
75×75×1281×1 conv
2×2 Average Pooling, stride 2DenseBlock(3) 75×75×1792 [1×1conv3×3conv]×48 
下载: 导出CSV
表 2 各种配准算法的APE值
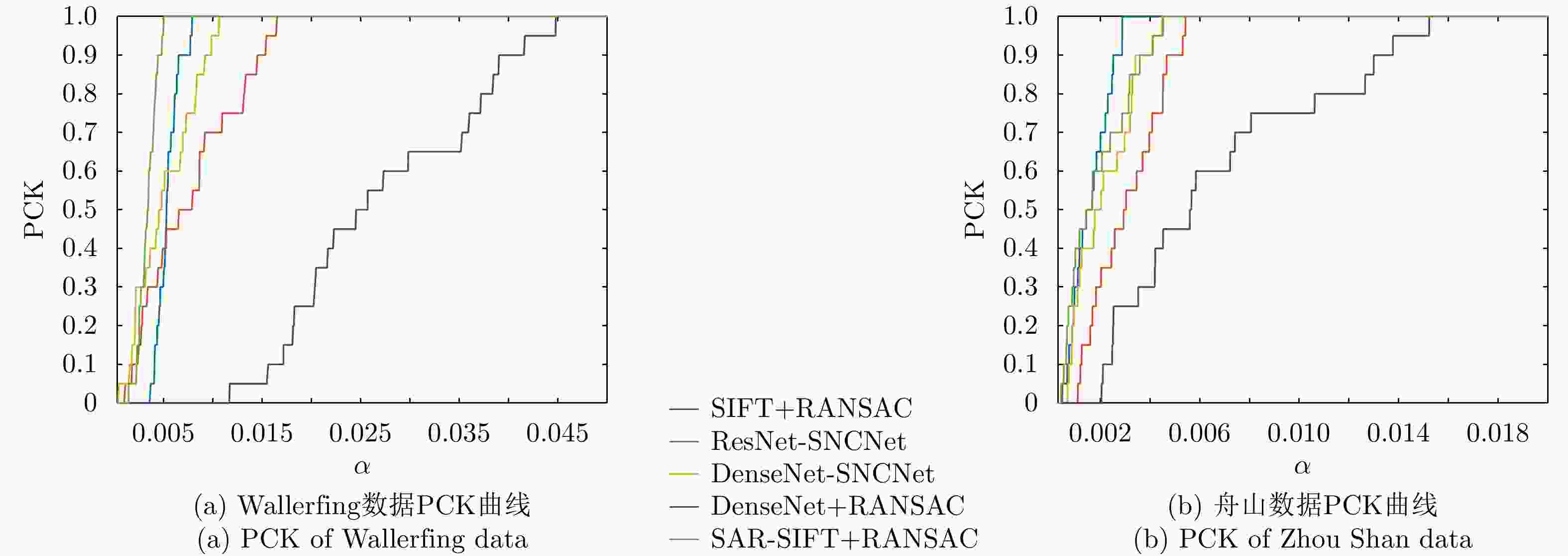
Table 2. APE of different registration algorithms
Method Wallerfing Pauli images Wallerfing Span images Zhou Shan images SIFT+RANSAC 6.521 9.058 1.924 SAR-SIFT+RANSAC 4.053 6.927 2.252 ResNet-SNCNet 9.222 9.641 3.677 DenseNet-SNCNet 6.175 7.545 2.553 DenseNet+RANSAC 32.715 40.042 7.988
下载: 导出CSV
表 3 k取不同值时，DenseNet+SNCNet配准结果的APE值
Table 3. APE of registration result by DenseNet+SNCNet with different k
k Wallerfing Pauli images Zhou Shan images 2 7.497 2.443 5 8.929 2.080 8 8.157 3.154 10 6.175 2.553 16 13.416 2.383
下载: 导出CSV
表 4 k取不同值时，基于GPU的DenseNet+SNCNet运算时间
Table 4. Time consuming of registration based on GPU by DenseNet+SNCNet with different k
k Wallerfing Pauli images Zhou Shan images 2 0.6267 0.6364 5 0.7335 0.7379 8 0.8525 0.9292 10 0.9943 0.9542 16 1.1793 1.2199
下载: 导出CSV
-
[1] WANG Shuang, QUAN Dou, LIANG Xuefeng, et al. A deep learning framework for remote sensing image registration[J]. ISPRS Journal of Photogrammetry and Remote Sensing, 2018, 145: 148–164. doi: 10.1016/j.isprsjprs.2017.12.012 [2] YANG Zhuoqian, DAN Tingting, and YANG Yang. Multi-temporal remote sensing image registration using deep convolutional features[J]. IEEE Access, 2018, 6: 38544–38555. doi: 10.1109/ACCESS.2018.2853100 [3] SARVAIYA J N, PATNAIK S, and BOMBAYWALA S. Image registration by template matching using normalized cross-correlation[C]. 2009 IEEE International Conference on Advances in Computing, Control, and Telecommunication Technologies, Trivandrum, India, 2009: 819–822. doi: 10.1109/ACT.2009.207. [4] GAN Rui, WU Jue, CHUNG A C S, et al. Multiresolution image registration based on Kullback-Leibler distance[C]. The 7th International Conference on Medical Image Computing and Computer-Assisted Intervention. Saint-Malo, France, 2004: 599–606. doi: 10.1007/978-3-540-30135-6_73. [5] 张涛, 王正勇, 张影, 等. 基于和声算法的图像配准技术[J]. 电视技术, 2014, 38(7): 9–12. doi: 10.16280/j.videoe.2014.07.032ZHANG Tao, WANG Zhengyong, ZHANG Ying, et al. Image registration techniques based on harmony search algorithm[J]. Video Engineering, 2014, 38(7): 9–12. doi: 10.16280/j.videoe.2014.07.032 [6] AVERBUCH A and KELLER Y. FFT based image registration[C]. 2002 IEEE International Conference on Acoustics, Speech, and Signal Processing, Orlando, USA, 2002: IV-3608–IV-3611. doi: 10.1109/ICASSP.2002.5745436. [7] HARRIS C and STEPHENS M. A combined corner and edge detector[C]. The 4th Alvey Vision Conference, Manchester, UK, 1988. doi: 10.5244/C.2.23. [8] LOWE D G. Distinctive image features from scale-invariant keypoints[J]. International Journal of Computer Vision, 2004, 60(2): 91–110. doi: 10.1023/B:VISI.0000029664.99615.94 [9] WANG Yufan, YU Qiuze, and YU Wenxian. An improved normalized cross correlation algorithm for SAR image registration[C]. 2012 IEEE International Geoscience and Remote Sensing Symposium, Munich, Germany, 2012: 2086–2089. doi: 10.1109/IGARSS.2012.6350961. [10] DELLINGER F, DELON J, GOUSSEAU Y, et al. SAR-SIFT: A SIFT-like algorithm for SAR images[J]. IEEE Transactions on Geoscience and Remote Sensing, 2015, 53(1): 453–466. doi: 10.1109/TGRS.2014.2323552 [11] MA Wenping, WEN Zelian, WU Yue, et al. Remote sensing image registration with modified SIFT and enhanced feature matching[J]. IEEE Geoscience and Remote Sensing Letters, 2017, 14(1): 3–7. doi: 10.1109/LGRS.2016.2600858 [12] KRIZHEVSKY A, SUTSKEVER I, and HINTON G. ImageNet classification with deep convolutional neural networks[C]. The 25th International Conference on Neural Information Processing Systems, Lake Tahoe, USA, 2012: 1097–1105. [13] 徐丰, 王海鹏, 金亚秋. 深度学习在SAR目标识别与地物分类中的应用[J]. 雷达学报, 2017, 6(2): 136–148. doi: 10.12000/JR16130XU Feng, WANG Haipeng, and JIN Yaqiu. Deep learning as applied in SAR target recognition and terrain classification[J]. Journal of Radars, 2017, 6(2): 136–148. doi: 10.12000/JR16130 [14] JIN Kan, CHEN Yilun, XU Bin, et al. A patch-to-pixel convolutional neural network for small ship detection with PolSAR images[J]. IEEE Transactions on Geoscience and Remote Sensing, 2020, 58(9): 6623–6638. doi: 10.1109/TGRS.2020.2978268 [15] DETONE D, MALISIEWICZ T, and RABINOVICH A. Deep image homography estimation[J]. arXiv: 1606.03798, 2016. [16] ROCCO I, ARANDJELOVIC R, and SIVIC J. Convolutional neural network architecture for geometric matching[J]. IEEE Transactions on Pattern Analysis and Machine Intelligence, 2019, 41(11): 2553–2567. doi: 10.1109/TPAMI.2018.2865351 [17] BALAKRISHNAN G, ZHAO A, SABUNCU M R, et al. VoxelMorph: A learning framework for deformable medical image registration[J]. IEEE Transactions on Medical Imaging, 2019, 38(8): 1788–1800. doi: 10.1109/TMI.2019.2897538 [18] ROCCO I, CIMPOI M, ARANDJELOVIĆ R, et al. Neighbourhood consensus networks[C]. Advances in Neural Information Processing Systems 31, Montréal, Canada, 2018: 1651–1662. [19] ROCCO I, ARANDJELOVIĆ R, and SIVIC J. Efficient neighbourhood consensus networks via submanifold sparse convolutions[J]. arXiv: 2004.10566, 2020. [20] HUANG Gao, LIU Zhuang, VAN DER MAATEN L, et al. Densely connected convolutional networks[C]. 2017 IEEE Conference on Computer Vision and Pattern Recognition, Honolulu, USA, 2017: 4700–4708. [21] CHOY C, GWAK J Y, and SAVARESE S. 4D Spatio-temporal Convnets: Minkowski convolutional neural networks[C]. IEEE/CVF Conference on Computer Vision and Pattern Recognition, Long Beach, USA, 2019: 3075–3084. [22] YANG Yi and RAMANAN D. Articulated human detection with flexible mixtures of parts[J]. IEEE Transactions on Pattern Analysis and Machine Intelligence, 2012, 35(12): 2878–2890. doi: 10.1109/TPAMI.2012.261 [23] 魏天华. 基于多核DSP的加速SAR-SIFT算法并行计算设计[D]. [硕士论文], 西安电子科技大学, 2020.WEI Tianhua. Parallel calculation of speed-up SAR-SIFT algorithm based on multi-score DSP[D]. [Master dissertation], Xidian University, 2020. 期刊类型引用(7)
1. 项德良，丁怀跃，管冬冬，程建达，孙晓坤. 结合极化白化滤波和SimSD-CapsuleNet的PolSAR图像配准. 测绘学报. 2024(03): 450-462 . 
百度学术2. 仇晓兰，罗一通，宋舒洁，彭凌霄，程遥，颜千程，上官松涛，焦泽坤，张柘，丁赤飚. 微波视觉三维SAR实验系统及其全极化数据处理方法. 雷达学报. 2024(05): 941-954 . 
本站查看3. 唐固城，谢丽芳，刘烜. 基于InSAR复数影像配准方法研究综述. 北京测绘. 2023(01): 1-7 . 百度学术4. 申亮，金添，黄晓涛. 结合形状信息的SAR图像特征匹配方法. 信号处理. 2023(02): 252-262 . 百度学术5. 王伟，陈颖，王嘉浩，张文成，李先静，张祺. 基于注意力和特征融合的光学遥感图像配准. 激光杂志. 2023(05): 174-181 . 百度学术6. 张永显，马国锐，訾栓紧，门行. 多源遥感影像学习型特征双向一致性配准. 测绘学报. 2023(11): 1906-1916 . 百度学术7. 王洪淼，杨健，殷君君. 基于Wishart梯度和SIFT方法的极化SAR图像配准. 中国科学:信息科学. 2022(04): 687-699 . 百度学术其他类型引用(3)
-
下载:
百度学术
计量
- 文章访问数: 2536
- HTML全文浏览量: 811
- PDF下载量: 246
- 被引次数: 10
