作者中心
专家审稿
责编办公
编辑办公
Consistency-based Air Target Height Estimation and Location in Distributed Space-based Radar Network
-
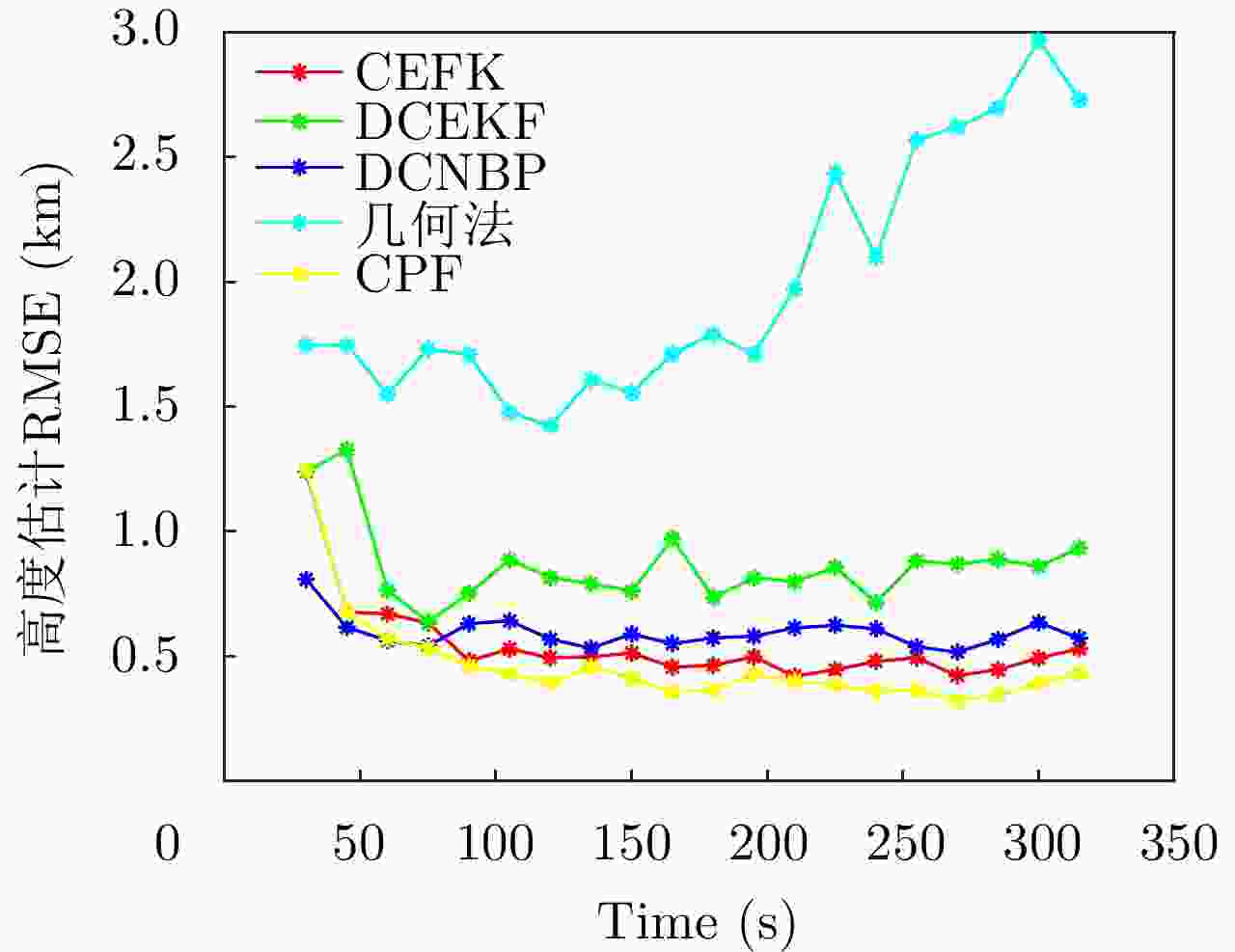
摘要: 单颗天基探测雷达对空中目标跟踪定位时，由于存在俯仰角信息缺失及量测的非线性等问题，目标高度估计误差大。多天基雷达组网为解决该问题提供了一种手段。同时，考虑系统的低计算复杂度、低通信开销、高精度、高可靠性等需求，该文提出了一种基于一致性的分布式天基雷达组网空中目标高度估计与定位方法。首先，给出了空中目标运动模型与天基雷达量测模型；然后，基于概率图模型理论，建立了多天基雷达组网融合多帧量测下目标跟踪定位问题的因子图模型；基于一致性融合，在多个局部目标运动状态之间建立耦合关系；结合粒子滤波与信度传播，建立了非参数信度传播在多天基雷达组网融合跟踪因子图上的消息表示与迭代计算规则；最后通过仿真验证了算法性能。仿真结果表明，与分布式一致扩展卡尔曼滤波算法相比，所提算法目标高度估计精度提升35.3%，有效提升了天基雷达目标定位性能。Abstract: When single space-based radar tracks and detects air targets, problems such as missing pitch angle information and nonlinear measurement lead to large target height estimation errors. Multi-space-based radar networking can solve this problem. Moreover, considering the system’s requirements for low computational complexity, low communication overhead, high accuracy, and high reliability, a consistency-based method for height estimation and location of air targets in a distributed space-based radar network is proposed. First, an air target motion model and a space-based radar measurement model are presented. Second, based on probabilistic graphical model theory, a factor graph for multi-frame measurement of target tracking and positioning in a space-based radar network is established. The coupling relationship between several local target motion states is established based on consistency fusion. Third, combining particle filtering and belief propagation establishes the message representation and iterative calculation rules of nonparametric belief propagation on the fusion tracking for factor graph of space-based radar networking. Finally, the performance of the algorithm is tested through simulation. The simulation results show that compared with the distributed consensus extended Kalman filter, the proposed algorithm improves the target height estimation accuracy by 35.3%, effectively improving the target localization performance of the space-based radar.
-
图 4 目标状态与量测联合概率分布函数的因子图分解
Figure 4. Factor graph decomposition of the joint probability distribution function of target states and measurements
图 7 DCNBP算法分布式实现结构图
Figure 7. Block diagram of the distributed implementation of DCNBP
图 9 空中目标高度估计RMSE(粒子数
$S = 400$ )Figure 9. RMSE of aerial target altitude estimation (particle number
$S = 400$ )
图 10 空中目标高度估计RMSE(粒子数
$S = 800$ )Figure 10. RMSE of aerial target altitude estimation (particle number
$S = 800$ )
图 11 不同测量误差空中目标高度估计RMSE
Figure 11. RMSE of aerial target height estimation with different measurement errors
图 12 不同高度误差空中目标定位估计RMSE
Figure 12. RMSE of aerial target position estimation with different altitude errors
1 天基雷达组网目标跟踪DCEKF算法
1. DCEKF algorithm for target tracking in space-based radar networks
1: 初始化：令 $ k = 0 $, 对每个雷达节点 $ j = 1,2,\cdots, N $，初始化
$ { {\hat {{\boldsymbol{x}}}}}_{0{{|}}0}^j $, $ {\boldsymbol{P}}_{0|0}^j $；2: for $ k = 1:K $ do 3: for $ j = 1,2,\cdots, N $ do 4: 计算预测分布： $ { {\hat {{\boldsymbol{x}}}}}_{k + 1|k}^j = {{\boldsymbol{F}}_k}{ {\hat {{\boldsymbol{x}}}}}_k^j $,
$ {\boldsymbol{P}}_{k + 1|k}^j{{ = }}{{\boldsymbol{F}}_k}{\boldsymbol{P}}_k^j{\boldsymbol{F}}_k^{\mathrm{T}} + {{\boldsymbol{Q}}_k} $；5: 根据式(18)、式(19)计算局部EKF更新 $ {\boldsymbol{\mu}} _k^j $和 $ {\boldsymbol{P}}_k^j $； 6: end for 7: 令 $ l = 0 $； 8: for $ j = 1,2,\cdots, N $ do 9: 初始化： $ {\boldsymbol{\mu}} _{ji}^l,{\boldsymbol{\varLambda}} _{ji}^l,\forall i \in {D_j} $； 10: end for 11: while $ l \le L $ do 12: $ l = l + 1 $； 13: for $ j = 1,2,\cdots, N $ do 14: 对节点 $ j $的每个邻居节点 $ i \in {D_j} $，采用式(22)、式(23)
计算 $ {\boldsymbol{\mu}} _{ji}^l $和 $ {\boldsymbol{\varLambda}} _{ji}^l $；15: end for 16: end while 17: for $ j = 1,2,\cdots, N $ do 18: 采用式(24)、式(25)计算 $ {\hat{\boldsymbol{x}}}_k^j $, $ {\boldsymbol{\varLambda}} _k^j $, $ {\boldsymbol{P}}_k^j = ({\boldsymbol{\varLambda}}_k^j)^{-1} $； 19: end for 20: end for 
下载: 导出CSV
2 基于重要性采样的消息乘积粒子化算法
2. Message product particleization algorithm based on importance sampling
Require: $ D $个输入消息，且每个输入消息 $ {m_i}\left( {{\boldsymbol{x}}} \right) $的粒子化形式
为 $ \left\{ {{{{\boldsymbol{x}}}_{i,s}},{w_{i,s}}} \right\}_{s = 1}^S $；Ensure: $ D $个输入消息乘积的粒子化形式 $ \left\{ {{{{\hat{{\boldsymbol{x}}}}}_s},{{\hat w}_s}} \right\}_{s = 1}^S $； 1: for $ i = 1,2, \cdots, D $ do 2: 构造输入消息 $ {m_i}\left( {{\boldsymbol{x}}} \right) $的高斯混合形式：
$ {m_i}\left( {{\boldsymbol{x}}} \right) = \displaystyle\sum\limits_{s = 1}^S {{w_{i,s}}{\cal{N}}\left( {{{\boldsymbol{x}}};{{{\boldsymbol{x}}}_{i,s}},{{\boldsymbol{P}}_i}} \right)} $；3: for $ s = 1,2, \cdots, S $ do 4: 设置均值： $ {{\boldsymbol{\mu}} _{i,s}} = {{\boldsymbol{x}}}_{i,s} $； 5: 设置协方差： $ {{\boldsymbol{P}}_i} = {S^{\textstyle\frac{1}{6}}}\displaystyle\sum\limits_{s = 1}^S {\displaystyle\sum\limits_{l = 1}^S{{w_{i,s}}{w_{i,l}}}} \left({{{{\boldsymbol{x}}}_{i,s}} - {{{\bar{{\boldsymbol{x}}}}}_i}} \right) {\left( {{{\boldsymbol{x}}_{i,l}} - \bar{\boldsymbol{x}}_i} \right)^{\mathrm{T}}} $； 6: end for 7: end for 8: for $ s = 1,2, \cdots, S $ do 9: for $ i = 1,2, \cdots, D $ do 10: 从建议性分布为 $ p\left( {{\zeta_{1:D}}} \right) $中获得辅助变量
$ {\zeta_{1:D}} \in {\left\{ {1,2, \cdots, S} \right\}^D} $的一组样本 $ l_{1:D} $；11: 根据式(46)和式(47)计算 $ \prod\nolimits_{i = 1}^D {{w_{i,{l_i}}}{\cal{N}}\left( {{\boldsymbol{x}};{{\boldsymbol{\mu}}_{i,{l_i}}},{{\boldsymbol{P}}_i}} \right)} $ 的
均值 $ {\bar {\boldsymbol{\mu}}} $、协方差 $ {\bar {\boldsymbol{P}} } $和权重 $ \bar w $；12: 采样一个粒子 $ {\hat {\boldsymbol{x}}} \sim {\cal{N}}\left( {{\boldsymbol{x}};{\bar {\boldsymbol{\mu}}} ,{\bar {\boldsymbol{P}} }} \right) $； 13: 计算权重 $ \hat w = \bar w/\prod {_{i = 1}^D{w_{i,{l_i}}}} $； 14: end for 15: end for 16: 归一化权重得到 $ D $个输入消息乘积的粒子化形式
$ \left\{ {{{{\hat {\boldsymbol{x}}}}_s},{{\hat w}_s}} \right\}_{s = 1}^S $。
下载: 导出CSV
3 天基雷达组网目标跟踪DCNBP算法
3. DCNBP algorithm for target tracking in space-based radar networks
1: 初始化：令 $ k = 0 $，对每个雷达节点 $ j = 1,2,\cdots, N $，初始化
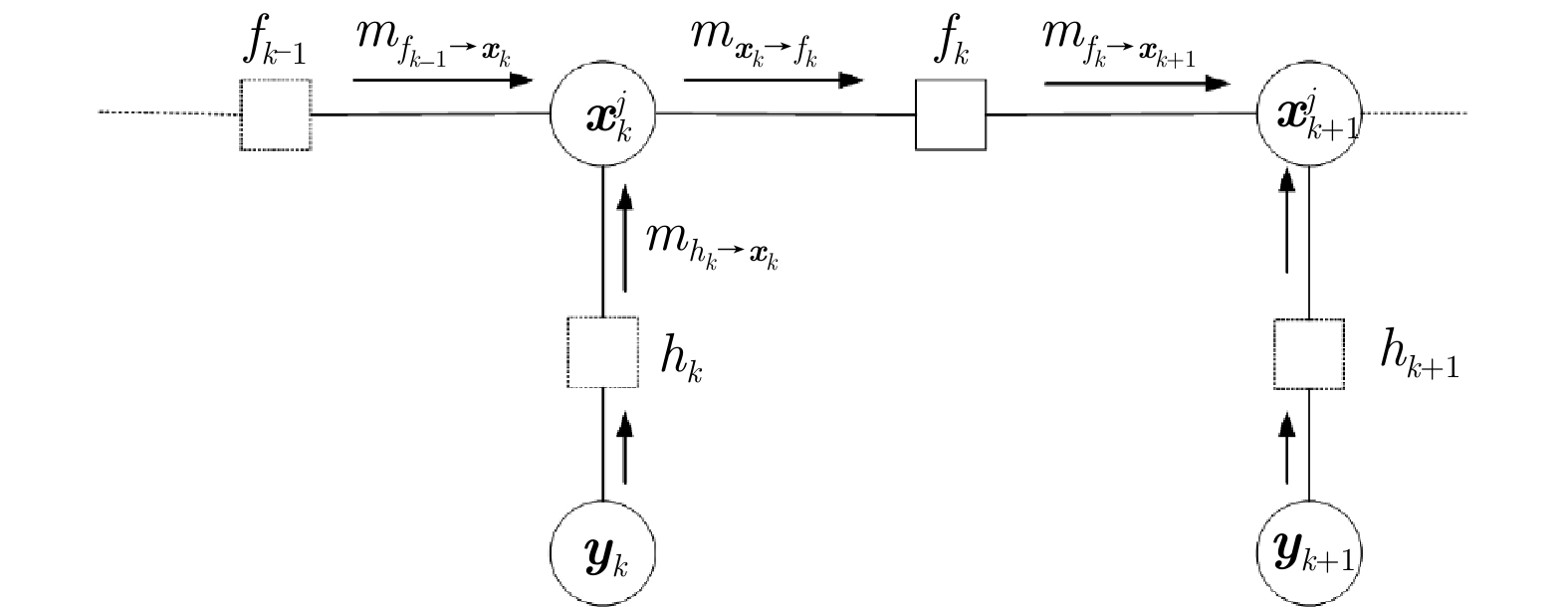
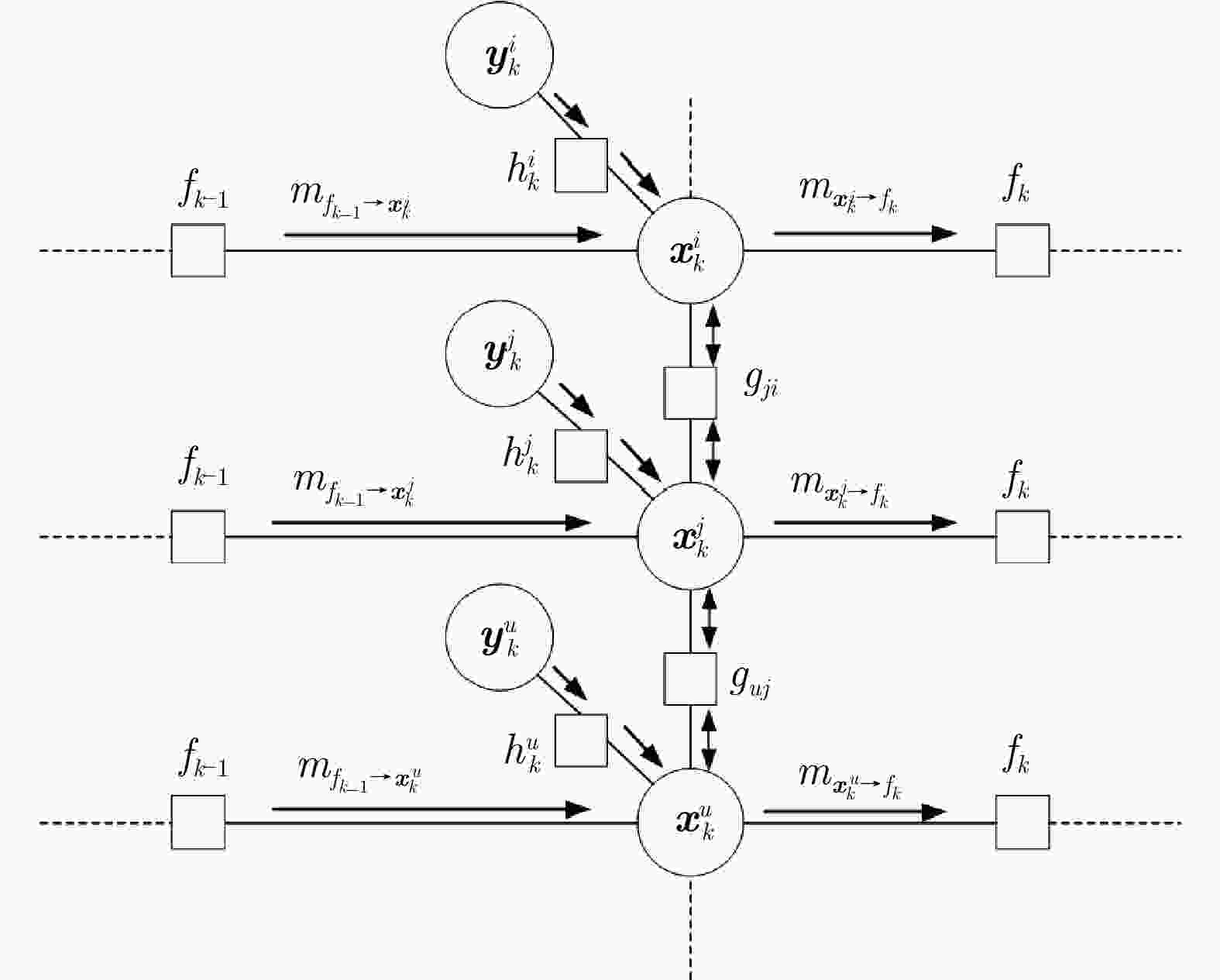
信度 $ {b_0}( {{{\boldsymbol{x}}}_0^j} ) = {p_0}( {{{\boldsymbol{x}}}_0^j} ) $；2: for $ k = 1:K $ do 3: for $ j = 1,2,\cdots, N $ do 4: 根据式(27)—式(29)建立消息 $ {m_{{f_{k - 1}} \to {{\boldsymbol{x}}}_k^j}} $的粒子化表示
$ \{ {{{\boldsymbol{x}}}_{k,s}^j,\bar w_{{f_k},s}^j} \}_{s = 1}^S $；5: 根据式(34)—式(37)建立消息 $ {m_{h_k^j \to {{\boldsymbol{x}}}_k^j}} $的粒子化表示
$ \{ {{\boldsymbol{x}}_{k,s}^j,w_{{h_k},s}^j} \}_{s = 1}^S $；6: 根据算法2建立消息乘积 $ {m_{{f_{k - 1}} \to {{\boldsymbol{x}}}_k^j}}{m_{h_k^j \to {{\boldsymbol{x}}}_k^j}} $的粒子化
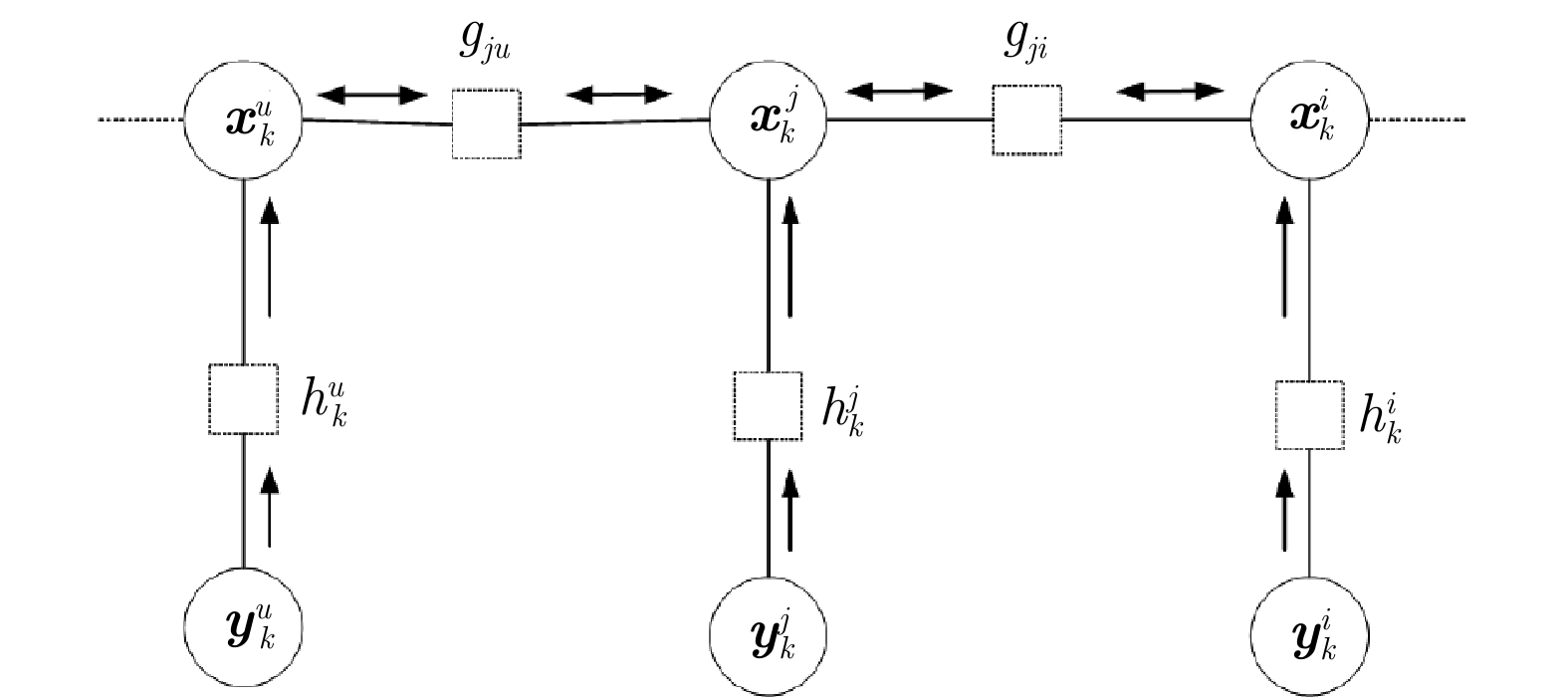
表示；7: end for 8: 令 $ l = 0 $； 9: for $ j = 1,2,\cdots, N $ do 10: 粒子初始化 $ m_{{g_{ji}} \to {{\boldsymbol{x}}}_k^j}^0 = \{ {{{\boldsymbol{x}}}_{ji,s}^0,w_{{g_{ji}},s}^0} \}_{s = 1}^S $； 11: end for 12: while $ l \le L $ do 13: $ l = l + 1 $；
14: 采用算法2计算 $ m_{{{\boldsymbol{x}}}_k^j \to {g_{ji}}}^l = {m_{h_k^j \to {{\boldsymbol{x}}}_k^j}}\prod\limits_{u \in {D_j}\backslash i} {m_{{g_{uj}} \to {{\boldsymbol{x}}}_k^j}^{l - 1}} $，
粒子化形式为 $ m_{{{\boldsymbol{x}}}_k^j \to {g_{ji}}}^l = \{ {\bar {\boldsymbol {x}}_{ji,s}^l,\bar w_{{g_{ji}},s}^l} \}_{s = 1}^S $；15: 根据耦合关系更新 $ m_{{g_{ji}} \to {{\boldsymbol{x}}}_k^j}^l = \{ {{{\boldsymbol{x}}}_{ji,s}^l,w_{{g_{ji}},s}^l} \}_{s = 1}^S $； 16: end while
17: 根据算法2计算消息乘积 $ {m_{{f_{k - 1}} \to {{\boldsymbol{x}}}_k^j}}{m_{h_k^j \to {{\boldsymbol{x}}}_k^j}}\prod\limits_{u \in {D_j}} {m_{{g_{uj}} \to {{\boldsymbol{x}}}_k^j}^L} $
的粒子化形式以表示后验分布 $ p( {{{\boldsymbol{x}}}_k^j} ) $，根据后验分布得到
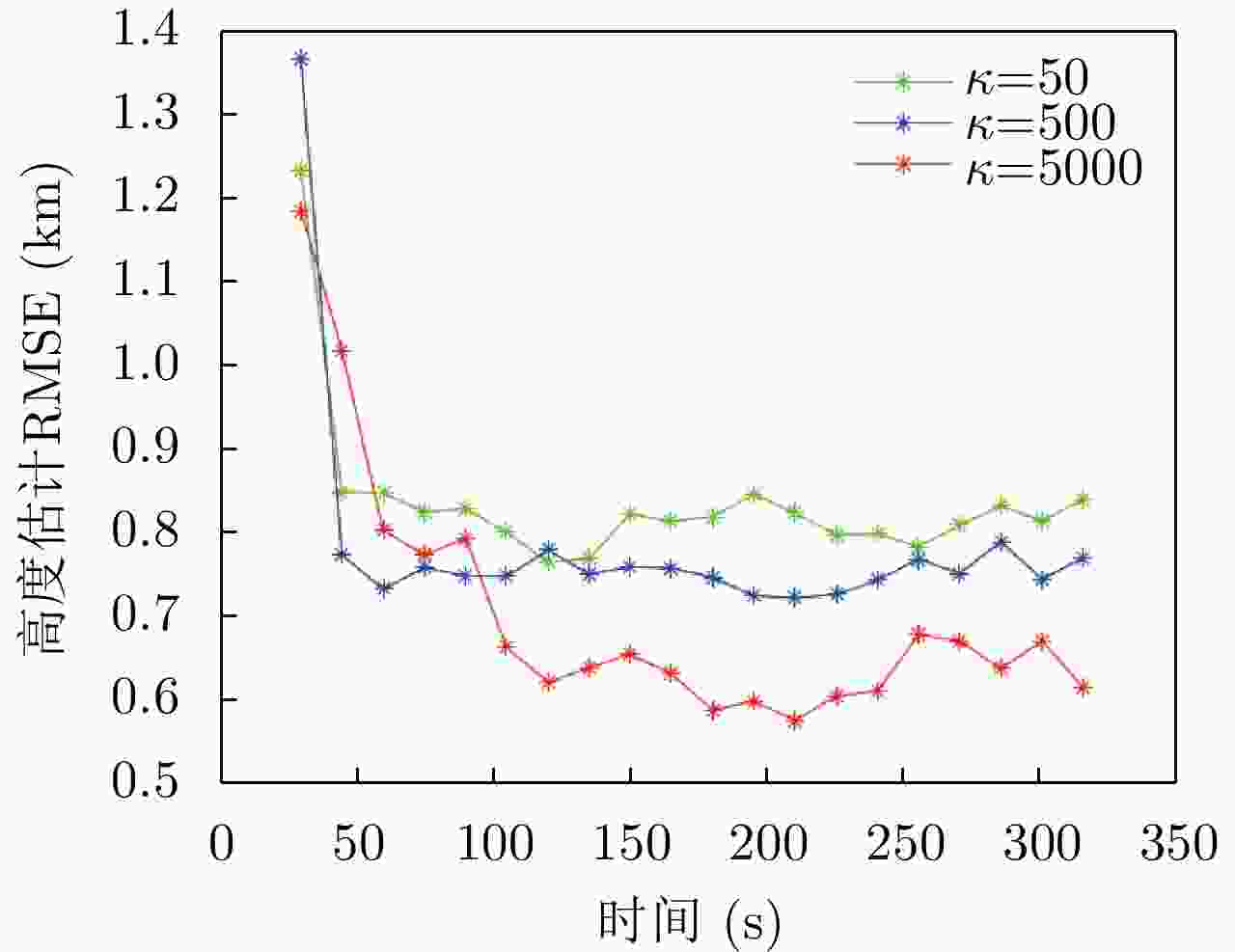
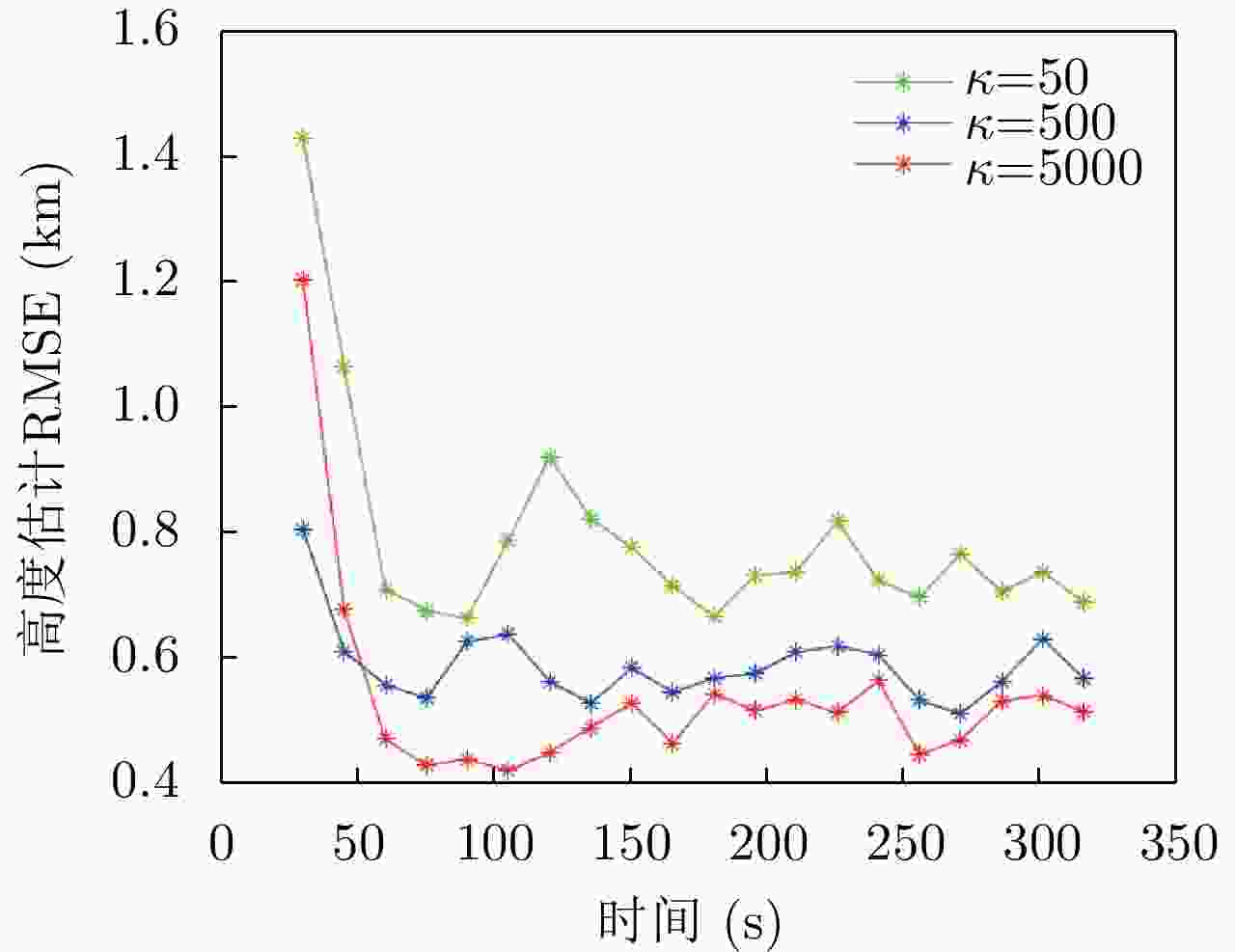
节点的估计值 $ \hat {\boldsymbol {x}}_{k}^j $；18: end for
下载: 导出CSV
表 1 不同参数下DCNBP算法估计的RMSE平均值(km)
Table 1. Average RMSE obtained by DCNBP with different parameters (km)
耦合参数( $\kappa$) $S = 400$ $S = 800$ $\kappa = 50$ 0.8196 0.6596 $\kappa = 500$ 0.7511 0.5506 $\kappa = 5000$ 0.6389 0.4661
下载: 导出CSV
-
[1] GRAVES R H W. Detection of airborne targets by a space-based radar using multipath interference[C]. 1991 IEEE National Radar Conference, Los Angeles, USA, 1991: 46–49. [2] KULIKOV G Y and KULIKOVA M V. The accurate continuous-discrete extended Kalman filter for radar tracking[J]. IEEE Transactions on Signal Processing, 2016, 64(4): 948–958. doi: 10.1109/TSP.2015.2493985 [3] KULIKOV G Y and KULIKOVA M V. Square-root accurate continuous-discrete extended-unscented Kalman filtering methods with embedded orthogonal and J-orthogonal QR decompositions for estimation of nonlinear continuous-time stochastic models in radar tracking[J]. Signal Processing, 2020, 166: 107253. doi: 10.1016/j.sigpro.2019.107253 [4] ZHANG Qian and SONG T L. Gaussian mixture presentation of measurements for long-range radar tracking[J]. Digital Signal Processing, 2016, 56: 110–122. doi: 10.1016/j.dsp.2016.06.008 [5] 张连仲, 王宝宝, 王超尘. 一种基于期望最大化去偏转换量测滤波的目标跟踪算法[J]. 中国惯性技术学报, 2020, 28(6): 829–833. doi: 10.13695/j.cnki.12-1222/o3.2020.06.020ZHANG Lianzhong, WANG Baobao, and WANG Chaochen. A target tracking algorithm based on expectation maximization debiased conversion measurement filter[J]. Journal of Chinese Inertial Technology, 2020, 28(6): 829–833. doi: 10.13695/j.cnki.12-1222/o3.2020.06.020 [6] WU Qisong, CHEN Lingjie, LI Yanping, et al. Reweighted robust particle filtering approach for target tracking in automotive radar application[J]. Remote Sensing, 2022, 14(21): 5477. doi: 10.3390/rs14215477 [7] AIT-EL-FQUIH B and HOTEIT I. A variational Bayesian multiple particle filtering scheme for large-dimensional systems[J]. IEEE Transactions on Signal Processing, 2016, 64(20): 5409–5422. doi: 10.1109/TSP.2016.2580524 [8] 闫文旭, 兰华, 王增福, 等. 基于变分贝叶斯的星载雷达非线性滤波[J]. 航空学报, 2020, 41(S2): 724395. doi: 10.7527/S1000-6893.2020.24395YAN Wenxu, LAN Hua, WANG Zengfu, et al. Nonlinear filtering for spaceborne radars based on variational Bayes[J]. Acta Aeronautica et Astronautica Sinica, 2020, 41(S2): 724395. doi: 10.7527/S1000-6893.2020.24395 [9] LAN Hua, MA Jirong, WANG Zengfu, et al. A message passing approach for multiple maneuvering target tracking[J]. Signal Processing, 2020, 174: 107621. doi: 10.1016/j.sigpro.2020.107621 [10] GUO Zhen, WANG Zengfu, LAN Hua, et al. OTHR multitarget tracking with a GMRF model of ionospheric parameters[J]. Signal Processing, 2021, 182: 107940. doi: 10.1016/j.sigpro.2020.107940 [11] XU Jing, YANG Gongliu, SUN Yiding, et al. A multi-sensor information fusion method based on factor graph for integrated navigation system[J]. IEEE Access, 2021, 9: 12044–12054. doi: 10.1109/ACCESS.2021.3051715 [12] YU Zehua, LI Jun, GUO Qinghua, et al. Efficient direct target localization for distributed MIMO radar with expectation propagation and belief propagation[J]. IEEE Transactions on Signal Processing, 2021, 69: 4055–4068. doi: 10.1109/TSP.2021.3092363 [13] DESINGH K, LU Shiyang, OPIPARI A, et al. Efficient nonparametric belief propagation for pose estimation and manipulation of articulated objects[J]. Science Robotics, 2019, 4(30): eaaw4523. doi: 10.1126/scirobotics.aaw4523 [14] 郭振, 王增福, 白向龙, 等. 消息传递方法及其在信息融合中的应用[J]. 控制与决策, 2022, 37(10): 2443–2455. doi: 10.13195/j.kzyjc.2021.0367GUO Zhen, WANG Zengfu, BAI Xianglong, et al. Message passing methods and their applications in information fusion[J]. Control and Decision, 2022, 37(10): 2443–2455. doi: 10.13195/j.kzyjc.2021.0367 [15] LAN Hua, WANG Zengfu, BAI Xianglong, et al. Measurement-level target tracking fusion for over-the-horizon radar network using message passing[J]. IEEE Transactions on Aerospace and Electronic Systems, 2021, 57(3): 1600–1623. doi: 10.1109/TAES.2020.3044109 [16] WU Yuanxin, WANG Ping, and HU Xiaoping. Algorithm of earth-centered earth-fixed coordinates to geodetic coordinates[J]. IEEE Transactions on Aerospace and Electronic Systems, 2003, 39(4): 1457–1461. doi: 10.1109/TAES.2003.1261144 [17] WANG Shengdi and DEKORSY A. A factor graph-based distributed consensus Kalman filter[J]. IEEE Signal Processing Letters, 2020, 27: 2039–2043. doi: 10.1109/LSP.2020.3036337 [18] LI Wei, YANG Zhen, and HU Haifeng. Sequential particle-based sum-product algorithm for distributed inference in wireless sensor networks[J]. IEEE Transactions on Vehicular Technology, 2013, 62(1): 341–348. doi: 10.1109/TVT.2012.2221484 [19] CHAHROUR H, DANSEREAU R M, RAJAN S, et al. Target detection through Riemannian geometric approach with application to drone detection[J]. IEEE Access, 2021, 9: 123950–123963. doi: 10.1109/ACCESS.2021.3105594 -
图(12) / 表(4)
计量
- 文章访问数: 585
- HTML全文浏览量: 394
- PDF下载量: 110
- 被引次数: 0
