A Range-angle Joint Imaging Algorithm for Automotive Radar Systems Based on Doppler Domain Compensation
-
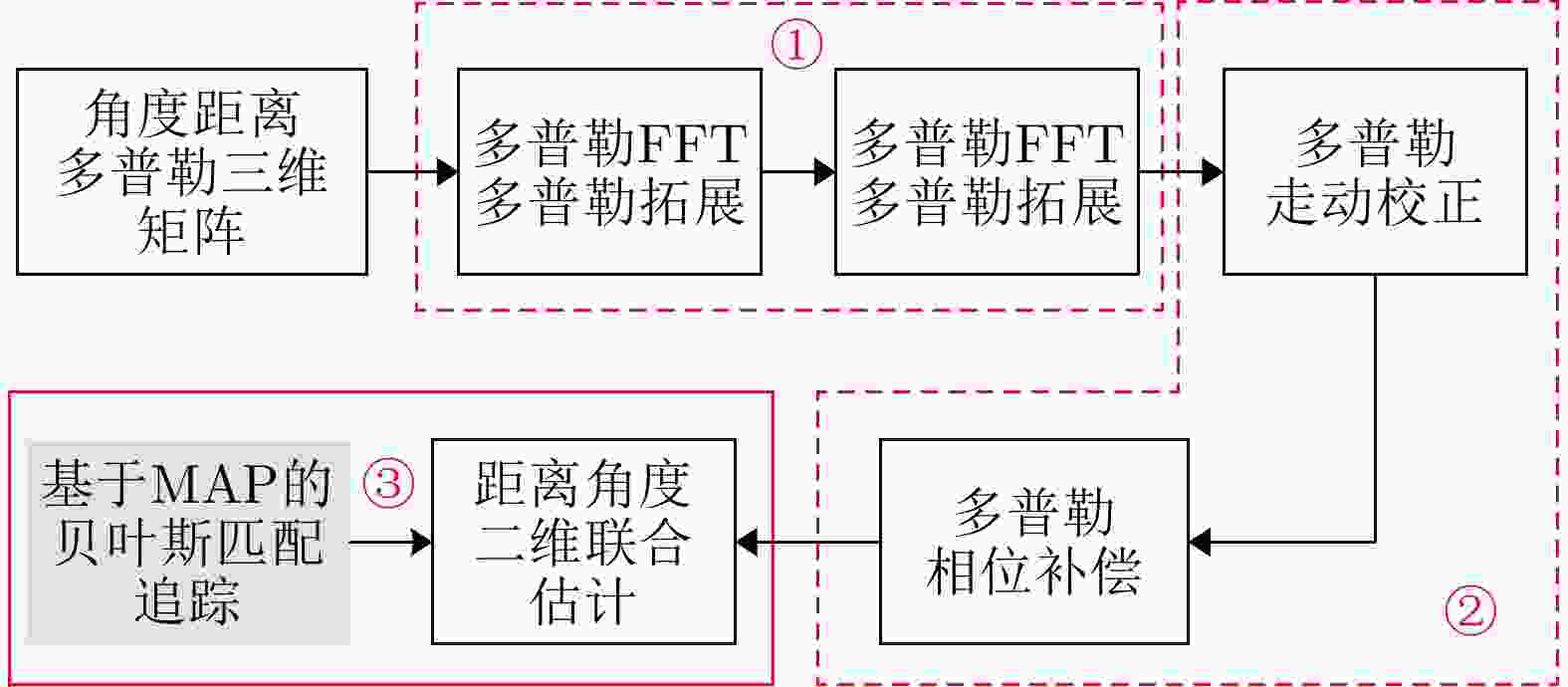
摘要: 高性能、高分辨率单快拍前视成像技术是赋能车载雷达发展的关键,但距离/多普勒走动问题会限制相干积分的实施,同时系统分辨率也往往受限于硬件参数难以提高。根据车载毫米波雷达时分多输入多输出(TDM-MIMO)的前视成像体制,该文提出多普勒域补偿和点对点回波校正方法,完成多域信号解耦合,同时完成距离多普勒走动校正和多普勒解模糊。由于有限阵元数及强噪声干扰限制了传统单维度距离角度成像准确性,因此,该文提出一种基于改进贝叶斯匹配追踪方法(IBMP)的多域联合估计算法。该方法基于伯努利-高斯(BG)模型,在最大后验(MAP)准则约束下迭代更新估计参数和支撑域,实现了多维联合信号的高精度重构。仿真和实测结果表明该文方法能够有效解决距离走动问题,并提高雷达前视成像的角度分辨率,具有较强噪声鲁棒性。
-
关键词:
- 毫米波雷达 /
- 距离走动 /
- 多普勒域补偿 /
- 多域联合估计 /
- 改进贝叶斯匹配追踪(IBMP)算法
Abstract: Single snapshot forward-looking imaging technology with high performance and resolution is crucial for enabling the development of automotive radars. However, range migration issues can limit the implementation of coherent integration methods, and improving system resolution is generally difficult due to hardware parameter limitations. Based on the Time-Division Multiplexing Multiple-Input-Multiple-Output (TDM-MIMO) forward-looking imaging systems of automotive millimeter wave radar, this paper proposes Doppler domain compensation and point-to-point echo correction measures for achieving multidomain signal decoupling. However, the accuracy of traditional single-dimension range and angle imaging is limited by the number of finite array elements and significant noise interference. Therefore, this paper proposes a multidomain joint estimation algorithm based on the Improved Bayesian Matching Pursuit (IBMP) method. The Bayesian method is based on the Bernoulli-Gaussian (BG) model, and the estimated parameters and support domain are iteratively updated in this method while adhering to the Maximum a Posteriori (MAP) criterion constraint to achieve the high-precision reconstruction of multidimensional joint signals. The final set of simulation and actual measurement results demonstrate that the proposed method can effectively solve the problem of range migration and improve the angle resolution of radar forward-looking imaging while exhibiting excellent noise robustness. -
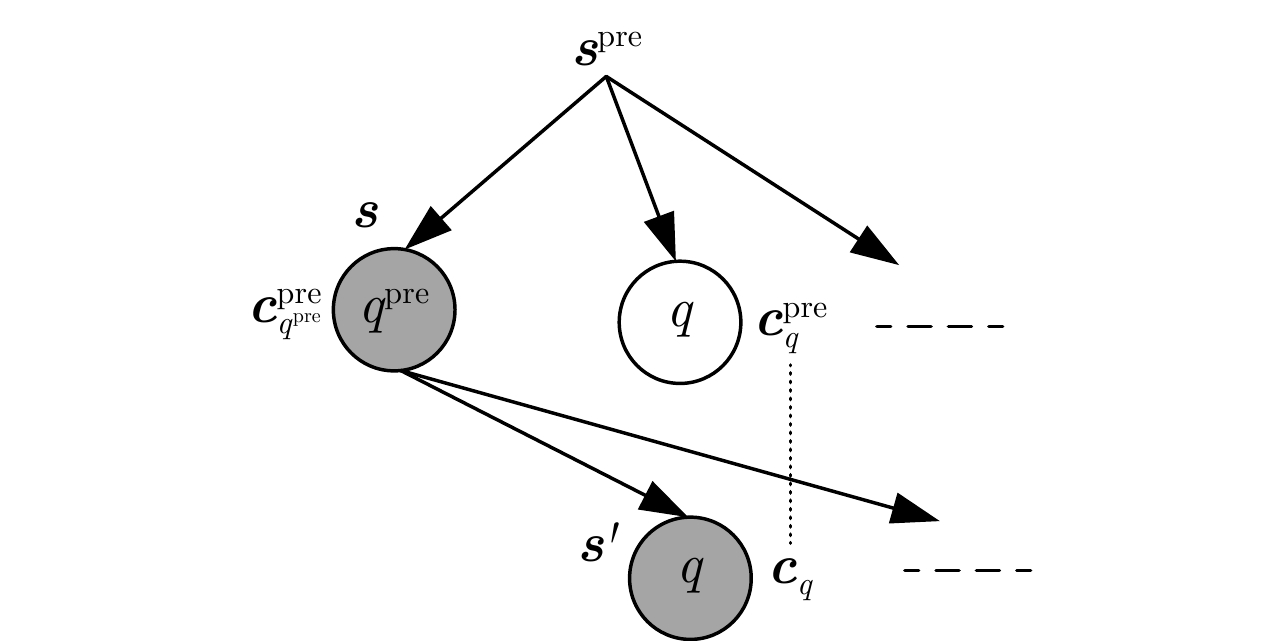
1 基于MAP的贝叶斯匹配追踪方法
1. The Bayesian Matching Pursuit (BMP) based on MAP
初始化:
$\partial \left( {\mathbf{0} } \right) = \left( { - M{\text{In} }\;\pi - M{\text{In} } \;{\sigma ^2} - \dfrac{1}{ { {\sigma ^2} } }\left\| { {\boldsymbol{Y} } } \right\|_2^2} \right) + Q{\text{In} }\left( {1 - {p_1} } \right)$${ { {\boldsymbol{c} } }_q} = \dfrac{ { { { {\boldsymbol{a} } }_q} } }{ { {\sigma ^2} } },{\beta _q} = \sigma _1^2{\left( {1 + \sigma _1^2{ {\boldsymbol{a} } }_q^{\text{H} }{ { {\boldsymbol{c} } }_q} } \right)^{ - 1} }$ ${\partial _q} = \partial \left( {\mathbf{0} } \right) + {\text{In} }\dfrac{ { {\beta _q} } }{ { \sigma _1^2} } + {\beta _q}\left\| {\left( { { { {\boldsymbol{Y} } }^{\text{H} } }{ { {\boldsymbol{c} } }_q} } \right)} \right\|_2^2 + {\text{In} }\left( {\dfrac{ { {p_1} } }{ {1 - {p_1} } } } \right)$ $\varOmega = [\;],\;{ { {\boldsymbol{s} } }^{\left( 0 \right)} } = {\mathbf{0} }$ 更新迭代过程: ${q^*} = {{{\rm{max}}\_{\rm{index}}} }\left( { {\partial _q} } \right)$ $\varOmega = \varOmega \cup {q^*},{ { {\boldsymbol{s} } }^{\left( { {d} } \right)} } = { { {\boldsymbol{s} } }^{\left( { { {d} } - 1} \right)} } + \delta \left[ { {q^*} } \right],{\partial ^{\left( d \right)} } = {\partial _{ {q^*} } }$ ${ { {\boldsymbol{c} } }_q} = { { {\boldsymbol{c} } }_q} - {\beta _{ {q^*} } }{ { {\boldsymbol{c} } }_{ {q^*} } }({ {\boldsymbol{c} } }_{ {q} })^{\text{H} }{ { {\boldsymbol{a} } }_q}$ ${\beta _q} = \sigma _1^2{\left( {1 + \sigma _1^2({ {\boldsymbol{a} } }_q)^{ {\rm{H} } }{ { {\boldsymbol{c} } }_q} } \right)^{ - 1} }$ ${\partial _q} = {\partial ^{\left( d \right)} } + {\rm{In} }\dfrac{ { {\beta _q} } }{ {\sigma _\Delta ^2} } + {\beta _q}\left\| { { { {\boldsymbol{Y} } }^{\text{H} } }{ { {\boldsymbol{c} } }_q} } \right\|_2^2 + {\text{In} }\left( {\dfrac{ { {p_1} } }{ {1 - {p_1} } } } \right)$ 输出: ${\hat { {\boldsymbol{x} } }_{ {\text{map} } } } = \sigma _1^2 \displaystyle\sum\limits_{i \in \varOmega } { {\delta _i}{ {\left( { {\boldsymbol{c} }_i^{} } \right)}^{\text{H} } }{ {\boldsymbol{Y} } } }$ 表 1 仿真实验雷达参数
Table 1. Radar parameters for simulation experiment
雷达参数 数值 载频(GHz) 77 带宽(MHz) 1500 MIMO天线配置 2T × 4R 脉冲宽度(μs) 55 脉冲采样点数K 256 脉冲个数L 256 角度分辨率(°) 15.7 距离分辨率(m) 0.1 最大不模糊速度(m/s) 8.85 表 2 AWR1642雷达关键参数
Table 2. Radar parameters of AWR1642
雷达参数 值 载频(GHz) 77 带宽(MHz) 1500 MIMO天线配置 2T × 4R 脉冲宽度(μs) 160 脉冲采样点数K 128 脉冲个数L 15.7 角度分辨率(°) 0.1 距离分辨率(m) 0.095 -
[1] BILIK I, LONGMAN O, VILLEVAL S, et al. The rise of radar for autonomous vehicles: Signal processing solutions and future research directions[J]. IEEE Signal Processing Magazine, 2019, 36(5): 20–31. doi: 10.1109/MSP.2019.2926573 [2] MUTSCHLER M A, SCHARF P A, RIPPL P, et al. River surface analysis and characterization using FMCW radar[J]. IEEE Journal of Selected Topics in Applied Earth Observations and Remote Sensing, 2022, 15: 2493–2502. doi: 10.1109/JSTARS.2022.3157469 [3] MERCURI M, LORATO I R, LIU Y H, et al. Vital-sign monitoring and spatial tracking of multiple people using a contactless radar-based sensor[J]. Nature Electronics, 2019, 2(6): 252–262. doi: 10.1038/s41928-019-0258-6 [4] XIA Weijie, LI Yi, and DONG Shiqi. Radar-based high-accuracy cardiac activity sensing[J]. IEEE Transactions on Instrumentation and Measurement, 2021, 70: 4003213. doi: 10.1109/TIM.2021.3050827 [5] SUN Hongbo, BRIGUI F, and LESTURGIE M. Analysis and comparison of MIMO radar waveforms[C]. 2014 International Radar Conference, Lille, France, 2014: 1–6. [6] RICHARDS M A. Fundamentals of Radar Signal Processing[M]. Dallas, USA: Tata McGraw-Hill Education, 2005. [7] PERRY R P, DIPIETRO R C, and FANTE R L. SAR imaging of moving targets[J]. IEEE Transactions on Aerospace and Electronic Systems, 1999, 35(1): 188–200. doi: 10.1109/7.745691 [8] HUANG Penghui, LIAO Guisheng, YANG Zhiwei, et al. Ground maneuvering target imaging and high-order motion parameter estimation based on second-order Keystone and generalized Hough-HAF transform[J]. IEEE Transactions on Geoscience and Remote Sensing, 2017, 55(1): 320–335. doi: 10.1109/TGRS.2016.2606436 [9] LONGMAN O and BILIK I. Spectral Radon-Fourier transform for automotive radar applications[J]. IEEE Transactions on Aerospace and Electronic Systems, 2021, 57(2): 1046–1056. doi: 10.1109/TAES.2020.3038245 [10] XIONG Kai, ZHAO Guanghui, and SHI Guangming. Radar high-speed target coherent detection method based on modified radon inverse Fourier transform[J]. IEEE Transactions on Aerospace and Electronic Systems, 2023, 59(2): 950–962. doi: 10.1109/TAES.2022.3193090 [11] ROBERTS W, STOICA P, LI Jian, et al. Iterative adaptive approaches to MIMO radar imaging[J]. IEEE Journal of Selected Topics in Signal Processing, 2010, 4(1): 5–20. doi: 10.1109/JSTSP.2009.2038964 [12] KIM S, OH D, and LEE J. Joint DFT-ESPRIT estimation for TOA and DOA in vehicle FMCW radars[J]. IEEE Antennas and Wireless Propagation Letters, 2015, 14: 1710–1713. doi: 10.1109/LAWP.2015.2420579 [13] FANG W H and FANG L D. Joint angle and range estimation with signal clustering in FMCW radar[J]. IEEE Sensors Journal, 2020, 20(4): 1882–1892. doi: 10.1109/JSEN.2019.2949367 [14] 杨建宇. 雷达对地成像技术多向演化趋势与规律分析[J]. 雷达学报, 2019, 8(6): 669–692. doi: 10.12000/JR19099YANG Jianyu. Multi-directional evolution trend and law analysis of radar ground imaging technology[J]. Journal of Radars, 2019, 8(6): 669–692. doi: 10.12000/JR19099 [15] 钟金荣, 文贡坚. 基于块稀疏贝叶斯学习的雷达目标压缩感知[J]. 雷达学报, 2016, 5(1): 99–108. doi: 10.12000/JR15056ZHONG Jinrong and WEN Gongjian. Compressive sensing for radar target signal recovery based on block sparse Bayesian learning[J]. Journal of Radars, 2016, 5(1): 99–108. doi: 10.12000/JR15056 [16] ANITORI L, OTTEN M, and HOOGEBOOM P. Compressive sensing for high resolution radar imaging[C]. 2010 Asia-Pacific Microwave Conference, Yokohama, Japan, 2010: 1809–1812. [17] WU Yang, ZHANG Yin, ZHANG Yongchao, et al. Outline reconstruction for radar forward-looking imaging based on total variation functional deconvloution methodxs[C]. IGARSS 2018–2018 IEEE International Geoscience and Remote Sensing Symposium, Valencia, Spain, 2018: 7267–7270. [18] 唐军奎, 刘峥, 冉磊, 等. 基于稀疏和低秩先验的雷达前视超分辨成像方法[J]. 雷达学报, 2023, 12(2): 332–342. doi: 10.12000/JR22199TANG Junkui, LIU Zheng, RAN Lei, et al. Radar forward-looking super-resolution imaging method based on sparse and low-rank priors[J]. Journal of Radars, 2023, 12(2): 332–342. doi: 10.12000/JR22199 [19] SHU Zhaowei, ZONG Zhulin, HUANG Libing, et al. Forward-looking radar super-resolution imaging combined TSVD with L1 norm constraint[C]. IGARSS 2019–2019 IEEE International Geoscience and Remote Sensing Symposium, Yokohama, Japan, 2019: 2559–2562. [20] JI Shihao, XUE Ya, and CARIN L. Bayesian compressive sensing[J]. IEEE Transactions on Signal Processing, 2008, 56(6): 2346–2356. doi: 10.1109/TSP.2007.914345 [21] XU Yanqin, SONG Yuan, WEI Shunjun, et al. A fast 2D super-resolution imaging method via Bayesian compressive sensing for mmWave automotive radar[C]. 2023 IEEE Radar Conference (RadarConf23), San Antonio, USA, 2023: 1–6. [22] SCHNITER P, POTTER L C, and ZINIEL J. Fast Bayesian matching pursuit[C]. 2008 Information Theory and Applications Workshop, San Diego, USA, 2008: 326–333. [23] YOU You, ZHANG Chuan, and ZHANG Li. Bayesian matching pursuit based estimation of off-grid channel for millimeter wave massive MIMO system[J]. IEEE Transactions on Vehicular Technology, 2022, 71(11): 11603–11614. doi: 10.1109/TVT.2022.3169721 [24] FIGUEIREDO M A T, NOWAK R D, and WRIGHT S J. Gradient projection for sparse reconstruction: Application to compressed sensing and other inverse problems[J]. IEEE Journal of Selected Topics in Signal Processing, 2007, 1(4): 586–597. doi: 10.1109/JSTSP.2007.910281 [25] MU Huilin, ZHANG Yun, JIANG Yicheng, et al. STAP-based GMTI for multichannel SAR with sparse sampling[C]. 2017 IEEE Radar Conference (RadarConf), Seattle, USA, 2017: 1483–1487. -



 作者中心
作者中心 专家审稿
专家审稿 责编办公
责编办公 编辑办公
编辑办公

 下载:
下载: