作者中心
专家审稿
责编办公
编辑办公
Waveform Selection Method of Cognitive Radar Target Tracking Based on Reinforcement Learning
-
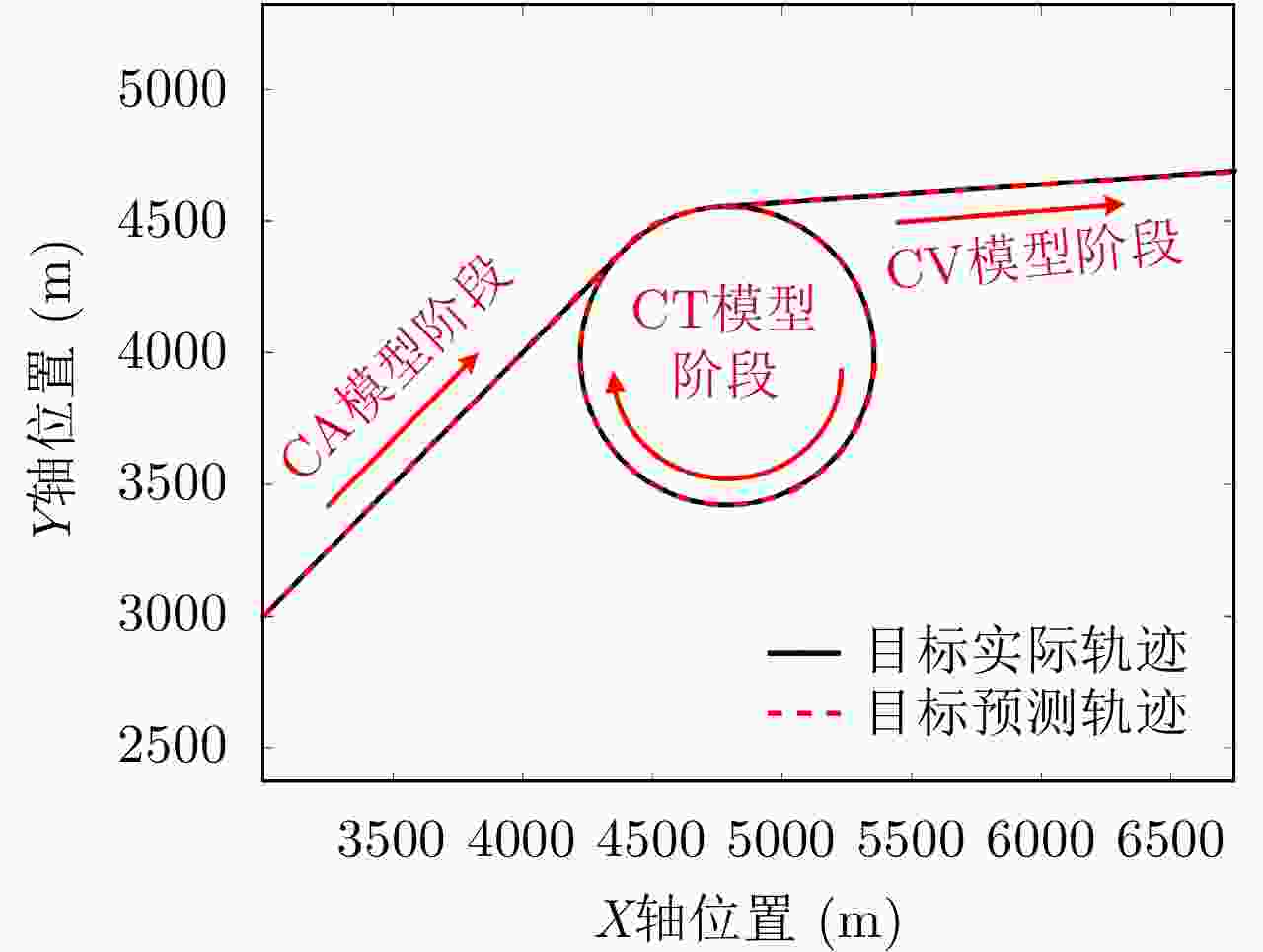
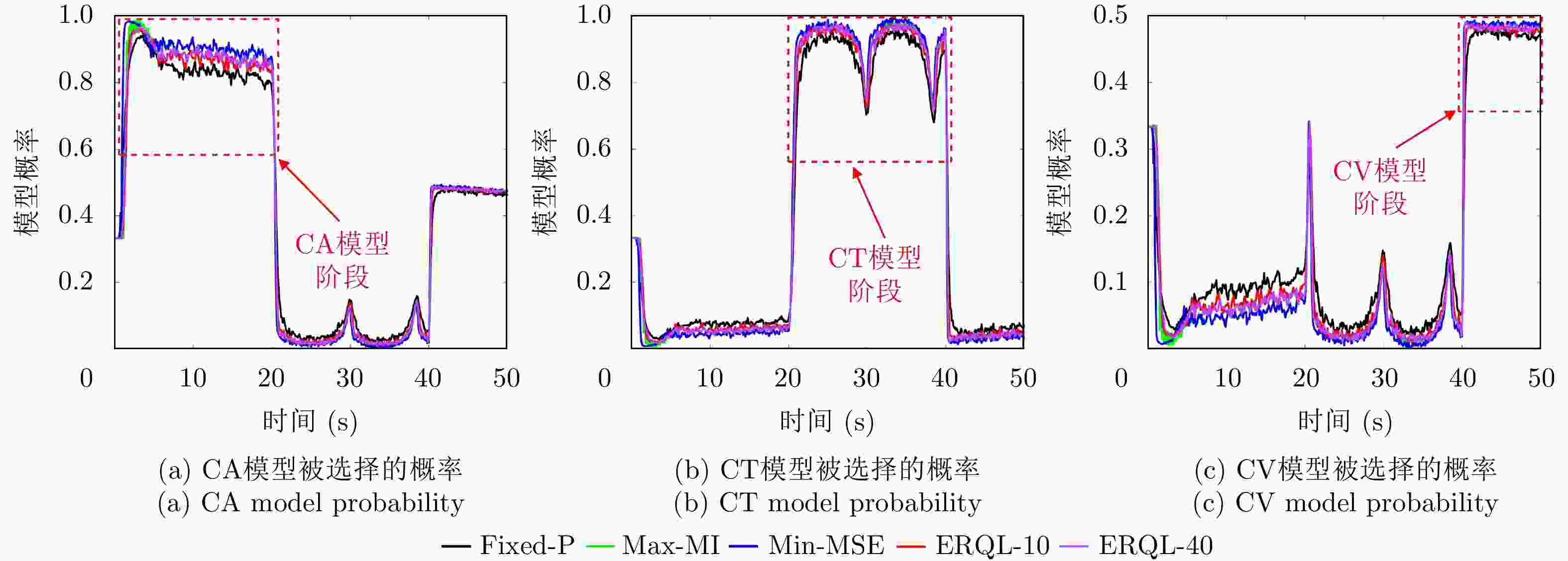
摘要: 认知雷达通过不断与环境互动并从经验中学习，根据获得的知识不断调整其波形、参数和照射策略，以在复杂多变的场景中实现稳健的目标跟踪，其波形设计在提高跟踪性能方面一直备受关注。该文提出了一种用于跟踪高机动目标的认知雷达波形选择框架，该框架考虑了恒定速度(CV)、恒定加速度(CA)和协同转弯(CT)模型的组合，在该框架的基础上设计了基于准则优化(CBO)和熵奖励Q学习(ERQL)方法进行最优波形选择。该方法将雷达与目标集成到一个闭环中，发射波形随目标状态的变化实时更新，从而达到对目标的最佳跟踪性能。数值结果表明，与CBO方法相比，所提出的ERQL方法大大减少了获取最优波形的处理时间，并实现了与CBO相近的跟踪性能，相比于固定参数(Fixed-P)方法，极大地提高了机动目标的跟踪精度。
-
关键词:
- 目标跟踪 /
- 认知雷达 /
- 波形挑选 /
- 基于准则优化(CBO) /
- 熵奖励Q学习(ERQL)
Abstract: Based on the obtained knowledge through ceaseless interaction with the environment and learning from the experience, cognitive radar continuously adjusts its waveform, parameters, and illumination strategies to achieve robust target tracking in complex and changing scenarios. Its waveform design has been receiving attention to improve tracking performance. In this paper, we propose a novel framework of cognitive radar waveform selection for the tracking of high-maneuvering targets. The framework considers the combination of Constant Velocity (CV), Constant Acceleration (CA), and Coordinate Turn (CT) motions. We also design Criterion-Based Optimization (CBO) and Entropy Reward Q-Learning (ERQL) methods to perform waveform selection based on this framework. To provide the optimum target tracking performance, it merges the radar and target into a closed loop, updating the broadcast waveform in real-time as the target state changes. The suggested ERQL technique achieves about the same tracking performance as the CBO while using much less processing time than the CBO, according to numerical results. The proposed ERQL method significantly increases the tracking accuracy of moving targets as compared to the fixed parameter approach. -
1. 引言
合成孔径雷达(Synthetic Aperture Radar, SAR)是一种主动式微波遥感探测技术，可实现全天时、全天候对地观测，并具有一定的地表穿透能力[1]。通过SAR系统获取目标的3维几何信息可用于对场景的精细化描述，相对于2维平面成像，具有十分重要的军事应用价值。目前较为成熟的3维重建技术是干涉SAR(Interferometric SAR, InSAR)技术[2,3]，利用两幅相干SAR复图像同名点的相位差反演高程。SAR层析成像(TomoSAR)技术则是在InSAR技术基础上发展起来的一种目标3维重建技术[4,5]。该技术弥补了InSAR技术在高度向分辨能力缺失的不足，真正实现了对目标的3维分辨。虽然InSAR和TomoSAR技术发展迅速，但其数据的获取需要通过多次航过或多个天线完成，增加了技术实现的难度和成本。
SAR多方位角观测是近年来提出的一种新的观测模式，对同一区域进行不同方位角的观测，不仅能获取场景内更丰富的目标特征信息，还使其具备了3维重建的潜力[6,7]。圆迹SAR(Circular SAR, CSAR)是多方位角观测的一种特殊形式，通过传感器平台的圆周运动，获取被观测目标多方位乃至360°全向观测信息，突破了常规直线轨迹SAR 2维成像的局限[8,9]。然而，对于星载SAR系统而言，难以实现单次航过环绕观测场景的多方位角观测。为实现全方位角观测，星载SAR系统需要依靠多航过或多星配合完成。尽管单次航过只能实现部分方位角的观测，但由于卫星轨道自身的弯曲特性，可将其等效为长3维曲线阵列[9,10]，因此观测数据中依然携带了目标3维几何信息。
实现3维成像的最直接方法是基于回波数据与散射目标系数间的傅里叶变换关系，通过3维FFT实现[11]。然而，由于多角度SAR数据在高度维是稀疏的，无法通过傅里叶变换实现无模糊3维成像。针对稀疏采样问题，文献[9,12]采用了稀疏重建技术恢复3维几何信息，但其方法基于多航过SAR数据，且运算量大，不适用于实时处理。文献[6]通过合理离散目标函数构造测量矩阵，然后采用稀疏重构算法实现多角度SAR 3维成像，但该方法受限于测量矩阵的设计，必须解决目标稀疏性与发射信息匹配的问题。文献[13]利用了高程相同的目标在多角度SAR图像序列上位置偏移一致的特性，提出了基于低秩和稀疏矩阵分解的目标3维重建方法，但其位置偏移与目标高度的传递关系建立在圆迹SAR观测几何下，不能直接推广至星载SAR系统。文献[14,15]分析了散射中心的分布特性，从非相干处理图像中提取轮廓线，从而估计目标的3维几何信息，但该方法需要建立在已知观测目标模型的基础上，无法重建未知目标。文献[16]通过分析TerraSAR-X凝视聚束模式数据，根据星载SAR轨道特性，给出了方位调频率误差与高程误差的函数关系，提出了一种基于参数估计的高程提取方法，但是其信号模型建立在正侧视几何下，未考虑多角度观测的斜视情况。
针对上述问题，本文提出了一种联合多方位角调频率估计的星载SAR3维成像方法。该方法根据星载SAR多方位角观测几何，首先给出了更精确且适用于斜视几何的多普勒调频率与高程误差间的传递函数，实现联合多方位角SAR子孔径数据的高程估计。然后，根据2维成像的投影几何，实现目标的3维成像。最后，仿真数据验证了方法的有效性。
本文结构如下：第2节介绍多方位角观测星载SAR系统的几何特性；第3节分析星载SAR多方位角观测几何下高程误差与多普勒调频率的关系；第4节，详细地阐述3维成像的全流程；第5节以圆柱点阵目标为例，给出3维成像结果；最后一节对全文进行总结。
2. 星载SAR多方位角观测几何
多方位角观测星载SAR系统通过波束方位向扫描实现对同一场景的长合成孔径观测，其数据录取几何如图1所示。图1中所有坐标都是建立在场景局部坐标系
O\raisebox1.5pt−XYZ 下；坐标系原点O 位于观测场景内某处，X 轴所指方向为地距向，Y 轴指向方位向，Z 轴指向高度向；卫星沿曲线轨道飞行，从P1 处开始持续对地面场景进行观测，直至P2 处停止观测，两处卫星速度矢量分别为V1 和V2 ,θ1 和θ2 为两处斜距矢量与速度矢量的夹角，观测方位角跨度为Δφ ；假设场景参考平面对应高程为0；场景内有一个目标位置矢量为T ，相对参考平面高程为h ，且目标到P1 和P2 的斜距分别为R1 和R2 。若以场景参考平面为成像地平面，对P1 所在方位角子孔径数据进行成像，该目标在成像平面内的投影位置为T1 ；对P2 所在方位角子孔径数据进行成像，则该目标在成像平面内的投影位置为T2 。目标真实位置和两投影位置满足距离-多普勒模型[17]
图 1 星载SAR多方位角观测几何示意图Figure 1. Space-borne SAR multiple azimuth angle observation geometry‖T−P1‖=‖T1−P1‖2(T−P1)V1λR1=2(T1−P1)V1λR1‖T−P2‖=‖T2−P2‖2(T−P2)V2λR2=2(T2−P2)V2λR2} (1) 式中，
λ 为雷达载波波长。从式(1)可以看出，投影方向与速度矢量垂直。由于卫星轨道的弯曲，速度矢量V1 和V2 不平行，因此两次投影方向不同，即有T1=/T2 ，可以根据投影位置偏移量提取目标高程。对于CSAR的圆轨迹，目标在不同方位角SAR图像中的偏移量与高程的关系可以通过几何关系求出[13]，但这在多方位角观测星载SAR系统中直接推导却十分复杂。因此，可以从信号模型出发，反推偏移量与高程的关系。3. 目标高程与方位向偏移量的关系
在多方位角星载SAR数据录取过程中，卫星的瞬时速度方向不断变化，对于距卫星同一斜距但高程不同的两个目标而言，多普勒历程是不同的。常见的多普勒频率表达式为
fd=2RS⋅VSλRst (2) 式中，
RS 为卫星到目标的瞬时斜距矢量，VS 为卫星的瞬时速度矢量，Rst 为卫星到目标的瞬时斜距。因此，多普勒调频率Kfd 可以表示为Kfd=2λ∂Rst∂t(RSVS)−Rst∂(RSVS)∂tR2st≈2λRst[∂Rst∂tVscosθ−(V2s+Rstascosαnad)]≈2λRst[−V2ssin2θ+Rstassinθcosαnad,c] (3) 式中，
Vs 为卫星瞬时速度，as 为卫星的瞬时加速度，αnad 为目标瞬时的雷达下视角，αnad,c 为目标在中心方位时刻(正侧视)的雷达下视角，θ 为斜距矢量与速度矢量的夹角之间的夹角。多方位角观测星载SAR对目标的观测经历了由前斜视到后斜视的过程，不同方位时刻目标的瞬时下视角与斜视情况相关，即cosαnad≈sinθcosαnad,c 。假设观测方位角跨度为[–20°, 20°]，如果在推导多普勒调频率时忽略斜视角的影响，最大将引入约6%的调频率误差。对于匀速直线飞行的SAR平台，式(3)中带有
as 的第2项不存在；对于卫星平台，as 为卫星的重力加速度。在二体模型下，根据开普勒第三定律，卫星重力加速度为as=GMR2sat (4) 式中，
G 为引力常量(6.674×10–11 N·m2/kg2),M 为地球质量(5.964×1024 kg),Rsat 为卫星轨道半径。假设目标的高程误差为
Δh ，则引入的调频率误差ΔKfd 为ΔKfd=Kfd,bias−Kfd=−2assinθλ[cos(αnad+Δαnad)−cosαnad]≈−2assinθλsinαnadΔαnad (5) 式中，
Kfd,bias 为存在偏差的多普勒调频率，Δαnad 为高度误差Δh 引起的雷达下视角误差。目标高程误差与雷达下视角的几何关系如图2所示。图2中
Hs 为卫星飞行轨道高度，Re 为该纬度对应的地球半径，αinc 为目标对应的局部入射角，T 和T′ 分别在目标真实位置和存在高程误差时位置。当Δαnad≈0 时，TT′ 可以近似看作直线。结合地球椭球模型[18]，高程误差引起的下视角误差可以表示为Δαnad≈|TT′|Rst=ΔhRstsinαinc=ReRe+HsΔhRstsinαnad (6) 联立式(5)和式(6)可得
ΔKfd≈−2asResinθλRst(Re+Hs)Δh (7) 式(7)中，多普勒调频率误差与高程误差呈线性关系，与斜距成反比。因此，在方位压缩后，通过对多普勒调频率误差进行估计，即可求出目标真实高程值。
图3为仿真实验与式(7)计算的对比结果。仿真使用的轨道高度为514 km，轨道倾角为97.4°，观测场景选在赤道附近。从图3(a)中可以看出，200 m以内的高程误差引起的调频率误差小于0.2 Hz/s2，调频率误差随下视角减小而增大；图3(b)显示，调频率误差仿真值与式(7)计算值存在约5%的残差。该残差的引入除了推导过程中的两次近似外，还有加速度
as 的近似。尽管使用更精确的as 可以提高计算精度，但这却不是必需的。虽然在as 不精确的情况下，单次计算将引入约5%的残差，但可以通过迭代使其快速收敛。假设初始高程残差为200 m，通过2次迭代，由参数不精确引入的高程残余误差即可收敛至2 m以内。目标高程估计的前提是多普勒调频率估计，常见多普勒调频率估计的方法有最大对比度法和视错位法(Map Drift, MD)[19]。因为前者无法直接估计调频率的误差方向及幅度，所以此处选用MD法。MD法认为多普勒调频率误差
ΔKfd 会导致两个方位子孔径图像之间出现方位向偏移。令数据实际的多普勒调频率为Kfd ，前后两子孔径的多普勒中心间隔为Δfd ，卫星地速为Vg ，则多普勒调频率误差可以近似为ΔKfd≈−K2fdΔfdVgΔdaz (8) 式中，
Δdaz 为子孔径图像间的方位向偏移量(距离)。结合式(7)和式(8)，可以得出高程误差估计表达式为Δh≈λRst(Re+Hs)K2fd2asReΔfdVgsinθΔdaz (9) 利用高程误差估计结果修正成像初始参考高程可获得目标真实高程。然后，将目标真实高程和目标在SAR图像中的像素坐标转换成目标3维几何信息，进而完成3维重建。在进行子孔径图像偏移量估计时，噪声的存在将引入偏移量的估计误差，从而影响高程测量精度，可通过切割多个子孔径，并通过对各子孔径的高程估计值求期望将该影响降低。对于多方位角观测SAR系统，由于其观测方位角跨度大，在确保足够子孔径分辨率的同时可以获得足够多的子孔径序列，可以获得更高的测高精度。在实际观测中，背景杂波对目标高程估计的影响相对较大。当杂波纹理特征明显，且杂波对应的场景高程与目标高程相同时，杂波在子孔径图像间的偏移量与目标的偏移量一致，不影响目标高程的估计；当杂波纹理特征明显，且杂波对应的场景高程与目标高程不同时，杂波在子孔径图像中的偏移量与目标不一致，即在计算偏移量时将出现两个峰值，分别属于杂波和目标，峰值大小与信杂比有关，峰值位置与杂波和目标的高程相关，不具有随机性，无法通过多角度观测提高高程估计精度；当杂波纹理特征不明显时，杂波在不同方位角子孔径图像间的配准偏移量具有随机性，可以通过对多方位角估计值求期望降低误差，即本文方法对于该类杂波的影响同样有一定的抑制效果。
4. 处理流程
本文给出了一种多方位角观测星载SAR的3维成像方法，其流程如图4所示。
图 4 多方位角观测星载SAR的3维成像方法流程图Figure 4. The schematic diagram of space-borne SAR 3-D imaging method by multiple azimuth angle observation该方法包含以下步骤：
步骤1 (数据子孔径分割) 根据星载多方位角观测SAR原始数据的孔径长度确定分割子孔径数。为确保各子孔径数据方位聚焦效果对高程的敏感性，子孔径方位角跨度应较大；同时，为了保证子孔径数据内的相干性和划分后子孔径数目足够多，子孔径方位角跨度不宜过大。根据经验，本文以2°作为子孔径分割的参考值，将全孔径数据分割成相同方位向点数的子孔径数据序列
S1,S2,···,SNsub ，其中Nsub 为分割后子孔径数。步骤2 (参考子孔径成像) 从
S1,S2,···,SNsub 中选取中间的子孔径数据作为参考子孔径数据Sref ，以场景参考平面为参考成像平面进行低分辨率2维成像，获得参考子孔径SAR图像Iref 。参考成像平面的高程可以通过先验粗DEM获取，作为高程估计的起始值。当缺少先验DEM时，也可以通过大尺度的高程搜索获取起始值。步骤3 (强散射点搜索) 考虑到照射场景内地形和地物的空变，先将
Iref 沿距离向和方位向进行分块，分别统计各块内的像素幅值，并设定相应的幅度门限，利用幅度提取强散射点。然后，合并所有强散射点，得到强点序列p1,p2,···,pNp ，其中Np 为强点个数。步骤4 (子孔径序列成像) 在参考成像平面内对子孔径序列
S1,S2,···,SNsub 进行2维成像，获得子孔径图像序列I1,I2,···,INsub 。步骤5 (相邻子孔径分块配准) 从每个子孔径图像中取出
Np 图像块，图像块的中心分别对应Np 个强散射点，图像块大小为5×5 个像素，整个孔径图像序列共可以获得Nsub×Np 个图像块。然后，对Nsub×Np 个图像块进行升采样，并配准插值后相邻子孔径图像同一强点所在的图像块，得到(Nsub−1)×Np 组偏移量。步骤6 (基于配准偏移量的高程估计) 将偏移量代入式(9)，估计出每个强散射点的
Nsub−1 个高程值。步骤7 (多方位角高程估计值平均) 对于每个强点，将
Nsub−1 高程估计值取平均，认为是该强点的最终高程估计结果。步骤8 (3维信息重建和点云显示) 根据强点在
Iref 中的位置和高程估计值，计算各点在场景中的3维坐标，最终以3维点云的形式显示。5. 仿真结果
仿真1 单点目标仿真 仿真参数如表1所示，表中的雷达波束中心下视角特指雷达波束正侧视照射场景时对应的波束中心下视角，仿真的点目标处于波束中心，设置不同信噪比和信杂比进行仿真实验。在不同信噪比的仿真实验中，SAR图像中加入的噪声为高斯白噪声，信噪比设有5 dB, 10 dB, 15 dB, 20 dB, 25 dB 5个梯度值，分别进行50次高程提取蒙特卡洛模拟实验，以高程估计的均方根误差(Root Means Square Error, RMSE)作为评价指标。在进行杂波仿真实验时，仿真方法与噪声的仿真方法不同，不直接向SAR图像中添加杂波。
κ 分布是目前应用最广的分布模型之一[20]，在高分辨情况下可以在很宽范围内匹配杂波数据的幅度分布。因此仿真实验中使用服从κ 分布的杂波模型生成场景的散射场。然后，用该散射场与目标进行多角度回波仿真。仿真数据的信杂比设有10 dB, 15 dB, 20 dB, 25 dB 4个梯度值(5 dB信杂比将导致目标淹没在杂波中)，各进行50次蒙特卡洛实验，同样以高程估计的均方根误差作为评价指标。本文中信杂比的定义为信号功率与杂波功率(杂波幅度的均方根)的比值。在不同信噪比仿真实验中，为验证本文方法在斜视处理时相对于文献[16]方法的优势，截取了中心方位角为16°，方位角跨度为4°对应的斜视回波数据，分别用文献[16]方法和本文方法进行处理，对比结果如图5(a)所示。由于文献[16]中方法的提出未考虑斜视几何，因此相比于本文方法在高程估计上存在更大的偏差。为进一步验证联合多方位角观测对提高测高精度的有效性，开展了单方位角观测和多方位角观测数据处理对比实验。其中，单方位角观测的方位角范围为[–2°, 2°]，处理时等分为两个子孔径，每个子孔径宽度为2°；多方位角观测的方位角范围为[–16°, 16°]，等分为16个子孔径，每个孔径宽度为2°，处理结果如图5(b)所示。可以看出，联合多方位角观测估计高程的RMSE比单方位角观测估计结果小，证明多方位角观测具有更好的抗噪性能；随着信噪比的升高，噪声的影响减弱，联合多方位角数据处理结果与单方位角数据处理结果逐渐逼近，且两者的RMSE不断下降，最终趋近于1 m，该残差与图3的分析一致。当信噪比大于10 dB时，多方位角观测高程估计精度优于2 m。
图 3 不同下视角对应的多普勒调频率误差与高程误差Figure 3. The relationship between Doppler frequency error and height in different nadir angles在不同信杂比仿真实验中，用上述方法仿真的匀质杂波如图6(a)所示。图6(b)给出了杂波像素幅值统计结果和
κ 分布概率密度曲线的对比，在统计时将杂波幅值范围等分成80个区间，对比结果显示仿真的杂波像素幅值服从κ 分布。实验数据后续的处理细节与信噪比仿真实验的数据处理细节一致，不赘述。图7(a)和图7(b)记录了50次单方位角数据处理和多方位角数据联合处理的蒙特卡洛实验结果，可以看出基于多方位角数据高程提取结果的波动范围要小于单方位角数据的高程提取结果的波动范围，即有更稳定的估计结果。图8给出了不同信杂比下50次蒙特卡洛实验的高程估计均方根误差，从图中的曲线可以看出基于多方位角数据联合高程估计结果精度优于单方位角数据高程估计精度，证明了本文所提方法在目标背景中含有纹理特征不明显杂波的条件下依旧有效。
图 7 不同信杂比下的蒙特卡洛高程估计结果记录Figure 7. Monte Carlo height estimation record in various signal clutter ratio仿真2 圆柱点阵仿真 主要仿真参数同表1，仿真的SAR图像信噪比为15 dB，在添加噪声时，参考的信号功率是点阵目标所在像素幅值的均方根值。图9显示了仿真的半径40 m、高20 m圆柱点阵模型，颜色对应高度。图10(a)是参考子孔径成像的幅度图，该图用于提取强散射点位置；图10(b)显示了强点提取结果，由于噪声存在和各点聚焦质量的差异，漏检了部分点目标，并且少量噪点被检测为目标；图10(c)和图10(d)分别是文献[16]方法和本文方法提取的强散射点最终的3维成像结果，两种方法都能在一定程度上还原点阵模型，其中本文所提方法的3维成像结果轮廓更清晰，证明本文方法的高程提取精度优于文献[16]。
表 1 仿真参数Table 1. Simulation parameters参数 数值 轨道高度(km) 514 轨道倾角(°) 97.4 雷达载频(GHz) 9.70 雷达带宽(MHz) 600 雷达波束中心下视角(°) 35 数据方位角跨度(°) [–16, +16] 观测场景纬度(°N) 0 6. 结论
针对星载SAR多方位角观测在高度维采样的稀疏性，无法直接通过3维FFT实现无模糊成像，且目标在不同方位角的投影与高程间的传递相对复杂等问题，本文提出了一种联合多方位角调频率估计的星载 SAR 3维成像方法。该方法首先给出了多普勒调频误差与高程误差进行关联，然后通过MD法估计多普勒调频率，接着通过联合多方位角高程估计值提高高程估计精度，最终根据高程估计结果和参考子孔径SAR图像恢复目标3维信息，实现3维成像。该方法利用了卫星轨道几何特点，建立了多普勒调频率与高程误差的关系，避免了求解目标在不同方位向投影位置的困难。同时，发挥了多方位角数据观测方位角大的优势，提高了高程测量精度，仿真实验验证其高程测量精度可达米级。本文3维成像的对象是强点目标，在实际场景中大多是扩展点目标(面目标)，如何实现对这些目标的3维成像将是下一步工作的重点。
-
图 5 各运动模型在不同运动阶段被选择的概率
Figure 5. Probability of each motion model being selected in different motion stages
图 11 各波形参数选择算法的平均耗时结果
Figure 11. The average time-consuming results of each waveform parameter selection algorithm
表 1 CBO/ERQL算法
Table 1. CBO/ERQL algorithm
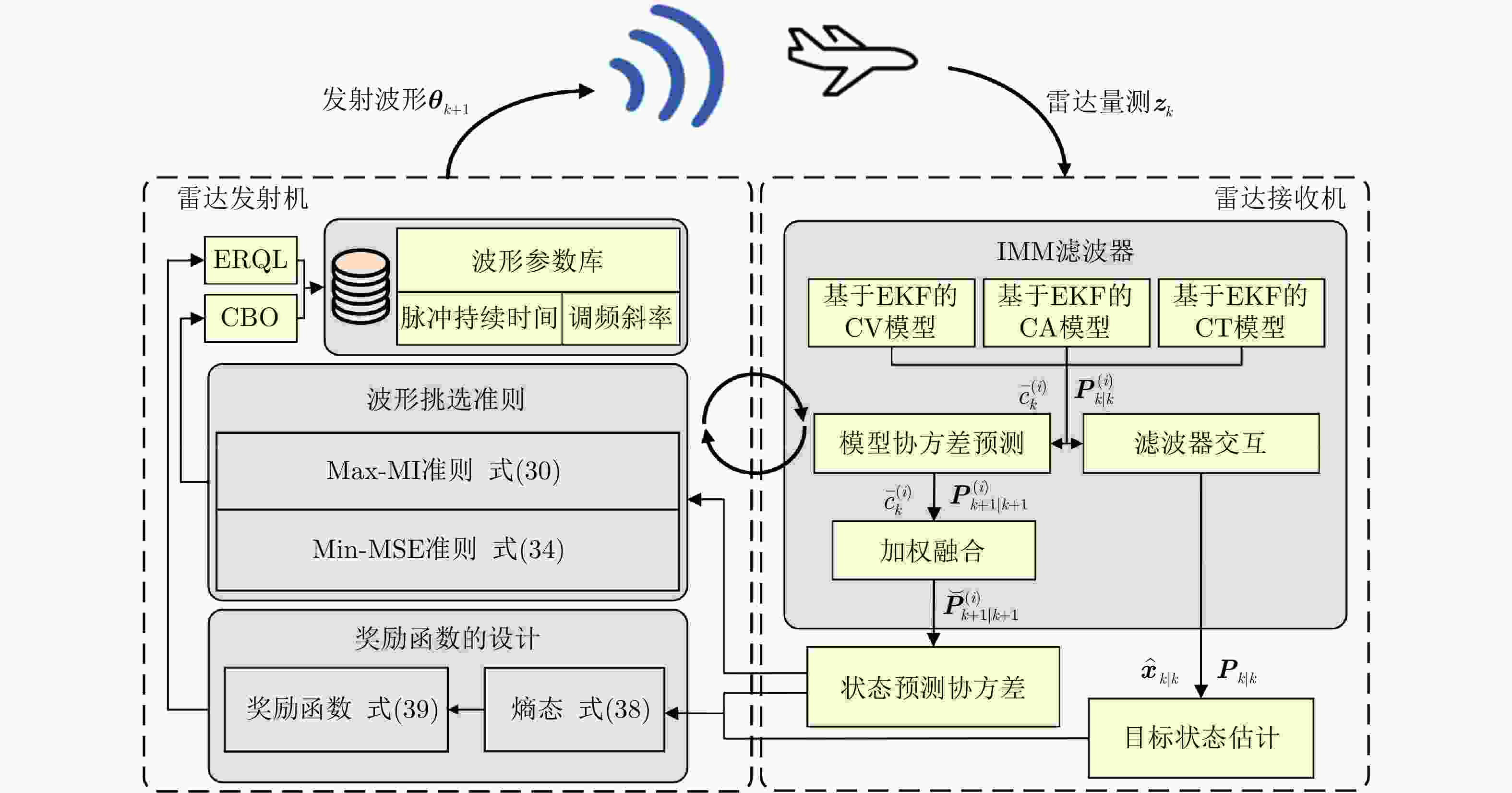
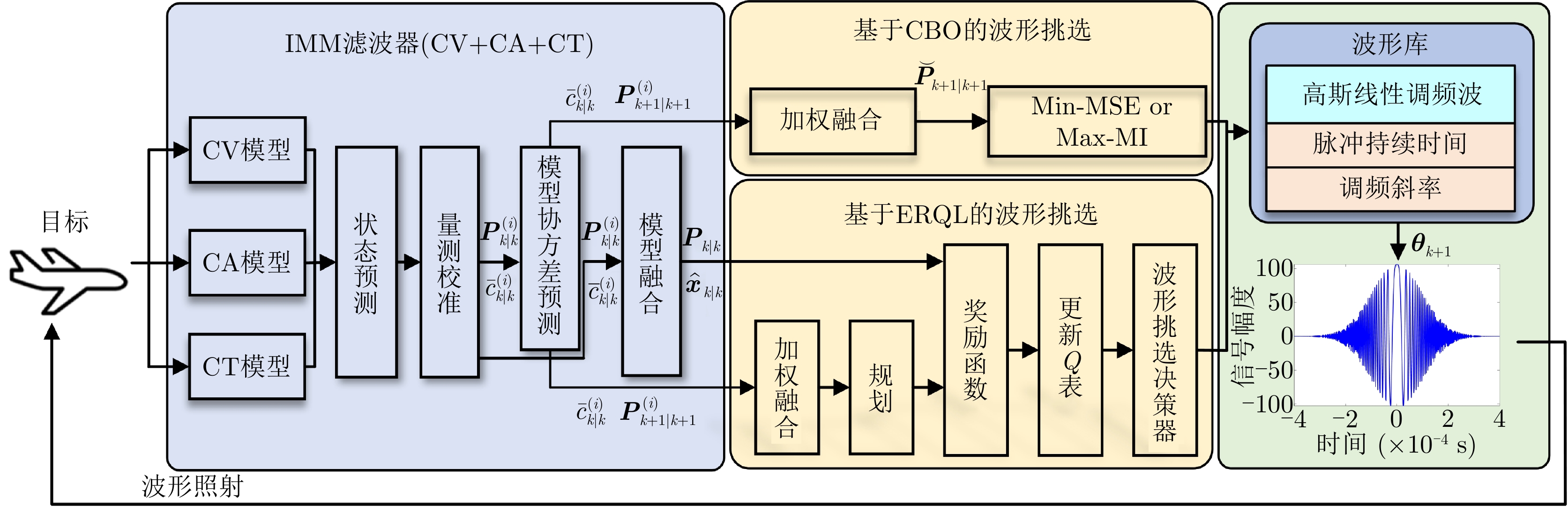
输入：k−1时刻的状态估计{\hat {\boldsymbol{x}}_{k - 1|k - 1} }, {{\boldsymbol{P}}_{k - 1|k - 1} }，k时刻的量
测{{\boldsymbol{z}}_k}。输出：最佳发射波形参数{{\boldsymbol{\theta}} _{k + 1} }。 (1) 通过IMM滤波器中的交互输入和模型滤波过程，计算每个模
型在时间k的估计值\hat {\boldsymbol{x}}_{k|k}^{{\rm{CV}}},{\text{ } }{\boldsymbol{P}}_{k|k}^{{\rm{CV}}}\\hat {\boldsymbol{x} }_{k|k}^{ {\rm{CA} }}, {\boldsymbol{P}}_{k|k}^{{\rm{CA}}}\\hat {\boldsymbol{x}}_{k|k}^{{\rm{CT}}},{\text{ } }{\boldsymbol{P}}_{k|k}^{{\rm{CT}}}。(2) 通过式(8)、式(10)、式(11)、式(13)计算各模型的预测概率
\bar c_k^{(i)}和预测状态估计误差协方差{\boldsymbol{P}}_{k + 1|k + 1}^{(i)}。(3) 通过式(37)的加权融合，得到{\overset{\lower0.5em\hbox{$\smash{\scriptscriptstyle\smile}$} }{{\boldsymbol{P}}} _{k + 1|k + 1} }。 (4) if (CBO) (5) 通过网格搜索找到式(30)或式(34)的最优波形参数{{\boldsymbol{\theta}} _{k + 1} }。 (6) else (ERQL) (7) 根据式(38)和式(39)计算预测奖励{r_{k + 1}}，通过式(35)更新每
个波形的Q表，重复此步骤，直到完成所需的单步预测次数或者
Q表收敛。(8) 选择Q表中最大Q值所对应的策略作为k + 1时刻的波形选择
策略 \pi _{k + 1}^{\text{*}}(s) 。(9) 根据波形选择策略 \pi _{k + 1}^*(s) 选择波形参数{{\boldsymbol{\theta}} _{k + 1} }。 (10) end if (11) 根据波形参数{{\boldsymbol{\theta}} _{k + 1} }，发射最优波形。 
下载: 导出CSV
表 2 不同方法的ARMSE对比结果
Table 2. ARMSE comparison results of different methods
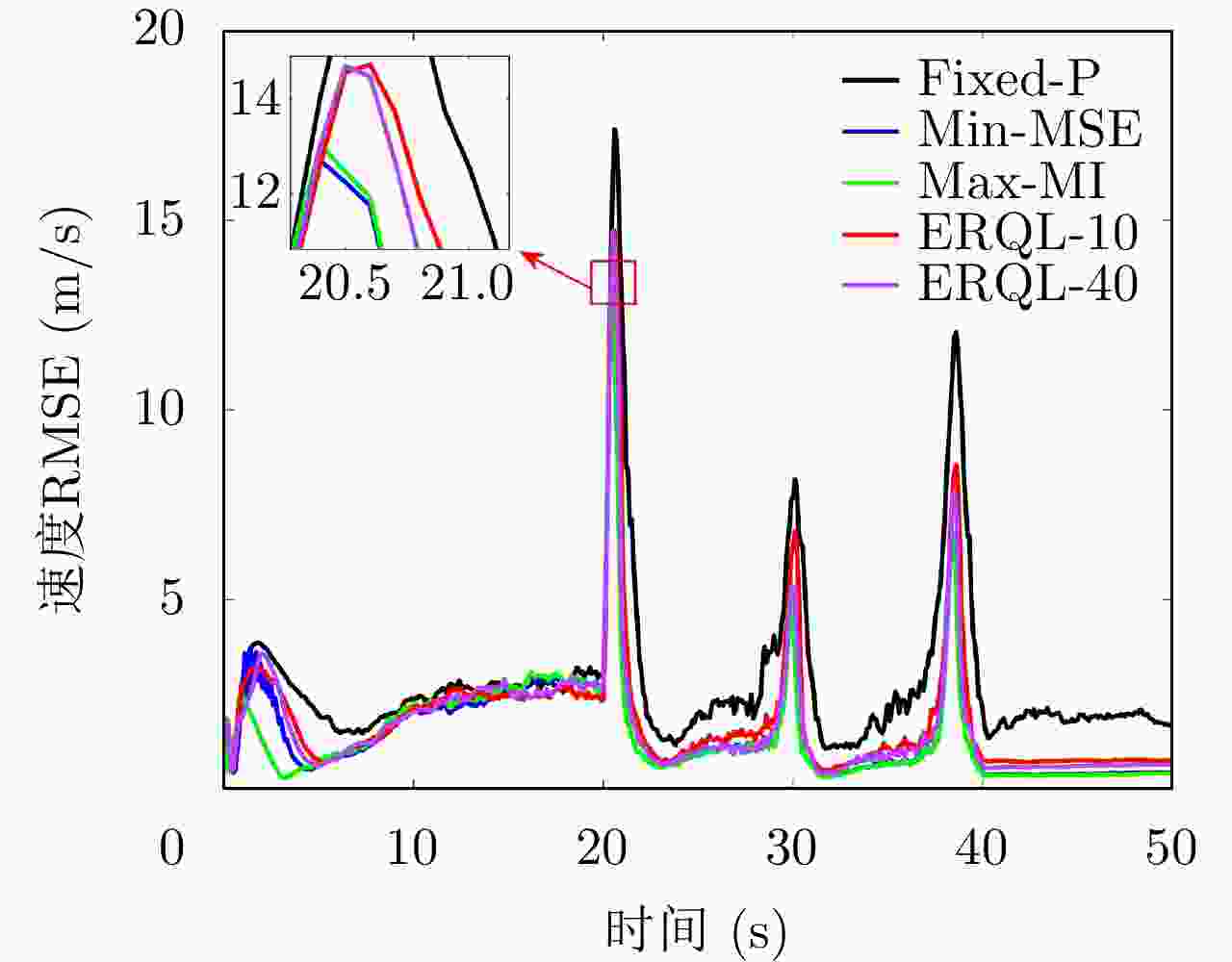
方法 {\bar X_{{\rm{pos}}} } {\bar Y_{{\rm{pos}}} } {\bar X_{{\rm{vel}}} } {\bar Y_{{\rm{vel}}} } Fixed-P 18.05 m 20.47 m 2.88 m/s 4.10 m/s Min-MSE 13.83 m 15.55 m 1.50 m/s 1.93 m/s Max-MI 14.44 m 15.79 m 1.46 m/s 1.92 m/s ERQL-10 15.40 m 17.98 m 1.87 m/s 2.55 m/s ERQL-40 14.25 m 15.95 m 1.71 m/s 2.32 m/s
下载: 导出CSV
表 3 CBO和ERQL方法相比于Fixed-P方法的跟踪性能改善与CPU时间比较(%)
Table 3. CBO and ERQL methods compared with Fixed-P methods for improved tracking performance and CPU time (%)
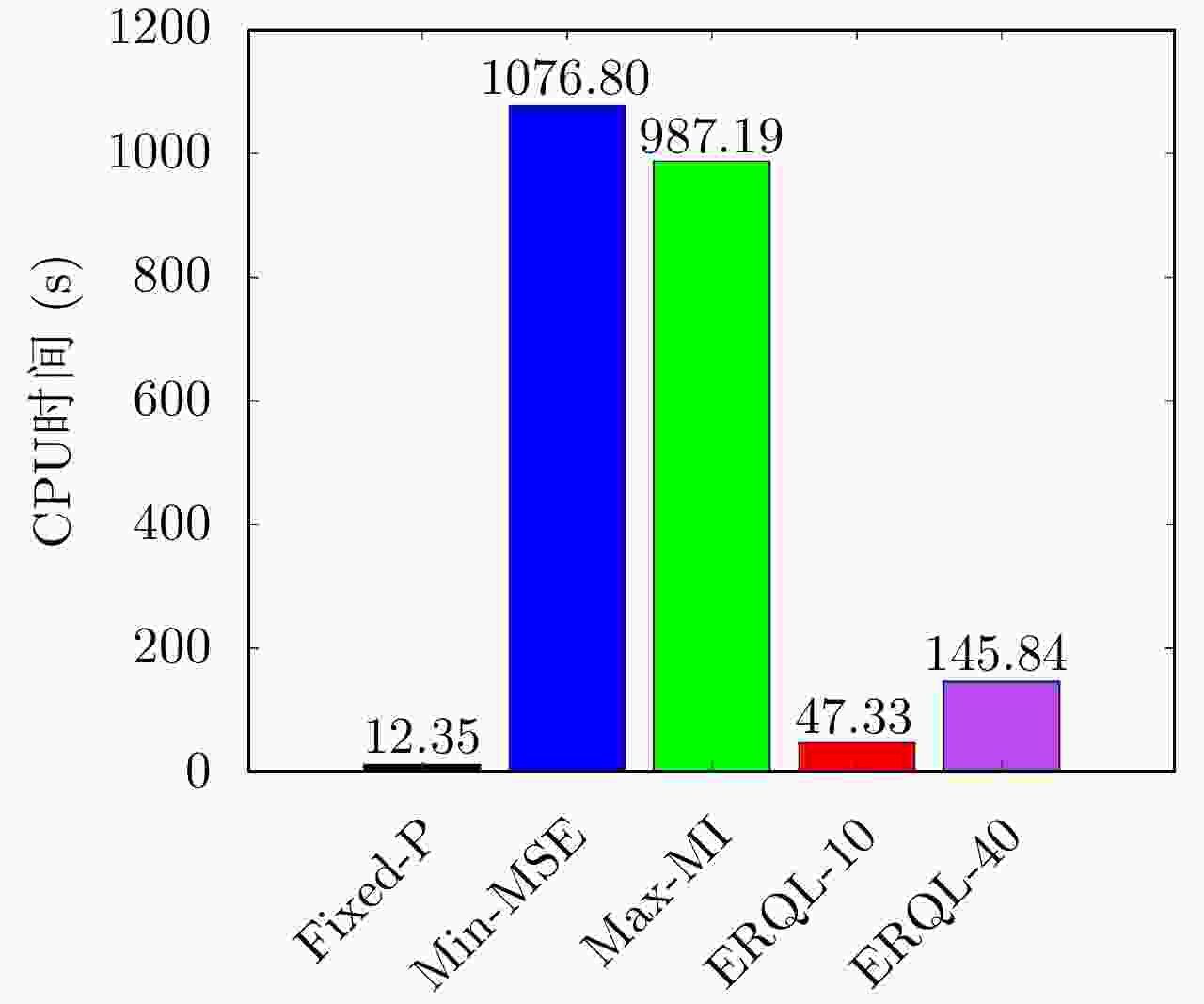
方法 {X_{{\rm{pos}}} } {Y_{{\rm{pos}}} } {X_{{\rm{vel}}} } {Y_{{\rm{vel}}} } CPU time Min-MSE 23.38 24.04 47.92 52.93 8619 Max-MI 20.61 22.86 49.13 53.17 7893 ERQL-10 14.68 12.16 34.84 37.80 283 ERQL-20 16.01 16.76 37.28 40.73 545 ERQL-40 21.05 22.08 40.63 43.41 1081 ERQL-80 15.51 15.68 41.11 47.07 2016
下载: 导出CSV
-
[1] YUAN Ye, YI Wei, HOSEINNEZHAD R, et al. Robust power allocation for resource-aware multi-target tracking with colocated MIMO radars[J]. IEEE Transactions on Signal Processing, 2021, 69: 443–458. doi: 10.1109/TSP.2020.3047519 [2] SUN Zhichao, YEN G G, WU Junjie, et al. Mission planning for energy-efficient passive UAV radar imaging system based on substage division collaborative search[J]. IEEE Transactions on Cybernetics, 2023, 53(1): 275–288. doi: 10.1109/TCYB.2021.3090662 [3] LIANG Jing and LIANG Qilian. Design and analysis of distributed radar sensor networks[J]. IEEE Transactions on Parallel and Distributed Systems, 2011, 22(11): 1926–1933. doi: 10.1109/TPDS.2011.45 [4] HAYKIN S. Cognitive radar: A way of the future[J]. IEEE Signal Processing Magazine, 2006, 23(1): 30–40. doi: 10.1109/MSP.2006.1593335 [5] LUO Zihan, LIANG Jing, and XU Zekai. Intelligent waveform optimization for target tracking in radar sensor networks[C]. 10th International Conference on Communications, Signal Processing, and Systems (CSPS), Changbaishan, China, 2021: 165–172. [6] HAYKIN S. Cognition is the key to the next generation of radar systems[C]. 2009 IEEE 13th Digital Signal Processing Workshop and 5th IEEE Signal Processing Education Workshop, Marco Island, USA, 2009: 463–467. [7] HAYKIN S, ZIA A, ARASARATNAM I, et al. Cognitive tracking radar[C]. 2010 IEEE Radar Conference, Arlington, USA, 2010: 1467–1470. [8] GUERCI J R. Cognitive radar: A knowledge-aided fully adaptive approach[C]. 2010 IEEE Radar Conference, Arlington, USA, 2010: 1365–1370. [9] GUERCI J R, GUERCI R M, RANAGASWAMY M, et al. CoFAR: Cognitive fully adaptive radar[C]. 2014 IEEE Radar Conference, Cincinnati, USA, 2014: 984–989. [10] GUERCI J R. Cognitive Radar: The Knowledge-Aided Fully Adaptive Approach[M]. 2nd ed. Norwood, USA: Artech House, 2020. [11] BELL K L, BAKER C J, SMITH G E, et al. Cognitive radar framework for target detection and tracking[J]. IEEE Journal of Selected Topics in Signal Processing, 2015, 9(8): 1427–1439. doi: 10.1109/JSTSP.2015.2465304 [12] SMITH G E, CAMMENGA Z, MITCHELL A, et al. Experiments with cognitive radar[C]. 2015 IEEE 6th International Workshop on Computational Advances in Multi-Sensor Adaptive Processing (CAMSAP), Cancun, Mexico, 2015: 293–296. [13] ZHANG Lingzhao and JIANG Min. Cognitive radar target tracking algorithm based on waveform selection[C]. 2021 IEEE 5th Advanced Information Technology, Electronic and Automation Control Conference (IAEAC), Chongqing, China, 2021: 1506–1510. [14] HULEIHEL W, TABRIKIAN J, and SHAVIT R. Optimal adaptive waveform design for cognitive MIMO radar[J]. IEEE Transactions on Signal Processing, 2013, 61(20): 5075–5089. doi: 10.1109/TSP.2013.2269045 [15] ALDAYEL O, MONGA V, and RANGASWAMY M. Successive QCQP refinement for MIMO radar waveform design under practical constraints[J]. IEEE Transactions on Signal Processing, 2016, 64(14): 3760–3774. doi: 10.1109/TSP.2016.2552501 [16] FENG Shuo and HAYKIN S. Cognitive risk control for transmit-waveform selection in vehicular radar systems[J]. IEEE Transactions on Vehicular Technology, 2018, 67(10): 9542–9556. doi: 10.1109/TVT.2018.2857718 [17] SAVAGE C O and MORAN B. Waveform selection for maneuvering targets within an IMM framework[J]. IEEE Transactions on Aerospace and Electronic Systems, 2007, 43(3): 1205–1214. doi: 10.1109/TAES.2007.4383612 [18] CLEMENTE C, SHOROKHOV I, PROUDLER I, et al. Radar waveform libraries using fractional Fourier transform[C]. 2014 IEEE Radar Conference, Cincinnati, USA, 2014: 855–858. [19] ZHAO Dehua, WEI Yinsheng, and LIU Yongtan. Real-time waveform adaption in spectral crowed environment using a sub-waveforms-based library[C]. 2016 CIE International Conference on Radar, Guangzhou, China, 2016: 1–5. [20] NGUYEN N H, DOGANCAY K, and DAVIS L M. Adaptive waveform selection for multistatic target tracking[J]. IEEE Transactions on Aerospace and Electronic Systems, 2015, 51(1): 688–701. doi: 10.1109/TAES.2014.130723 [21] ROMAN J. R., GARNHAM J. W. and ANTONIK P., Information Theoretic Criterion for Waveform Selection. Fourth IEEE Workshop on Sensor Array and Multichannel Processing, 2006., Waltham, MA, USA, 2006, 444-448, doi: 10.1109/SAM.2006.1706172. [22] CAO Xin, ZHENG Zhe, and AN Di. Adaptive waveform selection algorithm based on reinforcement learning for cognitive radar[C]. 2019 IEEE 2nd International Conference on Automation, Electronics and Electrical Engineering (AUTEEE), Shenyang, China, 2019: 208–213. [23] HAN Bo, HUANG Hanqiao, LEI Lei, et al. An improved IMM algorithm based on STSRCKF for maneuvering target tracking[J]. IEEE Access, 2019, 7: 57795–57804. doi: 10.1109/ACCESS.2019.2912983 [24] BLACKMAN S S, DEMPSTER R J, BUSCH M T, et al. IMM/MHT solution to radar benchmark tracking problem[J]. IEEE Transactions on Aerospace and Electronic Systems, 1999, 35(2): 730–738. doi: 10.1109/7.766953 [25] KERSHAW D J and EVANS R J. Optimal waveform selection for tracking systems[J]. IEEE Transactions on Information Theory, 1994, 40(5): 1536–1550. doi: 10.1109/18.333866 [26] SIRA S P, PAPANDREOU-SUPPAPPOLA A, and MORRELL D. Advances in Waveform-Agile Sensing for Tracking[M]. Cham: Springer, 2009: 59–60. [27] WILLIAMS J L. Information theoretic sensor management[D]. [Ph. D. dissertation], Massachusetts Institute of Technology, 2007: 41–42. [28] ATHANS M and TSE E. A direct derivation of the optimal linear filter using the maximum principle[J]. IEEE Transactions on Automatic Control, 1967, 12(6): 690–698. doi: 10.1109/TAC.1967.1098732 [29] THORNTON C E, KOZY M A, BUEHRER R M, et al. Deep reinforcement learning control for radar detection and tracking in congested spectral environments[J]. IEEE Transactions on Cognitive Communications and Networking, 2020, 6(4): 1335–1349. doi: 10.1109/TCCN.2020.3019605 [30] WANG Qing, QIAO Yanming, and GAO Lirong. A cognitive radar waveform optimization approach based on deep reinforcement learning[C]. 2019 IEEE International Conference on Signal, Information and Data Processing (ICSIDP), Chongqing, China, 2019: 1–6. 期刊类型引用(0)
其他类型引用(19)
-
下载:
计量
- 文章访问数: 1373
- HTML全文浏览量: 733
- PDF下载量: 363
- 被引次数: 19
