作者中心
专家审稿
责编办公
编辑办公
-
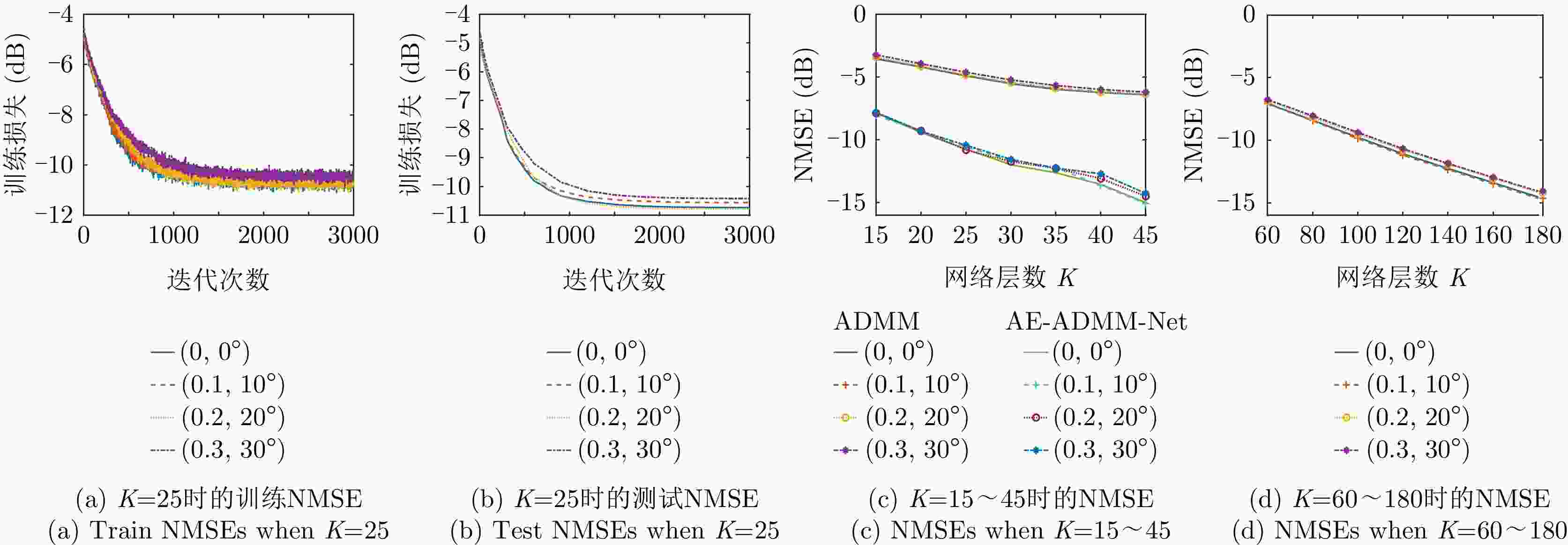
摘要: 稀疏恢复空时自适应处理(SR-STAP)方法能够利用少量训练距离单元实现对机载雷达杂波的有效抑制。然而，现有SR-STAP方法均基于模型驱动实现，存在着参数设置困难、运算复杂度高等问题。针对这些问题，该文将基于模型驱动的SR方法和基于数据驱动的深度学习方法相结合，首次将深度展开(DU)引入到机载雷达杂波抑制和目标检测之中。首先，建立了阵列误差(AE)条件下的杂波空时谱和阵列误差参数联合估计模型，并利用交替方向乘子法(ADMM)进行求解；接着，将ADMM算法展开为深度神经网络AE-ADMM-Net，利用充足完备的数据集对其迭代参数进行优化；最后，利用训练后的AE-ADMM-Net对训练距离单元数据进行处理，快速获得杂波空时谱和阵列误差参数的准确估计。仿真结果表明：与典型SR-STAP方法相比，该文所提出的DU-STAP方法能够在保持较低运算复杂度的同时提高杂波抑制性能。Abstract: The Sparse Recovery Space-Time Adaptive Processing (SR-STAP) method can use a small number of training range cells to effectively suppress the clutter of airborne radar. The SR-STAP approach may successfully eliminate airborne radar clutter using a limited number of training range cells. However, present SR-STAP approaches are all model-driven, limiting their practical applicability due to parameter adjustment difficulties and high computational cost. To address these problems, this study, for the first time, introduces the Deep Unfolding/Unrolling (DU) method to airborne radar clutter reduction and target recognition by merging the model-driven SR method and the data-driven deep learning method. Firstly, a combined estimation model for clutter space-time spectrum and Array Error (AE) parameters is established and solved using the Alternating Direction Method of Multipliers (ADMM) algorithm. Secondly, the ADMM algorithm is unfolded to a deep neural network, named AE-ADMM-Net, to optimize all iteration parameters using a complete training dataset. Finally, the training range cell data is processed by the trained AE-ADMM-Net, jointly estimating the clutter space-time spectrum and the radar AE parameters efficiently and accurately. Simulation results show that the proposed DU-STAP method can achieve higher clutter suppression performance with lower computational cost compared to typical SR-STAP methods.
-
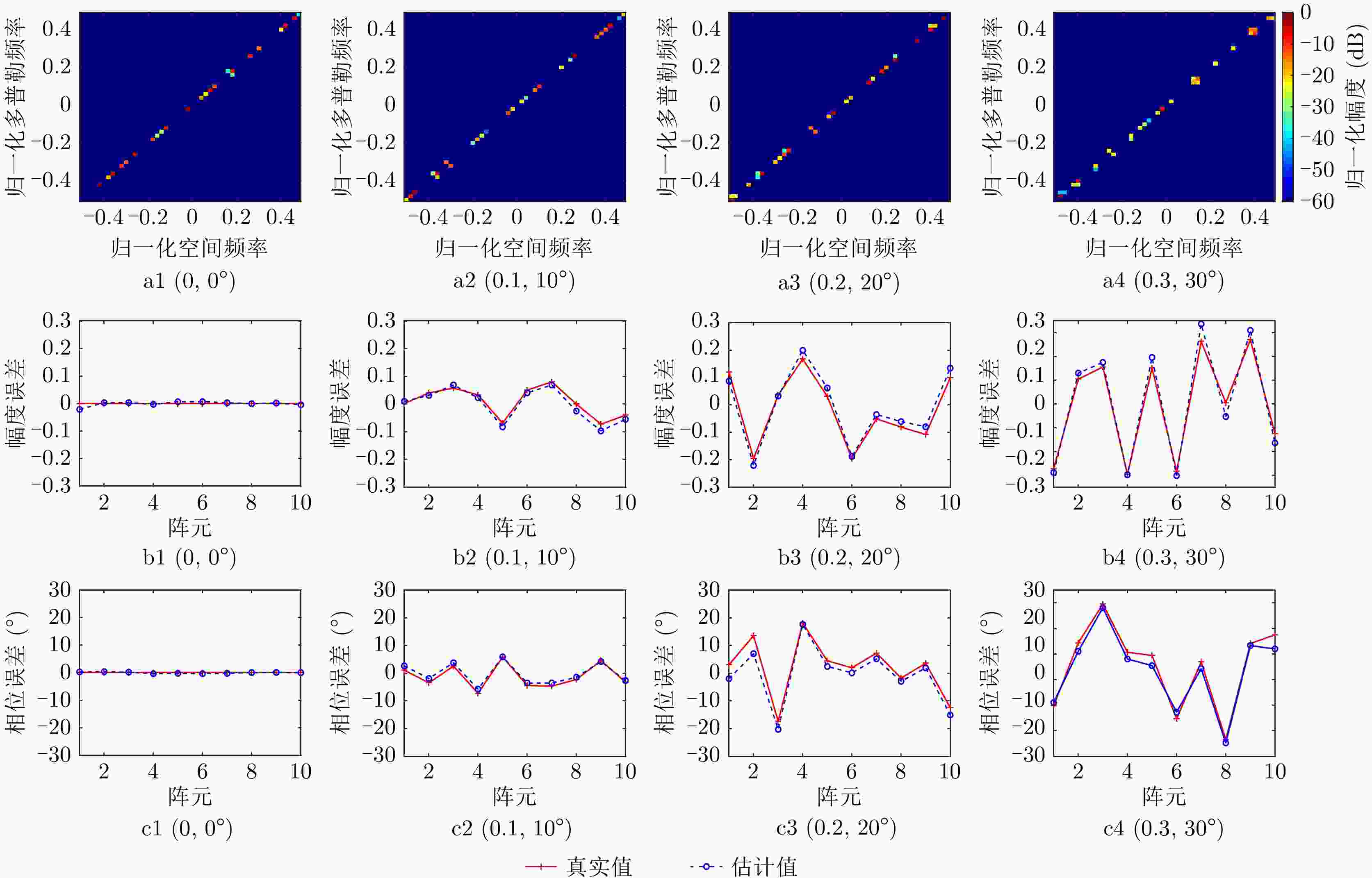
图 5 固定参数ADMM算法杂波空时谱和阵列误差参数估计结果(a1—a4：不同阵列误差参数下的空时谱估计结果，b1—b4：不同阵列误差参数下的幅度误差估计结果，c1—c4：不同阵列误差参数下的相位误差估计结果)
Figure 5. Clutter space-time spectra and array error parameters estimated via ADMM algorithm with fixed parameters (a1—a4: Clutter space-time spectra estimation results in different array error parameters, b1—b4: Amplitude error estimation results in different array error parameters, c1—c4: Phase error estimation results in different array error parameters)
图 6 AE-ADMM-Net的收敛性及其与ADMM算法的对比
Figure 6. Convergence performance of AE-ADMM-Net and its comparison with ADMM algorithm
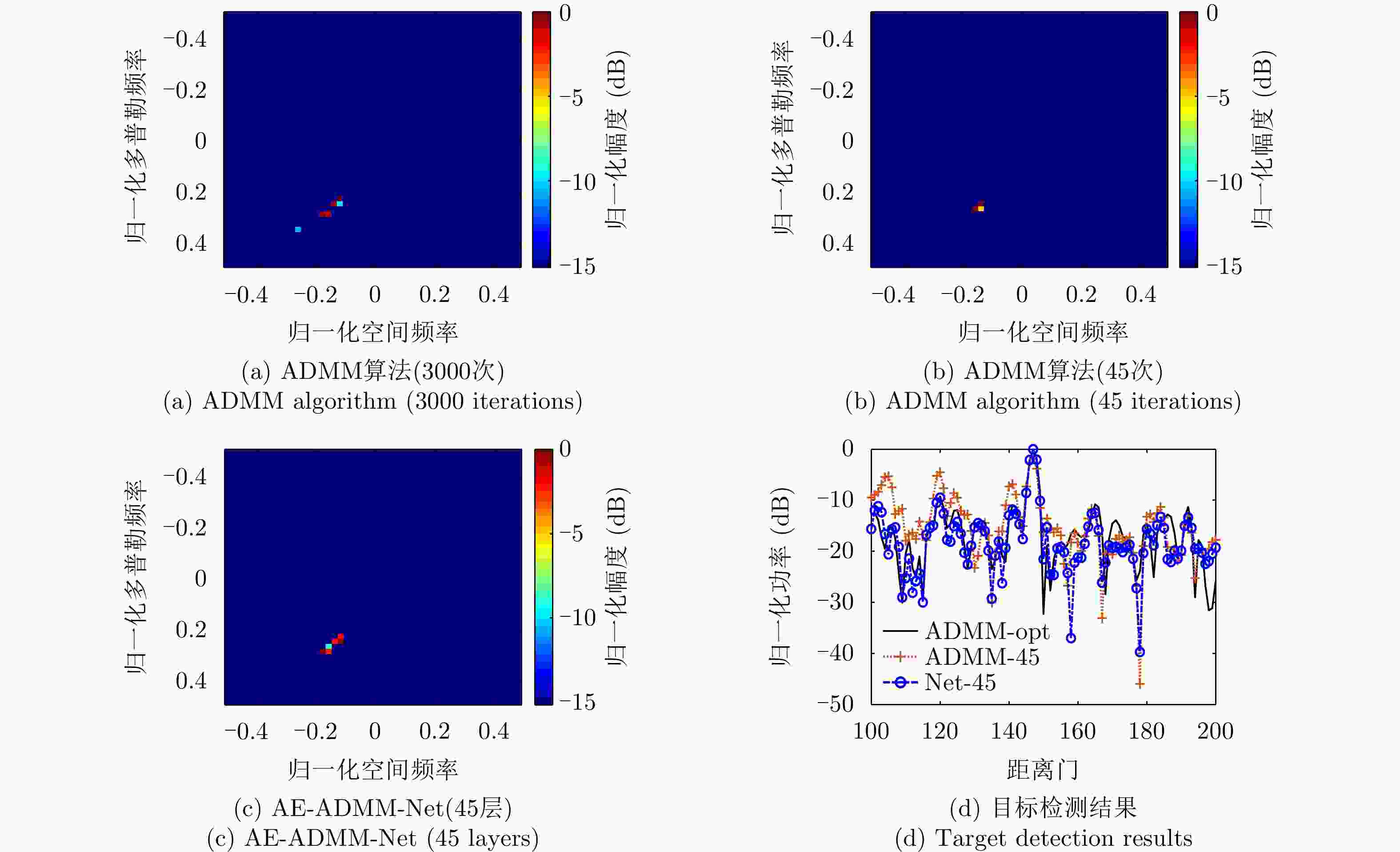
图 7 不同条件下不同算法的杂波空时谱估计结果(a1—a4：ADMM算法在不同阵列误差参数下的迭代25次的估计结果，b1—b4:ADMM算法在不同阵列误差参数下的迭代45次的估计结果，c1—c4：FOCUSS算法在不同阵列误差参数下的迭代200次的估计结果，d1—d4：SBL算法在不同阵列误差参数下的迭代400次的估计结果，e1—e4：25层的AE-ADMM-Net 在不同阵列误差参数下的的估计结果，f1—f4：45层的AE-ADMM-Net 在不同阵列误差参数下的估计结果)
Figure 7. Clutter space-time spectra estimated via different algorithms under different conditions (a1—a4: estimation results of ADMM algorithm with 25 iterations in different array error parameters, b1—b4: estimation results of ADMM algorithm with 45 iterations in different array error parameters, c1—c4: estimation results of FOCUSS algorithm with 200 iterations in different array error parameters, d1—d4: estimation results of SBL algorithm with 400 iterations in different array error parameters, e1—e4: estimation results of AE-ADMM-Net with 25 layers in different array error parameters, f1—f4: estimation results of AE-ADMM-Net with 45 layers in different array error parameters)
图 8 不同条件下AE-ADMM-Net的阵列误差参数估计结果(a1—a4：不同阵列误差参数下的幅度误差估计结果，b1—b4：不同阵列误差参数下的相位误差估计结果)
Figure 8. Array error parameters estimated by AE-ADMM-Net under different conditions (a1—a4: Amplitude error estimation results in different array error parameters, b1—b4: Phase error estimation results in different array error parameters)
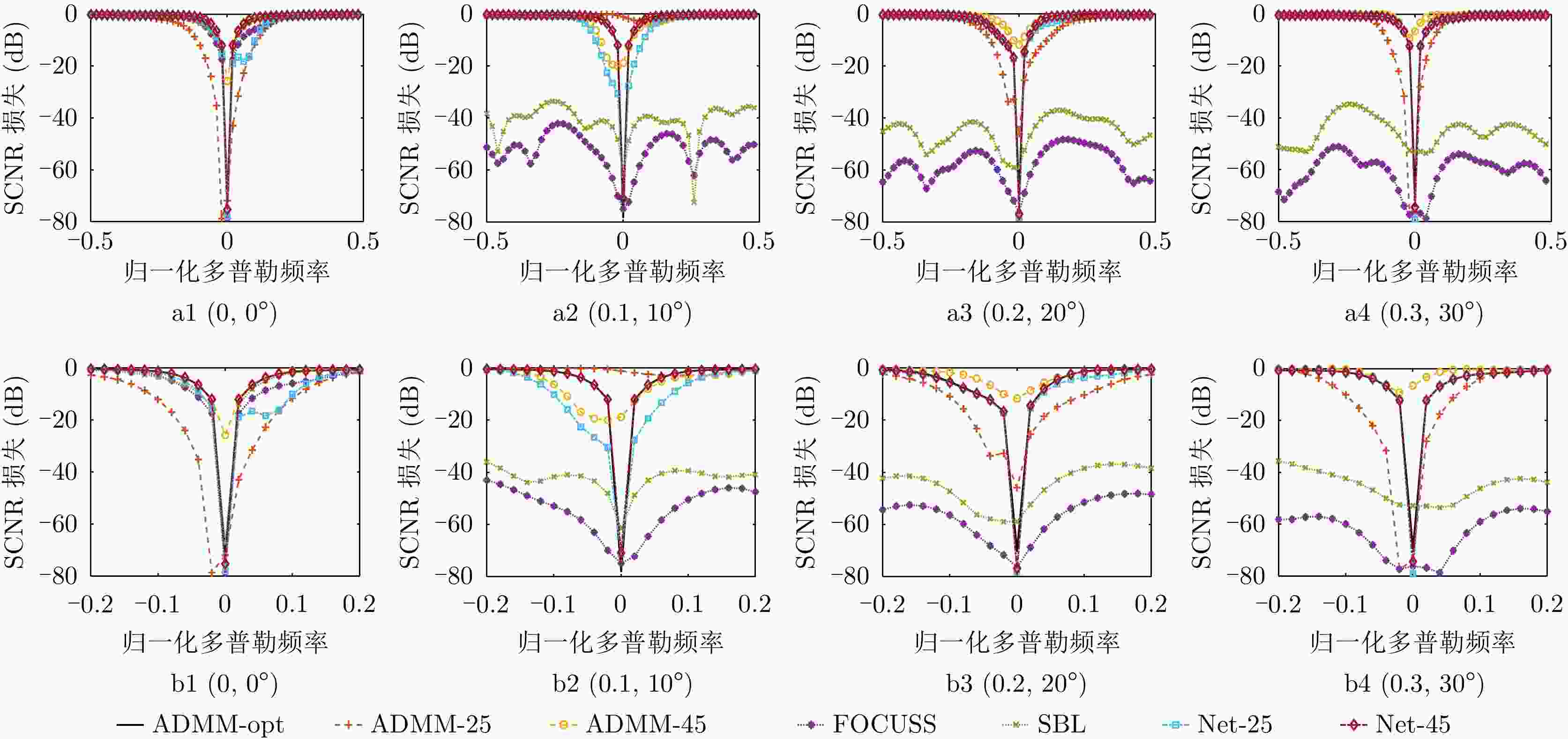
图 9 不同条件下不同方法对应的SCNR损失曲线(a1—a4：不同阵列误差参数下的SCNR曲线结果，b1—b4：不同阵列误差参数下的SCNR曲线局部放大结果)
Figure 9. SCNR loss curves corresponding to different methods under different conditions (a1—a4: SCNR loss curves results in different array error parameters, b1—b4: SCNR loss curves results with enlarged scale in different array error parameters)
图 10 不同条件下不同算法的运行时间
Figure 10. Running time of different algorithms under different conditions
图 11 Mountain Top实测数据处理结果
Figure 11. Processing results of Mountain Top actual measured data
表 1 ADMM算法
Table 1. ADMM algorithm
输入：A, y，迭代次数K，正则化因子$ \rho $，二次惩罚因子$ \gamma $，迭代步长$ \tau $，比例因子$ \delta $和w。 步骤1 初始化：${ {\boldsymbol{\alpha} } ^{(0)} } = { {\bf{0} }_{ {N_{{\rm{d}}} }{N_{{\rm{s}}} } } }$(${N_{{\rm{d}}} }{N_{{\rm{s}}} } \times 1$的全0列向量)，${{\boldsymbol{\lambda}} ^{(0)} } = {{\bf{0}}_{NM} }$($NM \times 1$的全0列向量)，${{\boldsymbol{t}}^{(0)} } = {{\bf{1}}_M}$($M \times 1$的全1列向量)，
${{\boldsymbol{T}}^{(0)} } = {{\boldsymbol{I}}_N} \otimes {\rm{diag}}({{\boldsymbol{t}}^{(0)} })$，$k = 0$；步骤2 ${ {\boldsymbol{\eta} } ^{(k + 1)} } = \rho \gamma /(1 + \rho \gamma )({ {\boldsymbol{\lambda} } ^{(k)} }/\gamma - {\boldsymbol{A} }{ {\boldsymbol{\alpha} } ^{(k)} } + { {\boldsymbol T}^{(k)} }{\boldsymbol{y} })$； 步骤3 ${{\boldsymbol{\alpha}} ^{(k + 1)} } = {\text{soft} }({{\boldsymbol{\alpha}} ^{(k)} } + \tau {{\boldsymbol{A}}^{{\rm{H}}} }{{\boldsymbol{\eta}} ^{(k + 1)} }/(\rho \gamma ),\tau /\gamma )$； 步骤4-1
${ {\boldsymbol{z} }^{(k)} } = {\boldsymbol{A} }{ {\boldsymbol{\alpha} } ^{(k + 1)} } + { {\boldsymbol{\eta} } ^{(k + 1)} } - {{\boldsymbol{\lambda}} ^{(k)} }/\gamma$, ${b_m} = \displaystyle\sum\nolimits_{n = 1}^N {y_{(n - 1)M + m}^ * z_{(n - 1)M + m}^{(k)} }$, ${a_m} = \displaystyle\sum\nolimits_{n = 1}^N {|{y_{(n - 1)M + m} }{|^2} }$,
$\beta = \left[\delta + {\rm{j}}w - \sum\nolimits_{m = 1}^M {({b_m}/{a_m}} )\right]/\sum\nolimits_{m = 1}^M {(1/{a_m})}$。步骤4-2 ${ {\boldsymbol{t} }^{(k + 1)} } = {\left[ {({b_1} + \beta )/{a_1},({b_2} + \beta )/{a_2}, \cdots ,({b_M} + \beta )/{a_M} } \right]^{\rm{T}}}$； 步骤5 ${ {\boldsymbol{\lambda} } ^{(k + 1)} } = { {\boldsymbol{\lambda} } ^{(k)} } - \gamma ({\boldsymbol{A} }{ {\boldsymbol{\alpha} } ^{(k + 1)} } + {{\boldsymbol{\eta}} ^{(k + 1)} } - { {\boldsymbol T}^{(k + 1)} }{\boldsymbol{y} })$； 步骤6 令$ k \leftarrow k + 1 $，若$k \le K - 1$，则返回步骤2，否则结束。 输出: ${\boldsymbol{\alpha}} = {{\boldsymbol{\alpha}} ^K}$, $ {e_m} = 1/t_m^K $, ${\boldsymbol{e} } = {[{e_1},{e_2}, \cdots ,{e_M}]^{\rm{T} } }$。 
下载: 导出CSV
表 2 仿真参数
Table 2. Simulation parameters
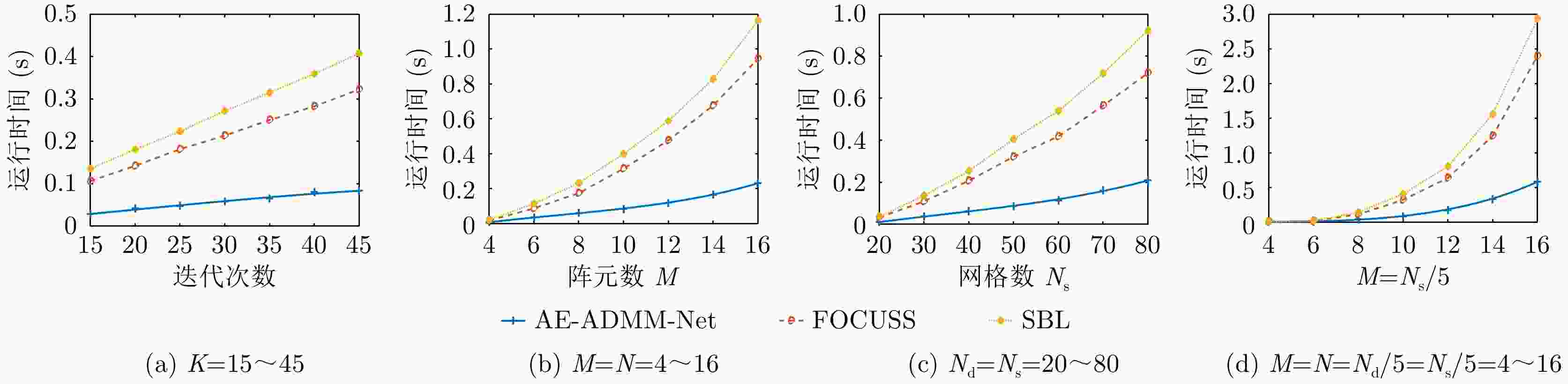
参数 数值 参数 数值 载机高度H 3000 m 载机速度v 100 ms–1 阵元数M 10 个 脉冲数N 10 个 阵元间距d 0.1 m 工作波长λ 0.2 m 脉冲重复频率fr 2000 Hz 距离范围[Rmin, Rmax] [21,31] km 距离单元数L 100 个 杂波块数Nc 361 个 阵元误差数P 100 个 杂噪比CNR 60 dB 训练数据集大小O 7500 测试数据集大小S 2500 频率范围f s和f d [–0.5,0.5] 网格数Ns和Nd 50 个
下载: 导出CSV
表 3 不同算法的运算复杂度
Table 3. Computational complexities of different algorithms
算法 运算复杂度 FOCUSS $O\left( {3NM{N_{{\rm{s}}} }{N_{{\rm{d}}} } + { {(NM)}^3} + 2{ {(NM)}^2}{N_{{\rm{s}}} }{N_{{\rm{d}}} } } \right)$ SBL $O\left( {5NM{N_{{\rm{s}}} }{N_{{\rm{d}}} } + { {(NM)}^3} + 2{ {(NM)}^2}{N_{{\rm{s}}} }{N_{{\rm{d}}} } + NM + {N_{{\rm{s}}} }{N_{{\rm{d}}} } } \right)$ AE-ADMM-Net $O\left( {2NM{N_{{\rm{s}}} }{N_{{\rm{d}}} } + { {(NM)}^2} + 2NM + {N_{{\rm{s}}} }{N_{{\rm{d}}} } } \right)$
下载: 导出CSV
-
[1] 谢文冲, 段克清, 王永良. 机载雷达空时自适应处理技术研究综述[J]. 雷达学报, 2017, 6(6): 575–586. doi: 10.12000/JR17073XIE Wenchong, DUAN Keqing, and WANG Yongliang. Space time adaptive processing technique for airborne radar: An overview of its development and prospects[J]. Journal of Radars, 2017, 6(6): 575–586. doi: 10.12000/JR17073 [2] BRENNAN L E and REED L S. Theory of adaptive radar[J]. IEEE Transactions on Aerospace and Electronic Systems, 1973, AES-9(2): 237–252. doi: 10.1109/TAES.1973.309792 [3] YANG Zhaocheng, WANG Zetao, LIU Weijian, et al. Reduced-dimension space-time adaptive processing with sparse constraints on beam-Doppler selection[J]. Signal Processing, 2019, 157: 78–87. doi: 10.1016/j.sigpro.2018.11.013 [4] PECKHAM C D, HAIMOVICH A M, AYOUB T F, et al. Reduced-rank STAP performance analysis[J]. IEEE Transactions on Aerospace and Electronic Systems, 2000, 36(2): 664–676. doi: 10.1109/7.845257 [5] SARKAR T K, WANG Hong, PARK S, et al. A deterministic least-squares approach to space-time adaptive processing (STAP)[J]. IEEE Transactions on Antennas and Propagation, 2001, 49(1): 91–103. doi: 10.1109/8.910535 [6] WU Yong, TANG Jun, and PENG Yingning. On the essence of knowledge-aided clutter covariance estimate and its convergence[J]. IEEE Transactions on Aerospace and Electronic Systems, 2011, 47(1): 569–585. doi: 10.1109/TAES.2011.5705692 [7] 段克清, 袁华东, 许红, 等. 稀疏恢复空时自适应处理技术研究综述[J]. 电子学报, 2019, 47(3): 748–756. doi: 10.3969/j.issn.0372-2112.2019.03.033DUAN Keqing, YUAN Huadong, XU Hong, et al. An overview on sparse recovery space-time adaptive processing technique[J]. Acta Electronica Sinica, 2019, 47(3): 748–756. doi: 10.3969/j.issn.0372-2112.2019.03.033 [8] JIANG Zhizhuo, WANG Xueqian, LI Gang, et al. Space-time adaptive processing by employing structure-aware two-level block sparsity[J]. IEEE Journal of Selected Topics in Applied Earth Observations and Remote Sensing, 2021, 14: 6386–6397. doi: 10.1109/JSTARS.2021.3090069 [9] 孙珂, 张颢, 李刚, 等. 基于杂波谱稀疏恢复的空时自适应处理[J]. 电子学报, 2011, 39(6): 1389–1393.SUN Ke, ZHANG Hao, LI Gang, et al. STAP via sparse recovery of clutter spectrum[J]. Acta Electronica Sinica, 2011, 39(6): 1389–1393. [10] SUN Ke, MENG Huadong, WANG Yongliang, et al. Direct data domain STAP using sparse representation of clutter spectrum[J]. Signal Processing, 2011, 91(9): 2222–2236. doi: 10.1016/j.sigpro.2011.04.006 [11] YANG Zhaocheng, LI Xiang, WANG Hongqiang, et al. On clutter sparsity analysis in space-time adaptive processing airborne radar[J]. IEEE Geoscience and Remote Sensing Letters, 2013, 10(5): 1214–1218. doi: 10.1109/LGRS.2012.2236639 [12] YANG Zhaocheng, LI Xiang, WANG Hongqiang, et al. Adaptive clutter suppression based on iterative adaptive approach for airborne radar[J]. Signal Processing, 2013, 93(12): 3567–3577. doi: 10.1016/j.sigpro.2013.03.033 [13] DUAN Keqing, WANG Zetao, XIE Wenchong, et al. Sparsity-based STAP algorithm with multiple measurement vectors via sparse Bayesian learning strategy for airborne radar[J]. IET Signal Processing, 2017, 11(5): 544–553. doi: 10.1049/iet-spr.2016.0183 [14] WANG Zetao, WANG Yongliang, DUAN Keqing, et al. Subspace-augmented clutter suppression technique for STAP radar[J]. IEEE Geoscience and Remote Sensing Letters, 2016, 13(3): 462–466. doi: 10.1109/LGRS.2016.2519765 [15] FENG Weike, GUO Yiduo, ZHANG Yongshun, et al. Airborne radar space time adaptive processing based on atomic norm minimization[J]. Signal Processing, 2018, 148: 31–40. doi: 10.1016/j.sigpro.2018.02.008 [16] GUO Yiduo, LIAO Guisheng, and FENG Weike. Sparse representation based algorithm for airborne radar in beam-space post-Doppler reduced-dimension space-time adaptive processing[J]. IEEE Access, 2017, 5: 5896–5903. doi: 10.1109/ACCESS.2017.2689325 [17] MA Zeqiang, LIU Yimin, MENG Huadong, et al. Sparse recovery-based space-time adaptive processing with array error self-calibration[J]. Electronics Letters, 2014, 50(13): 952–954. doi: 10.1049/el.2014.0315 [18] YANG Zhaocheng, DE LAMARE R C, and LIU Weijian. Sparsity-based STAP using alternating direction method with gain/phase errors[J]. IEEE Transactions on Aerospace and Electronic Systems, 2017, 53(6): 2756–2768. doi: 10.1109/TAES.2017.2714938 [19] GREGOR K and LECUN Y. Learning fast approximations of sparse coding[C]. The 27th International Conference on International Conference on Machine Learning, Haifa, Israel, 2010: 399–406. [20] LIU Jialin, CHEN Xiaohan, WANG Zhangyang, et al. ALISTA: Analytic weights are as good as learned weights in LISTA[C]. 7th International Conference on Learning Representations (ICLR), New Orleans, USA, 2019. [21] BORGERDING M, SCHNITER P, and RANGAN S. AMP-inspired deep networks for sparse linear inverse problems[J]. IEEE Transactions on Signal Processing, 2017, 65(16): 4293–4308. doi: 10.1109/TSP.2017.2708040 [22] YANG Chengzhu, GU Yuantao, CHEN Badong, et al. Learning proximal operator methods for nonconvex sparse recovery with theoretical guarantee[J]. IEEE Transactions on Signal Processing, 2020, 68: 5244–5259. doi: 10.1109/TSP.2020.2978615 [23] 朱晗归, 冯存前, 冯为可, 等. 一种深度学习稀疏单快拍DOA估计方法[J/OL]. 信号处理. https://kns.cnki.net/KCMS/detail/11.2406.TN.20220130.1421.006.ktml, 2022.ZHU Hangui, FENG Cunqian, FENG Weike, et al. A deep learning approach for sparse single snapshot DOA estimation[J/OL]. Journal of Signal Processing. https://kns.cnki.net/KCMS/detail/11.2406.TN.20220130.1421.006.ktml, 2022. [24] GUO Yiduo, LIAO Guisheng, GONG Jian, et al. Sparse recovery-based STAP method using prior information of azimuth-elevation[J]. Journal of Applied Remote Sensing, 2017, 11(3): 035004. doi: 10.1117/1.JRS.11.035004 [25] 段克清, 李想, 行坤, 等. 基于卷积神经网络的天基预警雷达杂波抑制方法[J]. 雷达学报, 2022, 11(3): 386–398. doi: 10.12000/JR21161DUAN Keqing, LI Xiang, XING Kun, et al. Clutter mitigation in space-based early warning radar using a convolutional neural network[J]. Journal of Radars, 2022, 11(3): 386–398. doi: 10.12000/JR21161 [26] Boyd S, Parikh N, Chu E, et al. Distributed optimization and statistical learning via the alternating direction method of multipliers[J]. Foundations and Trends in Machine learning, 2011, 3(1): 1–122. [27] YANG Junpeng and ZHANG Yin. Alternating direction algorithms for l1-problems in compressive sensing[J]. SIAM Journal on Scientific Computing, 2011, 33(1): 250–278. doi: 10.1137/090777761 [28] RUMELHART D E, HINTON G E, and WILLIAMS R J. Learning representations by back-propagating errors[J]. Nature, 1986, 323(6088): 533–536. doi: 10.1038/323533a0 [29] HU Xiaowei, XU Feng, GUO Yiduo, et al. MDLI-Net: Model-driven learning imaging network for high-resolution microwave imaging with large rotating angle and sparse sampling[J]. IEEE Transactions on Geoscience and Remote Sensing, 2022, 60: 5212617. doi: 10.1109/TGRS.2021.3110579 -
计量
- 文章访问数: 2205
- HTML全文浏览量: 1113
- PDF下载量: 281
- 被引次数: 0
