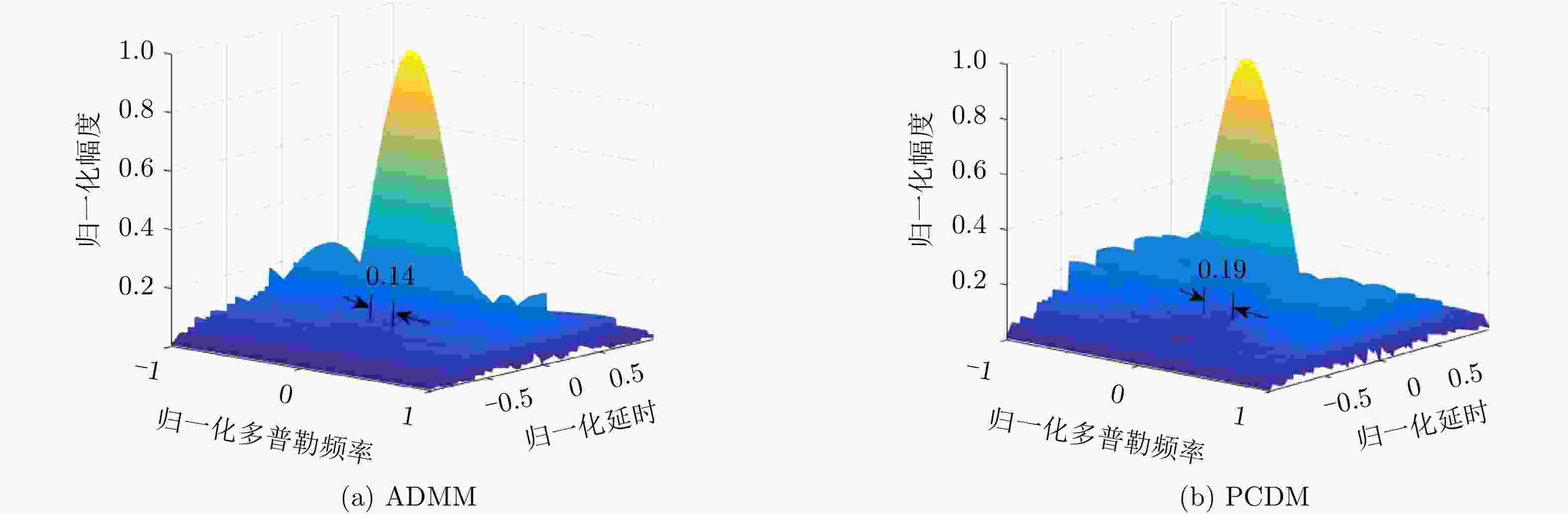
-
摘要: 雷达波形优化作为雷达领域中最重要的课题之一,受到广泛关注。雷达探测波形不仅要有恒定的幅度,还要有低的自相关副瓣。由于恒模约束是非凸的,所以针对低自相关旁瓣恒模波形优化问题复杂度很高。已有算法通常将包含波形幅度和相位信息的多维向量空间作为优化问题的可行解集合,计算过程需要恒模约束条件参与,导致寻优难度和计算量较大。该文提出了一种相位域低积分旁瓣恒模雷达波形优化方法,将对恒模波形寻优的可行解空间压缩至波形相位域的向量集合,对恒模波形向量中各元素相位与其他元素之间的关系进行深入分析并进行解析表示,进而基于坐标下降法的迭代优化思想对波形向量各元素依次更新。通过压缩可行集规模和采用闭式解更新变量的方法,获得了自相关积分旁瓣性能更优的波形序列,并有效降低了计算复杂度,提升了优化效率。最后该文通过数值仿真的方法验证所提方法的有效性。Abstract: Radar waveform optimization has recently drawn much attention. The radar waveform possesses not only constant amplitude but also a low autocorrelation sidelobe level. However, because of the presence of the constant modular constraint, the problem of optimizing the waveform is non-convex, which is difficult to address. The feasible domain used by the current methods usually contains the vector space with two dimensions: amplitude and phase. The optimization procedures accompanied by the constant constraint enlarge the difficulty and amount of calculation. Herein, the problem of designing unimodular sequences with low autocorrelation sidelobes is addressed, and a novel approach based on phase optimization is presented. The feasible domain is compressed into the vector space with only the phase dimension. The proposed method conducts a deep analysis of the relationship between the phases of the elements in the unimodular sequence and successively updates the vector with a closed-form solution in an element-by-element manner at each iteration using the coordinate descent method, which comprises low computational complexity. By compressing the feasible domain and updating the vector variable using the closed solution, the integrated sidelobe level and computation efficiency are improved. Representative numerical simulations are provided to verify the effectiveness of the proposed method.
-
表 1 PCDM算法
Table 1. PCDM algorithm
算法1:PCDM优化最优波形s 输入:$ {\boldsymbol{\varXi }} $, $ {{\boldsymbol{\kappa }}_0} $和$\varepsilon $,其中${\boldsymbol{\varXi } } = { {\boldsymbol{P} }^{\rm{H}}}{\boldsymbol{P} }$, $ {{\boldsymbol{\kappa }}_0} $为优化变量初始值,
$\varepsilon $为收敛常数;输出:优化问题(17)的最优波形序列${{\boldsymbol{s}}^\dagger }$; 步骤1:迭代计数变量t=0时,$ {\boldsymbol{\kappa }} = {{\boldsymbol{\kappa }}_0} $,${f_0} = {\boldsymbol{\kappa } }_0^{\rm{H}}{\boldsymbol{\varXi } }{ {\boldsymbol{\kappa } }_0}$; 步骤2:以${{\boldsymbol{\kappa }}_t}$为$ {\boldsymbol{\kappa }} $初始值,计算$ {\mu _i} $(i=0,1,···, 2N–1),循环更新
${{\boldsymbol{\kappa }}_t}$各维度分量;步骤3:${f_t} = {\boldsymbol{\kappa } }_t^{\rm{H}}{\boldsymbol{\varXi } }{ {\boldsymbol{\kappa } }_t}$。 步骤4:波形序列${{\boldsymbol{s}}_t} = {{\boldsymbol{\kappa }}_t}(0:N - 1)$; 步骤5:如果$\left| {{f_t} - {f_{t - 1}}} \right| \le \varepsilon $, ${f_{t - 1}}$为前一次迭代的目标函数
值,$ {{\boldsymbol{\kappa }}^\dagger } = {{\boldsymbol{\kappa }}_t} $,最优波形${{\boldsymbol{s}}^\dagger } = {{\boldsymbol{s}}_t}$,结束;
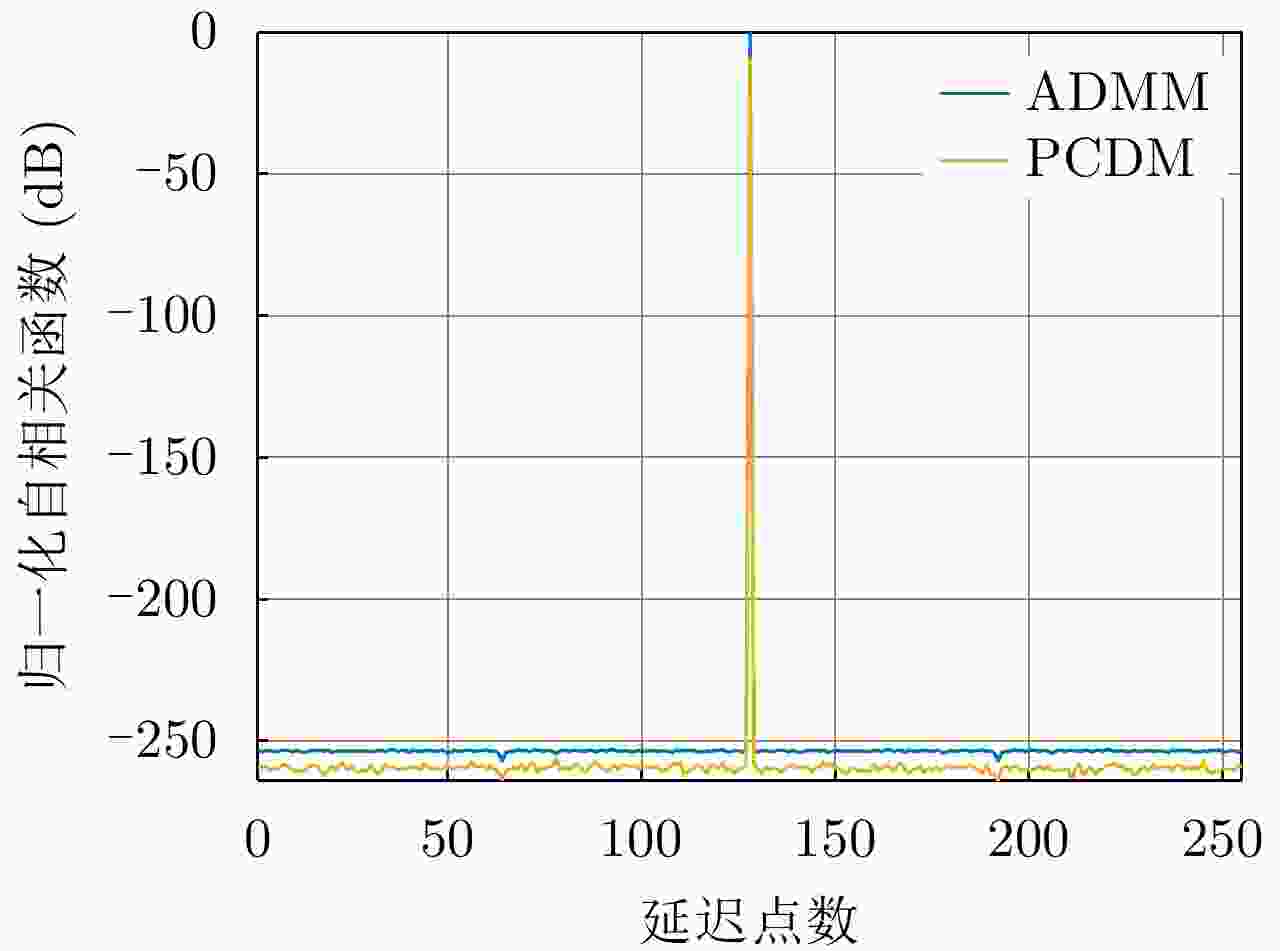
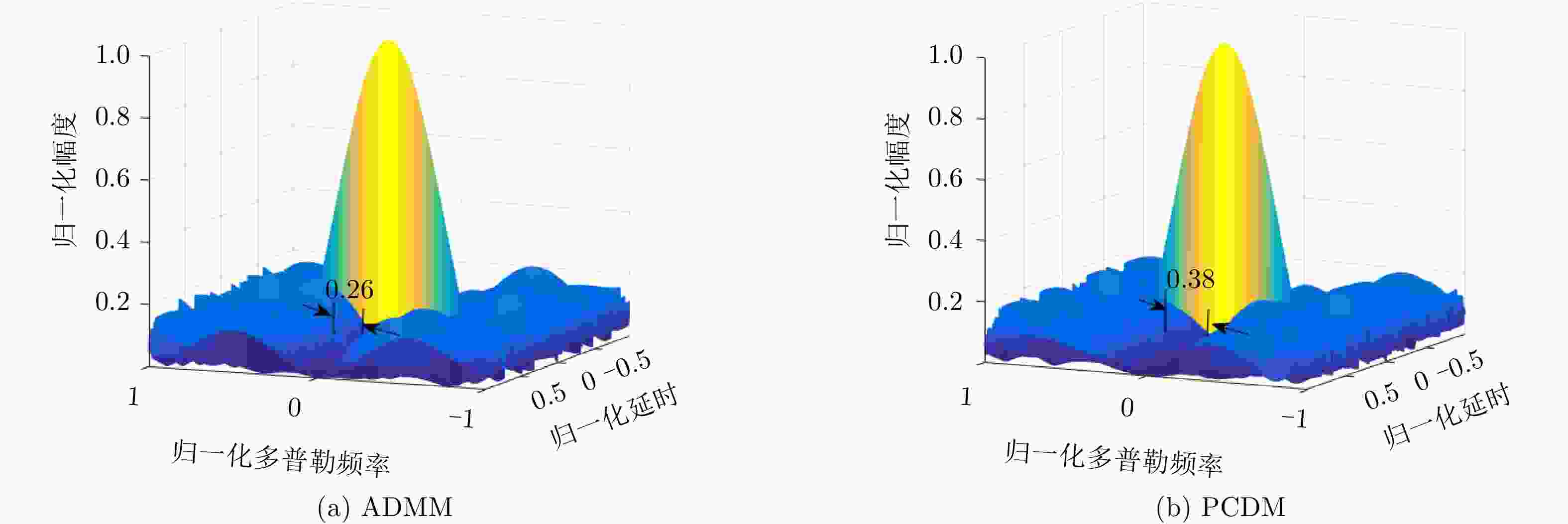
否则,${{\boldsymbol{\kappa }}_{t + 1}} = {{\boldsymbol{\kappa }}_t}$, $t = t + 1$,重复步骤2。表 2 周期波形优化两种算法所用参数
Table 2. Parameters used in two algorithms in periodic waveform optimization
参数名称 数值 序列长度 128 最大迭代次数 20000 收敛常数$\varepsilon $ 0.1 试验次数 600 表 3 对于周期波形优化ADMM算法与PCDM算法运算耗时比较
Table 3. Comparison of the computational time of ADMM and PCDM(Period)
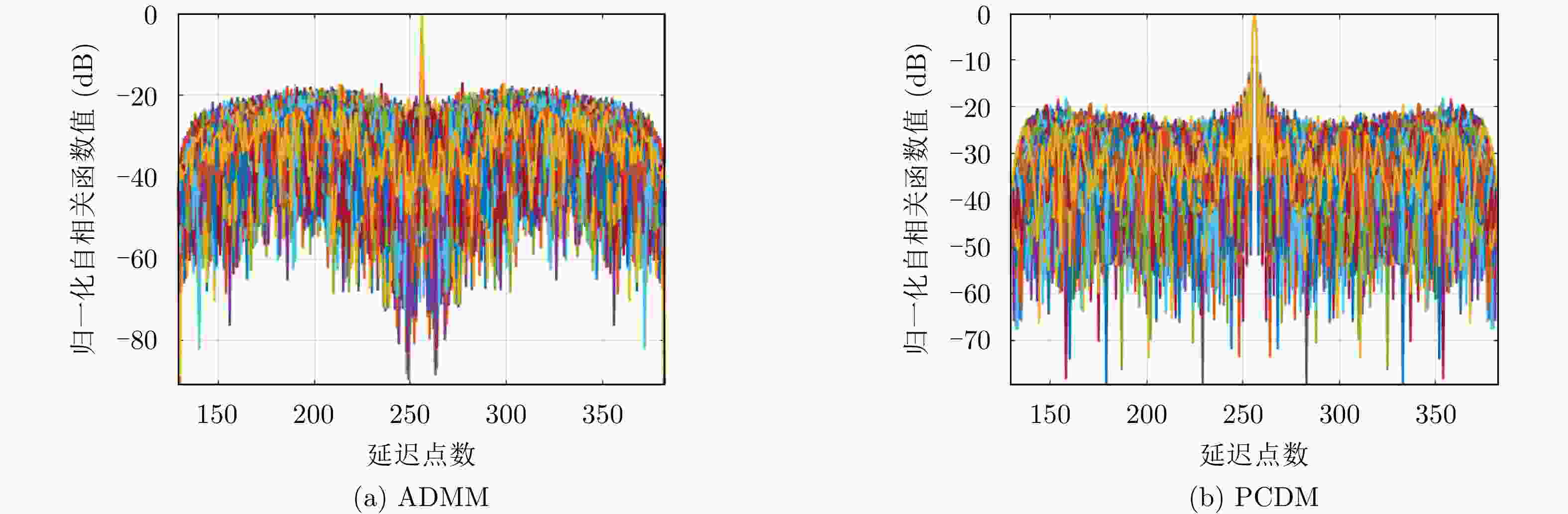
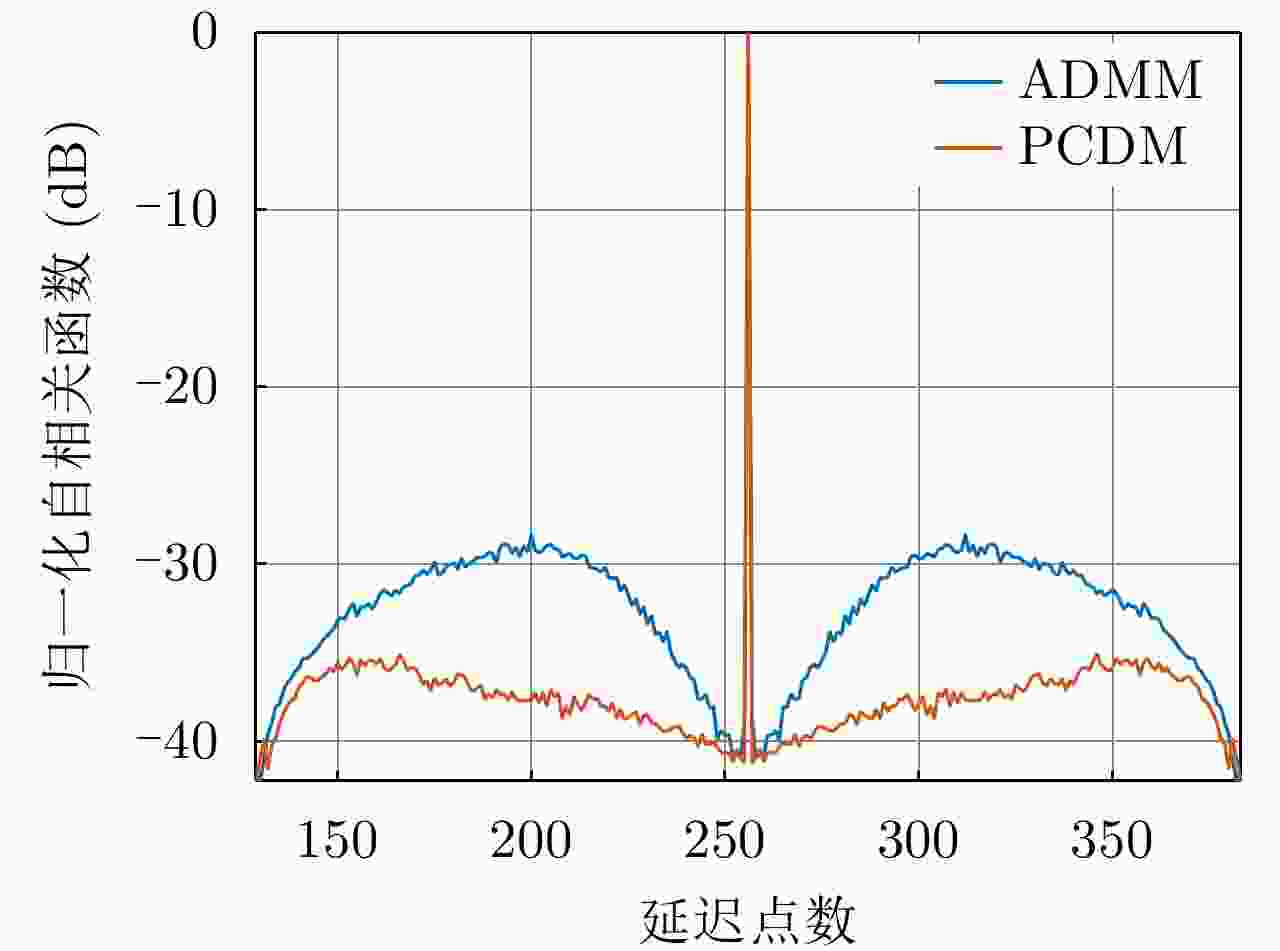
方法 计算时间 (s) 序列长度128点 序列长度1024点 ADMM 13.3487 1001.9395 PCDM 8.6281 844.8235 表 4 对非周期波形ADMM算法与PCDM算法运算耗时比较
Table 4. Comparison of the computational time of ADMM and PCDM (Aperiod)
方法 计算时间 (s) 序列长度128点 序列长度1024点 ADMM 67.3514 941.0294 PCDM 20.3676 380.6446 -
[1] GINI F, DE MAIO A, and PATTON L. Waveform Design and Diversity for Advanced Radar Systems[M]. London, UK: Institution of Engineering and Technology, 2012: 5. [2] SKOLNIK M I. Introduction to Radar Systems[M]. 3rd ed. New York, USA: McGraw-Hill Education (Asia) Co. , 2007. 10–56. [3] WANG Xinhai, ZHANG Gong, ZHANG Yu, et al. Design of spectrally compatible waveform with constant modulus for colocated multiple-input multiple-output radar[J]. IET Radar, Sonar & Navigation, 2019, 13(8): 1373–1388. doi: 10.1049/iet-rsn.2019.0009 [4] DAVIS M E and PILLAI S U. Waveform diversity for ultra-wide band surveillance radars[J]. IET Radar, Sonar & Navigation, 2014, 8(9): 1226–1233. doi: 10.1049/iet-rsn.2014.0366 [5] GOLAY M. A class of finite binary sequences with alternate auto-correlation values equal to zero (Corresp. )[J]. IEEE Transactions on Information Theory, 1972, 18(3): 449–450. doi: 10.1109/TIT.1972.1054797 [6] BARKER R H. Group Synchronizing of Binary Digital Systems[M]. JACKSON W. Communication Theory. New York: Academic Press, 1953: 273–287. [7] GOLAY M. Sieves for low autocorrelation binary sequences[J]. IEEE Transactions on Information Theory, 1977, 23(1): 43–51. doi: 10.1109/TIT.1977.1055653 [8] MERTENS S. Exhaustive search for low-autocorrelation binary sequences[J]. Journal of Physics A:Mathematical and General, 1996, 29(18): L473–L481. doi: 10.1088/0305-4470/29/18/005 [9] KOCABAS S E and ATALAR A. Binary sequences with low aperiodic autocorrelation for synchronization purposes[J]. IEEE Communications Letters, 2003, 7(1): 36–38. doi: 10.1109/LCOMM.2002.807438 [10] JEDWAB J. A survey of the merit factor problem for binary sequences[C]. Third International Conference on Sequences and Their Applications, Seoul, Korea, 2005: 30–55. doi: 10.1007/11423461_2. [11] WANG S. Efficient heuristic method of search for binary sequences with good aperiodic autocorrelations[J]. Electronics Letters, 2008, 44(12): 731–732. doi: 10.1049/el:20081058 [12] FRANK R. Polyphase codes with good nonperiodic correlation properties[J]. IEEE Transactions on Information Theory, 1963, 9(1): 43–45. doi: 10.1109/TIT.1963.1057798 [13] ZHANG N and GOLOMB S W. Polyphase sequence with low autocorrelations[J]. IEEE Transactions on Information Theory, 1993, 39(3): 1085–1089. doi: 10.1109/18.256535 [14] NUNN C J and COXSON G E. Polyphase pulse compression codes with optimal peak and integrated sidelobes[J]. IEEE Transactions on Aerospace and Electronic Systems, 2009, 45(2): 775–781. doi: 10.1109/TAES.2009.5089560 [15] DE MAIO A, DE NICOLA S, HUANG Yongwei, et al. Design of phase codes for radar performance optimization with a similarity constraint[J]. IEEE Transactions on Signal Processing, 2009, 57(2): 610–621. doi: 10.1109/TSP.2008.2008247 [16] CUI Guolong, JING Ying, LU Shuping, et al. Dual-Use Unimodular Sequence Design via Frequency Nulling Modulation[J]. IEEE Access, 2018(6): 62470–62481. doi: 10.1109/ACCESS.2018.2876644 [17] SOLTANALIAN M and STOICA P. Computational design of sequences with good correlation properties[J]. IEEE Transactions on Signal Processing, 2012, 60(5): 2180–2193. doi: 10.1109/TSP.2012.2186134 [18] STOICA P, HE Hao, and LI Jian. New algorithms for designing unimodular sequences with good correlation properties[J]. IEEE Transactions on Signal Processing, 2009, 57(4): 1415–1425. doi: 10.1109/TSP.2009.2012562 [19] STOICA P, HE Hao, and LI Jian. On designing sequences with impulse-like periodic correlation[J]. IEEE Signal Processing Letters, 2009, 16(8): 703–706. doi: 10.1109/LSP.2009.2021378 [20] SONG Junxiao, BABU P, and PALOMAR D P. Optimization methods for designing sequences with low autocorrelation sidelobes[J]. IEEE Transactions on Signal Processing, 2015, 63(15): 3998–4009. doi: 10.1109/TSP.2015.2425808 [21] BORWEIN P and FERGUSON R. Polyphase sequences with low autocorrelation[J]. IEEE Transactions on Information Theory, 2005, 51(4): 1564–1567. doi: 10.1109/TIT.2004.842778 [22] LIANG Junli, SO H C, LEUNG C S, et al. Waveform design with unit modulus and spectral shape constraints via Lagrange programming neural network[J]. IEEE Journal of Selected Topics in Signal Processing, 2015, 9(8): 1377–1386. doi: 10.1109/JSTSP.2015.2464178 [23] LIANG Junli, SO H C, LI Jian, et al. Unimodular sequence design based on alternating direction method of multipliers[J]. IEEE Transactions on Signal Processing, 2016, 64(20): 5367–5381. doi: 10.1109/TSP.2016.2597123 [24] BOYD S, PARIKH N, CHU E, et al. Distributed optimization and statistical learning via the alternating direction method of multipliers[J]. Foundations and Trends ® in Machine Learning, 2011, 3(1): 1–122. doi: 10.1561/2200000016 [25] ZHANG Jindong, ZHU Daiyin, and ZHANG Gong. New antivelocity deception jamming technique using pulses with adaptive initial phases[J]. IEEE Transactions on Aerospace and Electronic Systems, 2013, 49(2): 1290–1300. doi: 10.1109/TAES.2013.6494414 [26] BONNANS J F, GILBERT J C, LEMARÉCHAL C, et al. Numerical Optimization: Theoretical and Practical Aspects[M]. Berlin, Heidelberg: Springer, 2006, 67–76. doi: 10.1007/978-3-540-35447-5. [27] TANG Liang, ZHU Yongfeng, and FU Qiang. Fast algorithm for designing periodic/aperiodic sequences with good correlation and stopband properties[J]. EURASIP Journal on Advances in Signal Processing, 2018, 2018(1): 57. doi: 10.1186/s13634-018-0579-z [28] ESMAEILI-NAJAFABADI H, LEUNG H, and MOO P W. Unimodular waveform design with desired ambiguity function for cognitive radar[J]. IEEE Transactions on Aerospace and Electronic Systems, 2020, 56(3): 2489–2496. doi: 10.1109/TAES.2019.2942411 [29] GRANT M. CVX: MATLAB software for disciplined convex programming[EB/OL]. http://cvxr.com/cvx, 2020. [30] PEAUCELLE D, HENRION D, LABIT Y, et al. User’s guide for SEDUMI interface 1.04[J]. Siam Journal on Optimization - SIAMJO, 2002. -



 作者中心
作者中心 专家审稿
专家审稿 责编办公
责编办公 编辑办公
编辑办公
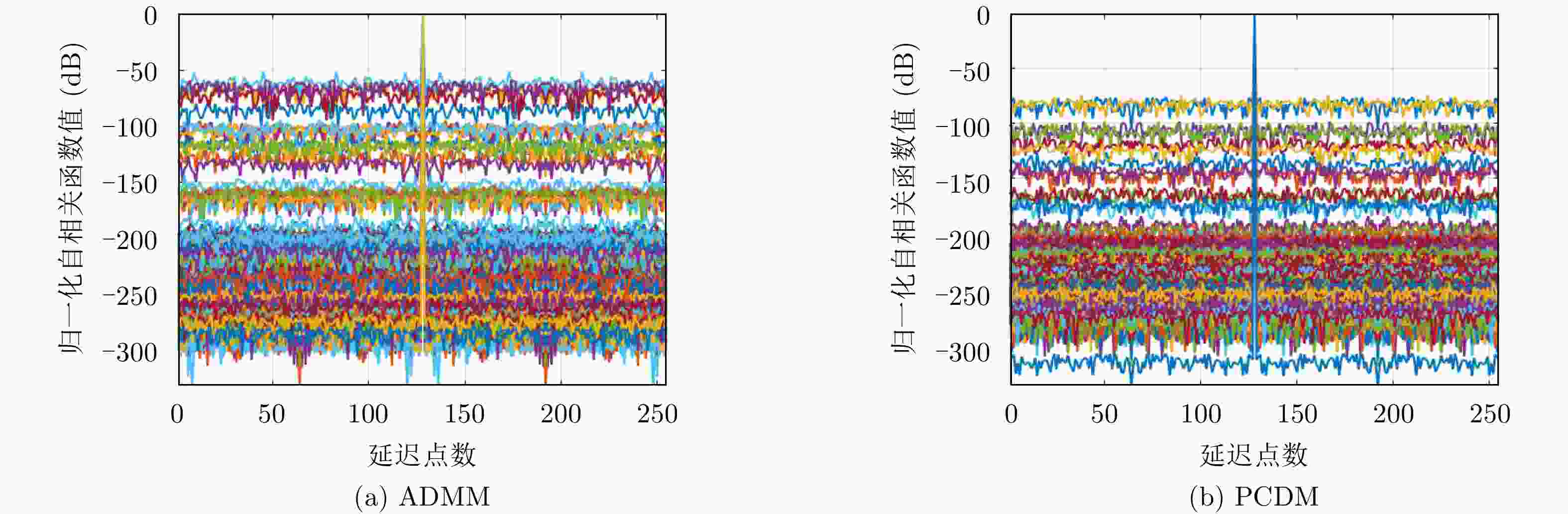
 下载:
下载: