基于深度学习的非线性空时自适应-脉冲压缩联合处理方法

廖志鹏; 段克清; 高飞

doi:10.12000/JR25096

基于深度学习的非线性空时自适应-脉冲压缩联合处理方法

DOI: 10.12000/JR25096 CSTR: 32380.14.JR25096

1.
中山大学电子与通信工程学院深圳 518107
2.
中国空间技术研究院西安分院西安 710100

基金项目: 雷达信号处理全国重点实验室支持计划(JKW202302)

详细信息

作者简介:
廖志鹏，博士生，主要研究方向为深度学习、阵列信号处理、空时自适应处理等

段克清，副教授，博士生导师，主要研究方向为机载/星载雷达信号处理、阵列信号处理、空时自适应处理等

高　飞，博士，高级工程师，主要研究方向为雷达系统仿真与设计、机载/星载雷达信号处理、阵列信号处理等

通讯作者:
段克清 duankeqing@aliyun.com

责任主编：谢文冲 Corresponding Editor: XIE Wenchong
中图分类号: TN957.51
计量
- 文章访问数:
- HTML全文浏览量:
- PDF下载量:
- 被引次数: 0
出版历程
- 收稿日期: 2025-05-23
- 修回日期: 2025-07-28
- 网络出版日期: 2025-08-29

Collaborative Nonlinear Space-time Adaptive Processing and Pulse Compression Based on Neural Networks

1.
School of Electronic and Communication Engineering, Sun Yat-sen University, Shenzhen 518107, China
2.
China Academy Space Technology Xian Branch, Xi’an 710100, China

Funds: The Foundation of National Key Laboratory of Radar Signal Processing (JKW202302)

More Information

Corresponding author: DUAN Keqing, duankeqing@aliyun.com

摘要

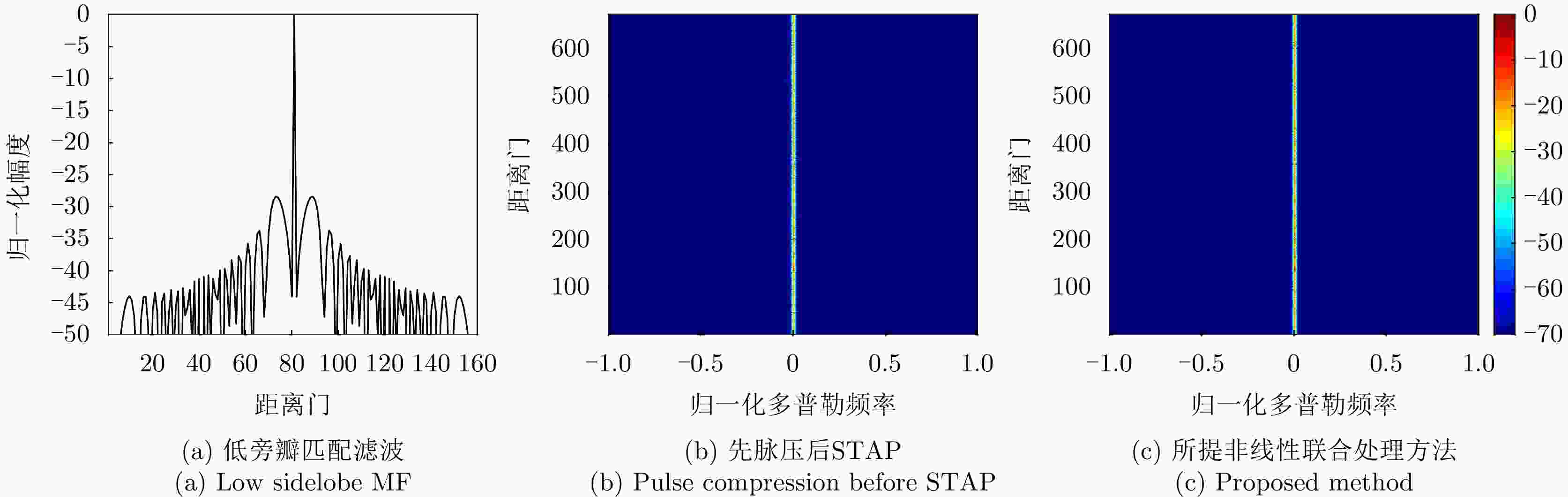
摘要: 在复杂目标和杂波环境下，传统机载雷达脉冲压缩和空时自适应处理均受限于预设线性模型而存在性能损失问题。针对该问题，该文提出一种基于深度学习的空时自适应-脉冲压缩联合处理技术，通过构建空时谱超分辨网络和脉冲压缩网络分别实现非线性杂波空时谱估计及非线性脉压，从而显著降低该信号处理流程中模型失配的影响，实现杂波抑制和目标检测性能的提升。同时，为避免非线性脉压在阵元和脉冲间引入相位误差的问题，该文从数学角度分析和讨论了脉压后置的可行性。在所提先滤波再脉压的非线性联合处理架构中，采用多模块卷积神经网络分别实现高分辨空时谱估计以及脉冲压缩处理，且所构建各网络模块功能均与相应数学解析式对应，因此具较高的可靠性。仿真实验结果表明，在密集弱目标和小样本环境下，所提非线性联合处理架构较相应传统处理流程可获得约20 dB的信杂噪比提升。
- 非线性信号处理 /
- 空时自适应处理(STAP) /
- 脉冲压缩 /
- 卷积神经网络(CNN) /
- 杂波抑制 /
- 目标检测
Abstract: Traditional airborne radar Pulse Compression (PC) and Space-Time Adaptive Processing (STAP) suffer performance degradation in complex target and clutter environments due to their reliance on predefined linear models. To address this issue, we developed a deep learning-based joint STAP-PC technique. This approach employed dedicated networks—a super-resolution space-time spectrum network for nonlinear clutter estimation and a PC network for nonlinear PC. The proposed architecture effectively mitigated model mismatch within the processing chain, leading to improved clutter suppression and target detection. Notably, we mathematically established the feasibility of post-pulse compensation to prevent nonlinear PC from introducing phase errors across elements and pulses. The implemented architecture utilized multimodule convolutional neural networks for super-resolution space-time spectrum estimation and PC, with each module’s functionality demonstrating clear mathematical correspondence, thereby ensuring the reliability of the overall processing chain. Simulation results revealed that in scenarios with dense weak targets and limited samples, the proposed nonlinear joint processing technique improved signal-to-clutter-plus-noise ratio by approximately 20 dB over traditional methods.
- Nonlinear signal processing /
- Space-Time Adaptive Processing (STAP) /
- Pulse Compression (PC) /
- Convolutional Neural Network (CNN) /
- Clutter suppression /
- Target detection

HTML全文

图 1 脉压前置的信号处理流程图

Figure 1. Signal processing flow with pulse compression at the front end

下载: 全尺寸图片幻灯片

图 2 脉压后置的信号处理流程图

Figure 2. Signal processing flow with pulse compression at the back end

下载: 全尺寸图片幻灯片

图 3 阵列与地面的几何关系

Figure 3. Airborne radar viewing geometry

下载: 全尺寸图片幻灯片

图 4 非线性空时自适应-脉压联合处理流程示意图

Figure 4. Schematic diagram of nonlinear pulse compression STAP joint processing flow

下载: 全尺寸图片幻灯片

图 5 空时谱超分辨网络示意图

Figure 5. Spatial-temporal spectrum super-resolution network schematic diagram

下载: 全尺寸图片幻灯片

图 6 脉冲压缩网络示意图

Figure 6. Pulse compression network schematic diagram

下载: 全尺寸图片幻灯片

图 7 多普勒模块数据流示意图

Figure 7. Illustration of the Doppler module data flow

下载: 全尺寸图片幻灯片

图 8 超参数模块滤波器可视化

Figure 8. The filters in the hyperparameter module

下载: 全尺寸图片幻灯片

图 9 各种方法重建的空时谱对比

Figure 9. Comparison of space-time spectra restored by various methods

下载: 全尺寸图片幻灯片

图 10 各种方法的距离多普勒谱对比

Figure 10. Comparison of range Doppler spectra of various methods

下载: 全尺寸图片幻灯片

图 11 脉冲压缩性能对比

Figure 11. Comparison of pulse compression performance

下载: 全尺寸图片幻灯片

图 12 不同程度多普勒频移的脉压性能对比

Figure 12. Comparison of pulse compression performance under different Doppler shift

下载: 全尺寸图片幻灯片

图 13 多普勒容忍度性能对比

Figure 13. Comparison of Doppler tolerance

下载: 全尺寸图片幻灯片

图 14 SCNR损失性能对比

Figure 14. Comparison of SCNR loss

下载: 全尺寸图片幻灯片

图 15 低脉压距离旁瓣的处理结果

Figure 15. The processing results under low pulse compression distance sidelobe

下载: 全尺寸图片幻灯片

图 16 高脉压距离旁瓣下的处理结果

Figure 16. The processing results under high pulse compression distance sidelobe

下载: 全尺寸图片幻灯片

图 17 非正侧视处理结果

Figure 17. The processing results for non-sidelooking condition

下载: 全尺寸图片幻灯片

表 1 非线性空时谱超分辨网络运算复杂度分析

Table 1. Analysis of computational complexity of nonlinear STAP spectrum estimation network

方法	运算复杂度	运行时间(s)
FOCUSS	$ O\left( {\left( {NK{N_{\text{S}}}{N_{\text{D}}} + {{\left( {NK} \right)}^3} + 2{{\left( {NK} \right)}^2}{N_{\text{S}}}{N_{\text{D}}} + NK{{\left( {{N_{\text{S}}}{N_{\text{D}}}} \right)}^2}} \right){I_{{\text{FOC}}}}} \right) $	61.87
SBL	$ O\left( {\left( {NK{N_{\text{S}}}{N_{\text{D}}} + {{\left( {NK} \right)}^3} + 3{{\left( {NK} \right)}^3}{N_{\text{S}}}{N_{\text{D}}} + 2NK{{\left( {{N_{\text{S}}}{N_{\text{D}}}} \right)}^2}} \right){I_{{\text{SBL}}}}} \right) $	130.40
CNN	$ O\left( {{\text{28777 }}{N_{\text{S}}}{N_{\text{D}}}} \right) $	1.53
所提非线性空时谱估计方法	$ O\left( {{\text{12960 }}{N_{\text{S}}}{N_{\text{D}}}} \right) $	0.79

下载: 导出CSV

表 2 脉冲压缩网络运算复杂度分析

Table 2. Analysis of computational complexity of end-to-end pulse compression network

方法	运算复杂度	运行时间(s)
MF	$O(P)$	0.02
APC	$O({P^3})$	1.70
DC-APC	$O({P^3})$	1.83
所提非线性脉冲压缩	$O(3744P)$	0.18

下载: 导出CSV

表 3 雷达系统参数

Table 3. Radar system parameters

参数	数值	参数	数值
飞行高度	3000 m	信号带宽	2.5 MHz
飞行速度	60 m/s	信号脉宽	32 μs
载波频率	9 GHz	脉冲重复频率	2500 Hz
阵元数	8	主波束方位角	0^o
脉冲数	16	主波束俯仰角	5^o

下载: 导出CSV

表 4 目标参数

Table 4. Targets parameters

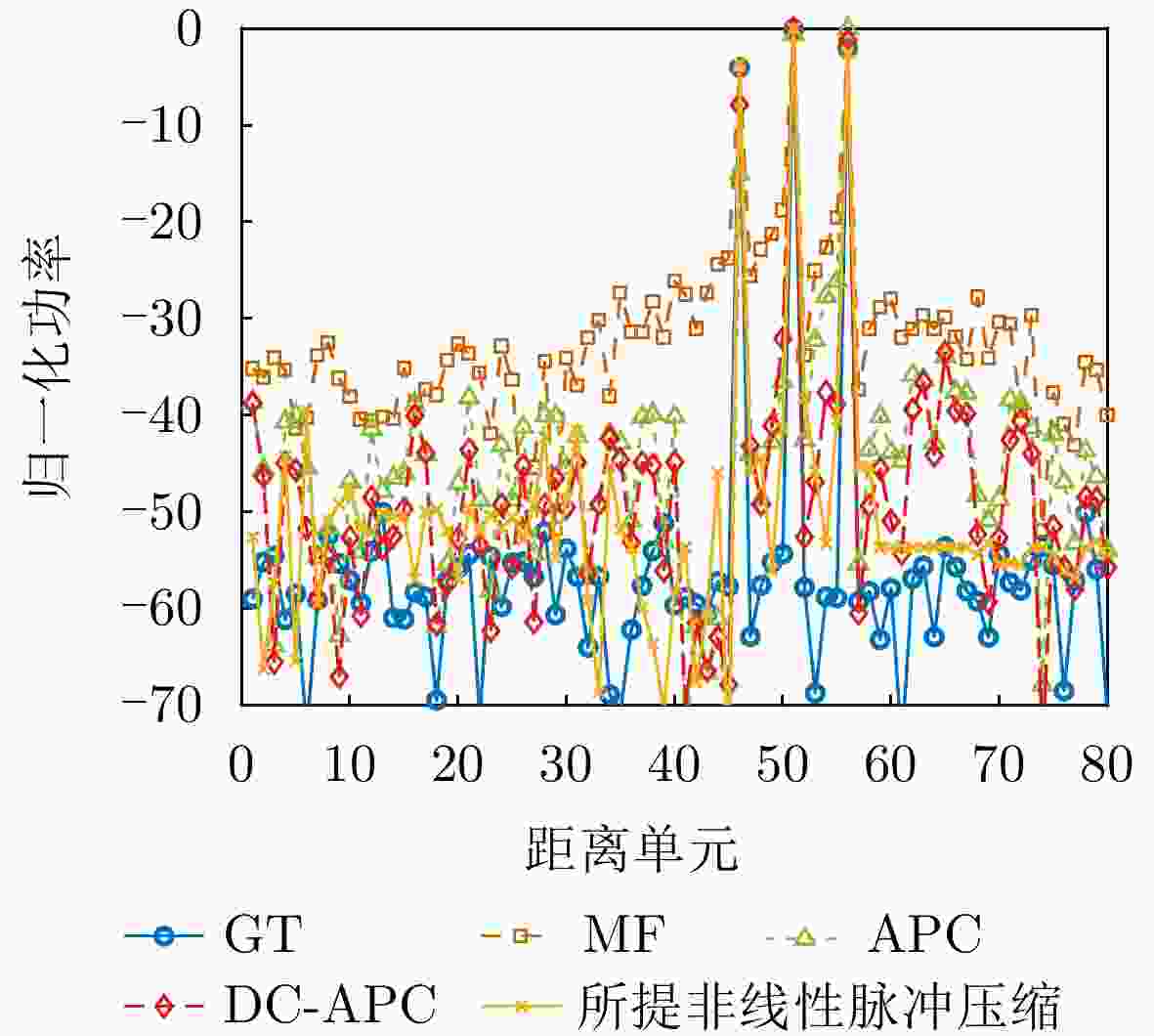
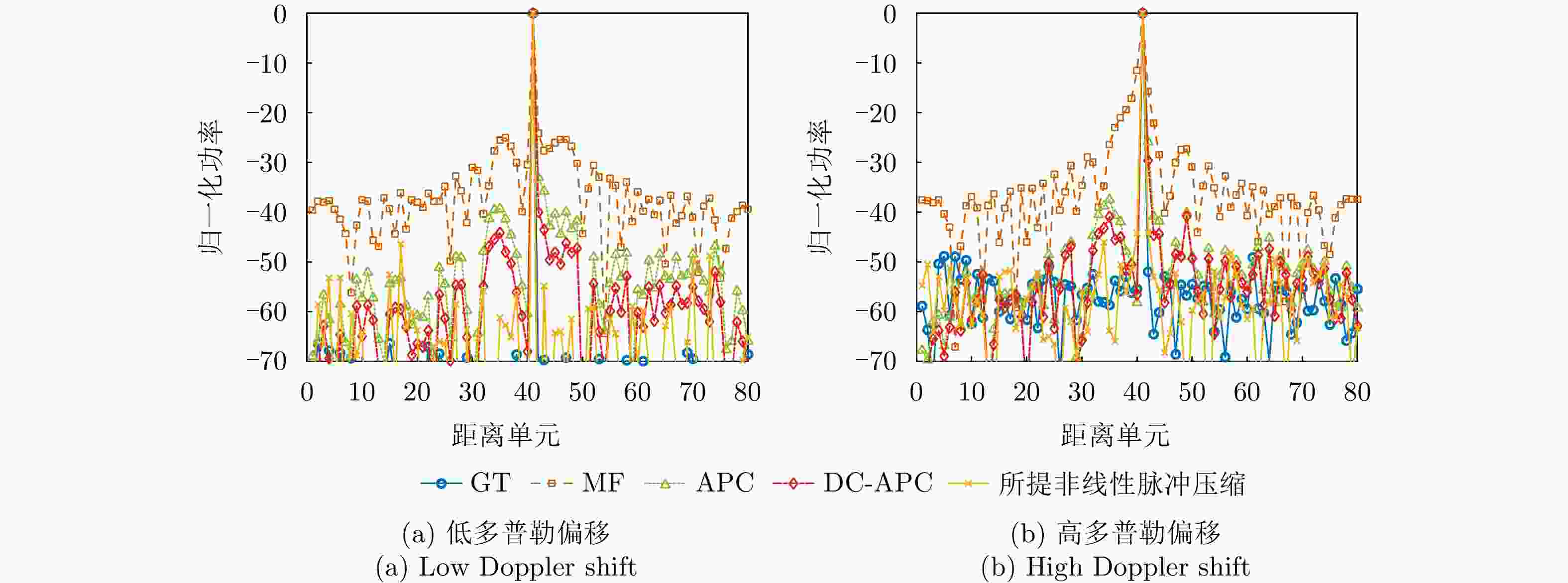
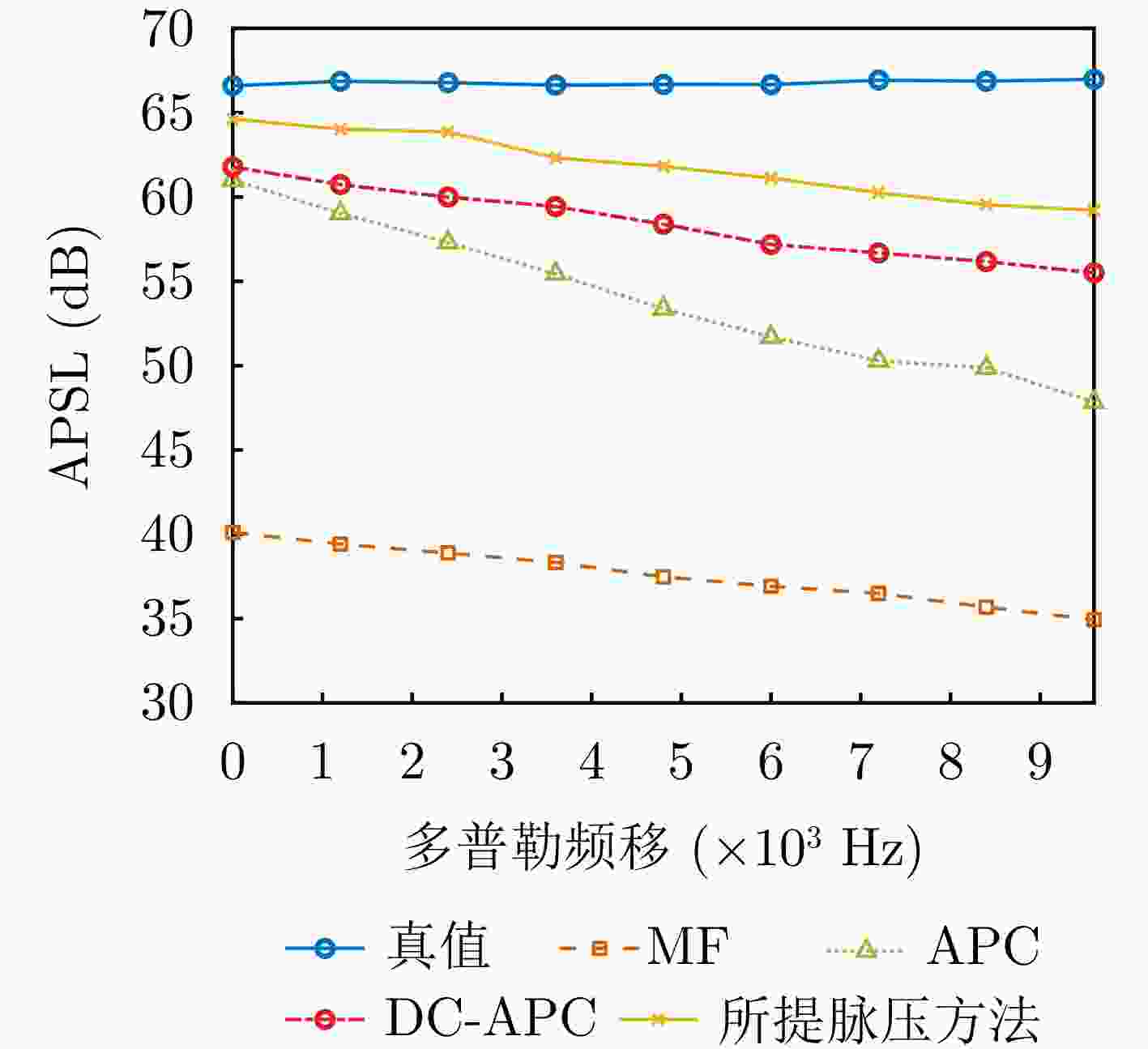
目标	距离门	SNR (dB)	多普勒频移(Hz)
目标1	46	25	120
目标2	51	29	1200
目标3	56	27	1920

下载: 导出CSV

表 5 各对比方法的APSL (dB)

Table 5. APSL of each comparison method (dB)

目标	MF	APC	DC-APC	CNN-APC	GT
目标1	28.86	30.55	41.41	48.07	53.58
目标2	32.86	45.01	49.30	51.68	57.48
目标3	30.90	45.56	48.10	49.20	55.37

下载: 导出CSV

参考文献(44)

[1]	SKOLNIK M I. Radar Handbook[M]. 3rd ed. New York: McGraw-Hill, 2008.
[2]	谢文冲, 段克清, 王永良. 机载雷达空时自适应处理技术研究综述[J]. 雷达学报, 2017, 6(6): 575–586. doi: 10.12000/JR17073. XIE Wenchong, DUAN Keqing, and WANG Yongliang. Space time adaptive processing technique for airborne radar: An overview of its development and prospects[J]. Journal of Radars, 2017, 6(6): 575–586. doi: 10.12000/JR17073.
[3]	RICHARDS M A. Fundamentals of Radar Signal Processing[M]. New York: McGraw-Hill, 2005.
[4]	ACKROYD M H and GHANI F. Optimum mismatched filters for sidelobe suppression[J]. IEEE Transactions on Aerospace and Electronic Systems, 1973, AES-9(2): 214–218. doi: 10.1109/TAES.1973.309769.
[5]	TSAO J and STEINBERG B D. Reduction of sidelobe and speckle artifacts in microwave imaging: The CLEAN technique[J]. IEEE Transactions on Antennas and Propagation, 1988, 36(4): 543–556. doi: 10.1109/8.1144.
[6]	RABASTE O and SAVY L. Mismatched filter optimization for radar applications using quadratically constrained quadratic programs[J]. IEEE Transactions on Aerospace and Electronic Systems, 2015, 51(4): 3107–3122. doi: 10.1109/TAES.2015.130769.
[7]	RABASTE O and BOSSE J. Robust mismatched filter for off-grid target[J]. IEEE Signal Processing Letters, 2019, 26(8): 1147–1151. doi: 10.1109/LSP.2019.2923054.
[8]	BLUNT S D and GERLACH K. Adaptive pulse compression via MMSE estimation[J]. IEEE Transactions on Aerospace and Electronic Systems, 2006, 42(2): 572–584. doi: 10.1109/TAES.2006.1642573.
[9]	GERLACH K and BLUNT S D. Radar pulse compression repair[J]. IEEE Transactions on Aerospace and Electronic Systems, 2007, 43(3): 1188–1195. doi: 10.1109/TAES.2007.4383610.
[10]	BLUNT S D and HIGGINS T. Achieving real-time efficiency for adaptive radar pulse compression[C]. 2007 IEEE Radar Conference, Waltham, USA, 2007: 116–121. doi: 10.1109/RADAR.2007.374201.
[11]	BLUNT S D and HIGGINS T. Dimensionality reduction techniques for efficient adaptive pulse compression[J]. IEEE Transactions on Aerospace and Electronic Systems, 2010, 46(1): 349–362. doi: 10.1109/TAES.2010.5417167.
[12]	HIGGINS T, BLUNT S D, and GERLACH K. Gain-constrained adaptive pulse compression via an MVDR framework[C]. 2009 IEEE Radar Conference, Pasadena, USA, 2009: 1–6. doi: 10.1109/RADAR.2009.4977011.
[13]	BLUNT S D, SHACKELFORD A K, GERLACH K, et al. Doppler compensation & single pulse imaging using adaptive pulse compression[J]. IEEE Transactions on Aerospace and Electronic Systems, 2009, 45(2): 647–659. doi: 10.1109/TAES.2009.5089547.
[14]	CUPRAK T D and WAGE K E. Efficient Doppler-compensated reiterative minimum mean-squared-error processing[J]. IEEE Transactions on Aerospace and Electronic Systems, 2017, 53(2): 562–574. doi: 10.1109/TAES.2017.2651480.
[15]	AKHTAR J. Neural network LFM pulse compression[C]. 2023 IEEE Radar Conference, San Antonio, USA, 2023: 1–6. doi: 10.1109/RadarConf2351548.2023.10149646.
[16]	GAO Yvyang and DONG Ganggang. Pulse compression based on learnable matched filtering[C]. IGARSS 2024 - 2024 IEEE International Geoscience and Remote Sensing Symposium, Athens, Greece, 2024: 2568–2571. doi: 10.1109/IGARSS53475.2024.10640745.
[17]	李秀友, 董云龙, 黄勇, 等. 基于迭代线性约束最小方差的稳健自适应脉冲压缩方法[J]. 电子与信息学报, 2015, 37(10): 2300–2306. doi: 10.11999/JEIT141631. LI Xiuyou, DONG Yunlong, HUANG Yong, et al. Robust adaptive pulse compression algorithm based on reiterative linearly constrained minimum variance[J]. Journal of Electronics & Information Technology, 2015, 37(10): 2300–2306. doi: 10.11999/JEIT141631.
[18]	裴家正, 黄勇, 陈宝欣, 等. 基于线性约束最小方差原则的稳健快速自适应脉冲压缩方法[J]. 系统工程与电子技术, 2022, 44(12): 3621–3630. doi: 10.12305/j.issn.1001-506X.2022.12.05. PEI Jiazheng, HUANG Yong, CHEN Baoxin, et al. Robust fast adaptive pulse compression method based on linearly constrained minimum variance principle[J]. Systems Engineering and Electronics, 2022, 44(12): 3621–3630. doi: 10.12305/j.issn.1001-506X.2022.12.05.
[19]	WANG Yongliang, CHEN Jianwen, BAO Zheng, et al. Robust space-time adaptive processing for airborne radar in nonhomogeneous clutter environments[J]. IEEE Transactions on Aerospace and Electronic Systems, 2003, 39(1): 71–81. doi: 10.1109/TAES.2003.1188894.
[20]	DIPIETRO R C. Extended factored space-time processing for airborne radar systems[C]. The 26th Asilomar Conference on Signals, Systems & Computers, Pacific Grove, USA, 1992: 425–430. doi: 10.1109/ACSSC.1992.269236.
[21]	DUAN Keqing, XU Hong, YUAN Huadong, et al. Reduced-DOF three-dimensional STAP via subarray synthesis for nonsidelooking planar array airborne radar[J]. IEEE Transactions on Aerospace and Electronic Systems, 2020, 56(4): 3311–3325. doi: 10.1109/TAES.2019.2958174.
[22]	MELVIN W L and GUERCI J R. Knowledge-aided signal processing: A new paradigm for radar and other advanced sensors[J]. IEEE Transactions on Aerospace and Electronic Systems, 2006, 42(3): 983–996. doi: 10.1109/TAES.2006.248215.
[23]	MELVIN W L and SHOWMAN G A. An approach to knowledge-aided covariance estimation[J]. IEEE Transactions on Aerospace and Electronic Systems, 2006, 42(3): 1021–1042. doi: 10.1109/TAES.2006.248216.
[24]	YANG Zhaocheng, DE LAMARE R C, and LIU Weijian. Sparsity-based STAP using alternating direction method with gain/phase errors[J]. IEEE Transactions on Aerospace and Electronic Systems, 2017, 53(6): 2756–2768. doi: 10.1109/TAES.2017.2714938.
[25]	DUAN Keqing, WANG Zetao, XIE Wenchong, et al. Sparsity-based STAP algorithm with multiple measurement vectors via sparse Bayesian learning strategy for airborne radar[J]. IET Signal Processing, 2017, 11(5): 544–553. doi: 10.1049/iet-spr.2016.0183.
[26]	CUI Ning, XING Kun, YU Zhongjun, et al. Reduced-complexity subarray-level sparse recovery STAP for multichannel airborne radar WGMTI application[J]. IEEE Transactions on Aerospace and Electronic Systems, 2023, 59(5): 6292–6313. doi: 10.1109/TAES.2023.3274104.
[27]	WANG Degen, WANG Tong, CUI Weichen, et al. A clutter suppression algorithm via enhanced sparse Bayesian learning for airborne radar[J]. IEEE Sensors Journal, 2023, 23(10): 10900–10911. doi: 10.1109/JSEN.2023.3263919.
[28]	DUAN Keqing, CHEN Hui, XIE Wenchong, et al. Deep learning for high-resolution estimation of clutter angle-Doppler spectrum in STAP[J]. IET Radar, Sonar & Navigation, 2022, 16(2): 193–207. doi: 10.1049/rsn2.12176.
[29]	VENKATASUBRAMANIAN S, WONGKAMTHONG C, SOLTANI M, et al. Toward data-driven stap radar[C]. 2022 IEEE Radar Conference (RadarConf22), New York City, USA, 2022: 1–5. doi: 10.1109/RadarConf2248738.2022.9764354.
[30]	LIU Jing, LIAO Guisheng, XU Jingwei, et al. Autoencoder neural network-based STAP algorithm for airborne radar with inadequate training samples[J]. Remote Sensing, 2022, 14(23): 6021. doi: 10.3390/rs14236021.
[31]	王俊, 郑彤, 雷鹏, 等. 深度学习在雷达中的研究综述[J]. 雷达学报, 2018, 7(4): 395–411. doi: 10.12000/JR18040. WANG Jun, ZHENG Tong, LEI Peng, et al. Study on deep learning in radar[J]. Journal of Radars, 2018, 7(4): 395–411. doi: 10.12000/JR18040.
[32]	RAJAN K and PATNAIK L M. Implementation of STAP algorithms on IBM SP2 and on ADSP 21062 dual digital signal processor systems[J]. Microprocessors and Microsystems, 2003, 27(4): 221–227. doi: 10.1016/S0141-9331(03)00022-X.
[33]	廖志鹏, 段克清, 何锦浚, 等. 基于可解释深度卷积网络的空时自适应处理方法[J]. 雷达学报, 2024, 13(4): 917–928. doi: 10.12000/JR24024. LIAO Zhipeng, DUAN Keqing, HE Jinjun, et al. Interpretable STAP algorithm based on deep convolutional neural network[J]. Journal of Radars, 2024, 13(4): 917–928. doi: 10.12000/JR24024.
[34]	ZOU Bo, WANG Xin, FENG Weike, et al. DU-CG-STAP method based on sparse recovery and unsupervised learning for airborne radar clutter suppression[J]. Remote Sensing, 2022, 14(14): 3472. doi: 10.3390/rs14143472.
[35]	朱晗归, 冯为可, 冯存前, 等. 机载雷达深度展开空时自适应处理方法[J]. 雷达学报, 2022, 11(4): 676–691. doi: 10.12000/JR22051. ZHU Hangui, FENG Weike, FENG Cunqian, et al. Deep unfolding based space-time adaptive processing method for airborne radar[J]. Journal of Radars, 2022, 11(4): 676–691. doi: 10.12000/JR22051.
[36]	LIAO Weikeng, CHOUDHARY A, WEINER D, et al. Design and evaluation of I/O strategies for parallel pipelined STAP applications[C]. 14th International Parallel and Distributed Processing Symposium, Cancun, Mexico, 2000: 655–662. doi: 10.1109/IPDPS.2000.846050.
[37]	LIAO Weikeng, CHOUDHARY A, WEINER D, et al. I/O implementation and evaluation of parallel pipelined STAP on high performance computers[C]. 6th International Conference on High Performance Computing, Calcutta, India, 1999: 354–358. doi: 10.1007/978-3-540-46642-0_51.
[38]	高飞, 陈辉, 任磊, 等. 一种新的机载雷达信号处理流程结构可行性证明及拓展性研究[J]. 信号处理, 2009, 25(11): 1785–1789. doi: 10.3969/j.issn.1003-0530.2009.11.023. GAO Fei, CHEN Hui, REN Lei, et al. Feasibility-proving of a new airborne radar signal processing architecture and extended research[J]. Journal of Signal Processing, 2009, 25(11): 1785–1789. doi: 10.3969/j.issn.1003-0530.2009.11.023.
[39]	YANG Yan, SUN Jian, LI Huibin, et al. ADMM-CSNet: A deep learning approach for image compressive sensing[J]. IEEE Transactions on Pattern Analysis and Machine Intelligence, 2020, 42(3): 521–538. doi: 10.1109/TPAMI.2018.2883941.
[40]	MA Jiawei, LIU Xiaoyang, SHOU Zheng, et al. Deep tensor ADMM-net for snapshot compressive imaging[C]. 2019 IEEE/CVF International Conference on Computer Vision, Seoul, Korea (South), 2019: 10222–10231. doi: 10.1109/ICCV.2019.01032.
[41]	MARQUES E C, MACIEL N, NAVINER L, et al. Deep learning approaches for sparse recovery in compressive sensing[C]. 2019 11th International Symposium on Image and Signal Processing and Analysis (ISPA), Dubrovnik, Croatia, 2019: 129–134. doi: 10.1109/ISPA.2019.8868841.
[42]	ZHANG Kai, VAN GOOL L, and TIMOFTE R. Deep unfolding network for image super-resolution[C]. 2020 IEEE/CVF Conference on Computer Vision and Pattern Recognition, Seattle, USA, 2020: 3214–3223. doi: 10.1109/CVPR42600.2020.00328.
[43]	BEN SAHEL Y, BRYAN J P, CLEARY B, et al. Deep unrolled recovery in sparse biological imaging: Achieving fast, accurate results[J]. IEEE Signal Processing Magazine, 2022, 39(2): 45–57. doi: 10.1109/MSP.2021.3129995.
[44]	TAN Xiao, YANG Zhiwei, LI Xianghai, et al. Gridless sparse recovery STAP algorithm with array amplitude-phase errors for non-uniform linear array[J]. Digital Signal Processing, 2024, 144: 104296. doi: 10.1016/j.dsp.2023.104296.