作者中心
专家审稿
责编办公
编辑办公
Moving Targets Detection with Low-bit Quantization in Distributed Radar on Moving Platforms
-
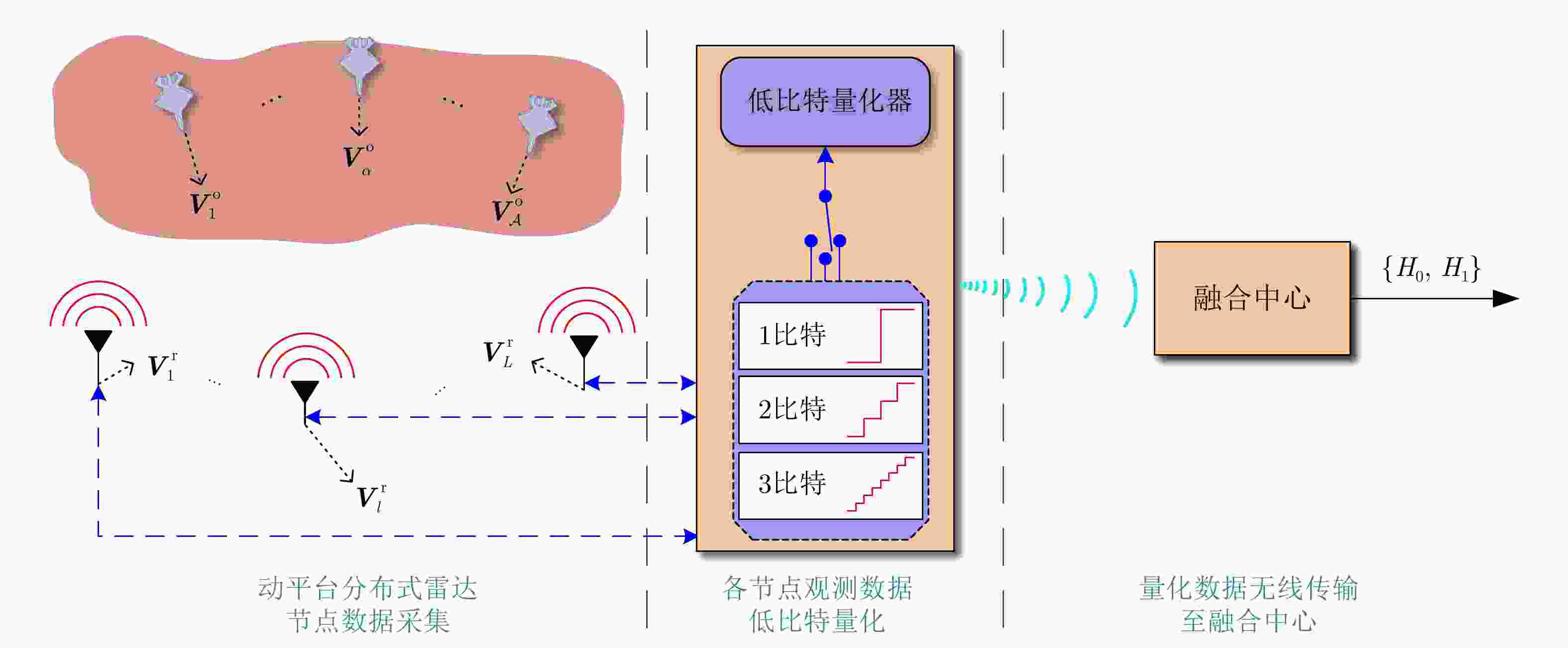
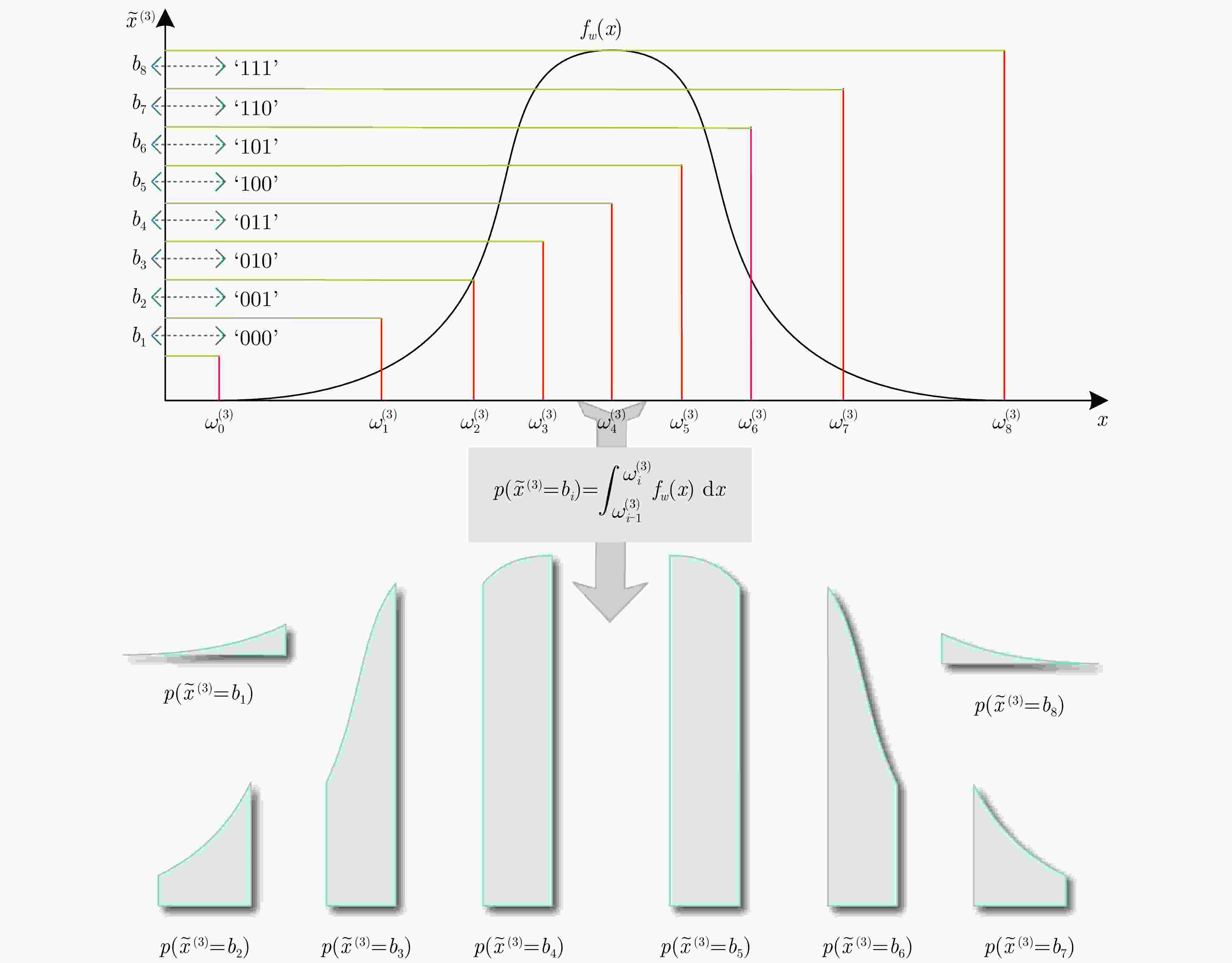
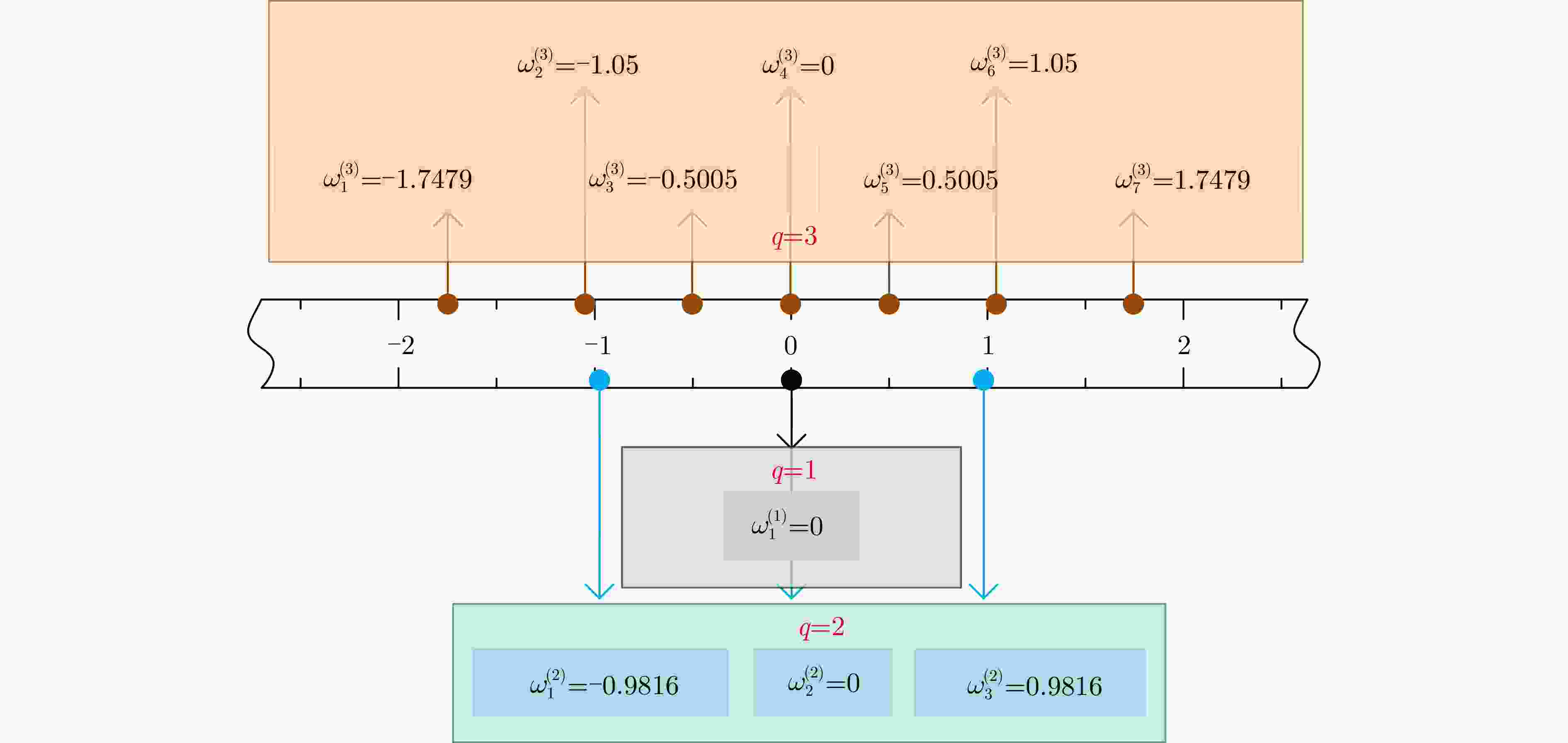
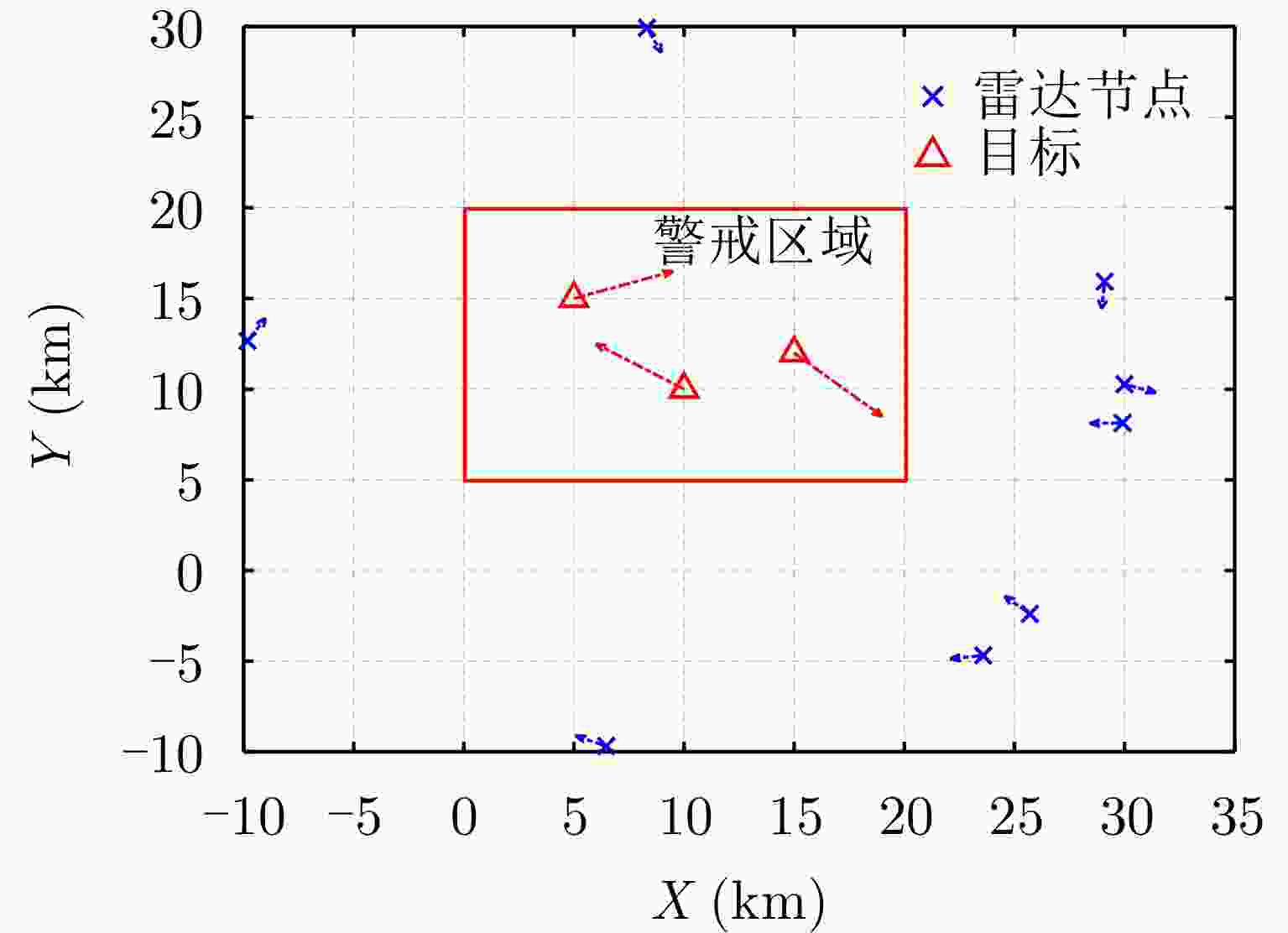
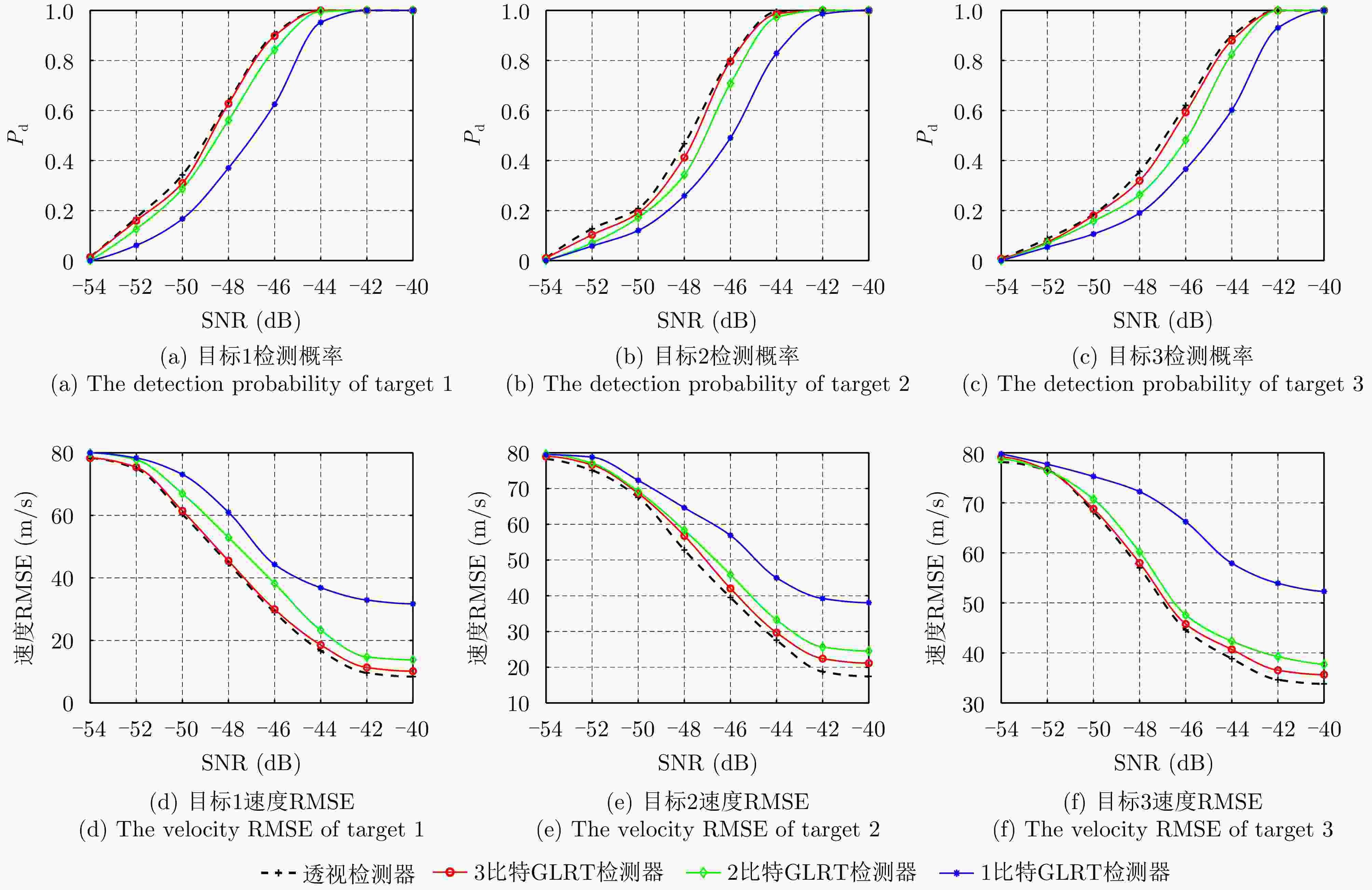
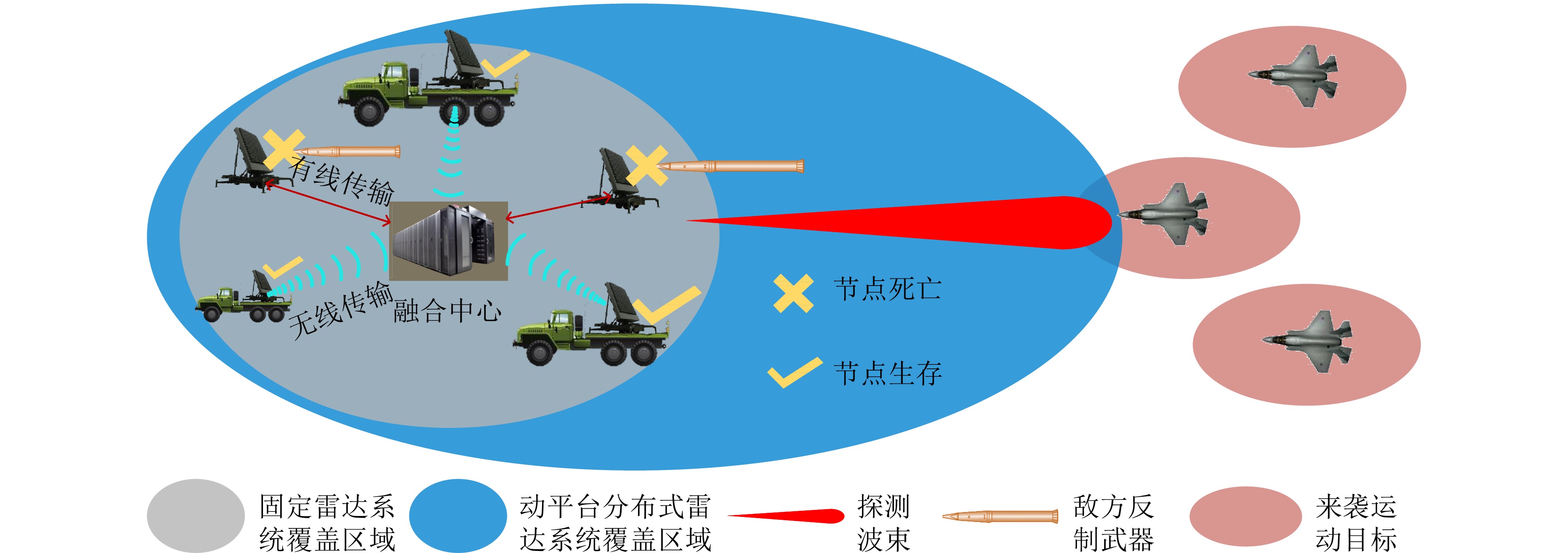
摘要: 动平台分布式雷达系统可有效提升系统的生存能力和探测性能，但运动平台之间通常采用无线传输方式，难以配备大通信带宽以传输完整的信号数据，给雷达系统的高性能检测带来极大挑战。由于低比特量化技术可显著降低分布式系统的通信传输代价和计算资源消耗，该文针对低信噪比弱信号环境下提出了动平台分布式雷达系统的低比特量化运动目标检测算法。首先，根据系统资源将各节点的多脉冲观测数据选择对应位数的低比特量化器进行量化，推导了关于量化器和多个目标状态的似然函数。其次，证明了低比特量化数据对应似然函数关于未知目标反射系数的凸性，并基于该特性设计了多普勒频移和反射系数的联合估计器。然后，针对探测区域中存在的多个状态未知目标设计了多目标检测器，推导了其恒虚警率门限。最后，通过推导系统的渐近性能设计了最优低比特量化器，在保证系统鲁棒性的同时有效提升了系统的检测性能。仿真实验分析了所提算法的检测与估计性能，结果证明了所提算法在低信噪比弱信号环境下的有效性，同时表明低比特量化数据可在仅占用低于20%通信带宽的基础上实现接近高精度(16比特量化)数据对应的检测和估计性能，且2比特量化策略可作为检测性能和雷达系统资源消耗的折中选择。Abstract: Distributed radar with moving platforms can enhance the survivability and detection performance of a system, however, it is difficult to equip these platforms with sufficient communication bandwidth to transmit high-precision observed data, posing a great challenge to the high-performance detection of a distributed radar system. Because low-bit quantization can effectively reduce the computation cost and resource consumption of distributed radar systems, in this paper, we investigate the high-performance detection of multiple moving targets using the distributed radar system on moving platforms by adopting the low-bit quantization strategy. First, according to system resources, multipulse observed data of each node may be quantized with a low-bit quantizer and the likelihood function relative to the quantizer and states of multiple targets are derived. Subsequently, based on the convexity of the likelihood function relative to the unknown reflection coefficients, a joint estimation algorithm is designed for the Doppler shifts and reflection coefficients. Then, a generalized likelihood ratio test based multi-target detector is designed for detecting multiple targets in the surveillance area with unknown states, and deriving the constant false alarm rate detection threshold. Finally, the optimal low-bit quantizer is designed by deriving the asymptotic detection performance of the system, which effectively improves the detection performance and ensures robustness. Simulation experiments are conducted to analyze the detection and estimation performance of the proposed algorithm, thereby demonstrating the effectiveness of the proposed algorithm for weak signals, and showing that the low-bit quantized data can achieve detection and estimation performance close to that of the high-precision (16-bit quantization) data while consuming a complementary 20% of the communication bandwidth. Besides, according to the simulated results, the two-bit quantization strategy may be a trade-off between the detection performance and resource consumption of the distributed radar system.
-
1. 引言
极化SAR图像分类作为极化SAR图像理解与解译的重要研究内容，近年来受到越来越多研究者的关注，并广泛应用到各个领域，如土地覆盖类型判别、地面目标检测、地质勘探、植被种类判别等[1–3]。根据分类方法中标记样本和无标记样本的利用方式，极化SAR地物分类方法主要可以分为3种类型：无监督分类方法[4,5]、监督分类方法[6,7]和半监督分类方法[8,9]。
对于极化SAR图像分类问题，监督分类方法通常比无监督分类更容易获得好的分类结果，但是监督分类方法通常需要充足的标记样本作为训练样本，而实际中标记样本的获取是非常困难，需要耗费大量的人力物力。而无标记数据获取相对容易，并且无标记的数据也能反映数据的某些信息，能够有效地帮助学习分类器。因此，如何利用大量的无标记样本对少量的标记样本进行补充辅助训练的半监督学习方法，引起了研究者的广泛关注，成为了当前研究的热点。近年来，很多半监督分类方法被提出来，如自训练(Self-training)方法[10]、协同训练方法(Co-training和Tri-training)[11,12]、标签传播聚类算法、基于图的半监督分类算法[13,14]和基于半监督的神经网络算法[15–17]等。然而针对极化SAR图像分类问题的半监督方法研究较少，Hansch[18]提出了一种基于聚类算法的半监督极化SAR分类方法，将半监督思想同聚类方法相结合，通过被选择未标记样本对聚类中心进行约束，利用未标记样本的约束影响聚类中心，获得更好的分类结果。为利用极化SAR数据中的空间信息，Liu等人[19]提出了基于邻域约束半监督特征提取的极化SAR图像分类方法。为使半监督训练中选择的未标记样本具有更高的可靠性和多样性，Wang等人[20]提出了基于改进协同训练的半监督极化SAR图像分类方法，通过协同训练的方式选择多样性的样本，通过预选择的方法增加被选择样本的可靠性。此外，结合深度学习方法和半监督学习思想，Geng等人[21]提出了基于超像素约束的深度神经网络半监督极化SAR分类方法。但是这些半监督分类方法都需要一定的标记样本，在标记样本非常少，只有几个标记像素的条件下，很难获得较好的分类结果。因此，本文针对此问题，提出一种基于邻域最小生成树的半监督极化SAR图像分类方法。该方法利用邻域最小生成树方法辅助半监督学习，在自训练的过程中通过邻域最小生成树辅助的方式选择更可靠的无标记样本扩大训练样本集，改善分类器的性能。
自训练学习方法是一种典型的半监督学习方法，该方法利用现有的标记数据训练得到的模型对无标记的样本进行预测，选择可靠性高的样本以及其被赋予的标签加入到标记样本集中，通过不断循环的自训练，逐渐增加训练集中的样本数量并逐步改善分类器性能，该方法的框架图如图1所示。由图1可以看出，自训练方法的关键是选择可靠性的样本，如果选择的样本不正确，使错误的样本加入到训练集中，不仅不能使分类器性能得到改善反而会降低分类器的性能。因此，如何选择高置信度的样本成为自训练算法的关键。而在极化SAR图像分类中，由于只有少量的标记样本，在少量标记样本下训练的分类器是一个弱分类器，直接在弱分类器的结果中选择的样本很难保证其可靠性。如果将错误标记的样本加入到标记样本集中，反而会使分类器的性能下降。因此，为增加被选择样本的可靠性，结合极化SAR图像像素间的空间信息，本文提出了基于邻域最小生成树的样本选择方法，通过邻域最小生成树辅助选择的方法增加被选择样本的可靠性。
因此，本文算法的主要贡献为：(1)针对极化SAR图像分类中标记样本非常少的问题，提出了一种新的基于邻域最小生成树的半监督极化SAR图像分类方法，该方法同时利用未标记样本和标记样本的信息有效地提高分类正确率；(2)为增加自训练过程中被选择样本的可靠性，结合极化SAR图像像素间的空间信息，在最小生成树的基础上针对极化SAR图像分类的特性，提出了基于邻域最小生成树样本选择方法。
2. 极化SAR数据
在极化SAR数据中，每个像素点都可以表示为一个相干矩阵T或协方差矩阵C
[C]=[⟨|SHH|2⟩√2⟨SHHS∗HV⟩⟨SHHS∗VV⟩√2⟨SHVS∗HH⟩2⟨|SHV|2⟩√2⟨SHVS∗VV⟩⟨SVVS∗HH⟩√2⟨SVVS∗HV⟩⟨|SVV|2⟩] (1)
其中，HH表示水平发射水平接收，VV表示垂直发射垂直接收，HV表示水平发射垂直接收。由协方差矩阵C的矩阵表示形式可以看出，协方差矩阵是一个对角线为实数的复共轭对称矩阵，并且由协方差矩阵转换的9维特征向量通常可以作为极化SAR数据特征的一种表示，并在极化图像处理中取得良好的效果[9]，该向量表示为
view=[C11,C22,C33,real(C12),imag(C12),real(C13),imag(C13),real(C23),imag(C23)] (2)
其中，real()表示实部，imag()表示虚部。
图2(a)为美国旧金山地区的极化SAR数据，图2(b)—图2(j)为由该数据的协方差矩阵转化的9维特征向量中每一元素增强10倍的灰度图。由9维特征向量每一元素的灰度图可以看出，每一元素都可以基本描述原始图像的大致信息，并且不同元素的灰度图都不相同，具有一定互补性，因此可以直接做为极化SAR图像的特征信息来描述极化SAR图像。
图 2 极化SAR协方差矩阵中9个元素的灰度值Figure 2. The gray value of 9 elements in PolSAR covariance matrix3. 邻域最小生成树
为增强自训练过程中被选样本的可靠性，在训练过程中逐步优化基分类器，结合极化SAR图像像素间的空间邻域信息，本文提出了基于邻域最小生成树的样本选择方法。
3.1 最小生成树
在图论问题中，对于连通且没有环路的连通图称为树，在一个连通图里删除所有的环路而形成的树叫做该图的生成树，其中具有最小总权重的树，被称为最小生成 (Minimum Spanning Tree, MST)[22]。定义为：在无带权的无向连通图G中，
W(vi,vj) 表示任意两个节点i和j之间边的权重的大小，若无向图G中存在着权重之和最小的生成树，则该树就是无向图G的最小生成树。图3为带权值的连通图G和其最小生成树。由图3(a)可以看出任意两个节点都通过带权重的边相连，对于无向图G来说，可以由不同的节点出发得到不同的生成树模型。图3(b)为由权重最小的边遍历所有节点得到的最小生成树，对于无向图G来说，图3(b)是其唯一的最小生成树。
本文采用Prim算法[23]计算最小生成树，该算法是一种产生最小生成树的算法。该算法从给定的顶点开始，每次选择一个与当前顶点最近的一个点，将该点与顶点之间的边加入到树中。其形式描述如下：
步骤1 输入：在一个加权无向图G中，顶点集合为V，权值边的集合为E；
步骤2 初始化：
Vr={x} ，其中x为初始顶点，Er={} 为空；步骤3 重复下列操作，直到所有的顶点都加入到集合
Vr 中：(1)在集合E中选择权重最小的边[u, v]，其中u为Vr 中的元素，v为集合V 中的元素，且v∉Vr ; (2)将v加入到集合Vr 中，将边[u, v]加入到集合Er 中；步骤4 输出：用集合
Vr 和Er 表示所得到的最小生成树。3.2 基于空间邻域信息的最小生成树
通过对最小生成树算法分析可以看出，最小生成树的生成过程非常符合极化SAR图像的分类过程，极化SAR图像中每一像素点对应生成树中的节点，像素之间的相似性关系类似于生成树中节点间的边的权重，因此最小生成树方法非常适用于极化SAR图像的分类。然而要生成最小生成树，首先要构建无向图G，顶点的集合V和边的集合E，然而对大小为
N×N 的极化SAR图像来说，需要计算N2(N2−1)/2 条边，需要耗费大量的时间。而极化SAR图像分类是对图像中每一个像素点分类，因此根据图像中像素点之间的空间关系，相邻的像素之间具有更高的相似性，提出了基于像素点空间邻域的Prim最小生成树算法，该算法描述如下：步骤1 构建无向图G(V, E)，其中V为顶点(已标记像素点)，用式(3)计算每一顶点于其8邻域边的集合E；
步骤2 选择顶点其8邻域内与其边的权值最小的边，并对与其权值最小的像素点进行标记，然后将其作为标记样本加入到顶点集合V中；
步骤3 重复步骤1—步骤2过程直到选择完整幅图像中所有的像素点。
该方法中需要计算各个顶点之间边的距离，由于极化SAR数据服从复Wishart分布，因此在极化SAR图像中，两个像素点之间的相似距离通常采用Wishart距离[24]表示
wi,j=12Tr((Ti)−1Tj+(Tj)−1Ti)−q (3) 其中，
Tr(⋅) 表示矩阵的迹，Ti 和Tj 分别表示像素点i 和j 的相干矩阵，对于发射与接收是一体的雷达，由于其互易性，则q=3 ，对于发射和接收不是一体的雷达，q=4 。图4为该算法的生成过程，图中绿色的矩形表示初始的顶点，灰色的矩形表示其邻域的顶点，矩形中的数字表示中心像素点与邻域像素点的距离，距离越小越相似。第1次学习过程，选择初始顶点邻域边最小的顶点，距离为‘1’的点，如图4(b)所示，然后再在新的顶点集合的邻域内选择边最小的顶点，如图4(c)所示，添加到以初始顶点为根的树的集合中，依次循环，直到选择完所有的顶点为止。
图 4 基于邻域的最小生成树生成过程Figure 4. The spanning process of neighborhood minimum spanning tree4. 本文所提方法
本文针对极化SAR图像分类中只有少量标记样本的问题，为在少量标记样本的条件下获得较高的分类正确率，在传统自训练方法的基础上提出了基于邻域最小生成树的半监督极化SAR图像分类方法。该方法的核心是在自训练的过程中由大量的无标记样本中选择可靠的样本，将其添加到标记样本中，扩大标记样本的数量，逐渐优化分类器性能，最终实现提高分类正确率的目的。为此，结合最小生成树方法和极化SAR图像中像素点的空间信息，提出了基于邻域最小生成的样本选择方法，增加被选择样本的可靠性。本文所提方法的整个框架图如图5所示，具体步骤如下：
图 5 基于邻域最小生成树的半监督极化SAR分类方法Figure 5. Semi-supervised PolSAR classification based on the neighborhood minimum spanning tree步骤1 为降低斑点噪声对极化SAR数据的影响，采用精致Lee滤波[25]对极化SAR数据滤波，滤波窗口大小为
7×7 。步骤2 以初始的标记像素点为初始顶点，构建无向图G，生成多个邻域最小生成树，每一个树中的像素点具有相同的标记；
步骤3 利用初始的标记样本点，以view为每一个像素点的特征信息训练SVM分类器，并用训练好的SVM分类器对邻域最小生成树标记的样本进行测试；
步骤4 挑选由分类器测试得到的结果中与邻域最小生成树生成的结果中标记一致的样本，添加到初始的标记样本集中，更新标记样本集；
步骤5 重复步骤2到步骤4过程t次，直到得到满意的分类器；
步骤6 用训练好的分类器对剩余样本进行测试。
5. 实验结果与分析
本文采用3组真实的极化SAR数据：(1)荷兰Flevoland 地区1989年8月由L波段的NASA/JPI AIRSAR 获得，该数据包含有
750×1024 个像素点，空间分辨率为6 m× 12.1 m，主要包含15类农作物，如图6所示；(2)荷兰地区2008年4月由C波段的Radarsat-2获取的极化SAR数据，该数据主要包含1400×1200 个像素点，空间分辨率为12 m× 8 m，主要包含城市、水域、深林和农田4种类别，如图7所示；(3)美国旧金山地区2008年由C波段的Radarsat-2获取的极化SAR数据，该数据主要包含1300×1300 个像素点，空间分辨率为12 m× 8 m，主要包含高密度城市、低密度城区、水域、植被和开发区域5种类别，如图8所示。
图 6 Flevoland地区AIRSAR L波段数据不同方法的分类结果Figure 6. Classification results of the Flevoland data acquired by AIRSAR
图 7 Flevoland地区Radarsat-2 C波段数据不同方法的分类结果Figure 7. Classification result of the Flevoland data acquired by Radarsat-2
图 8 旧金山地区Radarsat-2 C波段数据不同方法的分类结果Figure 8. Classification result of the San Francisco data acquired by Radarsat-2本文以SVM为基本分类器，采用径向基核函数和5倍的交叉验证，为了验证本文算法的有效性，将本文方法与传统的基于自训练的半监督方法(Self-training)[10]、基于SVM分类器的监督分类方法(采用径向基核函数和5倍的交叉验证)[26]和监督Wishart方法[27]进行比较，并用总分类正确率和Kappa系数对实验结果进行评估，所有的实验进行10次，用平均值表示最终的分类结果。
5.1 AIRSAR L波段荷兰地区的图像分类
本实验中每类别选择不同数量的标记样本(10, 8, 6, 4)作为训练样本。图6(a)为Pauli分解的RGB图，图6(a1)为真实地物。实验结果如图6，表1和表2所示。图6(b)为本文方法的分类结果，图6(c)为传统Self-training算法的分类结果，图6(d)为监督Wishart方法的分类结果，图6(e)为SVM方法的分类结果。 表1为每类训练样本数量为10时不同方法的分类正确率。
表 1 AIRSAR L波段的Felvoland地区不同分类算法的分类精度(%)Table 1. Classification accuracy of the Flevoland area acquired by AIRSAR L band (%)区域 方法 Wishart SVM Self-training 本文方法 Stembeans 91.48 70.07 90.82 98.75 Rapeseed 61.83 38.02 67.14 59.58 Bare soil 97.51 86.89 70.97 96.75 Potatoes 79.47 58.38 80.27 81.99 Beet 92.35 85.61 95.05 94.60 Wheat 2 67.43 71.80 67.39 89.86 Peas 93.10 77.70 95.24 97.56 Wheat 3 82.08 82.42 94.33 97.05 Lucerne 84.53 40.77 81.67 95.06 Barley 81.96 98.29 98.62 98.39 Wheat 81.46 68.28 85.34 85.41 Grasses 66.49 65.03 81.75 80.08 Forest 84.21 61.03 77.66 94.77 Water 46.85 65.32 69.39 93.35 Building 81.77 78.91 2.18 85.58 OA 79.40 70.30 77.19 89.92 表 2 AIRSAR L波段的Felvoland 地区不同训练样本的分类结果Table 2. Classification results of the Flevoland area acquired by AIRSAR L band with different number of training samples方法 训练样本数 4 6 8 10 OA (%) Kappa OA (%) Kappa OA (%) Kappa OA (%) Kappa Wishart 74.62 0.7215 76.19 0.7459 78.78 0.7656 80.26 0.7831 SVM 56.07 0.5423 58.12 0.5611 64.42 0.6102 70.30 0.6682 Self-training 63.36 0.6025 68.42 0.6569 73.89 0.7146 77.23 0.7489 本文方法 79.33 0.7888 83.06 0.8093 86.90 0.8416 89.92 0.8852 由表1可以看出，本文分类方法的分类正确率为89.92%，高于Self-training分类方法12.73%，高于SVM分类方法19.62%，高于监督Wishart方法10.52%，而且本文方法中大部分类别的分类正确率都高于其它的对比方法。这主要是因为本文所提出半监督分类算法能够有效地利用标记样本和无标记样本的信息，并采用邻域最小生成树的策略辅助选择高可靠性的样本，改善了基分类器的性能。但是本文方法在Rapeseed的分类正确率只有59.58%，低于Self-training方法7.56%。由图6(b)可以看出，在本文方法中一部分Rapeseed被分为了Wheat 2和Wheat 3，这主要是这几种农作物的叶子形状非常相近，很难区别。对比图6(c)可以看出，在Self-training方法中一部分Wheat 2和Wheat 3被错分为Rapeseed，因此虽然在Self-training方法中Rapeseed的分类正确率高，但是Wheat 2和Wheat 3分类正确率要低于本文方法的分类结果。此外本文方法在Bare soil区域的分类正确率虽然低于Wishart方法的分类正确率，但是分类正确率也已经大于96%。而且由图6(d)可以看出，Wishart方法将很大一部分Water区域错划分为Bare soil区域，使Water区域的分类正确率只有46.85%，远低于本文方法在该区域的分类正确率93.35%。由表2可以看出不同标记样本时本文方法的分类正确率都要高于对比方法的分类结果；本文方法的Kappa系数也高于对比方法的Kappa系数，而且通过对比图6中本文方法和对比方法的分类结果表示，也可以看出本文方法的分类结果的区域一致性也比其它的对比方法好。
5.2 Radarsat-2 C波段荷兰地区的图像分类
本实验中分别选择每类别为不同数量的标记样本(10, 8, 6, 4)作为训练样本。图7(a)为Pauli分解的RGB图，图7(a1)为真实地物。实验结果如图7，表3和表4所示。图7(b)为本文算法的分类结果，图7(c)为Self-training方法的分类结果，图7(d)为监督Wishart方法的分类结果，图7(e)为SVM方法的分类结果。 表3为每类选10个标记样本时，不同方法的分类正确率。
表 3 Radarsat-2 C波段的Felvoland地区不同分类算法的分类精度(%)Table 3. Classification accuracy of the Flevoland area acquired by Radarsat-2 C band (%)区域 方法 Wishart SVM Self-training 本文方法 Urban 69.61 54.75 63.93 71.44 Water 98.71 96.83 99.10 98.82 Forest 91.65 65.25 73.83 83.63 Cropland 55.27 78.97 79.23 82.24 OA 78.81 73.95 79.02 84.03 表 4 Radarsat-2 C波段的Felvoland 地区不同训练样本的分类结果Table 4. Classification results of the Flevoland area acquired by Radarsat-2 C band with different number of training samples方法 训练样本数 4 6 8 10 OA (%) Kappa OA (%) Kappa OA (%) Kappa OA (%) Kappa Wishart 69.21 0.5803 73.65 0.6239 76.81 0.6854 78.81 0.7026 SVM 50.79 0.4153 64.79 0.5471 70.05 0.5968 73.95 0.6394 Self-training 65.69 0.5233 70.41 0.5911 74.40 0.6605 79.45 0.7144 本文方法 76.71 0.6768 79.29 0.7235 82.02 0.7644 84.03 0.7882 由表3和表4可以看出，本文方法的分类结果明显高于传统的Self-training方法，SVM方法和Wishart分类方法。由表4可以看出当每类训练样本数量10时，本文分类方法的分类正确率为84.03%，高于Self-training分类方法4.58%，高于SVM分类方法10.08%，高于监督Wishart方法5.22%。由表3可以看出本文方法在Urban和Cropland区域的分类正确率都要高于对比方法，但是在Forest区域的分类正确率低于监督Wishart方法的分类正确率。由图7(d)可以看出，这主要是因为Wishart方法中一部分Cropland区域被分为了Forest类，虽然Wishart方法的Water区域分类正确率高，但是Cropland区域的分类正确率只有55.27%，明显低于本文所提方法，而且本文方法Forest和Cropland区域总的分类正确率也要高于Wishart方法。而由表4可以看出选择不同数量的标记样本时，本文方法的分类正确率都要高于对比方法；同时本文方法的Kappa系数也高于对比方法的Kappa系数，而且通过对比图7中本文方法和对比方法的分类结果图，也可以看出本文方法的分类结果的区域一致性也比其它的对比方法要好。因此可以得出相同的结论，本文所提方法要明显优于传统的分类方法，尤其是在标记样本较少的情况下。
5.3 Radarsat-2 C波段美国旧金山地区的图像分类
本实验分别选择每类别为不同数量的标记样本(10, 8, 6, 4)作为训练样本。图8(a)为Pauli分解的RGB图，图8(a1)为真实地物。实验结果如图8，表5和表6所示。图8(b)为本文方法的分类结果，图8(c)为Self-training方法的分类结果，图8(d)为监督Wishart方法的分类结果，图8(e)为SVM方法的分类结果。表5为每类选10个标记样本时，不同方法的分类正确率。
表 5 Radarsat-2 C波段的旧金山地区不同分类算法的分类结果(%)Table 5. Classification accuracy of the San Francisco area acquired by radarsat-2 C Band (%)区域 方法 Wishart SVM Self-training 本文方法 Water 98.70 90.04 98.04 99.92 Vegetation 91.03 78.51 84.45 91.50 Low-Density Urban 81.30 42.31 70.18 75.05 High-Density Urban 42.58 77.15 33.01 68.27 Developed 55.26 24.00 56.16 58.81 OA 73.77 62.40 68.37 78.71 表 6 Radarsat-2 C波段的旧金山地区不同训练样本的分类结果Table 6. Classification results of the San Francisco area acquired by Radarsat-2 C band with different number of training samples方法 训练样本数 4 6 8 10 OA (%) Kappa OA (%) Kappa OA (%) Kappa OA (%) Kappa Wishart 68.09 0.5181 70.44 0.5439 72.49 0.5867 73.77 0.6011 SVM 50.24 0.2817 51.25 0.2905 56.31 0.3628 62.40 0.4342 Self-training 52.34 0.3126 58.62 0.3669 63.27 0.4357 68.42 0.5308 本文方法 70.87 0.5482 73.15 0.5986 75.23 0.6284 78.71 0.6852 由表5和表6可以看出，本文方法的分类结果明显高于传统的Self-training方法，SVM方法和Wishart分类方法。由表6可以看出当每类训练样本数量10时，本文分类方法的分类正确率为78.71%，高于Self-training分类方法10.29%，高于SVM分类方法16.31%，高于监督Wishart方法4.94%。由表5可以看出本文方法在大部分区域的分类正确率都要高于对比方法，但是在Low-Density Urban区域的分类正确率低于监督Wishart方法的分类正确率。由图8(d)可以看出，这主要是因为Wishart方法中Low-Density Urban区域和High-Density Urban区域没有被有效地区分开，一部分的High-Density Urban区域被错分为Low-Density Urban，导致虽然Wishart方法的Low-Density Urban区域分类正确率高，但是High-Density Urban区域的分类正确率只有42.58%，明显低于本文所提方法，而且在本文方法中这两个区域总的分类正确率也要高于Wishart方法。而由表6可以看出当标记样本数量不同时，本文方法的分类正确率都要高于对比方法；对比本文方法的Kappa系数和对比方法的Kappa系数，可以发现本文方法的Kappa系数要明显高于对比方法的，而且通过对比图8中本文方法和对比方法的分类结果图，也可以看出本文方法的分类结果的区域一致性也比其它的对比方法要好。因此我们可以得出相同的结论，本文所提方法要明显优于传统的分类方法，尤其是在标记样本较少的情况下。
5.4 自训练次数对本文方法的影响
前面的实验已经验证了本文方法的有效性，本节分析迭代次数(自训练次数)对实验结果的影响。图9(a)为迭代次数对分类正确率的影响，由图9(a)可以看出随着迭代次数的增加分类正确率逐渐增加，当迭代次数大于8次的时候分类正确率的增长逐渐减小趋于平滑。图9(b)为迭代次数所消耗的时间成本，由图9(b)可以看出随着迭代次数的增加所耗费的时间迅速增加，这主要是因为随着迭代次数的增加，标记样本数量增加，最小生成树的种子点数量增加，最小生成树所需要的时间增加，自训练分类器的时间也增加。
6. 结论
本文提出了一种基于邻域最小生成树的半监督极化SAR图像分类方法。该方法能够有效地利用标记样本和无标记样本，通过邻域最小生成树辅助学习的方式选择高可靠性的样本，添加到标记样本集中，通过自训练的方式不断扩大标记样本集，优化分类器，使在只有少量标记样本时能够获得较高的分类正确率。并对3组真实极化SAR数据进行测试，实验结果表明本文方法能够获得满意的分类结果，尤其是在标记样本非常少的情况下。而且通过选择不同比例的训练样本实验表明相较于传统的方法本文方法获得的分类精度更高。此外，通过分析迭代次数对实验结果的影响实验表明，本文方法选择的无标记样本是可靠的，通过添加被选择的无标记样本扩大标记样本集逐渐改善分类器的性能。
-
图 1 动平台分布式雷达系统相较于传统固定节点的性能得益示意
Figure 1. Illustration of the performance benefits of a distributed radar system adopting moving platforms compared to the fixed nodes
图 2 分布式雷达系统低比特量化示意图
Figure 2. Schematic of low-bit quantization for distributed radar systems
图 4 1比特、2比特和3比特量化器对应的最优量化门限
Figure 4. Optimal quantization levels for the 1-bit, 2-bit and 3-bit quantizers
图 5 仿真场景示意(箭头表征雷达节点或者目标运动速度)
Figure 5. An illustration of the simulation scenario (arrows represent the velocities of nodes or targets)
图 7 不同量化位数对应各栅格的检测统计量
Figure 7. The test statistic for each grid cell with different quantization bits
图 8 不同量化位数对应的系统性能
Figure 8. System performance corresponding to different quantization bits
图 10 系统针对不同反射强度目标的检测和估计性能
Figure 10. Detection and estimation performance of the system for the targets with different power
1 基于BGDA的联合估计器设计
1. BGDA-based joint estimator design
输入：量化数据˜Y(q)l，初始状态˜αlG(0)=[˜αRlG,˜αIlG]T，学习率βl，容忍精度ηl。 输出：第l个通道的检测统计量ΛlG(˜Y(q)l)，未知参数的估计(ˆfdl,ˆαlG)。 for ˜fdl∈[fmin 初始赋值：{\widetilde {\boldsymbol{\alpha }}_{l\mathcal{G}}}\left( {\widetilde f_l^{\text{d}}} \right) \leftarrow {\widetilde {\boldsymbol{\alpha }}_{l\mathcal{G}}}\left( 0 \right) while {\left\| {\nabla {{\widetilde \ell }_1}\left( {\widetilde {\boldsymbol{Y}}_l^{\left( q \right)};\widetilde f_l^{\text{d}},{{\widetilde {\boldsymbol{\alpha }}}_{l\mathcal{G}}}\left( {\widetilde f_l^{\text{d}}} \right)} \right)} \right\|_2} > {\eta _l} {\widetilde {\boldsymbol{\alpha }}_{l\mathcal{G}}}\left( {\widetilde f_l^{\text{d}}} \right) \leftarrow {\widetilde {\boldsymbol{\alpha }}_{l\mathcal{G}}}\left( {\widetilde f_l^{\text{d}}} \right) + \beta _l^{\rm T} \nabla {\widetilde \ell _1}\left( {\widetilde {\boldsymbol{Y}}_l^{\left( q \right)};\widetilde f_l^{\text{d}},{{\widetilde {\boldsymbol{\alpha }}}_{l\mathcal{G}}}\left( {\widetilde f_l^{\text{d}}} \right)} \right) end {\varLambda _{l\mathcal{G}}}\left( {\widetilde {\boldsymbol{Y}}_l^{\left( q \right)};\widetilde f_l^{\text{d}},{{\widetilde {\boldsymbol{\alpha }}}_{l\mathcal{G}}}\left( {\widetilde f_l^{\text{d}}} \right)} \right) = {\widetilde \ell _1}\left( {\widetilde {\boldsymbol{Y}}_l^{\left( q \right)};\widetilde f_l^{\text{d}},{{\widetilde {\boldsymbol{\alpha }}}_{l\mathcal{G}}}\left( {\widetilde f_l^{\text{d}}} \right)} \right) end \left\{ \begin{gathered} \left( {\hat f_l^{\text{d}},{{\hat {\boldsymbol{\alpha}} }_{l\mathcal{G}}}} \right) = \mathop {\arg \max }\limits_{\left\{ {\widetilde f_l^{\text{d}},{{\widetilde {\boldsymbol{\alpha }}}_{l\mathcal{G}}}\left( {\widetilde f_l^{\text{d}}} \right)} \right\}} \left\{ {{\varLambda _{l\mathcal{G}}}\left( {\widetilde {\boldsymbol{Y}}_l^{\left( q \right)};\widetilde f_l^{\text{d}},{{\widetilde {\boldsymbol{\alpha }}}_{l\mathcal{G}}}\left( {\widetilde f_l^{\text{d}}} \right)} \right)} \right\} \\ {\varLambda _{l\mathcal{G}}}\left( {{{\boldsymbol{Y}}_l}} \right) = \max \left\{ {{\varLambda _{l\mathcal{G}}}\left( {\widetilde {\boldsymbol{Y}}_l^{\left( q \right)};\widetilde f_l^{\text{d}},{{\widetilde {\boldsymbol{\alpha }}}_{l\mathcal{G}}}\left( {\widetilde f_l^{\text{d}}} \right)} \right)} \right\} \\ \end{gathered} \right. 
下载: 导出CSV
-
[1] VISWANATHAN R and VARSHNEY P K. Distributed detection with multiple sensors Part I. Fundamentals[J]. Proceedings of the IEEE, 1997, 85(1): 54–63. doi: 10.1109/5.554208. [2] CHONG C Y and KUMAR S P. Sensor networks: Evolution, opportunities, and challenges[J]. Proceedings of the IEEE, 2003, 91(8): 1247–1256. doi: 10.1109/JPROC.2003.814918. [3] REIBMAN A R and NOLTE L W. Optimal detection and performance of distributed sensor systems[J]. IEEE Transactions on Aerospace and Electronic Systems, 1987, AES-23(1): 24–30. doi: 10.1109/TAES.1987.313355. [4] CHAKRABARTY K, IYENGAR S S, QI Hairong, et al. Grid coverage for surveillance and target location in distributed sensor networks[J]. IEEE Transactions on Computers, 2002, 51(12): 1448–1453. doi: 10.1109/TC.2002.1146711. [5] KAPLAN L M. Global node selection for localization in a distributed sensor network[J]. IEEE Transactions on Aerospace and Electronic Systems, 2006, 42(1): 113–135. doi: 10.1109/TAES.2006.1603409. [6] ZHOU Shidong, ZHAO Ming, XU Xibin, et al. Distributed wireless communication system: A new architecture for future public wireless access[J]. IEEE Communications Magazine, 2003, 41(3): 108–113. doi: 10.1109/MCOM.2003.1186553. [7] SHI Qingjiang, HE Chen, CHEN Hongyang, et al. Distributed wireless sensor network localization via sequential greedy optimization algorithm[J]. IEEE Transactions on Signal Processing, 2010, 58(6): 3328–3340. doi: 10.1109/TSP.2010.2045416. [8] 时晨光, 唐志诚, 周建江, 等. 非理想检测下多雷达网络节点选择与辐射资源联合优化分配算法[J]. 雷达学报, 2024, 13(3): 565–583. doi: 10.12000/JR23081.SHI Chenguang, TANG Zhicheng, ZHOU Jianjiang, et al. Joint collaborative radar selection and transmit resource allocation in multiple distributed radar networks with imperfect detection performance[J]. Journal of Radars, 2024, 13(3): 565–583. doi: 10.12000/JR23081. [9] 易伟, 袁野, 刘光宏, 等. 多雷达协同探测技术研究进展: 认知跟踪与资源调度算法[J]. 雷达学报, 2023, 12(3): 471–499. doi: 10.12000/JR23036.YI Wei, YUAN Ye, LIU Guanghong, et al. Recent advances in multi-radar collaborative surveillance: Cognitive tracking and resource scheduling algorithms[J]. Journal of Radars, 2023, 12(3): 471–499. doi: 10.12000/JR23036. [10] FISHLER E, HAIMOVICH A, BLUM R S, et al. Spatial diversity in radars-models and detection performance[J]. IEEE Transactions on Signal Processing, 2006, 54(3): 823–838. doi: 10.1109/TSP.2005.862813. [11] HAIMOVICH A M, BLUM R S, and CIMINI L J. MIMO radar with widely separated antennas[J]. IEEE Signal Processing Magazine, 2008, 25(1): 116–129. doi: 10.1109/MSP.2008.4408448. [12] 闵涛, 王象, 肖顺平. 基于复数指示角差异的多基地雷达密集多目标存在性检测[J]. 雷达学报, 2014, 3(4): 456–464. doi: 10.3724/SP.J.1300.2014.13116.MIN Tao, WANG Xiang, and XIAO Shunping. Detection of multiple unresolved targets based on complex indicated angle difference using multistatic radar[J]. Journal of Radars, 2014, 3(4): 456–464. doi: 10.3724/SP.J.1300.2014.13116. [13] ZHANG Shiyu, ZHOU Yu, SHA Minghui, et al. Moving multitarget detection using a multisite radar system with widely separated stations[J]. Remote Sensing, 2022, 14(11): 2660. doi: 10.3390/rs14112660. [14] LI Hongbin, WANG Zhe, LIU Jun, et al. Moving target detection in distributed MIMO radar on moving platforms[J]. IEEE Journal of Selected Topics in Signal Processing, 2015, 9(8): 1524–1535. doi: 10.1109/JSTSP.2015.2467355. [15] 严俊坤, 白舸, 黄佳沁, 等. 多机雷达协同区域动态覆盖航迹优化方法[J]. 雷达学报, 2023, 12(3): 541–549. doi: 10.12000/JR22196.YAN Junkun, BAI Ge, HUANG Jiaqin, et al. Flight path optimization method for dynamic area coverage based on multi-aircraft radars[J]. Journal of Radars, 2023, 12(3): 541–549. doi: 10.12000/JR22196. [16] CHEN Peng, ZHENG Le, WANG Xiaodong, et al. Moving target detection using colocated MIMO radar on multiple distributed moving platforms[J]. IEEE Transactions on Signal Processing, 2017, 65(17): 4670–4683. doi: 10.1109/TSP.2017.2714999. [17] 邢孟道, 林浩, 陈溅来, 等. 多平台合成孔径雷达成像算法综述[J]. 雷达学报, 2019, 8(6): 732–757. doi: 10.12000/JR19102.XING Mengdao, LIN Hao, CHEN Jianlai, et al. A review of imaging algorithms in multi-platform-borne synthetic aperture radar[J]. Journal of Radars, 2019, 8(6): 732–757. doi: 10.12000/JR19102. [18] HE Shaoming, SHIN H S, XU Shuoyuan, et al. Distributed estimation over a low-cost sensor network: A review of state-of-the-art[J]. Information Fusion, 2020, 54: 21–43. doi: 10.1016/j.inffus.2019.06.026. [19] RIBEIRO A and GIANNAKIS G B. Bandwidth-constrained distributed estimation for wireless sensor networks-part I: Gaussian case[J]. IEEE Transactions on Signal Processing, 2006, 54(3): 1131–1143. doi: 10.1109/TSP.2005.863009. [20] CIUONZO D, JAVADI S H, MOHAMMADI A, et al. Bandwidth-constrained decentralized detection of an unknown vector signal via multisensor fusion[J]. IEEE Transactions on Signal and Information Processing over Networks, 2020, 6: 744–758. doi: 10.1109/TSIPN.2020.3037832. [21] 张国鑫, 易伟, 孔令讲. 基于1比特量化的大规模MIMO雷达系统直接定位算法[J]. 雷达学报, 2021, 10(6): 970–981. doi: 10.12000/JR21062.ZHANG Guoxin, YI Wei, and KONG Lingjiang. Direct position determination for massive MIMO system with one-bit quantization[J]. Journal of Radars, 2021, 10(6): 970–981. doi: 10.12000/JR21062. [22] FANG Jun, LIU Yumeng, LI Hongbin, et al. One-bit quantizer design for multisensor GLRT fusion[J]. IEEE Signal Processing Letters, 2013, 20(3): 257–260. doi: 10.1109/LSP.2013.2243144. [23] RIBEIRO A and GIANNAKIS G B. Bandwidth-constrained distributed estimation for wireless sensor networks-part II: Unknown probability density function[J]. IEEE Transactions on Signal Processing, 2006, 54(7): 2784–2796. doi: 10.1109/TSP.2006.874366. [24] CIUONZO D, ROSSI P S, and WILLETT P. Generalized Rao test for decentralized detection of an uncooperative target[J]. IEEE Signal Processing Letters, 2017, 24(5): 678–682. doi: 10.1109/LSP.2017.2686377. [25] 万环, 余显祥, 全智, 等. 基于交替方向惩罚法的低精度量化MIMO雷达恒模波形设计方法[J]. 雷达学报, 2022, 11(4): 557–569. doi: 10.12000/JR22072.WAN Huan, YU Xianxiang, QUAN Zhi, et al. Constant modulus waveform design for low-resolution quantization MIMO radar based on an alternating direction penalty method[J]. Journal of Radars, 2022, 11(4): 557–569. doi: 10.12000/JR22072. [26] 赵博, 黄磊, 周汉飞, 等. 基于单频时变阈值的1-bit SAR成像方法研究[J]. 雷达学报, 2018, 7(4): 446–454. doi: 10.12000/JR18036.ZHAO Bo, HUANG Lei, ZHOU Hanfei, et al. 1-bit SAR imaging method based on single-frequency time-varying threshold[J]. Journal of Radars, 2018, 7(4): 446–454. doi: 10.12000/JR18036. [27] PAPADOPOULOS H C, WORNELL G W, and OPPENHEIM A V. Sequential signal encoding from noisy measurements using quantizers with dynamic bias control[J]. IEEE Transactions on Information Theory, 2001, 47(3): 978–1002. doi: 10.1109/18.915654. [28] STOICA P, SHANG Xiaolei, and CHENG Yuanbo. The Cramér-Rao bound for signal parameter estimation from quantized data [lecture notes][J]. IEEE Signal Processing Magazine, 2022, 39(1): 118–125. doi: 10.1109/MSP.2021.3116532. [29] GAO Fei, GUO Lili, LI Hongbin, et al. Quantizer design for distributed GLRT detection of weak signal in wireless sensor networks[J]. IEEE Transactions on Wireless Communications, 2015, 14(14): 2032–2042. doi: 10.1109/TWC.2014.2379279. [30] WANG Xueqian, LI Gang, and VARSHNEY P K. Detection of sparse stochastic signals with quantized measurements in sensor networks[J]. IEEE Transactions on Signal Processing, 2019, 67(8): 2210–2220. doi: 10.1109/TSP.2019.2903034. [31] WANG Xueqian, LI Gang, QUAN Chen, et al. Distributed detection of sparse stochastic signals with quantized measurements: The generalized Gaussian case[J]. IEEE Transactions on Signal Processing, 2019, 67(18): 4886–4898. doi: 10.1109/TSP.2019.2932884. [32] CHENG Xu, CIUONZO D, ROSSI P S, et al. Multi-bit & sequential decentralized detection of a noncooperative moving target through a generalized Rao test[J]. IEEE Transactions on Signal and Information Processing over Networks, 2021, 7: 740–753. doi: 10.1109/TSIPN.2021.3126930. [33] AMERI A, BOSE A, LI Jian, et al. One-bit radar processing with time-varying sampling thresholds[J]. IEEE Transactions on Signal Processing, 2019, 67(20): 5297–5308. doi: 10.1109/TSP.2019.2939086. [34] CHENG Ziyang, HE Zishu, and LIAO Bin. Target detection performance of collocated MIMO radar with one-bit ADCs[J]. IEEE Signal Processing Letters, 2019, 26(12): 1832–1836. doi: 10.1109/LSP.2019.2951496. [35] XIAO Yuhang, RAMÍREZ D, SCHREIER P J, et al. One-bit target detection in collocated MIMO radar and performance degradation analysis[J]. IEEE Transactions on Vehicular Technology, 2022, 71(9): 9363–9374. doi: 10.1109/TVT.2022.3178285. [36] WANG Zhen, HE Qian, and BLUM R S. Target detection using quantized cloud MIMO radar measurements[J]. IEEE Transactions on Signal Processing, 2022, 70: 1–16. doi: 10.1109/TSP.2021.3129364. [37] RICHARDS M A. Fundamentals of Radar Signal Processing[M]. 2nd ed. New York: McGraw-Hill Education, 2014. [38] XU Luzhou, LI Jian, and STOICA P. Target detection and parameter estimation for MIMO radar systems[J]. IEEE Transactions on Aerospace and Electronic Systems, 2008, 44(3): 927–939. doi: 10.1109/TAES.2008.4655353. [39] KAY S and ZHU Zhenghan. The complex parameter Rao test[J]. IEEE Trans. Signal Process, 2016, 64(24): 6580–6588. doi: 10.1109/TSP.2016.2613071. [40] YANG Shixing, YI Wei, JAKOBSSON A, et al. Weak signal detection with low-bit quantization in colocated MIMO radar[J]. IEEE Transactions on Signal Processing, 2023, 71: 447–460. doi: 10.1109/TSP.2023.3246233. [41] YANG Shixing, YI Wei, and JAKOBSSON A. Multitarget detection strategy for distributed MIMO radar with widely separated antennas[J]. IEEE Transactions on Geoscience and Remote Sensing, 2022, 60: 5113516. doi: 10.1109/TGRS.2022.3175046. [42] CHAO Shuyuan, CHEN Baixiao, and LI Caicai. Grid cell based detection strategy for MIMO radar with widely separated subarrays[J]. AEU - International Journal of Electronics and Communications, 2012, 66(9): 741–751. doi: 10.1016/j.aeue.2012.01.006. [43] YANG Shixing, LAI Yangming, JAKOBSSON A, et al. Hybrid quantized signal detection with a bandwidth-constrained distributed radar system[J]. IEEE Transactions on Aerospace and Electronic Systems, 2023, 59(6): 7835–7850. doi: 10.1109/TAES.2023.3296344. [44] WERNER K and JANSSON M. DOA estimation and detection in colored noise using additional noise-only data[J]. IEEE Transactions on Signal Processing, 2007, 55(11): 5309–5322. doi: 10.1109/TSP.2007.898758. [45] HE Qian, LEHMANN N H, BLUM R S, et al. MIMO radar moving target detection in homogeneous clutter[J]. IEEE Transactions on Aerospace and Electronic Systems, 2010, 46(3): 1290–1301. doi: 10.1109/TAES.2010.5545189. -
下载:
计量
- 文章访问数: 699
- HTML全文浏览量: 118
- PDF下载量: 322
- 被引次数: 0
