Target Parameter and Time-frequency Bias Estimation Method Based on Multitemporal Measurement Data for Distributed MIMO Radar
-
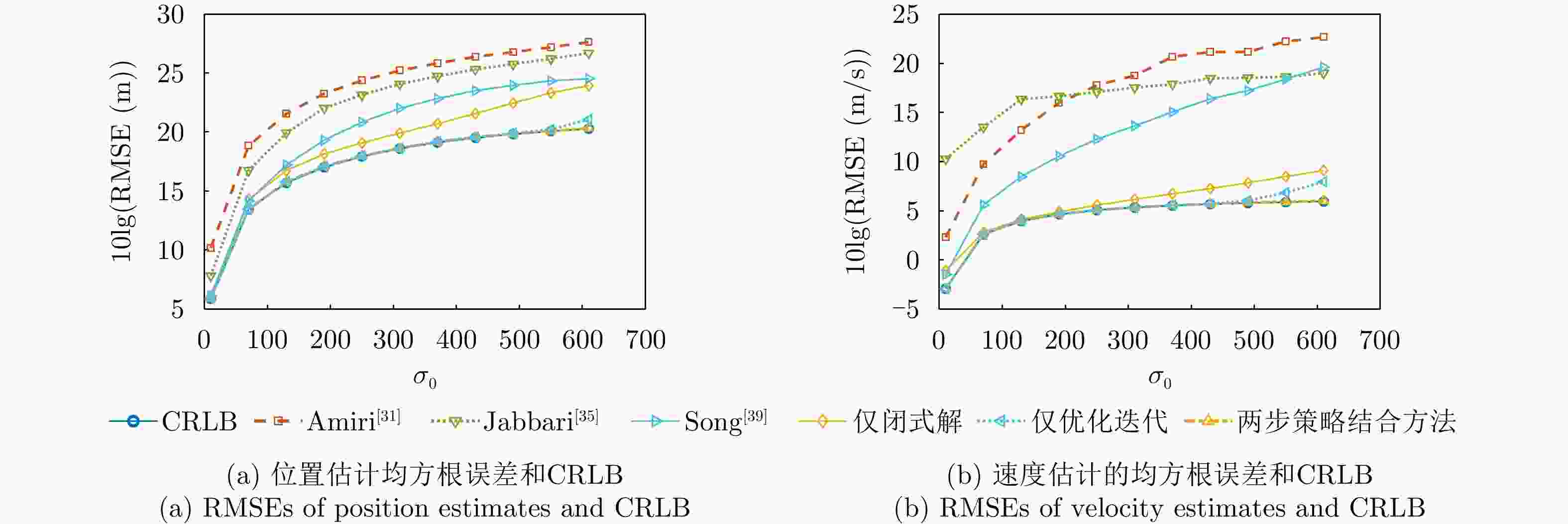
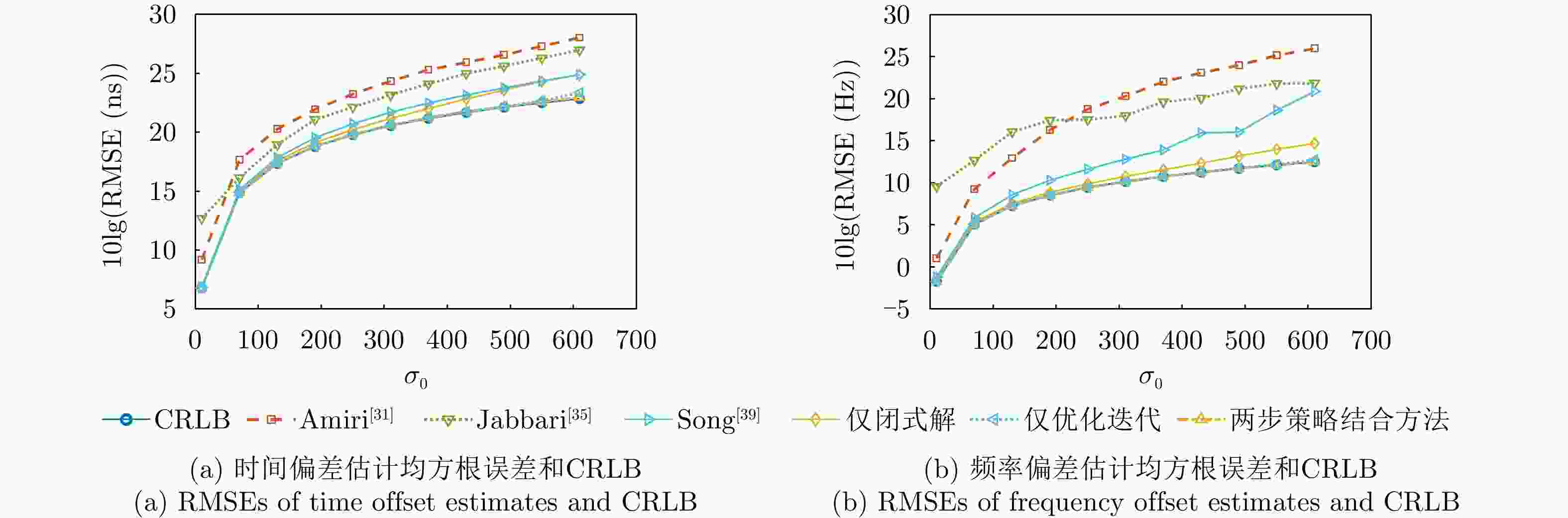
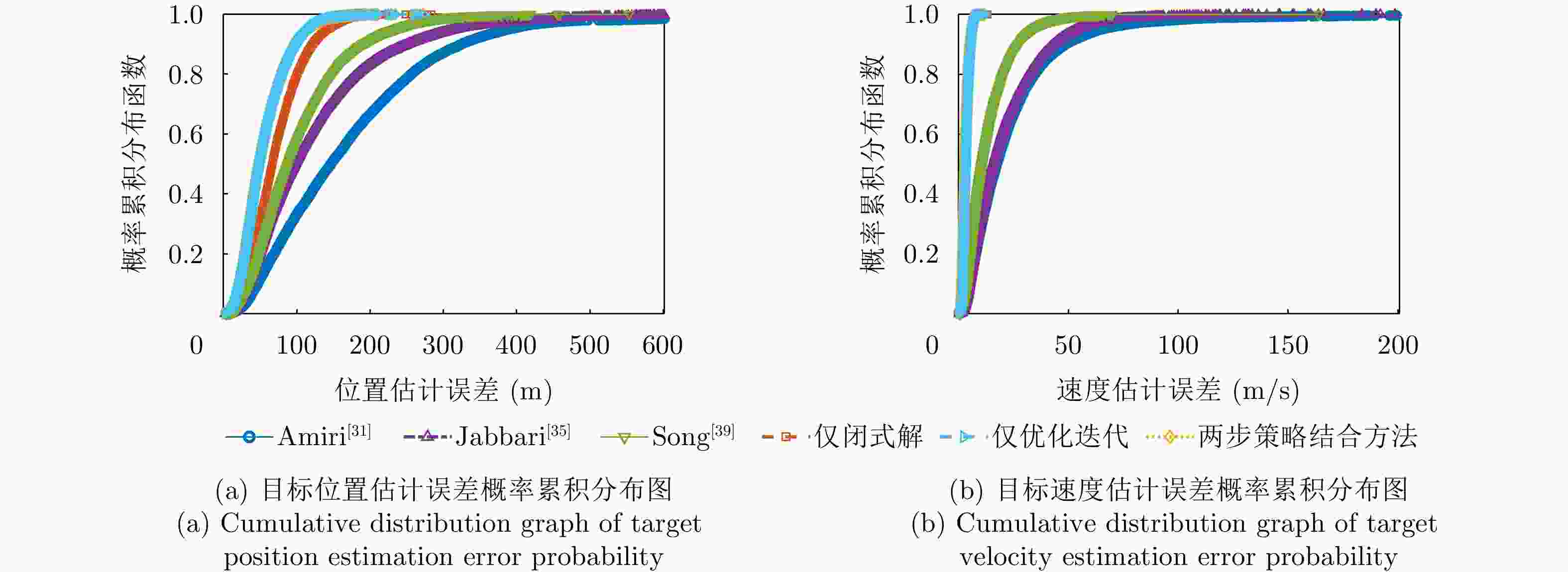
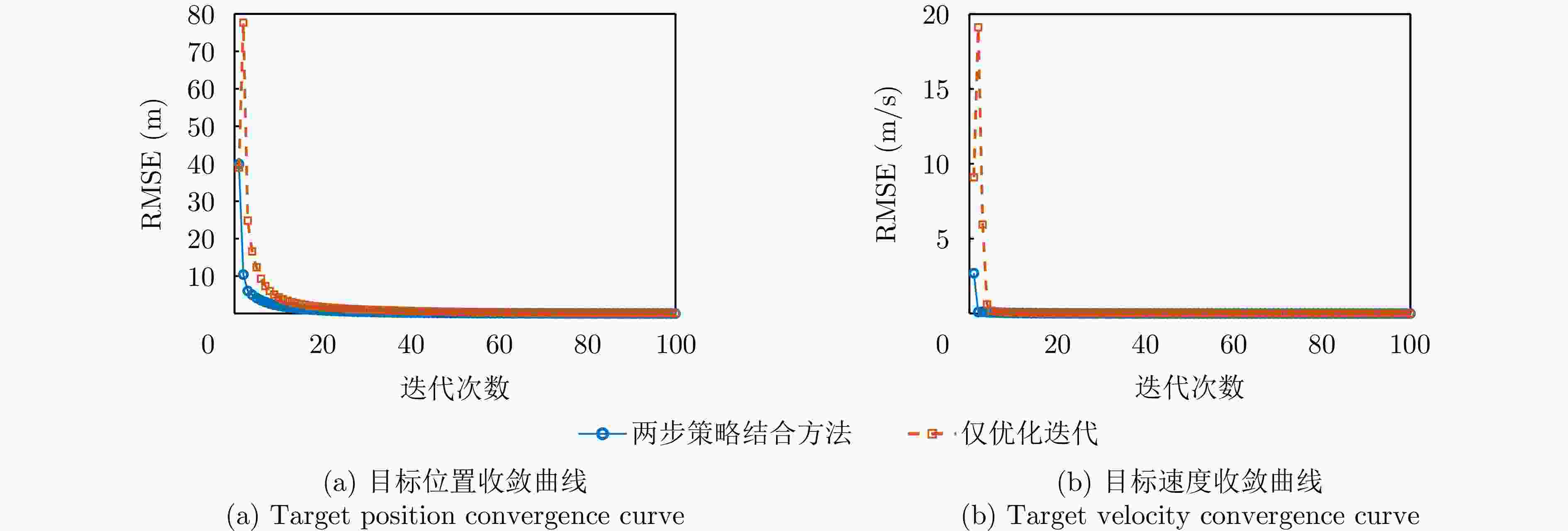
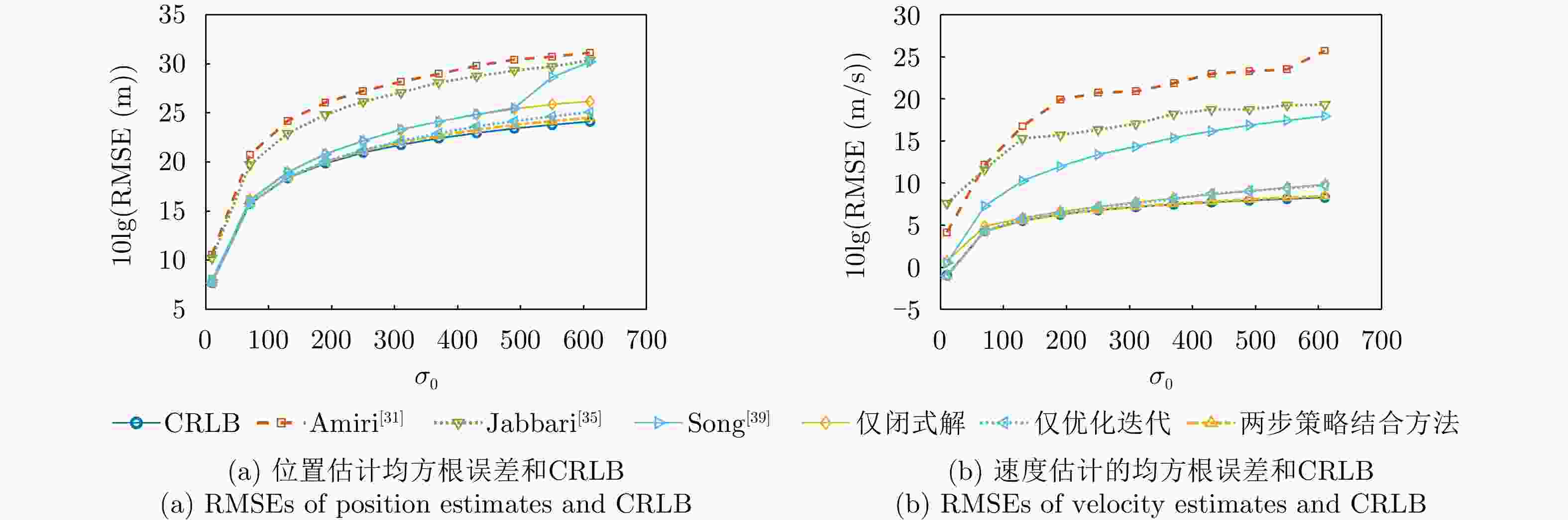
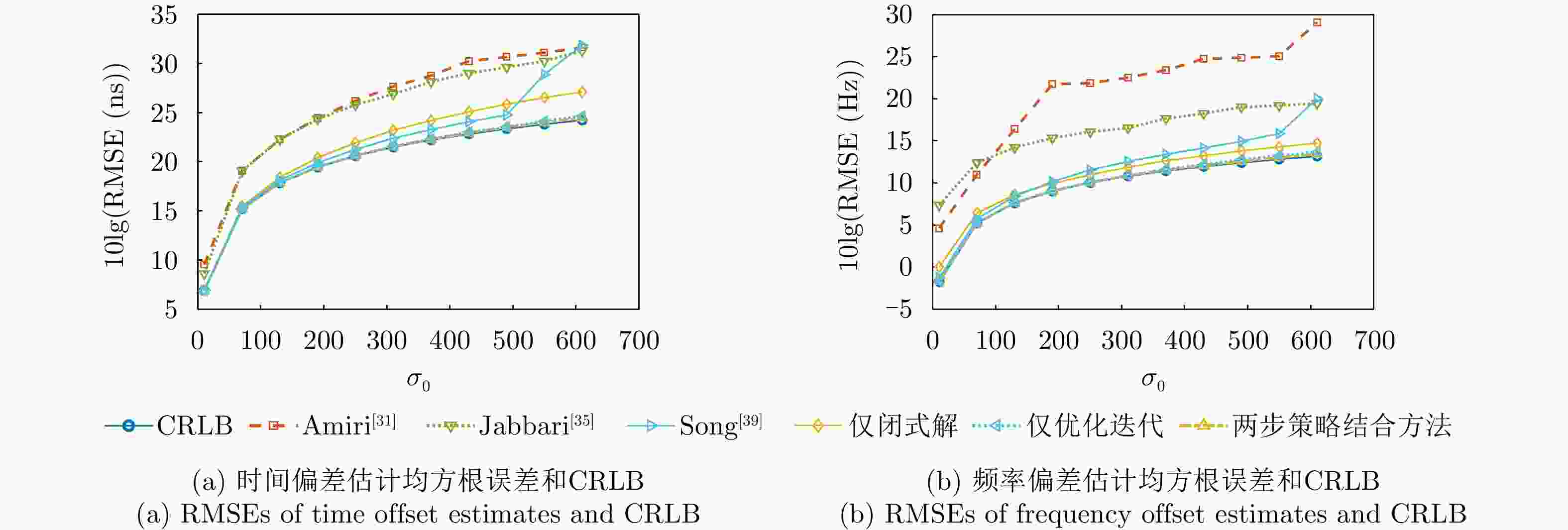
摘要: 该文针对分布式多输入多输出雷达系统中存在的时频同步误差问题,提出了一种基于多时刻测量数据的目标参数与系统时频偏差联合估计方法,突破了传统方法基于单时刻观测与依赖直达波数据的局限,实现了无须直达波的多时刻测量数据融合的高精度参数联合估计。该文采用“闭式解”和“迭代优化”两步策略结合方法,首先利用两阶段加权最小二乘框架构建闭式解,仅使用首尾两个时刻的观测数据获得目标位置、速度及辅助变量的初始估计,该方法显式地对误差项中的二阶分量进行了建模并优化了加权矩阵的构建,有效提高了算法在高误差水平条件下的精确性和鲁棒性;其次,以该闭式解作为初始值,基于多时刻测量数据构建最大似然-最大后验概率目标函数,采用信赖域迭代优化方法进一步优化估计结果,并且实现了时频偏差参数的估计校正。仿真实验表明,所提方法在多种实验误差水平和几何配置下均展现了优于对比方法的性能优势,显著提升了目标定位、测速及时频偏差估计的精度与鲁棒性,具有重要的理论价值与实际应用前景。Abstract: This study addresses time-frequency synchronization errors in distributed Multiple-Input Multiple-Output (MIMO) radar systems and proposes a joint estimation method for target parameters and system time-frequency biases based on multitemporal measurement data. The method overcomes the limitations of traditional approaches that rely on singletemporal measurement data and direct-path signals, enabling high-accuracy joint parameter estimation through multiepoch data fusion without requiring direct-path information. The proposed method adopts a two-step strategy that combines a closed-form solution with iterative optimization. First, a closed-form solution is derived within a two-stage weighted least-squares framework using only the first- and last-epoch observations to obtain initial estimates of the target position, velocity, and auxiliary variables. This stage explicitly models second-order error terms and optimizes the construction of the weighting matrix, significantly improving accuracy and robustness under high-error conditions. Second, using the closed-form estimates as initialization, a maximum likelihood-maximum a posteriori objective function is formulated based on the full multi-epoch measurement data, and a trust-region iterative optimization method is applied to refine the estimates and recover the time-frequency bias parameters. Simulation results show that the proposed method outperforms existing approaches across various error levels and geometric configurations, significantly enhancing the accuracy and robustness of target localization, velocity estimation, and time-frequency bias estimation. These results demonstrate strong theoretical significance and promising practical application potential.
-
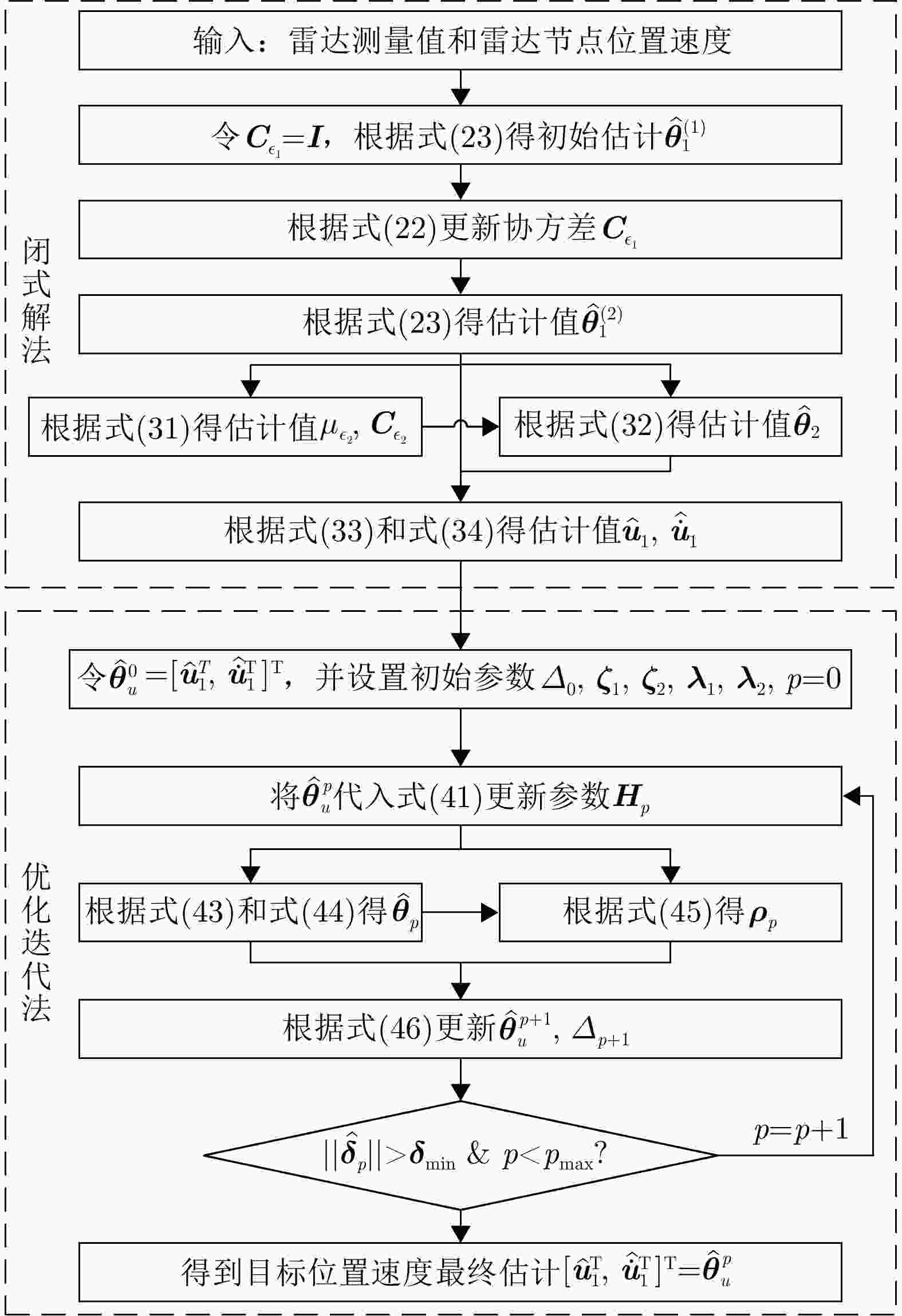
1 闭式解算法流程
1. Procedure of closed-form solution
输入:$ {r}_{1},{\dot{r}}_{1},{r}_{K},{\dot{r}}_{K},\boldsymbol{t},{\dot{\boldsymbol{t}}},\boldsymbol{s},{\dot{\boldsymbol{s}}},{T}_{s},K,{\boldsymbol{Q}}_{{\boldsymbol{\eta}} },{\boldsymbol{Q}}_{{\boldsymbol{\gamma}} } $ 输出:$ {{\hat{\boldsymbol{u}}}}_{1},{{\hat{\dot{\boldsymbol{u}} }}}_{1} $ 1:令$ {\boldsymbol{C}}_{{{\epsilon }_{1}}}=\boldsymbol{I} $,根据式(23)计算目标位置速度的初始估计
$ \hat{\boldsymbol{\theta }}_{1}^{(1)} $。2:根据式(22)更新初始估计协方差$ {\boldsymbol{C}}_{{{\epsilon }_{1}}} $。 3:根据式(23)得到加权最小二乘估计$ \hat{\boldsymbol{\theta }}_{1}^{(2)} $ 4:将$ {\hat{\boldsymbol{\theta }}}_{1}{}^{(2)} $代入式(31)得到$ {\boldsymbol{u}}_{{{\epsilon }_{2}}} $和$ {\boldsymbol{C}}_{{{\epsilon }_{2}}} $。 5:根据式(32)得到$ {\hat{\boldsymbol{\theta }}}_{2} $。 6:根据式(33)和式(34)得到目标位置速度的估计$ {{\hat{\boldsymbol{u}}}}_{1},{{\hat{\dot{\boldsymbol{u}} }}}_{1} $。 2 迭代优化算法流程
2. Procedure of iterative optimization
输入:$ r,\dot{r},\boldsymbol{t},{\dot{\boldsymbol{t}}},\boldsymbol{s},{\dot{\boldsymbol{s}}},{T}_{s},K,{\boldsymbol{Q}}_{\boldsymbol{\eta }},{\boldsymbol{Q}}_{\boldsymbol{\gamma }},\hat{\boldsymbol{\theta }}_{\boldsymbol{u}}^{0} $ 输出:$ {{\hat{\boldsymbol{u}}}}_{1},{{\hat{\dot{\boldsymbol{u}} }}}_{1} $ 步骤1:设置初始$ {\Delta }_{0},{\zeta }_{1},{\zeta }_{2},{\lambda }_{1},{\lambda }_{2},p=0 $。 步骤2:将目标位置速度估计$ \hat{\boldsymbol{\theta }}_{\boldsymbol{u}}^{p} $代入式(41)更新参数$ {\boldsymbol{H}}_{p} $。 步骤3:根据式(43)和式(44)求解并更新$ {\hat{\boldsymbol{\delta }}}_{p} $。 步骤4:根据式(45)求解$ {\rho }_{p} $,并通过式(46)得到$ \hat{\boldsymbol{\theta }}_{\boldsymbol{u}}^{p+1},{\Delta }_{p+1} $。 步骤5:根据式(47)判断是否收敛,收敛则执行6,否则令
$ p=p+1 $并重复执行步骤2—步骤4。步骤6:返回目标位置速度最终估计$ {[{{\hat{\boldsymbol{u}}}_{1}^{\rm T}},{{\hat{\dot{\boldsymbol{u}} }}_{1}^{\rm T}}]}^{\rm T}=\hat{\boldsymbol{\theta }}_{\boldsymbol{u}}^{p} $。 表 1 发射机和接收机位置速度表
Table 1. Positions and velocities of transmitters and receivers
节点 $ x_{i,0}^{t} $ (m) $ y_{i,0}^{t} $ (m) $ z_{i,0}^{t} $ (m) $ \dot{x}_{i,0}^{t} $ (m/s) $ \dot{y}_{i,0}^{t} $ (m/s) $ \dot{z}_{i,0}^{t}$ (m/s) $ {T}_{1} $ 0 0 200 0 20 10 $ {T}_{2} $ $ {R}_{0}\cos (\text{π} /3)/2 $ $ -{R}_{0} $ 350 –20 –40 40 $ {T}_{3} $ $ {R}_{0} $ $ -{R}_{0}\cos (\text{π} /6) $ 600 40 10 –20 $ {T}_{4} $ $ {R}_{0}\cos (\text{π} /4) $ $ {R}_{0}/2 $ 50 –40 –20 –10 $ {T}_{5} $ $ -{R}_{0} $ $ -{R}_{0}\cos (\text{π}/4) $ 50 30 –10 30 $ {T}_{6} $ $ -{R}_{0}\cos (\text{π} /6) $ $ -{R}_{0}/2 $ 350 50 –30 0 $ {T}_{7} $ $ {R}_{0}/2 $ $ {R}_{0}\cos (\text{π} /3) $ 200 –10 0 –30 $ {T}_{8} $ $ -{R}_{0}/2 $ $ {R}_{0} $ 600 10 40 20 $ {S}_{1} $ $ -{R}_{0} $ $ -{R}_{0}/2 $ 600 –20 20 –20 $ {S}_{2} $ $ -{R}_{0}\cos (\text{π} /3) $ 0 400 0 –30 30 $ {S}_{3} $ $ {R}_{0}/2 $ $ -{R}_{0} $ 350 30 20 20 $ {S}_{4} $ $ -{R}_{0}/2 $ $ {R}_{0}/2 $ 50 10 0 40 $ {S}_{5} $ $ {R}_{0}\cos (\text{π} /6) $ $ {R}_{0}\cos (\text{π}/4) $ 600 –10 –10 –30 $ {S}_{6} $ 0 $ -{R}_{0}\cos (\text{π} /3) $ 400 40 20 –10 $ {S}_{7} $ $ -{R}_{0}\cos (\text{π} /4) $ $ {R}_{0}\cos (\text{π} /6) $ 50 30 –30 10 $ {S}_{8} $ $ {R}_{0} $ $ {R}_{0} $ 350 –40 10 0 表 2 雷达节点与目标位置速度参数设置
Table 2. Radar node and target position and velocity parameter settings
节点类型 边界类型 位置$ x,y $ (m) 位置z (m) 速度$ \dot{x},\dot{y},\dot{z} $ (m/s) 雷达节点 下边界 $ -{R}_{0} $ 0 –20 上边界 $ {R}_{0} $ 500 20 目标 下边界 $ -{R}_{0} $ 500 –20 上边界 $ {R}_{0} $ 1000 20 -
[1] FISHLER E, HAIMOVICH A, BLUM R S, et al. Spatial diversity in radars-models and detection performance[J]. IEEE Transactions on Signal Processing, 2006, 54(3): 823–838. doi: 10.1109/TSP.2005.862813. [2] KRIEGER G. MIMO-SAR: Opportunities and pitfalls[J]. IEEE Transactions on Geoscience and Remote Sensing, 2014, 52(5): 2628–2645. doi: 10.1109/TGRS.2013.2263934. [3] WANG Wenqin. MIMO SAR OFDM chirp waveform diversity design with random matrix modulation[J]. IEEE Transactions on Geoscience and Remote Sensing, 2015, 53(3): 1615–1625. doi: 10.1109/TGRS.2014.2346478. [4] LIANG Yuanyuan, WEN Gongjian, ZHU Lingxiao, et al. Target detection performance of distributed MIMO radar systems under nonideal conditions[J]. IEEE Transactions on Aerospace and Electronic Systems, 2024, 60(2): 1951–1969. doi: 10.1109/TAES.2023.3344553. [5] CHEN Ruilin, GUO Shisheng, CHEN Jiahui, et al. Low-complexity multitarget detection and localization method for distributed MIMO radar[J]. IEEE Transactions on Radar Systems, 2025, 3: 599–614. doi: 10.1109/TRS.2025.3554198. [6] MA Cong, CAO Fengting, YANG Yue, et al. Distributed microwave photonic MIMO radar with accurate target position estimation[J]. IEEE Transactions on Microwave Theory and Techniques, 2023, 71(4): 1711–1719. doi: 10.1109/TMTT.2022.3218287. [7] ZHANG Guoxin, YI Wei, VARSHNEY P K, et al. Direct target localization with quantized measurements in noncoherent distributed MIMO radar systems[J]. IEEE Transactions on Geoscience and Remote Sensing, 2023, 61: 5103618. doi: 10.1109/TGRS.2023.3267499. [8] AMIRI R, KAZEMI S A R, BEHNIA F, et al. Efficient elliptic localization in the presence of antenna position uncertainties and clock parameter imperfections[J]. IEEE Transactions on Vehicular Technology, 2019, 68(10): 9797–9805. doi: 10.1109/TVT.2019.2933406. [9] KAZEMI S A R, AMIRI R, and BEHNIA F. Efficient joint localization and synchronization in distributed MIMO radars[J]. IEEE Signal Processing Letters, 2020, 27: 1200–1204. doi: 10.1109/LSP.2020.3007033. [10] LUO Shuai, WANG Yuexian, WANG Ling, et al. Direction finding for bistatic MIMO radar using a sparse moving array with sensor position errors[J]. IEEE Wireless Communications Letters, 2022, 11(9): 1840–1844. doi: 10.1109/LWC.2022.3184114. [11] BAR-SHALOM O and WEISS A J. Direct positioning of stationary targets using MIMO radar[J]. Signal Processing, 2011, 91(10): 2345–2358. doi: 10.1016/j.sigpro.2011.04.019. [12] HE Qian, BLUM R S, and HAIMOVICH A M. Noncoherent MIMO radar for location and velocity estimation: More antennas means better performance[J]. IEEE Transactions on Signal Processing, 2010, 58(7): 3661–3680. doi: 10.1109/TSP.2010.2044613. [13] NIU Ruixin, BLUM R S, VARSHNEY P K, et al. Target localization and tracking in noncoherent multiple-input multiple-output radar systems[J]. IEEE Transactions on Aerospace and Electronic Systems, 2012, 48(2): 1466–1489. doi: 10.1109/TAES.2012.6178073. [14] WEISS A J. Direct geolocation of wideband emitters based on delay and Doppler[J]. IEEE Transactions on Signal Processing, 2011, 59(6): 2513–2521. doi: 10.1109/TSP.2011.2128311. [15] ALAMDARI E, BEHNIA F, and AMIRI R. Conical localization from angle measurements: An approximate convex solution[J]. IEEE Sensors Letters, 2022, 6(5): 7001404. doi: 10.1109/LSENS.2022.3163186. [16] WANG Gang, XIANG Peng, and HO K C. Bias reduced semidefinite relaxation method for 3-D moving object localization using AOA[J]. IEEE Transactions on Wireless Communications, 2023, 22(11): 7377–7392. doi: 10.1109/TWC.2023.3250420. [17] SHI Zhanglei, WANG Hao, LEUNG C S, et al. Robust MIMO radar target localization based on Lagrange programming neural network[J]. Signal Processing, 2020, 174: 107574. doi: 10.1016/j.sigpro.2020.107574. [18] SUN Ting, DONG Chunxi, MAO Yu, et al. Moving target localization in multiple-input multiple-output radar systems without the prior knowledge of measurement noise powers[J]. IEEE Communications Letters, 2020, 24(9): 1957–1960. doi: 10.1109/LCOMM.2020.3001950. [19] SONG Haibo, WEN Gongjian, LIANG Yuanyuan, et al. Target localization and clock refinement in distributed MIMO radar systems with time synchronization errors[J]. IEEE Transactions on Signal Processing, 2021, 69: 3088–3103. doi: 10.1109/TSP.2021.3081038. [20] ZHENG Zhi, ZHANG Hongwang, and WANG Wenqin. Target localization in distributed MIMO radars via improved semidefinite relaxation[J]. Journal of the Franklin Institute, 2021, 358(10): 5588–5598. doi: 10.1016/j.jfranklin.2021.04.035. [21] SUN Bin, CHEN Haowen, WEI Xizhang, et al. Semidefinite relaxation method for target localization by MIMO radar using bistatic ranges[J]. International Journal of Distributed Sensor Networks, 2014, 10(8): 1–6. doi: 10.1155/2014/984812. [22] ZHENG Ruichao, WANG Gang, and HO K C. Accurate semidefinite relaxation method for elliptic localization with unknown transmitter position[J]. IEEE Transactions on Wireless Communications, 2021, 20(4): 2746–2760. doi: 10.1109/TWC.2020.3044217. [23] AMIRI R, BEHNIA F, and SADR M A M. Exact solution for elliptic localization in distributed MIMO radar systems[J]. IEEE Transactions on Vehicular Technology, 2018, 67(2): 1075–1086. doi: 10.1109/TVT.2017.2762631. [24] AMIRI R, BEHNIA F, and MALEKI SADR M A. Positioning in MIMO radars based on constrained least squares estimation[J]. IEEE Communications Letters, 2017, 21(10): 2222–2225. doi: 10.1109/LCOMM.2017.2724541. [25] QI Qinke, LI Youming, and GUO Qiang. A convex relaxation algorithm for source localization considering sensor motion in wireless sensor networks[J]. IEEE Communications Letters, 2021, 25(6): 1867–1871. doi: 10.1109/LCOMM.2021.3062668. [26] JIA Tianyi, HO K C, WANG Haiyan, et al. Effect of sensor motion on time delay and Doppler shift localization: Analysis and solution[J]. IEEE Transactions on Signal Processing, 2019, 67(22): 5881–5895. doi: 10.1109/TSP.2019.2946025. [27] QI Hengnian, WU Xiaoping, XIONG Naixue, et al. A source prediction system for dynamic networks based on TDOA measurements[J]. IEEE Transactions on Network Science and Engineering, 2021, 8(3): 2388–2401. doi: 10.1109/TNSE.2021.3092175. [28] MENG Xiangpei, LI Youming, WU Zhenqian, et al. A semidefinite relaxation approach for mobile target localization based on TOA and Doppler frequency shift measurements[J]. IEEE Sensors Journal, 2023, 23(14): 16051–16057. doi: 10.1109/JSEN.2023.3272565. [29] HO K C and XU Wenwei. An accurate algebraic solution for moving source location using TDOA and FDOA measurements[J]. IEEE Transactions on Signal Processing, 2004, 52(9): 2453–2463. doi: 10.1109/TSP.2004.831921. [30] YANG H and CHUN J. An improved algebraic solution for moving target localization in noncoherent MIMO radar systems[J]. IEEE Transactions on Signal Processing, 2016, 64(1): 258–270. doi: 10.1109/TSP.2015.2477803. [31] AMIRI R, BEHNIA F, and MALEKI SADR M A. Efficient positioning in MIMO radars with widely separated antennas[J]. IEEE Communications Letters, 2017, 21(7): 1569–1572. doi: 10.1109/LCOMM.2017.2688373. [32] NOROOZI A, AMIRI R, NAYEBI M M, et al. Efficient closed-form solution for moving target localization in MIMO radars with minimum number of antennas[J]. IEEE Transactions on Signal Processing, 2020, 68: 2545–2557. doi: 10.1109/TSP.2020.2986163. [33] KAZEMI S A R, AMIRI R, and BEHNIA F. Efficient closed-form solution for 3-D hybrid localization in multistatic radars[J]. IEEE Transactions on Aerospace and Electronic Systems, 2021, 57(6): 3886–3895. doi: 10.1109/TAES.2021.3082664. [34] NOROOZI A, SEBT M A, HOSSEINI S M, et al. Closed-form solution for elliptic localization in distributed MIMO radar systems with minimum number of sensors[J]. IEEE Transactions on Aerospace and Electronic Systems, 2020, 56(4): 3123–3133. doi: 10.1109/TAES.2020.2965668. [35] JABBARI M R, TABAN M R, and GAZOR S. A robust TSWLS localization of moving target in widely separated MIMO radars[J]. IEEE Transactions on Aerospace and Electronic Systems, 2023, 59(2): 897–906. doi: 10.1109/TAES.2022.3194112. [36] WU Xiaoping, MAO Xiaoting, and QI Hengnian. Semidefinite relaxation for moving target localization in asynchronous MIMO systems[J]. IEEE Transactions on Communications, 2024, 72(2): 1075–1089. doi: 10.1109/TCOMM.2023.3326492. [37] ZHANG Yang and HO K C. Multistatic moving object localization by a moving transmitter of unknown location and offset[J]. IEEE Transactions on Signal Processing, 2020, 68: 4438–4453. doi: 10.1109/TSP.2020.3008752. [38] ZHENG Ruichao, WANG Gang, HO K C, et al. Semidefinite relaxation method for moving object localization using a stationary transmitter at unknown position[C]. ICASSP 2022 - 2022 IEEE International Conference on Acoustics, Speech and Signal Processing (ICASSP), Singapore, Singapore, 2022: 5128–5132. doi: 10.1109/ICASSP43922.2022.9746393. [39] SONG Haibo, YUAN Fu, WANG Jie, et al. An algebraic solution for moving target localization in distributed MIMO radar systems with clock synchronization errors[C]. Proceedings Volume 13091, Fifteenth International Conference on Signal Processing Systems (ICSPS 2023), Xi’an, China, 2023. doi: 10.1117/12.3023350. -



 作者中心
作者中心 专家审稿
专家审稿 责编办公
责编办公 编辑办公
编辑办公
 下载:
下载: