作者中心
专家审稿
责编办公
编辑办公
A New Approach to High-order Range Cell Migration Correction for SAR Ground Moving Targets Based on Phase Tracking
-
摘要: 距离徙动校正(RCMC)是合成孔径雷达(SAR)实现运动目标参数估计和聚焦成像的关键环节。当目标或平台运动复杂时，传统低阶RCMC方法将不再适用，而现有基于参数化的高阶RCMC方法易存在模型失配和计算复杂度高的问题、现有非参数化方法在低信噪比下性能也将大幅下降。对此，该文借助扩展卡尔曼滤波(EKF)对造成RCM的相位进行追踪，进而构建RCM补偿函数实现RCMC。所提方法不依赖于RCM的具体模型，追踪得到的相位包含高阶分量，因此可以实现SAR运动目标的高阶RCMC。此外，EKF在进行相位追踪的同时能对信号进行滤波处理，可有效降低所提方法的信噪比(SNR)门限。与传统方法相比，该方法适用性广，计算量适中，且能校正不可忽略的高阶残余距离徙动。该文详细阐释了所提方法的原理及数学模型，并通过多组仿真和实测数据处理验证了所提方法的有效性和优越性。Abstract: Range Cell Migration Correction (RCMC) represents an important advancement in the estimation of moving target parameters and imaging of targets in high-resolution Synthetic Aperture Radar (SAR) systems. When the motion of a target or platform becomes complex, the traditional low-order RCMC method may no longer be suitable. Meanwhile, the existing high-order RCMC method based on parameterization is susceptible to issues such as model mismatch and high computational complexity. Additionally, its performance may decrease significantly under a low Signal-to-Noise Ratio (SNR). This research utilizes Extended Kalman Filter (EKF) to track the phase responsible for RCM and develop a phase compensation function to achieve RCMC. The proposed approach is model-independent and can track high-order components in the phase, thereby enabling high-order RCMC of moving targets in SAR. In addition, EKF can filter signals during phase tracking to effectively lower the SNR threshold of the proposed method. Thus, this method offers broad applicability, moderate computational complexity, and the ability to correct non-negligible high-order residual range cell migrations, thereby distinguishing it from traditional methods. This study thoroughly explains the principles and mathematical model behind the proposed method, demonstrating its effectiveness and superiority through multiple sets of simulations and measured data processing.
-
图 9 多频余弦耦合波动下的追踪结果
Figure 9. Phase tracking result under multifrequency cosine-coupled fluctuations
图 10 多频余弦耦合波动下点目标的处理结果
Figure 10. Processing results of point target under multifrequency cosine-coupled fluctuations
图 11 多频余弦耦合波动下多散射点目标的处理结果
Figure 11. Processing results of multi-point target under multifrequency cosine-coupled fluctuations
图 14 所提方法处理结果(人为加入噪声)
Figure 14. Processing results of the proposed method (artifical noise)
1 二元状态空间方程的迭代求解过程
1. Iterative solution of binary state-space equation
输入：目标所在距离单元的方位向采样信号$ s_{{\mathrm{T}}}(k) $ 输出：相位历程$ \phi(k) $的估计值$\tilde \phi(k) $：$\left\{ \begin{aligned} &\tilde \phi(k)=\hat{\boldsymbol{\varphi}}_k(1);\;k \ne N_{\mathrm{a}}-1\\ & \left[ \tilde \phi(N_{\mathrm{a}}-2) \;\;\hat{\boldsymbol{\phi}}(N_{\mathrm{a}}-1)\;\;\hat{\boldsymbol{\phi}}(N_{\mathrm{a}})\right]^{\rm{T}}= \hat{\boldsymbol{\varphi}}_{N_{\mathrm{a}}-1};\;k=N_{\mathrm{a}}-1 \end{aligned}\right. $。 $ O(1) $ 1. 初始化参数：相位状态向量$ {\boldsymbol{\varphi}}_{2} $，对应的协方差矩阵$ \boldsymbol{\varPhi}_{2} $，相位状态方程噪声协方差矩阵$ \boldsymbol{W}_{2} $；幅度状态向量$ {\boldsymbol{p}}_{2} $，对应的协方差矩阵
$ {\boldsymbol{P}}_{2} $，幅度状态方程噪声协方差矩阵$ {\boldsymbol{V}}_{2} $；观测方程噪声协方差矩阵$ \boldsymbol{R}_{2} $。2. EKF循环迭代开始，令 $ k={3} $ 3. 提取观测数据采样值：$ {\boldsymbol{s}}_{k}=\left[s_{{\mathrm{T}}}(k-1) \;\;s_{{\mathrm{T}}}(k) \;\;s_{{\mathrm{T}}}(k+1)\right]^{\mathrm{T}} $，并通过式(18)计算得$ {\boldsymbol{y}}_{k} $； $ O(1) $ 4. 状态向量预测值更新：$ \hat{{\boldsymbol{\varphi}}}_{k|k-1}={\boldsymbol{B}} \hat{{\boldsymbol{\varphi}}}_{k-1} ;\,\hat{{\boldsymbol{p}}}_{k| k-1}=\boldsymbol{B} {\hat{\boldsymbol{p}}_{k-1}} $； $ O\left(M^{2}\right) $ 5. 状态向量协方差矩阵计算：$ {\boldsymbol{\varPhi}}_{k|k-1}={\boldsymbol{B \varPhi}}_{k-1} {\boldsymbol{B}}^{{\mathrm{T}}}+{\boldsymbol{W}}_{k-1} ; {\boldsymbol{P}}_{k|k-1}={\boldsymbol{B P}}_{k|k-1} {\boldsymbol{B}}^{{\mathrm{T}}}+{\boldsymbol{V}}_{k-1} $； $ O\left(M^{3}+M^{2}\right) $ 6. 雅可比矩阵计算：$ {\boldsymbol{H}}_{1 k}=\partial f\left({\boldsymbol{p}}_{k}, {\boldsymbol{\varphi}}_{k}\right) / \partial {\boldsymbol{\varphi}}_{k };\, \boldsymbol{H}_{2k}=\partial f\left({\boldsymbol{p}}_{k}, {\boldsymbol{\varphi}}_{k}\right) / \partial {\boldsymbol{p}}_{k} $； $ O\left(M^{2}\right) $ 7. 卡尔曼增益计算：
${\boldsymbol{K}}_{1k}={\boldsymbol{\varPhi}}_{k|k-1} {\boldsymbol{H}}^{\mathrm{T}}_{1k}({\boldsymbol{H}}_{1k}{\boldsymbol{\varPhi}}_{k|k-1}{\boldsymbol{H}}^{\mathrm{T}}_{1k}+{\boldsymbol{R}}_{k-1})^{-1};\;{\boldsymbol{K}}_{2k}={\boldsymbol{P}}_{k|k-1}{\boldsymbol{H}}^{\mathrm{T}}_{2k}({\boldsymbol{H}}_{2k}{\boldsymbol{P}}_{k|k-1}{\boldsymbol{H}}^{\mathrm{T}}_{2k}+{\boldsymbol{R}}_{k-1})^{-1} $；$ O\left(M^{3}+M^{2}\right) $ 8. 根据ADMM策略，令幅度状态值为$ \hat{{\boldsymbol{p}}}_{k} \approx \hat{{\boldsymbol{p}}}_{k|k-1} $； $ O(1) $ 9. 状态向量更新：$ \hat{\boldsymbol{\varphi}}_k=\hat{\boldsymbol{\varphi}}_{k|k-1}+{\boldsymbol{K}}_{1k}\left[ {{{\boldsymbol{y}}_{{k}}} - \hat {\boldsymbol{A}}'_k \odot {{\boldsymbol{h}}_2}({{\hat {\boldsymbol{\varphi}} }_{k|k - 1}})} \right] ;{\hat {\boldsymbol{p}}_k} = {\hat {\boldsymbol{p}}_{k|{{k - 1}}}} + {\boldsymbol{K}}_{2k}\left[ {{{\boldsymbol{y}}_{{k}}} - \hat {\boldsymbol{A}}'_k \odot {{\boldsymbol{h}}_2}({{\hat {\boldsymbol{\varphi}} }_{k|k - 1}})} \right] $
其中，$ \hat{{\boldsymbol{A}}}_{k}^{\prime}=\left[{\boldsymbol{p}}_{k}\; {\boldsymbol{p}}_{k}\right]^{{\mathrm{T}}} $。$ O\left(M^{2}+M\right) $ 10. 状态向量协方差矩阵更新：${\boldsymbol{\varPhi}}_k=({\boldsymbol{I}}_{3 \times 3}-{\boldsymbol{K}}_{1k}{\boldsymbol{H}}_{1k}){\boldsymbol{\varPhi}}_{k|k-1};\;{\boldsymbol{P}}_k=({\boldsymbol{I}}_{3 \times 3 }-{\boldsymbol{K}}_{2k}{\boldsymbol{H}}_{2k}){\boldsymbol{P}}_{k|k-1} $； $ O\left(M^{3}+M^{2}\right) $ 11. 根据文献[36,37]，对噪声协方差矩阵进行自适应更新：
$ {\boldsymbol{W}}_{k}=\left(1-d_{k}\right) {\boldsymbol{W}}_{k-1}+d_{k} {\boldsymbol{K}}_{1 k}\left({\boldsymbol{\varepsilon}}_{k} {\boldsymbol{\varepsilon}}_{k}^{{\mathrm{T}}}\right) {\boldsymbol{K}}_{1k}^{{\mathrm{T}}};\; {\boldsymbol{V}}_{k}=\left(1-d_{k}\right) {\boldsymbol{V}}_{k-1}+d_{k} {\boldsymbol{K}}_{2k}\left({\boldsymbol{\varepsilon}}_{k} {\boldsymbol{\varepsilon}}_{k}^{{\mathrm{T}}}\right) {\boldsymbol{K}}_{2k}^{{\mathrm{T}}} $,
$ \boldsymbol{R}_{k}=\left(1-d_{k}\right) {\boldsymbol{R}}_{k-1}+d_{k}\left({\boldsymbol{\varepsilon}}_{k} {\boldsymbol{\varepsilon}}_{k}^{\mathrm{T}}-\boldsymbol{H}_{1k} {\boldsymbol{\varPhi}}_{k|k-1} \boldsymbol{H}_{1 k}^{\mathrm{T}}\right) $
其中，$ {\boldsymbol{\varepsilon}}_{k}={\boldsymbol{y}}_{k}-\hat{{\boldsymbol{A}}}'_{k} \odot {\boldsymbol{h}}_{2}\left(\hat{{\boldsymbol{\varphi}}}_{k|k-1}\right) $，且$ d_{k}=(1-b)/\left(1-b^{k}\right),(0<b<1) $，$ b $表示遗忘因子。$ O\left(M^{3}+M^{2}\right) $ 12. 更新EKF循环索引值：$ k=k+1 $； $ O(1) $ 13. 重复上述步骤3—步骤12，直至$ k=N_{\rm a}-1 $，结束循环迭代。 
下载: 导出CSV
表 1 计算复杂度
Table 1. Computation complexity
方法 计算复杂度 GRFT $ O\left(N_{\rm r} N_{\rm a} N_{0}^{L}\right) $ FAR $ O\left(N_{\rm a} N_{\rm r} \log N_{\rm r}\right) $ ACCF $ O\left(N_{\rm a} N_{\rm r} \log N_{\rm r}\right) $ ACCM $ O\left(N_{\rm a} N_{\rm r}\right) $ BFGS-WOA $ O\left(N_{I} N_{{\mathrm{r}}} N_{\rm a}\right)+O\left(N_{I} N_{\rm a}^{3}\right) $ 所提方法 $ O\left(N_{\rm r} N_{\rm a}^{2}\right)+O\left(M^{3} N_{\rm a}\right) $
下载: 导出CSV
表 2 雷达仿真参数
Table 2. Radar simulation parameters
参数 数值 中心频率(GHz) 10 信号带宽(MHz) 300 距离向采样率(MHz) 360 信号脉宽(μs) 10 脉冲重复频率(Hz) 2000 中心斜距(km) 10 距离向采样点数 4096 方位向采样点数 8192
下载: 导出CSV
表 3 平台与目标运动参数
Table 3. Platform and target motion parameters
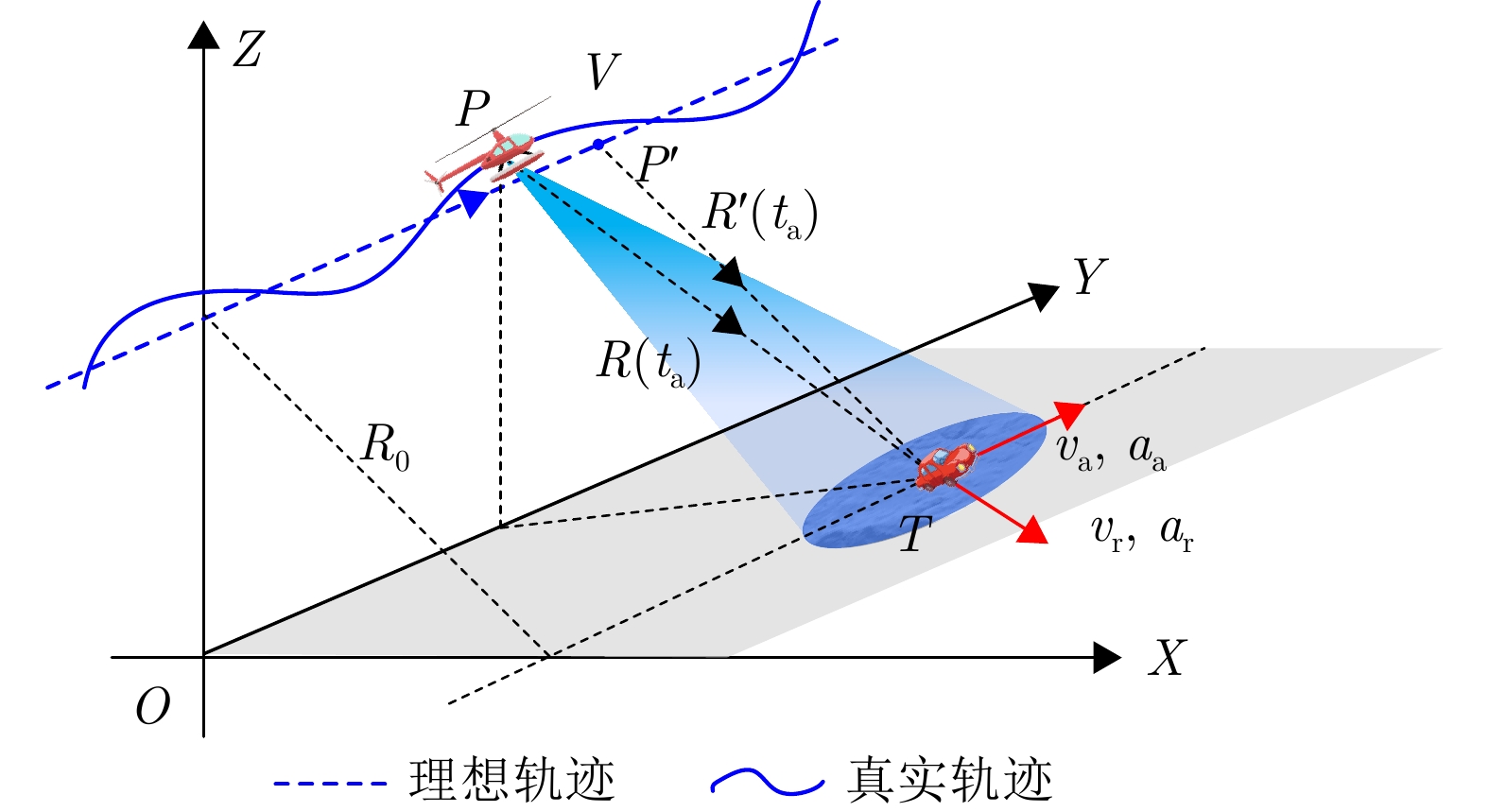
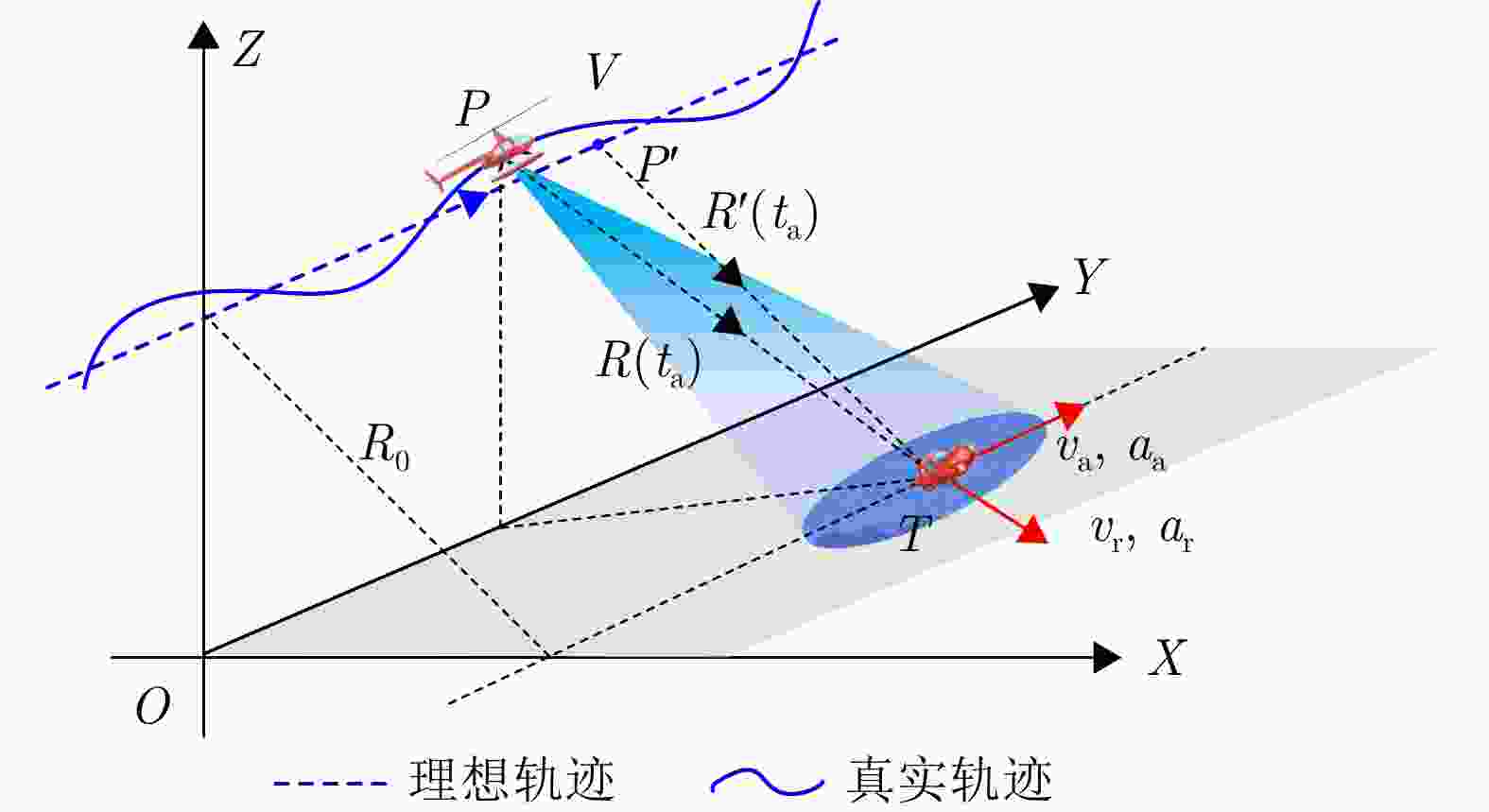
参数 数值 平台速度$ V $(m/s) 100 目标距离向速度$ v_{\rm r} $(m/s) –10 目标距离向加速度$ a_{\rm r} $(m/s2) –2 目标方位向速度$ v_{\rm a} $(m/s) 10 目标方位向加速度$ a_{\rm a} $(m/s2) 2
下载: 导出CSV
表 4 不同SNR下各方法的图像对比度
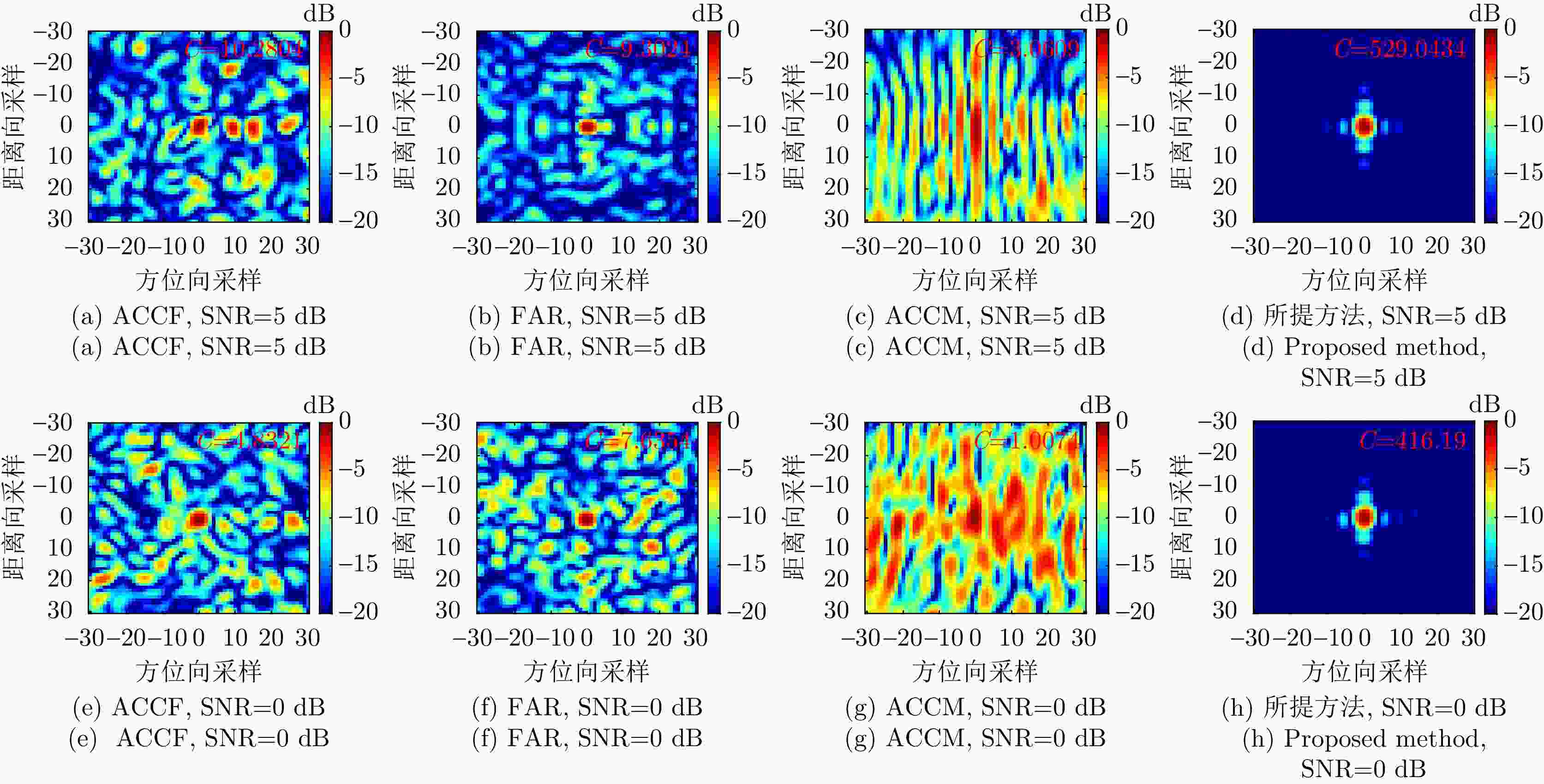
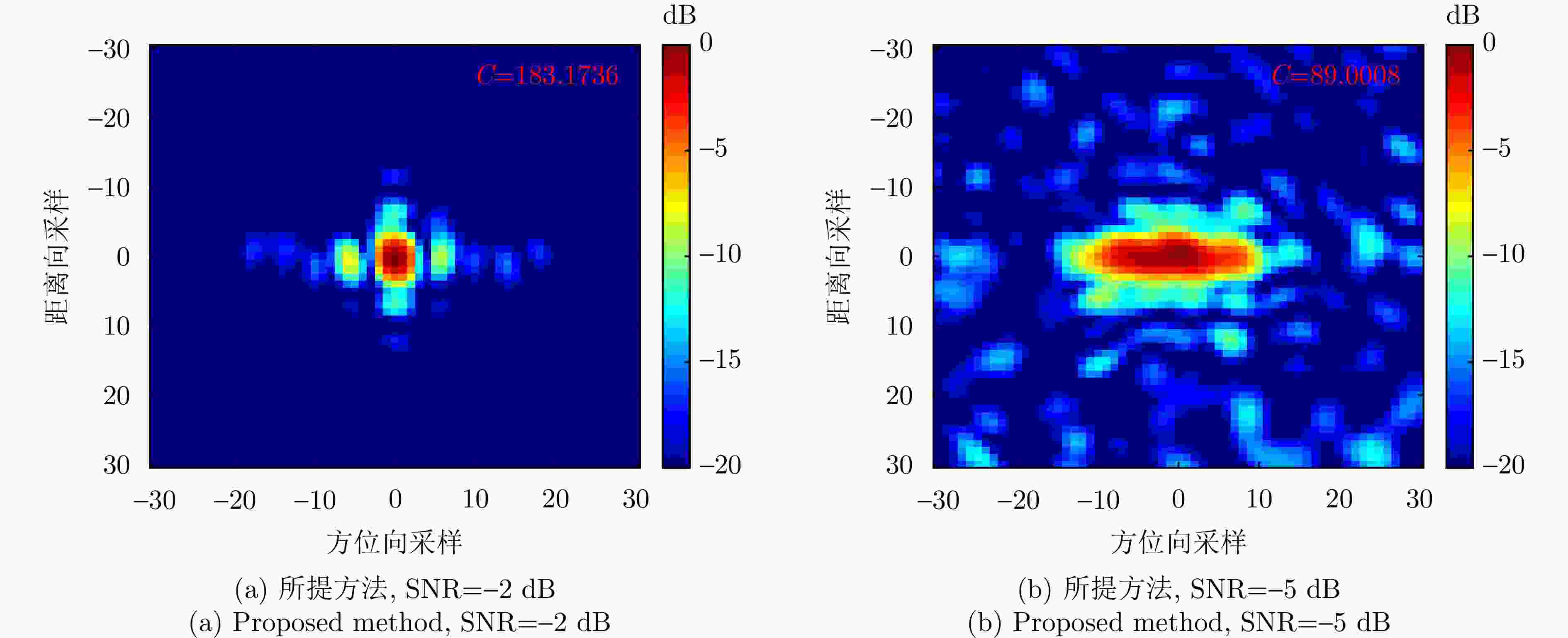
Table 4. Image contrast of each method under different SNR
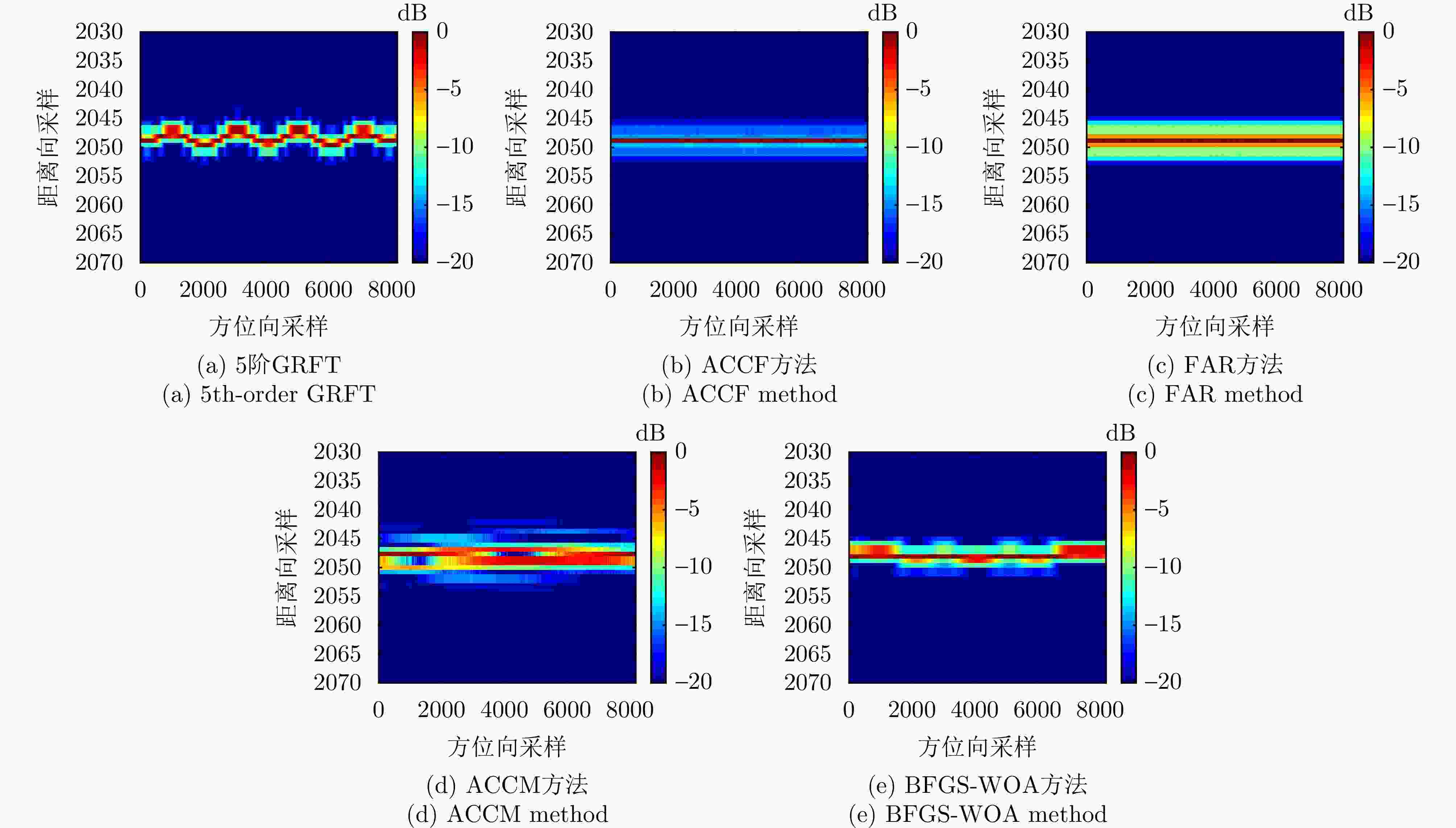
方法 SNR (dB) 5 2 0 –2 –4 –5 –6 5阶GRFT 210.76 136.79 115.13 86.72 30.70 28.74 1.08 FAR 10.05 8.32 7.56 7.43 5.31 3.48 1.36 ACCF 12.31 7.24 6.37 4.86 4.52 1.38 1.04 ACCM 10.61 6.15 2.61 1.22 1.08 1.05 1.04 BFGS-WOA 206.30 134.21 106.30 76.33 24.49 10.16 1.01 所提方法 491.58 243.74 157.03 112.70 110.76 100.62 100.22
下载: 导出CSV
表 5 各方法的计算时间
Table 5. Calculation time under different methods
方法 平均耗时(s) 5阶GRFT 8870.32 FAR 13.48 ACCF 12.86 ACCM 10.04 BFGS-WOA 36.25 所提方法 19.64
下载: 导出CSV
表 6 MMW雷达参数
Table 6. MMW radar parameters
参数 数值 中心频率(GHz) 77 信号带宽(GHz) 2.56 距离向采样率(MHz) 10 脉冲重复频率(Hz) 100 中心斜距(m) 10 雷达速度(cm/s) 2.13
下载: 导出CSV
表 7 Ka波段雷达参数
Table 7. Ka-band radar parameters
参数 数值 中心频率(GHz) Ka波段 距离分辨率(m) 0.15 观测时间(s) 70 飞行半径(m) 6000 飞行高度(km) 3 雷达速度(m/s) 80
下载: 导出CSV
-
[1] YANG Jian, LIU Chang, and WANG Yanfei. Detection and imaging of ground moving targets with real SAR data[J]. IEEE Transactions on Geoscience and Remote Sensing, 2015, 53(2): 920–932. doi: 10.1109/TGRS.2014.2330456. [2] DU Huagui, SONG Yongping, JIANG Nan, et al. A novel SAR ground maneuvering target imaging method based on adaptive phase tracking[J]. IEEE Transactions on Geoscience and Remote Sensing, 2023, 61: 5211916. doi: 10.1109/TGRS.2023.3294252. [3] PERRY R P, DIPIETRO R C, and FANTE R L. SAR imaging of moving targets[J]. IEEE Transactions on Aerospace and Electronic Systems, 1999, 35(1): 188–200. doi: 10.1109/7.745691. [4] ZHOU Feng, WU Renbiao, XING Mengdao, et al. Approach for single channel SAR ground moving target imaging and motion parameter estimation[J]. IET Radar, Sonar & Navigation, 2007, 1(1): 59–66. doi: 10.1049/iet-rsn:20060040. [5] TIAN Jing, CUI Wei, and WU Shuang. A novel method for parameter estimation of space moving targets[J]. IEEE Geoscience and Remote Sensing Letters, 2014, 11(2): 389–393. doi: 10.1109/LGRS.2013.2263332. [6] SUN Yan and WILLETT P. Hough transform for long chirp detection[J]. IEEE Transactions on Aerospace and Electronic Systems, 2002, 38(2): 553–569. doi: 10.1109/TAES.2002.1008986. [7] CARRETERO-MOYA J, GISMERO-MEN J, ASENSIO-LÓPEZ A, et al. Application of the radon transform to detect small-targets in sea clutter[J]. IET Radar, Sonar & Navigation, 2009, 3(2): 155–166. doi: 10.1049/iet-rsn:20080123. [8] XU Jia, YU Ji, PENG Yingning, et al. Radon-Fourier transform for radar target detection, (I:) Generalized Doppler filter bank[J]. IEEE Transactions on Aerospace and Electronic Systems, 2011, 47(2): 1186–1202. doi: 10.1109/TAES.2011.5751251. [9] XU Jia, YU Ji, PENG Yingning, et al. Radon-Fourier transform for radar target detection (II): Blind speed sidelobe suppression[J]. IEEE Transactions on Aerospace and Electronic Systems, 2011, 47(4): 2473–2489. doi: 10.1109/TAES.2011.6034645. [10] QIAN Lichang, XU Jia, SUN Wenfeng, et al. CLEAN based blind speed side lobe (BSSL) suppression in the Radon Fourier Transform (RFT) for multi-target detection[C]. IEEE 12th International Conference on Computer and Information Technology, Chengdu, China, 2012: 490–495. doi: 10.1109/CIT.2012.108. [11] CHEN Xiaolong, GUAN Jian, LIU Ningbo, et al. Maneuvering target detection via Radon-fractional Fourier transform-based long-time coherent integration[J]. IEEE Transactions on Signal Processing, 2014, 62(4): 939–953. doi: 10.1109/TSP.2013.2297682. [12] RAO Xuan, TAO Haihong, SU Jia, et al. Axis rotation MTD algorithm for weak target detection[J]. Digital Signal Processing, 2014, 26: 81–86. doi: 10.1016/j.dsp.2013.12.003. [13] SUN Zhi, LI Xiaolong, YI Wei, et al. A coherent detection and velocity estimation algorithm for the high-speed target based on the modified location rotation transform[J]. IEEE Journal of Selected Topics in Applied Earth Observations and Remote Sensing, 2018, 11(7): 2346–2361. doi: 10.1109/JSTARS.2018.2834535. [14] 王超, 王岩飞, 刘畅, 等. 基于参数估计的高分辨率SAR运动目标距离徙动校正方法[J]. 雷达学报, 2019, 8(1): 64–72. doi: 10.12000/JR18054.WANG Chao, WANG Yanfei, LIU Chang, et al. A new approach to range cell migration correction for ground moving targets in high-resolution SAR system based on parameter estimation[J]. Journal of Radars, 2019, 8(1): 64–72. doi: 10.12000/JR18054. [15] XU Jia, XIA Xianggen, PENG Shibao, et al. Radar maneuvering target motion estimation based on generalized Radon-Fourier transform[J]. IEEE Transactions on Signal Processing, 2012, 60(12): 6190–6201. doi: 10.1109/TSP.2012.2217137. [16] KONG Lingjiang, LI Xiaolong, CUI Guolong, et al. Coherent integration algorithm for a maneuvering target with high-order range migration[J]. IEEE Transactions on Signal Processing, 2015, 63(17): 4474–4486. doi: 10.1109/TSP.2015.2437844. [17] XIONG Wei, ZHANG Ying, DONG Xichao, et al. A novel ship imaging method with multiple sinusoidal functions to match rotation effects in geosynchronous SAR[J]. Remote Sensing, 2022, 12(14): 2249. doi: 10.3390/rs12142249. [18] LI Xiaolong, CUI Guolong, YI Wei, et al. A fast maneuvering target motion parameters estimation algorithm based on ACCF[J]. IEEE Signal Processing Letters, 2015, 22(3): 270–274. doi: 10.1109/LSP.2014.2358230. [19] LI Xiaolong, CUI Guolong, KONG Lingjiang, et al. Fast non-searching method for maneuvering target detection and motion parameters estimation[J]. IEEE Transactions on Signal Processing, 2016, 64(9): 2232–2244. doi: 10.1109/TSP.2016.2515066. [20] 贺雄鹏, 廖桂生, 许京伟, 等. 机动目标距离徙动校正与检测算法[J]. 系统工程与电子技术, 2018, 40(1): 1–8. doi: 10.3969/j.issn.1001-506X.2018.01.01.HE Xiongpeng, LIAO Guisheng, XU Jingwei, et al. Maneuvering target range migration correction and detection algorithm[J]. Systems Engineering and Electronics, 2018, 40(1): 1–8. doi: 10.3969/j.issn.1001-506X.2018.01.01. [21] 贺雄鹏, 廖桂生, 许京伟, 等. 基于频率轴反转的机动目标距离徙动补偿方法[J]. 电子学报, 2018, 46(6): 1496–1502. doi: 10.3969/j.issn.0372-2112.2018.06.032.HE Xiongpeng, LIAO Guisheng, XU Jingwei, et al. Range migration compensation method for maneuvering target based on frequency axis reversal[J]. Acta Electronica Sinica, 2018, 46(6): 1496–1502. doi: 10.3969/j.issn.0372-2112.2018.06.032. [22] CHEN C C and ANDREWS H C. Target-motion-induced RADAR imaging[J]. IEEE Transactions on Aerospace and Electronic Systems, 1980, AES-16(1): 2–14. doi: 10.1109/TAES.1980.308873. [23] 张泽. 空间目标的SAR/ISAR成像方法研究[D]. [硕士论文], 哈尔滨工业大学, 2019. doi: 10.27061/d.cnki.ghgdu.2019.000599.ZHANG Ze. Research on SAR/ISAR imaging method for space target[D]. [Master dissertation], Harbin Institute of Technology, 2019. doi: 10.27061/d.cnki.ghgdu.2019.000599. [24] ZHU Daiyin, WANG Ling, YU Yusheng, et al. Robust ISAR range alignment via minimizing the entropy of the average range profile[J]. IEEE Geoscience and Remote Sensing Letters, 2009, 6(2): 204–208. doi: 10.1109/LGRS.2008.2010562. [25] SAUER T and SCHROTH A. Robust range alignment algorithm via Hough transform in an ISAR imaging system[J]. IEEE Transactions on Aerospace and Electronic Systems, 1995, 31(3): 1173–1177. doi: 10.1109/7.395222. [26] ZHANG Lei, SHENG Jialian, DUAN Jia, et al. Translational motion compensation for ISAR imaging under low SNR by minimum entropy[J]. EURASIP Journal on Advances in Signal Processing, 2013, 2013(1): 33. doi: 10.1186/1687-6180-2013-33. [27] LIU Lei, ZHOU Feng, TAO Mingliang, et al. Adaptive translational motion compensation method for ISAR imaging under low SNR based on particle swarm optimization[J]. IEEE Journal of Selected Topics in Applied Earth Observations and Remote Sensing, 2015, 8(11): 5146–5157. doi: 10.1109/JSTARS.2015.2491307. [28] SHAO Shuai, LIU Hongwei, ZHANG Lei, et al. Integration of super-resolution ISAR imaging and fine motion compensation for complex maneuvering ship targets under high sea state[J]. IEEE Transactions on Geoscience and Remote Sensing, 2022, 60: 5222820. doi: 10.1109/TGRS.2022.3147266. [29] FU Jixiang, XING Mengdao, AMIN M, et al. ISAR translational motion compensation with simultaneous range alignment and phase adjustment in low SNR environments[C]. 2021 IEEE Radar Conference, Atlanta, USA, 2021: 1–6. doi: 10.1109/RadarConf2147009.2021.9455148. [30] LIU Fengkai, HUANG Darong, GUO Xinrong, et al. Joint range alignment and autofocus method based on combined Broyden-fletcher-Goldfarb-Shanno algorithm and whale optimization algorithm[J]. IEEE Transactions on Geoscience and Remote Sensing, 2023, 61: 5214617. doi: 10.1109/TGRS.2023.3306474. [31] DJEDDI M and BENIDIR M. A two parallel extended Kalman filtering algorithm for the estimation of chirp signals in non-Gaussian noise[C]. The 13th European Signal Processing Conference, Antalya, Turkey, 2005: 1–4. [32] YANG Jungang, HUANG Xiaotao, JIN Tian, et al. New approach for SAR imaging of ground moving targets based on a keystone transform[J]. IEEE Geoscience and Remote Sensing Letters, 2011, 8(4): 829–833. doi: 10.1109/LGRS.2011.2118739. [33] LI Gang, XIA Xianggen, and PENG Yingning. Doppler keystone transform: An approach suitable for parallel implementation of SAR moving target imaging[J]. IEEE Geoscience and Remote Sensing Letters, 2008, 5(4): 573–577. doi: 10.1109/LGRS.2008.2000621. [34] 黄小平, 王岩, 缪鹏程. 目标定位跟踪原理及应用—MATLAB仿真[M]. 北京: 电子工业出版社, 2018.HUANG Xiaoping, WANG Yan, and MIAO Pengcheng. Principles and Applications of Target Localization and Tracking—MATLAB Simulation[M]. Beijing: Publishing House of Electronics Industry, 2018. [35] LI Min, SUN Defeng, and TOH K C. A convergent 3-block semi-proximal ADMM for convex minimization problems with one strongly convex block[J]. Asia-Pacific Journal of Operational Research, 2015, 32(4): 1550024. doi: 10.1142/S0217595915500244. [36] CHEN Lin, JIANG Bowen, LIU Yuqi, et al. Application of adaptive EKF in real-time orbit determination[J]. Journal of the Brazilian Society of Mechanical Sciences and Engineering, 2021, 43(4): 187. doi: 10.1007/s40430-021-02867-z. [37] LIU Jianjuan, CHEN Hongmei, and LIU Nanbo. Effective Sage-Husa Kalman filter for sins/Doppler/platform compass integrated navigation system[C]. 2016 IEEE Chinese Guidance, Navigation and Control Conference, Nanjing, China, 2016: 541–546. doi: 10.1109/CGNCC.2016.7828843. [38] HUANG Penghui, LIAO Guisheng, YANG Zhiwei, et al. Ground maneuvering target imaging and high-order motion parameter estimation based on second-order Keystone and generalized Hough-HAF transform[J]. IEEE Transactions on Geoscience and Remote Sensing, 2017, 55(1): 320–335. doi: 10.1109/TGRS.2016.2606436. [39] 孙景波. 旋翼无人机雷达回波微动特征分析与提取[D]. [硕士论文], 中国民航大学, 2021. doi: 10.27627/d.cnki.gzmhy.2021.000057.SUN Jingbo. Micro-motion feature analysis and extraction of rotor UAV radar echoes[D]. [Master dissertation], Civil Aviation University of China, 2021. doi: 10.27627/d.cnki.gzmhy.2021.000057. [40] DU Huagui, SONG Yongping, ZHOU Jiwen, et al. A novel parameter estimation method for polynomial phase signals via adaptive EKF[J]. IEEE Internet of Things Journal, 2024, 11(11): 20816–20830. doi: 10.1109/JIOT.2024.3373642. [41] 王武. 机载圆周SAR-GMTI关键技术研究[D]. [博士论文], 国防科技大学, 2019. doi: 10.27052/d.cnki.gzjgu.2019.000357.WANG Wu. Study on key techniques for circular SAR-GMTI[D]. [Ph.D. dissertation], National University of Defense Technology, 2019. doi: 10.27052/d.cnki.gzjgu.2019.000357. -
图(18) / 表(8)
计量
- 文章访问数: 671
- HTML全文浏览量: 188
- PDF下载量: 196
- 被引次数: 0
