一种面向低成本轻量级雷达的单比特复用阵列信号收发框架

冯力方; 黄磊; 周汉飞; 李强; 刘仕奇; 张沛昌

doi:10.12000/JR23223

一种面向低成本轻量级雷达的单比特复用阵列信号收发框架

DOI: 10.12000/JR23223 CSTR: 32380.14.JR23223

冯力方^{1, 2, ,},
黄磊^{1, 2},
周汉飞^{1, 2},
李强^{1, 2},
刘仕奇^{1, 2},
张沛昌^{1, 2}

1.
深圳大学电子与信息工程学院深圳 518060
2.
深圳大学射频异质异构集成全国重点实验室深圳 518060

基金项目: 国家自然科学基金(62101347, 62371306)，国家杰出青年科学基金(61925108)，国家自然科学基金国际合作与交流重点项目(62220106009)，广东省基础与应用基础研究基金(2021A1515011855, 2022A1515110125)，深圳市孔雀团队项目(KQTD20210811090051046)，深圳大学2035卓越研究计划，湖州市太赫兹集成电路与系统重点实验室基金(HKLTICY23KF04)，深圳市基础研究项目(20220810142731001, 20200823154213001)

详细信息

作者简介:
冯力方，博士，助理教授，主要研究方向为雷达信号处理、雷达系统

黄　磊，博士，教授，主要研究方向为阵列信号处理、雷达信号处理

周汉飞，博士，副研究员，主要研究方向为雷达信号处理

李　强，博士，副教授，主要研究方向为阵列信号处理

刘仕奇，博士，副研究员，主要研究方向为雷达信号处理

张沛昌，博士，副教授，主要研究方向为MIMO多天线系统、毫米波信号处理

通讯作者:
冯力方 fenglifangf@163.com

责任主编：易伟 Corresponding Editor: YI Wei
中图分类号: TN974
计量
- 文章访问数: 686
- HTML全文浏览量: 153
- PDF下载量: 193
- 被引次数: 1
出版历程
- 收稿日期: 2023-11-17
- 修回日期: 2023-12-29
- 网络出版日期: 2024-01-08
- 刊出日期: 2024-02-28

A Single-bit Multiplexing Array Signal Transceiver Framework for Low-cost Lightweight Radar

FENG Lifang^{1, 2
, ,},
HUANG Lei^{1, 2},
ZHOU Hanfei^{1, 2},
LI Qiang^{1, 2},
LIU Shiqi^{1, 2},
ZHANG Peichang^{1, 2}

1.
College of Electronics and Information Engineering, Shenzhen University, Shenzhen 518060, China
2.
State Key Laboratory of Radio Frequency Heterogeneous Integration, Shenzhen University, Shenzhen 518060, China

Funds: The National Natural Science Foundation of China (62101347, 62371306), The National Science Fund for Distinguished Young Scholars (61925108), The Key Project of International Cooperation and Exchanges of the National Natural Science Foundation of China (62220106009), The Guangdong Basic and Applied Basic Research Foundation (2021A1515011855, 2022A1515110125), The project of Shenzhen Peacock Plan Teams (KQTD20210811090051046), The Shenzhen University 2035 Program for Excellent Research, The Huzhou Key Laboratory of Terahertz Integrated Circuits and Systems (HKLTICY23KF04), The Foundation of Shenzhen (20220810142731001, 20200823154213001)

More Information

Corresponding author: FENG Lifang, fenglifangf@163.com

摘要

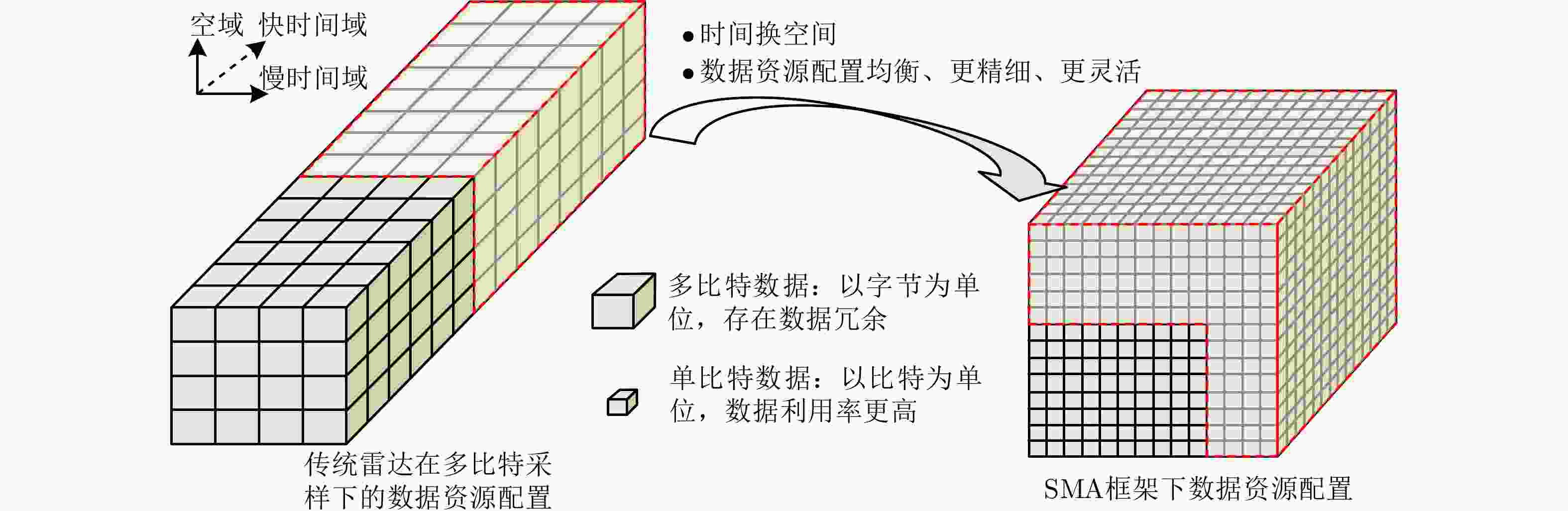
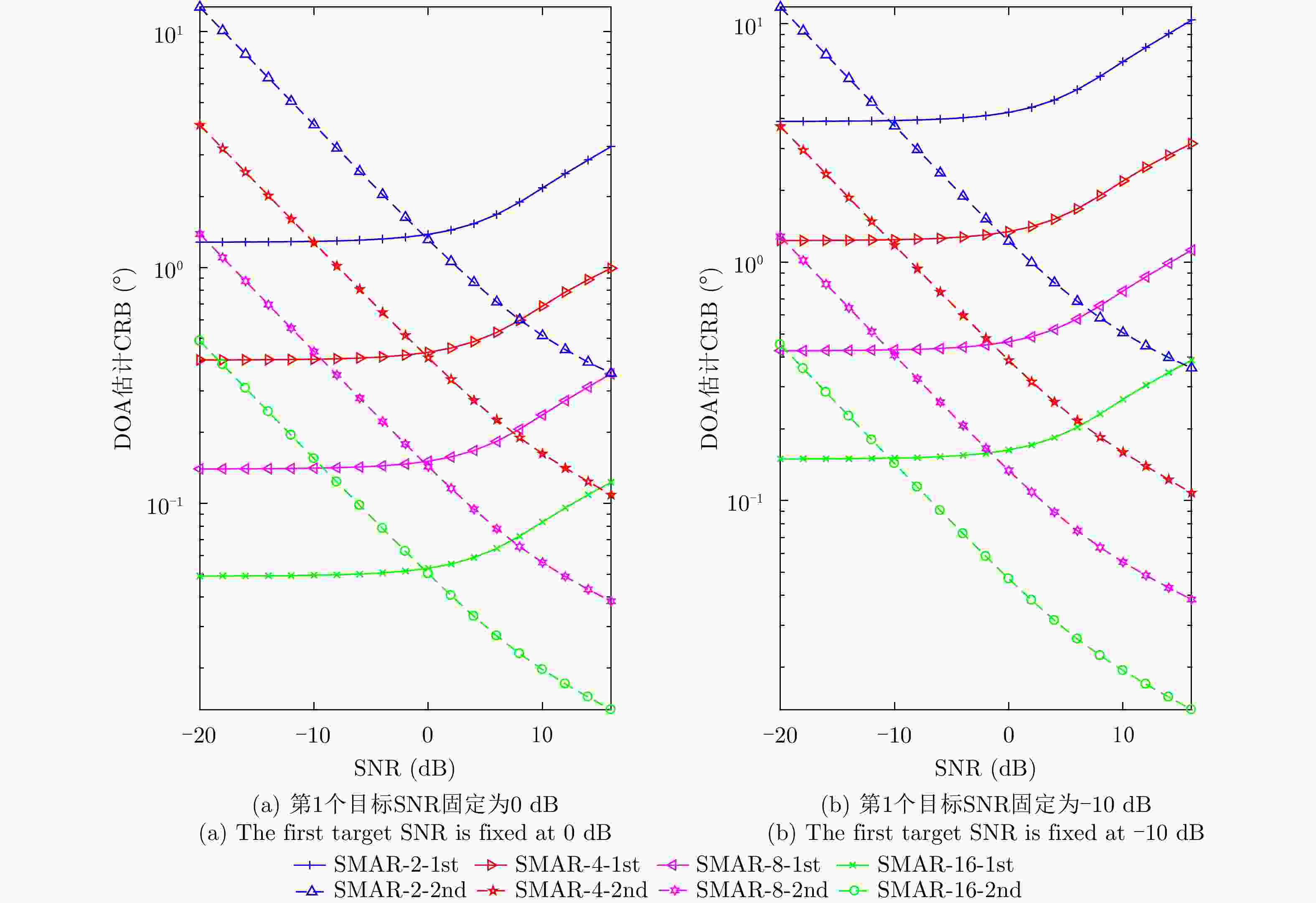
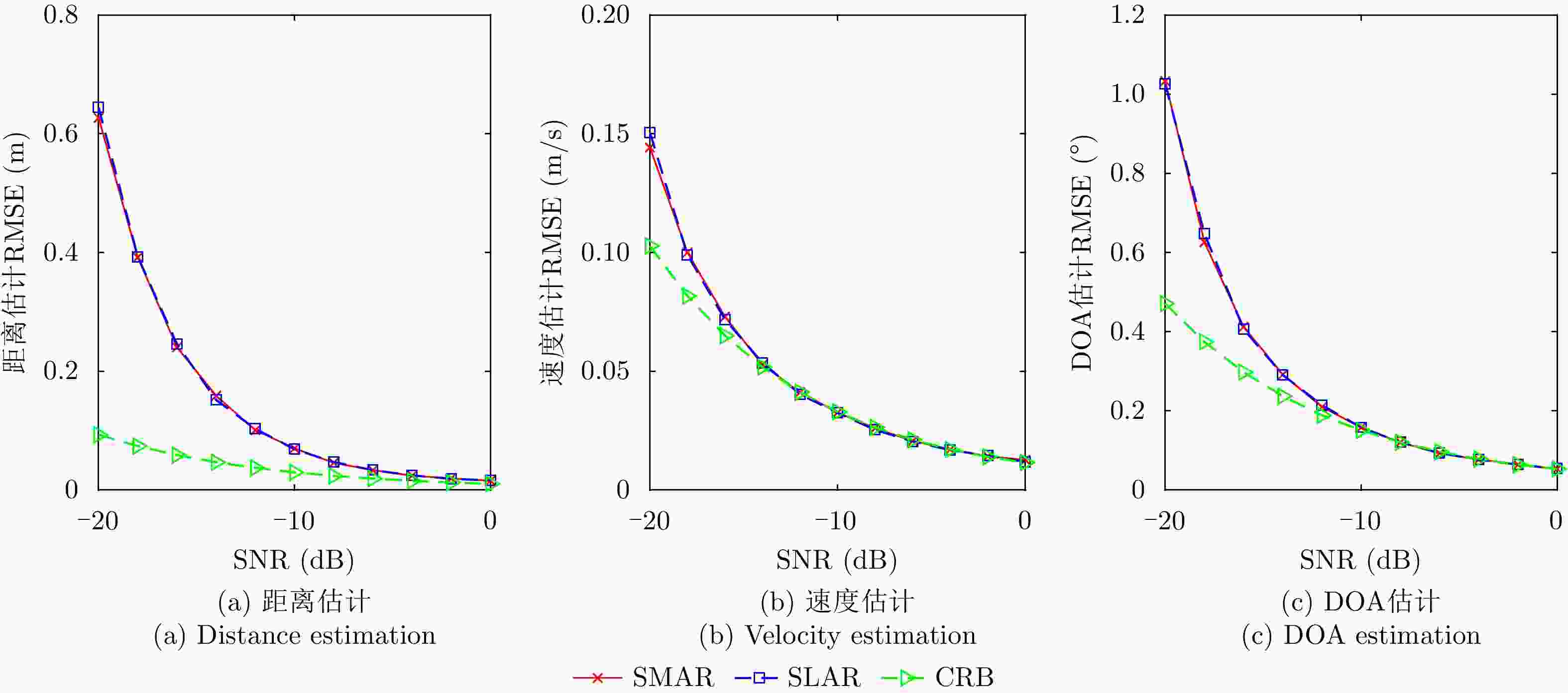
摘要: 面向低成本轻量级雷达的应用需求，该文提出了一种联合单比特采样量化和时分复用接收机的雷达信号收发框架。首先，通过介绍该框架的工作原理，阐述其在节省接收机数量方面的优势。从雷达资源配置的角度，分析了单比特采样量化在该框架中的重要性，并提出了该框架可利用时间换空间，获得比经典线性调频连续波雷达更好的探测性能。接着，推导了雷达测距、测速和测角公式，以及目标参数估计的克拉美罗界。在此基础上，验证了该框架的性能优势，同时也给出了其稳定工作的信噪比条件。最后，利用一种基于单比特二维多重信号分类的速度维配对算法，验证了该框架获取目标原理的正确性，以及性能分析的可靠性。
- 低成本轻量级雷达 /
- 线性调频连续波雷达 /
- 单比特采样 /
- 时分复用 /
- 雷达资源配置
Abstract: This paper proposes a radar signal transceiver framework that combines single-bit sampling and time division multiplexing receivers to satisfy the application requirements of low-cost lightweight radars. Firstly, this paper explains the advantages of saving the number of receivers by introducing the working principle of the framework. From the perspective of radar resource allocation, the importance of single-bit sampling in this framework was analyzed; additionally, the proposed framework can achieve better performance than a classical linear frequency modulation continuous wave radar using time and space exchange. Subsequently, the formulas for range, velocity and angle measurement were derived, along with the Cramér-Rao bound for estimating target parameters. Accordingly, the performance advantages of the proposed framework were verified, and the signal-to-noise ratio conditions for its stable operation were determined. Finally, this paper verifies the accuracy of the target acquisition principle of the proposed framework and the reliability of the performance analysis by using a velocity dimensional pairing algorithm based on single-bit two-dimensional multiple signal classification.
- Low-cost lightweight radar /
- Linear frequency modulation continuous wave radar /
- Single-bit sampling /
- Time division multiplexing /
- Radar resource allocation

HTML全文

1. 引言

极化干涉SAR^[1] 将SAR干涉测量能力和全极化探测能力相结合，可以获得地物目标更加丰富的观测信息，从而更好地反映地物目标结构特性，在森林高度反演、城区等复杂场景三维信息提取等方面有着良好的应用潜力，受到了国内外的普遍关注，并针对不同应用需求提出了不同的处理模型和方法。

在极化干涉SAR森林高度反演方面，一些学者提出了RVoG模型等经典物理模型^[2-4]，并开展了许多研究和验证。近年来，随着SAR系统分辨率的不断提高，极化干涉SAR在城区等复杂场景的应用潜力也受到了更多关注，并且已经发展了相关的处理方法，笔者总结为以下3种主要处理模型：(1)极化最优相干处理后干涉测高；(2)极化分解后干涉测高；(3)直接联立极化干涉观测方程以求解不同散射机制高度。其中，第1种处理模型应用广泛，通过极化最优相干可以提高干涉相干性，从而提升干涉测高的精度，但其只能获得一个综合意义上的高度，无法获悉不同散射机制的高度。第2种处理模型具有良好的物理可解释性，且已应用于城区建筑高度提取。例如，Garestier等人^[5]对建筑的结构及周围环境进行了理想化假设，基于Pauli基对建筑区域进行分解，利用Pauli分解后第1项和第3项的干涉相位差对建筑高度进行反演。王萍等人^[6]提出了一种基于Freeman三分量分解的极化干涉SAR建筑高度提取方法，分离了不同散射机制的相位中心。但该类方法在散射机制构成复杂的情况下难以得到有效的结果。为此，研究人员提出了第3类更具有普适性的方法。例如，Eric Pottier团队^[7]提出在极化干涉中使用基于旋转不变技术估计信号参数(Estimating Signal Parameters via Rotational Invariance Techniques, ESPRIT) 方法用于估计同一个像素内散射点的数目和位置，并以此获取建筑高度。Colin等人^[8]在ESPRIT分解基础上，提出了一种新的相干模型以区分同一像素内的3种散射机制，并应用于X波段极化干涉数据中以反演城区建筑高度。之后，Colin-koeniguer等人^[9]进一步改进模型，使其可以判断并区分同一个像素内的第1种到第3种散射机制。上述处理模型与方法的研究促进了极化干涉SAR在城区场景下的应用探索，然而，其模型方法研究均主要基于系统无误差的理想情况构建，并未考虑极化干涉SAR系统误差对模型和处理结果的影响，不利于对方法应用结果的分析和评价。为此，有必要对极化干涉SAR不同处理模型下的误差影响进行分析研究。

现有关于极化干涉SAR误差分析的研究，主要包括：在极化失真方面，Cloude^[10]分析了极化失真对极化干涉最优相干的影响；张林涛等人^[11]进一步提出了一个误差传递模型，分析了极化失真对极化干涉相位的影响；许丽颖^[12]分析了极化误差对极化干涉SAR反演林高的影响，还分析了极化误差对ESPRIT算法估计树高的影响。孙翔^[13]分析了极化误差对极化干涉SAR反演林高的影响。在干涉误差方面，文献[14-16]分析了基线、基线角和干涉通道相位对干涉的影响，文献[17-19]分析了运动补偿残余误差对干涉误差的影响；笔者前期工作^[20]进一步分析了极化失真和运动补偿残余误差对于极化最优相干下干涉相位的共同影响。综上，现有对极化干涉SAR误差影响分析的研究，在误差因素考虑以及与极化干涉SAR不同处理模型的结合上还不够全面，尚缺乏系统性的理论分析。

为此，本文针对极化干涉SAR系统误差进行了全面梳理和建模，并结合极化干涉SAR的3种处理模型推导了误差影响的规律，且通过仿真验证了误差影响模型的正确性。在此基础上，分析给出了极化干涉SAR 3种处理模型下反演的散射机制高度受极化失真、干涉误差、信噪比的影响程度。最后，使用实际无人机数据，给出了补偿误差后的高度反演结果。研究结果可为极化干涉SAR系统设计、极化干涉SAR处理方法选择以及处理结果分析理解提供理论方法支撑。

2. 不同处理模式下的基础模型与误差模型

2.1 极化干涉SAR处理模型

在介绍误差影响模型的推导之前，首先简要介绍本文涉及的3种极化干涉SAR处理模型。

2.1.1 极化最优相干处理模型

极化最优相干处理模型在文献[1]中有详细介绍，其目的是为极化观测矢量寻找一组最优的投影方向，以使得在该投影方向上获得最大的干涉相干性。

记全极化干涉图像组匹配后的某个像素位置Pauli分解后的极化向量分别为 ${{\boldsymbol{k}}}_{1},{{\boldsymbol{k}}}_{2}$ ：

$\left. \begin{split} & {{\boldsymbol{k}}}_{1}=\frac{1}{\sqrt{2}}{\bigr[\begin{array}{ccc}{S}_{{\rm{HH}}}^{1}+{S}_{{\rm{VV}}}^{1}\;\; {S}_{{\rm{HH}}}^{1}-{S}_{{\rm{VV}}}^{1}\;\;2{S}_{{\rm{HV}}}^{1}\end{array}\bigr]}^{{\rm{T}}} \\ &{{\boldsymbol{k}}}_{2}=\frac{1}{\sqrt{2}}{\bigr[\begin{array}{ccc}{S}_{{\rm{HH}}}^{2}+{S}_{{\rm{VV}}}^{2}\;\; {S}_{{\rm{HH}}}^{2}-{S}_{{\rm{VV}}}^{2}\;\; 2{S}_{{\rm{HV}}}^{2}\end{array}\bigr]}^{{\rm{T}}} \end{split}\right\}$

(1)

寻找使得干涉相干系数最大的投影向量，记为 ${{\boldsymbol{w}}}_{1}$ 和 ${{\boldsymbol{w}}}_{2}$ ，则得到最优极化相干对应的散射矢量为 ${{\boldsymbol{i}}}_{1},{{\boldsymbol{i}}}_{2}$ 。

${{\boldsymbol{i}}}_{1}={{\boldsymbol{w}}}_{1}^{\rm{H}}{{\boldsymbol{k}}}_{1},\; {{\boldsymbol{i}}}_{2}={{\boldsymbol{w}}}_{2}^{\rm{H}}{{\boldsymbol{k}}}_{2}$

(2)

其中，“H”表示共轭转置。极化最优相干后的干涉处理就是基于 ${{\boldsymbol{i}}}_{1},{{\boldsymbol{i}}}_{2}$ 进行干涉相位计算、相位解缠和高度反演等处理。

2.1.2 基于极化分解的极化干涉处理模型

基于极化分解的极化干涉处理模型，是先对相干的两组全极化图像数据各自进行极化分解，然后对分解后的每个极化分量各自进行干涉处理，从而可获得每个极化分量的相位中心高度。

Pauli分解是一种经典的极化分解方法，Pauli分解后的散射向量如式(1)所示，3个分量分别对应3种散射机制：第1个分量对应平坦表面的单次散射；第2个分量对应0°二面角散射，第3个分量对应45°的二面角散射。

由于Pauli分解在工程中应用普遍，且其为相干分解，可逐像素进行，对于建筑等人造目标比较适用，故本文重点结合Pauli分解后相干处理的模型分析误差影响。

2.1.3 基于极化干涉观测矩阵的处理模型

基于极化干涉观测矩阵的处理模型，是直接构建由主辅图像4种极化方式，共8个复数观测量所构成的观测方程，直接求解该像素内散射子的数量、每个散射子对应的干涉相位，进而反演每个散射子的高度。

该处理模型下，设匹配后的干涉图像组某个像素点内有d个散射子，则每个图像中的观测量可写为

$\left. \begin{split} & {s}_{pq}^{1}=\sum\limits_{m=1}^{d}{\sigma }_{m}{\varsigma }_{m}^{pq}{{\rm{e}}}^{{\rm{i}}{\textstyle\frac{4\pi }{\lambda }}R}+{n}_{1}^{pq} \\ & {s}_{pq}^{2}=\sum\limits_{m=1}^{d}{\sigma }'_{m}{\varsigma{'}_{ m} ^{pq}}{{\rm{e}}}^{{\rm{i}}{\textstyle\frac{4\pi }{\lambda }}\left(R+\Delta {R}_{m}\right)}+{n}_{2}^{pq} \end{split}\right\}$

(3)

其中， ${s}_{pq}^{1},{s}_{pq}^{2}$ 为两个干涉图像中该像素的复数值， $pq$ 表示极化通道(HH, HV, VH, VV)； ${\sigma }_{m}$ 和 ${\sigma }'_{m}$ 表示第m个散射子参考极化方式(如HH)下的散射系数，在基线较小的情况下，可认为 ${\sigma }_{m}\approx {\sigma }'_{m}$ ； ${\varsigma }_{m}^{pq}$ 和 ${\varsigma }_{m}'^{pq}$ 表示第m个散射子在 $pq$ 极化方式下的散射系数，通常也可认为 $\varsigma _m^{pq} \approx \varsigma_m'^{pq}$ ；R 表示该像素对应的干涉主图像中的斜距， ${\Delta }{R}_{m}$ 表示第m个散射子对应的干涉辅图像和主图像中的斜距差； ${n}_{1}^{pq},{n}_{2}^{pq}$ 为噪声。

式(3)在两个干涉通道散射矢量近似相等的假设下可以写为

${{\boldsymbol{s}}}_{1}={\boldsymbol{A}}{\boldsymbol{\sigma}} +{{\boldsymbol{n}}}_{1},\;{{\boldsymbol{s}}}_{2}\approx {\boldsymbol{A\varPhi}} {\boldsymbol{\sigma}} +{{\boldsymbol{n}}}_{2}$

(4)

其中

$\left. \begin{split} & {{\boldsymbol{s}}}_{1}={\bigr[\begin{array}{cccc}{s}_{{\rm{HH}}}^{1}& {s}_{{\rm{HV}}}^{1}& {s}_{{\rm{VH}}}^{1}& {s}_{{\rm{VV}}}^{1}\end{array}\bigr]}^{{\rm{T}}}\\ & {{\boldsymbol{s}}}_{2}={\bigr[\begin{array}{cccc}{s}_{{\rm{HH}}}^{2}& {s}_{{\rm{HV}}}^{2}& {s}_{{\rm{VH}}}^{2}& {s}_{{\rm{VV}}}^{2}\end{array}\bigr]}^{{\rm{T}}}\\ & {\boldsymbol{\varPhi}} ={\rm{diag}}\left\{{{\rm{e}}}^{{\rm{i}}{\phi }_{1}},{{\rm{e}}}^{{\rm{i}}{\phi }_{2}},\cdots ,{{\rm{e}}}^{{\rm{i}}{\phi }_{d}}\right\}\\ & {\phi }_{m}=\frac{4\pi }{\lambda }\Delta {R}_{m}\\ & {\boldsymbol{\sigma}} ={\left[{\sigma }_{1},{\sigma }_{2},\cdots,{\sigma }_{d}\right]}^{{\rm{T}}}\\ & {\boldsymbol{A}}=\left[\begin{array}{cccc}{\varsigma }_{1}^{{\rm{HH}}}& {\varsigma }_{1}^{{\rm{HV}}}& {\varsigma }_{1}^{{\rm{VH}}}& {\varsigma }_{1}^{{\rm{VV}}}\\ {\varsigma }_{2}^{{\rm{HH}}}& {\varsigma }_{2}^{{\rm{HV}}}& {\varsigma }_{2}^{{\rm{VH}}}& {\varsigma }_{2}^{{\rm{VV}}}\\ \vdots & \vdots & \vdots & \vdots \\ {\varsigma }_{d}^{{\rm{HH}}}& {\varsigma }_{d}^{{\rm{HV}}}& {\varsigma }_{d}^{{\rm{VH}}}& {\varsigma }_{d}^{{\rm{VV}}}\end{array}\right] \end{split}\right\}$

(5)

式中，d具体需要根据矩阵性质判定，待求量是 ${\boldsymbol{\varPhi}}$ 。在 ${S}_{\mathrm{V}\mathrm{H}}\approx {S}_{\mathrm{H}\mathrm{V}}$ 的假设下，协方差矩阵为

${{\boldsymbol{R}}}_{{\boldsymbol{XX}}}=\left\langle{{\boldsymbol{XX}}}^+\right\rangle$

(6)

其中

${\boldsymbol{X}}={\left[\begin{array}{ccc}{s}_{{\rm{HH}}}^{1}& {s}_{{\rm{HV}}}^{1}& \begin{array}{cccc}{s}_{{\rm{VV}}}^{1}& {s}_{{\rm{HH}}}^{2}& {s}_{{\rm{HV}}}^{2}& {s}_{{\rm{VV}}}^{2}\end{array}\end{array}\right]}^{{\rm{T}}}$

(7)

使用文献[7]中的TLS-ESPRIT算法求解，对矩阵 ${{\boldsymbol{R}}}_{{\boldsymbol{XX}}}$ 进行SVD分解，可以得到：

${{\boldsymbol{R}}}_{{\boldsymbol{XX}}}={\boldsymbol{E}}{\boldsymbol{\varLambda}} {{\boldsymbol{E}}}^{\rm{H}}=\sum\limits_{m=1}^{6}{\lambda }_{m}{e}_{m}{e}_{m}^{\rm{H}}$

(8)

其中， $\boldsymbol{\varLambda }=\mathrm{d}\mathrm{i}\mathrm{a}\mathrm{g}\left\{{\lambda }_{1},{\lambda }_{2},\cdots ,{\lambda }_{6}\right\}$ , $\boldsymbol{E}=\left[{e}_{1},{e}_{2},\cdots ,{e}_{6}\right]$ 。定义同一个像素中散射子的个数为d，一般假设d小于极化通道的总数，即 $d\le 3$ 。

矩阵E的前d列就是d个散射子对应的特征向量，将它们组合成新矩阵 ${\boldsymbol{E}}_{\boldsymbol{S}}$ ，并将它按行平均拆分为矩阵 ${\boldsymbol{E}}_{\boldsymbol{X}}$ 和 ${\boldsymbol{E}}_{\boldsymbol{Y}}$ 。矩阵 ${{\boldsymbol{E}}}_{{\boldsymbol{S}}}$ 的前3行为 ${\boldsymbol{E}}_{\boldsymbol{X}}$ ，后3行为 ${\boldsymbol{E}}_{\boldsymbol{Y}}$ 。

${{\boldsymbol{E}}}_{{\boldsymbol{S}}}=\left[\sqrt{{\lambda }_{1}}{e}_{1},\sqrt{{\lambda }_{2}}{e}_{2},\cdots ,\sqrt{{\lambda }_{d}}{e}_{d}\right]=\left[\begin{array}{c}{{\boldsymbol{E}}}_{{\boldsymbol{X}}}\\ {{\boldsymbol{E}}}_{{\boldsymbol{Y}}}\end{array}\right]$

(9)

将矩阵 ${\boldsymbol{E}}_{\boldsymbol{X}}$ 和 ${\boldsymbol{E}}_{\boldsymbol{Y}}$ 重新写为矩阵 ${\boldsymbol{E}}_{\boldsymbol{X}\boldsymbol{Y}}$ ，并对矩阵 ${\boldsymbol{E}}_{\boldsymbol{X}\boldsymbol{Y}}$ 进行SVD分解。

${{\boldsymbol{E}}}_{{\boldsymbol{XY}}}^{\rm{H}}{{\boldsymbol{E}}}_{{\boldsymbol{XY}}}=\left[\begin{array}{c}{{\boldsymbol{E}}}_{X}^{\rm{H}}\\ {{\boldsymbol{E}}}_{{\boldsymbol{Y}}}^{\rm{H}}\end{array}\right]\left[\begin{array}{cc}{{\boldsymbol{E}}}_{{\boldsymbol{X}}}& {{\boldsymbol{E}}}_{{\boldsymbol{Y}}}\end{array}\right]={{\boldsymbol{E}}}_{1}{\boldsymbol{\varLambda}} {{\boldsymbol{E}}}_{1}^{\rm{H}}$

(10)

将矩阵 ${\boldsymbol{E}}_{1}$ 拆分为4个 $d \times d$ 的子矩阵，并构造矩阵 ${\boldsymbol{\varPsi}}$ ，构造 ${\boldsymbol{\varPsi}}$ 的推导过程详见文献[21]中的式(26)。

${{\boldsymbol{E}}}_{1}=\left[\begin{array}{cc}{{\boldsymbol{E}}}_{11}& {{\boldsymbol{E}}}_{12}\\ {{\boldsymbol{E}}}_{21}& {{\boldsymbol{E}}}_{22}\end{array}\right],\quad {\boldsymbol{\varPsi}} =-{{\boldsymbol{E}}}_{12}{{\boldsymbol{E}}}_{22}^{-1}$

(11)

Roy和Kailath^[21]推导出矩阵 ${\boldsymbol{\varPsi}}$ 的特征值 ${\lambda }'_{m}$ 就是矩阵 ${\boldsymbol{\varPhi}}$ 的对角线元素。因此，每个散射子的干涉相位 ${\phi }_{m}$ 可以写为

${\phi }_{m}={\rm{arg}}\left({\lambda }'_{m}\right)$

(12)

由式(12)求解得到每个散射子的干涉相位 ${\phi }_{m}, (m=1,2,\cdots ,d)$ 后，根据干涉SAR高度反演的公式即可得到每个散射子的高度。

TLS-ESPRIT方法只能解出对应散射机制的干涉相位，无法解出对应散射机制的散射强度，后向散射系数等其他参数。因此，本文提出通过相关推导，解出ESPRIT模型中的其他参数。

将式(4)中得到的两个子阵模型合并。

${\boldsymbol{X}}=\left[\begin{array}{c}{\boldsymbol{A}}\\ {\boldsymbol{A\varPhi}} \end{array}\right]{\boldsymbol{S}}+{\boldsymbol{N}}=\bar {\boldsymbol{A}}{\boldsymbol{S}}+{\boldsymbol{N}}$

(13)

得到协方差矩阵如式(14)所示。

$\left. \begin{split} & {\boldsymbol{R}}={\rm{E}}\left[{{\boldsymbol{XX}}}^{\rm{H}}\right]=\bar{{\boldsymbol{A}}}{{\boldsymbol{R}}}_{{\boldsymbol{S}}}\bar{\boldsymbol{A}}^{\rm{H}}+{{\boldsymbol{R}}}_{{\boldsymbol{N}}}\\ & {\boldsymbol{R}}={{\boldsymbol{U}}}_{{\boldsymbol{S}}}{{\boldsymbol{\varSigma}}}_{{\boldsymbol{S}}}{{{\boldsymbol{U}}}_{\boldsymbol{S}}^{\rm{H}}} +{{\boldsymbol{U}}}_{{{{\boldsymbol{N}}}}}{{\boldsymbol{\varSigma}} }_{{\boldsymbol{N}}}{{{\boldsymbol{U}}}_{{\boldsymbol{N}}}^{\rm{H}}} \end{split} \right\}$

(14)

其中，E为期望算子， ${\boldsymbol{U}}_{\boldsymbol{S}}$ 为大特征值对应的特征向量， ${\boldsymbol{U}}_{\boldsymbol{N}}$ 为小特征值对应的特征向量。 ${\boldsymbol{\varSigma}}_{\boldsymbol{S}}$ , ${\boldsymbol{\varSigma}}_{\boldsymbol{N}}$ 为对应的奇异值矩阵。从式(14)看出 ${\boldsymbol{U}}_{\boldsymbol{S}}$ 张成的信号子空间与 $\bar{\boldsymbol{A}}$ 张成的信号子空间是相等的。

${\rm{span}}\left\{{{\boldsymbol{U}}}_{{\boldsymbol{S}}}\right\}={\rm{span}}\left\{\bar{{\boldsymbol{A}}}\right\}$

(15)

此时，存在一个唯一的非奇异矩阵T，使得

${{\boldsymbol{U}}}_{{\boldsymbol{S}}}=\bar{{\boldsymbol{A}}}{\boldsymbol{T}}$

(16)

式(16)对两个子阵都成立，所以有

${{\boldsymbol{U}}}_{{\boldsymbol{S}}}=\left[\begin{array}{c}{{\boldsymbol{U}}}_{S1}\\ {{\boldsymbol{U}}}_{S2}\end{array}\right]=\left[\begin{array}{c}{\boldsymbol{AT}}\\ {\boldsymbol{A\varPhi}} {\boldsymbol{T}}\end{array}\right]$

(17)

根据式(17)可以得到

${{\boldsymbol{U}}}_{S2}={{\boldsymbol{U}}}_{S1}{{\boldsymbol{T}}}^{-1}{\boldsymbol{\varPhi T}}={{\boldsymbol{U}}}_{S1}{\boldsymbol{\varPsi}}$

(18)

由式(18)可以得到

${\boldsymbol{\varPhi}} ={{\boldsymbol{T}}}^{-1}{\boldsymbol{\varPsi T}}$

(19)

其中， ${\boldsymbol{\varPsi }}$ 特征值组成的对角阵为 ${\boldsymbol{\varPhi}}$ ，矩阵T 的各列就是 ${\boldsymbol{\varPsi}}$ 的特征矢量。

因此根据式(13)—式(19)，逆向求解相关参数。步骤如下：

步骤1　根据式(11)，求解 ${\boldsymbol{\varPsi}}$ 。

步骤2　根据式(19)，求解T， ${\boldsymbol{\varPsi}}$ 的特征向量组合就是T。

步骤3　根据式(17)求解A。

${\boldsymbol{A}}={{\boldsymbol{U}}}_{S1}{{\boldsymbol{T}}}^{-1}$

(20)

2.2 误差类型

极化干涉SAR系统误差可以分为极化失真和干涉误差两大类，下面分别进行梳理和建模。

2.2.1 极化失真模型

极化SAR系统的失真模型为

${\boldsymbol{M}}=K{{\rm{e}}}^{{\rm{j}}\phi }\left[\begin{array}{cc}1& {\delta }_{1}\\ {\delta }_{2}& {f}_{1}\end{array}\right]\left[\begin{array}{cc}{S}_{{\rm{HH}}}& {S}_{{\rm{VH}}}\\ {S}_{{\rm{HV}}}& {S}_{{\rm{VV}}}\end{array}\right]\left[\begin{array}{cc}1& {\delta }_{3}\\ {\delta }_{4}& {f}_{2}\end{array}\right]+{\boldsymbol{N}}$

(21)

其中， ${\delta }_{1}$ , ${\delta }_{2}$ , ${\delta }_{3}$ , ${\delta }_{4}$ 是极化串扰， ${f}_{1}$ , ${f}_{2}$ 表示幅相不平衡，这些系数均为复数，K是系统增益因子， $\phi$ 是系统相位。

不考虑系统增益和相位这些一致量，式(21)可以简化写为

$\left. \begin{split} & {\boldsymbol{m}}={{\boldsymbol{P}}}''{\boldsymbol{s}} \\ & {{\boldsymbol{P}}}''=\left[\begin{array}{cccc}1& {\delta }_{4}& {\delta }_{1}& {\delta }_{1}{\delta }_{4}\\ {\delta }_{3}& {f}_{2}& {\delta }_{1}{\delta }_{3}& {\delta }_{1}{f}_{2}\\ {\delta }_{2}& {\delta }_{2}{\delta }_{4}& {f}_{1}& {\delta }_{4}{f}_{1}\\ {\delta }_{2}{\delta }_{3}& {\delta }_{2}{f}_{2}& {\delta }_{3}{f}_{1}& {f}_{1}{f}_{2}\end{array}\right] \end{split} \right\}$

(22)

其中， $\boldsymbol{m} = {\left[{m}_{\mathrm{H}\mathrm{H}}\,{m}_{\mathrm{H}\mathrm{V}}\,{m}_{\mathrm{V}\mathrm{H}}\,{m}_{\mathrm{V}\mathrm{V}} \right]}^{\mathrm{T}}$ , $\boldsymbol{s} = {\left[{s}_{\mathrm{H}\mathrm{H}}\,{s}_{\mathrm{H}\mathrm{V}}\,{s}_{\mathrm{V}\mathrm{H}}\,{s}_{\mathrm{V}\mathrm{V}} \right]}^{\mathrm{T}}$ , ${\boldsymbol{P}}''$ 为失真矩阵。

Pauli基下散射向量k可以表示为

${\boldsymbol{k}}=\frac{1}{\sqrt{2}}{{\boldsymbol{B}}}'{\boldsymbol{s}}$

(23)

其中， $\boldsymbol{k} = {1}/{\sqrt{2}}[{s}_{\mathrm{H}\mathrm{H}} + {s}_{\mathrm{HV}\mathrm{V}}\;{s}_{\mathrm{H}\mathrm{H}} - {s}_{\mathrm{V}\mathrm{V}}\;{s}_{\mathrm{H}\mathrm{V}} + {s}_{\mathrm{V}\mathrm{H}}\;\mathrm{j} ({s}_{\mathrm{H}\mathrm{V}}- {s}_{\mathrm{V}\mathrm{H}})]^{\mathrm{T}}$ ，则在极化失真影响下，含误差的散射向量 ${\boldsymbol{k}}'$ 可以表示为

${{\boldsymbol{k}}}'=\frac{1}{\sqrt{2}}{{\boldsymbol{B}}}' {\boldsymbol{m}}=\frac{1}{\sqrt{2}}{{\boldsymbol{B}}}'{{\boldsymbol{P}}}''{\boldsymbol{s}}={{\boldsymbol{B}}}'{{\boldsymbol{P}}}''{{\boldsymbol{B}}}'^{-1} {\boldsymbol{k}}={\boldsymbol{Zk}}$

(24)

其中， $\boldsymbol{Z}={\boldsymbol{B}}'{\boldsymbol{P}}''{\boldsymbol{B}}'^{-1}$ 是Pauli基下的极化失真矩阵。

在互易介质情况下，根据互易定理将相干散射矢量简化为三维矢量，会有类似的表达式，此时Z可以表示为 $\boldsymbol{Z}=\boldsymbol{B}\boldsymbol{P}{\boldsymbol{B}}^{-1}$ 。其中：

$\begin{split} & {\boldsymbol{P}} = \left[ \begin{array}{ccc}1& {\delta }_{1}+{\delta }_{4}& {\delta }_{1}{\delta }_{4}\\ \dfrac{{\delta }_{2}+{\delta }_{3}}{2}& \dfrac{{\delta }_{1}{\delta }_{3}+{\delta }_{2}{\delta }_{4}+{f}_{1}+{f}_{2}}{2}& \dfrac{{\delta }_{1}{f}_{2}+{\delta }_{4}{f}_{1}}{2}\\ {\delta }_{2}{\delta }_{3}& {\delta }_{2}{f}_{2}+{\delta }_{3}{f}_{1}& {f}_{1}{f}_{2}\end{array} \right],\\ & {\boldsymbol{B}}=\left[\begin{array}{ccc}1& 0& 1\\ 1& 0& -1\\ 0& 2& 0\end{array}\right]\\[-21pt] \end{split}$

(25)

2.2.2 干涉误差模型

干涉SAR系统误差主要包括系统延迟误差、基线长度误差、基线角误差和干涉相位误差。其中系统延迟误差是极化干涉SAR各个通道共有的误差，故此处不予考虑。

本文重点考虑能引起各个通道间不一致的误差量，即重点考虑基线长度误差、基线角误差和干涉相位误差，其中干涉相位误差包括了系统干涉通道引入的相位误差和运动补偿残余导致的干涉相位误差。因此，本节推导干涉相位、基线和基线角误差对反演高度的影响。

干涉SAR的观测几何如图1所示。

图 1 干涉SAR观测几何示意图

Figure 1. The schematic diagram of InSAR

下载: 全尺寸图片幻灯片

其中，H表示雷达高度，M和N为两个天线。P为目标点，h为目标点高度， ${\theta }_{1}$ 表示天线的视角，B为基线长度， $\alpha$ 为基线角， ${R}_{1},{R}_{2}$ 为 $M,N$ 与目标P的距离。

配准后的干涉图像 ${s}_{1}$ 和 ${s}_{2}$ 进行干涉可得到范围为 $[-\pi ,\pi ]$ 的缠绕相位为

${\phi }_{\omega }={\rm{arg}}({s}_{1}{s}_{2}^{{\rm{H}}})$

(26)

其中， $\mathrm{a}\mathrm{r}\mathrm{g}$ 表示取相位。通过相位解缠得到解缠后的干涉相位 $\phi$ 如下：

$\phi =-\frac{2\pi Q}{\lambda }({R}_{1}-{R}_{2})$

(27)

其中，雷达一发双收模式下 $Q=1$ ；如果雷达双发双收模式下 $Q=2$ 。根据图1的几何关系有

${\sin}\left({\theta }_{1}-\alpha \right)=\frac{{R}_{1}^{2}-{R}_{2}^{2}+{B}^{2}}{2{R}_{1}B}$

(28)

将式(27)代入式(28)，可以得到：

${\theta }_{1}=\alpha + {\arcsin}\left(\frac{B}{2{R}_{1}}-\frac{\lambda \phi }{2\pi QB}-\frac{{\lambda }^{2}{\phi }^{2}}{8{\pi }^{2}{Q}^{2}{R}_{1}B}\right)$

(29)

当存在基线误差 ${\Delta }B$ 、基线角误差 ${\Delta }\alpha$ 和干涉相位误差 ${\Delta }\phi$ 时，有

$\begin{split} {{\theta }'_{1}}=& (\alpha +\Delta \alpha )+ {{\rm{arcsin}}}\left(\frac{B+\Delta B}{2{R}_{1}}\right.\\ & \left. -\frac{\lambda (\phi +\Delta \phi )}{2\pi Q(B+\Delta B)}-\frac{{\lambda }^{2}(\phi +\Delta \phi {)}^{2}}{8{\pi }^{2}{Q}^{2}{R}_{1}(B+\Delta B)}\right) \end{split}$

(30)

目标高度可以表示为

$h=H-{R}_{1}{{\cos}{\theta }'_{1}}$

(31)

基于以上公式，求解的目标高度对基线长度、基线角和干涉相位误差的敏感度为

$\left. \begin{split} & \frac{\partial h}{\partial \phi }=\frac{\lambda {R}_{1}{\sin}{\theta }_{1}}{2\pi QB{\cos}\left({\theta }_{1}-\alpha \right)}\\ & \frac{\partial h}{\partial B}=\frac{\lambda \phi {R}_{1}{\sin}{\theta }_{1}}{2\pi Q{B}^{2}{\cos}\left({\theta }_{1}-\alpha \right)}\\ & \frac{\partial h}{\partial \alpha }={R}_{1}{\sin}{\theta }_{1} \end{split}\right\}$

(32)

2.3 不同处理模式下的误差影响分析

基于上述极化失真和干涉误差的模型，本节进一步结合极化干涉SAR不同处理方法进行误差影响的理论分析。

2.3.1 基于极化最优相干的极化干涉误差影响

基于笔者前期工作^[20]，我们已得到极化失真和干涉相位误差两者共存下对基于极化最优相干的干涉相位影响。考虑极化失真与干涉相位误差后Pauli基下的失真矩阵为

$\begin{split} & {{\boldsymbol{Z}}'_i} = {{\boldsymbol{BEPB}}^{{\boldsymbol{ - 1}}}} = \exp ( - {\rm{j}}{{\Delta }}{\varphi _{ei}}) \times \frac{1}{2} \\ & \qquad \times\left[ {\begin{array}{*{20}{c}} {1 + \delta _2^i\delta _3^i + \delta _1^i\delta _4^i + f_1^if_2^i}&{1 + \delta _2^i\delta _3^i - \delta _1^i\delta _4^i - f_1^if_2^i}&{\delta _1^i + \delta _4^i + \delta _2^if_2^i + \delta _3^if_1^i} \\ {1 - \delta _2^i\delta _3^i + \delta _1^i\delta _4^i - f_1^if_2^i}&{1 - \delta _2^i\delta _3^i - \delta _1^i\delta _4^i + f_1^if_2^i}&{\delta _1^i + \delta _4^i - \delta _2^if_2^i - \delta _3^if_1^i} \\ {\delta _2^i + \delta _3^i + \delta _4^if_1^i + \delta _1^if_2^i}&{\delta _2^i + \delta _3^i - \delta _4^if_1^i - \delta _1^if_2^i}&{\delta _1^i\delta _3^i + \delta _2^i\delta _4^i + f_1^i + f_2^i} \end{array}} \right],\;\;i = 1,2 \end{split}$

(33)

其中， ${\Delta \varphi }_{e1},{\Delta \varphi }_{e2}$ 分别是两个干涉天线各自的相位误差， ${{\boldsymbol{Z}}}'_{1},{{\boldsymbol{Z}}}'_{2}$ 分别是两个干涉天线的极化失真矩阵。右上角的i表示第i个天线，例如 ${\delta }_{1}^{i}$ 表示第i个天线的 ${\delta }_{1}$ ， ${f}_{1}^{i}$ 表示第i个天线的 ${f}_{1}$ 。 ${\boldsymbol{E}}$ 矩阵意义详见文献[20]。

基于式(2)、式(24)和式(33)，可以推导得到极化最优相干下的干涉相位误差。给出极化失真和干涉相位误差对基于极化最优相干的干涉相位的影响公式，如式(34)所示。

$\begin{split} & \Delta {\phi }_{j}=-(\Delta {\varphi }_{e1}-\Delta {\varphi }_{e2})-{{\rm{arg}}}\left({{\boldsymbol{v}}}_{1j}^{{\rm{H}}}{{{\boldsymbol{Z}}}'}_{2}^{{\rm{H}}}{{\boldsymbol{Z}}}_{1}'{{\boldsymbol{v}}}_{2j}\right),\\ & j=\mathrm{1,2},3\\[-10pt] \end{split}$

(34)

其中， $\left|{{{\boldsymbol{v}}}}_{1{j}}\right|=\left|{\boldsymbol{v}}_{2{j}}\right|=1$ , $\mathrm{arg}\left({\boldsymbol{v}}_{1{j}}^{\rm{H}}{\boldsymbol{v}}_{2{j}}\right)=0$ ， ${{\boldsymbol{v}}}_{1{j}}$ 和 ${{\boldsymbol{v}}}_{2{j}}$ 表示极化最优相干的投影方向，具体意义参见文献[20]中的说明。

本文进一步考虑极化失真和干涉基线、基线角、干涉相位误差共存时对高度的影响。对于极化最优相干后的干涉而言，高度的求解公式同式(29)—式(31)，只是式中的 ${\Delta }\phi$ 换成了 ${\Delta }{\phi }_{j}$ 。因此在极化最优相干处理模型下，高度误差对基线、基线角和干涉相位的敏感度同式(32)，影响规律与干涉SAR误差影响规律相同，但由于极化失真带来了干涉相位误差的变化，故误差数值会存在差别，具体数值可基于式(29)—式(34)进行计算分析。

2.3.2 基于Pauli分解的极化干涉误差影响

根据式(24)和式(33)，对于Pauli分解后的散射矢量 ${\boldsymbol{k}}_{1}$ , ${\boldsymbol{k}}_{2}$ ，其在极化失真矩阵作用的 ${\boldsymbol{k}}'_{1}$ , ${\boldsymbol{k}}'_{2}$ 为

${{{\boldsymbol{k}}}'_{i}}={\exp}(-{\rm{j}}\Delta {\varphi }_{ei})\times \frac{1}{\sqrt{2}} \times \left[\begin{array}{c}{s}_{{\rm{HH}}}^{i}+\left({\delta }_{1}^{i}+{\delta }_{4}^{i}+{\delta }_{2}^{i}{f}_{2}^{i}+{\delta }_{3}^{i}{f}_{1}^{i}\right){s}_{{\rm{HV}}}^{i}+{f}_{1}^{i}{f}_{2}^{i}{s}_{{\rm{VV}}}^{i}\\ {s}_{{\rm{HH}}}^{i}+\left({\delta }_{1}^{i}+{\delta }_{4}^{i}-{\delta }_{2}^{i}{f}_{2}^{i}-{\delta }_{3}^{i}{f}_{1}^{i}\right){s}_{{\rm{HV}}}^{i}-{f}_{1}^{i}{f}_{2}^{i}{s}_{{\rm{VV}}}^{i}\\ 2\left({\delta }_{2}^{i}+{\delta }_{3}^{i}\right){s}_{{\rm{HH}}}^{i}+\left({f}_{1}^{i}+{f}_{2}^{i}\right){s}_{{\rm{HV}}}^{i}+\left({\delta }_{1}^{i}{f}_{2}^{i}+{\delta }_{4}^{i}{f}_{1}^{i}\right){s}_{{\rm{VV}}}^{i}\end{array}\right] ,\;\; i={1,2}$

(35)

则每个散射机制对应的干涉相位为

$\left. \begin{split} & {\phi }'_{p1}={{\rm{arg}}}\left\{{{k}'_{1}}\left(1\right){{k}'_{2}}{\left(1\right)}^{\rm{H}}\right\}=-\left(\Delta {\varphi }_{e1}-\Delta {\varphi }_{e2}\right)+{{\rm{arg}}}\Bigr\{\left[{s}_{{\rm{HH}}}^{1}+\left({\delta }_{1}^{1}+{\delta }_{4}^{1}+{\delta }_{2}^{1}{f}_{2}^{1}+{\delta }_{3}^{1}{f}_{1}^{1}\right){s}_{{\rm{HV}}}^{1}+{f}_{1}^{1}{f}_{2}^{1}{s}_{{\rm{VV}}}^{1}\right]\ \\ & \left.\qquad\;\;\times {\left[{s}_{{\rm{HH}}}^{2}+\left({\delta }_{1}^{2}+{\delta }_{4}^{2}+{\delta }_{2}^{2}{f}_{2}^{2}+{\delta }_{3}^{2}{f}_{1}^{2}\right){s}_{{\rm{HV}}}^{2}+{f}_{1}^{2}{f}_{2}^{2}{s}_{{\rm{VV}}}^{2}\right]}^{\rm{H}}\right\} \\ & {\phi }'_{p2}=-\left(\Delta {\varphi }_{e1}-\Delta {\varphi }_{e2}\right)+{{\rm{arg}}}\Bigr\{\left[{s}_{{\rm{HH}}}^{1}+\left({\delta }_{1}^{1}+{\delta }_{4}^{1}-{\delta }_{2}^{1}{f}_{2}^{1}-{\delta }_{3}^{1}{f}_{1}^{1}\right){s}_{{\rm{HV}}}^{1}-{f}_{1}^{1}{f}_{2}^{1}{s}_{{\rm{VV}}}^{1}\right] \\ & \qquad\;\;\times\left.{\left[{s}_{{\rm{HH}}}^{2}+\left({\delta }_{1}^{2}+{\delta }_{4}^{2}-{\delta }_{2}^{2}{f}_{2}^{2}-{\delta }_{3}^{2}{f}_{1}^{2}\right){s}_{{\rm{HV}}}^{2}-{f}_{1}^{2}{f}_{2}^{2}{s}_{{\rm{VV}}}^{2}\right]}^{\rm{H}}\right\} \\ & {\phi }'_{p3} =-\left(\Delta {\varphi }_{e1}-\Delta {\varphi }_{e2}\right)+{{\rm{arg}}}\Bigr\{\left[2\left({\delta }_{2}^{1}+{\delta }_{3}^{1}\right){s}_{{\rm{HH}}}^{1}+\left({f}_{1}^{1}+{f}_{2}^{1}\right){s}_{{\rm{HV}}}^{1}+\left({\delta }_{1}^{1}{f}_{2}^{1}+{\delta }_{4}^{1}{f}_{1}^{1}\right){s}_{{\rm{VV}}}^{1}\right] \\ & \qquad\;\;\times\left.{\left[2\left({\delta }_{2}^{2}+{\delta }_{3}^{2}\right){s}_{{\rm{HH}}}^{2}+\left({f}_{1}^{2}+{f}_{2}^{2}\right){s}_{{\rm{HV}}}^{2}+\left({\delta }_{1}^{2}{f}_{2}^{2}+{\delta }_{4}^{2}{f}_{1}^{2}\right){s}_{{\rm{VV}}}^{2}\right]}^{\rm{H}}\right\} \end{split}\right\}$

(36)

干涉相位误差为

$\left. \begin{split} & \Delta {\phi }'_{p1}=-\left(\Delta {\varphi }_{e1}-\Delta {\varphi }_{e2}\right)+{{\rm{arg}}}\Bigr\{\left[{s}_{{\rm{HH}}}^{1}+\left({\delta }_{1}^{1}+{\delta }_{4}^{1}+{\delta }_{2}^{1}{f}_{2}^{1}+{\delta }_{3}^{1}{f}_{1}^{1}\right){s}_{{\rm{HV}}}^{1}+{f}_{1}^{1}{f}_{2}^{1}{s}_{{\rm{VV}}}^{1}\right] \\ & \qquad\quad\times\left.{\left[{s}_{{\rm{HH}}}^{2}+\left({\delta }_{1}^{2}+{\delta }_{4}^{2}+{\delta }_{2}^{2}{f}_{2}^{2}+{\delta }_{3}^{2}{f}_{1}^{2}\right){s}_{{\rm{HV}}}^{2}+{f}_{1}^{2}{f}_{2}^{2}{s}_{{\rm{VV}}}^{2}\right]}^{\rm{H}}\right\}-{{\rm{arg}}}\left\{\left[{s}_{{\rm{HH}}}^{1}+{s}_{{\rm{VV}}}^{1}\right]{\left[{s}_{{\rm{HH}}}^{2}+{s}_{{\rm{VV}}}^{2}\right]}^{\rm{H}}\right\} \\ & \Delta {\phi }'_{p2}=-\left(\Delta {\varphi }_{e1}-\Delta {\varphi }_{e2}\right)+{{\rm{arg}}}\Bigr\{\left[{s}_{{\rm{HH}}}^{1}+\left({\delta }_{1}^{1}+{\delta }_{4}^{1}-{\delta }_{2}^{1}{f}_{2}^{1}-{\delta }_{3}^{1}{f}_{1}^{1}\right){s}_{{\rm{HV}}}^{1}-{f}_{1}^{1}{f}_{2}^{1}{s}_{{\rm{VV}}}^{1}\right] \\ & \qquad\quad\times\left.{\left[{s}_{{\rm{HH}}}^{2}+\left({\delta }_{1}^{2}+{\delta }_{4}^{2}-{\delta }_{2}^{2}{f}_{2}^{2}-{\delta }_{3}^{2}{f}_{1}^{2}\right){s}_{{\rm{HV}}}^{2}-{f}_{1}^{2}{f}_{2}^{2}{s}_{{\rm{VV}}}^{2}\right]}^{\rm{H}}\right\}-{{\rm{arg}}}\left\{\left[{s}_{{\rm{HH}}}^{1}-{s}_{{\rm{VV}}}^{1}\right]{\left[{s}_{{\rm{HH}}}^{2}-{s}_{{\rm{VV}}}^{2}\right]}^{\rm{H}}\right\} \\ & \Delta {\phi }'_{p3}=-\left(\Delta {\varphi }_{e1}-\Delta {\varphi }_{e2}\right)+{\rm{arg}}\Bigr\{\left[2\left({\delta }_{2}^{1}+{\delta }_{3}^{1}\right){s}_{{\rm{HH}}}^{1}+\left({f}_{1}^{1}+{f}_{2}^{1}\right){s}_{{\rm{HV}}}^{1}+\left({\delta }_{1}^{1}{f}_{2}^{1}+{\delta }_{4}^{1}{f}_{1}^{1}\right){s}_{{\rm{VV}}}^{1}\right] \\ & \qquad\quad\times\left.{\left[2\left({\delta }_{2}^{2}+{\delta }_{3}^{2}\right){s}_{{\rm{HH}}}^{2}+\left({f}_{1}^{2}+{f}_{2}^{2}\right){s}_{{\rm{HV}}}^{2}+\left({\delta }_{1}^{2}{f}_{2}^{2}+{\delta }_{4}^{2}{f}_{1}^{2}\right){s}_{{\rm{VV}}}^{2}\right]}^{\rm{H}}\right\}-{{\rm{arg}}}\left\{\left[2{s}_{{\rm{HV}}}^{1}\right]{\left[2{s}_{{\rm{HV}}}^{2}\right]}^{\rm{H}}\right\} \end{split}\right\}$

(37)

可见每个极化分量的干涉相位误差除了 $\left({\Delta }{\varphi }_{e1}- {\Delta }{\varphi }_{e2}\right)$ 外，还受到了极化失真的影响，且影响关系在不同散射机制下不尽相同。此外，对于每个散射机制的高程求解公式同式(29)—式(31)，只是式中的 ${\Delta }\phi$ 换成了 ${\Delta }{\phi }_{pj},\left(j=\mathrm{1,2},3\right)$ 。基于Pauli分解的极化干涉处理可以得到不同散射机制的高度，因此我们还关心各种误差对不同极化散射机制间高度差的影响，其可有助于指导极化干涉SAR的应用。

根据式(31)，散射机制 ${p}_{1}$ , ${p}_{2}$ 的高度差 ${\Delta }h$ 为

$\Delta h=-{R}_{1}\left({\cos}{\theta }_{1p1}-{\cos}{\theta }_{1p2}\right)$

(38)

其中， ${\theta }_{1p1},{\theta }_{1p2}$ 分别为两种散射机制的散射子对应于干涉主天线的视角。当存在极化失真和干涉误差时，高度差变为

$\Delta {h}'=-{R}_{1}\left({{\cos}\theta }'_{1p1}-{{\cos}\theta }'_{1p2}\right)$

(39)

故高度差的误差为

$\begin{split} \Delta {h}'-\Delta h=& \frac{\lambda {R}_{1}{\sin}{\theta }_{1p1}}{2\pi QB{\cos}\left({\theta }_{1p1}-\alpha \right)}\Delta {\phi }'_{p1}\\ & -\frac{\lambda {R}_{1}{\sin}{\theta }_{1p2}}{2\pi QB{\cos}\left({\theta }_{1p2}-\alpha \right)}\Delta {\phi }'_{p2} +\frac{\lambda {R}_{1}}{2\pi Q{B}^{2}}\\ & \times\left(\frac{{\phi }_{p1}{\sin}{\theta }_{1p1}}{{\cos}\left({\theta }_{1p1}-\alpha \right)}-\frac{{\phi }_{p2}{\sin}{\theta }_{1p2}}{{\cos}\left({\theta }_{1p2}-\alpha \right)}\right)\Delta B\\ &+{R}_{1}\left({\sin}{\theta }_{1p1}-{\sin}{\theta }_{1p2}\right)\Delta \alpha \\[-10pt] \end{split}$

(40)

可见，如不同散射子本身的高度差较大，则视角差异较大，故对基线长度、基线角和干涉相位误差的敏感度较大，同时受到极化失真的影响；如果散射子自身的高度差异很小，则高度差的误差基本不受基线、基线角和干涉相位误差的影响，主要受到极化失真的影响。3.2.2节分析了散射子高度差异较大和较小的情况下，各种误差对Pauli分解的影响。

2.3.3 极化干涉观测矩阵直接求解高度的误差影响

3.1.3节用仿真分析了极化串扰对ESPRIT的影响，得到极化串扰对ESPRIT的影响很小的结论，因此此处忽略串扰下进行推导。

若忽略串扰，根据式(22)，P可以简化为

${\boldsymbol{P}}=\left[\begin{array}{ccc}1& 0& 0\\ 0& \dfrac{{f}_{1}+{f}_{2}}{2}& 0\\ 0& 0& {f}_{1}{f}_{2}\end{array}\right]$

(41)

对于式(7)的散射矢量X，记考虑误差后的散射矢量 $\boldsymbol{X}'$ 为

${{\boldsymbol{X}}}'={\left[\begin{array}{ccc}{m}_{{\rm{HH}}}^{1}& {m}_{{\rm{HV}}}^{1}& \begin{array}{cccc}{m}_{{\rm{VV}}}^{1}& {m}_{{\rm{HH}}}^{2}& {m}_{{\rm{HV}}}^{2}& {m}_{{\rm{VV}}}^{2}\end{array}\end{array}\right]}^{{\rm{T}}}$

(42)

其与X的关系为

${{\boldsymbol{X}}}'={{\boldsymbol{P}}}'{\boldsymbol{X}}$

(43)

其中

$\begin{split} & {{\boldsymbol{P}}}'=\left[\begin{array}{cc}{\exp}(-{\rm{j}}\Delta {\varphi }_{e1})\times {{\boldsymbol{P}}}_{1}& 0\\ 0& {\exp}(-{\rm{j}}\Delta {\varphi }_{e2})\times {{\boldsymbol{P}}}_{2}\end{array}\right],\\ & {{\boldsymbol{P}}}_{1}=\left[\begin{array}{ccc}1& 0& 0\\ 0& \dfrac{{f}_{1}^{1}+{f}_{2}^{1}}{2}& 0\\ 0& 0& {f}_{1}^{1}{f}_{2}^{1}\end{array}\right],\\ & {{\boldsymbol{P}}}_{2}=\left[\begin{array}{ccc}1& 0& 0\\ 0& \dfrac{{f}_{1}^{2}+{f}_{2}^{2}}{2}& 0\\ 0& 0& {f}_{1}^{2}{f}_{2}^{2}\end{array}\right]\\[-25pt] \end{split}$

(44)

考虑误差后的相干矩阵为

${{\boldsymbol{R}}}'=\left\langle{{\boldsymbol{X}}}'\times {{\boldsymbol{X}}}'^{\rm{H}}\right\rangle =\left\langle{{\boldsymbol{P}}}'{{\boldsymbol{X}}}'{{\boldsymbol{X}}}'^{\rm{H}}{{\boldsymbol{P}}'}^{\rm{H}}\right\rangle ={{\boldsymbol{P}}}'{\boldsymbol{R}}{{\boldsymbol{P}}'}^{\rm{H}}$

(45)

对相干矩阵 ${\boldsymbol{R}}'$ 进行SVD分解：

${{\boldsymbol{R}}}'={{\boldsymbol{E}}}'{\boldsymbol{\varLambda}} {{\boldsymbol{E}}}'^{{\rm{H}}}={\sum \limits_{m=1}^{6}{\lambda }_{m}{{\boldsymbol{P}}}'{e}_{m}\left({{\boldsymbol{P}}}'{e}_{m}\right)^{\rm{H}}}$

(46)

将前d列向量写成一个新矩阵 ${\boldsymbol{E}}'_{\boldsymbol{S}}$ ， $d\le 3$ 。

$\begin{split} {{\boldsymbol{E}}}_{{\boldsymbol{S}}}'=& \left[\sqrt{{\lambda }_{1}}{{\boldsymbol{P}}}'_{{e}_{1}},\sqrt{{\lambda }_{2}}{{\boldsymbol{P}}}'_{{e}_{2}},\cdots ,\sqrt{{\lambda }_{d}}{{\boldsymbol{P}}}'_{{e}_{d}}\right]\\ =& \left[\begin{array}{c}{\exp}(-{\rm{j}}\Delta {\varphi }_{e1})\times {{\boldsymbol{P}}}_{1}\times {{\boldsymbol{E}}}_{{\boldsymbol{X}}}\\ {\exp}(-{\rm{j}}\Delta {\varphi }_{e2})\times {{\boldsymbol{P}}}_{2}\times {{\boldsymbol{E}}}_{{\boldsymbol{Y}}}\end{array}\right]=\left[\begin{array}{c}{{\boldsymbol{E}}}_{{\boldsymbol{X}}}'\\ {{\boldsymbol{E}}}_{{\boldsymbol{Y}}}'\end{array}\right] \end{split}$

(47)

将矩阵 ${\boldsymbol{E}}'_{\boldsymbol{X}}$ 和 ${\boldsymbol{E}}'_{\boldsymbol{Y}}$ 重新写为矩阵 ${\boldsymbol{E}}'_{\boldsymbol{X}\boldsymbol{Y}}$ ，并进行SVD分解。

$\begin{split} {\boldsymbol{E}}{}_{\boldsymbol{XY}}'^{\rm{H}}{{\boldsymbol{E}}}_{{\boldsymbol{XY}}}'=& \left[\begin{array}{c}{{{\boldsymbol{E}}}}_{{\boldsymbol{X}}}'^{\rm{H}}\\ {{{\boldsymbol{E}}}}_{Y}'^{\rm{H}}\end{array}\right]\Bigr[\begin{array}{cc}{{\boldsymbol{E}}}_{{\boldsymbol{X}}}'& {{\boldsymbol{E}}}_{{\boldsymbol{Y}}}'\end{array}\Bigr] = \left[\begin{array}{cc}{{\boldsymbol{E}}}_{{\boldsymbol{X}}}^{\rm{H}}{{\boldsymbol{P}}}_{1}^{\rm{H}}{{\boldsymbol{P}}}_1{{\boldsymbol{E}}}_{{\boldsymbol{X}}}& {{\rm{e}}}^{{\rm{j}}\left(\Delta {\varphi }_{e2}-\Delta {\varphi }_{e1}\right)}{{\boldsymbol{E}}}_{{\boldsymbol{X}}}^{\rm{H}}{{\boldsymbol{P}}}_{1}^{\rm{H}}{{\boldsymbol{P}}}_{2}{{\boldsymbol{E}}}_{{\boldsymbol{Y}}}\\ {{\rm{e}}}^{{\rm{j}}\left(\Delta {\varphi }_{e1}-\Delta {\varphi }_{e2}\right)}{{\boldsymbol{E}}}_{{\boldsymbol{Y}}}^{\rm{H}}{{\boldsymbol{P}}}_{2}^{\rm{H}}{{\boldsymbol{P}}}_{1}{{\boldsymbol{E}}}_{{\boldsymbol{X}}}& {{\boldsymbol{E}}}_{{\boldsymbol{Y}}}^{\rm{H}}{{\boldsymbol{P}}}_{2}^{\rm{H}}{{\boldsymbol{P}}}_{2}{{\boldsymbol{E}}}_{{\boldsymbol{Y}}}\end{array}\right]\\ =& \left[\begin{array}{cc}{c}_{11}{{\boldsymbol{E}}}_{{\boldsymbol{X}}}^{\rm{H}}{{\boldsymbol{E}}}_{{\boldsymbol{X}}}& {c}_{12}{\boldsymbol{{E}}}_{{\boldsymbol{X}}}^{\rm{H}}{{\boldsymbol{E}}}_{{\boldsymbol{Y}}}\\ {c}_{21}{{\boldsymbol{E}}}_{{\boldsymbol{Y}}}^{\rm{H}}{{\boldsymbol{E}}}_{{\boldsymbol{X}}}& {c}_{22}{{\boldsymbol{E}}}_{{\boldsymbol{Y}}}^{\rm{H}}{{\boldsymbol{E}}}_{{\boldsymbol{Y}}}\end{array}\right]={{\boldsymbol{E}}}_{1}'{\boldsymbol{\varLambda}} {{\boldsymbol{E}}}_{1}'^{\rm{H}} \end{split}$

(48)

因为矩阵 ${\boldsymbol{P}}_{1}$ 和 ${\boldsymbol{P}}_{2}$ 是对角阵，所以可以将它们的乘积提出来，计算后作为系数，即 ${c}_{11},{c}_{12},{c}_{21},{c}_{22}$ 。其中

$\begin{split} & {c}_{11}=1 + \frac{\left({f}_{1}^{1} + {f}_{2}^{1}\right){\left({f}_{1}^{1} + {f}_{2}^{1}\right)}^{\rm{H}}}{4} + {f}_{1}^{1}{f}_{2}^{1}{\left({f}_{1}^{1}{f}_{2}^{1}\right)}^{\rm{H}}, {c}_{12}={{\rm{e}}}^{{\rm{j}}\left(\Delta {\varphi }_{e2}-\Delta {\varphi }_{e1}\right)}\left(1+\frac{{\left({f}_{1}^{1}+{f}_{2}^{1}\right)}^{\rm{H}}\left({f}_{1}^{2}+{f}_{2}^{2}\right)}{4}+{\left({f}_{1}^{1}{f}_{2}^{1}\right)}^{\rm{H}}{f}_{1}^{2}{f}_{2}^{2}\right),\\ & {c}_{21} = {{\rm{e}}}^{{\rm{j}}\left(\Delta {\varphi }_{e1}-\Delta {\varphi }_{e2}\right)}\left(1+\frac{\left({f}_{1}^{1}+{f}_{2}^{1}\right){\left({f}_{1}^{2}+{f}_{2}^{2}\right)}^{\rm{H}}}{4}+{f}_{1}^{1}{f}_{2}^{1}{\left({f}_{1}^{2}{f}_{2}^{2}\right)}^{\rm{H}}\right) , {c}_{22} = 1+\frac{\left({f}_{1}^{2}+{f}_{2}^{2}\right){\left({f}_{1}^{2}+{f}_{2}^{2}\right)}^{\rm{H}}}{4} + {f}_{1}^{2}{f}_{2}^{2}{\left({f}_{1}^{2}{f}_{2}^{2}\right)}^{\rm{H}} \end{split}$

(49)

将矩阵 ${\boldsymbol{E}}'_{1}$ 拆分为4个 $d\times d$ 的子矩阵，并构造矩阵 ${\boldsymbol{\varPsi}} '$ 。

$\left. \begin{split} & {{\boldsymbol{E}}}'_{1}=\left[\begin{array}{cc}{c}_{11}{{\boldsymbol{E}}}_{11}& {c}_{12}{{\boldsymbol{E}}}_{12}\\ {c}_{21}{{\boldsymbol{E}}}_{21}& {c}_{22}{{\boldsymbol{E}}}_{22}\end{array}\right]\\ & {{\boldsymbol{\varPsi}} }'=-\frac{{c}_{12}}{{c}_{22}}{{\boldsymbol{E}}}_{12}{{\boldsymbol{E}}}_{22}^{-1}=\frac{{c}_{12}}{{c}_{22}}{\boldsymbol{\varPsi}} \end{split} \right\}$

(50)

${\boldsymbol{\varPsi}} '$ 的特征值为 ${\lambda }''_{m}$ ，每个散射子的干涉相位可以写为

${\phi }'_{m}={\arg}\left({\lambda }''_{m} \right)$

(51)

得到分解的干涉相位，进而通过干涉SAR高度反演公式得到对应的高度。

若两个天线的极化误差一致，则 ${c}_{12}/{c}_{22}= {{\rm{e}}}^{{\rm{j}}\left({\Delta }{\varphi }_{e2}-{\Delta }{\varphi }_{e1}\right)}$ ，即 ${{\boldsymbol{\varPsi}} }'={{\rm{e}}}^{{\rm{j}}\left(\Delta {\varphi }_{e1}-\Delta {\varphi }_{e2}\right)}{\boldsymbol{\varPsi}}$ ，干涉相位 ${\phi }'_{m}= {\phi }_{m}+\left({\Delta }{\varphi }_{e2}-{\Delta }{\varphi }_{e1}\right)$ 。

当两个天线极化失真一致并忽略极化串扰时，极化失真对基于ESPRIT的极化干涉处理方法无影响，不会引入高程误差。3.1.3节对这一结论进行了验证。

由于本方法得到了不同散射机制的高度，可直接基于式(51)进一步分析不同散射机制间高度差受误差的影响。

3. 仿真验证与分析

3.1 模型正确性验证

为了检验本文提出的误差模型的正确性，本文采用仿真的方法对2.3节的模型进行验证。

本文仿真的系统参数采用实验室Ku波段无人机载极化干涉SAR的实际参数，该无人机采用双天线构型，参数已在表1列出。

表 1 系统仿真参数

Table 1. Simulation parameters of system

参数	数值
中心频率	15.2 GHz
飞行高度	205 m
斜距	889 m
基线	0.6 m
基线角	–1°

下载: 导出CSV

| 显示表格

仿真区域示意图如图2所示，左边蓝色部分为地面，高度0 m，作为基准；右边绿色部分为具备一定高度的建筑混合区。混合区由Pauli分解的3种机制混合而成，包括单次散射，0°二面角的二次散射，45°二面角的二次散射，高度分别为20 m(模拟建筑屋顶高度)、0 m(模拟建筑与地面二面角散射高度)、10 m(模拟建筑区植被的体散射高度)，3种机制的散射强度设置相同。

图 2 仿真图像

Figure 2. Simulation image

下载: 全尺寸图片幻灯片

以单次散射为例，仿真的过程如式(52)所示。首先给定天线与目标的位置，通过斜距来计算目标的相位 ${\phi }_{s}$ 。给定其中一种散射机制的强度 ${A}_{1}$ 与Pauli基的散射矩阵 ${{\boldsymbol{s}}}_{g1}$ ，将其乘积作为4种极化方式(HH, HV, VH, VV)散射值的幅度，这样就可以得到单次散射的散射值 ${sm}_{1}$ 。同理可以得到Pauli分解另两种散射机制的散射值 ${sm}_{2}$ 和 ${sm}_{3}$ ，然后将同一分辨单元内3种散射机制的散射值相加，并加入一定信噪比的高斯白噪声N，最终得到每个像素的散射值 ${{sm}}$ ，其中， $sm={sm}_{1}+{sm}_{2}+{sm}_{3}+N$ 。

$\begin{split} & {{\boldsymbol{sm}}}_{1}={{\boldsymbol{A}}}_{1}\times {{\boldsymbol{s}}}_{g1}\times {{\rm{e}}}^{-{\rm{j}}{\varphi }_{s}},\\ & {{\boldsymbol{sm}}}_{1}={\left[\begin{array}{cccc}{{{sm}}}_{1}^{{\rm{HH}}}& {{{sm}}}_{1}^{{\rm{HV}}}& {{{sm}}}_{1}^{{\rm{VH}}}& {{{sm}}}_{1}^{{\rm{VV}}}\end{array}\right]}^{{\rm{T}}},\\ & {{{\boldsymbol{s}}}}_{g1}={\left[\begin{array}{cccc}1& 0& 0& 1\end{array}\right]}^{{\rm{T}}},\\ & {\phi }_{s}=-\frac{2\pi Q{R}_{{\rm{sm}}}}{{\lambda }_{{\rm{sm}}}} \end{split}$

(52)

其中， ${R}_{{\rm{sm}}}$ 为斜距， ${\lambda }_{{\rm{sm}}}$ 为波长，若系统一发双收，则 $Q=1$ 。

以无误差、信噪比为30 dB的理想情况计算出的高度为真值，以存在极化失真和干涉误差、信噪比同为30 dB情况下计算出的高度减去上述真值为高度误差结果。

3.1.1 极化最优相干下的极化干涉误差模型验证

为了验证模型的正确性，本文采用两种方式加入极化误差与干涉误差。一种是在仿真数据中加入，另一种是通过2.3节的推导，按照误差的表达式加入误差，得到了高度误差与目标高度的关系。

由于误差因素众多，为了验证的全面性，现分别采用如下两组典型参数进行验证。

(1) 基线B误差2 mm，基线角 $\alpha$ 误差0.03°，幅度不平衡1 dB，信噪比30 dB，极化串扰为–30 dB。

(2) 基线B误差1 mm，基线角 $\alpha$ 误差0.01°，幅度不平衡0.5 dB，信噪比30 dB，极化串扰为–30 dB。

图3给出了上述两组参数极化最优相干下极化干涉得到的高度误差与干涉相位误差和极化通道相位不平衡两个主要因素的关系。

图 3 极化干涉误差模型的验证

Figure 3. Verification of PolInSAR error model

下载: 全尺寸图片幻灯片

图3三维曲面为按照2.3.1节式(34)的误差模型得到的误差，红色散点表示在仿真数据上直接加入误差得到的结果。从图中可以看出两种方式得到的高度误差比较接近，两种方式得到的误差相差约0.5 m，说明了本文极化干涉误差模型的正确性。

3.1.2 Pauli分解下的极化干涉误差模型验证

通过仿真得到极化干涉数据，对这个数据进行Pauli分解，计算Pauli分解后3种散射机制的高度。将单次散射、0°二面角的二次散射、45°二面角的二次散射的高度分别记为 ${H}_{p1},{H}_{p2},{H}_{p3}$ 。

首先验证绝对高程误差模型，即由式(37)计算的高度，同3.1.1节第1组参数的仿真条件，得到误差对3种散射机制的影响如图4。

图 4 Pauli分解下的极化干涉误差模型验证(单一高度)

Figure 4. Verification of error model under Pauli decomposition (Single height)

下载: 全尺寸图片幻灯片

图4三维曲面为按照2.3.2节式(36)，式(37)的误差模型得到的误差结果，红色散点表示在仿真数据上直接加入误差得到的结果。可见两者高度吻合，说明了本文误差模型的正确性。

进一步对不同散射机制高度差的误差模型式(40)进行验证，即给出 ${H}_{p1}-{H}_{p2}$ , ${H}_{p1}-{H}_{p3}$ , ${H}_{p3}- {H}_{p2}$ 的验证结果如图5所示。

图 5 Pauli分解下的极化干涉误差模型验证(高度差)

Figure 5. Verification of error model under Pauli decomposition (Height difference)

下载: 全尺寸图片幻灯片

同样，图5中三维曲面为按照2.3.2节中式(40)的误差模型得到的误差，红色散点表示在数据上直接加入误差。从图5可以看出两种方式得到的高度误差十分接近，说明了误差模型的正确性。

3.1.3 结合ESPRIT的极化相干误差模型验证

对于Pauli分解而言，即使一个区域内混合的散射机制数量小于3，其也是按照散射机制为3的方式处理。然而，基于ESPRIT分解的方法则与散射机制数量有关，混合的散射机制数量越多得到的分解结果越难以解释。为此，本小节将混合的散射机制变成两种，即表面单次散射(高度为20 m)和45°二面角散射(高度为10 m)。

下面首先给出两种散射机制的高度误差的验证结果，仿真条件如3.1.1节中参数(1)，为了与误差模型一致，这部分不考虑串扰。

图6中三维曲面为按照2.3.3节中式(51)的误差模型得到的误差，红色散点表示在数据上直接加入误差的结果。图7给出了两种散射机制高度差的误差验证结果，从图7可以看出两种方式得到的高度误差比较接近，说明了误差模型的正确性。

图 6 结合ESPRIT的极化相干误差模型验证(单一高度)

Figure 6. Verification of error model of PolInSAR combined with ESPRIT (Single Height)

下载: 全尺寸图片幻灯片

图 7 结合ESPRIT的极化相干误差模型验证

Figure 7. Verification of error model of PolInSAR combined with ESPRIT

下载: 全尺寸图片幻灯片

2.3.3节推导了结合ESPRIT的极化干涉误差模型，推导的前提是忽略极化串扰的影响。此处仿真给出极化串扰对ESPRIT分解的两种散射机制的高度的影响，结果如图8所示。图8(a)是串扰对单次散射机制的影响，图8(b)是串扰对45°二面角二次散射的影响。从图中可以看出，极化串扰对ESPRIT很小，确实可以忽略。

图 8 极化串扰对ESPRIT分解得到的高度的影响

Figure 8. Effects of crosstalk on height obtained by ESPRIT decomposition

下载: 全尺寸图片幻灯片

由2.3.3节式(51)得出结论，当两个天线极化失真一致情况下，极化失真对基于ESPRIT的极化干涉的高度没有影响。本部分对这个结论进行验证，结果如图9所示。图9(a)，图9(c)是极化失真对单次散射机制的影响，图9(b)，图9(d)是极化失真对45°二面角二次散射的影响，可见对高度的影响均在毫米级，可以忽略。

图 9 两天线极化失真一致时，极化失真对ESPRIT误差模型的影响

Figure 9. Effects of polarization distortion on ESPRIT error model when distortion is equal on two antennas

下载: 全尺寸图片幻灯片

3.2 误差影响程度分析

3.1节在验证模型正确性的同时，可以获得高度误差与干涉相位和极化相位不平衡的关系，但高度误差与其他误差因素的关系曲线并未给出。因此，在上述模型验证正确的基础上，下面进一步分析不同处理方法下不同误差的影响程度。

3.2.1 极化最优相干处理下误差影响结果

在极化最优相干处理下，极化失真、干涉误差及信噪比的影响分析结果分别如图10和图11所示。

图 10 极化失真对极化干涉高度反演的影响

Figure 10. Effects of polarization distortion on height obtained by PolInSAR

下载: 全尺寸图片幻灯片

图 11 干涉误差对极化干涉高度反演的影响

Figure 11. Effects of interferometric error on height obtained by PolInSAR

下载: 全尺寸图片幻灯片

从图10可以看出，在极化最优相干处理模型下，极化幅相不平衡对高度反演结果的影响较小，极化串扰在小于–20 dB的情况下，对极化干涉影响较小，但如果极化串扰较大，也会引起较大的高度误差。

从图11可以看出，相比于极化误差，极化最优相干处理模型下对干涉误差的敏感程度更高。基线长度、基线角和干涉相位误差对反演高度影响均较大。由图11可知，信噪比大于24 dB后，误差标准差小于0.5 m，误差的影响比较稳定。

3.2.2 Pauli分解处理下的误差影响结果

图12和图13给出Pauli分解处理下，极化失真和干涉误差对各散射机制间相对高度误差的影响结果。

图 12 极化失真对Pauli分解下高度反演结果的影响

Figure 12. Effects of polarization distortion on height obtained by Pauli decomposition

下载: 全尺寸图片幻灯片

图 13 干涉误差对Pauli分解下高度反演结果的影响

Figure 13. Effects of interferometric error on height obtained by PolInSAR

下载: 全尺寸图片幻灯片

从图12可以看出，极化幅度相不平衡和极化串扰对于Pauli分解下各散射机制的相对高度有非常大的影响，因此如要采用该方法分离不同散射机制并得到正确的高度，需首先保证数据的极化质量。

从图13可以看出，在本仿真的系统参数下，干涉误差中的基线长度对散射机制间高度差的结果影响较大，基线角和干涉相位误差则对结果影响较小。此外，信噪比大于26 dB，误差标准差小于0.5 m，误差的影响较为稳定。

由2.3.3节式(40)可知，散射子高度差异不同会导致误差影响的不同。为此，此处给出单次散射、0°二面角二次散射、45°二面角二次散射3种散射机制混合，对应高度分别为20 m, 18 m, 19 m情况下的极化失真、干涉误差和信噪比的影响。结果如图14和图15所示。

图 14 极化失真对Pauli分解的影响

Figure 14. Effects of polarization distortion on Pauli decomposition

下载: 全尺寸图片幻灯片

图 15 干涉误差与信噪比对Pauli分解的影响

Figure 15. Effects of interferometric error on Pauli decomposition

下载: 全尺寸图片幻灯片

对比图12和图13可见，在基于Pauli分解的处理模型下，散射子高度差异较小时，极化误差与干涉误差造成的影响也明显减小。

3.2.3 ESPRIT分解处理下的误差影响结果

此处与3.1.3节一致，考虑两类散射机制混合的情况，分析两类散射机制高度差，即 ${H}_{i2}-{H}_{i1}$ ，受极化失真和干涉误差的影响程度。结果如图16和图17所示。

图 16 极化失真对ESPRIT分解的影响

Figure 16. Effects of polarization distortion on ESPRIT

下载: 全尺寸图片幻灯片

图 17 干涉误差对ESPRIT分解的影响

Figure 17. Effects of interferometric error on ESPRIT

下载: 全尺寸图片幻灯片

从图16可以看出，极化幅相不平衡和串扰对结果的影响都很小。从图17可以看出，本文仿真条件下，基线长度误差对结果的影响较大，基线角误差对结果的影响较小，干涉相位误差对结果的影响较大。信噪比大于11 dB以后，误差标准差小于0.5 m，误差的影响变得稳定。

3.3 讨论

3.3.1 对Pauli分解与ESPRIT误差影响分析的比较

由3.1.2节和3.2.2节可知，Pauli分解处理模式下对极化误差影响非常敏感，而在基于ESPRIT分解的处理模式下，则对极化误差的影响不甚敏感。为了更好地对比分析和解释，此处进一步给出仿真结果，结果如图18和图19所示。仿真预设建筑区域由单次散射和45°二次散射混合而成，高度分别为20 m和10 m。

图 18 极化失真对散射机制高度差的影响

Figure 18. Effects of polarization distortion on height difference of scattering mechanisms

下载: 全尺寸图片幻灯片

图 19 干涉误差对散射机制高度差的影响

Figure 19. Effects of interferometric error on height difference of scattering mechanisms

下载: 全尺寸图片幻灯片

图18，图19分别给出了两种处理模型下极化误差和干涉误差对反演的散射机制高度差的影响。图中红线表示Pauli分解，蓝线表示ESPRIT分解。从图19可以看出，对于Pauli分解，信噪比大于26 dB以后，误差标准差小于0.5 m，误差的影响变得稳定。

由图18可见，极化串扰对基于Pauli分解方式的高度反演结果影响要比对基于ESPRIT分解方式的影响大很多。为了解释这种差异，我们以极化串扰为–20 dB为例，采用2.3.3节提出的方法，给出考虑误差前后分解得到的散射机制。同时预设Pauli分解和ESPRIT分解中单次散射和45°二次散射的强度分别为10 dB和30 dB。

基于ESPRIT分解得到的考虑误差前后主图像的散射矢量，结果如表2。

表 2 ESPRIT方法得到散射机制的结果

Table 2. Scattering mechanisms obtained by ESPRIT

极化方式	主图像	辅图像	含串扰的主图像	含串扰的辅图像
单次散射	–0.89 +0.11i	–0.85 –0.25	–0.54 +0.03i	–0.45 –0.33i
0°二次散射	0.02 –0.01i	0.02 –0.01i	0.02 +0.01i	0.02 +0.01i
45°二次散射	1	1	1	1

下载: 导出CSV

| 显示表格

经过ESPRIT分解，得到的两个散射机制的干涉相位如表3。

表 3 ESPRIT方法得到的干涉相位

Table 3. Interferometric phase obtained by ESPRIT

极化方式	理想(°)	含串扰(°)
单次散射	58.90	58.41
45°二次散射	84.87	84.24

下载: 导出CSV

| 显示表格

基于Pauli分解得到的考虑误差前后的散射矢量如表4。得到的干涉相位误差如表5所示。

表 4 Pauli分解得到散射机制的结果

Table 4. Scattering mechanisms obtained by Pauli decomposition

极化方式	主图像	辅图像	含串扰的主图像	含串扰的辅图像
单次散射	0.10	0.29	0.09+0.04i	0.28+0.04i
0°二次散射	0.002	0.001i	–0.001i	0.003
45°二次散射	1	1	1	1

下载: 导出CSV

| 显示表格

表 5 –20 dB串扰误差下两种分解的干涉相位误差

Table 5. Interferometric phase error of two decompositions under –20 dB crosstalk

极化方式	ESPRIT (°)	Pauli (°)
单次散射	0.49	15.69
45°二次散射	0.63	–0.45

下载: 导出CSV

| 显示表格

从表2—表5可知，基于ESPRIT分解的处理方式下，分解得到的散射机制强度与仿真预设值一致，其对应的干涉相位几乎不受串扰的影响。而在Pauli分解条件下，散射机制的干涉相位受到串扰影响较大。

这里需要说明本文仿真中按照式(5)预先给定的两个散射机制的强度 ${\sigma }_{1}$ 和 ${\sigma }_{2}$ 相差较大， ${\sigma }_{1}=10\;{\rm{dB}}$ , ${\sigma }_{2}=30\;{\rm{dB}}$ 。如果预先给定的两个散射机制的强度 ${\sigma }_{1}$ 和 ${\sigma }_{2}$ 相差不大，如 ${\sigma }_{1}=20\;{\rm{dB}}$ , ${\sigma }_{2}=30\;{\rm{dB}}$ 。这会导致ESPRIT分解得到散射机制的强度存在误差。也就是说表2中主图像的散射机制不是 ${\left[\begin{array}{ccc}1& 0& 1\end{array}\right]}^{\mathrm{T}}$ ，而是 ${\left[\begin{array}{ccc}0.5& 0& 1.0\end{array}\right]}^{\mathrm{T}}$ 。

3.3.2 3类散射机制混合下的ESPRIT误差影响分析

前文对ESPRIT的分析都是考虑两类散射机制混合的情况，实际中一个分辨单元内散射体的个数常大于两个。因此，为了更贴合实际情况，我们给出一个分辨单元内存在3种散射机制的情况下，极化误差与干涉误差对ESPRIT的影响。

本文给定的散射机制包括单次散射，0°二面角的二次散射，45°二面角的二次散射，高度分别为20 m, 0 m和10 m。对应的仿真的高度为 ${H}_{e1}$ , ${H}_{e2}$ , ${H}_{e3}$ 。

在这种情况下，极化误差与干涉误差对ESPRIT的影响如图20和图21所示。

图 20 3类机制混合的极化误差对ESPRIT分解的影响

Figure 20. Effects of polarization distortion on ESPRIT mixed by 3 mechanisms

下载: 全尺寸图片幻灯片

图 21 3类机制混合的干涉误差对ESPRIT分解的影响

Figure 21. Effects of interferometric error on ESPRIT mixed by 3 mechanisms

下载: 全尺寸图片幻灯片

从图(20)中可知，极化误差对ESPRIT的影响很小，基线误差与干涉相位误差的影响较大。相较于两种散射机制混合的情况，3种散射机制混合情况下，极化误差与干涉的影响与两种散射机制混合情况基本一致，唯独信噪比的影响与两种散射机制混合情况不一致。可以看出，信噪比对不同机制间的高度差影响不一致。

4. 实际数据结果

第3节给出了误差影响的仿真结果，在这部分，本文补偿实际数据的极化误差与干涉误差，进而提高高程反演的精度。

本文采用的无人机载极化干涉SAR系统是由中国科学院空天信息创新研究院和中科宇达公司于2020年共同研制的，该系统如图22所示。系统中心频率15.2 GHz，工作于Ku波段，基线0.62 m，飞行高度206 m。

图 22 无人机载极化干涉SAR系统

Figure 22. UAV-borne PolInSAR system

下载: 全尺寸图片幻灯片

成像区域位于上海复旦大学校区周边，如图23所示。

图 23 无人机载极化干涉SAR系统成像区域

Figure 23. Imaging area of UAV-borne system

下载: 全尺寸图片幻灯片

真实高度是由倾斜摄影测量并通过与SAR图像配准得到的，真实高度如图24所示。

图 24 真实高度

Figure 24. Real height

下载: 全尺寸图片幻灯片

通过测量，我们得到发射通道的幅度不平衡–7.727 dB，相位不平衡–6.303°。接收通道幅度不平衡3.76 dB，相位不平衡–23.479°。极化串扰为–7.811 dB。通过未补偿误差前反演得到的高度与航迹，计算出了运动补偿残余导致的干涉相位误差。

分别根据式(34)、式(37)和式(51)，我们给出了补偿极化失真与干涉误差后，基于极化最优相干、Pauli分解和ESPRIT分解的高度反演结果。高度反演的结果主要通过干涉算法得到，具体步骤已在笔者的文章[22]中列出。

补偿误差前后，极化最优相干的高度反演结果如图25所示。

图 25 极化最优相干反演的高度图

Figure 25. Height retrieved by polarimetric optimal coherence

下载: 全尺寸图片幻灯片

根据真实高度，我们通过计算得到，补偿误差前极化最优相干在建筑区域的RMSE(均方根误差)为2.88 m，补偿误差后建筑区域的RMSE为2.77 m。

为了简化篇幅，本文只展示了补偿误差前后Pauli分解中单次散射的高度反演结果，如图26所示。

图 26 单次散射反演的高度图

Figure 26. Height retrieved by single scattering

下载: 全尺寸图片幻灯片

补偿误差前Pauli分解中单次散射、0°二面角的二次散射和45°二面角的二次散射的RMSE为3.16 m, 3.21 m和3.39 m。补偿误差后对应的RMSE为2.96 m, 2.90 m, 2.95 m。

对于ESPRIT，同一个分辨单元内有3种散射机制，将分离出的3个干涉相位中差值最大的两个作为屋顶相位和地面相位，并通过干涉反演高度。由于ESPRIT分解的过程比较耗时，本文只截取了SAR图像中右下角的一片密集建筑区，补偿误差前后ESPRIT的高度反演结果如图27所示。

图 27 ESPRIT反演的高度图

Figure 27. Height retrieved by ESPRIT

下载: 全尺寸图片幻灯片

补偿误差前ESPRIT分解的RMSE为2.92 m，补偿后RMSE为2.87 m。

从这3组结果可以看出，补偿极化误差与干涉误差后，高程反演精度都有了一定的提升。其中，Pauli分解的反演精度提升较大，ESPRIT的反演精度提升较小，ESPRIT算法反演得到的高度对误差不敏感且更加稳定。

5. 结语

本文建立了极化干涉、Pauli分解和极化干涉结合ESPRIT 3种情况下的误差模型，并通过仿真进行了验证。之后分析了极化误差、干涉误差和信噪比对于3种情况的影响。此外，为了求解ESPRIT除干涉相位以外的其他参数，本文给出了一种逆向求解相关参数的方法。本文在讨论部分还分析了同一像素点内有两种散射机制的情况，并与ESPRIT分解和存在3种散射机制的Pauli分解的结果做对比。最后，通过补偿极化误差与干涉误差，提升了高度反演精度。

本文的分析为Ku波段无人机系统提供了误差分析结果，提高了反演的精度并支撑了该系统的应用。

图 1 SMA框架示意图

Figure 1. The schematic diagram of SMA framework

下载: 全尺寸图片幻灯片

图 2 SMA在TDM-MIMO中应用的示意图

Figure 2. Schematic diagram of SMA application in TDM-MIMO

下载: 全尺寸图片幻灯片

图 3 SMA-MIMO天线工作原理

Figure 3. Working principle of SMA-MIMO antenna

下载: 全尺寸图片幻灯片

图 4 雷达资源配置对比示意图

Figure 4. Schematic diagram of radar resource allocation comparison

下载: 全尺寸图片幻灯片

图 5 发射信号的时频曲线和接收阵元分时接入的时序

Figure 5. Time-frequency curve of the transmitting signal and sequential of the time-division access of receiving elements

下载: 全尺寸图片幻灯片

图 6 距离估计性能

Figure 6. Distance estimation performance

下载: 全尺寸图片幻灯片

图 7 速度估计性能

Figure 7. Velocity estimation performance

下载: 全尺寸图片幻灯片

图 8 DOA估计性能

Figure 8. DOA estimation performance

下载: 全尺寸图片幻灯片

图 9 固定第1个目标SNR下的距离估计性能

Figure 9. Distance estimation performance under fixed first target SNR

下载: 全尺寸图片幻灯片

图 10 固定第1个目标SNR下的速度估计性能

Figure 10. Velocity estimation performance under fixed first target SNR

下载: 全尺寸图片幻灯片

图 11 固定第1个目标SNR下的DOA估计性能

Figure 11. DOA estimation performance under fixed first target SNR

下载: 全尺寸图片幻灯片

图 12 归一化2D-MUSIC伪谱俯视图

Figure 12. Normalized 2D-MUSIC pseudospectral top view

下载: 全尺寸图片幻灯片

图 13 提出算法的估计性能

Figure 13. The estimation performance of the proposed algorithm

下载: 全尺寸图片幻灯片

表 1 不同收发框架需要收发机的数量

Table 1. Number of transceivers required for different frameworks

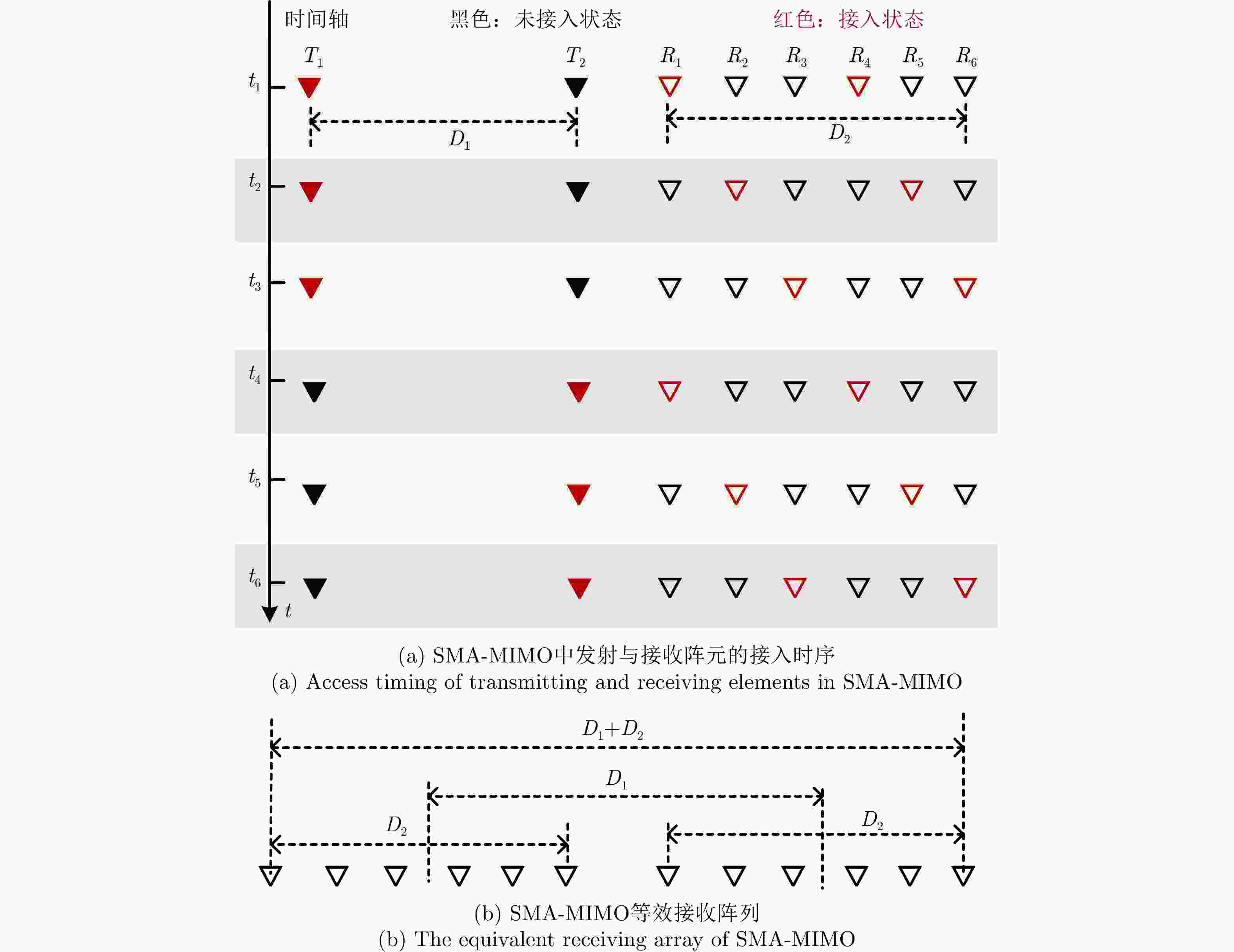
收发框架类型	发射机数量(个)	接收机数量(个)
SIMO	1	12
TDM-MIMO	1	6
SMA-MIMO	1	2

下载: 导出CSV

表 2 不同雷达类型的参数

Table 2. Parameters of different radar types

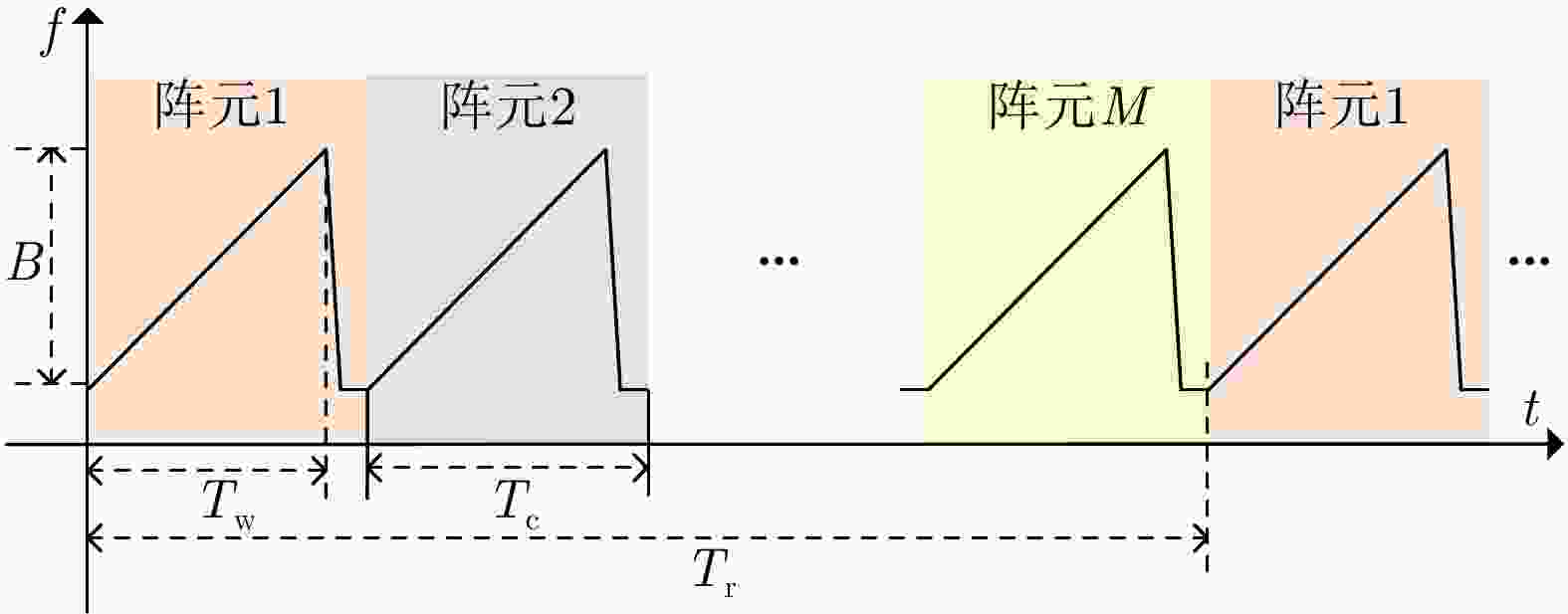
案例名	接收机数量	阵元数量M	CPI (ms)	脉冲重复周期(μs)	脉冲个数P	脉冲宽度(μs)	ADC采样频率(MHz)	单周期采样点数L
TMLR	1	1	1.2	97.4026	12	97.4026	0.6844	66
SMAR-2	1	2	1.2	97.4026	12	48.7013	1.3689	66
SMAR-4	1	4	1.2	97.4026	12	24.3506	2.7378	66
SMAR-8	1	8	1.2	97.4026	12	12.1753	5.4756	66
SMAR-16	1	16	1.2	97.4026	12	6.0877	10.9511	66
SLAR-2	2	2	1.2	97.4026	12	48.7013	1.3689	66
SLAR-4	4	4	1.2	97.4026	12	24.3506	2.7378	66
SLAR-8	8	8	1.2	97.4026	12	12.1753	5.4756	66
SLAR-16	16	16	1.2	97.4026	12	6.0877	10.9511	66

下载: 导出CSV

参考文献(42)

[1]	LIANG Junli, ZHANG Xuan, SO H C, et al. Sparse array beampattern synthesis via alternating direction method of multipliers[J]. IEEE Transactions on Antennas and Propagation, 2018, 66(5): 2333–2345. doi: 10.1109/TAP.2018.2811778
[2]	WANG Xiangrong, ABOUTANIOS E, and AMIN M G. Thinned array beampattern synthesis by iterative soft-thresholding-based optimization algorithms[J]. IEEE Transactions on Antennas and Propagation, 2014, 62(12): 6102–6113. doi: 10.1109/TAP.2014.2364048
[3]	CHEN Kesong, YUN Xiaohua, HE Zishu, et al. Synthesis of sparse planar arrays using modified real genetic algorithm[J]. IEEE Transactions on Antennas and Propagation, 2007, 55(4): 1067–1073. doi: 10.1109/TAP.2007.893375
[4]	FENG Lifang, CUI Guolong, YU Xianxiang, et al. Beampattern synthesis via the constrained subarray layout optimization[J]. IEEE Transactions on Antennas and Propagation, 2021, 69(1): 182–194. doi: 10.1109/TAP.2020.3008652
[5]	ZHANG Ruoyu, SHIM B, and WU Wen. Direction-of-arrival estimation for large antenna arrays with hybrid analog and digital architectures[J]. IEEE Transactions on Signal Processing, 2022, 70: 72–88. doi: 10.1109/TSP.2021.3119768
[6]	QIN Si, ZHANG Y D, and AMIN M G, et al. Generalized coprime array configurations for direction-of-arrival estimation[J]. IEEE Transactions on Signal Processing, 2015, 63(6): 1377–1390. doi: 10.1109/TSP.2015.2393838
[7]	PAL P and VAIDYANATHAN P P. Nested arrays: A novel approach to array processing with enhanced degrees of freedom[J]. IEEE Transactions on Signal Processing, 2010, 58(8): 4167–4181. doi: 10.1109/TSP.2010.2049264
[8]	BARAL A B and TORLAK M. Joint Doppler frequency and direction of arrival estimation for TDM MIMO automotive radars[J]. IEEE Journal of Selected Topics in Signal Processing, 2021, 15(4): 980–995. doi: 10.1109/JSTSP.2021.3073572
[9]	HU Xueyao, LI Yang, LU Man, et al. A multi-carrier-frequency random-transmission chirp sequence for TDM MIMO automotive radar[J]. IEEE Transactions on Vehicular Technology, 2019, 68(4): 3672–3685. doi: 10.1109/TVT.2019.2900357
[10]	HONG Lang and HONG S. Systems and methods for virtual aperature radar tracking[P]. US, EP3746809A4, 2021.
[11]	LEE M S and KIM Y H. Design and performance of a 24-GHz switch-antenna array FMCW radar system for automotive applications[J]. IEEE Transactions on Vehicular Technology, 2010, 59(5): 2290–2297. doi: 10.1109/TVT.2010.2045665
[12]	FANG Jun, LIU Yumeng, LI Hongbin, et al. One-bit quantizer design for multisensor GLRT fusion[J]. IEEE Signal Processing Letters, 2013, 20(3): 257–260. doi: 10.1109/LSP.2013.2243144
[13]	黄广佳, 程旭, 饶彬, 等. 基于广义Rao检验的单/多比特MIMO雷达运动目标检测方法[J/OL]. 系统工程与电子技术, 1–12. http://kns.cnki.net/kcms/detail/11.2422.TN.20230201.1510.001.html, 2023. HUANG Guangjia, CHENG Xu, RAO Bin, et al. One/multi-bit MIMO radar detection of a moving target based on generalized Rao test[J/OL]. Systems Engineering and Electronics, 1–12. http://kns.cnki.net/kcms/detail/11.2422.TN.20230201.1510.001.html, 2023.
[14]	CHENG Xu, CIUONZO D, ROSSI P S, et al. Multi-bit & sequential decentralized detection of a noncooperative moving target through a generalized Rao test[J]. IEEE Transactions on Signal and Information Processing over Networks, 2021, 7: 740–753. doi: 10.1109/TSIPN.2021.3126930
[15]	CHENG Xu, CIUONZO D, and ROSSI P S. Multibit decentralized detection through fusing smart and dumb sensors based on Rao test[J]. IEEE Transactions on Aerospace and Electronic Systems, 2020, 56(2): 1391–1405. doi: 10.1109/TAES.2019.2936777
[16]	WANG Xueqian, LI Gang, and VARSHNEY P K. Distributed detection of weak signals from one-bit measurements under observation model uncertainties[J]. IEEE Signal Processing Letters, 2019, 26(3): 415–419. doi: 10.1109/LSP.2019.2892196
[17]	LI Chengxi, HE You, WANG Xueqian, et al. Distributed detection of sparse stochastic signals via fusion of 1-bit local likelihood ratios[J]. IEEE Signal Processing Letters, 2019, 26(12): 1738–1742. doi: 10.1109/LSP.2019.2945193
[18]	LI Chengxi, LI Gang, and VARSHNEY P K. Distributed detection of sparse stochastic signals with 1-bit data in tree-structured sensor networks[J]. IEEE Transactions on Signal Processing, 2020, 68: 2963–2976. doi: 10.1109/TSP.2020.2988598
[19]	XIAO Yuhang, RAMÍREZ D, SCHREIER P J, et al. One-bit target detection in collocated MIMO radar and performance degradation analysis[J]. IEEE Transactions on Vehicular Technology, 2022, 71(9): 9363–9374. doi: 10.1109/TVT.2022.3178285
[20]	REN Jiaying, ZHANG Tianyi, LI Jian, et al. Sinusoidal parameter estimation from signed measurements via majorization-minimization based RELAX[J]. IEEE Transactions on Signal Processing, 2019, 67(8): 2173–2186. doi: 10.1109/TSP.2019.2899804
[21]	STOICA P, SHANG Xiaolei, and CHENG Yuanbo. The Cramér-Rao bound for signal parameter estimation from quantized data [Lecture Notes][J]. IEEE Signal Processing Magazine, 2022, 39(1): 118–125. doi: 10.1109/MSP.2021.3116532
[22]	FENG Lifang, HUANG Lei, LI Qiang, et al. An off-grid iterative reweighted approach to one-bit direction of arrival estimation[J]. IEEE Transactions on Vehicular Technology, 2023, 72(6): 8134–8139. doi: 10.1109/TVT.2023.3239003
[23]	BAR-SHALOM O and WEISS A J. DOA estimation using one-bit quantized measurements[J]. IEEE Transactions on Aerospace and Electronic Systems, 2002, 38(3): 868–884. doi: 10.1109/TAES.2002.1039405
[24]	HUANG Xiaodong and LIAO Bin. One-bit MUSIC[J]. IEEE Signal Processing Letters, 2019, 26(7): 961–965. doi: 10.1109/LSP.2019.2913452
[25]	CHEN Xinzhu, HUANG Lei, ZHOU Hanfei, et al. One-bit digital beamforming[J]. IEEE Transactions on Aerospace and Electronic Systems, 2023, 59(1): 555–567. doi: 10.1109/TAES.2022.3181257
[26]	FU Haoyu and CHI Yuejie. Quantized spectral compressed sensing: Cramer-Rao bounds and recovery algorithms[J]. IEEE Transactions on Signal Processing, 2018, 66(12): 3268–3279. doi: 10.1109/TSP.2018.2827326
[27]	ZAYYANI H, HADDADI F, and KORKI M. Double detector for sparse signal detection from one-bit compressed sensing measurements[J]. IEEE Signal Processing Letters, 2016, 23(11): 1637–1641. doi: 10.1109/LSP.2016.2613898
[28]	SHANG Xiaolei, LI Jian, and STOICA P. Weighted SPICE algorithms for range-Doppler imaging using one-bit automotive radar[J]. IEEE Journal of Selected Topics in Signal Processing, 2021, 15(4): 1041–1054. doi: 10.1109/JSTSP.2021.3071601
[29]	ZAHABI S J, NAGHSH M M, MODARRES-HASHEMI M, et al. One-bit compressive radar sensing in the presence of clutter[J]. IEEE Transactions on Aerospace and Electronic Systems, 2020, 56(1): 167–185. doi: 10.1109/TAES.2019.2916532
[30]	ZHANG Rong, LI Changheng, LI Jian, et al. Range estimation and range-Doppler imaging using signed measurements in LFMCW radar[J]. IEEE Transactions on Aerospace and Electronic Systems, 2019, 55(6): 3531–3550. doi: 10.1109/TAES.2019.2907395
[31]	JIN Benzhou, ZHU Jiang, WU Qihui, et al. One-bit LFMCW radar: Spectrum analysis and target detection[J]. IEEE Transactions on Aerospace and Electronic Systems, 2020, 56(4): 2732–2750. doi: 10.1109/TAES.2020.2978374
[32]	AMERI A, BOSE A, LI Jian, et al. One-bit radar processing with time-varying sampling thresholds[J]. IEEE Transactions on Signal Processing, 2019, 67(20): 5297–5308. doi: 10.1109/TSP.2019.2939086
[33]	XI Feng, XIANG Yijian, ZHANG Zhen, et al. Joint angle and Doppler frequency estimation for MIMO radar with one-bit sampling: A maximum likelihood-based method[J]. IEEE Transactions on Aerospace and Electronic Systems, 2020, 56(6): 4734–4748. doi: 10.1109/TAES.2020.3000841
[34]	CHENG Ziyang, HE Zishu, and LIAO Bin. Target detection performance of collocated MIMO radar with one-bit ADCs[J]. IEEE Signal Processing Letters, 2019, 26(12): 1832–1836. doi: 10.1109/LSP.2019.2951496
[35]	XI Feng, XIANG Yijian, CHEN Shengyao, et al. Gridless parameter estimation for one-bit MIMO radar with time-varying thresholds[J]. IEEE Transactions on Signal Processing, 2020, 68: 1048–1063. doi: 10.1109/TSP.2020.2970343
[36]	LIU Bingfan, CHEN Baixiao, and YANG Minglei. Parameter estimation and CRB analysis of 1-bit colocated MIMO radar[J]. IET Radar, Sonar & Navigation, 2021, 15(6): 592–604. doi: 10.1049/rsn2.12076
[37]	张国鑫, 易伟, 孔令讲. 基于1比特量化的大规模MIMO雷达系统直接定位算法[J]. 雷达学报, 2021, 10(6): 970–981. doi: 10.12000/JR21062 ZHANG Guoxin, YI Wei, and KONG Lingjiang. Direct position determination for massive MIMO system with one-bit quantization[J]. Journal of Radars, 2021, 10(6): 970–981. doi: 10.12000/JR21062
[38]	王峥. 单比特压缩感知雷达成像关键技术的研究[D]. [博士论文], 中国科学技术大学, 2021. WANG Zheng. One-bit compressed sensing radar imaging research on key technologies[D]. [Ph.D. dissertation], University of Science and Technology of China, 2021.
[39]	赵博, 黄磊, 周汉飞, 等. 基于单频时变阈值的1-bit SAR成像方法研究[J]. 雷达学报, 2018, 7(4): 446–454. doi: 10.12000/JR18036 ZHAO Bo, HUANG Lei, ZHOU Hanfei, et al. 1-bit SAR imaging method based on single-frequency time-varying threshold[J]. Journal of Radars, 2018, 7(4): 446–454. doi: 10.12000/JR18036
[40]	ZHAO Bo, HUANG Lei, and BAO Weimin. One-bit SAR imaging based on single-frequency thresholds[J]. IEEE Transactions on Geoscience and Remote Sensing, 2019, 57(9): 7017–7032. doi: 10.1109/TGRS.2019.2910284
[41]	ZHAO Bo, HUANG Lei, LI Jian, et al. Deceptive SAR jamming based on 1-bit sampling and time-varying thresholds[J]. IEEE Journal of Selected Topics in Applied Earth Observations and Remote Sensing, 2018, 11(3): 939–950. doi: 10.1109/JSTARS.2018.2793247
[42]	VAN VLECK J H and MIDDLETON D. The spectrum of clipped noise[J]. Proceedings of the IEEE, 1966, 54(1): 2–19. doi: 10.1109/PROC.1966.4567

施引文献

期刊类型引用(1)
1. 徐慧智，常梦莹，陈祎楠，郝东升. 目标检测下的车型对交通流速度影响研究. 计算机工程与应用. 2024(24): 314-321 . 百度学术
其他类型引用(0)

资源附件(0)

访问统计

图(13) / 表(2)

计量

文章访问数: 686
HTML全文浏览量: 153
PDF下载量: 193
被引次数: 1

1. 引言
2. 不同处理模式下的基础模型与误差模型
2.1 极化干涉SAR处理模型
2.2 误差类型
2.3 不同处理模式下的误差影响分析
3. 仿真验证与分析
3.1 模型正确性验证
3.2 误差影响程度分析
3.3 讨论
4. 实际数据结果
5. 结语

一种面向低成本轻量级雷达的单比特复用阵列信号收发框架

DOI: 10.12000/JR23223 CSTR: 32380.14.JR23223

通讯作者: 冯力方 fenglifangf@163.com

计量

出版历程

A Single-bit Multiplexing Array Signal Transceiver Framework for Low-cost Lightweight Radar

Corresponding author: FENG Lifang, fenglifangf@163.com

1. 引言

2. 不同处理模式下的基础模型与误差模型

2.1 极化干涉SAR处理模型

2.1.1 极化最优相干处理模型

2.1.2 基于极化分解的极化干涉处理模型

2.1.3 基于极化干涉观测矩阵的处理模型

2.2 误差类型

2.2.1 极化失真模型

2.2.2 干涉误差模型

2.3 不同处理模式下的误差影响分析

2.3.1 基于极化最优相干的极化干涉误差影响

2.3.2 基于Pauli分解的极化干涉误差影响

2.3.3 极化干涉观测矩阵直接求解高度的误差影响

3. 仿真验证与分析

3.1 模型正确性验证

3.1.1 极化最优相干下的极化干涉误差模型验证

3.1.2 Pauli分解下的极化干涉误差模型验证

3.1.3 结合ESPRIT的极化相干误差模型验证

3.2 误差影响程度分析

3.2.1 极化最优相干处理下误差影响结果

3.2.2 Pauli分解处理下的误差影响结果

3.2.3 ESPRIT分解处理下的误差影响结果

3.3 讨论

3.3.1 对Pauli分解与ESPRIT误差影响分析的比较

3.3.2 3类散射机制混合下的ESPRIT误差影响分析

4. 实际数据结果

5. 结语

期刊类型引用(1)

其他类型引用(0)

计量

出版历程

目录

1. 引言

2. 不同处理模式下的基础模型与误差模型

2.1 极化干涉SAR处理模型

2.2 误差类型

2.3 不同处理模式下的误差影响分析

3. 仿真验证与分析

3.1 模型正确性验证

3.2 误差影响程度分析

3.3 讨论

4. 实际数据结果

5. 结语

期刊介绍

联系我们

通讯作者:
冯力方 fenglifangf@163.com