基于稀疏重构的全极化SAR联合多维重建

孙豆; 路东伟; 邢世其; 杨潇; 李永祯; 王雪松

doi:10.12000/JR20092

基于稀疏重构的全极化SAR联合多维重建

DOI: 10.12000/JR20092

孙豆^1,,
路东伟^1,,
邢世其^1, ,,
杨潇^2,,
李永祯^1,,
王雪松^1,

1.
国防科技大学电子信息系统复杂电磁环境效应国家重点实验室长沙 410073
2.
国防科技大学电子科学系长沙 410073

基金项目: 国家自然科学基金(61971429, 61901499)

详细信息

作者简介:
孙　豆(1992–)，女，博士研究生，主要研究方向为极化雷达成像和雷达信号处理。E-mail: sundou14@nudt.edu.cn

路东伟(1992–)，男，博士研究生，主要研究方向为合成孔径雷达对抗和雷达目标识别。E-mail: bookwormldw@qq.com

邢世其(1984–)，男，副研究员，主要研究方向为极化雷达成像、雷达信号处理以及合成孔径雷达对抗。E-mail: xingshiqi_paper@163.com

杨　潇(1983–)，男，助教，主要研究方向为雷达信号处理和雷达目标识别。E-mail: 297414430@qq.com

李永祯(1977–)，男，研究员，博士生导师，主要研究方向为极化雷达与电子对抗。E-mail: e0061@sina.com

王雪松(1972–)，男，教授，博士生导师，主要研究方向为极化雷达、目标识别与电子对抗。E-mail: wxs1019@vip.sina.com

通讯作者:
邢世其 xingshiqi_paper@163.com

责任主编：仇晓兰 Corresponding Editor: QIU Xiaolan
中图分类号: TN95
计量
- 文章访问数: 2727
- HTML全文浏览量: 780
- PDF下载量: 227
- 被引次数: 23
出版历程
- 收稿日期: 2020-07-06
- 修回日期: 2020-09-24
- 网络出版日期: 2020-10-28

Full-polarization SAR Joint Multidimensional Reconstruction Based on Sparse Reconstruction

SUN Dou^1
,,
LU Dongwei^1
,,
XING Shiqi^{1
, ,},
YANG Xiao^2
,,
LI Yongzhen^1
,,
WANG Xuesong^1
,

1.
State Key Laboratory of Complex Electromagnetic Environment Effects on Electronics and Information System, National University of Defense Technology, Changsha 410073, China
2.
Department of Electronic Science, National University of Defense Technology, Changsha 410073, China

Funds: The National Natural Science Foundation of China (61971429, 61901499)

More Information

Corresponding author: XING Shiqi, xingshiqi_paper@163.com

摘要

摘要: 各极化通道独立处理和三维分步成像会忽视数据之间的关联性，造成散射中心的失配以及极化散射矩阵获取的不准确。鉴于此，该文提出一种基于稀疏重构的全极化联合多维重建方法。该方法通过设置联合稀疏约束对所有极化通道及所有维度进行联合，将全极化多维重建建模为多通道联合稀疏重构问题。通过数据插值对模型简化后，结合三维快速傅里叶变换、共轭梯度法和牛顿迭代法给出一种高效的模型求解方法，可以同时得到极化散射矩阵和目标三维信息。该文方法保证了不同极化通道、不同维度的稀疏支撑集一致，且充分利用了数据之间的关联性带来的额外信息。基于仿真数据和电磁计算数据的实验结果表明，该方法的性能不受目标类型影响，具有一定的抗噪性，能有效地获取目标的多维重建结果，得到的三维成像结果分辨率高且极化散射矩阵估计精度高。
- 合成孔径雷达 /
- 全极化 /
- 稀疏重构 /
- 三维成像 /
- 联合重建
Abstract: Independent processing of each polarization channel and three-dimensional multistage imaging ignore the correlation between data, resulting in the mismatch between scattering centers and the inaccurate acquisition of polarization scattering matrices. To address these issues, a full-polarization Synthetic Aperture Radar (SAR) joint multidimensional reconstruction method based on sparse reconstruction is proposed in this study. In this method, all polarization channels and dimensions are integrated by setting the joint sparse constraints, and the full-polarization SAR joint multidimensional reconstruction is modeled as a multichannel joint sparse reconstruction problem. After the model is simplified by data interpolation, an efficient model-solving method is proposed by combining the three-dimensional fast Fourier transform, conjugate gradient method, and Newton iteration method, where the polarization scattering matrix and three-dimensional information of the target can be obtained at the same time. The proposed method ensures that the sparse support sets of different polarization channels and dimensions are consistent and utilizes the additional information generated by the correlation between data. On the basis of the simulation and electromagnetic calculation data, the experimental results indicate that the proposed method is tolerant of noise and immune to the types of targets. Moreover, the proposed method can effectively obtain the multidimensional reconstruction results of the target, where both the resolution of the imaging results and the estimation accuracy of the polarization scattering matrix are high.
- Synthetic Aperture Radar (SAR) /
- Full-polarimetric /
- Sparse reconstruction /
- Three-dimensional imaging /
- Joint reconstruction

HTML全文

1. 引言

合成孔径雷达地面动目标显示(Synthetic Aperture Radar-Ground Moving Target Indication, SAR-GMTI)结合了SAR能对地面全天时、全天候高分辨成像和GMTI能够检测、跟踪地面运动目标的优点，能对任意地面动目标进行检测、识别、跟踪、定位和成像^[1]，已成为先进体制SAR必备的功能。随着SAR-GMTI的快速发展，已对军事运动目标构成了严重威胁，因此，对SAR-GMTI系统干扰技术的研究具有重要意义^[2]。

SAR-GMTI通常用多个通道对杂波和静止目标进行对消^[3]，仅留下具有运动信息的目标，从而完成对运动目标的检测。常规的SAR干扰方法^[4,5]经过多通道对消后，会失去干扰效果，这使得对SAR-GMTI干扰必须有别于SAR干扰。文献[6,7]提出利用多干扰机对抗SAR双通道干扰对消技术，为多通道SAR-GMTI干扰提供了新的思路，但多个干扰机的协同工作难度较大；文献[8,9]提出了针对SAR-GMTI的虚假动目标欺骗干扰方法，这一类干扰需侦测SAR信号，并在此基础上进行复杂调制后转发出去，产生此类干扰对收发隔离度要求高，工程上较难实现；文献[10]就相干干扰工程实现难的问题，提出了间歇采样处理的干扰方法，利用收发分时避开了收发高隔离度的难以实现的难题；文献[11,12]提出了对SAR-GMTI的无源压制干扰，其干扰成本低且具有一定压制干扰效果，但无源干扰设备摆放受地形的限制，无法针对重要目标位置进行灵活压制，干扰灵活性不足。基于上述背景，本文提出了一种对常规的通道干涉对消SAR-GMTI的遮蔽干扰方法，该方法可以控制遮蔽区域的大小和出现的位置，达到对指定运动目标进行遮蔽的效果，通过遮蔽运动目标，影响运动目标回波的相位和幅度，从而无法检测运动目标，无法正确估计参数，无法正确定位动目标，最终达到对SAR-GMTI干扰的目的。文章首先给出了干扰模型，然后分析了该方法对SAR-GMTI的干扰原理，并分析了采样周期、占空比、运动调制参数和干扰能量对干扰效果的影响，最后通过仿真验证了干扰的正确性和有效性。

2. 运动调制间歇采样遮蔽干扰模型

如图1，SAR处于正侧视工作模式，设SAR平台以速度v沿x轴方向做匀速直线运动，其高度为H，合成孔径长度为L，合成孔径时间为 ${T_L} = L/v$ 。干扰机J位置为 $({x_j},{y_j},0)$ , t_a=0时干扰机到SAR的斜距为 ${R_j} = \sqrt {{x_j}\!^2 + {y_j}\!^2 + {H^2}}$ ，任意时刻t_a干扰机到SAR的斜距为 ${R_j}\left( {{t_{\rm{a}}}} \right)$ 。

图 1 SAR成像场景图

Figure 1. The imaging scene of SAR

下载: 全尺寸图片幻灯片

2.1 运动调制干扰模型

对SAR运动调制干扰是指利用干扰机模拟运动目标的反射回波相位特征的干扰方法。运动目标相对于静止目标的反射回波会存在一个运动附加相位，只要将此附加相位求得，并利用干扰机在截获SAR信号的基础上，调制上这个运动附加相位，然后转发出去，就能模拟产生运动假目标回波信号。下面重点推导匀加速运动目标的运动附加相位 $\Delta \phi \left( {{t_{\rm{a}}}} \right)$ 。

如图1，假设一个运动点目标P在t_a=0时刻坐标为 $({x_j},{y_j},0)$ (即与干扰机同坐标)，在地面上做匀加速运动，它沿方位向和距离向的速度、加速度分别为v_x, a_x和v_y, a_y，任意t_a时刻，P坐标为 $\left( {{x_j} + {v_x}{t_{\rm{a}}} + {a_x}t_{\rm{a}}^2/2,{y_j} + {v_y}{t_{\rm{a}}} + {a_y}t_{\rm{a}}^2/2,0} \right)$ , t_a=0时P到SAR的斜距为R_j, P与SAR间距离 ${R_j}\left( {{t_{\rm{a}}}} \right)$ 表达式为：

$\begin{aligned} & \!\!\!\!\!\!\!{R_j}\left( {{t_{\rm a}}} \right) \\ = & \!\! \sqrt {{{\left( {{x_j} \!\!+\! \!{v_x}{t_{\rm{a}}} \!\!+\!\! \frac{1}{2}{a_x}{t_{\rm{a}}}\!\!^2 \!\!-\!\! v{t_{\rm{a}}}} \right)}^2} \!\!\!\!+\!\! {{\left( {{y_j} \!+\! {v_y}{t_{\rm{a}}} \!\!+\!\! \frac{1}{2}{a_y}{t_{\rm{a}}}\!\!^2} \right)}^2} \!\!\!\!+\!\! {H^2}} \\ \approx & {R_j} \!+\!\! \frac{{{x_j}\left( {{v_x} \!\!-\!\! v} \right) \!\!+\!\! E{v_y}}}{{{R_j}}}{t_{\rm{a}}} \!+\! \frac{{{{\left( {{v_x} \!\!-\!\! v} \right)}^2} \!\!+\!\! {v_y}\!\!^2 \!+\! {x_j}{a_x} \!\!+\!\! {y_j}{a_y}}}{{2{R_j}}}{t_{\rm a}}\!^2\\ & + \frac{{{a_x}\left( {{v_x} - v} \right) + {a_y}{v_y}}}{{2{R_j}}}{t_{\rm{a}}}\!^3 + \frac{{{a_x}\!\!^2 + {a_y}\!\!^2}}{{8{R_j}}}{t_{\rm a}}\!^4 \end{aligned}$

(1)

若目标P静止，任意t_a时刻，P坐标为 $({x_j},{y_j},0)$ ，则P与SAR间距离 ${R_0}\left( {{t_{\rm{a}}}} \right)$ 表达式为：

$\begin{aligned} {R_0}\left( {{t_\rm{a}}} \right) & = \sqrt {{{\left( {{x_j} - v{t_\rm{a}}} \right)}^2} + {y_j}^2 \!+ {H^2}} \\ & \approx {R_j} - \frac{{{x_j}v}}{{{R_j}}}{t_\rm{a}} +\frac{{{v^2}}}{{2{R_j}}}{t_\rm{a}}\!\!^2 \end{aligned}$

(2)

根据式(1)和式(2)，可以得到运动附加相位的表达式为：

$\begin{aligned} \Delta \phi \left( {{t_{\rm{a}}}} \right) = & \! \frac{{2{{π}}}}{\lambda }\left[ {2R\left( {{t_{\rm{a}}}} \right) - 2{R_0}\left( {{t_{\rm{a}}}} \right)} \right]\\ = & \! 4{{π}}\frac{{{x_j}{v_x} \!+\! {y_j}{v_y}}}{{\lambda {R_j}}}{t_{\rm{a}}}\\ & + 2{{π}}\frac{{{v_x}\!^2 \!-\! 2{v_x}v \!+\! {v_y}\!^2 \!+\! {x_j}{a_x} \!+\! {y_j}{a_y}}}{{\lambda {R_j}}}{t_{\rm{a}}}\!\!^2\\ & + \! 2{{π}}\frac{{{a_x}\left( {{v_x} \!-\! v} \right) \!+\! {a_y}{v_y}}}{{\lambda {R_j}}}\!{t_{\rm{a}}}\!^3 \!+\! {{π}} \! \frac{{{a_x}\!^2 \!+\! {a_y}\!^2}}{{2\lambda {R_j}}}{t_{\rm{a}}}\!^4 \end{aligned}$

(3)

将推导出的运动附加相位 $\Delta \phi \left( {{t_{\rm{a}}}} \right)$ 调制在截获到的SAR信号上，可以得到运动调制干扰信号，其基带形式为：

$\begin{array}{l} {s _j}\left( {{t_{\rm{r}}},{t_{\rm{a}}}} \right) = {\rm{rect}}\left[ {\frac{{{t_{\rm{r}}} - 2{R_j}\left( {{t_{\rm a}}} \right){\rm{/}}{\rm c}}}{{{T_{\rm{p}}}}}} \right]{\rm{rect}}\left( {\frac{{{t_{\rm{a}}} - {x_j}/v}}{{{T_L}}}} \right)\\ \quad\quad\quad\quad\;\; \cdot \exp \left\{ {\left. {{\rm{j{{π}} }}{\mu _{\rm{r}}}{{\left[ {{t_{\rm{a}}} - \frac{{2{R_j}\left( {{t_{\rm{a}}}} \right)}}{{\rm{c}}}} \right]}^2}} \right\}} \right. \\ \quad\quad\quad\quad\;\; \cdot \exp \left[ { - {\rm{j}}\frac{{4{{π}}}}{\lambda }{R_j}\left( {{t_{\rm{a}}}} \right)} \right] \cdot \exp \left[ {{\rm{j}}\Delta \phi \left( {{t_{\rm{a}}}} \right)} \right] \end{array}$

(4)

其中， ${\mathop{\rm rect}\nolimits} \left( u \right) = \left\{ \begin{array}{l} 1,\quad \left| u \right| \le 1/2\\ 0,\quad {\rm{else}} \end{array} \right.$ , t_r为快时间，t_a为慢时间，f₀为中心频率，μ_r为调频率，T_p为脉宽，c为光速，v_x, a_x和v_y, a_y在式(4)中分别称为方位向调制速度、调制加速度和距离向调制速度、调制加速度。

2.2 间歇采样转发干扰模型

间歇采样干扰指干扰机接收SAR信号后，高保真度地采样其中一小段信号后进行转发处理，再采样下一段并进行转发，如此收发分时、采样和转发交替工作直至大时宽信号结束^[13]。设间歇采样脉冲信号 $p({t_{\rm{r}}})$ 为矩形包络脉冲串(如图2)，其表达式为：

图 2 距离向间歇采样脉冲串

Figure 2. Azimuth intermittent sampling pulse series

下载: 全尺寸图片幻灯片

$\begin{aligned} p({t_{\rm{r}}}) = & {\rm{rect}}\left(\frac{{{t_{\rm{r}}}}}{{{T_{\rm{w}}}}}\right) \otimes \sum\limits_{ - \infty }^{ + \infty } {\delta ({t_{\rm{r}}} - n{T_{\rm{s}}})} \\ = & {D_{\rm{r}}} + \sum\limits_{n = 1}^\infty {2{a_n}} {\rm{cos}}2{{π}}n{f_{\rm{s}}}{t_{\rm{r}}} \end{aligned}$

(5)

其中。“ $\otimes$ ”为卷积符号， $\delta ( \cdot )$ 为冲击函数，T_w为采样脉冲宽度，T_s为采样周期， ${D_{\rm{r}}} = {T_{\rm{w}}}/{T_{\rm{s}}} = {T_{\rm{w}}}{f_{\rm{s}}}$ 为占空比， ${a_n} = {T_{\rm{w}}}{f_{\rm{s}}}{\rm{sinc}}(n{{π}}{T_{\rm{w}}}{f_{\rm{s}}}) = {D_{\rm{r}}}{\rm{sinc}}(n{{π}}{D_{\rm{r}}})$ 为幅度加权系数，通常情况下T_w, T_s远小于雷达信号的脉冲宽度。

对截获的SAR信号 ${s_0}({t_{\rm{r}}},{t_{\rm{a}}})$ 进行距离向间歇采样后，就得到了间歇采样干扰信号，其表达式为：

${s_{j{\rm{r}}}}({t_{\rm{r}}},{t_{\rm{a}}}) = {s_0}({t_{\rm{r}}},{t_{\rm{a}}}) \cdot p({t_{\rm{r}}})$

(6)

间歇采样干扰基于天线收发分时体制，能够改善干扰机收发隔离问题，可在距离向产生密集的多假目标干扰效果。

2.3 运动调制间歇采样遮蔽干扰模型

运动调制间歇采样干扰详细产生步骤是在接收到的SAR信号上调制匀加速运动附加相位 $\Delta \phi \left( {{t_{\rm{a}}}} \right)$ ，并对其距离向间歇采样，然后转发出去，此干扰信号的基带形式为：

$\begin{split} {s_j}\left( {{t_{\rm{r}}},{t_{\rm{a}}}} \right) =\!\!\!\! & {\rm{rect}}\left[ {\frac{{{t_{\rm{r}}} - 2{R_j}\left( {{t_{\rm{a}}}} \right){\rm{/}}{\rm c}}}{{{T_{\rm{p}}}}}} \right]{\rm{rect}}\left( {\frac{{{t_{\rm{a}}} - {x_j}/v}}{{{T_{L{\rm{p}}}}}}} \right)\\ & \cdot \exp \left\{ {\left. {{\rm{j{{π}} }}{\mu _{\rm{r}}}{{\left[ {{t_{\rm{r}}} - \frac{{2{R_j}\left( {{t_{\rm{a}}}} \right)}}{{\rm{c}}}} \right]}^2}} \right\}} \right. \\ & \cdot {\rm{exp}}\left[ { - {\rm{j}}2k{R_j}\left( {{t_{\rm{a}}}} \right)} \right] \exp \left[ {\Delta \phi \left( {{t_{\rm a}}} \right)} \right]\! \\ & \cdot \left\{\!\! {{D_{\rm r}} \!+\!\! \sum\limits_{n = 1}^\infty {2{a_n}} {\rm{cos}}2{{π}}n{f_{\rm{s}}}\left[ \! {{t_{\rm{r}}} \!-\! \frac{{2{R_j}\left( {{t_{\rm a}}} \right)}}{{\rm{c}}}} \right]} \!\! \right\} \end{split}$

(7)

运动调制间歇采样干扰在方位向上利用运动调制效应实现展宽和偏移，在距离向上利用间歇采样产生距离向多假目标，二者相结合能实现2维区域遮蔽干扰，因此将这种新的干扰样式称为运动调制间歇采样遮蔽干扰。

3. 对SAR-GMTI干扰原理

GMTI按实现方式的不同可分为两类：一是单通道GMTI，该方式对硬件需求较低，运算量相对较小，但是对弱目标或慢速目标的检测性能较差；二是多通道GMTI，该方式通过增加雷达系统空间维信息对杂波实现良好的抑制和对消，能够在低信噪比条件下对慢速运动目标进行有效检测，主要包括DPCA, STAP, ATI等^[14]。这里采用三通道干涉技术为例分析对SAR-GMTI的干扰原理，其几何模型如图3所示。

图 3 三通道SAR-GMTI干涉处理几何模型

Figure 3. The sketch map of tri-antenna interference cancelling technique

下载: 全尺寸图片幻灯片

三通道子孔径天线沿航迹以等间隔D_a排列，天线2发射信号，天线1、天线2、天线3同时接收信号。由图3可知，干扰信号到3个通道的传播路程分别为 ${R_{j1}} \!=\! ({R_{j{\rm{a}}2}} \!+\! {R_{j{\rm{a}}1}})$ , ${R_{j2}} \!=\! 2{R_{j{\rm{a}}2}}$ , ${R_{j3}} \!=\! ({R_{j{\rm{a}}2}} \!+\! {R_{j{\rm{a}}3}})$ 。忽略干扰机延迟，3个通道接收到的干扰信号分别为(略去窗函数)：

$\left\{\! \begin{aligned} {s _{j1}}({t_{\rm{r}}},{t_{\rm{a}}}) = & \cdot \exp \left\{ {\left. {{\rm{j{{π}} }}{\mu _{\rm{r}}}{{\left[ {{t_{\rm{a}}} - \frac{{{R_{j1}}\left( {{t_{\rm{a}}}} \right)}}{{\rm{c}}}} \right]}^2}} \right\}} \right. \\& \cdot \exp \left[ { - {\rm{j}}k{R_{j1}}\left( {{t_{\rm{a}}}} \right)} \right] \cdot \exp \left[ {{\rm{j}}\Delta \phi \left( {{t_{\rm{a}}}} \right)} \right] \\ &\cdot \left\{ {{D_{\rm r}} \!+\! \sum\limits_{n = 1}^\infty {2{a_n}} {\rm{cos}}2{{π}}n{f_{\rm{s}}}\left[ {{t_{\rm{r}}} \!-\! \frac{{{R_{j1}}\left( {{t_{\rm{a}}}} \right)}}{{\rm{c}}}} \right]} \!\!\right\}\\ {s _{j2}}({t_{\rm{r}}},{t_{\rm{a}}}) = & \exp \left\{ {\left. {{\rm{j{{π}} }}{\mu _{\rm{r}}}{{\left[ {{t_{\rm{a}}} - \frac{{{R_{j2}}\left( {{t_{\rm{a}}}} \right)}}{{\rm{c}}}} \right]}^2}} \right\}} \right. \\&\cdot \exp \left[ { - {\rm{j}}k{R_{j2}}\left( {{t_{\rm{a}}}} \right)} \right] \cdot \exp \left[ {{\rm{j}}\Delta \phi \left( {{t_{\rm{a}}}} \right)} \right] \\&\cdot \left\{ {{D_{\rm{r}}} \!+\! \sum\limits_{n = 1}^\infty {2{a_n}} {\rm{cos}}2{{π}}n{f_{\rm{s}}}\left[ {{t_{\rm{r}}} \!-\! \frac{{{R_{j2}}\left( {{t_{\rm{a}}}} \right)}}{{\rm{c}}}} \right]} \!\!\right\}\\ {s _{j3}}({t_{\rm{r}}},{t_{\rm{a}}}) = & \exp \left\{ {\left. {{\rm{j{{π}} }}{\mu _{\rm{r}}}{{\left[ {{t_{\rm{a}}} - \frac{{{R_{j3}}\left( {{t_a}} \right)}}{{\rm{c}}}} \right]}^2}} \right\}} \right. \\ &\cdot\exp \left[ { - {\rm{j}}k{R_{j3}}\left( {{t_{\rm{a}}}} \right)} \right] \cdot \exp \left[ {{\rm{j}}\Delta \phi \left( {{t_{\rm{a}}}} \right)} \right] \\ &\cdot \left\{ {{D_{\rm{r}}} \!+\! \sum\limits_{n = 1}^\infty {2{a_n}} {\rm{cos}}2{{π}}n{f_{\rm{s}}}\left[ {{t_{\rm{r}}} \!-\! \frac{{{R_{j3}}\left( {{t_{\rm{a}}}} \right)}}{{\rm{c}}}} \right]}\!\! \right\} \end{aligned} \right.$

(8)

利用RD算法对3个通道成像进行分析，3个通道信号经距离向匹配滤波可得

$\left\{ \begin{aligned} {s _{j{\rm r}1}}({t_{\rm{r}}},{t_{\rm{a}}}) \approx & {s _{j{\rm r}2}}({t_{\rm{r}}},{t_{\rm{a}}}) \\&\cdot \exp \left[ { \!\!- {\rm{j}}\frac{{2{{π}}}}{\lambda } \left(\frac{{{D_{\rm{a}}}\!\!^2 - 2{D_{\rm{a}}}{x_j}}}{{2{R_j}}} \!+\! \frac{{{D_{\rm{a}}}v{t_{\rm{a}}}}}{{{R_j}}} \right)} \right]\\ {s _{j{\rm r}2}}({t_{\rm{r}}},{t_{\rm{a}}}) = &\exp \left[ { - {\rm{j}}k{R_{j2}}\left( {{t_{\rm{a}}}} \right)} \right] \cdot \exp \left[ {{\rm{j}}\Delta \phi \left( {{t_{\rm{a}}}} \right)} \right]\\ & \cdot \sum\limits_{n = - \infty }^{ + \infty } {{a_n}\chi \left( {{t_{\rm{r}}} - \frac{{{R_{j2}}\left( {{t_{\rm{a}}}} \right)}}{{\rm{c}}}, - n{f_{\rm{s}}}} \right)} \\ {s _{j{\rm r}3}}({t_{\rm r}},{t_{\rm a}}) \approx &{s _{j{\rm r}2}}({t_{\rm{r}}},{t_{\rm{a}}}) \\&\cdot \exp \! \left[ {\! - {\rm{j}}\frac{{2{{π}}}}{\lambda }\! \left(\frac{{{D_{\rm{a}}}\!\!^2 \!+\! 2{D_{\rm{a}}}{x_j}}}{{2{R_j}}} \!-\! \frac{{{D_{\rm{a}}}v{t_{\rm{a}}}}}{{{R_j}}} \right)} \right] \end{aligned} \right.$

(9)

其中， $\chi \left( \cdot \right)$ 为SAR线性调频脉冲信号的模糊函数^[10]，其表达式为：

$\begin{aligned} \chi \left( {\tau ,{f_{\rm{d}}}} \right) = & \exp \left( { \!-\! {\rm{j{{π}} }}{f_{\rm{d}}}\tau } \right) \cdot \left( {1 \!-\! \frac{{\left| \tau \right|}}{{{T_{\rm{p}}}}}} \right) \\&\cdot {\mathop{\rm sinc}\nolimits} \left[ {\left( {{f_{\rm{d}}} - {\mu _{\rm{r}}}\tau } \right)\left( {{T_{\rm{p}}} - \left| \tau \right|} \right)} \right] \end{aligned}$

(10)

经距离徙动校正，忽略接收通道的位置差异对距离向成像的影响，在进行方位向匹配滤波前，必须补偿通道位置间隔产生的多普勒中心频率偏差，以通道2为参考，则通道1和通道3的补偿函数分别为：

$\left\{ \begin{array}{l} {C_1}({t_{\rm{a}}}) = \exp ({\rm{j}}2{{π}}v{D_{\rm{a}}}{t_{\rm{a}}}/\lambda {R_j})\\ {C_3}({t_{\rm{a}}}) = \exp ( - {\rm{j}}2{{π}}v{D_{\rm{a}}}{t_{\rm{a}}}/\lambda {R_j}) \end{array} \right.$

(11)

对通道1、通道3进行多普勒中心偏差补偿后，可得方位向匹配滤波输出包络为：

$\left\{ \begin{aligned} { s_{j{\rm a}1}}({t_{\rm{r}}},{t_{\rm{a}}}) \approx &{s _{j{\rm a}2}}({t_{\rm{r}}},{t_{\rm{a}}})\! \cdot \! \exp \left[ { \!-\! {\rm{j}}\frac{{2{{π}}}}{\lambda }\left(\frac{{{D_{\rm{a}}}\!\!^2\! -\! 2{D_{\rm{a}}}{x_j}}}{{2{R_j}}}\right)}\! \right]\\ {s _{j{\rm a}2}}({t_{\rm{r}}},{t_{\rm{a}}}) =& \left( {1 - \left| {{t_{\rm{r}}}\!^ * } \right|/{T_{\rm{p}}}} \right) \cdot \left( {1 - \left| {{t_{\rm{a}}}\!^ * } \right|/{T_L}} \right) \\&\cdot {\mathop{\rm sinc}\nolimits} \left[ {{{π}}{\mu _{\rm{a}}}{t_{\rm{a}}}\!^ * \left( {{T_L} - \left| {{t_{\rm{a}}}\!^ * } \right|} \right)} \right]\\ &\cdot \sum\limits_{n = - \infty }^{ + \infty } {a_n}\exp \left( { - {\rm{j{{π}} }}n{f_{\rm{s}}}{t_{\rm{r}}}\!^*} \right) \\&\cdot {\mathop{\rm sinc}\nolimits} \left[ {{{π}}\left( {n{f_{\rm{s}}} + {\mu _{\rm r}}{t_{\rm{r}}}\!^ * } \right)\left( {{T_{\rm{p}}} - \left| {{t_{\rm{r}}}\!^ * } \right|} \right)} \right] \\ {s _{j{\rm{a}}3}}({t_{\rm{r}}},{t_{\rm{a}}}) \approx & {s _{j{\rm{a}}2}}({t_{\rm{r}}},{t_{\rm{a}}}) \!\cdot\! \exp\! \left[ { -\! {\rm{j}}\frac{{2{{π}}}}{\lambda }\left(\frac{{{D_{\rm{a}}}\!\!^2 \!+\! 2{D_{\rm{a}}}{x_j}}}{{2{R_j}}}\right)}\! \right] \end{aligned} \right.$

(12)

其中， ${t_{\rm{r}}}\!^ * \!\!=\!\! {t_{\rm{r}}} \!-\! 2{R_j}/{\rm{c}}$ , ${t_{\rm{a}}}\!^ * \!=\!\! {t_{\rm{a}}} \!-\! {t_{{\rm{am}}}}$ , ${a_n} \!\!=\!\! {D_{\rm{r}}}{\mathop{\rm sinc}\nolimits} (n{{π}}{D_{\rm{r}}})$ , D_r是间歇采样脉冲串的占空比，t_am为驻相点 ${\tau ^ * }$ 处对应的方位向时刻，在t_a=t_am时各通道有最大输出值，t_am的表达式为^[9]：

$\begin{aligned} {t_{{\rm{am}}}} = &\frac{{{x_j}}}{v} - \frac{{{x_j}{v_x} + {y_j}{v_y}}}{{{v^2}}}\\ & - \frac{{{v_x}\!^2 - 2{v_x}v + {y_y}\!^2 + {x_j}{a_x} + {y_j}{a_y}}}{{{v^2}}}{\tau ^ * }\\ & -\! \frac{{3{a_x}\left( {{v_x} \!\!-\!\! v} \right) +\! 3{a_y}{v_y}}}{{2{v^2}}}{\tau ^{ * 2}} \!-\!\! \frac{{{a_x}\!^2 \!+\! {a_y}\!^2}}{{2{v^2}}}{\tau ^{ * 3}} \end{aligned}$

(13)

t_am关于 ${\tau ^ * }$ 的常数项体现了目标方位像的峰值偏移位置，关于 ${\tau ^ * }$ 的1次、2次和3次项可使方位向目标像展宽和散焦。

由式(12)通道2成像表达式可见，由运动调制效应产生的干扰条带在距离向以间隔为 $n{\rm{c}}{f_{\rm{s}}}/2{\mu _{\rm{r}}}$ 周期延拓出现，能量较强的干扰条带数为 ${\mathop{\rm floor}\nolimits} \left( {2/{D_{\rm{r}}}} \right) - 1$ ，因此会产生区域遮蔽干扰效果。根据运动目标SAR成像效应^[9]知干扰条带方位向中心偏移位置和展宽量分别为：

$\!\!\!\!\!\!\!\!\!\!\!\!\!\!\!\!\!\!\!\!\!\!\!\!\!\!\!\!\!\!\!\!\!\!\!\!\!\!\!\!\!\!\!\! x = {x_j} - \frac{{{x_j}{v_x} + {y_j}{v_y}}}{v} \quad\quad\quad$

(14)

$\begin{array}{l} \delta x = \left| { - \frac{{{v_x}\!^2 - 2{v_x}v + {v_y}\!^2 + {x_j}{a_x} + {y_j}{a_y}}}{v}{T_L}} \right.\\ \;\;\;\;\;\;\;\left. { - \frac{{3\left( {{a_x}{v_x} - {a_x}v + {a_y}{v_y}} \right)}}{{4v}}{T_L}\!^2 - \frac{{{a_x}\!^2 + {a_y}\!^2}}{{8v}}{T_L}\!^3} \right|\quad \end{array}$

(15)

由此可以计算出形成有效干扰的面积为：

${S_j} = \delta x \cdot \frac{{n{\rm{c}}{f_{\rm{s}}}}}{{2{\mu _{\rm{r}}}}} \cdot \left[ {{\mathop{\rm floor}\nolimits} \left( {\frac{2}{{{D_{\rm{r}}}}}} \right) - 2} \right]$

(16)

由于各接收通道存在沿航迹方向位置偏差，在进行杂波对消之前，必须补偿由位置偏差引起的相位偏差，相应的补偿函数为：

$\left\{ { \begin{aligned} {C _{12}}({t_{\rm{a}}}) = \exp \left[ {{\rm{j{{π}} }}{D_{\rm{a}}}({D_{\rm{a}}} - 2v{t_{\rm{a}}})/\lambda {R_j}} \right]\\ {C _{23}}({t_{\rm{a}}}) = \exp \left[ {{\rm{j{{π}} }}{D_{\rm{a}}}({D_{\rm{a}}} + 2v{t_{\rm{a}}})/\lambda {R_j}} \right] \end{aligned}} \right.$

(17)

利用式(15)进行位置偏差相位补偿，并进行杂波对消可得

$\left\{ \begin{array}{l} {y _{12}}({t_{\rm{r}}},{t_{\rm{a}}}) = {s _{j{\rm a}1}}({t_{\rm{r}}},{t_{\rm{a}}}){C _{12}} - {s _{j{\rm a}2}}({t_{\rm{r}}},{t_{\rm{a}}}) \\ = {s _{j{\rm a}2}}({t_{\rm{r}}},{t_{\rm{a}}})\\ \quad\cdot \left[ {\exp \left( {{\rm{j}}\frac{{2{{π}}{D_{\rm{a}}}v}}{{\lambda {R_j}}}\left(\frac{{{x_j}}}{v} - {t_{\rm{a}}} \right)} \right) - 1} \right]\\ {y _{23}}({t_{\rm{r}}},{t_{\rm{a}}}) = {s _{j{\rm a}2}}({t_{\rm{r}}},{t_{\rm{a}}}) - {s _{j{\rm a}3}}({t_{\rm{r}}},{t_{\rm{a}}}){C _{23}}\\ = {s _{j{\rm a}2}}({t_{\rm{r}}},{t_{\rm{a}}}) \\ \quad\cdot \left[ {1 - \exp \left( {{\rm{j}}\frac{{2{{π}}{D_{\rm{a}}}v}}{{\lambda {R_j}}}\left(\frac{{{x_j}}}{v} - {t_{\rm{a}}} \right)} \right)} \right] \end{array} \right.$

(18)

对式(18)取模，则干扰信号通过SAR-GMTI系统后的输出幅度为：

$\begin{aligned} \left| {{y _{12}}({t_{\rm{r}}},{t_{\rm{a}}})} \right| = &\left| {{y _{23}}({t_{\rm{r}}},{t_{\rm{a}}})} \right| = 2\left| {{s _{j{\rm a}2}}({t_{\rm{r}}},{t_{\rm{a}}})} \right| \\ &\cdot \left| {\sin \left[ {\frac{{{{π}}{D_{\rm{a}}}v}}{{\lambda {R_j}}} \left ({t_{\rm{a}}} - \frac{{{x_j}}}{v} \right)} \right] } \right| \end{aligned}$

(19)

一般情况下，t_am表达式中 $- \displaystyle\frac{{{v_x}\!^2 - 2{v_x}v + {v_y}\!^2}}{{{v^2}}}{\tau\! ^*}$ $- \displaystyle\frac{{3{a_x}\left( {{v_x} - v} \right) + 3{a_y}{v_y}}}{{2{v^2}}}{\tau ^{*2}} - \frac{{{a_x}\!^2 + {a_y}\!^2}}{{2{v^2}}}{\tau ^{*3}}$ 对成像能量的影响较小，可忽略不计^[9]，此时对消后输出幅度近似为：

$\begin{aligned} \left| {{y _{12}}({t_{\rm{r}}},{t_{\rm{a}}})} \right| =& \left| {{y _{23}}({t_{\rm{r}}},{t_{\rm{a}}})} \right| = 2\left| {{s _{j{\rm a}2}}({t_{\rm{r}}},{t_{\rm{a}}})} \right| \\ & \!\!\!\cdot \left| {\sin \left[\! {\frac{{{{π}}{D_{\rm{a}}}}}{{\lambda {R_j}v}}({x_j}{v_x} \!\!+\!\! {y_j}{v_y} \!\!+\!\! \left( {{x_j}{a_x} \!\!+\!\! {y_j}{a_y}} \right){\tau ^ * })} \right] } \right| \end{aligned}$

(20)

由式(20)可知，干扰机位置，距离向和方位向速度、加速度取值将直接影响到杂波对消后运动目标的保留能量的大小。当 ${x_j}{v_x} \!+\! {y_j}{v_y} \!+\! \left( {{x_j}{a_x} \!+\! {y_j}{a_y}} \right){\tau ^ * } \!=$ $n\lambda {R_j}v/{D_{\rm{a}}}$ 时，干扰能量将被全部对消，干扰位于对消特性的凹口处；当 ${x_j}{v_x} \!+\! {y_j}{v_y} \!+\! \left( {{x_j}{a_x} \!+\! {y_j}{a_y}} \right){\tau ^ * } \!=$ $\left( {n + 1/2} \right)\lambda {R_j}v/{D_{\rm{a}}}$ 时，干扰位于对消特性的凸口处，干扰幅度得到最大程度地增强，可达到对消前的2倍；其余均介于凸口和凹口之间。这说明运动调制间歇采样干扰经过GMTI处理后不会被完全对消，能够对SAR-GMTI达到干扰效果。

4. 干扰参数和干扰功率分析

运动调制间歇采样遮蔽干扰经过SAR-GMTI处理后的输出与采样周期、占空比、运动调制参数和干扰能量4个干扰指标有关。因此需要进一步理解这些干扰参数的影响。

(1) 间歇采样周期T_s

间歇采样周期影响遮蔽面积，遮蔽疏密程度，是一个关键的干扰指标。当间歇采样周期越大时，假目标条带越密集，所形成的遮蔽面积越小，干扰能量越集中；当间歇采样周期越小时，假目标条带越稀疏，所形成的遮蔽面积越大，干扰能量越分散。

(2) 占空比D_r

占空比影响干扰输出加权系数a_n，因而会影响到干扰输出幅度。设n=0为距离向中心假目标，其余为距离向第n阶次假目标。当 $n{{π}}{D_{\rm{r}}} = k{{π}}$ (k为整数)时，a_n=0，此时图像上将看不到该次级假目标。由于a_n=D_r，所以占空比越大，距离向中心假目标幅度越大，次级假目标幅度相对中心假目标会降低。占空比减小时，中心假目标幅度下降较快，次级假目标幅度下降较慢。

(3) 运动调制参数v_x, v_y, a_x, a_y

运动调制参数主要影响方位向假目标峰值中心位置及展宽量。一般地，干扰机位置纵坐标y_j远大于横坐标x_j，由式(14)和式(15)知，v_x影响方位向均匀展宽量，v_y影响假目标峰值中心位置在方位向上发生偏移的大小，a_x对偏移和展宽影响均不大，a_y是使方位向发生非均匀展宽的原因。

(4) 干扰能量分析

干扰能量影响干扰信号处理后的幅度，因而决定了对目标遮蔽的好坏。干扰能量过小，则无法有效遮蔽目标；干扰能量过大，则影响干扰效率。由于干扰信号在距离维间歇采样和方位维运动调制，因而会导致2维部分失配，为了选择合适的干扰功率，需要根据匹配滤波的信号处理过程，对所需干扰能量进行分析。根据式(12)，单位幅度干扰信号经过距离向匹配滤波后的幅度A_r为 $\left( {1 - \left| {{t_{\rm{r}}}\!^ * } \right|/{T_{\rm{p}}}} \right) \cdot$ $\displaystyle\sum\nolimits_{n = - \infty }^{ + \infty } {{{a_n}{\mathop{\rm sinc}\nolimits} \left[ {{{π}}\left( {n{f_{\rm{s}}} + {\mu _{\rm r}}{t_{\rm{r}}}\!^ * } \right)\left( {{T_{\rm{p}}} - \left| {{t_{\rm{r}}}\!^ * } \right|} \right)} \right]} }$ ，而经过方位向匹配滤波后的幅度A_a为 $\left( {1 - \left| {{t_{\rm{a}}}^ * } \right|/{T_L}} \right) \cdot {\mathop{\rm sinc}\nolimits}$ $\left[ {{{π}}{\mu _{\rm{a}}}{t_{\rm{a}}}\!^ * \left( {{T_L} - \left| {{t_{\rm{a}}}\!^ * } \right|} \right)} \right]$ ，从而经过2维匹配滤波处理后的幅度为 ${A_{\rm{r}}} \cdot {A_{\rm{a}}}$ 。干扰信号2维处理后的幅度大于被保护目标回波2维处理后幅度的 $\sqrt 2$ 倍时，一般能达到有效遮蔽^[15]。根据上述能量分析，可以得到合适的干扰功率。

由于干扰机与待保护目标成像后的相对位置是已知的，结合待保护区域大小，选择合适的干扰参数和干扰功率，可使得目标恰好被遮蔽。

5. 仿真实验

为了验证理论分析的正确性和干扰的有效性，根据式(12)生成的干扰信号按照RD成像算法进行干扰仿真。设SAR-GMTI工作于正侧视，其主要实验参数如表1所示，SAR干扰机放置坐标为(0, 10000, 0)，干扰实验参数如表2所示，设置干信比为15 dB。

表 1 SAR-GMTI实验参数

Table 1. The simulation experiment parameters

SAR参数名称	数值
信号载频(GHz)	10
信号脉宽(μs)	20
距离向信号带宽(MHz)	100
方位向信号带宽(Hz)	400
各通道天线间距(m)	1
飞行高度(m)	6000
合成孔径长度(m)	300
载机速度(m/s)	200
脉冲重复周期(Hz)	480
通道数目	3

下载: 导出CSV

| 显示表格

表 2 干扰实验参数

Table 2. The jamming experiment parameters

干扰参数名称	符号
采样周期(μs)	T_s
距离向调制速度(m/s)	v_y
距离向调制加速度(m/s²)	a_y
占空比	D_r
方位向调制速度(m/s)	v_x
方位向调制加速度(m/s²)	a_x

下载: 导出CSV

| 显示表格

5.1 对运动装甲车干扰遮蔽效果

因为干扰机和待保护目标相对位置是已知的，对干扰机设置合理的运动参数，可使干扰能量仅出现在待保护目标上，从而有效利用了干扰能量。

现需保护6辆具有较强反射特性的运动装甲车，其坐标分别为(–110, 9975, 0), (–110, 10000, 0), (–110, 10025, 0), (–100, 9975, 0), (–100, 10000, 0), (–100, 10025, 0)，均以 ${v_{{\rm T}x} = 0$ , $a_{{\rm T}x} = 0$ , $v_{{\rm T}y} = - 3\;{\rm{m}}/{\rm{s}}$ , $a_{{\rm T}y} = 0$ 行进。运动装甲车SAR成像后会发生偏移或展宽，其方位向偏移量 $\Delta x$ 和展宽量 $\delta x$ 由式(14)和式(15)可以计算得出。将装甲车运动参数代入，可得各装甲车偏移量 $\Delta x{\rm{ = }}150\;{\rm{m}}$ 、展宽量 $\delta x{\rm{ = }}0$ ，因此装甲车SAR成像后的坐标分别为(40, 9975, 0), (40, 10000, 0), (40, 10025, 0), (50, 9975, 0), (50, 10000, 0), (50, 10025, 0)成像仿真图如图4(a)所示，运动装甲车和静止参考点均清晰可见；图4(b)表示经过GMTI对消后的成像图，静止参考点被对消，运动装甲车仍清晰可见。

图 4 遮蔽6辆装甲车干扰效果图

Figure 4. The jamming images effect of shading six armored car

下载: 全尺寸图片幻灯片

用运动调制间歇采样干扰对SAR-GMTI进行转发，按上述实验参数进行仿真。根据计算出的待保护目标成像后的位置信息，干扰参数设置为v_x=0, a_x=0, v_y=–0.85 m/s, a_y=–0.15 m/s², D_r=10%, T_s=8 μs；根据第3节干扰能量分析，选择干信比为15 dB。经SAR-GMTI对消处理后干扰仿真效果如图4(c)所示，可见在干信比为15 dB时，干扰能量没有被对消，并且将运动装甲车完全遮盖，而对一般的噪声干扰要达到相同的遮盖干扰效果，干信比至少要达到50 dB^[4]，说明此干扰方法能量利用效率较高。遮蔽面积约为1600 m²，与式(16)计算结果基本一致，说明了理论分析的正确性。

5.2 各参数对干扰效果影响仿真

(1) 间歇采样周期

取v_x=0, a_x=0, v_y=–0.85 m/s, a_y=–0.3 m/s², D_r=10%，采样周期依次为T_s=4 μs, T_s=8 μs进行对比仿真，对GMTI干扰成像结果如图5。可见，随着采样周期的变大，干扰条带在距离向上分布越密集，干扰区域越小，能量越集中。

图 5 不同采样周期下的干扰图像

Figure 5. Jamming images with different sampling periods

下载: 全尺寸图片幻灯片

(2) 占空比

取v_x=0, a_x=0, v_y=–0.85 m/s, a_y=–0.3 m/s², T_s=6 μs，占空比依次为D_r=10%, D_r=15%，进行对比仿真，结果如图6。可见，随着占空比的增大，干扰条带数目减少，遮蔽面积减小，各干扰条带强度差别变大。

图 6 不同占空比下的干扰图像

Figure 6. Jamming images with different duty ratio

下载: 全尺寸图片幻灯片

(3) 运动调制参数

取v_x=0, a_x=0, v_y=–0.85 m/s, T_s=8 μs, D_r=10%，当a_y=–0.30 m/s², a_y=–0.45 m/s²时，结果如图7(a)–图7(b)；再取v_x=0, a_x=0, a_y=–0.15 m/s², T_s=8 μs, D_r=10%，当距离向速度依次为v_y=0.3 m/s, v_y=–0.6 m/s时，结果如图7(c)–图7(d)。可见，距离向调制加速度对干扰条带长度影响很大，其绝对值越大，干扰条带越长；距离向调制速度主要影响遮蔽面中心的方位向出现位置。

图 7 不同运动调制参数下的干扰图像

Figure 7. Jamming images with different motion modulation parameters

下载: 全尺寸图片幻灯片

6. 结束语

本文提出一种基于运动调制的SAR-GMTI间歇采样遮蔽干扰方法，建立了干扰模型，并进行了理论分析和仿真实验。理论分析表明，该方法能够对SAR-GMTI产生遮蔽干扰效果，且其遮蔽面的大小、疏密程度和覆盖位置可以通过改变采样周期、占空比和运动调制参数进行灵活地控制；仿真实验表明，该方法对强反射目标群具有较好的遮蔽效果，且所需干扰能量较小。此干扰方法改善了干扰机收发隔离的问题，能产生灵活可控的遮蔽面，且干扰能量较一般噪声压制干扰更低，因此具有较高的研究与运用价值。

图 1 各个极化通道的仿真目标成像结果

Figure 1. Each polarization channel’s imaging results of simulated targets

下载: 全尺寸图片幻灯片

图 2 仿真目标全极化联合多维重建结果

Figure 2. Full polarization joint multi-dimensional reconstruction results of simulated targets

下载: 全尺寸图片幻灯片

图 3 Slicy的CAD模型

Figure 3. CAD model of Slicy

下载: 全尺寸图片幻灯片

图 4 各个极化通道的Slicy成像结果

Figure 4. Each polarization channel’s imaging results of Slicy

下载: 全尺寸图片幻灯片

图 5 Slicy全极化联合多维重建结果

Figure 5. Full polarization joint multi-dimensional reconstruction results of Slicy

下载: 全尺寸图片幻灯片

图 6 卫星的CAD模型

Figure 6. CAD model of satellite

下载: 全尺寸图片幻灯片

图 7 各个极化通道的卫星成像结果

Figure 7. Each polarization channel’s imaging results of satellite

下载: 全尺寸图片幻灯片

图 8 卫星全极化联合多维重建结果

Figure 8. Full polarization joint multi-dimensional reconstruction results of satellite

下载: 全尺寸图片幻灯片

表 1 全极化联合多维重建方法的步骤

Table 1. Steps of full polarization joint multi-dimensional reconstruction method

　(1) 设定初值：

${{\tilde{ \beta }}^n} = {{0}}$ ；

　(2) 对每个极化通道，

　　　(a) 使用3-D NUFFT对

${G_l}(k_x^{},k_y^{},k_z^{})$ 进行插值，得到
　　　　

${\hat G_l}(\hat k_x^{},\hat k_y^{},\hat k_z^{})$ ，

　　　(b) 对

${\hat G_l}(\hat k_x^{},\hat k_y^{},\hat k_z^{})$ 进行3-D IFFT，并向量化结果得到
　　　　

${{\hat{ A}}^{\rm{H}}}{{\hat{ b}}_l}$ ；

　(3) 根据所有极化通道的

${{\hat{ A}}^{\rm{H}}}{{\hat{ b}}_l}$ ，得到

${{\hat{ A}}^{\rm{H}}}{\hat{ b}}$ ；

　(4) 结合3-D FFT，3-D IFFT和共轭梯度法计算
　　

${(2{{\hat{ A}}^{\rm{H}}}{\hat{ A}} + \mu p{{D}}({{\tilde{ \beta }}^n}))^{ - 1}}$ ；

　(5) 根据

${{\hat{ A}}^{\rm{H}}}{\hat{ b}}$ ，计算

${(2{{\hat{ A}}^{\rm{H}}}{\hat{ A}} + \mu p{{D}}({{\tilde{ \beta }}^n}))^{ - 1}}2{{\hat{ A}}^{\rm{H}}}{\hat{ b}}$ ；

　(6) 按式(17)迭代计算

${{\tilde{ \beta }}^{n + 1}}$ ，当

${ {\left\| { { { {\tilde{ \beta } } }^{n + 1} } - { { {\tilde{ \beta } } }^n} } \right\|_2^2} \Bigr/ {\left\| { { { {\tilde{ \beta } } }^n} } \right\|_2^2} } < \tau$ 时
　　得到解

${\tilde{ \beta }} = {{\tilde{ \beta }}^{n + 1}}$ ；

　(7) 对

${\tilde{ \beta }}$ 进行Cameron分解，得到全极化联合多维重建结果。

下载: 导出CSV

表 2 仿真目标信息

Table 2. Information of simulated targets

类型	散射矩阵	幅度	位置
三面角	$\left[ {\begin{array}{*{20}{c}} 1&0 \\ 0&1 \end{array}} \right]$	1	$x = 1.0\,{\rm{m} },y = - 0.5\,{\rm{m} },z = 0.7\,{\rm{m} }$
偶极子	$\left[ {\begin{array}{*{20}{c}} 1&0 \\ 0&0 \end{array}} \right]$	1	$x = - 1.0\,{\rm{m} },y = 0.5\,{\rm{m} },z = - 0.7\,{\rm{m} }$
30°二面角	$\left[ {\begin{array}{*{20}{c}} {0.5}&{0.866} \\ {0.866}&{ - 0.5} \end{array}} \right]$	1	$x = - 0.5\,{\rm{m} },y = - 1.0\,{\rm{m} },z = 0.7\,{\rm{m} }$
45°二面角	$\left[ {\begin{array}{*{20}{c}} 0&1 \\ 1&0 \end{array}} \right]$	1	$x = 0.5\,{\rm{m} },y = 1.0\,{\rm{m} },z = - 0.7\,{\rm{m} }$

下载: 导出CSV

表 3 目标的仿真参数

Table 3. Simulation parameters of simulated targets

雷达扫描参数	值
频率范围	[8 GHz, 12 GHz]
频率采样间隔	20 MHz
方位角范围	[–4°, 6°]
方位角采样间隔	1/14°
俯仰角范围	[18°, 42°]
俯仰角采样间隔	1/14°
极化方式	HH, HV, VH, VV

下载: 导出CSV

表 4 仿真目标的极化散射矩阵估计结果

Table 4. Polarization scattering matrix estimation results of simulated targets

方法	目标类型	三面角	偶极子	30°二面角	45°二面角
联合多维重建	变型前	$\left[ {\begin{array}{*{20}{c}} {0.4\operatorname{j} }&0 \\ 0&{0.4{\rm{j}}} \end{array}} \right]$	$\left[ {\begin{array}{*{20}{c}} { - 0.38{\rm{j}}}&0 \\ 0&0 \end{array}} \right]$	$\left[ {\begin{array}{*{20}{c}} { - 0.21}&{ - 0.37} \\ { - 0.37}&{0.21} \end{array}} \right]$	$\left[ {\begin{array}{*{20}{c}} 0&{ - 0.42} \\ { - 0.42}&0 \end{array}} \right]$
联合多维重建	变型后	${\color{Blue}{0.4} }{ {\rm{e} }^{ {\rm{j} }{ {90}^ \circ } } }{\color{red}{\left[ {\begin{array}{*{20}{c} } 1&0 \\ 0&1 \end{array} } \right] } }$	${\color{Blue}{0.38} }{ {\rm{e} }^{ {\rm{j} }( - { {90}^ \circ })} }{\color{red}{\left[ {\begin{array}{*{20}{c} } 1&0 \\ 0&0 \end{array} } \right] } }$	${\color{Blue}{0.42} }{ {\rm{e} }^{ {\rm{j} }{ {180}^ \circ } } }{\color{red}{\left[ {\begin{array}{*{20}{c} } {0.5}&{0.88} \\ {0.88}&{ - 0.5} \end{array} } \right]} }$	${\color{Blue}{0.42} }{ {\rm{e} }^{ {\rm{j} }{ {180}^ \circ } } }{\color{red}{\left[ {\begin{array}{*{20}{c} } 0&1 \\ 1&0 \end{array} } \right]}}$
独立多维重建	变型前	$\left[ {\begin{array}{*{20}{c}} {0.38{\rm{j}}}&0 \\ 0&{0.38{\rm{j}}} \end{array}} \right]$	$\left[ {\begin{array}{*{20}{c}} { - 0.38{\rm{j}}}&0 \\ 0&0 \end{array}} \right]$	$\left[ {\begin{array}{*{20}{c}} { - 0.13 + 0.02{\rm{j}}}&{ - 0.34 + 0.06{\rm{j}}} \\ { - 0.34 + 0.06{\rm{j}}}&{0.13 - 0.02{\rm{j}}} \end{array}} \right]$	$\left[ {\begin{array}{*{20}{c}} 0&{ - 0.4 - 0.07{\rm{j}}} \\ { - 0.4 - 0.07{\rm{j}}}&0 \end{array}} \right]$
独立多维重建	变型后	${\color{Blue}{0.38} }{ {\rm{e} }^{ {\rm{j} }{ {89}^ \circ } } }{\color{red}{\left[ {\begin{array}{*{20}{c} } 1&0 \\ 0&1 \end{array} } \right]}}$	${\color{Blue}{0.38} }{ {\rm{e} }^{ {\rm{j} }( - { {89}^ \circ })} }{\color{red}{\left[ {\begin{array}{*{20}{c} } 1&0 \\ 0&0 \end{array} } \right]}}$	${\color{Blue}{0.26} }{ {\rm{e} }^{ {\rm{j} }{ {170}^ \circ } } }{\color{red}{\left[ {\begin{array}{*{20}{c} } {0.5}&{1.35} \\ {1.35}&{ - 0.5} \end{array} } \right]}}$	${\color{Blue}{0.41} }{ {\rm{e} }^{ {\rm{j} }( - { {170}^ \circ })} }{\color{red}{\left[ {\begin{array}{*{20}{c} } 0&1 \\ 1&0 \end{array} } \right]}}$

下载: 导出CSV

表 5 不同SNR下仿真目标的极化散射矩阵估计结果

Table 5. Polarization scattering matrix estimation results of simulated targets under different SNR

目标类型		SNR=13 dB	SNR=18 dB	SNR=23 dB
三面角	变型前	$\left[\!\! {\begin{array}{*{20}{c}} {0.01 + 0.39{\rm{j}}} \!\!\!&\!\!\! {0.02} \\ {0.01 + 0.01{\rm{j}}} \!\!\!&\!\!\! { - 0.02 + 0.39{\rm{j}}} \end{array}} \!\!\right]$	$\left[\!\! {\begin{array}{*{20}{c}} { - 0.02 + 0.4{\rm{j}}} \!\!\!&\!\!\! {0.01 - 0.02{\rm{j}}} \\ {0.03{\rm{j}}} \!\!\!&\!\!\! {0.01 + 0.4{\rm{j}}} \end{array}} \!\!\right]$	$\left[\!\! {\begin{array}{*{20}{c}} {0.01 + 0.41{\rm{j}}} \!\!\!&\!\!\! {0.02{\rm{j}}} \\ { - 0.01} \!\!\!&\!\!\! {0.01 + 0.40{\rm{j}}} \end{array}} \!\!\right]$
三面角	变型后	${\color{blue}{0.39}}{ {\rm{e} }^{ {\rm{j8} }{ {8.7}^ \circ } } }{\color{red}{\left[\!\! {\begin{array}{*{20}{c} } 1 \!\!\!&\!\!\! {0.02 - 0.06{\rm{j} } } \\ {0.03 - 0.04{\rm{j} } } \!\!\!&\!\!\! {1.03 + 0.07{\rm{j} } } \end{array} } \!\!\right]}}$	${\color{blue}{0.4}}{ {\rm{e} }^{ {\rm{j92} }{\rm{.} }{ {\rm{2} }^{\rm{o} } } }}{\color{red}{\left[\!\! {\begin{array}{*{20}{c} } 1 \!\!\!&\!\!\! { - 0.04 - 0.03{\rm{j} } } \\ {0.09 - 0.01{\rm{j} } } \!\!\!&\!\!\! {1.01 - 0.06{\rm{j} } } \end{array} } \!\!\right] }}$	${\color{blue}{0.41} }{ {\rm{e} }^{ {\rm{j} }{ {88.6}^ \circ } } }{\color{red}{\left[\!\! {\begin{array}{*{20}{c} } 1 \!\!\!&\!\!\! {0.04} \\ {0.02 + 0.03{\rm{j} } } \!\!\!&\!\!\! {0.97 - 0.01{\rm{j} } } \end{array} } \!\!\right]} }$
偶极子	变型前	$\left[\!\! {\begin{array}{*{20}{c}} {0.02 - 0.38{\rm{j}}} \!\!\!&\!\!\! {0.01{\rm{j}}} \\ { - 0.02 + 0.02{\rm{j}}} \!\!\!&\!\!\! { - 0.03{\rm{j}}} \end{array}} \!\!\right]$	$\left[\!\! {\begin{array}{*{20}{c}} {0.02 - 0.41{\rm{j}}} \!\!\!&\!\!\! {0.02 + 0.01{\rm{j}}} \\ { - 0.01 + 0.01{\rm{j}}} \!\!\!&\!\!\! {0.01} \end{array}} \!\!\right]$	$\left[\!\! {\begin{array}{*{20}{c}} { - 0.4{\rm{j}}} \!\!\!&\!\!\! {0.02{\rm{j}}} \\ 0 \!\!\!&\!\!\! 0 \end{array}} \!\!\right]$
偶极子	变型后	${\color{blue}{0.3} }{\rm{8} }{ {\rm{e} }^{ {\rm{j( - 86} }{\rm{.} }{ {\rm{8} }^{\rm{o} } }{\rm{)} } } }\!{\color{red}{\left[\!\!\!\! {\begin{array}{*{20}{c} } 1 \!\!\!&\!\!\! { - 0.03} \\ { - 0.05 \!-\! 0.05{\rm{j} } } \!\!\!&\!\!\! {0.08 \!-\! 0.13{\rm{j} } } \end{array} } \!\!\!\right]} }$	$\;{\color{blue}{0.41} }{ {\rm{e} }^{ {\rm{j( - 87} }{\rm{.} }{ {\rm{3} }^{\rm{o} } }{\rm{)} } } }\!{\color{red}{\left[\!\!\!\! {\begin{array}{*{20}{c} } 1 \!\!\!&\!\!\! { - 0.02 \!+\! 0.06{\rm{j} } } \\ { - 0.02 \!-\! 0.01{\rm{j} } } \!\!\!&\!\!\! { - 0.01 \!+\! 0.01{\rm{j} } } \end{array} } \!\!\!\!\right]} }$	${\color{blue}{0.4} }{ {\rm{e} }^{ {\rm{j - 9} }{ {\rm{0} }^{\rm{o} } } } }{\color{red}{\left[\!\! {\begin{array}{*{20}{c} } 1 \!\!\!&\!\!\! { - 0.05} \\ 0 \!\!\!&\!\!\! 0 \end{array} } \!\!\right]} }$
30° 二面角	变型前	$\left[\!\! {\begin{array}{*{20}{c}} { - 0.16 + 0.02{\rm{j}}} \!\!\!&\!\!\! { - 0.28 + 0.04{\rm{j}}} \\ { - 0.39 + 0.07{\rm{j}}} \!\!\!&\!\!\! {0.2 - 0.04{\rm{j}}} \end{array}} \!\!\right]$	$\left[\!\! {\begin{array}{*{20}{c}} { - 0.22 + 0.03{\rm{j}}} \!\!\!&\!\!\! { - 0.37 + 0.06{\rm{j}}} \\ { - 0.39 + 0.06{\rm{j}}} \!\!\!&\!\!\! {0.24 - 0.04{\rm{j}}} \end{array}} \!\!\right]$	$\left[\!\! {\begin{array}{*{20}{c}} { - 0.22 + 0.04{\rm{j}}} \!\!\!&\!\!\! { - 0.39 + 0.06{\rm{j}}} \\ { - 0.37 + 0.05{\rm{j}}} \!\!\!&\!\!\! {0.22 - 0.04{\rm{j}}} \end{array}} \!\!\right]$
30° 二面角	变型后	${\color{blue}{0.33} }{ {\rm{e} }^{ {\rm{j172} }{\rm{.} }{ {\rm{4} }^{\rm{o} } } } }{\color{red}{\left[\!\! {\begin{array}{*{20}{c} } {0.5} \!\!\!&\!\!\! {0.84} \\ {1.18 - 0.07{\rm{j} } } \!\!\!&\!\!\! { - 0.6 + 0.04{\rm{j} } } \end{array} } \!\!\right]} }$	${\color{blue}{0.45} }{ {\rm{e} }^{ {\rm{j172} }{\rm{.} }{ {\rm{3} }^{\rm{o} } } } }{\color{red}{\left[\!\! {\begin{array}{*{20}{c} } {0.5} \!\!\!&\!\!\! {0.85 - 0.03{\rm{j} } } \\ {0.89 - 0.02{\rm{j} } } \!\!\!&\!\!\! { - 0.53 + 0.03{\rm{j} } } \end{array} } \!\!\right]} }$	${\color{blue}{0.45} }{ {\rm{e} }^{ {\rm{j169} }{\rm{.} }{ {\rm{4} }^{\rm{o} } } } }{\color{red}{\left[\!\! {\begin{array}{*{20}{c} } {0.5} \!\!\!&\!\!\! {0.87 + 0.02{\rm{j} } } \\ {0.84 + 0.04{\rm{j} } } \!\!\!&\!\!\! { - 0.5} \end{array} } \!\!\right]} }$
45° 二面角	变型前	$\left[\!\! {\begin{array}{*{20}{c}} {0.02} \!\!\!&\!\!\! { - 0.41 - 0.06{\rm{j}}} \\ { - 0.45 - 0.06{\rm{j}}} \!\!\!&\!\!\! { - 0.02} \end{array}} \!\!\right]$	$\left[\!\! {\begin{array}{*{20}{c}} { - 0.01 + 0.01{\rm{j}}} \!\!\!&\!\!\! { - 0.46 - 0.06{\rm{j}}} \\ { - 0.44 - 0.08{\rm{j}}} \!\!\!&\!\!\! { - 0.01{\rm{j}}} \end{array}} \!\!\right]$	$\left[\!\! {\begin{array}{*{20}{c}} 0 \!\!\!&\!\!\! { - 0.43 - 0.01{\rm{j}}} \\ { - 0.42 - 0.08{\rm{j}}} \!\!\!&\!\!\! {0.02{\rm{j}}} \end{array}} \!\!\right]$
45° 二面角	变型后	${\color{blue}{0.42} }{ {\rm{e} }^{ {\rm{j( - 171} }{\rm{.} }{ {\rm{8} }^{\rm{o} } }{\rm{)} } } }{\color{red}{\left[\!\! {\begin{array}{*{20}{c} } { - 0.05} \!\!\!&\!\!\! 1 \\ {1.01} \!\!\!&\!\!\! {0.04} \end{array} } \!\!\right]} }$	${\color{blue}{0.46} }{ {\rm{e} }^{ {\rm{j( - 172} }{\rm{.} }{ {\rm{4} }^{\rm{o} } }{\rm{)} } } }{\color{red}{\left[\!\! {\begin{array}{*{20}{c} } {0.02 \!-\! 0.01{\rm{j} } } \!\! & \!\! 1 \\ {0.96 \!+\! 0.05{\rm{j} } } \!\! & \!\! {0.01 \!+\! 0.02{\rm{j} } } \end{array} } \!\!\right]} }$	${\color{blue}{0.44} }{ {\rm{e} }^{ {\rm{j( - 170} }{\rm{.} }{ {\rm{7} }^{\rm{o} } }{\rm{)} } } }{\color{red}{\left[\!\! {\begin{array}{*{20}{c} } 0 \!\!\!&\!\!\! 1 \\ {0.98 \!+\! 0.01{\rm{j} } } \!\!\!&\!\!\! { - 0.02 \!-\! 0.05{\rm{j} } } \end{array} } \!\!\right]} }$

下载: 导出CSV

表 6 Slicy的仿真参数

Table 6. Simulation parameters of Slicy

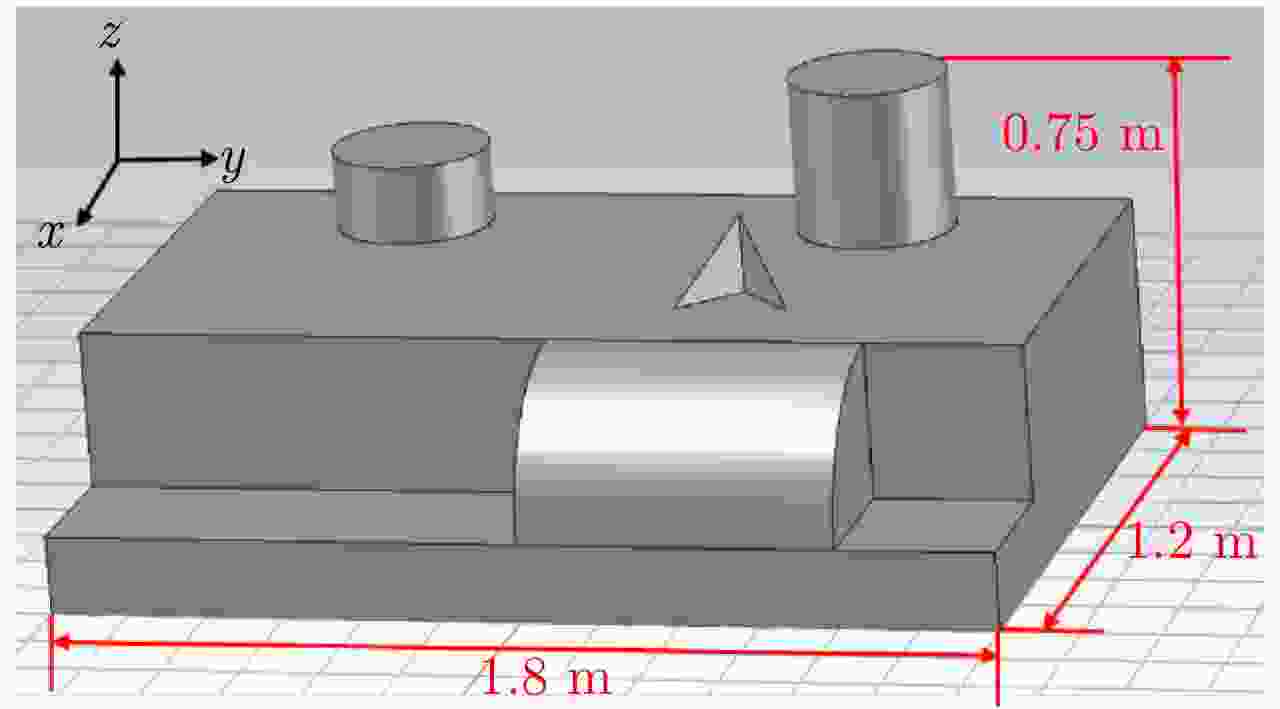
参数类型	参数	取值
雷达扫描参数	频率范围	[8 GHz, 12 GHz]
	频率采样间隔	20 MHz
	方位角范围	[–4°, 6°]
	方位角采样间隔	1/14°
	俯仰角范围	[18°, 42°]
	俯仰角采样间隔	1/14°
	极化方式	HH, HV, VH, VV
场景参数	方位角0°	沿x 轴正方向
	俯仰角0°	沿z 轴正方向
	x 轴方向场景范围	[–0.6 m, 0.6 m]
	y 轴方向场景范围	[–0.9 m, 0.9 m]
	z 轴方向场景范围	[0 m, 0.75 m]

下载: 导出CSV

表 7 卫星的仿真参数

Table 7. Simulation parameters of satellite

参数类型	参数	取值
雷达扫描参数	频率范围	[9 GHz, 11 GHz]
	频率采样间隔	20 MHz
	方位角范围	[–20°, 20°]
	方位角采样间隔	0.1°
	俯仰角范围	[45°, 65°]
	俯仰角采样间隔	0.2°
	极化方式	HH, HV, VH, VV
场景参数	方位角0°	沿x 轴正方向
	俯仰角0°	沿z 轴正方向
	x 轴方向场景范围	[–0.5 m, 0.5 m]
	y 轴方向场景范围	[–4.105 m, 4.105 m]
	z 轴方向场景范围	[–1.775 m, 1.775 m]

下载: 导出CSV

参考文献(23)

[1]	保铮, 邢孟道, 王彤. 雷达成像技术[M]. 北京: 电子工业出版社, 2005. BAO Zheng, XING Mengdao, and WANG Tong. Radar Imaging[M] Beijing: Publishing House of Electronics Industry, 2005.
[2]	CUMMING I G and WONG F H. Digital Processing of Synthetic Aperture Radar Data: Algorithm and Implementation[M]. Boston: Artech House, 2005.
[3]	LEE J S and POTTIER E. Polarimetric Radar Imaging: From Basics to Applications[M]. Boca Raton, FL: CRC Press, 2009.
[4]	庄钊文, 肖顺平, 王雪松. 雷达极化信息处理及其应用[M]. 北京: 国防工业出版社, 1999. ZHUANG Zhaowen, XIAO Shunping, and WANG Xuesong. Radar Polarization Information Processing and Application[M] Beijing: National Defense Industry Press, 1999.
[5]	FREY O and MEIER E. Analyzing tomographic SAR data of a forest with respect to frequency, polarization, and focusing technique[J]. IEEE Transactions on Geoscience and Remote Sensing, 2011, 49(10): 3648–3659. doi: 10.1109/TGRS.2011.2125972
[6]	GUILLASO S, FERRO-FAMIL L, REIGBER A, et al. Building characterization using L-band polarimetric interferometric SAR data[J]. IEEE Geoscience and Remote Sensing Letters, 2005, 2(3): 347–351. doi: 10.1109/LGRS.2005.851543
[7]	PONCE O, PRATS-IRAOLA P, SCHEIBER R, et al. First airborne demonstration of holographic SAR tomography with fully polarimetric multicircular acquisitions at L-band[J]. IEEE Transactions on Geoscience and Remote Sensing, 2016, 54(10): 6170–6196. doi: 10.1109/TGRS.2016.2582959
[8]	丁赤飚, 仇晓兰, 吴一戎. 全息合成孔径雷达的概念、体制和方法[J]. 雷达学报, 2020, 9(3): 399–408. doi: 10.12000/JR20063 DING Chibiao, QIU Xiaolan, and WU Yirong. Concept, system, and method of holographic synthetic aperture radar[J]. Journal of Radars, 2020, 9(3): 399–408. doi: 10.12000/JR20063
[9]	FENG Dong, AN Daoxiang, HUANG Xiaotao, et al. A phase calibration method based on phase gradient autofocus for airborne holographic SAR imaging[J]. IEEE Geoscience and Remote Sensing Letters, 2019, 16(12): 1864–1868. doi: 10.1109/LGRS.2019.2911932
[10]	SUN Dou, XING Shiqi, LI Yongzhen, et al. Sub-aperture partitioning method for three-dimensional wide-angle synthetic aperture radar imaging with non-uniform sampling[J]. Electronics, 2019, 8(6): 629. doi: 10.3390/electronics8060629
[11]	XING Shiqi, LI Yongzhen, DAI Dahai, et al. Three-dimensional reconstruction of man-made objects using polarimetric tomographic SAR[J]. IEEE Transactions on Geoscience and Remote Sensing, 2013, 51(6): 3694–3705. doi: 10.1109/TGRS.2012.2220145
[12]	AUSTIN C D, ERTIN E, and MOSES R L. Sparse signal methods for 3-D radar imaging[J]. IEEE Journal of Selected Topics in Signal Processing, 2011, 5(3): 408–423. doi: 10.1109/JSTSP.2010.2090128
[13]	SUN Dou, PANG Bo, XING Shiqi, et al. Direct 3-D sparse imaging using non-uniform samples without data interpolation[J]. Electronics, 2020, 9(2): 321. doi: 10.3390/electronics9020321
[14]	ERTIN E, MOSES R L, and POTTER L C. Interferometric methods for three-dimensional target reconstruction with multipass circular SAR[J]. IET Radar, Sonar & Navigation, 2010, 4(3): 464–473.
[15]	HU Xiaowei, TONG Ningning, GUO Yiduo, et al. MIMO radar 3-D imaging based on multi-dimensional sparse recovery and signal support prior information[J]. IEEE Sensors Journal, 2018, 18(8): 3152–3162. doi: 10.1109/JSEN.2018.2810705
[16]	NANNINI M, SCHEIBER R, HORN R, et al. First 3-D reconstructions of targets hidden beneath foliage by means of polarimetric SAR tomography[J]. IEEE Geoscience and Remote Sensing Letters, 2012, 9(1): 60–64. doi: 10.1109/LGRS.2011.2160329
[17]	NANNINI M, SCHEIBER R, and HORN R. Imaging of targets beneath foliage with SAR tomography[C]. The 7th European Conference on Synthetic Aperture Radar, Friedrichshafen, Germany, 2008: 1–4.
[18]	SAUER S, FERRO-FAMIL L, REIGBER A, et al. Three-dimensional imaging and scattering mechanism estimation over urban scenes using dual-baseline polarimetric InSAR observations at L-band[J]. IEEE Transactions on Geoscience and Remote Sensing, 2011, 49(11): 4616–4629. doi: 10.1109/TGRS.2011.2147321
[19]	NGUYEN N H, BERRY P, and TRAN H T. Compressive sensing for tomographic imaging of a target with a narrowband bistatic radar[J]. Sensors, 2019, 19(24): 5515. doi: 10.3390/s19245515
[20]	ZHU Xiaoxiang and BAMLER R. Super-resolution power and robustness of compressive sensing for spectral estimation with application to spaceborne tomographic SAR[J]. IEEE Transactions on Geoscience and Remote Sensing, 2012, 50(1): 247–258. doi: 10.1109/TGRS.2011.2160183
[21]	CETIN M and KARL W C. Feature-enhanced synthetic aperture radar image formation based on nonquadratic regularization[J]. IEEE Transactions on Image Processing, 2001, 10(4): 623–631. doi: 10.1109/83.913596
[22]	CAMERON W L and LEUNG L K. Feature motivated polarization scattering matrix decomposition[C]. Proceedings of IEEE International Conference on Radar, Arlington, USA, 1990: 549–557.
[23]	阙肖峰, 聂在平, 胡俊. 混合场积分方程结合MLFMA分析导体介质复合目标电磁散射问题[J]. 电子学报, 2007, 35(11): 2062–2066. doi: 10.3321/j.issn:0372-2112.2007.11.006 QUE Xiaofeng, NIE Zaiping, and HU Jun. Analysis of EM scattering by composite conducting and dielectric object using combined field integral equation with MLFMA[J]. Acta Electronica Sinica, 2007, 35(11): 2062–2066. doi: 10.3321/j.issn:0372-2112.2007.11.006

施引文献

期刊类型引用(15)

1.	潘小义，刘晓斌，陈吉源，冯学文，顾赵宇，肖顺平. 间歇采样转发干扰技术研究述评. 系统工程与电子技术. 2024(09): 2887-2901 . 百度学术
2.	胡泽宾. SAR干扰技术综述. 雷达科学与技术. 2024(04): 369-376 . 百度学术
3.	何金阳，程子扬，李绽蕾，何子述，沙明辉. 低多普勒敏感的抗间歇采样转发干扰波形设计方法. 系统工程与电子技术. 2023(05): 1333-1341 . 百度学术
4.	张家运，李文海，孙伟超，王洪春. 基于灰狼优化算法的间歇采样移频转发干扰优化方法. 电子信息对抗技术. 2023(05): 14-20 . 百度学术
5.	纪朋徽，邢世其，徐伟，代大海，冯德军. 基于相干两点源的虚假运动目标生成方法. 电子与信息学报. 2022(04): 1343-1350 . 百度学术
6.	王福来，庞晨，殷加鹏，李楠君，李永祯，王雪松. 一种多普勒容忍的抗间歇采样转发干扰恒模互补波形和接收滤波器联合设计方法. 雷达学报. 2022(02): 278-288 . 本站查看
7.	邢世其，黄大通，徐伟，李永祯，肖顺平. 一种反多通道对消的多干扰机协同干扰方法. 电子与信息学报. 2022(09): 3144-3154 . 百度学术
8.	孙光，邢世其，黄大通，李永祯，王雪松. 基于噪声乘积调制的SAR-GMTI间歇采样干扰方法. 系统工程与电子技术. 2022(10): 3059-3071 . 百度学术
9.	黄大通，邢世其，庞礴，李永祯，王雪松. 对SAR-GMTI的二维单音调制散射波干扰. 系统工程与电子技术. 2020(08): 1685-1694 . 百度学术
10.	李永祯，黄大通，邢世其，王雪松. 合成孔径雷达干扰技术研究综述. 雷达学报. 2020(05): 753-764 . 本站查看
11.	降佳伟，王宏艳，吴彦鸿. 对地面动目标检测雷达的干扰技术综述. 系统工程与电子技术. 2020(11): 2471-2480 . 百度学术
12.	周超，刘泉华，胡程. 间歇采样转发式干扰的时频域辨识与抑制. 雷达学报. 2019(01): 100-106 . 本站查看
13.	周阳，毕大平，沈爱国. 对SAR-GMTI的大区域遮蔽有源-无源协同干扰方法. 系统工程与电子技术. 2018(05): 1004-1011 . 百度学术
14.	畅鑫，董春曦，唐峥钊，董阳阳，刘明明. 基于双站幅度调制的虚假运动场景对SAR-GMTI的欺骗方法. 电子与信息学报. 2018(09): 2190-2197 . 百度学术
15.	张静克，汪亚，戚宗锋，曾勇虎，汪连栋. 多通道SAR-GMTI虚假运动目标成像特性分析. 航天电子对抗. 2018(05): 9-13+33 . 百度学术

其他类型引用(8)

资源附件(0)

访问统计

图(8) / 表(7)

计量

文章访问数: 2727
HTML全文浏览量: 780
PDF下载量: 227
被引次数: 23

1. 引言
2. 运动调制间歇采样遮蔽干扰模型
2.1 运动调制干扰模型
2.2 间歇采样转发干扰模型
2.3 运动调制间歇采样遮蔽干扰模型
3. 对SAR-GMTI干扰原理
4. 干扰参数和干扰功率分析
5. 仿真实验
5.1 对运动装甲车干扰遮蔽效果
5.2 各参数对干扰效果影响仿真
6. 结束语

1. 引言
2. 运动调制间歇采样遮蔽干扰模型
2.1 运动调制干扰模型
2.2 间歇采样转发干扰模型
2.3 运动调制间歇采样遮蔽干扰模型
3. 对SAR-GMTI干扰原理
4. 干扰参数和干扰功率分析
5. 仿真实验
5.1 对运动装甲车干扰遮蔽效果
5.2 各参数对干扰效果影响仿真
6. 结束语

参考文献(23)

施引文献

资源附件(0)

访问统计

基于稀疏重构的全极化SAR联合多维重建

DOI: 10.12000/JR20092

通讯作者:
邢世其 xingshiqi_paper@163.com

计量

Full-polarization SAR Joint Multidimensional Reconstruction Based on Sparse Reconstruction

Corresponding author: XING Shiqi, xingshiqi_paper@163.com

1. 引言

2. 运动调制间歇采样遮蔽干扰模型

2.1 运动调制干扰模型

2.2 间歇采样转发干扰模型

2.3 运动调制间歇采样遮蔽干扰模型

3. 对SAR-GMTI干扰原理

4. 干扰参数和干扰功率分析

5. 仿真实验

5.1 对运动装甲车干扰遮蔽效果

5.2 各参数对干扰效果影响仿真

6. 结束语

期刊类型引用(15)

其他类型引用(8)

计量

目录

1. 引言

2. 运动调制间歇采样遮蔽干扰模型

2.1 运动调制干扰模型

2.2 间歇采样转发干扰模型

2.3 运动调制间歇采样遮蔽干扰模型

3. 对SAR-GMTI干扰原理

4. 干扰参数和干扰功率分析

5. 仿真实验

5.1 对运动装甲车干扰遮蔽效果

5.2 各参数对干扰效果影响仿真

6. 结束语

期刊介绍

联系我们

基于稀疏重构的全极化SAR联合多维重建

DOI: 10.12000/JR20092

通讯作者: 邢世其 xingshiqi_paper@163.com

计量

出版历程

Full-polarization SAR Joint Multidimensional Reconstruction Based on Sparse Reconstruction

Corresponding author: XING Shiqi, xingshiqi_paper@163.com

1. 引言

2. 运动调制间歇采样遮蔽干扰模型

2.1 运动调制干扰模型

2.2 间歇采样转发干扰模型

2.3 运动调制间歇采样遮蔽干扰模型

3. 对SAR-GMTI干扰原理

4. 干扰参数和干扰功率分析

5. 仿真实验

5.1 对运动装甲车干扰遮蔽效果

5.2 各参数对干扰效果影响仿真

6. 结束语

期刊类型引用(15)

其他类型引用(8)

计量

出版历程

目录

1. 引言

2. 运动调制间歇采样遮蔽干扰模型

2.1 运动调制干扰模型

2.2 间歇采样转发干扰模型

2.3 运动调制间歇采样遮蔽干扰模型

3. 对SAR-GMTI干扰原理

4. 干扰参数和干扰功率分析

5. 仿真实验

5.1 对运动装甲车干扰遮蔽效果

5.2 各参数对干扰效果影响仿真

6. 结束语

期刊介绍

联系我们

通讯作者:
邢世其 xingshiqi_paper@163.com