Approximate Maximum Likelihood Estimator of Multi-target Motion Parameters for Orthogonal Frequency Division Multiplexing Radar
-
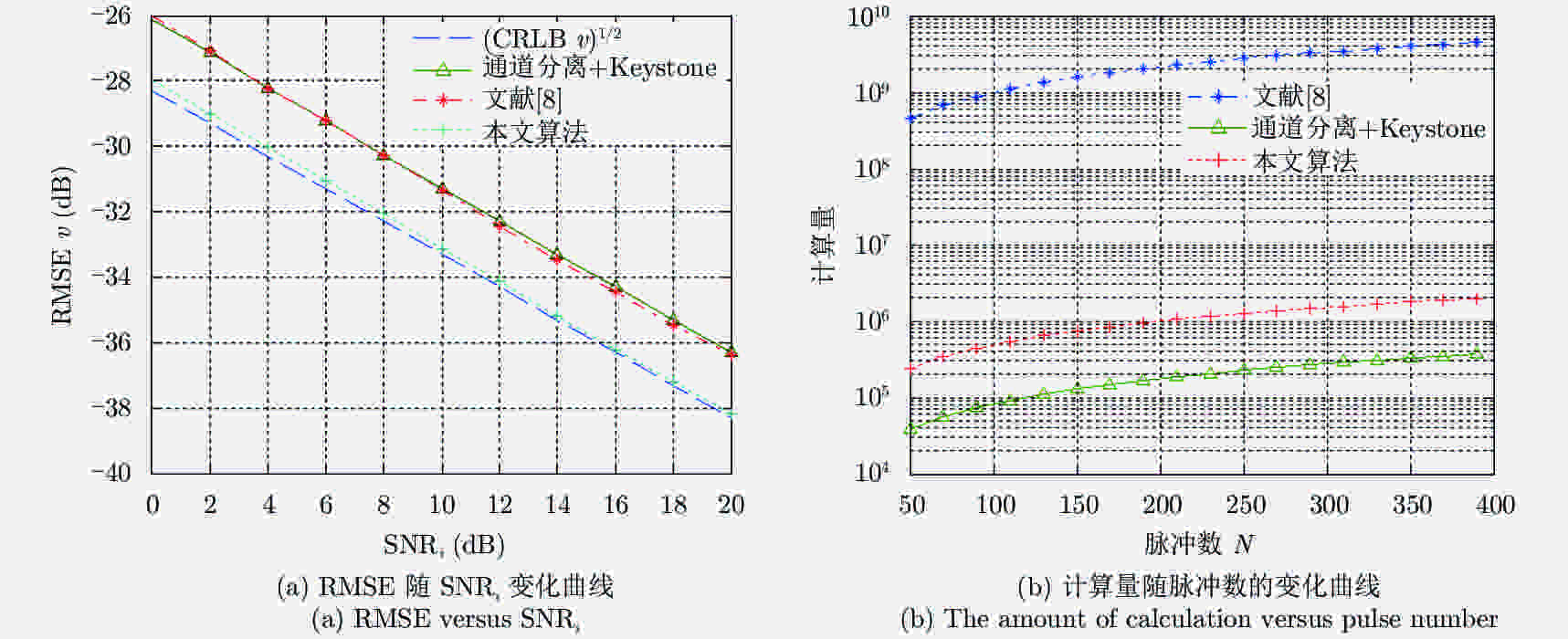
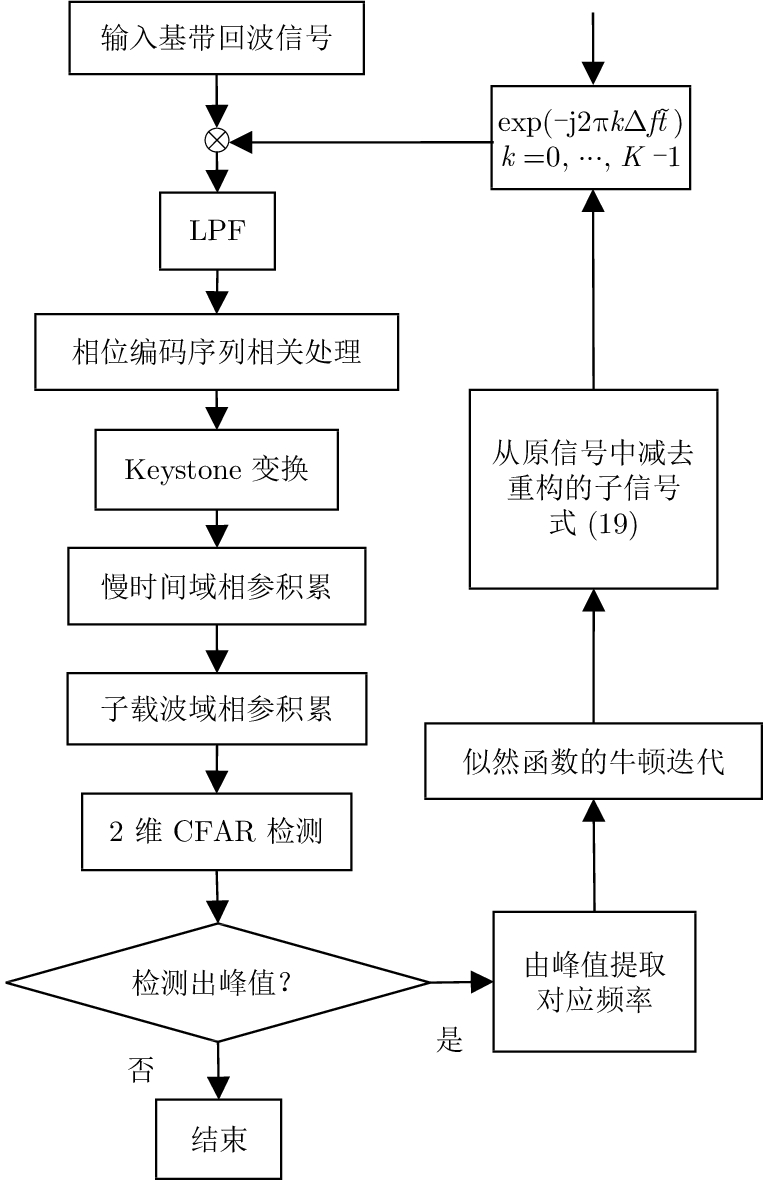
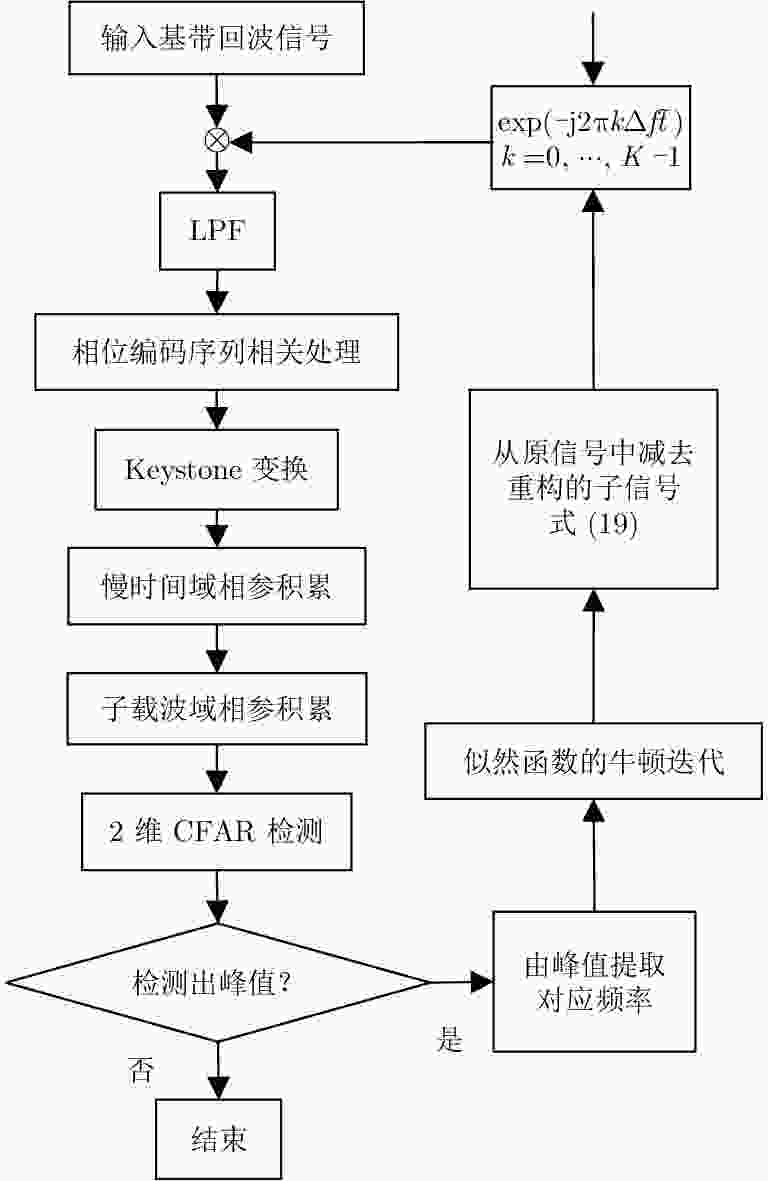
摘要: 针对相位编码正交频分复用(Orthogonal Frequency Division Multiplexing, OFDM)雷达动目标探测问题,该文提出了一种基于通道分离和最大似然原理相结合的运动参数估计方法。首先,利用OFDM信号的正交性分离出多通道信号,并与相位编码参考信号在快时间域相关后获得各通道的1维距离像。随后,利用Keystone变换校正子载波多普勒偏移与慢时间之间的耦合,并在慢时间域和子载波域进行相参积累得到距离-多普勒2维谱。结合CLEAN技术对距离-多普勒2维谱进行谱峰搜索,获得各个目标的位置和速度参数估计量。以此为初值,利用牛顿迭代算法对似然函数进行优化,最终获得运动参数的近似最大似然估计(Approximate Maximum Likelihood Estimator, AMLE)。仿真实验表明,该文算法在计算复杂性和参数估计精度上都优于传统的Keystone估计算法,在相同均方根误差(Root-Mean-Square Error, RMSE)下其输入信噪比改善了约4 dB,且均方误差接近Cramer-Rao下限。
-
关键词:
- 相位编码 /
- 正交频分复用 /
- 通道分离 /
- Keystone变换 /
- 最大似然估计
Abstract: To detect multiple targets on a phase-coded Orthogonal Frequency Division Multiplexing (OFDM) radar, this paper proposes a parameter estimation method based on channel separation and maximum likelihood principle. First, the multi-channel signals were separated because of the orthogonality of the OFDM system, and then the separated signals were correlated with the phase-coded reference signal in the fast time domain to acquire a 1-D range profile from each channel. Subsequently, Keystone transform was used to correct the effect of the coupling between Doppler shift of the subcarrier and the slow time domain. Simultaneously, coherent accumulation was conducted jointly in the slow time and subcarrier domains to obtain a 2-D range-Doppler spectrum. Using CLEAN technique, the peaks of this spectrum were examined to obtain the range cells and velocities of each target. Using these parameters as the initial values, the likelihood function was maximized using Newton’s iterative algorithm to yield an approximate maximum likelihood estimator of the motion parameters. Simulation results demonstrate that the proposed algorithm outperforms the traditional Keystone-based estimation algorithm both in computational complexity and parameter estimation accuracy. The algorithm improved the input SNR by approximately 4 dB under the same root mean square error, and the mean square error approached the Cramer-Rao lower bound. -
表 1 仿真参数
Table 1. Simulation parameters
参数 数值 工作频率 ${f_{\rm c}}$ (GHz) 5 带宽B (MHz) 64 脉冲重复周期 ${T_{\rm r}}$ (ms) 2 脉冲数N 250 载波数K 64 -
[1] Mazahir S, Chaaban A, Elgala H, et al.. Effective information rates of single-carrier and multi-carrier modulation schemes for bandwidth constrained IM/DD systems[C]. Proceedings of the 2017 IEEE International Conference on Communications (ICC), Paris, France, 2017: 1–6. DOI: 10.1109/ICC.2017.7997325 [2] Shi C G, Wang F, Sellathurai M, et al. Power minimization-based robust OFDM radar waveform design for radar and communication systems in coexistence[J]. IEEE Transactions on Signal Processing, 2018, 66(5): 1316–1330. DOI: 10.1109/TSP.2017.2770086 [3] Patel V V and Patil R N. Minimization of PAPR in OFDM system using IDWT/DWT, clipping and filtering combined with huffman coding method[C]. Proceedings of the 2013 International Conference on Communications and Signal Processing (ICCSP), Melmaruvathur, India, 2013: 250–254. DOI: 10.1109/iccsp.2013.6577053 [4] Omar S M, Kassem F, Mitri R, et al.. A novel barker code algorithm for resolving range ambiguity in high PRF radars[C]. Proceedings of the 2015 European Radar Conference (EuRAD), Paris, France, 2015: 81–84. DOI: 10.1109/EuRAD.2015.7346242 [5] 霍凯, 赵晶晶. OFDM新体制雷达研究现状与发展趋势[J]. 电子与信息学报, 2015, 37(11): 2776–2789. DOI: 10.11999/JEIT150335Huo Kai and Zhao Jing-jing. The development and prospect of the new OFDM radar[J]. Journal of Electronics&Information Technology, 2015, 37(11): 2776–2789. DOI: 10.11999/JEIT150335 [6] Lellouch G, Mishra A K, and Inggs M. Design of OFDM radar pulses using genetic algorithm based techniques[J]. IEEE Transactions on Aerospace and Electronic Systems, 2016, 52(4): 1953–1966. DOI: 10.1109/TAES.2016.140671 [7] Liu Y J, Liao G S, Yang Z W, et al. Design of integrated radar and communication system based on MIMO-OFDM waveform[J]. Journal of Systems Engineering and Electronics, 2017, 28(4): 669–680. DOI: 10.21629/JSEE.2017.04.06 [8] 张卫, 顾红, 苏卫民. 基于Keystone变换的OFDM信号距离走动校正方法[J]. 数据采集与处理, 2013, 28(4): 421–424. DOI: 10.3969/j.issn.1004-9037.2013.04.006Zhang Wei, Gu Hong, and Su Wei-min. Range walk correction of OFDM signal radar with Keystone transform[J]. Journal of Data Acquisition and Processing, 2013, 28(4): 421–424. DOI: 10.3969/j.issn.1004-9037.2013.04.006 [9] Lellouch G, Mishra A, and Inggs M. Impact of the Doppler modulation on the range and Doppler processing in OFDM radar[C]. 2014 IEEE Radar Conference, Cincinnati, OH, USA, 2014: 803–808. DOI: 10.1109/RADAR.2014.6875700 [10] 李升远, 张馨恬, 唐世阳. 采用OFDM-LFM的MIMO雷达高速目标波形设计[J]. 西安电子科技大学学报, 2018, 45(3): 8–13. DOI: 10.3969/j.issn.1001-2400.2018.03.002Li Sheng-yuan, Zhang Xin-tian, and Tang Shi-yang. MIMO radar waveform design via OFDM-LFM for high speed target[J]. Journal of Xidian University, 2018, 45(3): 8–13. DOI: 10.3969/j.issn.1001-2400.2018.03.002 [11] Liu L, Zhou F, Tao M L, et al. A novel method for multi-targets ISAR imaging based on particle swarm optimization and modified CLEAN technique[J]. IEEE Sensors Journal, 2016, 16(1): 97–108. DOI: 10.1109/JSEN.2015.2478808 [12] 霍凯. 基于OFDM新体制雷达信号的微动目标特征提取研究[D]. [博士论文], 国防科学技术大学, 2011Huo Kai. Research on feature extraction for target with micro-motion based on new OFDM radar signals[D]. [Ph.D. dissertation], National University of Defense Technology, 2011 -



 作者中心
作者中心 专家审稿
专家审稿 责编办公
责编办公 编辑办公
编辑办公
 下载:
下载: