作者中心
专家审稿
责编办公
编辑办公
Theoretical Extension of a Microwave EM Method for Predicting the Terahertz Scattering of Electrically Large Complex Target
-
摘要: 微波方法到太赫兹散射特性建模的延拓面临两个关键的科学问题研究，其一是材料响应特性延拓，包括金属属性向合金属性过渡导致Drude模型无法准确描述，以及介质材料在太赫兹频段的响应模型研究；其二是表面随机粗糙结构、以及复杂细微精细结构在太赫兹频段下的散射行为建模方法的延拓研究。微波频段下可视同为光滑的金属表面在太赫兹频段可能呈现出表面微粗糙特性。此外，针对含介质涂覆或全介质表面太赫兹散射特性的建模，需要结合随机边界散射理论，建立多层描述模型，以涵盖其中的面散射和体散射现象。该文首先采用积分方程方法描述和分析了金属粗糙表面的太赫兹散射规律，与实测数据吻合较好。其次，对于含涂覆或介质材料的目标表面，除表面粗糙的影响外，材料内部的微小粒子成分(如碳粉、石墨、金属粉等)的电尺寸与太赫兹波长相比拟，实验显示其体散射贡献不可忽视。该文尝试用矢量辐射传输理论与积分方程方法结合的多层模型来描述含介质材料表面的散射特性，很好地解释了实测规律。最后，该文提出基于“半确定性”描述的射线追踪高频算法，实现了复杂目标表面相干和非相干散射特性的一体化快速建模，为超电大复杂目标太赫兹散射特性的建模分析提供有效手段。Abstract: Two important issues must be considered when modeling the terahertz (THz) wave scattering behavior using microwave EM methods. The first is the material response characteristics, including the metallic materials that may be beyond the scope of the Drude model’s description and the dielectric materials that may lack appropriate description models. The second is the modeling method for investigating the THz scattering behavior of the surface random roughness and the complex fine structures. Several theoretical endeavors are presented in this paper to elucidate the surface- and volume-scattering phenomenon observed in the experiment data. First, we employ the Integral Equation Method (IEM) to fit the measured data of an aluminum plate. Good agreements confirm the superior applicability of IEM to the metallic materials. Nevertheless, for dielectric materials, the volume-scattering contributions of the inner microstructures or particles whose sizes are comparable to the THz wavelength are required to be considered. Furthermore, our findings state that, for dielectric materials, it can be fit to the experimental data with the help of the Vector Radiative Transfer (VRT) theory. Finally, this research proposes a semi-deterministic description-based ray-tracing high-frequency algorithm to realize the rapid modeling of the coherent and incoherent scattering of electrically large complex targets at THz bands.
-
图 1 单层随机粗糙边界散射示意图
Figure 1. The scattering geometry of one-layer randomly rough boundary
图 2 单层粗糙表面模型散射模拟与STL实测对比结果
Figure 2. Comparison between the simulated data by one-layer rough boundary scattering model and the experiment data by STL
图 3 多层随机粗糙边界散射示意图
Figure 3. The scattering geometry of multi-layer randomly rough boundary
图 4 多层模型和单层模型实验校验对比
Figure 4. Experimental validation of one-layer and multi-layer scattering model
图 5 采用多种内部粒子描述的多层模型实测校验(240 GHz，粒子直径分别为24 μm和100 μm)
Figure 5. Experimental validation of multi-layer scattering model with hybrid particles (240 GHz, the particle size is set by 24 μm and 100 μm respectively)
图 6 微波方法对复杂目标太赫兹散射特性建模思路
Figure 6. Theoretical extension of microwave EM method for the terahertz scattering prediction of extremely large electric size target
图 7 基于射线追踪散射几何描述示意图(大尺度外形由小面元表示；路径1为1次直接散射，路径2为多次散射)
Figure 7. The scattering geometry of ray tracing (Large scale profile is descript by myriads of small patches; Path 1 denotes the single scattering, path 2 denotes the multiple scattering)
图 8 基于面边界(2维粗糙纹理)电磁模型的复杂目标太赫兹成像仿真结果
Figure 8. Simulated THz image data of complex target under the description of surface scattering model (with two-dimensional texture)
图 9 基于体边界(3维粗糙纹理)电磁模型的复杂目标太赫兹成像仿真结果
Figure 9. Simulated THz image data of complex target under the description of volume scattering model (with three-dimensional texture)
图 11 光滑与粗糙表面弹头模型成像结果对比
Figure 11. Comparison on imaging data between rough and smooth missile warheads
图 12 不同粗糙程度表面立方体RCS结果对比
Figure 12. Comparison on RCS by cubes with different kinds of rough surface
图 13 光滑与粗糙表面模型RCS极化响应结果对比
Figure 13. Comparison on polarized RCS between rough and smooth cubes
图 14 某“全向角反射器”几何结构示意图
Figure 14. The geometry of kind of “Omni-directional corner reflector”
-
[1] Siegel P H. Terahertz technology[J]. IEEE Transactions on Microwave Theory and Techniques, 2002, 50(3): 910–928. DOI: 10.1109/22.989974 [2] 许景周, 张希成. 太赫兹科学技术和应用[M]. 北京: 北京大学出版社, 2007.Xu Jing-zhou and Zhang Xicheng. Terahertz Science and Technology and its Application[M]. Beijing: Beijing University Press, 2007. [3] 刘盛纲. 太赫兹科学技术的新发展[J]. 中国基础科学科学前沿, 2006, 8(1): 7–12. DOI: 10.3969/j.issn.1009-2412.2006.01.003Liu Sheng-gang. Recent development of terahertz science and technology[J]. China Basic Science, 2006, 8(1): 7–12. DOI: 10.3969/j.issn.1009-2412.2006.01.003 [4] Ferguson B and Zhang X C. Materials for terahertz science and technology[J]. Nature Materials, 2002, 1(1): 26–33. DOI: 10.1038/nmat708 [5] Goyette T M, Gatesman A, Horgan T M, et al.. THz compact range radar systems[C]. Proceedings of IEEE International Microwave Symposium, Philadelphia, 2003. [6] Goyette T M, Dickinson J C, Waldman J, et al.. Three-dimensional fully polarimetric W-band ISAR imagery of scale-model tactical targets using a 1.56-THz compact range[C]. Proceedings of the SPIE 5095, Algorithms for Synthetic Aperture Radar Imagery X, Orlando, Florida, United States, 2003. [7] Digiovanni D A, Gatesman A J, and Giles R H. Backscattering of ground terrain and building materials at submillimeter-wave and terahertz frequencies[C]. Proceedings of the SPIE 8715, Passive and Active Millimeter-Wave Imaging XVI, Baltimore, Maryland, United States, 2013, 8715: 871507. [8] Tamminen A, Ala-Laurinaho J, and Räisänen A V. Indirect holographic imaging: Evaluation of image quality at 310 GHz[C]. Proceedings of the SPIE 7670, Passive Millimeter-Wave Imaging Technology XIII, Orlando, Florida, United States, 2010, 7670: 76700A. [9] Tamminen A, Lonnqvist A, Mallat J, et al. Monostatic reflectivity and transmittance of radar absorbing materials at 650 GHz[J]. IEEE Transactions on Microwave Theory and Techniques, 2008, 56(3): 632–637. DOI: 10.1109/TMTT.2008.916881 [10] Iwaszczuk K, Heiselberg H, and Jepsen P U. Terahertz radar cross section measurements[J]. Optics Express, 2010, 18(25): 26399–26408. DOI: 10.1364/OE.18.026399 [11] Iwaszczuk K, Strikwerda A C, Fan K B, et al. Flexible metamaterial absorbers for stealth applications at terahertz frequencies[J]. Optics Express, 2012, 20(1): 635–643. DOI: 10.1364/OE.20.000635 [12] Gente R, Jansen C, Geise R, et al. Scaled bistatic radar cross section measurements of aircraft with a fiber-coupled THz time-domain spectrometer[J]. IEEE Transactions on Terahertz Science and Technology, 2012, 2(4): 424–431. DOI: 10.1109/TTHZ.2012.2192929 [13] 王瑞君, 王宏强, 庄钊文, 等. 太赫兹雷达技术研究进展[J]. 激光与光电子学进展, 2013, 50(4): 040001Wang Rui-jun, Wang Hong-qiang, Zhuang Zhao-wen, et al. Research progress of Terahertz radar technology[J]. Laser&Optoelectronics Progress, 2013, 50(4): 040001 [14] 武亚君, 黄欣, 徐秀丽, 等. 太赫兹目标RCS缩比测量技术[J]. 强激光与粒子束, 2013, 25(6): 1541–1544. DOI: 10.3788/HPLPB20132506.1541Wu Ya-jun, Huang Xin, Xu Xiu-li, et al. Radar cross section measurement technique of scale-model targets at terahertz[J]. High Power Laser and Particle Beams, 2013, 25(6): 1541–1544. DOI: 10.3788/HPLPB20132506.1541 [15] 梁达川, 谷建强, 韩家广, 等. 宽频太赫兹时域雷达系统[J]. 空间电子技术, 2013(4): 99–103. DOI: 10.3969/j.issn.1674-7135.2013.04.023Liang Da-chuan, Gu Jian-qiang, Han Jia-guang, et al. Terahertz time-domain radar system[J]. Space Electronic Technology, 2013(4): 99–103. DOI: 10.3969/j.issn.1674-7135.2013.04.023 [16] 江舸, 成彬彬, 张健. 基于0.14 THz成像雷达的RCS测量[J]. 太赫兹科学与电子信息学报, 2014, 12(1): 19–23. DOI: 10.11805/TKYDA201401.0019Jiang Ge, Cheng Bin-bin, and Zhang Jian. 0.14 THz radar imaging based Radar Cross Section measurement[J]. Journal of Terahertz Science and Electronic Information Technology, 2014, 12(1): 19–23. DOI: 10.11805/TKYDA201401.0019 [17] DiGiovanni D A, Gatesman A J, Giles R H, et al.. Electromagnetic scattering from dielectric surfaces at millimeter wave and terahertz frequencies[C]. Proceedings of the SPIE 9462, Passive and Active Millimeter-Wave Imaging XVIII, Baltimore, Maryland, United States, 2015, 9462: 94620H. 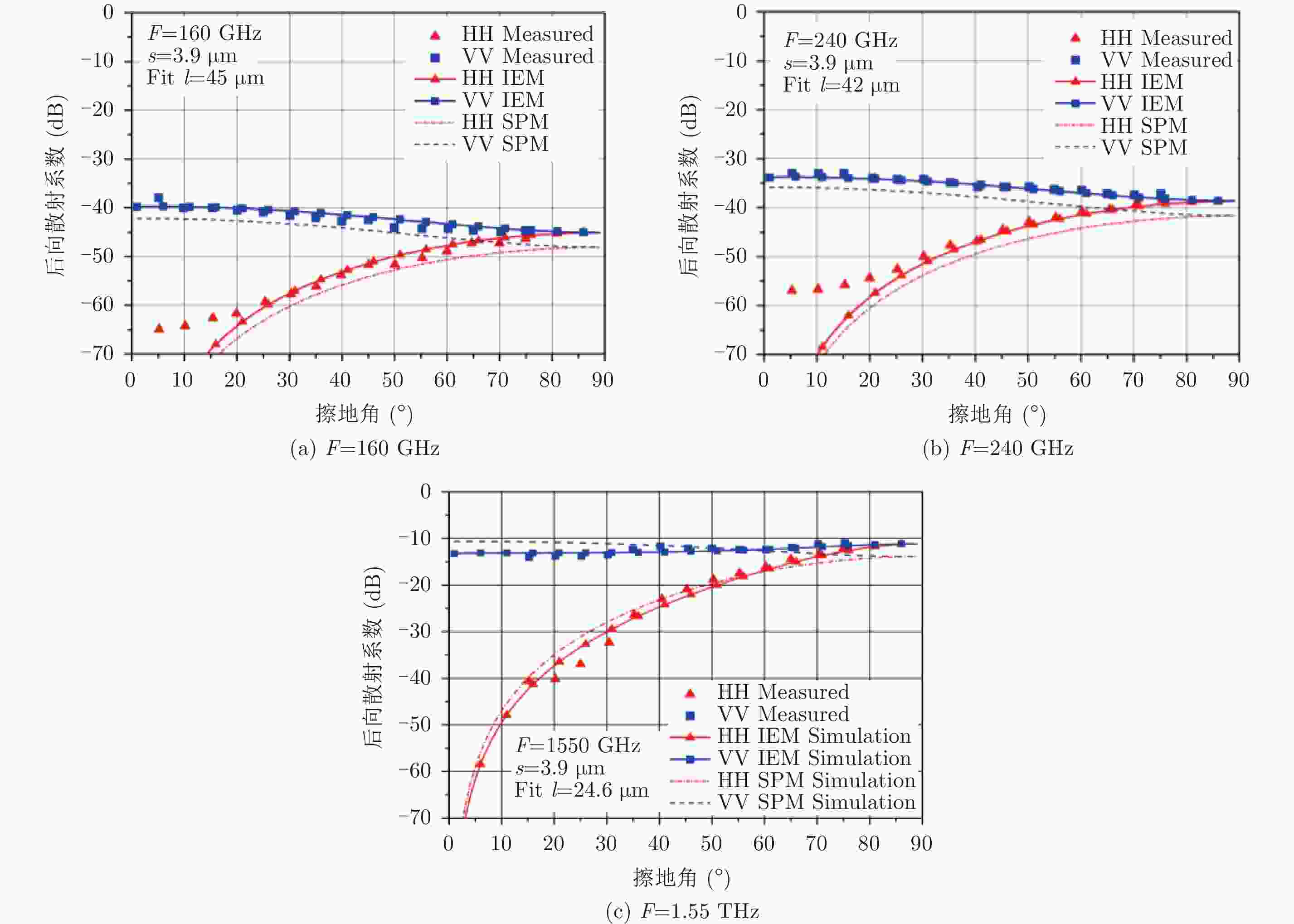[18] DiGiovanni D A, Gatesman A J, Goyette T M, et al.. Surface and volumetric backscattering between 100 GHz and 1.6 THz[C]. Proceedings of the SPIE 9078, Passive and Active Millimeter-Wave Imaging XVII, Baltimore, Maryland, United States, 2014, 9078: 90780A. [19] Soto-Crespo J M, Nieto-Vesperinas M, and Friberg A T. Scattering from slightly rough random surfaces: A detailed study on the validity of the small perturbation method[J]. Journal of the Optical Society of America A, 1990, 7(7): 1185–1201. DOI: 10.1364/JOSAA.7.001185 [20] Hsieh C Y, Fung A K, Nesti G, et al. A further study of the IEM surface scattering model[J]. IEEE Transactions on Geoscience and Remote Sensing, 1997, 35(4): 901–909. DOI: 10.1109/36.602532 [21] Jin Y Q. Electromagnetic Scattering Modelling for Quantitative Remote Sensing[M]. Singapore: World Scientific, 1993. [22] 金亚秋. 矢量辐射传输理论和参数反演[M]. 郑州: 河南科学技术出版社, 1994.Jin Ya-qiu. Theory of Vector Radiation Transmission and Parameter Inversion[M]. Zhengzhou: Henan Science and Technology Press, 1994. [23] 金亚秋. 电磁散射和热辐射的遥感理论[M]. 北京: 科学出版社, 1993.Jin Ya-qiu. Remote Sensing Theory of Electromagnetic Scattering and Thermal Radiation[M]. Beijing: Science Press, 1993. [24] Kozlov A I, Ligthart L P, Logvin A I, et al.. Mathematical and Physical Modelling of Microwave Scattering and Polarimetric Remote Sensing: Monitoring the Earth’s Environment Using Polarimetric Radar: Formulation and Potential Applications[M]. New York: Kluwer Academic Publishers, 2001: 43–65. 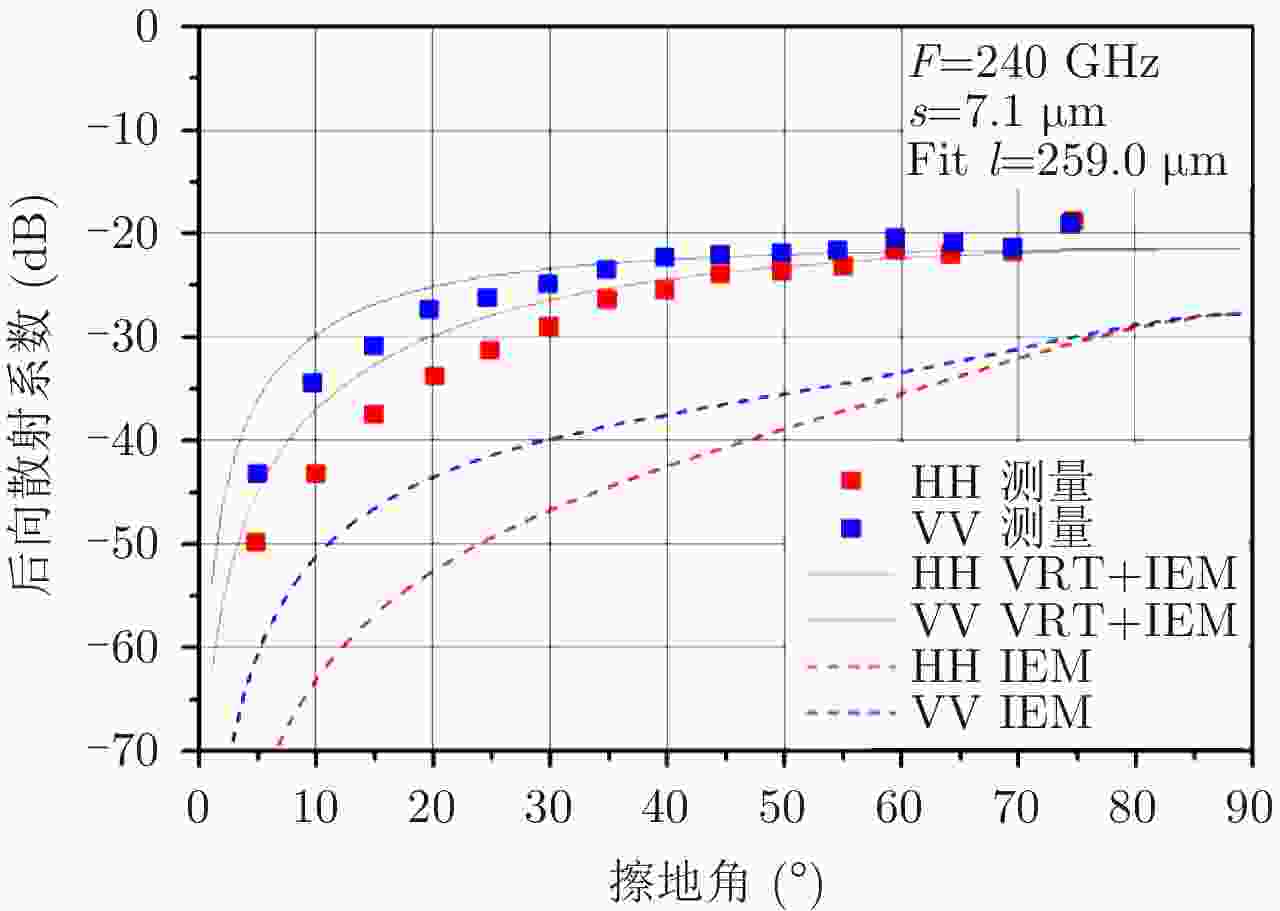[25] Xu F and Jin Y Q. Bidirectional analytic ray tracing for fast computation of composite scattering from electric-large target over a randomly rough surface[J]. IEEE Transactions on Antennas and Propagation, 2009, 57(5): 1495–1505. DOI: 10.1109/TAP.2009.2016691 [26] Chen H, Zhang M, Zhao Y W, et al. An efficient slope-deterministic facet model for SAR imagery simulation of marine scene[J]. IEEE Transactions on Antennas and Propagation, 2010, 58(11): 3751–3756. DOI: 10.1109/TAP.2010.2071349 -
下载:
计量
- 文章访问数: 3064
- HTML全文浏览量: 785
- PDF下载量: 476
- 被引次数: 0
