作者中心
专家审稿
责编办公
编辑办公
A Novel Cooperative Positioning Method for Over-the-horizon Shortwave Emitter Based on Two-dimensional Direction-of-arrival and Time-difference-of-arrival Measurements
-
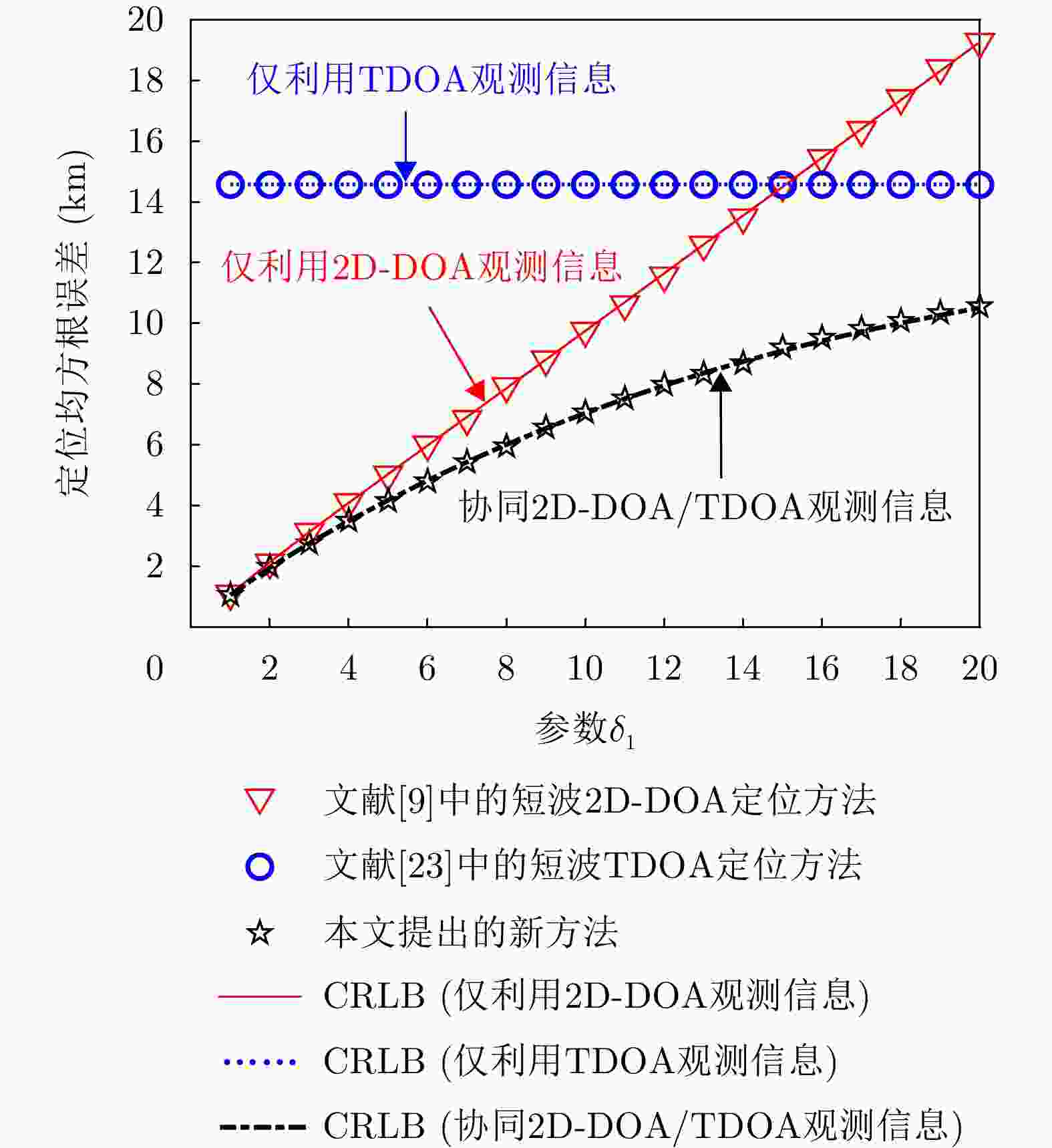
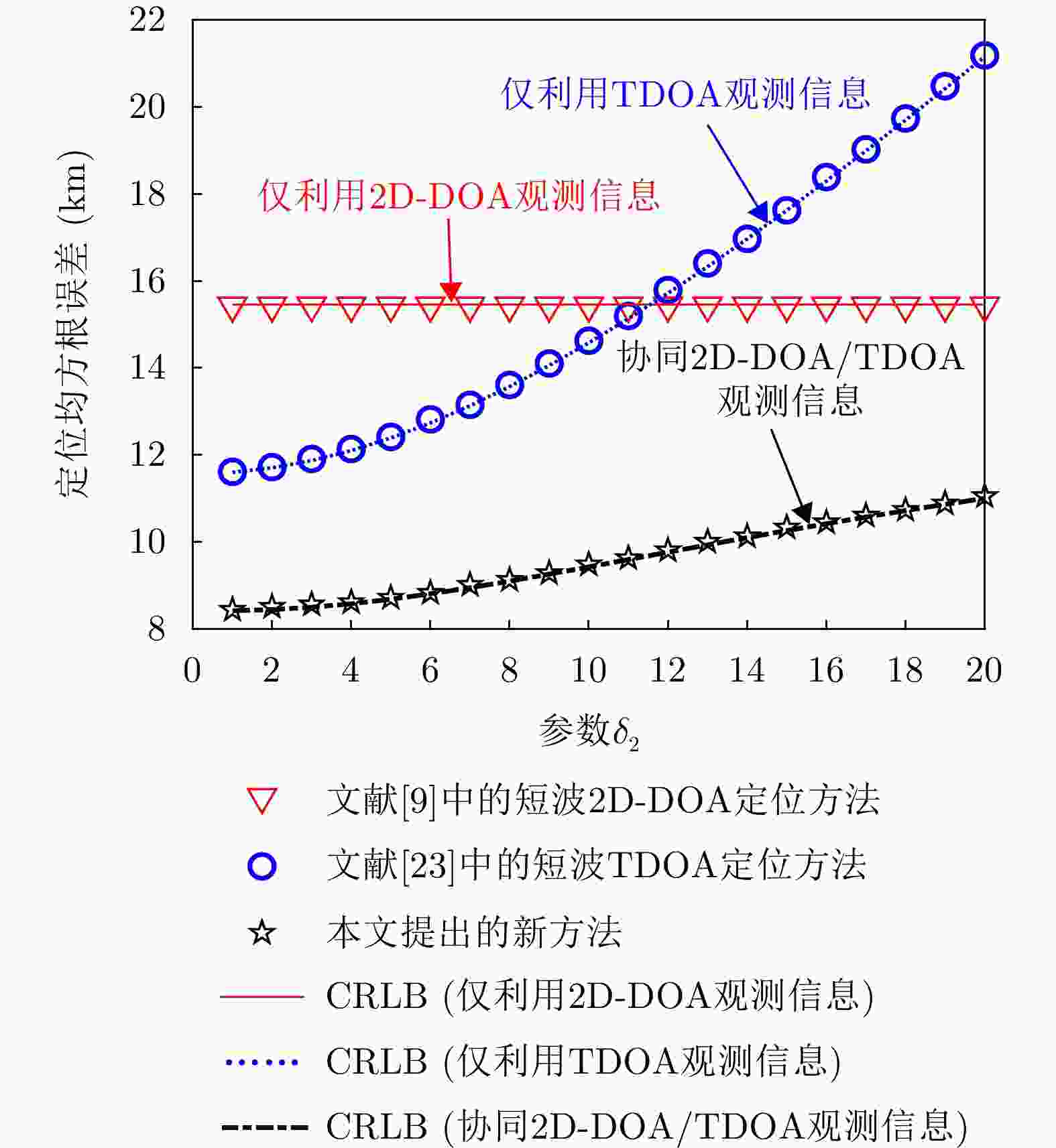
摘要: 针对超视距远距离短波辐射源定位误差较大的问题，该文在观测站同时获得二维到达角度和到达时间差参数的场景下，提出一种协同这两种观测量的定位新方法。首先，基于单跳电离层虚高模型构建面向短波辐射源的二维到达角度和到达时间差的非线性观测方程。然后，将超视距定位几何模型与代数模型相结合，并依次将两种非线性观测方程转化为伪线性观测方程，进而提出一种无需迭代的两阶段协同定位方法。阶段1通过求解一元六次多项式的根获得目标位置向量闭式解，阶段2通过构建等式约束优化模型对阶段1的估计误差进行改良，并利用拉格朗日乘子技术得到精度更高的定位结果。最后，利用约束误差扰动理论对新提出的协同定位方法的估计性能进行理论分析，证明新方法具有渐近统计最优性，同时还利用约束误差扰动理论定量分析短波辐射源高度信息误差对定位精度产生的影响，并推导能确保地球椭圆约束产生性能增益的短波辐射源高度信息误差最大门限值。仿真实验结果验证该文新方法能够获得显著的协同增益。Abstract: To reduce the large over-the-horizon localization errors of long-range shortwave emitter, a novel cooperative positioning method is proposed. This method combines two-Dimensional (2D) Direction-Of-Arrival (DOA) and Time-Difference-Of-Arrival (TDOA) measurements under scenarios in which observation stations can simultaneously obtain the two types of parameters. Initially, based on the single-hop ionospheric virtual height model, the nonlinear measurement models of 2D DOA and TDOA are established for over-the-horizon shortwave localization. Subsequently, by combining the over-the-horizon localization geometric and algebraic model, the two types of nonlinear measurement equations are successively transformed into the corresponding pseudo-linear measurement equations. On this basis, a novel two-stage cooperative positioning method is proposed without iteration. In the first stage, the closed-form solution of the target position vector is obtained by solving the roots of a sixth-order polynomial. In the second stage, an equality-constrained optimization problem is established to refine the localization result obtained in the first stage, yielding a more accurate target position estimate using the Lagrange multiplier technique. In addition, the estimation performance of the proposed cooperative positioning method is theoretically analyzed based on the constrained error perturbation theory, and the asymptotic efficiency of the new estimator is proved. Meanwhile, the influence of the altitude information error of the emitter on the positioning accuracy is quantitatively analyzed by applying the theory of constrained error perturbation, and the maximum threshold value of this error, which ensures that the constrained solution remains better than the unconstrained one, is deduced. Simulation results show that the newly proposed method can achieve significant cooperative gain.
-
图 1 短波辐射源2D-DOA和TDOA几何模型示意图
Figure 1. Schematic diagram of 2D-DOA and TDOA geometric models of shortwave radiation source
图 2 在ECEF坐标系下的X-Y平面中的定位结果散布图与定位误差椭圆曲线
Figure 2. Scatter plot of positioning results and elliptical curve of positioning errors in the X-Y plane in the ECEF coordinate system
图 3 正确的根、与正确的根最邻近的假根以及门限值$ - 1/{\kappa _{\max }}$
Figure 3. Correct root, the closest false root to the correct root and threshold value $ - 1/{\kappa _{\max }}$
图 7 定位均方根误差随着相关系数cDT的变化曲线
Figure 7. Localization RMSE as a function of correlation coefficient cDT
表 1 新方法的计算步骤及其所需的乘法次数
Table 1. Calculation steps of the new method and the number of multiplications required
序号 计算内容 乘法次数 步骤1 利用式(18)计算矩阵${{\boldsymbol{Q}}_\theta }$和向量${{\boldsymbol{p}}_\theta }$；利用式(22)计算矩阵${{\boldsymbol{Q}}_\beta }$和向量${{\boldsymbol{p}}_\beta }$；
利用式(26)计算矩阵${{\boldsymbol{Q}}_t}$和向量${{\boldsymbol{p}}_t}$$27N - 8$ 步骤2 利用式(27)构造矩阵${\boldsymbol{Q}}({\boldsymbol{\hat z}},{\boldsymbol{\hat d}})$和向量${\boldsymbol{p}}({\boldsymbol{\hat z}},{\boldsymbol{\hat d}})$ 无实质乘法计算 步骤3 利用式(30)计算矩阵${{\boldsymbol{C}}_z}$和${{\boldsymbol{C}}_d}$ $48{N^2} - 4N - 13$ 步骤4 利用式(34)计算协方差矩阵${\bf{COV}}({\boldsymbol{e}})$及其逆矩阵${({\bf{COV}}({\boldsymbol{e}}))^{ - 1}}$ $\begin{gathered} O[{(3N - 1)^3}] + 66{N^3} \\[-3pt] - 61{N^2} + 19N - 2 \end{gathered} $ 步骤5 利用式(38)计算矩阵${\boldsymbol{W}}({\boldsymbol{\hat z}},{\boldsymbol{\hat d}})$及其逆矩阵${({\boldsymbol{W}}({\boldsymbol{\hat z}},{\boldsymbol{\hat d}}))^{ - 1}}$ $\begin{gathered} O(64) + 36{N^2} \\[-3pt] + 24N - 12 \end{gathered} $ 步骤6 对矩阵${({\boldsymbol{W}}({\boldsymbol{\hat z}},{\boldsymbol{\hat d}}))^{ - 1}}{{\boldsymbol{\varOmega }}_1}$进行特征值分解得到特征值对角矩阵${{\boldsymbol{\varLambda }}_{\text{w}}}$和特征矩阵${{\boldsymbol{H}}_{\text{w}}}$ $O(64) + 4$ 步骤7 利用式(43)计算向量${{\boldsymbol{h}}_1}$和${{\boldsymbol{h}}_2}$ $\begin{gathered} O(64) + 9{N^2} \\ + 6N + 45 \\ \end{gathered} $ 步骤8 利用式(46)—式(50)计算多项式系数$ {\{ {\alpha _j}\} _{0 \le j \le 6}} $ $82$ 步骤9 求解式(45)中的一元六次多项式的根，并利用式(53)选择正确的根 $\begin{gathered} J \cdot O[{(3N - 1)^3}] + O(6) \\[-3pt] + J(12{N^3} + 2{N^2} - 2N) \end{gathered} $ 步骤10 利用式(37)计算向量${{\boldsymbol{\hat v}}_{{\text{o,f}}}}$，并进而构造向量$ {{{\hat {\bar {\boldsymbol{v}}}}}_{{\text{o,f}}}} $和${{\boldsymbol{\hat u}}_{{\text{o,f}}}}$ $O(64) + 16$ 步骤11 利用式(62)计算均方误差矩阵${\bf{MSE}}({{{\hat {\bar {\boldsymbol{v}}}}}_{{\text{o,f}}}})$及其逆矩阵${({\bf{MSE}}({{{\hat {\bar {\boldsymbol{v}}}}}_{{\text{o,f}}}}))^{ - 1}}$ $O(64) + O(27) + 145$ 步骤12 利用式(65)计算标量$ \hat \mu $和向量$ {\boldsymbol{\hat \eta }} $ 6 步骤13 利用式(66)构造矩阵$ {\boldsymbol{\bar J}}({{\boldsymbol{\hat u}}_{{\text{o,f}}}}) $ 5 步骤14 利用式(69)计算向量$ \Delta {{{\hat {\bar {\boldsymbol{v}}}}}_{{\text{o,f}}}} $ $28$ 步骤15 利用式(70)计算向量$ {{{\hat{ \bar {\boldsymbol{u}}}}}_{{\text{o,s}}}} $ 无实质乘法计算 步骤16 利用式(71)计算最终定位结果$ {{\boldsymbol{\hat u}}_{{\text{o,s}}}} $ 3 
下载: 导出CSV
表 2 观测站的经纬度与电离层虚高数值
Table 2. Longitude, latitude and ionospheric virtual height of shortwave observer
观测站 经度(°) 纬度(°) 电离层虚高(km) 1 123.04 40.94 273 2 115.66 40.27 316 3 114.61 34.98 358 4 113.47 30.09 347 5 115.75 26.22 255
下载: 导出CSV
表 3 多项式方程的根及其对应的MLE目标函数值
Table 3. Roots of polynomial equation and their corresponding MLE objective function values
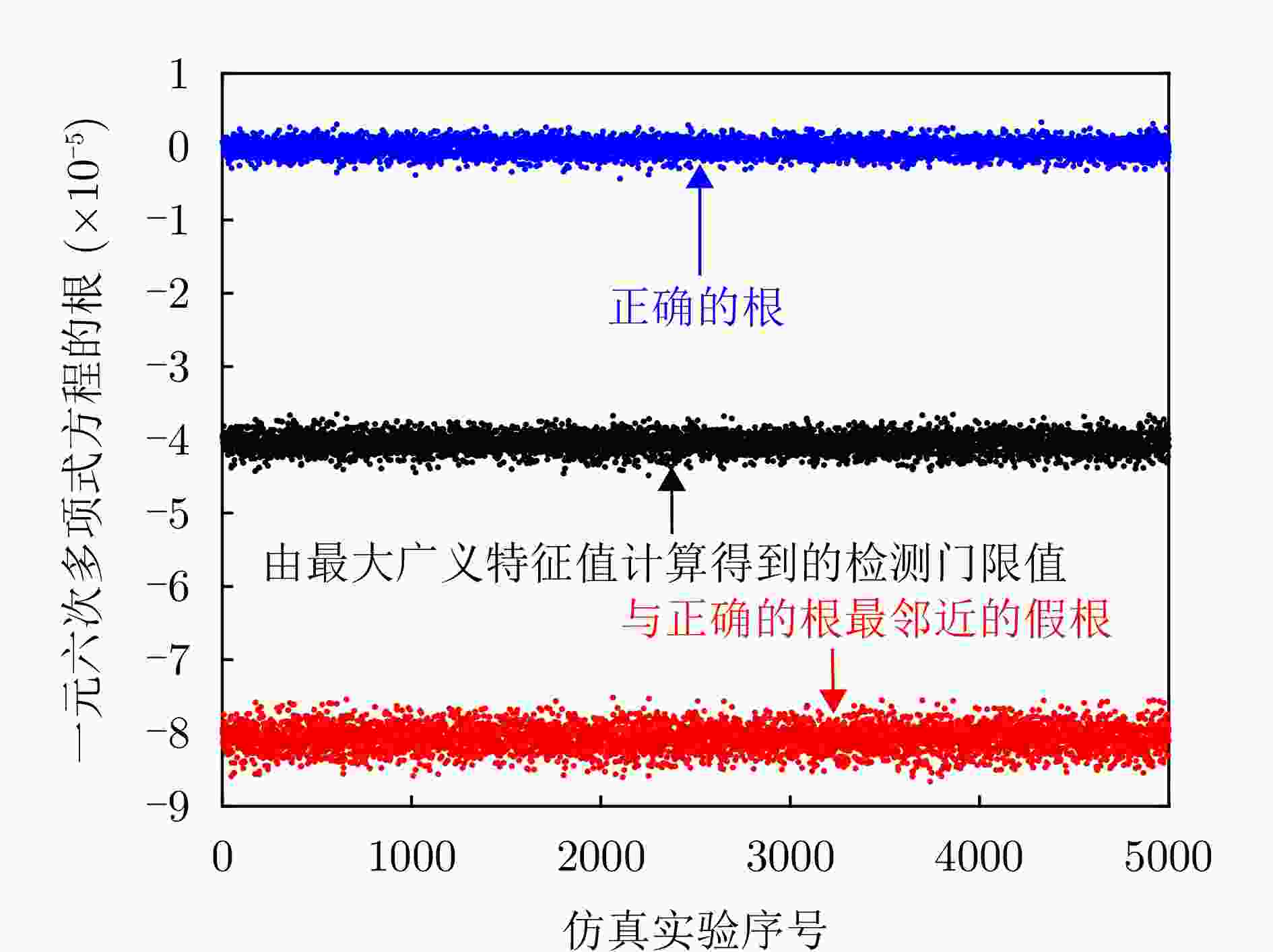
序号 一元六次多项式方程的根 与门限值–1/$ {\kappa _{\max }} $= –4.02×10–5的关系 由式(53)给出的MLE目标函数值 1 –8.12×10–2 小于 3.34×106 2 –7.98×10–2 小于 3.22×106 3 –1.81×10–2 小于 7.56×105 4 –1.73×10–2 小于 6.90×105 5 –8.08×10–5 小于 6.60×103 6 2.89×10–7 唯一大于 1.23×101 唯一的最小值
下载: 导出CSV
-
[1] 王金龙, 陈瑾, 徐煜华. 短波通信技术研究进展与发展需求[J]. 陆军工程大学学报, 2022, 1(1): 1–7. doi: 10.12018/j.issn.2097-0730.20211218001.WANG Jinlong, CHEN Jin, and XU Yuhua. On research advances and development requirements of high frequency communication technologies[J]. Journal of Army Engineering University of PLA, 2022, 1(1): 1–7. doi: 10.12018/j.issn.2097-0730.20211218001. [2] PANG Feifei, DOĞANÇAY K, NGUYEN N H, et al. AOA pseudolinear target motion analysis in the presence of sensor location errors[J]. IEEE Transactions on Signal Processing, 2020, 68: 3385–3399. doi: 10.1109/TSP.2020.2998896. [3] YAN Qingli, CHEN Jianfeng, ZHANG Jie, et al. Robust AOA-based source localization using outlier sparsity regularization[J]. Digital Signal Processing, 2021, 112: 103006. doi: 10.1016/j.dsp.2021.103006. [4] SUN Yimao, HO K C, and WAN Qun. Eigenspace solution for AOA localization in modified polar representation[J]. IEEE Transactions on Signal Processing, 2020, 68: 2256–2271. doi: 10.1109/TSP.2020.2981773. [5] CHEN Xianjing, WANG Gang, and HO K C. Semidefinite relaxation method for unified near-field and far-field localization by AOA[J]. Signal Processing, 2021, 181: 107916. doi: 10.1016/j.sigpro.2020.107916. [6] ZOU Yanbin, WU Liehu, FAN Jingna, et al. A convergent iteration method for 3-D AOA localization[J]. IEEE Transactions on Vehicular Technology, 2023, 72(6): 8267–8271. doi: 10.1109/TVT.2023.3242054. [7] CHEN Yonghua, YU Hua, LI Jie, et al. Three-dimensional source localization based on 1-D AOA measurements: Low-complexity and effective estimator[J]. IEEE Transactions on Instrumentation and Measurement, 2023, 72: 9510615. doi: 10.1109/TIM.2023.3298680. [8] 王鼎, 尹洁昕, 朱中梁. 针对超视距短波辐射源的测角与测时差协同定位方法[J]. 中国科学: 信息科学, 2022, 52(11): 1942–1973. doi: 10.1360/SSI-2021-0331.WANG Ding, YIN Jiexin, and ZHU Zhongliang. Novel cooperative localization method of over-the-horizon shortwave emitters based on direction-of-arrival and time-difference-of-arrival measurements[J]. Scientia Sinica Informationis, 2022, 52(11): 1942–1973. doi: 10.1360/SSI-2021-0331. [9] JIANG Linqiang, TANG Tao, WU Zhidong, et al. An iterative method for short-wave source localization using direction of arrival measurements[C]. The 18th Chinese National Symposium on Radio Propogation, Qingdao, China, 2023: 595–600. doi: 10.26914/c.cnkihy.2023.050995. [10] 贺承杰. 天波超视距雷达海面目标定位方法研究[J]. 雷达科学与技术, 2020, 18(5): 568–572, 578. doi: 10.3969/j.issn.1672-2337.2020.05.017.HE Chengjie. Surface target location method of sky wave over-the-horizon radar[J]. Radar Science and Technology, 2020, 18(5): 568–572, 578. doi: 10.3969/j.issn.1672-2337.2020.05.017. [11] GUO Fucheng and HO K C. A quadratic constraint solution method for TDOA and FDOA localization[C]. 2011 IEEE International Conference on Acoustics, Speech and Signal Processing (ICASSP), Prague, Czech Republic, 2011: 2588–2591. doi: 10.1109/ICASSP.2011.5947014. [12] LI Qian, CHEN Baixiao, and YANG Minglei. Improved two-step constrained total least-squares TDOA localization algorithm based on the alternating direction method of multipliers[J]. IEEE Sensors Journal, 2020, 20(22): 13666–13673. doi: 10.1109/JSEN.2020.3004235. [13] 王鼎, 尹洁昕, 高路, 等. 一种同步时钟偏差和传感器位置误差存在下的TDOA定位新方法[J]. 航空学报, 2022, 43(7): 325405. doi: 10.7527/S1000-6893.2021.25405.WANG Ding, YIN Jiexin, GAO Lu, et al. A novel method for TDOA localization in presence of synchronization clock bias and sensor position uncertainty[J]. Acta Aeronautica et Astronautica Sinica, 2022, 43(7): 325405. doi: 10.7527/S1000-6893.2021.25405. [14] JAIN A, PAGANI P, FLEURY R, et al. Accurate time difference of arrival estimation for HF radio broadcast signals[J]. Microwave and Optical Technology Letters, 2018, 60(6): 1406–1410. doi: 10.1002/mop.31178. [15] WANG Ting, HONG Xueli, LIU Wen, et al. Geolocation of unknown emitters using TDOA of path rays through the ionosphere by multiple coordinated distant receivers[C]. 2018 IEEE International Conference on Acoustics, Speech and Signal Processing (ICASSP), Calgary, Canada, 2018: 3509–3513. doi: 10.1109/ICASSP.2018.8462106. [16] HUANG Sen, PUN Y M, SO A M C, et al. A provably convergent projected gradient-type algorithm for TDOA-based geolocation under the quasi-parabolic ionosphere model[J]. IEEE Signal Processing Letters, 2020, 27: 1335–1339. doi: 10.1109/LSP.2020.3010676. [17] XIONG Wenxin, SCHINDELHAUER C, and SO H C. Globally optimized TDOA high-frequency source localization based on quasi-parabolic ionosphere modeling and collaborative gradient projection[J]. IEEE Transactions on Aerospace and Electronic Systems, 2023, 59(1): 580–590. doi: 10.1109/TAES.2022.3185971. [18] YANG Lijuan, GAO Huotao, LING Yun, et al. Localization method of wide-area distribution multistatic sky-wave over-the-horizon radar[J]. IEEE Geoscience and Remote Sensing Letters, 2022, 19(1): 3500305. doi: 10.1109/LGRS.2020.3018322. [19] 李琛, 周晨, 王君明, 等. 基于经验电离层模型的短波时差定位理论分析[J]. 系统工程与电子技术, 2023, 45(7): 1911–1919. doi: 10.12305/j.issn.1001-506X.2023.07.01.LI Chen, ZHOU Chen, WANG Junming, et al. Theoretical analysis of shortwave TDOA geolocation based on empirical ionospheric model[J]. Systems Engineering and Electronics, 2023, 45(7): 1911–1919. doi: 10.12305/j.issn.1001-506X.2023.07.01. [20] JAIN A, PAGANI P, FLEURY R, et al. Efficient time domain HF geolocation using multiple distributed receivers[C]. The 11th European Conference on Antennas and Propagation (EUCAP), Paris, France, 2017: 1852–1856. doi: 10.23919/EuCAP.2017.7928069. [21] JAIN A, PAGANI P, FLEURY R, et al. HF source geolocation using an operational TDoA receiver network: Experimental results[J]. IEEE Antennas and Wireless Propagation Letters, 2018, 17(9): 1643–1647. doi: 10.1109/LAWP.2018.2860459. [22] XU Chen, CAI Hongtao, GAO Shunzu, et al. A method for HF skywave source geolocation in unknown ionosphere environments and experimental results[J]. IEEE Antennas and Wireless Propagation Letters, 2023, 22(5): 1059–1063. doi: 10.1109/LAWP.2022.3232399. [23] ZHANG Tienan, MAO Xingpeng, ZHAO Chunlei, et al. A novel grid selection method for sky-wave time difference of arrival localisation[J]. IET Radar, Sonar & Navigation, 2019, 13(4): 538–549. doi: 10.1049/iet-rsn.2018.5308. [24] ZHANG Fengrui, SUN Yimao, and WAN Qun. Calibrating the error from sensor position uncertainty in TDOA-AOA localization[J]. Signal Processing, 2020, 166: 107213. doi: 10.1016/j.sigpro.2019.07.006. [25] KANG XU, WANG Dejiang, SHAO Yu, et al. An efficient hybrid multi-station TDOA and single-station AOA localization method[J]. IEEE Transactions on Wireless Communications, 2023, 22(8): 5657–5670. doi: 10.1109/TWC.2023.3235753. [26] XU Zhezhen, LI Hui, YANG Kunde, et al. A robust constrained total least squares algorithm for three-dimensional target localization with hybrid TDOA-AOA measurements[J]. Circuits, Systems, and Signal Processing, 2023, 42(6): 3412–3436. doi: 10.1007/s00034-022-02270-6. [27] CAO Yalu, LI Peng, LI Jinzhou, et al. A new iterative algorithm for geolocating a known altitude target using TDOA and FDOA measurements in the presence of satellite location uncertainty[J]. Chinese Journal of Aeronautics, 2015, 28(5): 1510–1518. doi: 10.1016/j.cja.2015.08.015. [28] PEI Yuhao, WU Guizhou, and GUO Fucheng. Geolocation a known-altitude moving source by TDOA and FDOA measurements[J]. Electronics Letters, 2022, 58(13): 514–516. doi: 10.1049/ell2.12508. [29] MORE J J. Generalizations of the trust region problem[J]. Optimization Methods and Software, 1993, 2(3/4): 189–209. doi: 10.1080/10556789308805542. [30] HO K C and CHAN Y T. Geolocation of a known altitude object from TDOA and FDOA measurements[J]. IEEE Transactions on Aerospace and Electronic Systems, 1997, 33(3): 770–783. doi: 10.1109/7.599239. -
图(9) / 表(3)
计量
- 文章访问数: 310
- HTML全文浏览量: 144
- PDF下载量: 228
- 被引次数: 0
