作者中心
专家审稿
责编办公
编辑办公
Coherent Detection Method for Moving Platform Based Distributed Aperture Radar and Experimental Verification
-
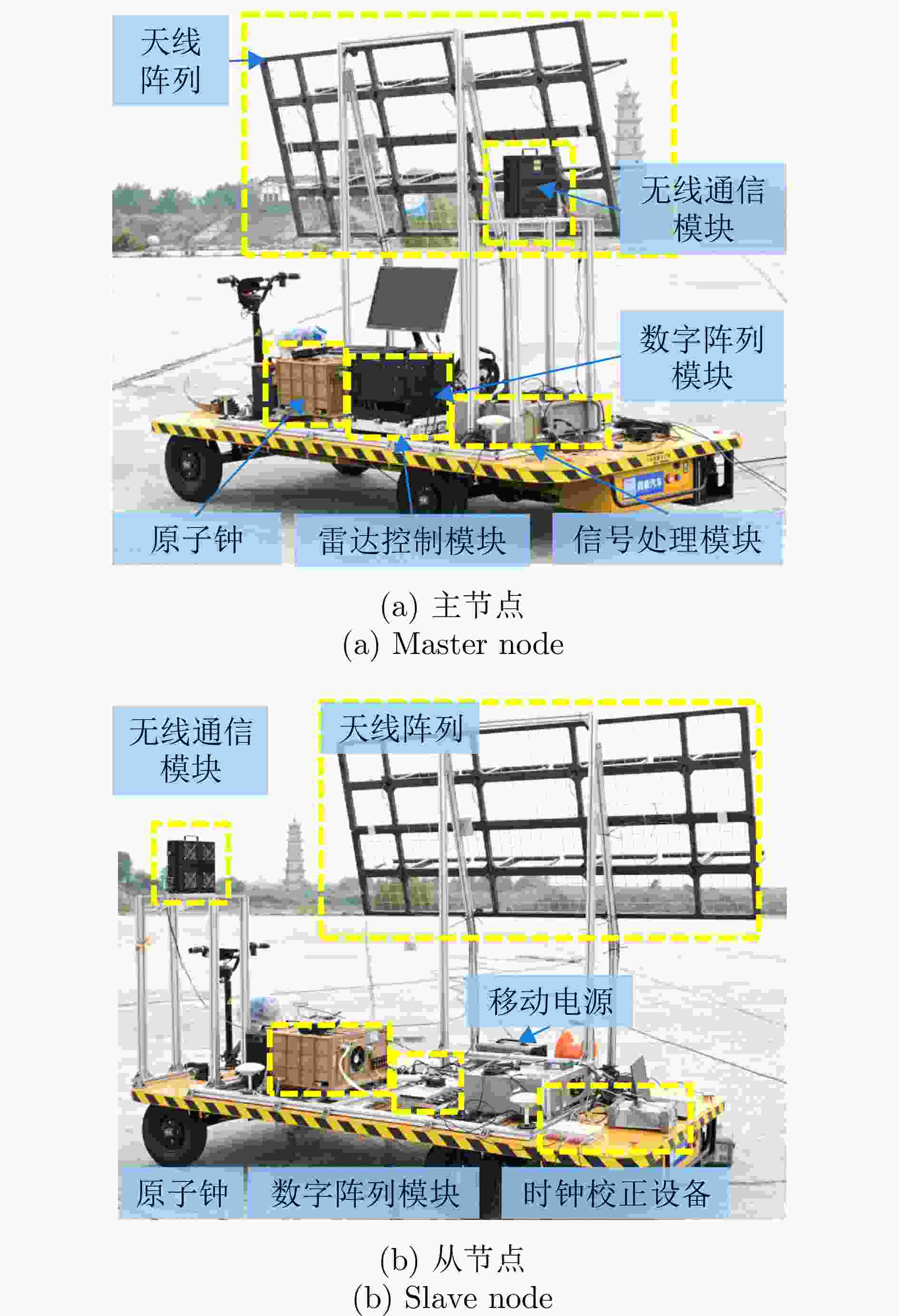
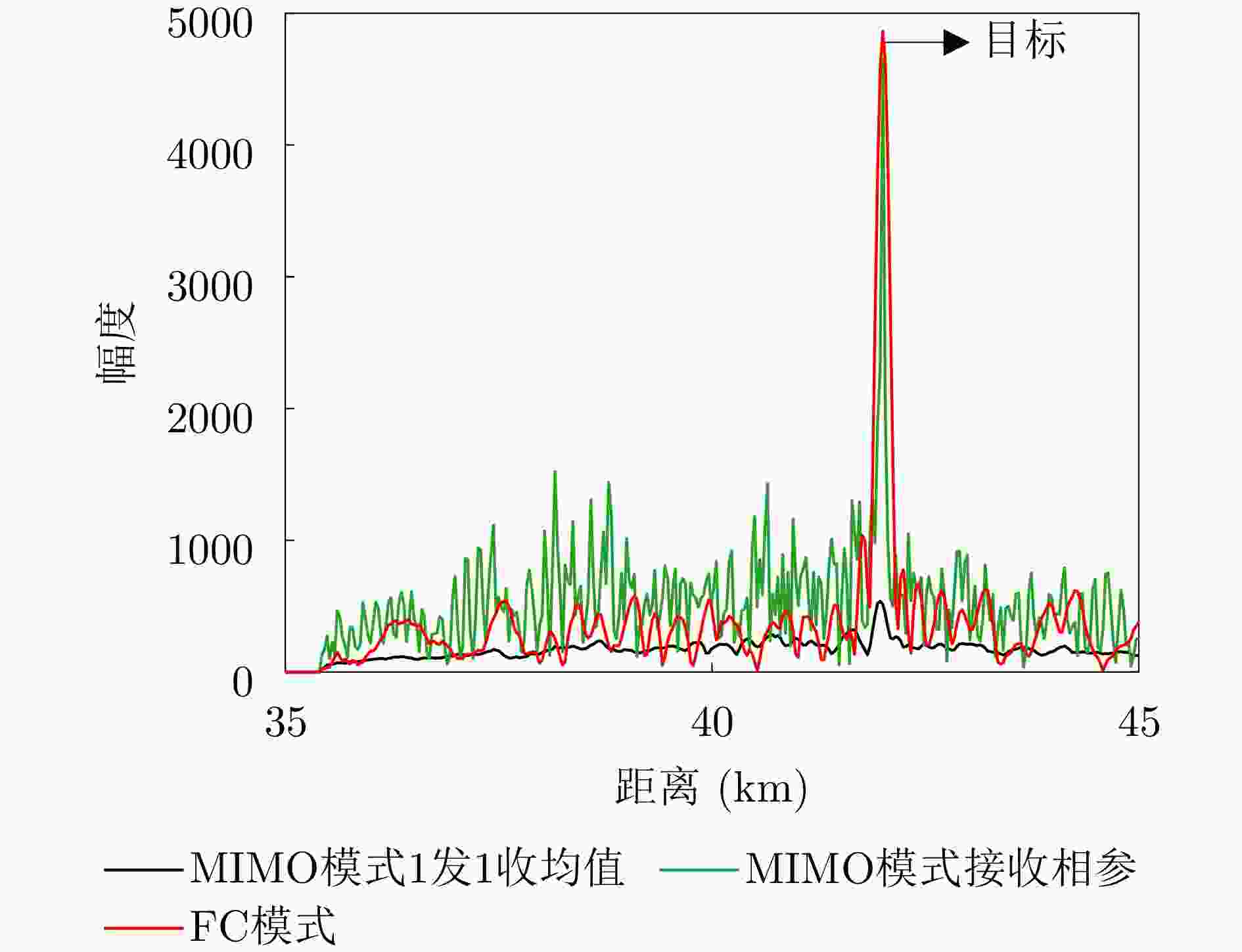
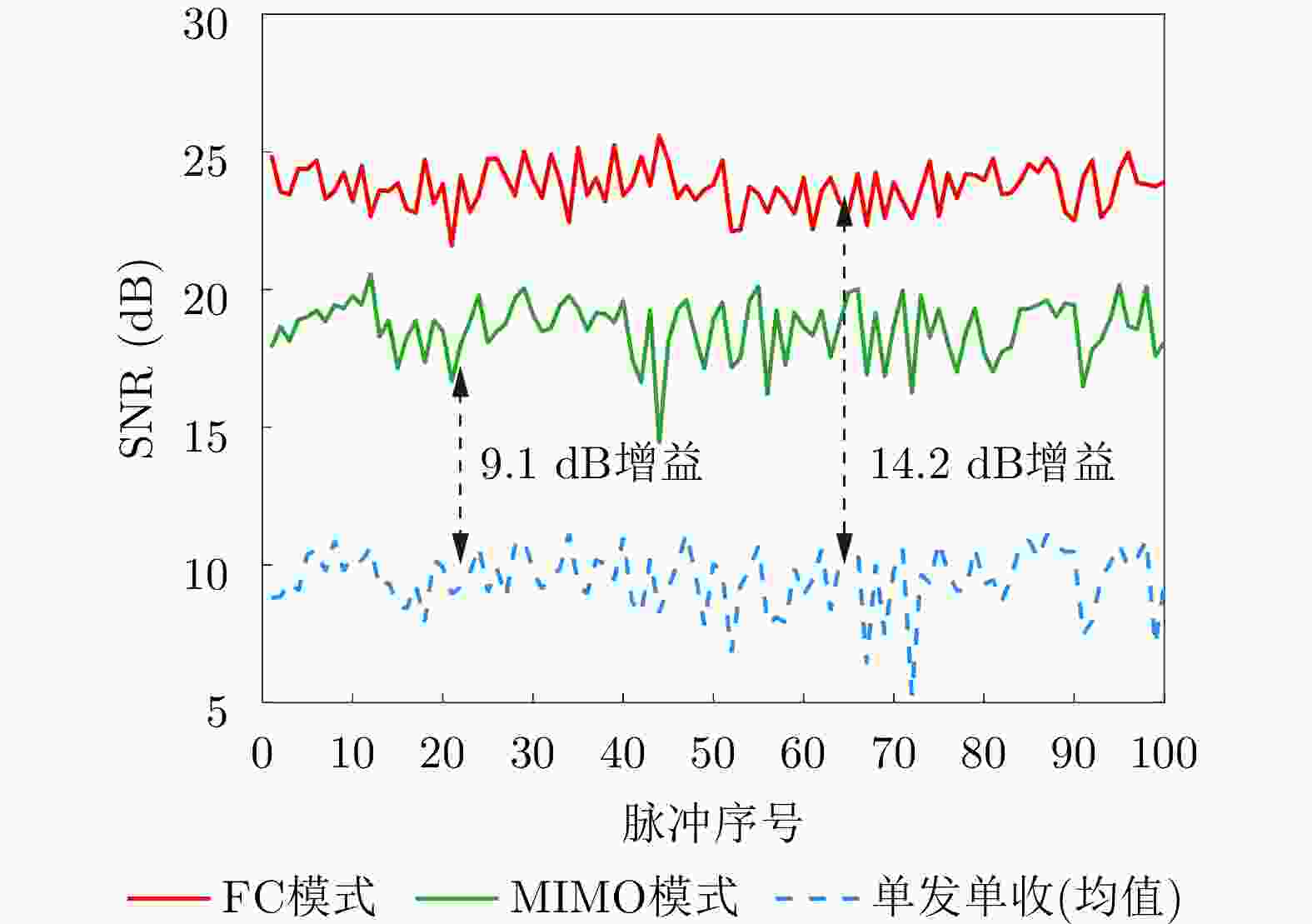
摘要: 动平台分布孔径雷达不仅可以通过多部小孔径雷达相参合成等效获得大孔径雷达的探测性能，也可进一步通过机动性和灵活部署增强探测与抗毁伤能力，是未来雷达重要发展方向之一。但由于多雷达间存在内部钟差和外部传播路径差，各雷达发射信号无法直接相参合成，需进行必要的时间和相位相参参数校正，且分布孔径雷达间距通常远超半波长，合成方向图将存在栅瓣问题，影响目标角度估计。为获得相参参数，该文以闭环式框架为基础，给出动平台分布孔径雷达认知相参框架，并结合运动条件下相参参数的变化规律，提出多脉冲关联相参参数估计方法以提升参数估计精度。同时，针对栅瓣问题，结合平台运动特性提出一种基于阵列构型累积的无模糊角度估计方法。最后，在仿真验证基础上基于所提框架设计了3节点地面动平台分布孔径雷达原理样机并开展了试验验证，试验结果表明在运动场景下，相比单部孔径雷达可以实现最高14.2 dB的信噪比增益，从而提升了目标的测距精度，同时在一定条件下实现了目标角度的无模糊测量，证明了所提方法和框架的有效性。该文工作将对未来分布孔径雷达的工程化实现及发展起到一定的引导作用。Abstract: As one of the most promising next-generation radars, Moving platform based Distributed Aperture Radar (MDAR) cannot only coherently combining distributed apertures to obtain the same detection performance of a large aperture, but also enhance the detection and anti-damage capabilities through mobility and flexible deployment. However, time and phase synchronization among radars should be done before coherently combining due to internal clock differences and external propagation path differences. Moreover, grating lobes will generate as the distance between multiple radars usually exceeds half a wavelength, which affects the estimation accuracy of target angle. To obtain Coherent Parameters (CPs), this paper established a cognitive framework for MDAR based on closed-loop structure. And a multi-pulse correlation CPs estimation method considering motion conditions is proposed to improve estimation accuracy. In the meanwhile, an unambiguous angle estimation method based on array configuration accumulation is proposed considering platform motion characteristics. Finally, based on the simulation verification and the proposed framework, a prototype of a 3-node ground Moving platform based Distributed Coherent Aperture Radar (MDCAR) system is designed and experiments are conducted. Compared to a single radar, a maximum value of 14.2 dB signal-to-noise ratio improvement can be achieved, which can further enhance range detection accuracy. Besides, unambiguous angle estimation is also realized under certain conditions. This work is expected to provide support for the research and development of MDCAR.
-
1. 引言
潮间带区域是一种位于陆地与海洋之间的特殊海岸区域，在低潮时露出水面而在高潮时被水淹没[1]，其构成了一个独特的湿地生态系统，提供了多种植被必需的生长环境，是水产养殖、海洋环境观测、海洋经济开发以及海岸防御的重点区域。为了更好地开发利用潮间带区域，利用遥感对潮间带进行观测和研究的工作已得到开展[2–5]。如何基于遥感图像自动准确地将潮间带区域与水域及其他陆地区域分开，并能够准确区分潮间带区域不同植被或养殖类型，是潮间带区域监测所关心的问题。合成孔径雷达(Synthetic Aperture Radar, SAR)尤其是全极化SAR，由于其全天时全天候工作的优势和分类能力强的特点，在该方面的应用得到了关注[6–8]。
针对极化SAR数据，通过特征值分解以及散射分析等手段，可以从中提取出大量的多极化特征来描述地物的散射信息[9,10]。这些特征为极化SAR数据的应用提供了新的视角。近年来，基于极化特征的研究有了突破性的进展，广泛地应用在地物分类、典型目标检测提取等领域[11–13]。相比于其他特征，极化熵被证实可以更好地描述地物的极化相关的纹理信息(polarization-dependent variation of texture)[14]和表面粗糙度[15]，并且有较好的目标识别能力[16]。因此，极化熵广泛地应用在地物分类、海岸带典型目标检测[3,17]等领域。比较典型的有Cloude和Pottier1997年提出的基于极化熵的地物分类框架[16]以及Eun-Sung等人利用极化熵基于GEV分布实现对水下养殖区域的检测等[3]。
另外，从对极化SAR数据的统计特性的分析出发，已有研究将有限混合模型(Finite Mixture Models, FMM)等理论引入到基于极化SAR地物分类应用中[18]。从传统的混合Wishart模型[18]到混合U分布模型[19]，基于FMM的极化SAR地物分类方法在城区、农田以及海洋等区域达到较好的分类效果。
在潮间带区域，其在退潮后露出水面的部分主要由淤泥滩、浅留水体以及水产养殖等部分组成，而上述部分的电磁散射强度与水面差别不大，因此在极化SAR图像中表现为类似的散射强度和散射机制，不易区分。现有针对极化SAR数据进行地物分类的算法在潮间带这种特殊的地物场景中并不能得到很好的分类结果。现有基于SAR数据对于潮间带区域也有较多的研究，主要针对有潮海域的地貌变动监控[7,20–22]、土壤湿度分析[1,8]以及特定地物的散射特性分析[3,17,23,24]等。比较典型的有Li Zhen等人针对1999–2006年波罗的海海域的潮间带地貌演变研究[7,20–22]以及Hoonyol Lee等人对于韩国南部海域潮间带的土壤湿度变化研究[1]等。
本文针对潮间带的特点，基于极化特征和FMM提出了一种新的地物分类方法。首先，本文针对4种典型的极化特征进行分析和筛选，得到一组最适合描述潮间带区域的多极化特征：极化熵和反熵。在此基础上，基于对极化熵图像的统计特性分析和极值理论，本文优选GEV分布对潮间带区域的极化熵分布进行描述[20,25]。随后构建了一种基于GEV混合模型(GEV Mixture Model, GEVMM)在极化熵特征中对潮间带地物进行标记。最后结合反熵的信息实现潮间带地物分类。本文利用RadarSAT-2获取的上海崇明岛东滩区域数据进行实验验证。与经典多极化SAR分类方法结果及实地考察真值的对比结果表明，本文方法能够有效地将潮间带区域与水域进行区分，并对潮间带内部不同场景类型进行分类，效果优于Wishart-H/A/α等经典方法。
本文的结构如下：第2节详细介绍本文提出的分类方法，第3节基于实测数据对方法进行验证，并对结果进行分析讨论，第4节总结全文。
2. 极化熵结合GEV模型的分类方法
2.1 信号建模与极化特征
在全极化SAR模式中，SAR系统以水平极化和垂直极化两种模式的组合来发射和接收电磁波[26]。极化散射矩阵为：
S=[SHHSHVSVHSVV] (1) 一般来说， SHV=SVH，因此Pauli散射矢量定义为：
k=1√2[SHH+SVVSHH−SVV2SHV]T (2) 其中，T表示转置。基于k可以得到极化相干矩阵T3：
T3=1LL∑n=1kk∗T (3) 其中，L为视数，上标 ∗代表了复共轭。从极化散射矩阵S和极化相干矩阵T3中可以提取出来很多极化特征，其中4个最典型的多极化特征(Span, H, A, α)如下。
极化总功率Span是一个典型的极化特征，其定义可以从极化散射矩阵S得到：
Span=|SHH|2+|SHV|2+|SVH|2+|SVV|2 (4) Span影像为4个极化通道图像的功率之和，其中包含了各通道图像的信息。
从极化相干矩阵T3中获取极化特征一般通过特征值分解，其中比较典型的为 H/A/α分解。 H/A/α已经在极化图像分类领域广泛使用，其定义为：
T3=3∑i=1λiT3i=3∑i=1λiuiui∗T (5) 其中， λi是T3矩阵的特征值，代表着第i个归一化分量 T3i的比重，其概率可以用Pi来表示：
Pi=λi/λi3∑i=1λi3∑i=1λi (6) 极化熵和反熵是 H/A/α分解后得到的两个重要特征，可以通过对 λi进行计算得到：
H=−3∑i=1PilogPi (7) A=λ2−λ3λ2+λ3 (8) 其中，H是极化熵，A是反熵，计算时特征值按照 λ1>λ2>λ3来排序。其中极化熵H描述了散射的随机性，其取值范围为0到1。当极化熵值较低时，可以认为只有一种主导散射机制；当极化熵值较高时，此时表现出较为强烈的去极化特性，散射机制趋向随机；当极化熵接近于1时，散射机制接近于噪声。反熵A是对极化熵H的一个有效补充，是对第2个和第3个特征值的差异的描述，并且对极化熵值大于0.7的高熵区域有着较好的识别性能[26]。一般来说，潮间带的大多数区域对于反熵的响应较弱，只有部分高熵区域，例如露出水面的金属隔离网，才有较高的反熵值。
另外一个重要的 H/A/α分解特征是平均散射角，可以通过特征向量计算得到：
α=3∑i=1Picos−1(|ui(1)|) (9) 其中，α为平均散射角，其值域范围为0° and 90°[26]。
2.2 极化特征比较与选择
在潮间带区域，退潮残留的水体、淤泥滩和水下农场等构成了复杂的地貌。残留水体和淤泥滩均有相对光滑的表面，且绝大部分的水下农场养殖区域可以被称为“浅层水域”，仅有少量的隔离网和部分植被的枝叶露出水面。因此，该区域在各个通道的雷达功率图像中均会表现出和海水相似的图像灰度值，如图1(a)所示。所以Span图虽然综合了全极化SAR的4个通道功率图像的幅度信息，但是这种简单的功率和并不能增强潮间带区域和海水的区分能力。
潮间带混杂的地物也导致了其散射机制的随机性变化较大，而极化熵H和反熵A均是对散射随机性的描述，因此这两个特征均有可能用来描述在潮间带区域。潮间带区域的极化熵和反熵示例分别如图1(b)和图1(c)所示。可以看出，相比于Span，极化熵可以较好地区分海洋和潮间带区域，并且可以区分潮间带内部地物类型。而反熵则可以明显将高熵和低熵区域区分开来。因此对于潮间带区域，理论上来说极化熵是一种更普适的特征，而反熵更适合用来区分一些高熵区域。
平均散射角α则是对潮间带区域的散射机制的直接描述。较为光滑的表面会产生较低的α值，随着α值的增大，散射机制依次从表面散射，体散射到二次散射过渡。简而言之，对于潮间带区域，平均散射角α可以认为是一种对表面粗糙度的衡量。淤泥滩和露出水面的水下植被与水面相比拥有不同粗糙度的表面，从而在α特征图中会有不同的表现，如图1(d)所示。但是，由于在潮汐作用下潮间带区域的地物表面相对平滑，其散射机制大多为不同程度的布拉格表面散射，因此这种粗糙度带来的差异性不足以用来对潮间带区域的地物分类。
基于上述分析，本文优选极化熵H和反熵A来进行潮间带的分类，其中H为主要特征，A则作为补充。
2.3 极化熵的统计特性分析与混合GEV模型
极化熵是一种对极化散射机制随机性的衡量。然而，对于中等分辨率(如Radarsat-2全极化模式分辨率为8 m)图像，一个像素点中可能包含多种地物，即有着较强的散射随机性，意味着比较高的极化熵值，当散射随机性很强时，极化熵值趋近于1，接近噪声水平。在潮间带中，虽然总体上来说其极化熵值不是很高，但是部分露出水面的植被以及金属隔离网区域有着较强的散射随机性会产生接近于1的极高熵值。这些高熵值在极化熵图像的统计直方图中导致一种long-tails现象。long-tails现象是风险预测或者灾害预警等极端事件研究中的重点，包括“左拖尾(厚尾)”和“右拖尾(薄尾)”[27]。对于这两种现象，传统的统计分布模型例如高斯分布模型或者Gamma分布模型难以给出好的拟合效果[25]。而常用的一些描述long-tails现象的模型，包括广义Gamma分布和k分布，均对“右拖尾”有较好的描述能力，但是不能很好地适应“左拖尾”。而且，k分布是基于乘性噪声模型提出，仅适用于均匀区域和弱纹理区域，对于极化熵图像不太适用[26]。极值理论方面的研究表明，GEV分布可以很好地描述有极端事件发生的随机过程。在近年来的研究中GEV分布已经被大量地用在SAR图像对特殊目标的分析中[3,20,25]。其中Eun-Sung的论文中对比了广义Gamma分布族中的Weibull分布和log-normal分布，证明了GEV分布能够更好地描述水下养殖等类似区域[3]。因此本文采用GEV来描述潮间带区域的极化熵图像。GEV分布是一族连续的极值概率分布，并且具有有限分布和稳定的特性。GEV分布的概率密度函数如式(10)所示：
gev(x,μ,σ,ξ)={e−(ξx−μσ+1)−1/ξ(ξx−μσ+1)−1−1/ξσ,ξx−μσ+1>0, σ>0, ξ≠0e−(x−μσ)−e−(x−μσ)σ,σ>0, ξ=0 (10) GEV分布的参数有3个：即形状参数 ξ，尺度参数σ和位置参数μ。图2中给出了对于不同 ξ下的GEV分布的形态，其中 ξ分别为–0.5, 0, 0.5, σ和μ均为0.1和0.5。当 ξ等于0时为Gumbel分布，当 ξ大于0时为Weibull分布，而当 ξ小于0时为Frechet分布。其中Weibull描述的是一种“右拖尾分布”，Frechet描述的是一种“左拖尾分布”[27]，而Gumbel分布为两者之间的过渡。因此，GEV分布对long-tails有着广泛的适应性以及较好的描述能力。
通过上面的分析可以得出，GEV分布能够较好地描述潮间带区域的极化熵图像。由于单个概率分布只有一个峰值，而对于潮间带区域，多种地物必然会导致多个峰值的出现。因此基于GEV分布，可以通过建立一个有限混合模型(Finite Mixture Model, FMM)来实现对潮间带的地物分类。有限混合GEV模型(GEV Mixture Models, GEVMM)n个GEV分布的线性叠加，其定义如式(11)所示：
f(x;ξ,σ,μ)=n∑i=1aifi(x;ξi,σi,μi) (11) 其中，n为GEV分布的个数，在潮间带地物分类中代表着潮间带的地物种类，fi(·)代表着第i个种地物所服从的GEV分布。
2.4 基于GEV模型的分类方法
对于潮间带区域的极化熵图像H的地物分类可以分为两个步骤：首先是GEV混合模型的计算，然后将模型映射到图像空间中实现分类。其中最重要的一步是GEVMM的计算。本文以EM算法为基础，来实现对GEVMM的构建。
EM算法是一种极大似然估计算法，以迭代的方式来实现对模型的估计。算法的每一次迭代都是由E步(求期望)和M步(将期望最大化)构成[28]。在本文中，首先给定类别个数和参数的初始值，然后在E步，依照当前模型参数，计算分模型i对图像中每个点xj的响应度 ˆγji，其计算公式为：
ˆγji=aifi(xj;ξi,σi,μi|θi)n∑iaifi(xj;ξi,σi,μi|θi) (12) 其中，j为样本标记，i为类别标记，式中θi指在第i个分模型。在M步中，我们先根据响应度大小对图像像素进行归类，然后用最小二乘法估计出每个分模型的参数[29]。实验中最小二乘法估计通过MATLAB函数gevfit实现。如此迭代，直到参数收敛。
另一方面，传统的FMM进行模型估计时分模型个数是固定的，难以适应不同的地物类型的特征值分布。因此，本文采用了自适应的的GEVMM估计方法。在迭代的过程中，如果对某一个类别产生最大响应的点的数目少于某个阈值时，该类别即认为无意义并删除。在本文的实验中，这个阈值被设为50。迭代收敛后得到GEVMM以及其中的各个分量，然后通过计算图像中的每个点对模型各分量的响应度，得到一个分类标记图。
反熵作为极化熵的补充，其在高于0.7时采用较好的识别能力[26]。因此可以通过0.7这个阈值对反熵图像进行阈值分割，实现二值分类。基于此，本文通过将两个特征得到的结果进行融合，更好地实现潮间带的地物分类。假设极化熵得到的M类集合为 {A1,A2,⋅⋅⋅,AM}，反熵得到的两类为 {B1,B2}，融合算法要处理的集合为各类的交集，即：
C={Ai∩Bj,Ai∩Bj≠∅,i∈[1,M],j∈[1,2]} (13) 对于C中的每一个像素x，分别计算其对Ai与Bj的从属度 mx(Ai)和 mx(Bj)：
mx(Ai)=|H(x)−xAi| (14) mx(Bj)=|A(x)−xBj| (15) 其中，H(x)为极化熵在x位置的值， xAi为极化熵图像中 Ai类所有像素的均值，即类别中心。同理， A(x)为反熵在x位置的值， xBj为反熵图像中 Bj类所有像素的均值。本文中采用如下准则来对交集C进行判决：如果 ∑x∈Cmx(Ai)>∑x∈Cmx(Bj)，那么C属于Ai类，反之C属于Bj类。这样就实现了分类结果的融合。
GEVMM的构建流程以及图像分类算法流程如图3所示。
3. 实验与分析
基于本文的方法，利用Radarsat-2卫星的全极化数据进行了实验验证，实验数据的分辨率为8 m。研究区域位于上海崇明岛东滩潮间带，其卫星数据获取时间为2015年5月16日，此时的潮水处于低潮状态。图4描述了实验区域，其中图4(a)给出了整幅数据的Pauli伪彩色图像，其中的黄色矩形框代表着我们选定的实验区域，大小为20.0 km×5.6 km。数据获取时的实验区域的实时状态如图4(b)所示，从近到远依次是低矮植被区域，淤泥滩以及露出水面的水产养殖场的隔离网。
实验中，本文首先基于实测数据对潮间带区域的极化特征进行目视解译与定量衡量来佐证前面的分析；然后基于所示的流程对潮间带进行地物分类；最后利用PolSAR Pro软件对研究区域进行Wishart-H/A/α分类，并和本文方法的实验结果进行对比和分析。
3.1 基于实测数据的极化特征分析
图5给出了图4(a)黄框所示的研究区域的极化特征。基于上面的分析，下面结合实地考察结果以及图4(a)中所示的Pauli伪彩色图对4个特征进行目视解译。在图5(a)所示的Span影像中，我们可以识别出潮间带的大致轮廓以及金属隔离网等，但是潮间带内部细节的识别能力较差，并且潮间带和海洋的边界比较模糊。图5(b)给出了极化熵图像，从图中我们可以识别出海面，以及潮间带中的淤泥滩，草地以及暗色的残留水体等，并且和海面的区分较为显著，但是对金属隔离网的识别能力较差。图5(c)中的反熵可以很好地识别金属隔离网，但是无法识别出其他地物。而对于图5(d)，平均散射角可以对潮间带区域中的地物进行一定的识别，但是不能很好地区分海面和潮间带中的水产养殖。对比Span、极化熵、反熵和平均散射角4张图，可以发现极化熵可以对除去金属隔离网之外的地物有着最好的视觉判别而反熵作为补充可以很好地识别出金属隔离网区域。因此，极化熵结合反熵，可以给出最好的视觉判别效果。
为了进一步地佐证，本文采用Michelson对比度准则来衡量上述图像的类间对比度(between-region contrast)[30]。 Michelson准则是一种经典的图像衡量标准，并且广泛地用在SAR图像评价中[3,31]。其定义如下：
C=Fmax−FminFmax+Fmin (16) 其中，Fmax和Fmin分别为图像的最大值和最小值。对比度值C位于[0, 1]区间。一般来说，C越高，对比度越强，区分能力也越强。表1给出了4个极化特征的类间对比度，从表中可以看出，反熵拥有最高的对比度值，极化熵的对比度紧随其后且高于其他两个特征。从前面的分析中可以得知，反熵对高熵部分响应强烈并且抑制了低熵部分的值，导致了较高的对比度值，也确保了其对潮间带的高熵部分的识别能力。从图5(c)可以看出，反熵对于具有高熵值的金属隔离网有着很好的区分能力，但是对其他低熵区域，区分能力很差。极化熵有着第二高的对比度值，从图5(b)中也可以看出极化熵对整个潮间带区域的细节有着很好的描述以及较好的区分能力。平均散射角α的对比度低于极化熵，从图5(d)中也可以看出其对潮间带的细节有一定的描述能力，但是无论是边缘的清晰度还是Michelson对比度都明显弱于极化熵。而Span图像在视觉判别能力和对比度方面表现最差。综上所述，极化熵和反熵的组合可以对潮间带区域地物进行很好的区分。
表 1 各极化特征的Michelson类间对比度Table 1. Michelson between-region contrast of different features极化特征 类间对比度 Span 0.4092 Entropy 0.7703 Anisotropy 0.9959 α 0.6757 3.2 基于GEVMM的极化熵统计建模
基于图5(b)所示的极化熵图像，我们按照图3所示的流程进行GEVMM建模和地物分类。在GEVMM构建中，根据实地考察结果结合极化熵图像我们初始指定模型的分量数目为8，经过迭代收敛后得到的模型中有5个分量，图6(f)给出了最终的GEVMM和极化熵直方图以及模型中各分量的图示。为了确保GEVMM的优越性，本文用Gamma分布和log-normal分布分别来拟合GEVMM得到的标记图中对应的每种类别的归一化直方图，与GEVMM的各个分量的拟合效果进行对比，如图6(a)–图6(e)所示。图6(a)–图6(e)展示了拟合对比结果，其中蓝色部分为各类别的直方图，绿线代表GEVMM的对应分量拟合结果，黑线代表Gamma模型拟合结果，红线代表了log-normal模型拟合结果。可以看出，GEV分布可以很好地拟合图6(d)和图6(e)两图的“左拖尾现象”，明显优于其他两种模型。同样，图6(b)中GEV分布的拟合效果也明显优于其他两种分布。
图 6 GEVMM及其各分量与Gamma分布和log-normal分布的对比：(a)–(e)分别为5个分量与Gamma分布，log-normal分布以及对应标记区域的直方图的对比，其中蓝色区域为归一化直方图，绿线是GEV拟合结果，黑线是Gamma拟合结果，红线是log-normal拟合结果，(f)给出了GEVMM及其各个分量与研究区域直方图的对比结果，其中蓝线为归一化直方图，红线为GEVMM，绿线为GEVMM的各个分量Figure 6. Fitness comparison among GEV distribution and Gamma distribution and Log-normal distribution of each component in GEVMM: (a)–(e) represent the five components of the GEVMM and the fitting results by the Gamma distribution and log-normal distribution for the histograms, which are marked as blue, the green lines represent the GEV fitting results, the black lines represent the most fitted Gamma distribution and the red lines represent the most fitted log-normal distribution, (f) shows the five components of GEVMN as green lines and the respective histograms as blue lines, the red line represents the final model为了进一步确认GEVMM的准确性，本文采用赤池信息量准则(Akaike Information Criterion, AIC)对各个模型进行衡量[32]。AIC准则的定义如下：
AIC=2k−2Ln (17) 其中，k为参数个数，n为样本个数，L为对数相似度(log likelihood)。对数相似度的定义如下：
L=−n2ln(2π)−n2ln(ssen)−n2 (18) 其中，sse为直方图和拟合结果之间的残差和。对于AIC准则来说，k越小或者L越大，AIC的值越小，模型的正确性也越高。其中k越小，模型越简洁，而L越大，模型越准确。表2给出了3种分布在每个类别对应的AIC值，可以看出GEV分布明显优于其他两种分布。结合图6和表2，可以得出GEV分布模型有着最好的拟合能力。另外，最终得到的GEVMM和统计直方图之间的AIC值为4.0661，也说明了模型的有效性。
表 2 GEV分布，Gamma分布和log-normal分布在每种类别中的拟合结果的AIC值Table 2. The AIC values of the fitting results between the GEV distribution, the Gamma distribution and log-normal distributionAIC 1 2 3 4 5 GEV 6.3988 4.0095 4.1105 4.7009 6.2093 Gamma 11.3878 9.3573 7.6928 9.0210 8.3989 log-normal 11.3878 9.3573 7.6928 9.0213 8.3997 3.3 地物分类结果与分析
图7展示了地物分类实验结果，其中图7(a)给出了研究区域的Pauli伪彩色图。基于极化熵的GEVMM得到的图像分类标记图如图7(b)所示，通过融合图7(c)给出的反熵的分割结果，得到的最终分类结果如图7(d)所示。图7(e)给出了Wishart-H/A/α方法的分类结果。研究区域真值图如图7(f)所示，其中蓝色为海洋区域，浅蓝色和浅绿色区域分别为潮间带中的水下养殖与残留水体，黄色和棕黄色代表植被散射区域和淤泥滩，深红色代表金属隔离网。
对比发现极化熵得到的结果可以很好地识别出潮间带区域的大多地物类型，与真值较为一致，但是该图中地物只是分为5类，不能很好地识别出图7(f)中深红色的金属隔离网区域。而在图7(c)的反熵的阈值分割结果可以较好地提取出金属隔离网区域。图7(d)中融合后得到的分类结果和真值图相比有较为一致分类效果，并优于图7(b)和图7(c)的结果。而图7(e)所示的Wishart-H/A/α的分类结果和真值图有着较大的不同。在研究区域，图7(e)只能将金属隔离网区域和其他地物区分，对于潮间带的其他5类，均不具备较好的区分度，并且潮间带区域和海洋区域未能进行很好地区分。
针对本文提出的方法和Wishart-H/A/α分类方法，实验中采用Kappa系数来衡量两种方法的分类效果。结合真值数据，两种方法的Kappa系数分别为0.9019和0.3662，总体分类精度分别为0.8912和0.3712，也验证了本文方法的准确性。可见，在潮间带区域的地物分类中，本文的方法要优于Wishart-H/A/α分类。
4. 结束语
针对潮间带区域的地物分类问题，本文提出了结合极化熵和反熵的潮间带地物分类方法。基于极化熵图像，本文对潮间带区域建立GEVMM。在此基础上通过和反熵的信息融合得到最终的分类结果。实验中利用C波段Radarsat-2全极化数据实现了对上海崇明岛东滩潮间带区域的地物分类。对比真值图，本文方法可以给出较好目视结果并优于Wishart-H/A/α方法。最后的定量分析证明本文方法具有较好的准确性。
-
图 5 方向图与阵列构型关系示意
Figure 5. Illustration of the relationship between array geometry and beam pattern
图 8 平台运动控制精度与相参合成效率的关系
Figure 8. Impact of platform control errors on coherent efficiency
图 13 原子钟频率随时间变化情况
Figure 13. Relationship between the frequency of the atomic clock and the time
表 1 相参参数估计仿真参数
Table 1. Simulation parameters of CPs estimation
参数 数值 节点数目 2 信号波形 正负线性调频信号 节点初始位置 [0, 0; 0, 50] m 发射中心频率 300 MHz 发射带宽 10 MHz 脉冲重复频率 2000 Hz 仿真持续时间 1 s 节点运动速度 [0, 10] m/s 目标初始位置 [ 10000 ,8000 ] m目标运动速度 [–200, 0] m/s 初始内部相位误差 0° 
下载: 导出CSV
表 2 角度估计主要仿真参数
Table 2. Simulation parameters of angle estimation
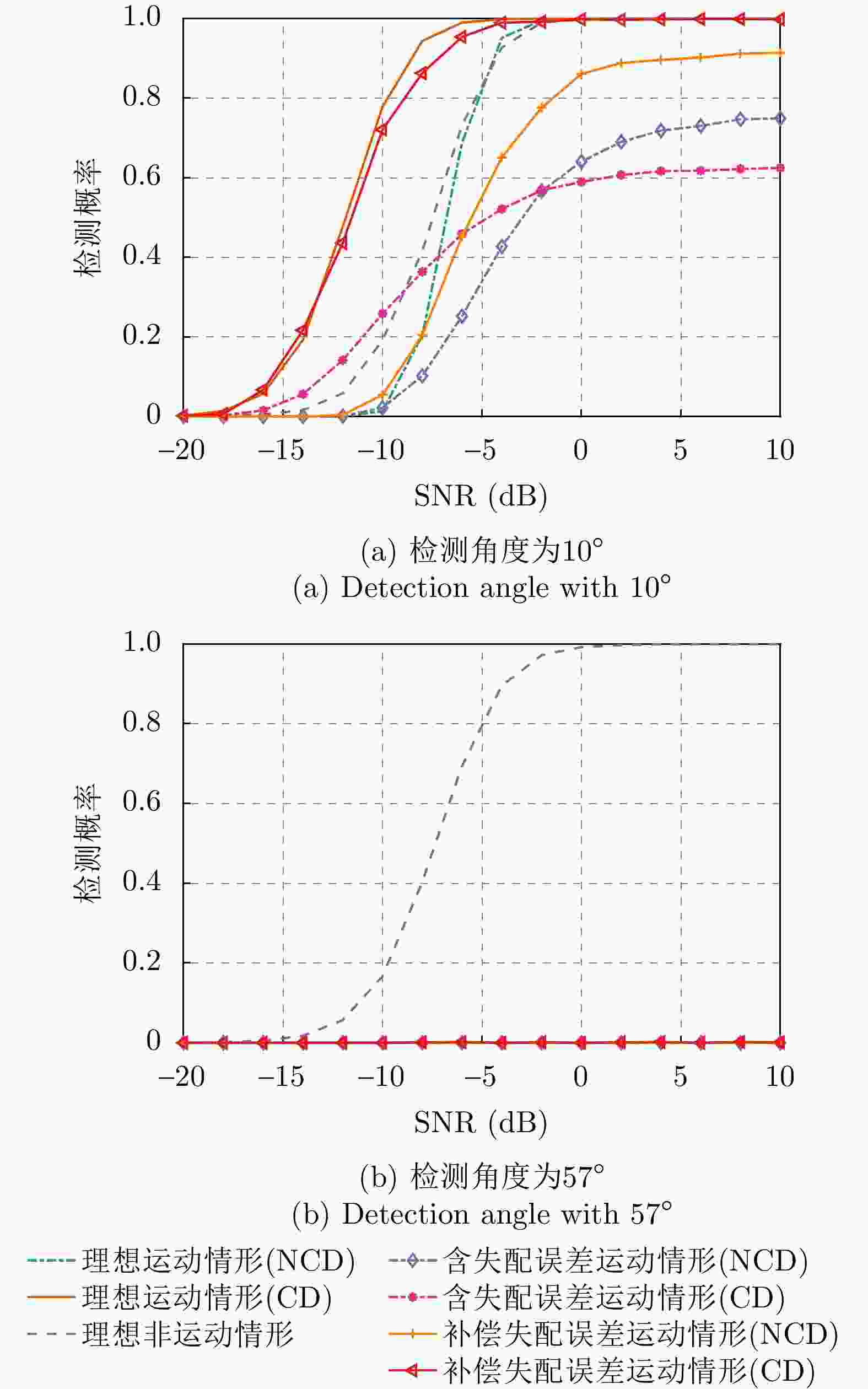
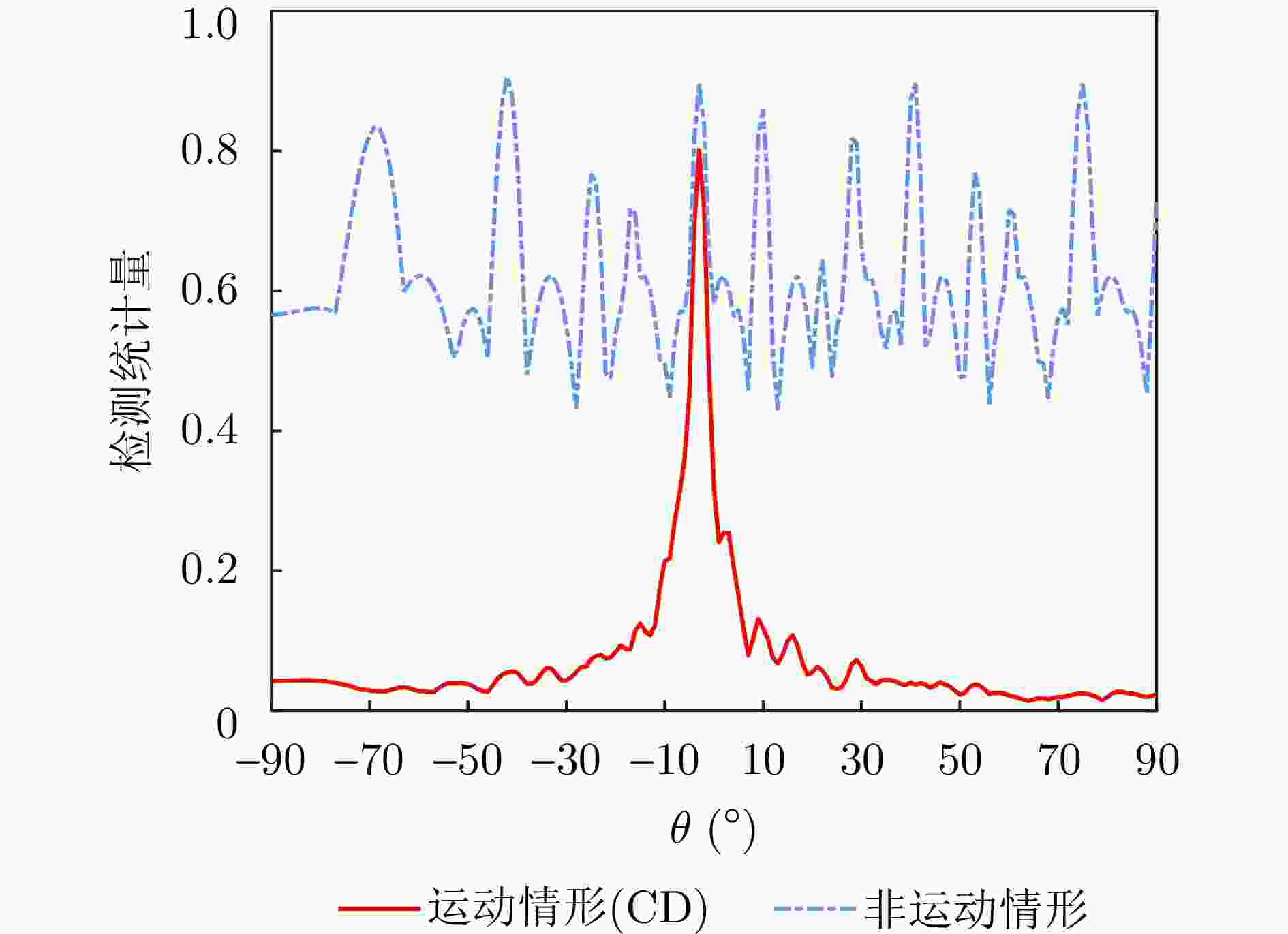
参数 数值 节点数目 3 节点初始位置 [0, 0; 0, 1.5; 0, 3.0] m 发射中心频率 300 MHz 节点运动速度(相参情形) [0, 10; 0, 10; 0, 10] m/s 节点运动速度(非相参情形) [0, 10; 0, 20; 0, 30] m/s 脉冲重复间隔 25 ms 目标角度 10° 所用脉冲个数 3
下载: 导出CSV
表 3 雷达参数
Table 3. Radar parameters
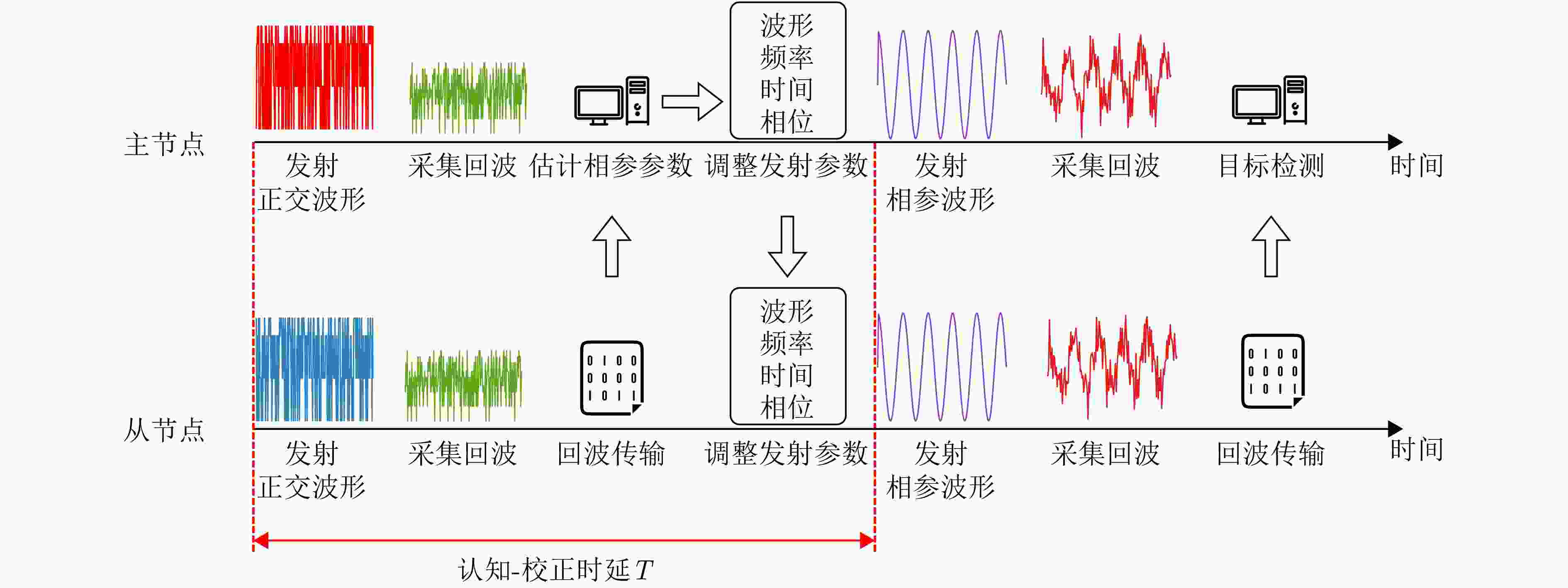
参数 数值 节点数目 3 发射中心频率 230 MHz 信号带宽 1 MHz 脉冲宽度 30 μs 脉冲重复频率 2000 Hz 认知-校正时延 0.5 s
下载: 导出CSV
-
[1] CUOMO K M, COUTTS S D, MCHARG J C, et al. Wideband aperture coherence processing for next generation radar (NexGen)[R]. MIT Lincoln Laboratory Report NG-3, 2004. [2] 鲁耀兵, 高红卫. 分布孔径雷达[M]. 北京: 国防工业出版社, 2017: 216–217.LU Yaobing and GAO Hongwei. Distributed Aperture Radar[M]. Beijing: National Defense Industry Press, 2017: 216–217. [3] KORDIK A M, METCALF J G, CURTIS D D, et al. Graceful performance degradation and improved error tolerance via mixed-mode distributed coherent radar[J]. IEEE Sensors Journal, 2023, 23(5): 5251–5262. doi: 10.1109/JSEN.2023.3236487. [4] NANZER J A, MGHABGHAB S R, ELLISON S M, et al. Distributed phased arrays: Challenges and recent advances[J]. IEEE Transactions on Microwave Theory and Techniques, 2021, 69(11): 4893–4907. doi: 10.1109/TMTT.2021.3092401. [5] 刘泉华, 张凯翔, 梁振楠, 等. 地基分布式相参雷达技术研究综述[J]. 信号处理, 2022, 38(12): 2443–2459. doi: 10.16798/j.issn.1003-0530.2022.12.001.LIU Quanhua, ZHANG Kaixiang, LIANG Zhennan, et al. Research overview of ground-based distributed coherent aperture radar[J]. Journal of Signal Processing, 2022, 38(12): 2443–2459. doi: 10.16798/j.issn.1003-0530.2022.12.001. [6] 刘兴华, 王国玉, 徐振海, 等. 分布式孔径相参合成原理、发展与技术实现综述[J]. 雷达学报, 2023, 12(6): 1229–1248. doi: 10.12000/JR23195.LIU Xinghua, WANG Guoyu, XU Zhenhai, et al. Review of principles, development and technical implementation of coherently combining distributed apertures[J]. Journal of Radars, 2023, 12(6): 1229–1248. doi: 10.12000/JR23195. [7] 卢佳欣, 刘飞峰, 缪颖杰, 等. 动平台分布式相参雷达系统分析[J]. 信号处理, 2019, 35(5): 825–830. doi: 10.16798/j.issn.1003-0530.2019.05.013.LU Jiaxin, LIU Feifeng, MIAO Yingjie, et al. Analysis on distributed coherent radar system with moving platforms[J]. Journal of Signal Processing, 2019, 35(5): 825–830. doi: 10.16798/j.issn.1003-0530.2019.05.013. [8] MUDUMBAI R, BARRIAC G, and MADHOW U. On the feasibility of distributed beamforming in wireless networks[J]. IEEE Transactions on Wireless Communications, 2007, 6(5): 1754–1763. doi: 10.1109/TWC.2007.360377. [9] GAO Hongwei, ZHOU Baoliang, ZHOU Dongming, et al. Performance analysis and experimental study on distributed aperture coherence-synthetic radar[C]. 2016 CIE International Conference on Radar, Guangzhou, China, 2016: 1–5. doi: 10.1109/RADAR.2016.8059191. [10] SUN Palin, TANG Jun, HE Qian, et al. Cramer-Rao bound of parameters estimation and coherence performance for next generation radar[J]. IET Radar, Sonar & Navigation, 2013, 7(5): 553–567. doi: 10.1049/iet-rsn.2012.0139. [11] 宋靖, 周青松, 张剑云. 基于相关法的分布式全相参雷达相干参数估计及相参性能[J]. 电子与信息学报, 2015, 37(7): 1710–1715. doi: 10.11999/JEIT141339.SONG Jing, ZHOU Qingsong, and ZHANG Jianyun. Coherent parameters estimation by cross-correlation for distributed aperture fully coherent radar[J]. Journal of Electronics & Information Technology, 2015, 37(7): 1710–1715. doi: 10.11999/JEIT141339. [12] 张洪纲, 雷子健, 刘泉华. 基于MUSIC法的宽带分布式全相参雷达相参参数估计方法[J]. 信号处理, 2015, 31(2): 208–214. doi: 10.3969/j.issn.1003-0530.2015.02.011.ZHANG Honggang, LEI Zijian, and LIU Quanhua. Coherent parameters estimation method based on MUSIC in wideband distributed coherent aperture radar[J]. Journal of Signal Processing, 2015, 31(2): 208–214. doi: 10.3969/j.issn.1003-0530.2015.02.011. [13] 刘兴华, 徐振海, 王罗胜斌, 等. 基于信号重建的分布式相参雷达相参参数估计算法[J]. 系统工程与电子技术, 2018, 40(9): 1931–1938. doi: 10.3969/j.issn.1001-506X.2018.09.06.LIU Xinghua, XU Zhenhai, WANG Luoshengbin, et al. Coherent parameters estimation algorithm for distributed coherent aperture radar based on signal reconstruction[J]. Systems Engineering and Electronics, 2018, 40(9): 1931–1938. doi: 10.3969/j.issn.1001-506X.2018.09.06. [14] LIU Xinghua, XU Zhenhai, LIU Xiang, et al. A clean signal reconstruction approach for coherently combining multiple radars[J]. EURASIP Journal on Advances in Signal Processing, 2018, 2018(1): 47. doi: 10.1186/s13634-018-0569-1. [15] 殷丕磊, 张洪纲, 翟腾普, 等. 基于Kalman滤波的分布式全相参雷达相参参数估计方法[J]. 北京理工大学学报, 2016, 36(3): 282–288. doi: 10.15918/j.tbit1001-0645.2016.03.012.YIN Pilei, ZHANG Honggang, ZHAI Tengpu, et al. Coherent parameters estimation using Kalman filter in distributed coherent aperture radar[J]. Transactions of Beijing Institute of Technology, 2016, 36(3): 282–288. doi: 10.15918/j.tbit1001-0645.2016.03.012. [16] LIU Xinghua, XU Zhenhai, WANG Luoshengbin, et al. Dual-radar coherently combining: Generalised paradigm and verification example[J]. IET Radar, Sonar & Navigation, 2019, 13(5): 689–699. doi: 10.1049/iet-rsn.2018.5089. [17] 陈金铭, 王彤, 吴建新, 等. 基于特显点的机载分布式相参雷达同步误差校正方法[J]. 电子与信息学报, 2021, 43(2): 356–363. doi: 10.11999/JEIT190694.CHEN Jinming, WANG Tong, WU Jianxin, et al. Airborne distributed coherent aperture radar synchronization error calibration method based on prominent points[J]. Journal of Electronics & Information Technology, 2021, 43(2): 356–363. doi: 10.11999/JEIT190694. [18] CHEN Jinming, WANG Tong, LIU Xiaoyu, et al. Time and phase synchronization using clutter observations in airborne distributed coherent aperture radars[J]. Chinese Journal of Aeronautics, 2022, 35(3): 432–449. doi: 10.1016/j.cja.2021.08.040. [19] CHEN Jinming, WANG Tong, LIU Xiaoyu, et al. Identifiability analysis of positioning and synchronization errors in airborne distributed coherence aperture radars[J]. IEEE Sensors Journal, 2022, 22(6): 5978–5993. doi: 10.1109/JSEN.2022.3144481. [20] LIU Xiaoyu, WANG Tong, CHEN Jinming, et al. Efficient configuration calibration using ground auxiliary receivers at inaccurate locations[J]. Digital Signal Processing, 2022, 129: 103675. doi: 10.1016/j.dsp.2022.103675. [21] ZHANG Yuxuan, WU Jianxin, and ZHANG Lei. Joint multierror calibration by merging errors in distributed coherent aperture radar using strong scatter echoes[J]. IEEE Transactions on Aerospace and Electronic Systems, 2024, 60(1): 1148–1158. doi: 10.1109/TAES.2023.3335186. [22] ZENG Tao, YIN Pilei, and LIU Quanhua. Wideband distributed coherent aperture radar based on stepped frequency signal: Theory and experimental results[J]. IET Radar, Sonar & Navigation, 2016, 10(4): 672–688. doi: 10.1049/iet-rsn.2015.0221. [23] WANG Yan, DING Zegang, LI Linghao, et al. First demonstration of single-pass distributed SAR tomographic imaging with a P-band UAV SAR prototype[J]. IEEE Transactions on Geoscience and Remote Sensing, 2022, 60: 5238618. doi: 10.1109/TGRS.2022.3221859. [24] LIU Ruitao, ZHANG Wei, YU Xianxiang, et al. Transmit-receive beamforming for distributed phased-MIMO radar system[J]. IEEE Transactions on Vehicular Technology, 2022, 71(2): 1439–1453. doi: 10.1109/TVT.2021.3133596. [25] FENG Bokai and DAVID C J. Two-way pattern grating lobe control for distributed digital subarray antennas[J]. IEEE Transactions on Antennas and Propagation, 2015, 63(10): 4375–4383. doi: 10.1109/TAP.2015.2465863. [26] MASSA A, ROCCA P, and OLIVERI G. Compressive sensing in electromagnetics—a review[J]. IEEE Antennas and Propagation Magazine, 2015, 57(1): 224–238. doi: 10.1109/MAP.2015.2397092. [27] LIU Yanhui, NIE Zaiping, and LIU Qinghuo. Reducing the number of elements in a linear antenna array by the matrix pencil method[J]. IEEE Transactions on Antennas and Propagation, 2008, 56(9): 2955–2962. doi: 10.1109/TAP.2008.928801. [28] LIU Yanhui, LIU Qinghuo and NIE Zaiping. Reducing the number of elements in multiple-pattern linear arrays by the extended matrix pencil methods[J]. IEEE Transactions on Antennas and Propagation, 2014, 62(2): 652–660. doi: 10.1109/TAP.2013.2292529. [29] PINCHERA D, MIGLIORE M D, and PANARIELLO G. Synthesis of large sparse arrays using IDEA (inflating-deflating exploration algorithm)[J]. IEEE Transactions on Antennas and Propagation, 2018, 66(9): 4658–4668. doi: 10.1109/TAP.2018.2846777. [30] YAN Chuang, YANG Peng, XING Zhiyu, et al. Synthesis of planar sparse arrays with minimum spacing constraint[J] IEEE Antennas and Wireless Propagation Letters, 2018, 17(6): 1095–1098. doi: 10.1109/LAWP.2018.2833962. [31] MOHAN A and RAJ A A B. Array thinning of Beamformers using simple genetic algorithm[C]. 2020 International Conference on Computational Intelligence for Smart Power System and Sustainable Energy, Keonjhar, India: IEEE, 2020: 1–4. doi: 10.1109/CISPSSE49931.2020.9212258. [32] OLIVERI G, ROCCA P, and MASSA A. Reliable diagnosis of large linear arrays-a Bayesian compressive sensing approach[J]. IEEE Transactions on Antennas and Propagation, 2012, 60(10): 4627–4636. doi: 10.1109/TAP.2012.2207344. [33] HU Liubo, WU Jianxin, and ZHANG Lei. Efficient transceiving search scheme and implementation method for collocated distributed coherent aperture radar via grating lobes exploitation[J]. Remote Sensing, 2023, 15(9): 2262. doi: 10.3390/rs15092262. [34] NANZER J A. Spatial filtering of grating lobes in mobile sparse arrays[C]. 2016 IEEE Radio and Wireless Symposium, Austin, USA: IEEE, 2016: 26–28. doi: 10.1109/RWS.2016.7444354. [35] CHATTERJEE P and NANZER J A. Using platform motion for improved spatial filtering in distributed antenna arrays[C]. 2018 IEEE Radio and Wireless Symposium, Anaheim, USA, 2018: 253–255. doi: 10.1109/RWS.2018.8305002. [36] WANG Yuanhao, YANG Qi, Wang Hongqiang, et al. Grating lobe suppression for distributed phased array via accumulated array pattern synthesis[J]. IEEE Antennas and Wireless Propagation Letters, 2023, 22(7): 1527–1531. doi: 10.1109/LAWP.2023.3249908. [37] MA Penghui, LI Jianfeng, PAN Jingjing, et al. Enhanced DOA estimation with augmented CADiS by exploiting array motion strategies[J]. IEEE Transactions on Vehicular Technology, 2023, 72(4): 4713–4727. doi: 10.1109/TVT.2022.3224908. [38] LUO Shuai, WANG Yuexian, LI Jianying, et al. Angle estimation for bistatic MIMO radar with a sparse moving array in the presence of position errors and gain-phase perturbation[J]. IEEE Transactions on Vehicular Technology, 2023, 72(12): 16006–16020. doi: 10.1109/TVT.2023.3294605. [39] 刘兴华, 徐振海, 肖顺平. 分布式相参雷达几何布置约束条件[J]. 系统工程与电子技术, 2017, 39(8): 1723–1731. doi: 10.3969/j.issn.1001-506X.2017.08.09.LIU Xinghua, XU Zhenhai, and XIAO Shunping. Geometric arrangement constraints of distributed coherent aperture radar[J]. Systems Engineering and Electronics, 2017, 39(8): 1723–1731. doi: 10.3969/j.issn.1001-506X.2017.08.09. [40] CHEN C C and ANDREWS H C. Target-motion-induced radar imaging[J]. IEEE Transactions on Aerospace and Electronic Systems, 1980, AES-16(1): 2–14. doi: 10.1109/TAES.1980.308873. [41] KELLY E J. An adaptive detection algorithm[J]. IEEE Transactions on Aerospace and Electronic Systems, 1986, AES-22(2): 115–127. doi: 10.1109/TAES.1986.310745. [42] XU Luzhou, LI Jian, and STOICA P. Target detection and parameter estimation for MIMO radar systems[J]. IEEE Transactions on Aerospace and Electronic Systems, 2008, 44(3): 927–939. doi: 10.1109/TAES.2008.4655353. [43] MGHABGHAB S and NANZER J A. Ranging requirements for open-loop coherent distributed arrays with wireless frequency synchronization[C]. 2020 IEEE USNC-CNC-URSI North American Radio Science Meeting, Montreal, Canada: IEEE, 2020: 69–70. doi: 10.23919/USNC/URSI49741.2020.9321643. [44] CHATTERJEE P and NANZER J A. Effects of time alignment errors in coherent distributed radar[C]. 2018 IEEE Radar Conference, Oklahoma City, USA, 2018: 727–731. doi: 10.1109/RADAR.2018.8378649. [45] CHALLA S, MORELANDE M R, MUŠICKID, et al. Fundamentals of Object Tracking[M]. Cambridge, UK: Cambridge University Press, 2011. doi: 10.1017/CBO9780511975837. 期刊类型引用(0)
其他类型引用(2)
-
下载:
计量
- 文章访问数: 344
- HTML全文浏览量: 199
- PDF下载量: 187
- 被引次数: 2
