面向毫米波动作识别的视觉辅助信道仿真技术

任振裕; 吉辰卿; 余潮; 陈万里; 王锐

doi:10.12000/JR24101

面向毫米波动作识别的视觉辅助信道仿真技术

DOI: 10.12000/JR24101

任振裕¹,
吉辰卿¹,
余潮¹,
陈万里^2, ,,
王锐^1, ,

1.
南方科技大学电子与电气工程系深圳 518055
2.
深圳技术大学深圳 518118

基金项目: 国家自然科学基金(62171213)，高水平专项资金(G030230001, G03034K004)

详细信息

作者简介:
任振裕，硕士生，主要研究方向为毫米波人体动作识别技术

吉辰卿，硕士生，主要研究方向为毫米波轨迹重构技术

余　潮，硕士，主要研究方向为通信感知一体化、毫米波被动感知

陈万里，高级实验师，主要研究方向为软件无线电通信、毫米波雷达技术、通信感知一体化技术

王　锐，博士，副教授，主要研究方向为通信系统的随机优化与资源调度、近似马尔可夫决策过程、智能无线感知技术

通讯作者:
陈万里 chenwanli@sztu.edu.cn

王锐 wang.r@sustech.edu.cn

责任主编：陈彦 Corresponding Editor: CHEN Yan
中图分类号: TN957.52
计量
- 文章访问数: 207
- HTML全文浏览量: 94
- PDF下载量: 31
- 被引次数: 0
出版历程
- 收稿日期: 2024-05-25
- 修回日期: 2024-08-26
- 网络出版日期: 2024-09-14

Computer Vision-assisted Wireless Channel Simulation for Millimeter Wave Human Motion Recognition

REN Zhenyu¹,
JI Chenqing¹,
YU Chao¹,
CHEN Wanli^{2
, ,},
WANG Rui^{1
, ,}

1.
Department of Electronic and Electrical Engineering, Southern University of Science and Technology (SUSTech), Shenzhen 518055, China
2.
Shenzhen Technology University, Shenzhen 518118, China

Funds: The National Natural Science Foundation of China (62171213), High Level of Special Funds (G030230001, G03034K004)

More Information

Corresponding author: CHEN Wanli, chenwanli@sztu.edu.cn; WANG Rui, wang.r@sustech.edu.cn

摘要

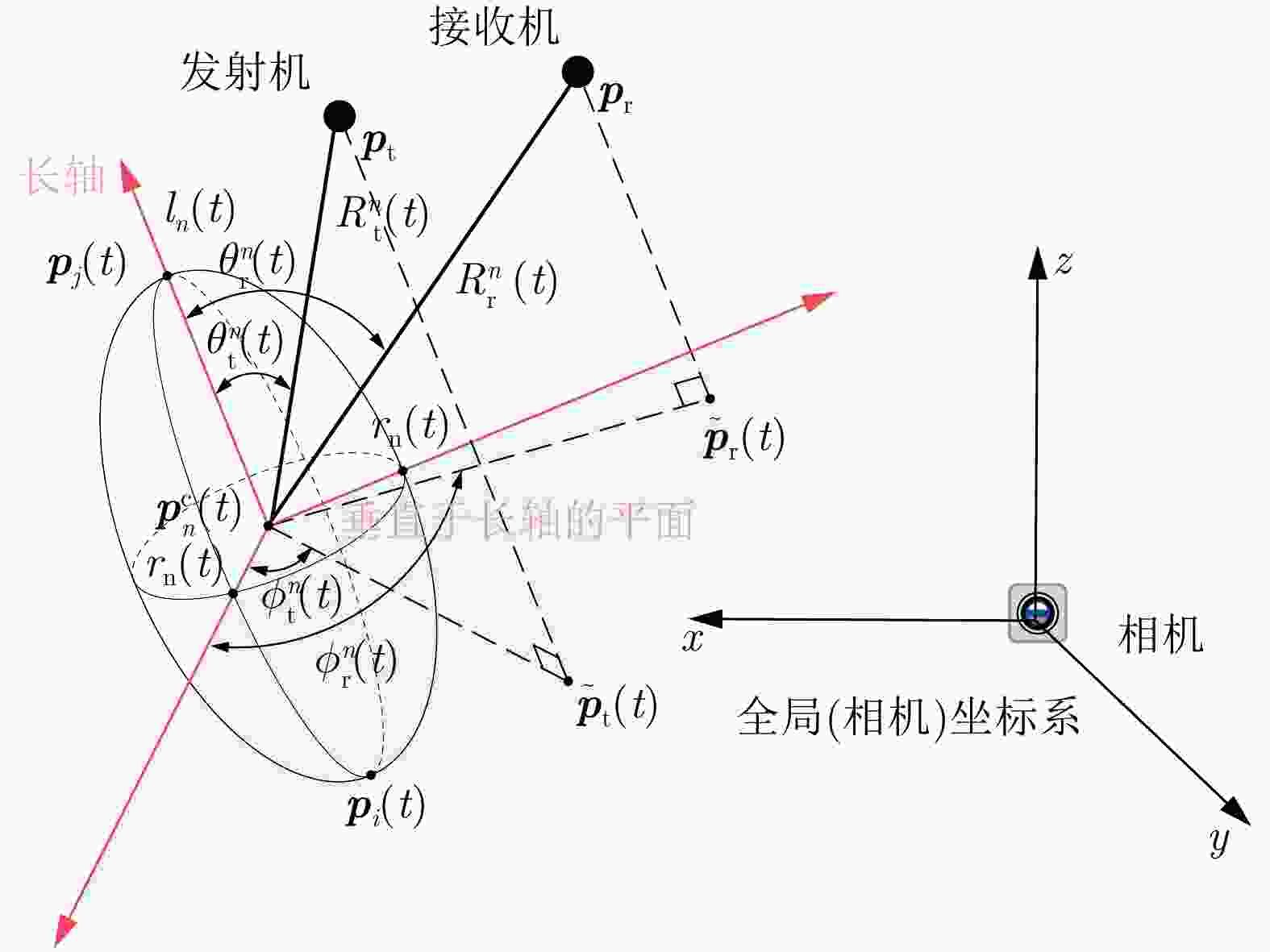
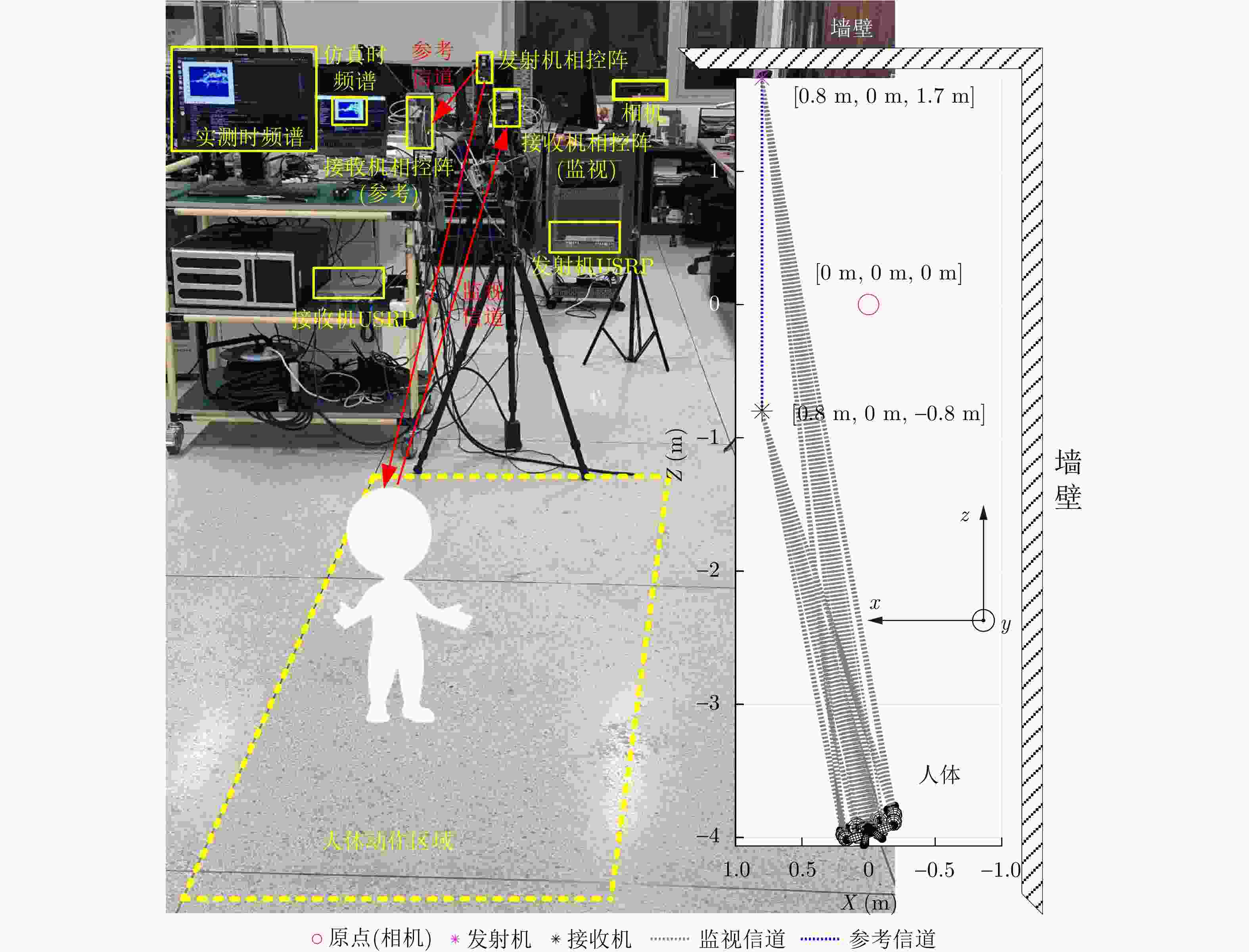
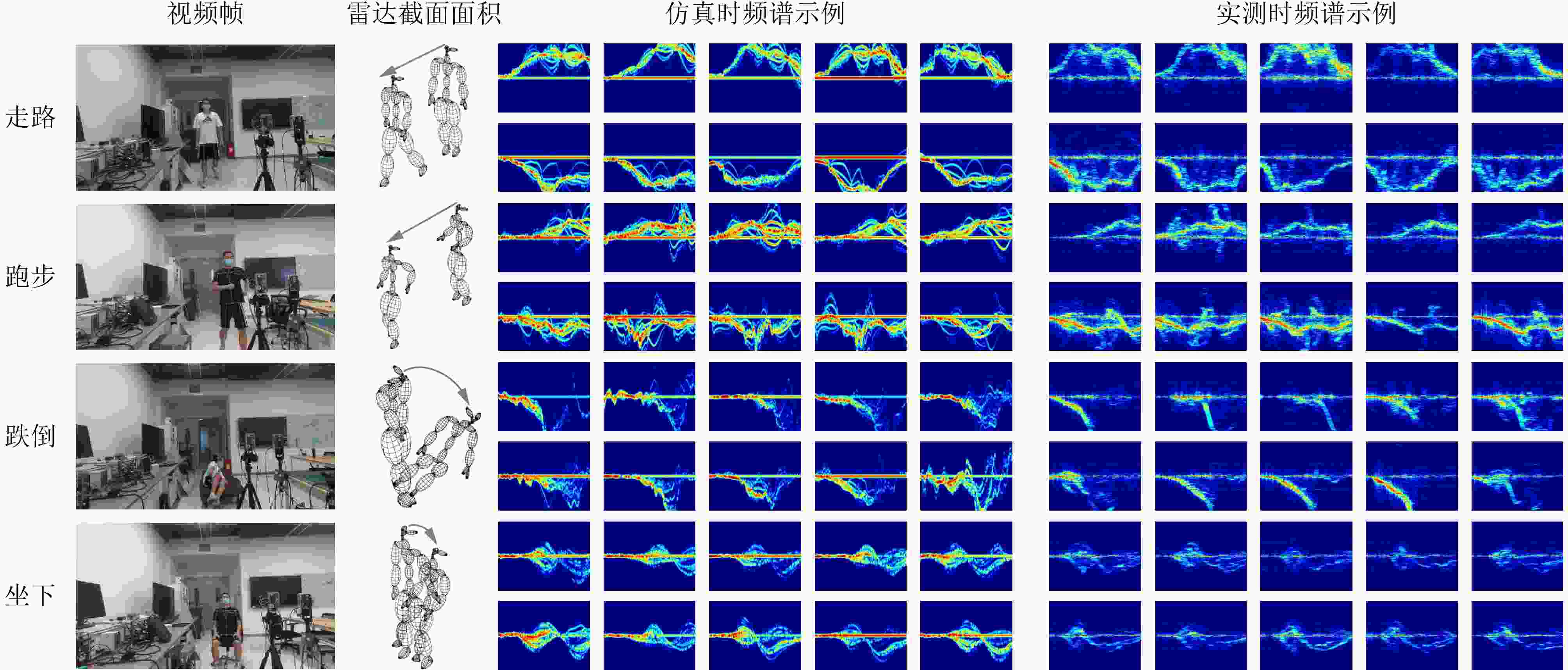
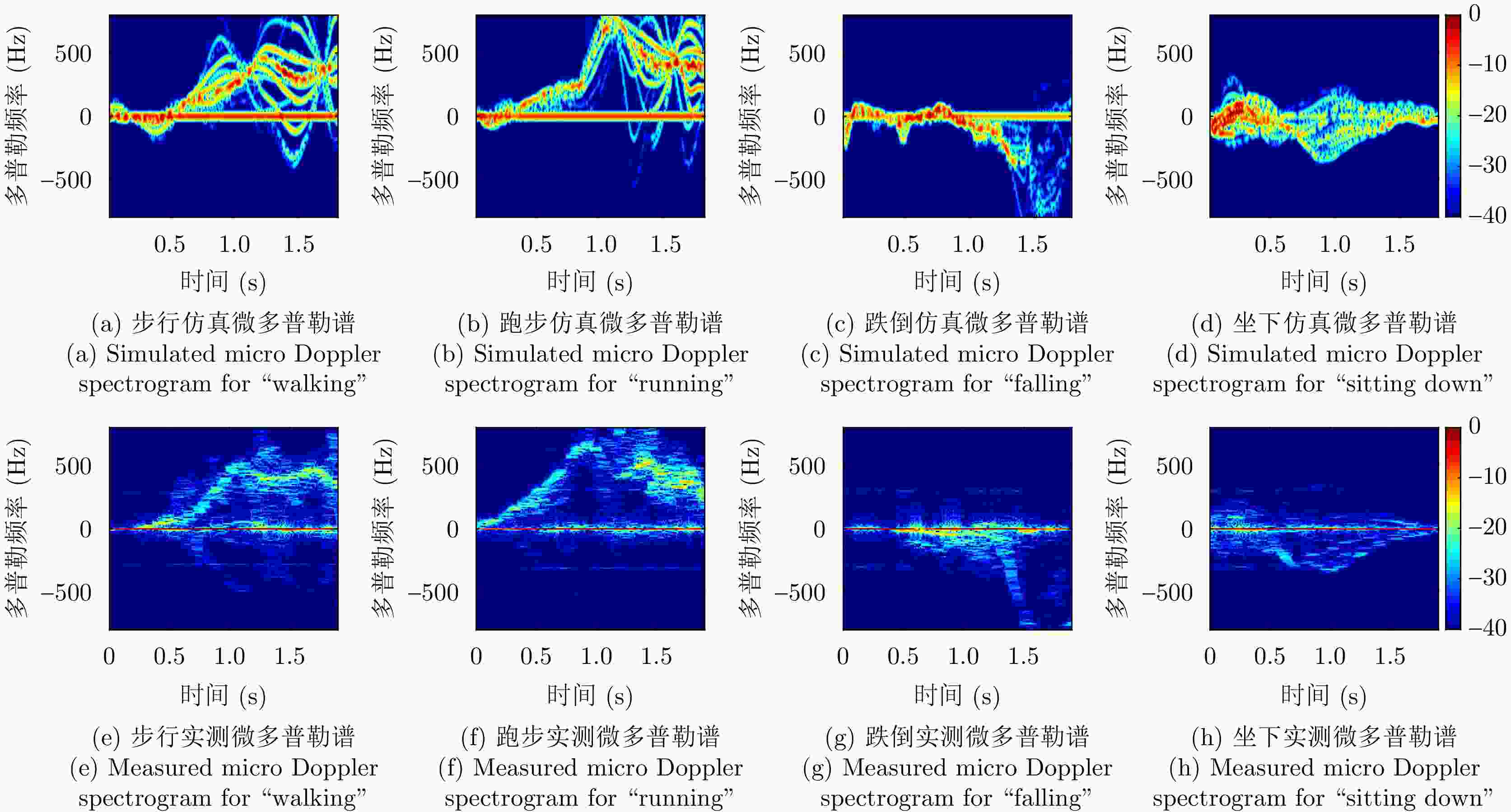
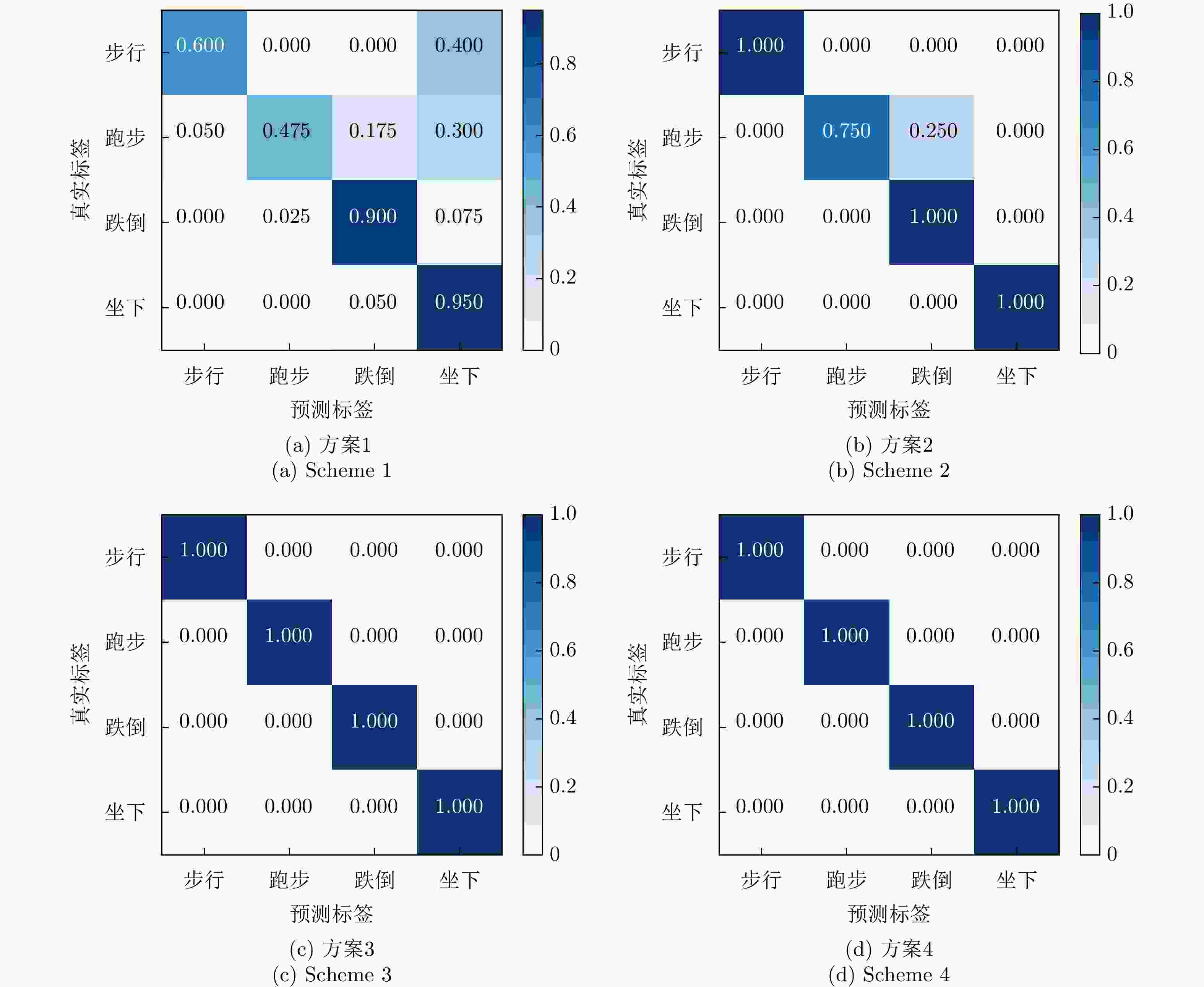
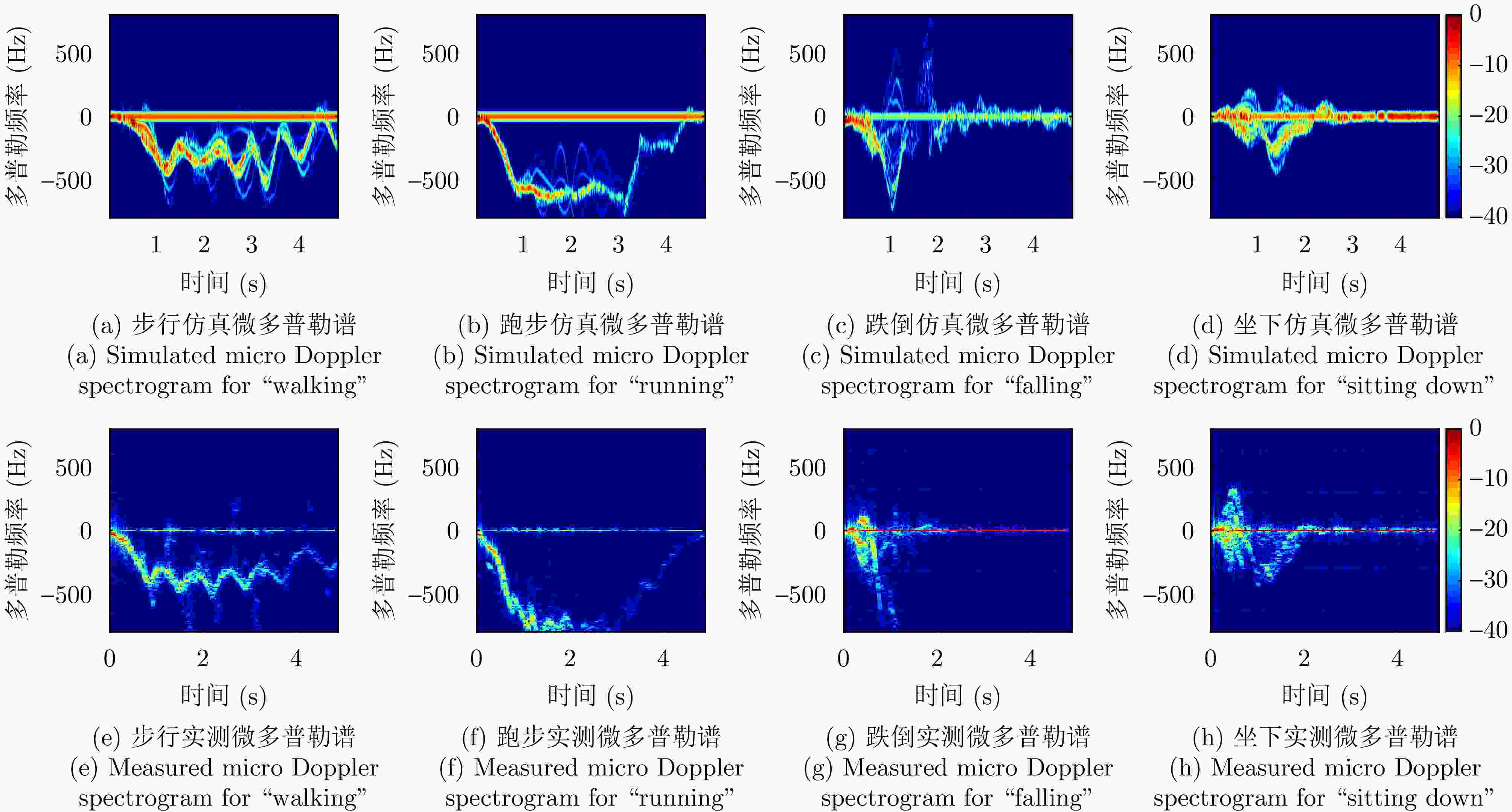
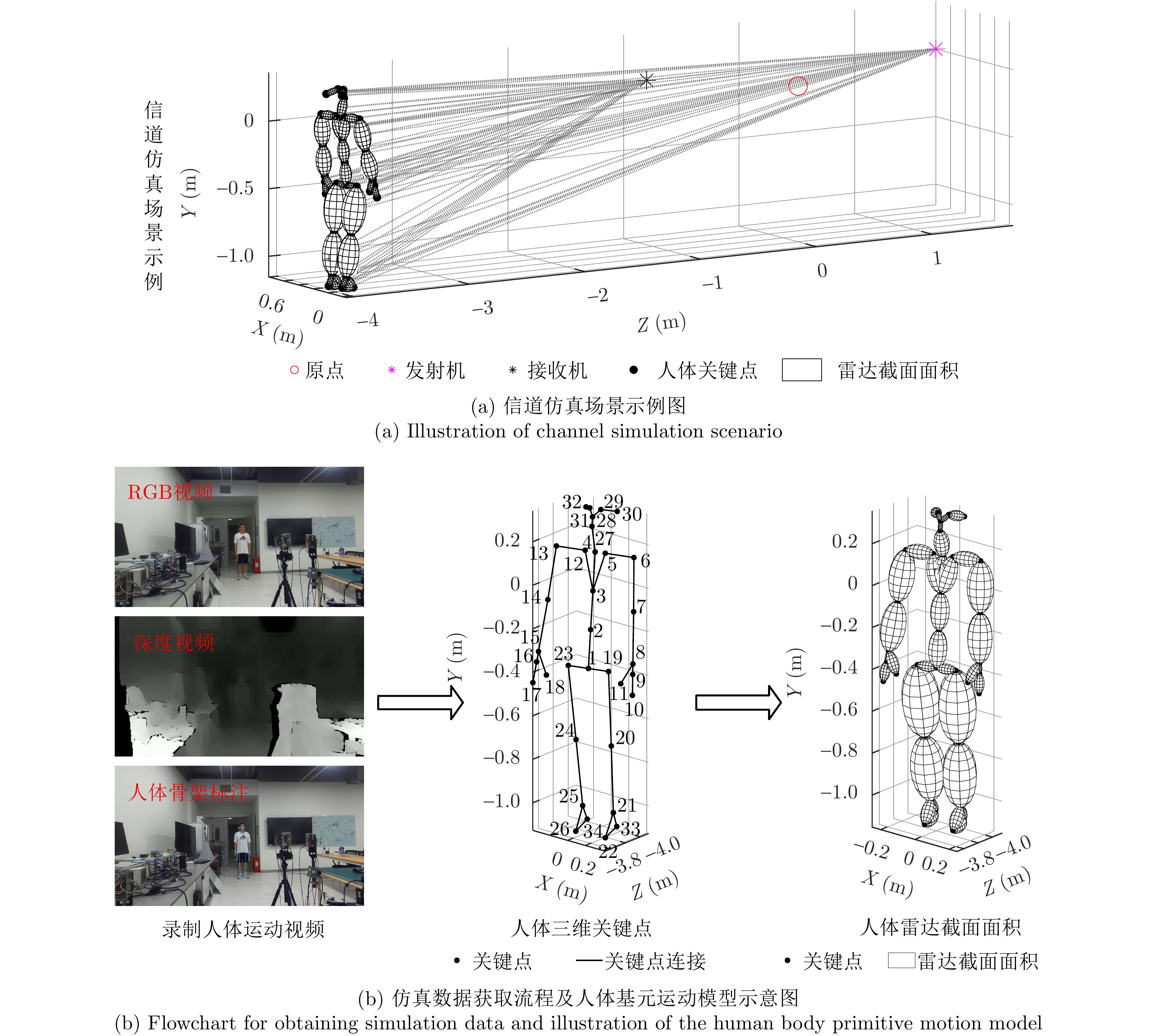
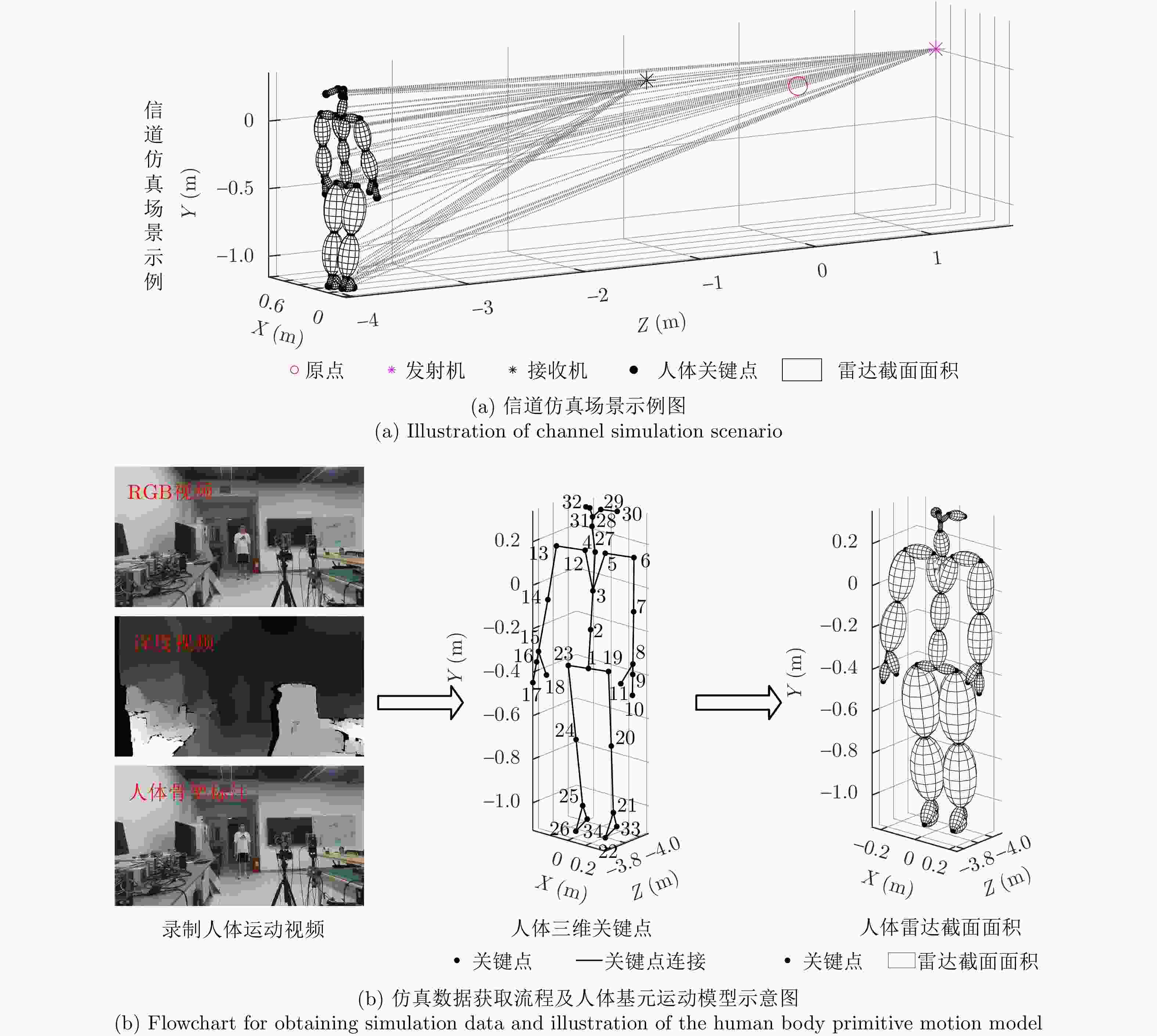
摘要: 该文提出了一种利用计算机视觉技术辅助实现包含运动人体散射特征的毫米波无线信道仿真方法。该方法旨在为毫米波无线人体动作识别场景之下，快速且低成本地生成仿真训练数据集，避免当前实测采集数据集的巨大开销。首先利用基元模型将人体建模为35个相互连接的椭球，并从包含人体动作的视频中提取出人体在进行对应动作时各个椭球的运动数据；其次利用简化的射线追踪方法，针对动作中基元模型的每一帧计算对应的信道响应；最后对信道响应进行多普勒分析，获得对应动作的微多普勒时频谱。上述仿真获得的微多普勒时频谱数据集可以用于训练无线动作识别的深度神经网络。该文针对“步行”“跑步”“跌倒”“坐下”这4种常见的人体动作在60 GHz频段上进行了信道仿真及动作识别的测试。实验结果表明，通过仿真训练的深度神经网络在实际无线动作识别中平均识别准确率可以达到73.0%。此外，借助无标签迁移学习，通过少量无标签实测数据的微调，上述准确率可以进一步提高到93.75%。
- 无线信道建模 /
- 无线动作识别 /
- 无标签迁移学习 /
- 毫米波 /
- 计算机视觉
Abstract: This study proposes a computer vision-assisted millimeter wave wireless channel simulation method incorporating the scattering characteristics of human motions. The aim is to rapidly and cost-effectively generate a training dataset for wireless human motion recognition, thereby avoiding the laborious and cost-intensive efforts associated with physical measurements. Specifically, the simulation process includes the following steps. First, the human body is modeled as 35 interconnected ellipsoids using a primitive-based model, and motion data of these ellipsoids are extracted from videos of human motion. A simplified ray tracing method is then used to obtain the channel response for each snapshot of the primitive model during the motion process. Finally, Doppler analysis is performed on the channel responses of the snapshots to obtain the Doppler spectrograms. The Doppler spectrograms obtained from the simulation can be used to train deep neural network for real wireless human motion recognition. This study examines the channel simulation and action recognition results for four common human actions (“walking” “running” “falling” and “sitting down”) in the 60 GHz band. Experimental results indicate that the deep neural network trained with the simulated dataset achieves an average recognition accuracy of 73.0% in real-world wireless motion recognition. Furthermore, he recognition accuracy can be increased to 93.75% via unlabeled transfer learning and fine-tuning with a small amount of actual data.
- Wireless channel simulation /
- Wireless human motion recognition /
- Unlabeled transfer learning /
- Millimeter wave /
- Computer vision

HTML全文

图 1 信道仿真场景及具有34个关键点，35个基元的人体模型示意图

Figure 1. Illustration of channel simulation scenario and primitive-based human model with 34 keypoints and 35 primitives

下载: 全尺寸图片幻灯片

图 2 对第n个椭球的双基地雷达截面面积的计算参数示意图

Figure 2. Illustration of bistatic radar cross section (RCS) calculation parameters for n-th ellipsoid

下载: 全尺寸图片幻灯片

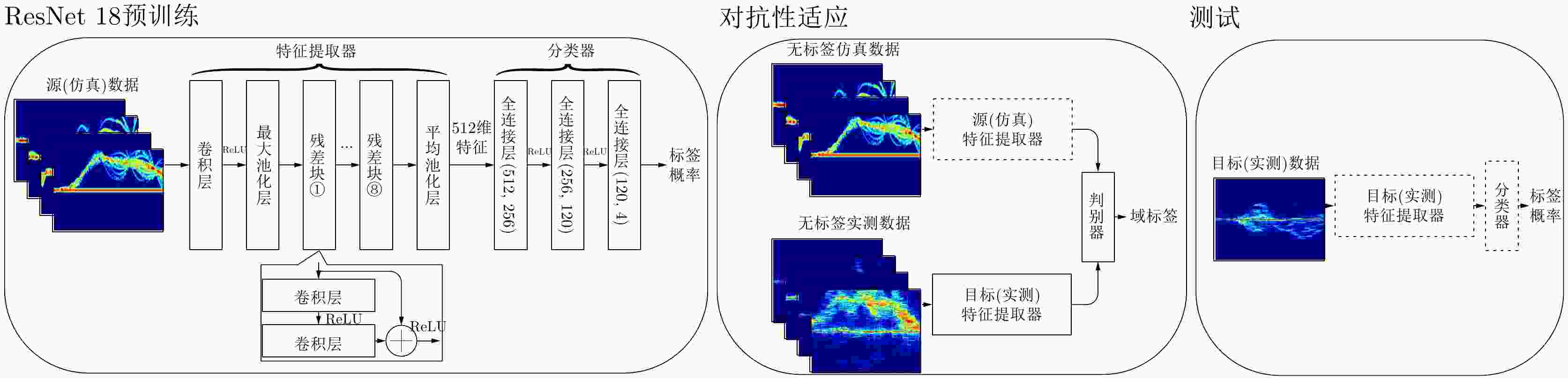
图 3 无标签迁移学习框架(虚线框格代表着训练或测试阶段神经网络的参数保持不变，而实线框格表示神经网络的参数随着训练的过程不断更新)

Figure 3. An overview of unsupervised transfer learning (dashed boxes represent the neural network parameters that remain unchanged during training or testing phases, while solid boxes indicate neural network parameters that are continuously updated throughout the training process)

下载: 全尺寸图片幻灯片

图 4 实验设备及实验场景示意图

Figure 4. Illustration of facilities and scenario of experiment

下载: 全尺寸图片幻灯片

图 5 仿真与实测数据集微多普勒谱示意图

Figure 5. Illustration of the simulated and experimental spectrogram datasets

下载: 全尺寸图片幻灯片

图 6 4个人体动作的仿真与实测微多普勒谱对比

Figure 6. Spectrogram comparison of four human motions generated by simulation and experiment

下载: 全尺寸图片幻灯片

图 7 不同人体动作仿真与实测样本间SSIM值的CDF曲线

Figure 7. The CDF curves of SSIM values between simulated and measured samples for different human motions

下载: 全尺寸图片幻灯片

图 8 人体动作识别结果

Figure 8. Human motion recognition result

下载: 全尺寸图片幻灯片

图 9 4个人体动作的仿真与实测微多普勒谱对比(样本时长5 s)

Figure 9. Spectrogram comparison of four human motions generated by simulation (experiment for 5 seconds)

下载: 全尺寸图片幻灯片

参考文献(29)

[1]	LI Chenning, CAO Zhichao, and LIU Yunhao. Deep AI enabled ubiquitous wireless sensing: A survey[J]. ACM Computing Surveys (CSUR), 2022, 54(2): 32. doi: 10.1145/3436729.
[2]	LIU Jian, LIU Hongbo, CHEN Yingying, et al. Wireless sensing for human activity: A survey[J]. IEEE Communications Surveys & Tutorials, 2020, 22(3): 1629–1645. doi: 10.1109/COMST.2019.2934489.
[3]	ZHANG Yi, ZHENG Yue, QIAN Kun, et al. Widar3.0: Zero-effort cross-domain gesture recognition with Wi-Fi[J]. IEEE Transactions on Pattern Analysis and Machine Intelligence, 2022, 44(11): 8671–8688. doi: 10.1109/TPAMI.2021.3105387.
[4]	元志安, 周笑宇, 刘心溥, 等. 基于RDSNet的毫米波雷达人体跌倒检测方法[J]. 雷达学报, 2021, 10(4): 656–664. doi: 10.12000/JR21015. YUAN Zhian, ZHOU Xiaoyu, LIU Xinpu, et al. Human fall detection method using millimeter-wave radar based on RDSNet[J]. Journal of Radars, 2021, 10(4): 656–664. doi: 10.12000/JR21015.
[5]	金添, 何元, 李新羽, 等. 超宽带雷达人体行为感知研究进展[J]. 电子与信息学报, 2022, 44(4): 1147–1155. doi: 10.11999/JEIT211044. JIN Tian, HE Yuan, LI Xinyu, et al. Advances in human activity sensing using ultra-wide band radar[J]. Journal of Electronics & Information Technology, 2022, 44(4): 1147–1155. doi: 10.11999/JEIT211044.
[6]	SUN Hongbo, CHIA L G, and RAZUL S G. Through-wall human sensing with WiFi passive radar[J]. IEEE Transactions on Aerospace and Electronic Systems, 2021, 57(4): 2135–2148. doi: 10.1109/TAES.2021.3069767.
[7]	LI Jie, YU Chao, LUO Yan, et al. Passive motion detection via mmWave communication system[C]. IEEE 95th Vehicular Technology Conference: (VTC2022-Spring), Helsinki, Finland, 2022: 1–6. doi: 10.1109/VTC2022-Spring54318.2022.9860809.
[8]	DU Rui, HUA Haocheng, XIE Hailiang, et al. An overview on IEEE 802.11bf: WLAN sensing[J]. IEEE Communications Surveys & Tutorials, 2024. doi: 10.1109/COMST.2024.3408899.
[9]	ZHANG Meihong, DU Rui, PENG Xiaohui, et al. Channel models for WLAN sensing systems[R]. IEEE 802.11-21/0782r5, 2021.
[10]	LI Guoliang, WANG Shuai, LI Jie, et al. Wireless sensing with deep spectrogram network and primitive based autoregressive hybrid channel model[C]. IEEE 22nd International Workshop on Signal Processing Advances in Wireless Communications (SPAWC), Lucca, Italy, 2021: 481–485. doi: 10.1109/SPAWC51858.2021.9593198.
[11]	ZHOU Pei, CHENG Kaijun, HAN Xiao, et al. IEEE 802.11ay-based mmWave WLANs: Design challenges and solutions[J]. IEEE Communications Surveys & Tutorials, 2018, 20(3): 1654–1681. doi: 10.1109/COMST.2018.2816920.
[12]	ASSASA Hany, et al. A collection of open-source tools to simulate IEEE 802.11ad/ay WLAN networks in network simulator ns-3[EB/OL]. https://github.com/wigig-tools.
[13]	LI Guoliang, WANG Shuai, LI Jie, et al. Integrated sensing and communication from learning perspective: An SDP3 approach[J]. IEEE Internet of Things Journal, 2024, 11(4): 5589–5603. doi: 10.1109/JIOT.2023.3309837.
[14]	VISHWAKARMA S, LI Wenda, TANG Chong, et al. SimHumalator: An open-source end-to-end radar simulator for human activity recognition[J]. IEEE Aerospace and Electronic Systems Magazine, 2022, 37(3): 6–22. doi: 10.1109/MAES.2021.3138948.
[15]	BOULIC R, THALMANN N M, and THALMANN D. A global human walking model with real-time kinematic personification[J]. The Visual Computer, 1990, 6(6): 344–358. doi: 10.1007/BF01901021.
[16]	LI Jiamu, ZHANG Dongheng, CHEN Qi, et al. SIMFALL: A data generator for RF-based fall detection[C]. ICASSP 2024 - 2024 IEEE International Conference on Acoustics, Speech and Signal Processing (ICASSP), Seoul, Korea, 2024: 8165–8169. doi: 10.1109/ICASSP48485.2024.10446234.
[17]	CHI Guoxuan, YANG Zheng, WU Chenshu, et al. RF-diffusion: Radio signal generation via time-frequency diffusion[C]. The 30th Annual International Conference on Mobile Computing and Networking, Washington, USA, 2024: 77–92. doi: 10.1145/3636534.3649348.
[18]	REN Zhenyu, LI Guoliang, JI Chenqing, et al. CASTER: A computer-vision-assisted wireless channel simulator for gesture recognition[J]. IEEE Open Journal of the Communications Society, 2024, 5: 3185–3195. doi: 10.1109/OJCOMS.2024.3398016.
[19]	WANG Jinbao, TAN Shujie, ZHEN Xiaotong, et al. Deep 3D human pose estimation: A review[J]. Computer Vision and Image Understanding, 2021, 210: 103225. doi: 10.1016/j.cviu.2021.103225.
[20]	StereoLabs. Stereolabs docs: API reference, tutorials, and integration[EB/OL]. https://www.stereolabs.com/docs.
[21]	ZHENG Ce, WU Wenhan, CHEN Chen, et al. Deep learning-based human pose estimation: A survey[J]. ACM Computing Surveys, 2024, 56(1): 11. doi: 10.1145/3603618.
[22]	TROTT K D. Stationary phase derivation for RCS of an ellipsoid[J]. IEEE Antennas and Wireless Propagation Letters, 2007, 6: 240–243. doi: 10.1109/LAWP.2007.891521.
[23]	DE BOOR C. A Practical Guide to Splines[M]. New York, USA: Springer, 1978: 40–48.
[24]	ZHUANG Fuzhen, QI Zhiyuan, DUAN Keyu, et al. A comprehensive survey on transfer learning[J]. Proceedings of the IEEE, 2021, 109(1): 43–76. doi: 10.1109/JPROC.2020.3004555.
[25]	HE Kaiming, ZHANG Xiangyu, REN Shaoqing, et al. Deep residual learning for image recognition[C]. 2016 IEEE Conference on Computer Vision and Pattern Recognition (CVPR), Las Vegas, USA, 2016: 770–778. doi: 10.1109/CVPR.2016.90.
[26]	TZENG E, HOFFMAN J, SAENKO K, et al. Adversarial discriminative domain adaptation[C]. 2017 IEEE Conference on Computer Vision and Pattern Recognition (CVPR), Honolulu, USA, 2017: 2962–2971. doi: 10.1109/CVPR.2017.316.
[27]	National Instruments. USRP-2954[EB/OL]. https://www.ni.com/en-us/shop/model/usrp-2954.html.
[28]	Sivers IMA. EVK 06002/00[EB/OL]. https://www.siversima.com/product/evk-06002-00/.
[29]	WANG Zhou, BOVIK A C, SHEIKH H R, et al. Image quality assessment: From error visibility to structural similarity[J]. IEEE Transactions on Image Processing, 2004, 13(4): 600–612. doi: 10.1109/TIP.2003.819861.