Volume 12 Issue 4
Aug.  2023
Turn off MathJax
Article Contents
Article Navigation >  Journal of Radars  > 2023  >  12(4): 906-922
WANG Zhirui, KANG Yuzhuo, ZENG Xuan, et al. SAR-AIRcraft-1.0: High-resolution SAR aircraft detection and recognition dataset[J]. Journal of Radars, 2023, 12(4): 906–922. doi: 10.12000/JR23043
Citation: WANG Zhirui, KANG Yuzhuo, ZENG Xuan, et al. SAR-AIRcraft-1.0: High-resolution SAR aircraft detection and recognition dataset[J]. Journal of Radars, 2023, 12(4): 906–922. doi: 10.12000/JR23043
shu

SAR-AIRcraft-1.0: High-resolution SAR Aircraft Detection and Recognition Dataset

doi: 10.12000/JR23043
  • 1.

    Aerospace Information Research Institute, Chinese Academy of Sciences, Beijing 100094, China

  • 2.

    University of Chinese Academy of Sciences, Beijing 100049, China

  • 3.

    School of Electronic, Electrical and Communication Engineering, University of Chinese Academy of Sciences, Beijing 100049, China

  • 4.

    Key Laboratory of Network Information System Technology (NIST), Chinese Academy of Sciences, Beijing 100190, China

Funds:  The National Natural Science Foundation of China (62076241, 62171436)
More Information
  • Corresponding author: SUN Xian, sunxian@aircas.ac.cn
  • Received Date: 2023-04-17
  • Rev Recd Date: 2023-06-27
    • Available Online: 2023-07-04
  • Publish Date: 2023-07-17
    Abstract
  • This study proposes a Synthetic Aperture Radar (SAR) aircraft detection and recognition method combined with scattering perception to address the problem of target discreteness and false alarms caused by strong background interference in SAR images. The global information is enhanced through a context-guided feature pyramid module, which suppresses strong disturbances in complex images and improves the accuracy of detection and recognition. Additionally, scatter key points are used to locate targets, and a scatter-aware detection module is designed to realize the fine correction of the regression boxes to improve target localization accuracy. This study generates and presents a high-resolution SAR-AIRcraft-1.0 dataset to verify the effectiveness of the proposed method and promote the research on SAR aircraft detection and recognition. The images in this dataset are obtained from the satellite Gaofen-3, which contains 4,368 images and 16,463 aircraft instances, covering seven aircraft categories, namely A220, A320/321, A330, ARJ21, Boeing737, Boeing787, and other. We apply the proposed method and common deep learning algorithms to the constructed dataset. The experimental results demonstrate the excellent effectiveness of our method combined with scattering perception. Furthermore, we establish benchmarks for the performance indicators of the dataset in different tasks such as SAR aircraft detection, recognition, and integrated detection and recognition.

     

    • FullText(HTML)
  • loading
    • References(41)
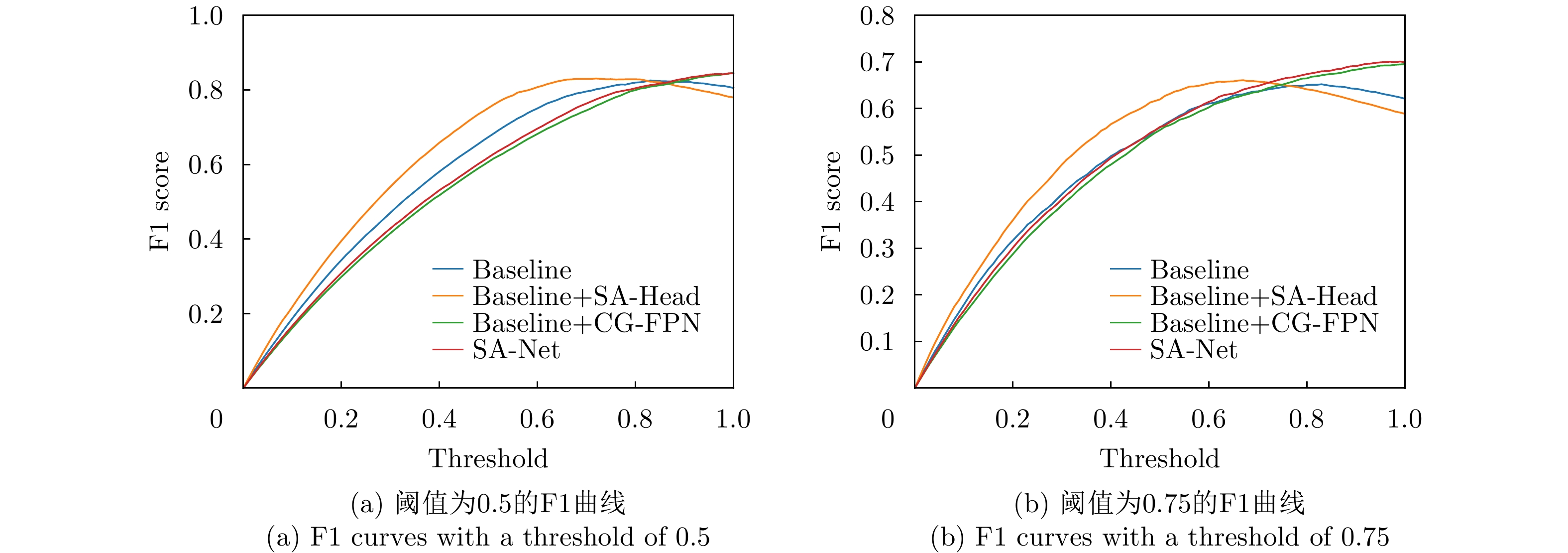
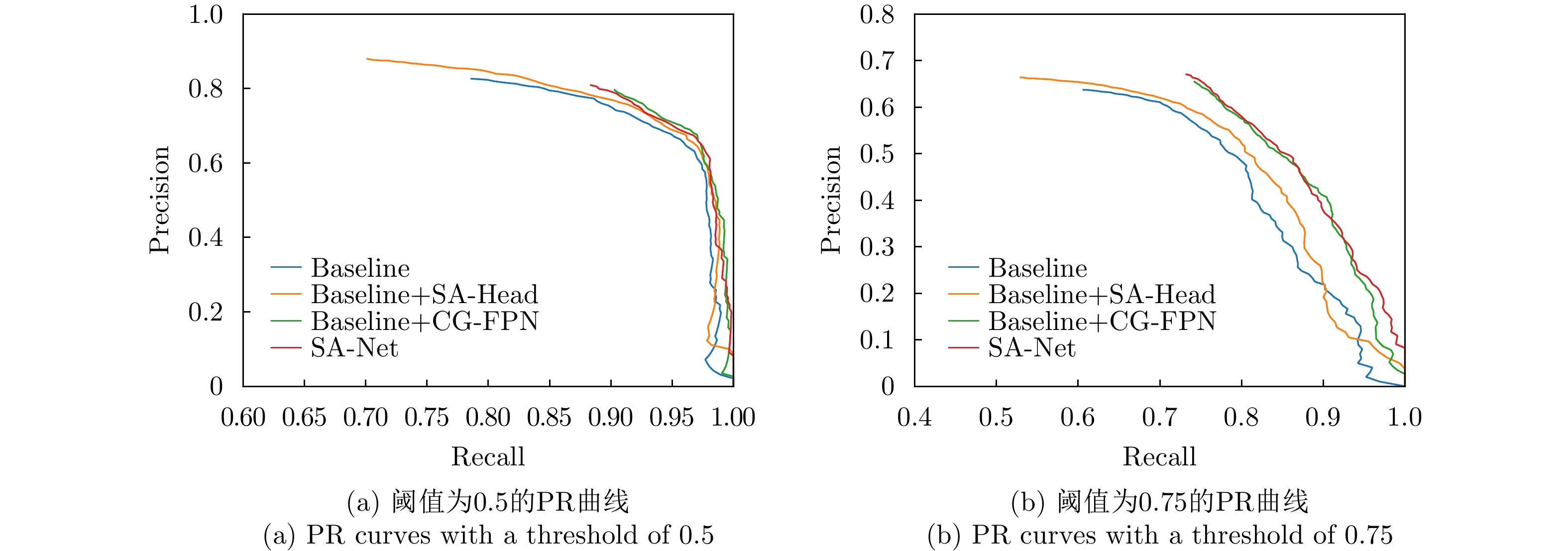
  • [1]
    FU Kun, FU Jiamei, WANG Zhirui, et al. Scattering-keypoint-guided network for oriented ship detection in high-resolution and large-scale SAR images[J]. IEEE Journal of Selected Topics in Applied Earth Observations and Remote Sensing, 2021, 14: 11162–11178. doi: 10.1109/JSTARS.2021.3109469
    [2]
    GUO Qian, WANG Haipeng, and XU Feng. Scattering enhanced attention pyramid network for aircraft detection in SAR images[J]. IEEE Transactions on Geoscience and Remote Sensing, 2021, 59(9): 7570–7587. doi: 10.1109/TGRS.2020.3027762
    [3]
    SHAHZAD M, MAURER M, FRAUNDORFER F, et al. Buildings detection in VHR SAR images using fully convolution neural networks[J]. IEEE Transactions on Geoscience and Remote Sensing, 2019, 57(2): 1100–1116. doi: 10.1109/TGRS.2018.2864716
    [4]
    ZHANG Zhimian, WANG Haipeng, XU Feng, et al. Complex-valued convolutional neural network and its application in polarimetric SAR image classification[J]. IEEE Transactions on Geoscience and Remote Sensing, 2017, 55(12): 7177–7188. doi: 10.1109/TGRS.2017.2743222
    [5]
    FU Kun, DOU Fangzheng, LI Hengchao, et al. Aircraft recognition in SAR images based on scattering structure feature and template matching[J]. IEEE Journal of Selected Topics in Applied Earth Observations and Remote Sensing, 2018, 11(11): 4206–4217. doi: 10.1109/JSTARS.2018.2872018
    [6]
    DU Lan, DAI Hui, WANG Yan, et al. Target discrimination based on weakly supervised learning for high-resolution SAR images in complex scenes[J]. IEEE Transactions on Geoscience and Remote Sensing, 2020, 58(1): 461–472. doi: 10.1109/TGRS.2019.2937175
    [7]
    CUI Zongyong, LI Qi, CAO Zongjie, et al. Dense attention pyramid networks for multi-scale ship detection in SAR images[J]. IEEE Transactions on Geoscience and Remote Sensing, 2019, 11: 8983–8997. doi: 10.1109/TGRS.2019.2923988
    [8]
    ZHANG Jinsong, XING Mengdao, and XIE Yiyuan. FEC: A feature fusion framework for SAR target recognition based on electromagnetic scattering features and deep CNN features[J]. IEEE Transactions on Geoscience and Remote Sensing, 2021, 59(3): 2174–2187. doi: 10.1109/TGRS.2020.3003264
    [9]
    ZHAO Yan, ZHAO Lingjun, LI Chuyin, et al. Pyramid attention dilated network for aircraft detection in SAR images[J]. IEEE Geoscience and Remote Sensing Letters, 2021, 18(4): 662–666. doi: 10.1109/LGRS.2020.2981255
    [10]
    ZHAO Yan, ZHAO Lingjun, LIU Zhong, et al. Attentional feature refinement and alignment network for aircraft detection in SAR imagery[J]. IEEE Transactions on Geoscience and Remote Sensing, 2022, 60: 5220616. doi: 10.1109/TGRS.2021.3139994
    [11]
    FU Jiamei, SUN Xian, WANG Zhirui, et al. An anchor-free method based on feature balancing and refinement network for multiscale ship detection in SAR images[J]. IEEE Transactions on Geoscience and Remote Sensing, 2021, 59(2): 1331–1344. doi: 10.1109/TGRS.2020.3005151
    [12]
    SUN Yuanrui, WANG Zhirui, SUN Xian, et al. SPAN: Strong scattering point aware network for ship detection and classification in large-scale SAR imagery[J]. IEEE Journal of Selected Topics in Applied Earth Observations and Remote Sensing, 2022, 15: 1188–1204. doi: 10.1109/JSTARS.2022.3142025
    [13]
    郭倩, 王海鹏, 徐丰. SAR图像飞机目标检测识别进展[J]. 雷达学报, 2020, 9(3): 497–513. doi: 10.12000/JR20020

    GUO Qian, WANG Haipeng, and XU Feng. Research progress on aircraft detection and recognition in SAR imagery[J]. Journal of Radars, 2020, 9(3): 497–513. doi: 10.12000/JR20020
    [14]
    吕艺璇, 王智睿, 王佩瑾, 等. 基于散射信息和元学习的SAR图像飞机目标识别[J]. 雷达学报, 2022, 11(4): 652–665. doi: 10.12000/JR22044

    LYU Yixuan, WANG Zhirui, WANG Peijin, et al. Scattering information and meta-learning based SAR images interpretation for aircraft target recognition[J]. Journal of Radars, 2022, 11(4): 652–665. doi: 10.12000/JR22044
    [15]
    KANG Yuzhuo, WANG Zhirui, FU Jiamei, et al. SFR-Net: Scattering feature relation network for aircraft detection in complex SAR images[J]. IEEE Transactions on Geoscience and Remote Sensing, 2022, 60: 5218317. doi: 10.1109/TGRS.2021.3130899
    [16]
    CHEN Jiehong, ZHANG Bo, and WANG Chao. Backscattering feature analysis and recognition of civilian aircraft in TerraSAR-X images[J]. IEEE Geoscience and Remote Sensing Letters, 2015, 12(4): 796–800. doi: 10.1109/LGRS.2014.2362845
    [17]
    SUN Xian, LV Yixuan, WANG Zhirui, et al. SCAN: Scattering characteristics analysis network for few-shot aircraft classification in high-resolution SAR images[J]. IEEE Transactions on Geoscience and Remote Sensing, 2022, 60: 5226517. doi: 10.1109/TGRS.2022.3166174
    [18]
    KEYDEL E R, LEE S W, and MOORE J T. MSTAR extended operating conditions: A tutorial[C]. The SPIE 2757, Algorithms for Synthetic Aperture Radar Imagery III, Orlando, USA, 1996: 228–242.
    [19]
    HUANG Lanqing, LIU Bin, LI Boying, et al. OpenSARShip: A dataset dedicated to Sentinel-1 ship interpretation[J]. IEEE Journal of Selected Topics in Applied Earth Observations and Remote Sensing, 2018, 11(1): 195–208. doi: 10.1109/JSTARS.2017.2755672
    [20]
    LI Jianwei, QU Changwen, and SHAO Jiaqi. Ship detection in SAR images based on an improved faster R-CNN[C]. 2017 SAR in Big Data Era: Models, Methods and Applications (BIGSARDATA), Beijing, China, 2017: 1–6.
    [21]
    WANG Yuanyuan, WANG Chao, ZHANG Hong, et al. A SAR dataset of ship detection for deep learning under complex backgrounds[J]. Remote Sensing, 2019, 11(7): 765. doi: 10.3390/rs11070765
    [22]
    孙显, 王智睿, 孙元睿, 等. AIR-SARShip-1.0: 高分辨率SAR舰船检测数据集[J]. 雷达学报, 2019, 8(6): 852–862. doi: 10.12000/JR19097

    SUN Xian, WANG Zhirui, SUN Yuanrui, et al. AIR-SARShip-1.0: High-resolution SAR ship detection dataset[J]. Journal of Radars, 2019, 8(6): 852–862. doi: 10.12000/JR19097
    [23]
    WEI Shunjun, ZENG Xiangfeng, QU Qizhe, et al. HRSID: A high-resolution SAR images dataset for ship detection and instance segmentation[J]. IEEE Access, 2020, 8: 120234–120254. doi: 10.1109/ACCESS.2020.3005861
    [24]
    HOU Xiyue, AO Wei, SONG Qian, et al. FUSAR-Ship: Building a high-resolution SAR-AIS matchup dataset of Gaofen-3 for ship detection and recognition[J]. Science China Information Sciences, 2020, 63(4): 140303. doi: 10.1007/s11432-019-2772-5
    [25]
    ZHANG Peng, XU Hao, TIAN Tian, et al. SEFEPNet: Scale expansion and feature enhancement pyramid network for SAR aircraft detection with small sample dataset[J]. IEEE Journal of Selected Topics in Applied Earth Observations and Remote Sensing, 2022, 15: 3365–3375. doi: 10.1109/JSTARS.2022.3169339
    [26]
    陈杰, 黄志祥, 夏润繁, 等. 大规模多类SAR目标检测数据集-1.0[J/OL]. 雷达学报. https://radars.ac.cn/web/data/getData?dataType=MSAR, 2022.

    CHEN Jie, HUANG Zhixiang, XIA Runfan, et al. Large-scale multi-class SAR image target detection dataset-1.0[J/OL]. Journal of Radars. https://radars.ac.cn/web/data/getData?dataType=MSAR, 2022.
    [27]
    HU Jie, SHEN Li, and SUN Gang. Squeeze-and-excitation networks[C]. IEEE/CVF Conference on Computer Vision and Pattern Recognition, Salt Lake City, USA, 2018: 7132–7141.
    [28]
    SUN Yuanrui, SUN Xian, WANG Zhirui, et al. Oriented ship detection based on strong scattering points network in large-scale SAR images[J]. IEEE Transactions on Geoscience and Remote Sensing, 2021, 60: 5218018. doi: 10.1109/TGRS.2021.3130117
    [29]
    HUANG Lichao, YANG Yi, DENG Yafeng, et al. DenseBox: Unifying landmark localization with end to end object detection[J]. arXiv preprint arXiv: 1509.04874, 2015.
    [30]
    MIKOLAJCZYK K and SCHMID C. Scale & affine invariant interest point detectors[J]. International Journal of Computer Vision, 2004, 60(1): 63–86. doi: 10.1023/B:VISI.0000027790.02288.f2
    [31]
    OLUKANMI P O, NELWAMONDO F, and MARWALA T. K-means-MIND: An efficient alternative to repetitive k-means runs[C]. 2020 7th International Conference on Soft Computing & Machine Intelligence (ISCMI), Stockholm, Sweden, 2020: 172–176.
    [32]
    DAI Jifeng, QI Haozhi, XIONG Yuwen, et al. Deformable convolutional networks[C]. 2017 IEEE International Conference on Computer Vision, Venice, Italy, 2017: 764–773.
    [33]
    FAN Haoqiang, SU Hao, and GUIBAS L. A point set generation network for 3d object reconstruction from a single image[C]. 2017 IEEE Conference on Computer Vision and Pattern Recognition, Honolulu, USA, 2017: 2463–2471.
    [34]
    LIN T Y, GOYAL P, GIRSHICK R, et al. Focal loss for dense object detection[C]. 2017 IEEE International Conference on Computer Vision, Venice, Italy, 2017: 2999–3007.
    [35]
    HE Kaiming, ZHANG Xiangyu, REN Shaoqing, et al. Deep residual learning for image recognition[C]. 2016 IEEE Conference on Computer Vision and Pattern Recognition, Las Vegas, USA, 2016: 770–778.
    [36]
    GIRSHICK R. Fast R-CNN[C]. 2015 IEEE International Conference on Computer Vision, Santiago, Chile, 2015: 1440–1448.
    [37]
    CAI Zhaowei and VASCONCELOS N. Cascade R-CNN: Delving into high quality object detection[C]. 2018 IEEE/CVF Conference on Computer Vision and Pattern Recognition, Salt Lake City, USA, 2018: 6154–6162.
    [38]
    YANG Ze, LIU Shaohui, HU Han, et al. RepPoints: Point set representation for object detection[C]. 2019 IEEE/CVF International Conference on Computer Vision, Seoul, Korea, 2019: 9656–9665.
    [39]
    XIE Saining, GIRSHICK R, DOLLÁR P, et al. Aggregated residual transformations for deep neural networks[C]. 2017 IEEE Conference on Computer Vision and Pattern Recognition, Honolulu, USA, 2017: 5987–5995.
    [40]
    LIU Ze, LIN Yutong, CAO Yue, et al. Swin transformer: Hierarchical vision transformer using shifted windows[C]. 2021 IEEE/CVF International Conference on Computer Vision, Montreal, Canada, 2021: 9992–10002.
    [41]
    TIAN Zhi, SHEN Chunhua, CHEN Hao, et al. FCOS: Fully convolutional one-stage object detection[C]. 2019 IEEE/CVF International Conference on Computer Vision, Seoul, Korea, 2019: 9626–9635.
    • Relative Articles
    • Supplements(0)
    • Cited By
  • 加载中

Catalog

    通讯作者: 陈斌, bchen63@163.com
    • 1. 

      沈阳化工大学材料科学与工程学院 沈阳 110142

    1. 本站搜索
    2. 百度学术搜索
    3. 万方数据库搜索
    4. CNKI搜索
    Get Citation
    PDF
    XML
    Article views(5282) PDF downloads(569) Cited by()
    Proportional views
    Related

    京ICP备20021838号-8   Supported by: Beijing Renhe Information Technology Co. Ltd     百度统计

    /

    DownLoad:  Full-Size Img  PowerPoint
    Return