基于子阵波束设计的空时二维杂波抑制方法

万福海; 许京伟; 廖桂生; 王伟伟

doi:10.12000/JR24064

基于子阵波束设计的空时二维杂波抑制方法

DOI: 10.12000/JR24064 CSTR: 32380.14.JR24064

1.
西安电子科技大学雷达信号处理国家重点实验室西安 710071
2.
中国空间技术研究院西安分院西安 710000

基金项目: 国家自然科学基金(61931016, 62071344)，陕西省自然科学基础研究计划(2023-JC-JQ-55)

详细信息

作者简介:
万福海，博士生，主要研究方向为空时自适应处理、阵列信号处理

许京伟，博士，副教授，主要研究方向为雷达系统建模、阵列信号处理、波形分集雷达(频率分集阵和空时编码阵列)等

廖桂生，博士，教授，主要研究方向为雷达系统技术与阵列处理、雷达稀疏成像处理等

王伟伟，研究员，主要研究方向为星载雷达技术、雷达动目标检测、合成孔径雷达成像、阵列信号处理等

通讯作者:
许京伟 xujingwei1987@163.com

责任主编：谢文冲 Corresponding Editor: XIE Wenchong
中图分类号: TN957.51
计量
- 文章访问数: 437
- HTML全文浏览量: 129
- PDF下载量: 153
- 被引次数: 0
出版历程
- 收稿日期: 2024-04-11
- 修回日期: 2024-05-09
- 网络出版日期: 2024-06-12
- 刊出日期: 2024-09-28

Space-time Two-dimensional Clutter Suppression Method Based on Subarray Beam Pattern Design

1.
National Key Laboratory of Radar Signal Processing, Xidian University, Xi’an 710071, China
2.
China Academy of Space Technology (Xi’an), Xi’an 710000, China

Funds: The National Natural Science Foundation of China (61931016, 62071344), Natural Science Basic Research Project of Shaanxi Province (2023-JC-JQ-55)

More Information

Corresponding author: XU Jingwei, xujingwei1987@163.com

摘要

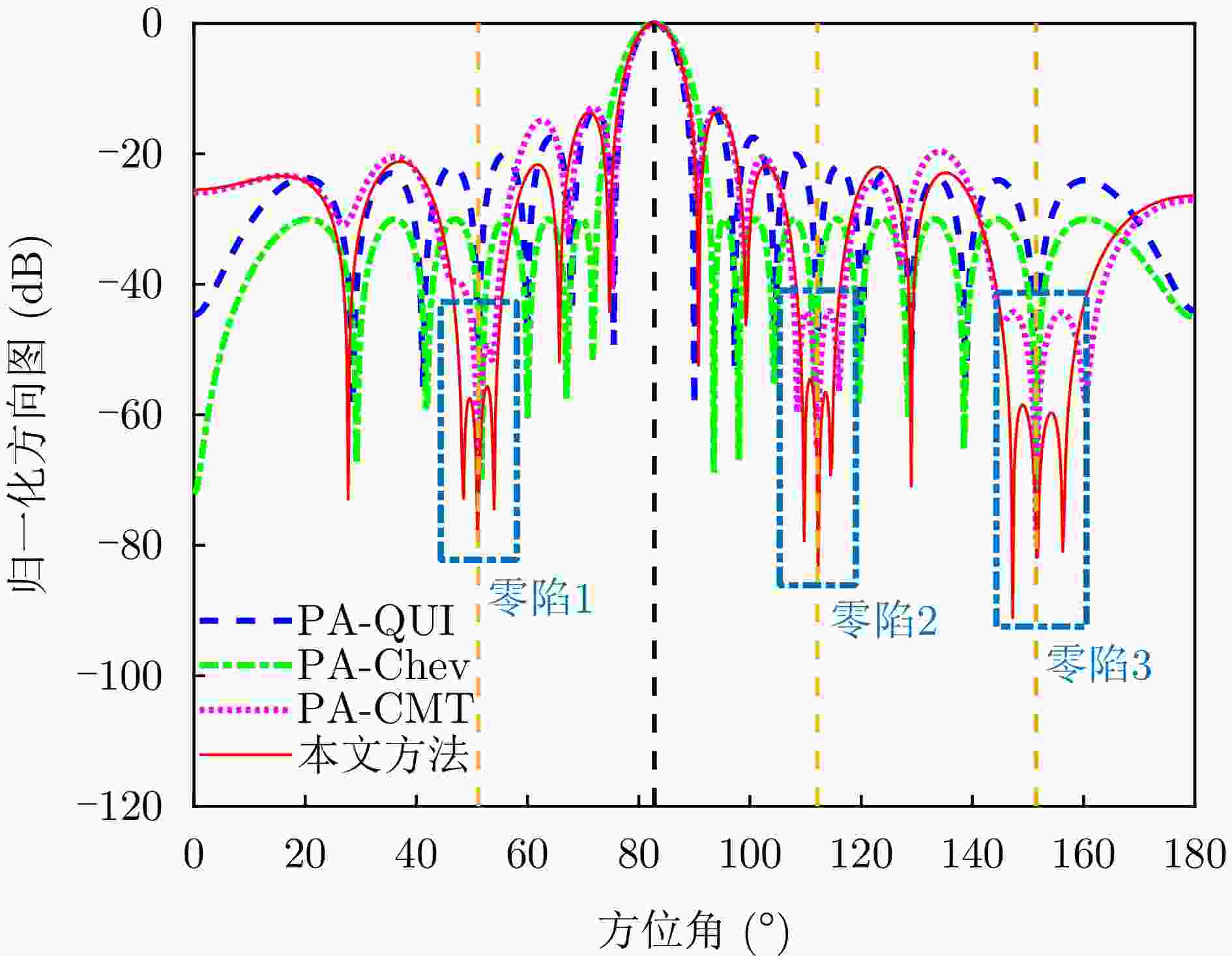
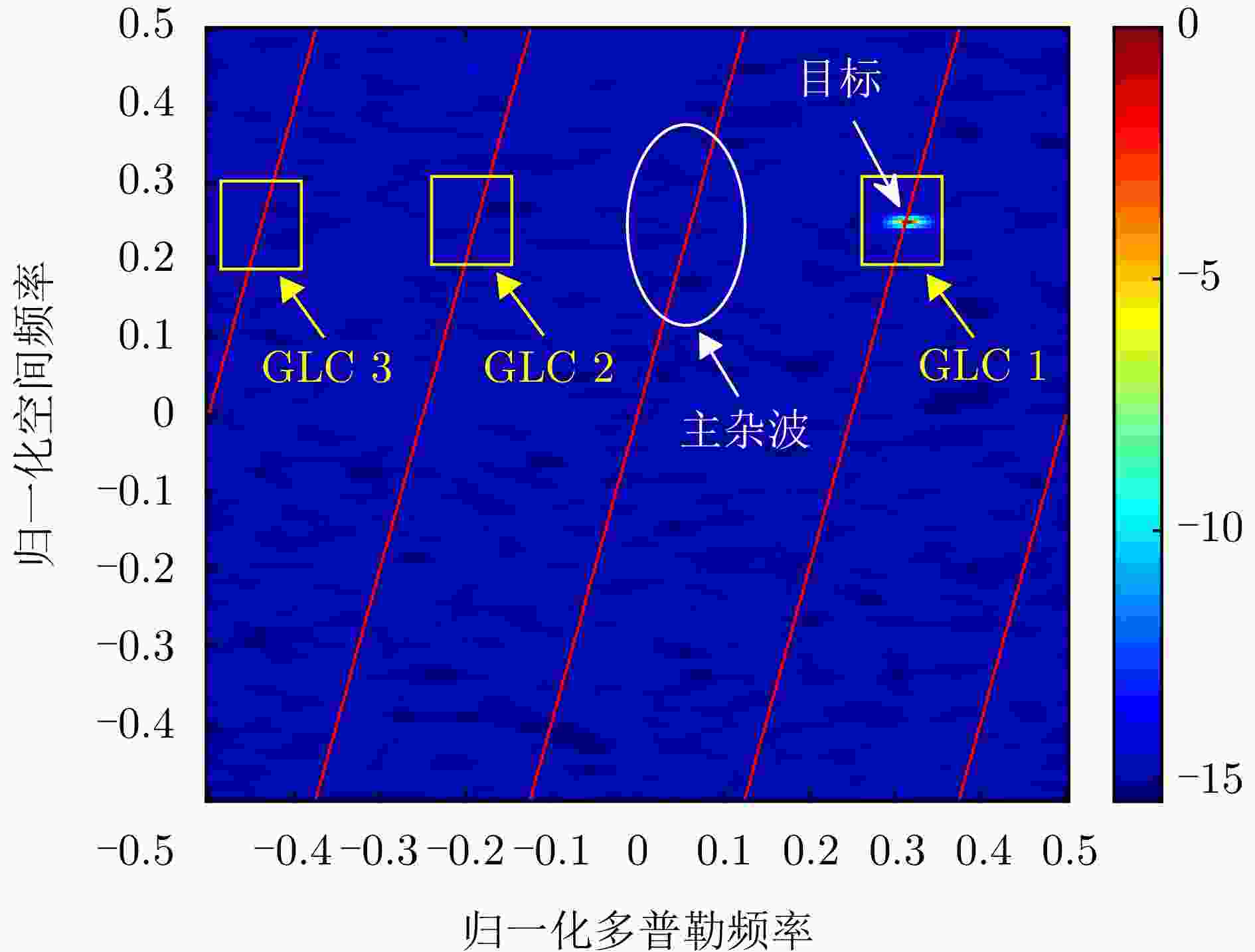
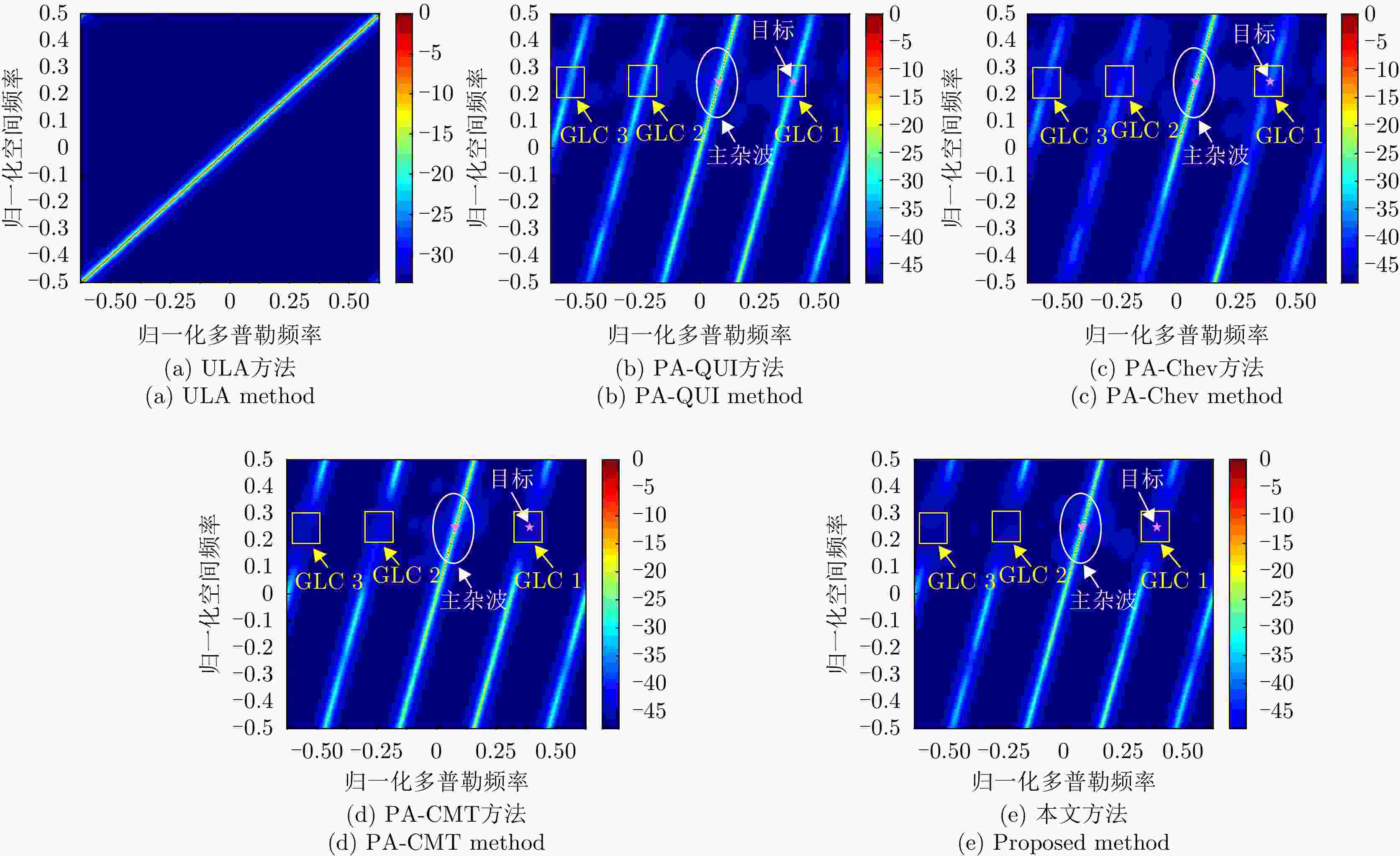
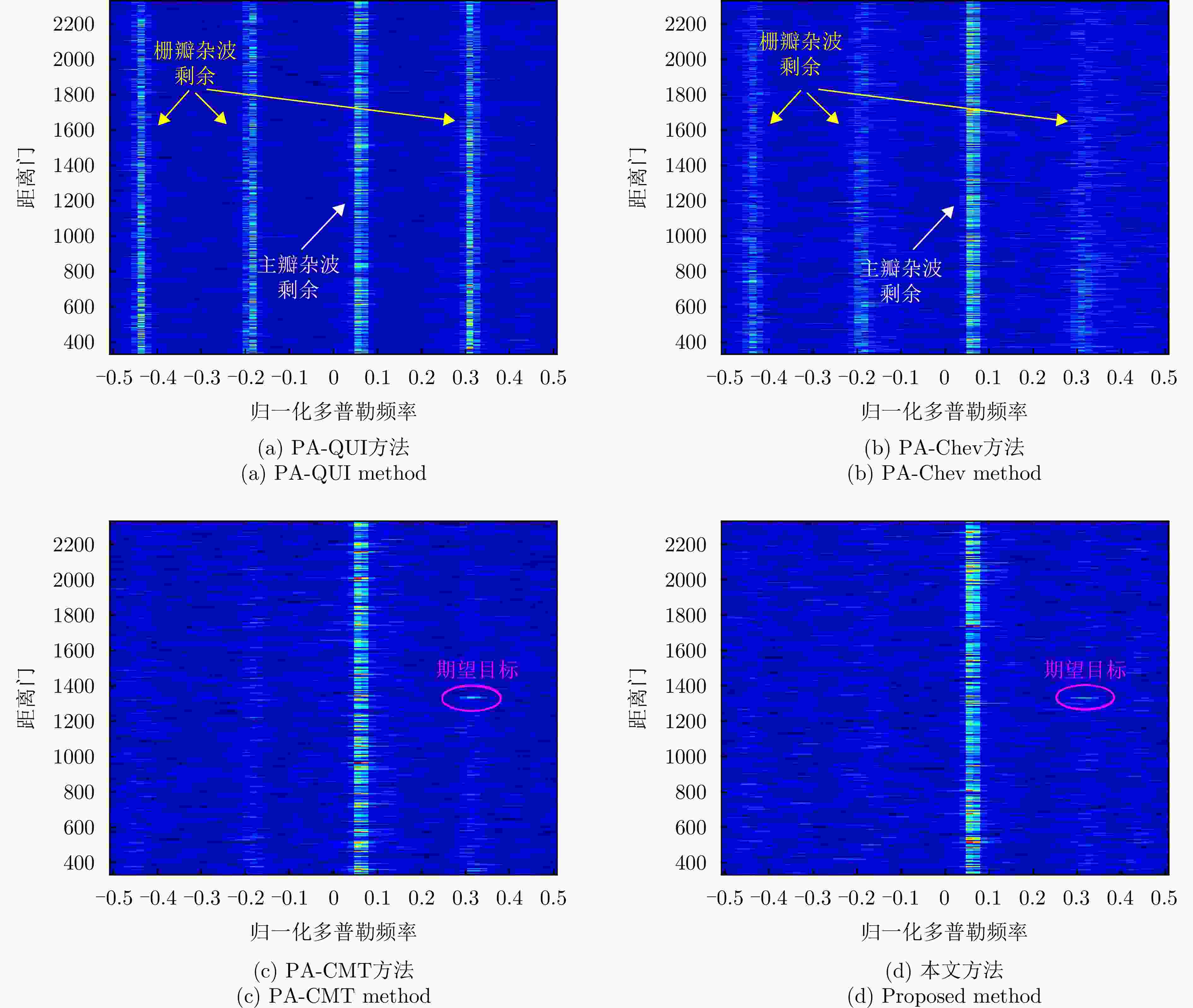
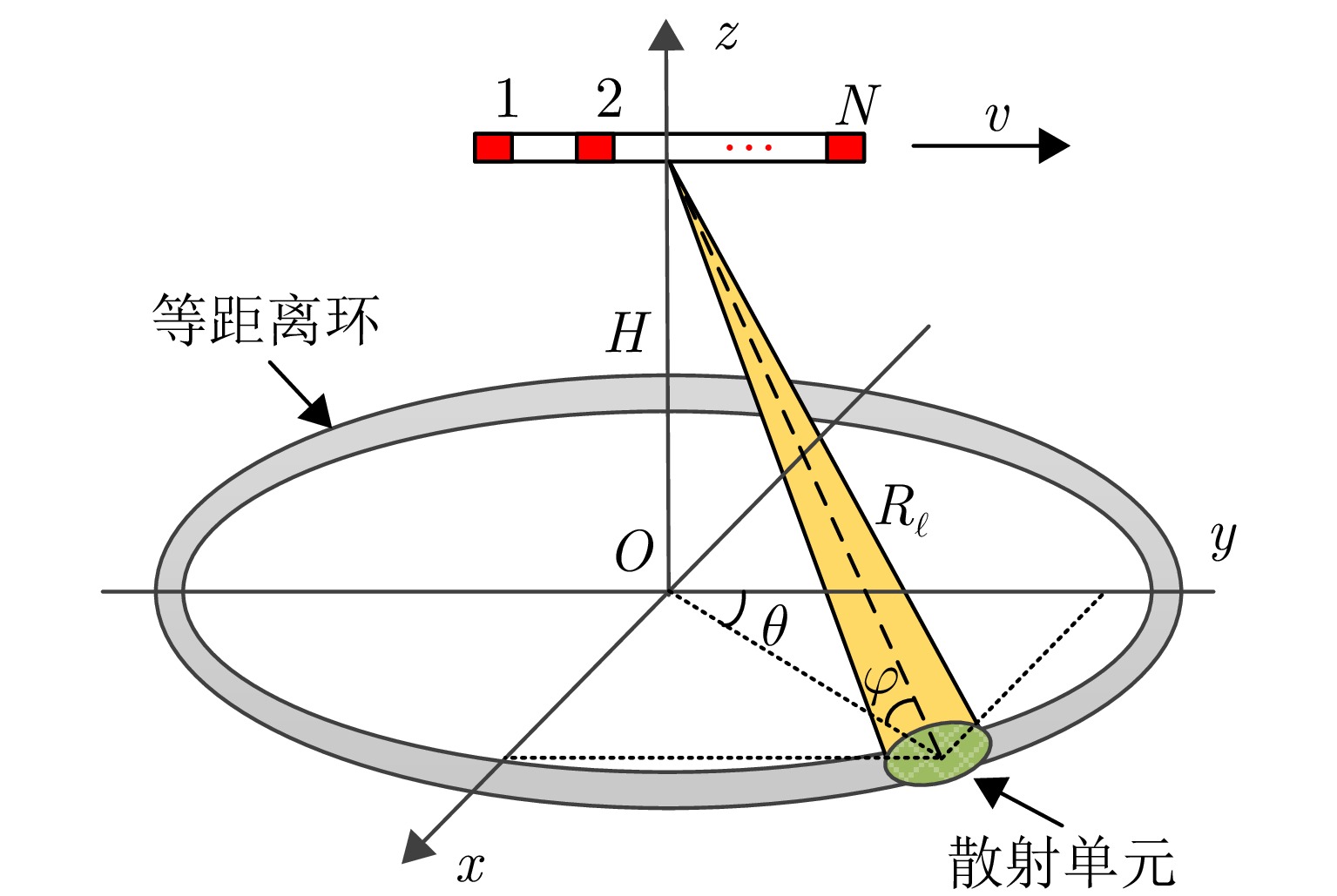
摘要: 机载雷达接收端采用子阵处理时面临栅瓣杂波导致的复杂空时耦合分布，使主瓣波束方向存在多个由栅瓣杂波导致的检测性能凹口，目标检测性能恶化严重。针对此问题，该文首先分析了子阵处理中栅瓣杂波空时谱分布特性，并在此基础上提出了基于接收子阵波束设计的空时二维杂波抑制方法。该方法采用重叠子阵构型方案，通过子阵方向图设计形成在子阵间栅瓣区域处的宽凹口，实现对子阵间栅瓣区域杂波的预滤波。进一步构建子阵级空时处理器，由于栅瓣杂波已经在子阵内完成预滤波，避免了栅瓣杂波在空时二维平面上的耦合扩散，从而提高了杂波抑制和动目标检测性能。仿真结果表明，所提方法显著改善了栅瓣杂波区的输出信杂噪比损失性能。
- 空时自适应处理 /
- 重叠子阵 /
- 栅瓣杂波抑制 /
- 子阵方向图 /
- 预滤波
Abstract: Airborne radar receivers that utilize subarray processing face challenges owing to the complex space-time coupling distribution caused by grating-lobe clutter. This results in multiple performance notches in the main beam, which severely affects target detection performance. To address this issue, we analyze the characteristics of grating-lobe clutter distribution in subarray processing and propose an approach for space-time clutter suppression based on the design of a receiving subarray beam pattern. Our approach leverages an overlapping subarray scheme to form wide nulls in the regions between subarrays where grating-lobe clutter is prevalent through beam pattern design. This design facilitates grating-lobe clutter pre-filtering between subarrays. Furthermore, we develop a subarray-level space-time processor that avoids the grating-lobe clutter coupling diffusion in the space-time two-dimensional plane by performing clutter pre-filtering within each subarray. This strategy enhances clutter suppression and moving-target-detection capabilities. Simulation results verify that the proposed method can remarkably improve the output signal to clutter plus noise ratio loss performance in grating-lobe clutter regions.
- Space-Time Adaptive Processing (STAP) /
- Overlapping subarray /
- Grating-lobe clutter suppression /
- Subarray beampattern /
- Pre-filtering

HTML全文

图 1 正侧视机载雷达几何构型

Figure 1. Side-looking airborne radar geometry model

下载: 全尺寸图片幻灯片

图 2 阵列接收信号处理流程图

Figure 2. Flowchart of array receiving signal processing

下载: 全尺寸图片幻灯片

图 3 杂波模糊示意图

Figure 3. Schematic of clutter ambiguity

下载: 全尺寸图片幻灯片

图 4 不同阵元重叠数时杂波空时谱示意图

Figure 4. Space-time clutter spectrum diagram with different array overlapping numbers

下载: 全尺寸图片幻灯片

图 5 不同阵元重叠数下的杂波谱分布

Figure 5. Space-time clutter spectrum with different array overlapping numbers

下载: 全尺寸图片幻灯片

图 6 接收子阵方向图

Figure 6. Receive subarray beampattern

下载: 全尺寸图片幻灯片

图 7 目标在空时平面位置分布

Figure 7. Space-time distribution of the target

下载: 全尺寸图片幻灯片

图 8 杂波空时Capon谱

Figure 8. Clutter space-time Capon spectrum

下载: 全尺寸图片幻灯片

图 9 距离-多普勒谱结果

Figure 9. Range-Doppler spectrum

下载: 全尺寸图片幻灯片

图 10 有无幅相误差情形下输出SCNR与输入CNR曲线

Figure 10. Output SCNR versus input CNR with or without amplitude and phase error

下载: 全尺寸图片幻灯片

图 11 输出SCNR损失与多普勒频率变化关系

Figure 11. Output SCNR loss versus Doppler frequency

下载: 全尺寸图片幻灯片

表 1 雷达系统仿真参数

Table 1. Simulation parameters of radar system

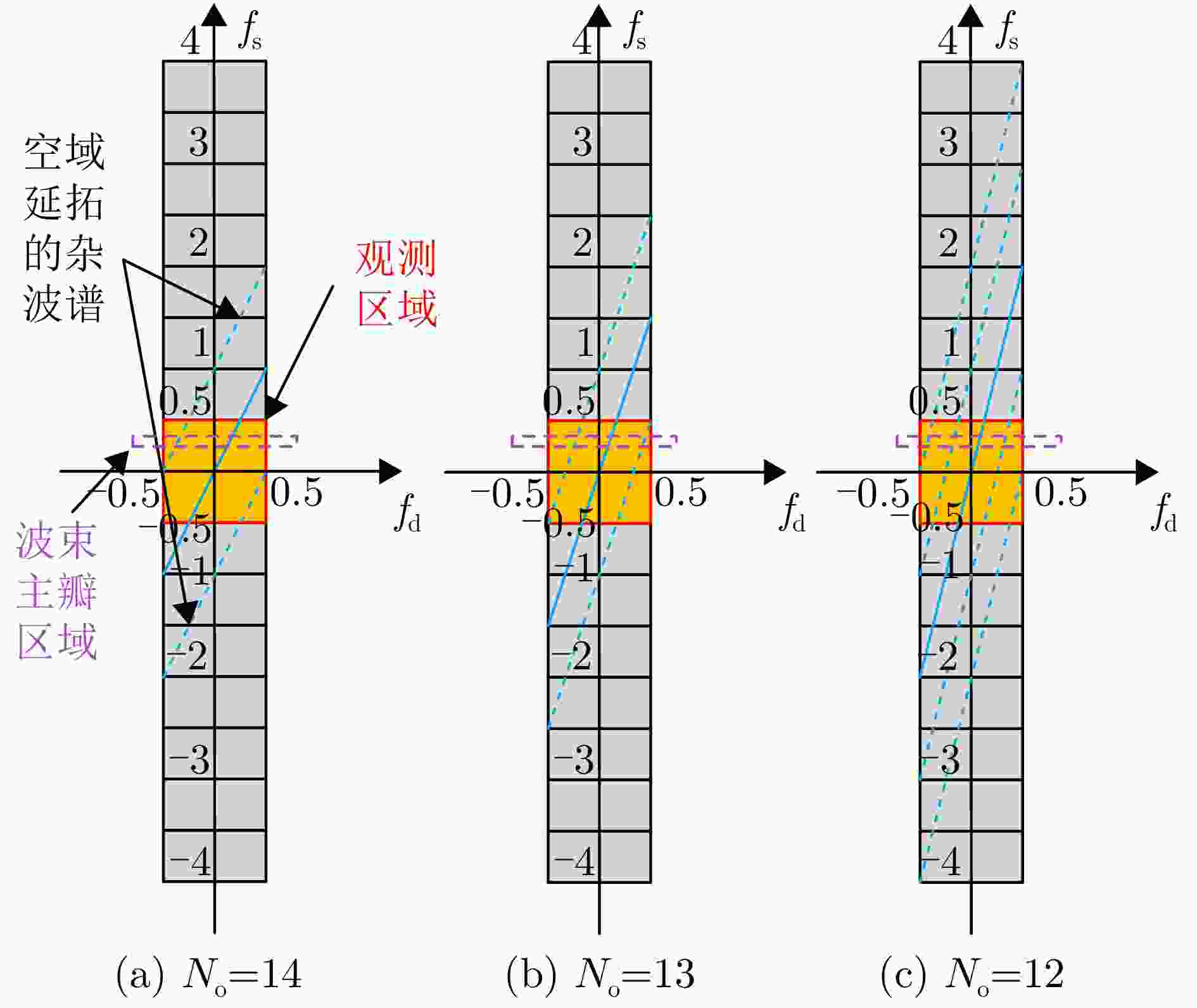
参数	数值	参数	数值
阵元总数	52	子阵数	10
子阵内阵元数	16	重叠阵元数	12
脉冲数	16	工作载频	1.2 GHz
波长	0.25 m	脉冲重频	2 kHz
信号带宽	5 MHz	平台高度	10 km
平台速度	125 m/s	目标方位角	82.79°
目标俯仰角	4.99°	目标斜距	115 km
空间频率展宽	0.1	多普勒滤波器带宽	0.06
幅度误差	0.03	相位误差	3°
信噪比	–5 dB	杂噪比	50 dB

下载: 导出CSV

参考文献(36)

[1]	BRENNAN L, MALLETT J, and REED I. Adaptive arrays in airborne MTI radar[J]. IEEE Transactions on Antennas and Propagation, 1976, 24(5): 607–615. doi: 10.1109/TAP.1976.1141412.
[2]	谢文冲, 王永良, 熊元燚. 机载雷达空时自适应处理[M]. 北京: 清华大学出版社, 2024: 86–95. XIE Wenchong, WANG Yongliang, and XIONG Yuanyi. Space Time Adaptive Processing Technique for Airborne Radar[M]. Beijing: Tsinghua University Press, 2024: 86–95.
[3]	XU Jingwei, LIAO Guisheng, and SO H C. Space-time adaptive processing with vertical frequency diverse array for range-ambiguous clutter suppression[J]. IEEE Transactions on Geoscience and Remote Sensing, 2016, 54(9): 5352–5364. doi: 10.1109/TGRS.2016.2561308.
[4]	WEN Cai, HUANG Yan, PENG Jinye, et al. Slow-time FDA-MIMO technique with application to STAP radar[J]. IEEE Transactions on Aerospace and Electronic Systems, 2022, 58(1): 74–95. doi: 10.1109/TAES.2021.3098100.
[5]	SONG Di, FENG Qi, CHEN Shengyao, et al. Space-time adaptive processing using deep neural network-based shrinkage algorithm under small training samples[J]. IEEE Transactions on Aerospace and Electronic Systems, 2023, 59(6): 9697–9703. doi: 10.1109/TAES.2023.3255840.
[6]	阚庆云, 许京伟, 廖桂生. 和差天线空时自适应测角方法及性能分析[J]. 电子学报, 2023, 51(1): 42–49. doi: 10.12263/DZXB. 20211458. KAN Qingyun, XU Jingwei, and LIAO Guisheng. Angle estimation approach and performance analysis for STAP with sum-difference antenna[J]. Acta Electronica Sinica, 2023, 51(1): 42–49. doi: 10.12263/DZXB.20211458.
[7]	XIE Lei, HE Zishu, TONG Jun, et al. A recursive angle-Doppler channel selection method for reduced-dimension space-time adaptive processing[J]. IEEE Transactions on Aerospace and Electronic Systems, 2020, 56(5): 3985–4000. doi: 10.1109/TAES.2020.2983533.
[8]	HUANG Penghui, ZOU Zihao, XIA Xianggen, et al. A novel dimension-reduced space-time adaptive processing algorithm for spaceborne multichannel surveillance radar systems based on spatial-temporal 2-D sliding window[J]. IEEE Transactions on Geoscience and Remote Sensing, 2022, 60: 5109721. doi: 10.1109/TGRS.2022.3144668.
[9]	GOLDSTEIN J S and REED I S. Reduced-rank adaptive filtering[J]. IEEE Transactions on Signal Processing, 1997, 45(2): 492–496. doi: 10.1109/78.554317.
[10]	HERD J S and CONWAY M D. The evolution to modern phased array architectures[J]. Proceedings of the IEEE, 2016, 104(3): 519–529. doi: 10.1109/JPROC.2015.2494879.
[11]	HE Xiongpeng, LIAO Guisheng, ZHU Shengqi, et al. Range ambiguous clutter suppression approach with elevation time diverse array[J]. IEEE Transactions on Aerospace and Electronic Systems, 2022, 58(1): 359–373. doi: 10.1109/TAES.2021.3101786.
[12]	ZHANG Tianfu, WANG Zhihao, XING Mengdao, et al. Research on multi-domain dimensionality reduction joint adaptive processing method for range ambiguous clutter of FDA-Phase-MIMO space-based early warning radar[J]. Remote Sensing, 2022, 14(21): 5536. doi: 10.3390/rs14215536.
[13]	LI Yuanshuai, CHANG Shaoqiang, LIU Zihao, et al. Range ambiguity suppression under high-resolution estimation using the MUSIC-AP algorithm for pulse-Doppler radar[J]. Signal Processing, 2024, 214: 109237. doi: 10.1016/j.sigpro.2023.109237.
[14]	WU Yong, TANG Jun, and PENG Yingning. On the essence of knowledge-aided clutter covariance estimate and its convergence[J]. IEEE Transactions on Aerospace and Electronic Systems, 2011, 47(1): 569–585. doi: 10.1109/TAES.2011.5705692.
[15]	WANG Degen, WANG Tong, CUI Wenchen, et al. A clutter suppression algorithm via enhanced sparse Bayesian learning for airborne radar[J]. IEEE Sensors Journal, 2023, 23(10): 10900–10911. doi: 10.1109/JSEN.2023.3263919.
[16]	VARADARAJAN V and KROLIK J L. Joint space-time interpolation for distorted linear and bistatic array geometries[J]. IEEE Transactions on Signal Processing, 2006, 54(3): 848–860. doi: 10.1109/TSP.2005.862941.
[17]	WANG Yongliang, DUAN Keqing, and XIE Wenchong. Cross beam STAP for nonstationary clutter suppression in airborne radar[J]. International Journal of Antennas and Propagation, 2013, 2013: 276310. doi: 10.1155/2013/276310.
[18]	MAILLOUX R J, SANTARELLI S G, ROBERTS T M, et al. Irregular polyomino-shaped subarrays for space-based active arrays[J]. International Journal of Antennas and Propagation, 2009, 2009: 956524. doi: 10.1155/2009/956524.
[19]	黄飞, 盛卫星, 马晓峰. 随机错位子阵阵列天线及其优化设计[J]. 电波科学学报, 2008, 23(5): 917–921. doi: 10.3969/j.issn.1005-0388.2008.05.023. HUANG Fei, SHENG Weixing, and MA Xiaofeng. Plane antenna arrays with randomly staggered subarrays and its optimal design[J]. Chinese Journal of Radio Science, 2008, 23(5): 917–921. doi: 10.3969/j.issn.1005-0388.2008.05.023.
[20]	XIONG Ziyuan, XU Zhenhai, CHEN Siwei, et al. Subarray partition in array antenna based on the algorithm X[J]. IEEE Antennas and Wireless Propagation Letters, 2013, 12: 906–909. doi: 10.1109/LAWP.2013.2272793.
[21]	KARADEMIR S, PROKOPYEV O A, and MAILLOUX R J. Irregular polyomino tiling via integer programming with application in phased array antenna design[J]. Journal of Global Optimization, 2016, 65(2): 137–173. doi: 10.1007/s10898-015-0354-8.
[22]	DONG Wei, XU Zhenhai, LIU Xinghua, et al. Irregular subarray tiling via heuristic iterative convex relaxation programming[J]. IEEE Transactions on Antennas and Propagation, 2020, 68(4): 2842–2852. doi: 10.1109/TAP.2019.2955070.
[23]	ROCCA P, ANSELMI N, POLO A, et al. An irregular two-sizes square tiling method for the design of isophoric phased arrays[J]. IEEE Transactions on Antennas and Propagation, 2020, 68(6): 4437–4449. doi: 10.1109/TAP.2020.2970088.
[24]	ZHOU Jian, WANG Yiqing, WANG Zhangling, et al. Irregular subarray tiling via rotational symmetry[J]. IEEE Antennas and Wireless Propagation Letters, 2023, 22(4): 903–907. doi: 10.1109/LAWP.2022.3228108.
[25]	MA Yankai, YANG Shiwen, CHEN Yikai, et al. High-directivity optimization technique for irregular arrays combined with maximum entropy model[J]. IEEE Transactions on Antennas and Propagation, 2021, 69(7): 3913–3923. doi: 10.1109/TAP.2020.3044653.
[26]	YANG Feng, MA Yankai, LONG Weijun, et al. Synthesis of irregular phased arrays subject to constraint on directivity via convex optimization[J]. IEEE Transactions on Antennas and Propagation, 2021, 69(7): 4235–4240. doi: 10.1109/TAP.2020.3044632.
[27]	JIANG Hailing, GONG Yu, ZHANG Junyi, et al. Irregular modular subarrayed phased array tiling by algorithm X and differential evolution algorithm[J]. IEEE Antennas and Wireless Propagation Letters, 2023, 22(7): 1532–1536. doi: 10.1109/LAWP.2023.3250260.
[28]	TOYAMA N. Optimization of aperiodic array patterns using GA and SDA[C]. 2005 IEEE Antennas and Propagation Society International Symposium, Washington, USA, 2005: 69–72. doi: 10.1109/APS.2005.1551737.
[29]	WANG Hao, FANG Dagang, and CHOW Y L. Grating lobe reduction in a phased array of limited scanning[J]. IEEE Transactions on Antennas and Propagation, 2008, 56(6): 1581–1586. doi: 10.1109/TAP.2008.923354.
[30]	程乃平, 潘点飞. 大型阵列天线子阵划分及栅瓣抑制方法[J]. 信号处理, 2014, 30(5): 535–543. doi: 10.3969/j.issn.1003-0530.2014.05.007. CHENG Naiping and PAN Dianfei. Subarray partition method and grating lobe suppression for large array antenna[J]. Journal of Signal Processing, 2014, 30(5): 535–543. doi: 10.3969/j.issn.1003-0530.2014.05.007.
[31]	KRIVOSHEEV Y V, SHISHLOV A V, and DENISENKO V V. Grating lobe suppression in aperiodic phased array antennas composed of periodic subarrays with large element spacing[J]. IEEE Antennas and propagation Magazine, 2015, 57(1): 76–85. doi: 10.1109/MAP.2015.2397155.
[32]	XU Xiaomin, LIAO Cheng, ZHOU Liang, et al. Grating lobe suppression of non-uniform arrays based on position gradient and sigmoid function[J]. IEEE Access, 2019, 7: 106407–106416. doi: 10.1109/ACCESS.2019.2932123.
[33]	YANG Gongqing, ZENG Hui, and XU Zhenhai. Adaptive gradient search algorithm for displaced subarrays with large element spacing[J]. IEEE Antennas and Wireless Propagation Letters, 2021, 20(7): 1155–1159. doi: 10.1109/LAWP.2021.3074253.
[34]	ELAYAPERUMAL S and RAJAGOPAL S. Design of antenna array architecture with large inter element spacing and low grating lobes[C]. 2021 IEEE International Conference on Electronics, Computing and Communication Technologies, Bangalore, India, 2021: 1–6. doi: 10.1109/CONECCT52877.2021.9622535.
[35]	LIU Zhixin, ZHU Shengqi, XU Jingwei, et al. Range-ambiguous clutter suppression for STAP-based radar with vertical coherent frequency diverse array[J]. IEEE Transactions on Geoscience and Remote Sensing, 2023, 61: 5106517. doi: 10.1109/TGRS.2023.3291738.
[36]	GUERCI J R. Theory and application of covariance matrix tapers for robust adaptive beamforming[J]. IEEE Transactions on Signal Processing, 1999, 47(4): 977–985. doi: 10.1109/78.752596.