IAA-Net：一种实孔径扫描雷达迭代自适应角超分辨成像方法

毛德庆; 杨建宇; 杨明杰; 张永超; 张寅; 黄钰林

doi:10.12000/JR24063

IAA-Net：一种实孔径扫描雷达迭代自适应角超分辨成像方法

DOI: 10.12000/JR24063 CSTR: 32380.14.JR24063

电子科技大学信息与通信工程学院成都 611731

基金项目: 国家自然科学基金(62301131)，博士后科学基金(BX20220055, 2022M720667)

详细信息

作者简介:
毛德庆，博士，副研究员，主要研究方向为雷达前视成像、雷达超分辨成像等

杨建宇，博士，教授，主要研究方向为合成孔径雷达和统计信号处理等

杨明杰，硕士生，主要研究方向为机载雷达前视智能化超分辨成像等

张永超，博士，副研究员，主要研究方向为阵列信号处理和雷达应用中的逆问题等

张　寅，博士，研究员，主要研究方向为信号处理和雷达成像等

黄钰林，博士，教授，主要研究方向为雷达成像、检测与识别和机器学习等

通讯作者:
毛德庆 deqingmao@uestc.edu.cn

张寅 yinzhang@uestc.edu.cn

责任主编：朱岱寅 Corresponding Editor: ZHU Daiyin
中图分类号: TN957
计量
- 文章访问数: 437
- HTML全文浏览量: 213
- PDF下载量: 142
- 被引次数: 0
出版历程
- 收稿日期: 2024-04-09
- 修回日期: 2024-06-23
- 网络出版日期: 2024-07-22
- 刊出日期: 2024-09-28

IAA-Net: An Iterative Adaptive Approach for Angular Super-resolution Imaging of Real Aperture Scanning Radar

School of Information and Communication Engineering, University of Electronic Science and Technology of China, Chengdu 611731, China

Funds: The National Natural Science Foundation of China (62301131), The China Postdoctoral Science Foundation (BX20220055, 2022M720667)

More Information

Corresponding author: MAO Deqing, deqingmao@uestc.edu.cn; ZHANG Yin, yinzhang@uestc.edu.cn

摘要

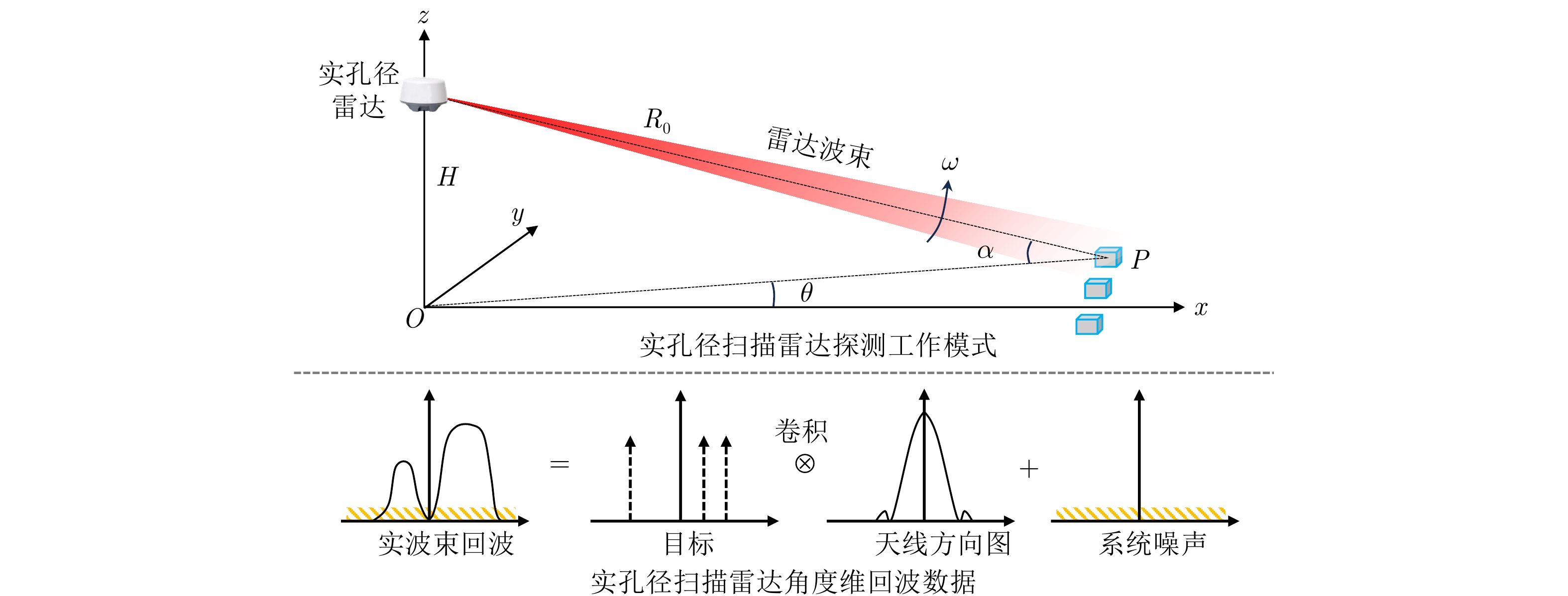
摘要: 实孔径雷达(RAR)通过天线扫描工作，以获取大范围探测区域内目标的观测信息。但是，由于雷达天线尺寸小，受天线衍射机理限制，与距离分辨率相比，其角分辨率通常较低。角超分辨处理方法，可利用天线方向图与目标散射间的卷积关系，通过求解卷积反演问题，以提高扫描雷达角分辨率。但是，由于测量矩阵的低秩特性，传统角超分辨处理方法，存在正则化参数选择难、迭代更新慢等问题，并且在低信噪比条件下，角超分辨处理性能明显下降。针对上述问题，该文提出了一种基于深度网络的迭代自适应实孔径扫描雷达角超分辨成像方法。首先，该文将实孔径扫描雷达的卷积反演问题转化为回波自相关矩阵反演求解问题，以改善求逆矩阵的病态性；其次，将可学习的修正矩阵引入到迭代自适应求解方法中，以实现迭代自适应求解方法与深度网络的结合；最后，通过迭代学习更新回波自相关矩阵，降低噪声对反演结果的影响，提高实孔径雷达的角分辨率。仿真及实测数据结果表明，所提方法可避免传统算法中的手动参数选择和迭代更新慢等问题。同时，由于深度网络的学习拟合能力，所提方法可在低信噪比条件下保持良好的角超分辨性能。
- 实孔径雷达 /
- 角超分辨重建 /
- 深度网络 /
- 迭代自适应 /
- 参数选择
Abstract: Real Aperture Radar (RAR) observes wide-scope target information by scanning its antenna. However, because of the limited antenna size, the angular resolution of RAR is much lower than the range resolution. Angular super-resolution methods can be applied to enhance the angular resolution of RAR by inverting the low-rank steering matrix based on the convolution relationship between the antenna pattern and target scatterings. Because of the low-rank characteristics of the antenna steering matrix, traditional angular super-resolution methods suffer from manual parameter selection and high computational complexity. In particular, these methods exhibit poor super-resolution angular resolution at low signal-to-noise ratios. To address these problems, an iterative adaptive approach for angular super-resolution imaging of scanning RAR is proposed by combining the traditional Iterative Adaptive Approach (IAA) with a deep network framework, namely IAA-Net. First, the angular super-resolution problem for RAR is transformed into an echo autocorrelation matrix inversion problem to mitigate the ill-posed condition of the inverse matrix. Second, a learnable repairing matrix is introduced into the IAA procedure to combine the IAA algorithm with the deep network framework. Finally, the echo autocorrelation matrix is updated via iterative learning to improve the angular resolution. Simulation and experimental results demonstrate that the proposed method avoids manual parameter selection and reduces computational complexity. The proposed method provides high angular resolution under a low signal-to-noise ratio because of the learning ability of the deep network.
- Real Aperture Radar (RAR) /
- Angular super-resolution reconstruction /
- Deep network framework /
- Iterative Adaptive Approach (IAA) /
- Parameter selection

HTML全文

图 1 实孔径雷达波束扫描探测工作模式与角度维回波数据示意图

Figure 1. Beam scanning working mode and echo data in the azimuthal direction of RAR

下载: 全尺寸图片幻灯片

图 2 传统IAA算法与IAA-Net深度网络结构对比

Figure 2. Comparison of the traditional IAA algorithm and the proposed IAA-Net method

下载: 全尺寸图片幻灯片

图 3 IAA-Net深度网络迭代结构

Figure 3. Iterative framework of the proposed IAA-Net method

下载: 全尺寸图片幻灯片

图 4 目标重建更新模块

Figure 4. Target reconstructing and updating module

下载: 全尺寸图片幻灯片

图 5 参数训练更新模块

Figure 5. Parameter training and updating module

下载: 全尺寸图片幻灯片

图 6 部分训练样本示例

Figure 6. Examples of some training samples

下载: 全尺寸图片幻灯片

图 7 V形目标不同超分辨成像方法处理结果对比

Figure 7. Comparison of different super-resolution imaging methods for V points

下载: 全尺寸图片幻灯片

图 8 V形目标不同超分辨成像方法处理结果剖面对比

Figure 8. Result profile comparison of different super-resolution imaging methods for V points

下载: 全尺寸图片幻灯片

图 9 点阵目标不同超分辨成像方法结果对比

Figure 9. Comparison of different super-resolution imaging methods for multiple point targets

下载: 全尺寸图片幻灯片

图 10 点阵目标不同超分辨成像方法结果剖面对比

Figure 10. Profile comparison of different super-resolution imaging methods for multiple point targets

下载: 全尺寸图片幻灯片

图 11 不同超分辨方法在不同信噪比下重建结果的平均主瓣宽度

Figure 11. Average mainlobe width of different super-resolution methods under different SNRs

下载: 全尺寸图片幻灯片

图 12 不同方位向采样点数下超分辨处理运行时间

Figure 12. Operational time of different super-resolution methods with different azimuthal samples

下载: 全尺寸图片幻灯片

图 13 不同算法实测数据角超分辨结果

Figure 13. Experimental results of different super-resolution methods

下载: 全尺寸图片幻灯片

图 14 环扫监视雷达不同算法实测数据角超分辨结果

Figure 14. Experimental results of different superresolution methods for circular scanning radar

下载: 全尺寸图片幻灯片

表 1 雷达系统仿真参数

Table 1. Radar system simulation parameters

参数	数值
扫描速度	50°/s
扫描范围	–8°～+8°
脉冲重复频率	1000 Hz
主瓣波束宽度	5.1°
载波频率	9.6 GHz
信号带宽	45 MHz
信号时宽	2 μs
采样率	90 MHz
平台速度	30 m/s

下载: 导出CSV

表 2 V型场景不同超分辨方法的MSE对比

Table 2. MSE comparison of different super-resolution methods

方法	MSE
Tikhonov L2方法	26.4810
分裂Bregman L1方法	3.3306
IAA方法($\gamma = $0.2)	13.2678
IAA方法($\gamma = $0.05)	8.0262
所提IAA-Net方法	2.2932

下载: 导出CSV

参考文献(53)

[1]	SKOLNIK M I. Introduction to Radar Systems[M]. New York: McGraw-Hill, 1980.
[2]	杨建宇. 雷达对地成像技术多向演化趋势与规律分析[J]. 雷达学报, 2019, 8(6): 669–692. doi: 10.12000/JR19099. YANG Jianyu. Multi-directional evolution trend and law analysis of radar ground imaging technology[J]. Journal of Radars, 2019, 8(6): 669–692. doi: 10.12000/JR19099.
[3]	RICHARDS M A, 邢孟道, 王彤, 李真芳, 等译. 雷达信号处理基础[M]. 北京: 电子工业出版社, 2008. RICHARDS M A, XING Mengdao, WANG Tong, LI Zhenfang, et al. translation. Fundamentals of Radar Signal Processing[M]. Beijing: Publishing House of Electronics Industry, 2008.
[4]	CUMMING I G, WONG F H, 洪文, 胡东辉, 等译. 合成孔径雷达成像: 算法与实现[M]. 北京: 电子工业出版社, 2007. CUMMING I G, WONG F H, HONG Wen, HU Donghui, et al. translation. Digital Processing of Synthetic Aperture Radar Data: Algorithms and Implementation[M]. Beijing: Publishing House of Electronics Industry, 2007.
[5]	李亚超, 王家东, 张廷豪, 等. 弹载雷达成像技术发展现状与趋势[J]. 雷达学报, 2022, 11(6): 943–973. doi: 10.12000/JR22119. LI Yachao, WANG Jiadong, ZHANG Tinghao, et al. Present situation and prospect of missile-borne radar imaging technology[J]. Journal of Radars, 2022, 11(6): 943–973. doi: 10.12000/JR22119.
[6]	SADJADI F. Enhancing angular resolution in non-coherent radar imagery[C]. International Radar Conference, Beijing, China, 1996: 330–333. doi: 10.1109/ICR.1996.574454.
[7]	FOUETTILLOUX R, FERRO-FAMIL L, MÉRIE S, et al. Improving the angular resolution of a scanning radar with imperfectly known antenna patterns[C]. 2019 IEEE Conference on Antenna Measurements & Applications (CAMA), Kuta, Bali, Indonesia, 2019: 231–234. doi: 10.1109/CAMA47423.2019.8959779.
[8]	丁义元, 杨建宇, 张卫华, 等. 改进实孔径雷达角分辨力的广义逆滤波方法[J]. 电子学报, 1993, 21(9): 15–19. doi: 10.3321/j.issn:0372-2112.1993.09.003. DING Yiyuan, YANG Jianyu, ZHANG Weihua, et al. Improvement of angular resolution of real aperture radar via generalized inverse filtering[J]. Acta Electronica Sinica, 1993, 21(9): 15–19. doi: 10.3321/j.issn:0372-2112.1993. 09.003.
[9]	单荣光, 李士国, 朱力. 去卷积实现雷达方位超分辨[J]. 现代雷达, 1993, 15(6): 25–32. doi: 10.16592/j.cnki.1004-7859.1993.06.004. SHAN Rongguang, LI Shiguo, and ZHU Li. Radar azimuth super-resolution using deconvolution[J]. Modern Radar, 1993, 15(6): 25–32. doi: 10.16592/j.cnki.1004-7859.1993.06.004.
[10]	盛卫星, 方大纲, 杨正龙, 等. 一般非综合孔径雷达方位超分辨研究[J]. 南京理工大学学报, 2000, 24(4): 289–295. doi: 10.14177/j.cnki.32-1397n.2000.04.001. SHENG Weixing, FANG Dagang, YANG Zhenglong, et al. Angular super-resolution for real aperture radars[J]. Journal of Nanjing University of Science and Technology, 2000, 24(4): 289–295. doi: 10.14177/j.cnki.32-1397n.2000.04.001.
[11]	许然. 提高雷达成像质量的若干新体制和新方法研究[D]. [博士论文], 西安电子科技大学, 2015. doi: 10.7666/d.Y2954050. XU Ran. Study on new systems and techniques for improving radar imaging performances[D]. [Ph.D. dissertation], Xidian University, 2015. doi: 10.7666/d.Y2954050.
[12]	DUNCAN M J. Design of a repeater-jammer experiment for a monopulse radar[D]. [Master dissertation], NAVAL Postgraduate School, 1975.
[13]	谭珂. 机载前视雷达扫描波束锐化方法研究[D]. [博士论文], 电子科技大学, 2018. TAN Ke. Research on beam sharpening method of airborne forward-looking scanning radar[D]. [Ph.D. dissertation], University of Electronic Science and Technology of China, 2018.
[14]	吴迪, 朱岱寅, 朱兆达. 机载雷达单脉冲前视成像算法[J]. 中国图象图形学报, 2010, 15(3): 462–469. doi: 10.11834/jig.20100317. WU Di, ZHU Daiyin, and ZHU Zhaoda. Research on nomopulse forward-looking imaging algorithm for airborne radar[J]. Journal of Image and Graphics, 2010, 15(3): 462–469. doi: 10.11834/jig.20100317.
[15]	徐浩. 基于空间谱理论和时空两维随机辐射场的雷达成像研究[D]. [博士论文], 中国科学技术大学, 2011. doi: 10.7666/d.d141340. XU Hao. The radar imaging based on space spectrum and temporal-spatial stochastic radiation field[D]. [Ph.D. dissertation], University of Science and Technology of China, 2011. doi: 10.7666/d.d141340.
[16]	王建秋, 刘康, 王煜, 等. 涡旋电磁波雷达成像分辨力研究[J]. 雷达学报, 2021, 10(5): 680–690. doi: 10.12000/JR21054. WANG Jianqiu, LIU Kang, WANG Yu, et al. Resolution analysis of vortex electromagnetic radar imaging[J]. Journal of Radars, 2021, 10(5): 680–690. doi: 10.12000/JR21054.
[17]	付江南. 涡旋电磁场高分辨成像方法研究[D]. [硕士论文], 电子科技大学, 2022. doi: 10.27005/d.cnki.gdzku.2022.002306. FU Jiangnan. Study on high resolution imaging method of vortex electromagnetic field[D]. [Master dissertation], University of Electronic Science and Technology of China, 2022. doi: 10.27005/d.cnki.gdzku.2022.002306.
[18]	毛德庆. 机载雷达扫描波束超分辨成像方法研究[D]. [博士论文], 电子科技大学, 2022. doi: 10.27005/d.cnki.gdzku.2022.004148. MAO Deqing. Research on scanning beam super-resolution imaging methods for airborne radar[D]. [Ph.D. dissertation], University of Electronic Science and Technology of China, 2022. doi: 10.27005/d.cnki.gdzku.2022.004148.
[19]	赵正义, 侯颖妮. 基于TSVD的块稀疏重构雷达前视超分辨成像[J]. 系统工程与电子技术, 2023, 45(7): 2051–2059. doi: 10.12305/j.issn.1001-506X.2023.07.15. ZHAO Zhengyi and HOU Yingni. Radar forward-looking super resolution imaging based on block sparse reconstruction with TSVD[J]. Systems Engineering and Electronics, 2023, 45(7): 2051–2059. doi: 10.12305/j.issn.1001-506X.2023.07.15.
[20]	FARINA A, PRODI F, and VINELLI F. Application of superresolution techniques to radar imaging[J]. Journal of Systems Engineering and Electronics, 1994, 5(1): 1–14.
[21]	RICHARDSON W H. Bayesian-based iterative method of image restoration[J]. Journal of the Optical Society of America, 1972, 62(1): 55–59. doi: 10.1364/JOSA.62.000055.
[22]	LUCY L B. An iterative technique for the rectification of observed distributions[J]. The Astronomical Journal, 1974, 79(6): 745. doi: 10.1086/111605.
[23]	GUAN Jinchen, YANG Jianyu, HUANG Yulin, et al. Maximum a posteriori-based angular superresolution for scanning radar imaging[J]. IEEE Transactions on Aerospace and Electronic Systems, 2014, 50(3): 2389–2398. doi: 10.1109/TAES.2014.120555.
[24]	ZHANG Yin, ZHANG Qiping, LI Changlin, et al. Sea-surface target angular superresolution in forward-looking radar imaging based on maximum A posteriori algorithm[J]. IEEE Journal of Selected Topics in Applied Earth Observations and Remote Sensing, 2019, 12(8): 2822–2834. doi: 10.1109/JSTARS.2019.2918189.
[25]	ZHANG Yin, SHEN Jiahao, TUO Xingyu, et al. Scanning radar forward-looking superresolution imaging based on the Weibull distribution for a sea-surface target[J]. IEEE Transactions on Geoscience and Remote Sensing, 2022, 60: 5116111. doi: 10.1109/TGRS.2022.3194118.
[26]	马静雯. 基于反卷积的雷达角超分辨成像方法研究[D]. [硕士论文], 西安电子科技大学, 2018. doi: 10.7666/d.D01663882. MA Jingwen. Research on radar angular super-resolution imaging method based on deconvolution[D]. [Master dissertation], Xidian University, 2018. doi: 10.7666/d.D01663882.
[27]	LI Weixin, LI Ming, ZUO Lei, et al. Forward-looking super-resolution imaging for sea-surface target with multi-prior Bayesian method[J]. Remote Sensing, 2022, 14(1): 26. doi: 10.3390/rs14010026.
[28]	李维新, 李明, 陈洪猛, 等. 针对回波数据异常时的雷达前视超分辨快速成像方法[J]. 雷达学报, 2024, 13(3): 667–681. doi: 10.12000/JR23209. LI Weixin, LI Ming, CHEN Hongmeng, et al. Fast radar forward-looking super-resolution imaging for abnormal echo data[J]. Journal of Radars, 2024, 13(3): 667–681. doi: 10.12000/JR23209.
[29]	LI Weixin, LI Ming, ZUO Lei, et al. Real aperture radar forward-looking imaging based on variational Bayesian in presence of outliers[J]. IEEE Transactions on Geoscience and Remote Sensing, 2022, 60: 5117113. doi: 10.1109/TGRS.2022.3203807.
[30]	TAN Ke, LU Xingyu, YANG Jianchao, et al. A novel Bayesian super-resolution method for radar forward-looking imaging based on Markov random field model[J]. Remote Sensing, 2021, 13(20): 4115. doi: 10.3390/rs13204115.
[31]	CHEN Hongmeng, LI Yachao, GAO Wenquan, et al. Bayesian forward-looking superresolution imaging using Doppler deconvolution in expanded beam space for high-speed platform[J]. IEEE Transactions on Geoscience and Remote Sensing, 2022, 60: 5105113. doi: 10.1109/TGRS.2021.3107717.
[32]	陈洪猛, 余继周, 张文杰, 等. 基于概率模型驱动的机载贝叶斯前视超分辨多目标成像方法[J]. 雷达学报, 2023, 12(6): 1125–1137. doi: 10.12000/JR23080. CHEN Hongmeng, YU Jizhou, ZHANG Wenjie, et al. Probability model-driven airborne Bayesian forward-looking super-resolution imaging for multitarget scenario[J]. Journal of Radars, 2023, 12(6): 1125–1137. doi: 10.12000/JR23080.
[33]	HUANG Yulin, ZHA Yuebo, WANG Yue, et al. Forward looking radar imaging by truncated singular value decomposition and its application for adverse weather aircraft landing[J]. Sensors, 2015, 15(6): 14397–14414. doi: 10.3390/s150614397.
[34]	张启平. 雷达实孔径超分辨成像中的正则化方法研究[D]. [博士论文], 电子科技大学, 2021. doi: 10.27005/d.cnki.gdzku.2021.005078. ZHANG Qiping. Research on regularization method in radar real-aperture super-resolution imaging[D]. [Ph.D. dissertation], University of Electronic Science and Technology of China, 2021. doi: 10.27005/d.cnki.gdzku.2021.005078.
[35]	周静. 相控阵雷达前视成像算法研究[D]. [硕士论文], 西安电子科技大学, 2021. doi: 10.27389/d.cnki.gxadu.2021.001024. ZHOU Jing. Research on forward-looking imaging method of phased array radar[D]. [Master dissertation], Xidian University, 2021. doi: 10.27389/d.cnki.gxadu.2021.001024.
[36]	张鑫. 雷达方位超分辨关键技术研究[D]. [博士论文], 大连海事大学, 2018. doi: 10.7666/d.Y3368947. ZHANG Xin. Research on the key technology of radar azimuth super-resolution[D]. [Ph.D. dissertation], Dalian Maritime University, 2018. doi: 10.7666/d.Y3368947.
[37]	王子曦. 基于正则化的雷达前视超分辨成像算法工程应用分析[J]. 电子技术与软件工程, 2021(17): 89–92. WANG Zixi. An engineering application analysis of regularization-based radar forward-looking super-resolution imaging algorithm[J]. Electronic Technology & Software Engineering, 2021(17): 89–92.
[38]	樊晨阳, 贺思三, 李西敏, 等. 基于阵列雷达扫描的正则化前视成像方法[J]. 电光与控制, 2022, 29(10): 76–81. doi: 10.3969/j.issn.1671-637X.2022.10.014. FAN Chenyang, HE Sisan, LI Ximin, et al. A regularized forward-looking imaging method based on array radar scanning[J]. Electronics Optics & Control, 2022, 29(10): 76–81. doi: 10.3969/j.issn.1671-637X.2022.10.014.
[39]	唐军奎, 刘峥, 冉磊, 等. 基于稀疏和低秩先验的雷达前视超分辨成像方法[J]. 雷达学报, 2023, 12(2): 332–342. doi: 10.12000/JR22199. TANG Junkui, LIU Zheng, RAN Lei, et al. Radar forward-looking super-resolution imaging method based on sparse and low-rank priors[J]. Journal of Radars, 2023, 12(2): 332–342. doi: 10.12000/JR22199.
[40]	吴阳. 基于正则化理论的运动平台雷达超分辨成像方法研究[D]. [硕士论文], 电子科技大学, 2019. WU Yang. Radar super-resolution imaging method of moving platform based on the regularization theory[D]. [Master dissertation], University of Electronic Science and Technology of China, 2019.
[41]	杨志伟, 贺顺, 廖桂生. 机载单通道雷达实波束扫描的前视探测[J]. 航空学报, 2012, 33(12): 2240–2245. YANG Zhiwei, HE Shun, and LIAO Guisheng. Forward-looking detection for airborne single-channel radar with beam scanning[J]. Acta Aeronautica et Astronautica Sinica, 2012, 33(12): 2240–2245.
[42]	张洁, 吴迪, 朱岱寅. 一种机载/弹载阵列雷达前视超分辨成像算法[J]. 雷达科学与技术, 2018, 16(2): 119–124. doi: 10.3969/j.issn.1672-2337.2018.02.001. ZHANG Jie, WU Di, and ZHU Daiyin. A forward-looking super-resolution imaging algorithm for airborne/missile-borne array radar[J]. Radar Science and Technology, 2018, 16(2): 119–124. doi: 10.3969/j.issn.1672-2337.2018.02.001.
[43]	YARDIBI T, LI Jian, STOICA P, et al. Source localization and sensing: A nonparametric iterative adaptive approach based on weighted least squares[J]. IEEE Transactions on Aerospace and Electronic Systems, 2010, 46(1): 425–443. doi: 10.1109/TAES.2010.5417172.
[44]	ZHANG Yongchao, ZHANG Yin, LI Wenchao, et al. Super-resolution surface mapping for scanning radar: Inverse filtering based on the fast iterative adaptive approach[J]. IEEE Transactions on Geoscience and Remote Sensing, 2018, 56(1): 127–144. doi: 10.1109/TGRS.2017.2743263.
[45]	ZHANG Yongchao, MAO Deqing, ZHANG Qian, et al. Airborne forward-looking radar super-resolution imaging using iterative adaptive approach[J]. IEEE Journal of Selected Topics in Applied Earth Observations and Remote Sensing, 2019, 12(7): 2044–2054. doi: 10.1109/JSTARS.2019.2920859.
[46]	MAO Deqing, ZHANG Yongchao, ZHANG Yin, et al. Target fast reconstruction of real aperture radar using data extrapolation-based parallel iterative adaptive approach[J]. IEEE Journal of Selected Topics in Applied Earth Observations and Remote Sensing, 2021, 14: 2258–2269. doi: 10.1109/JSTARS.2021.3054046.
[47]	LI Yueli, LIU Jianguo, JIANG Xiaoqing, et al. Angular superresol for signal model in coherent scanning radars[J]. IEEE Transactions on Aerospace and Electronic Systems, 2019, 55(6): 3103–3116. doi: 10.1109/TAES.2019.2900133.
[48]	任凌云, 吴迪, 朱岱寅, 等. 基于机载多通道雷达迭代超分辨估计的前视成像[J]. 雷达学报, 2023, 12(6): 1166–1178. doi: 10.12000/JR23085. REN Lingyun, WU Di, ZHU Daiyin, et al. Forward-looking imaging via iterative super-resolution estimation in airborne multi-channel radar[J]. Journal of Radars, 2023, 12(6): 1166–1178. doi: 10.12000/JR23085.
[49]	张永超. 机载雷达前视虚拟阵列超分辨成像方法研究[D]. [博士论文], 电子科技大学, 2018. ZHANG Yongchao. Research on virtual-array approach for airborne radar forward-looking super-resolution imaging[D]. [Ph.D. dissertation], University of Electronic Science and Technology of China, 2018.
[50]	STOICA P, ZACHARIAH D, and LI Jian. Weighted SPICE: A unifying approach for hyperparameter-free sparse estimation[J]. Digital Signal Processing, 2014, 33: 1–12. doi: 10.1016/j.dsp.2014.06.010.
[51]	QI Lijuan, ZHENG Mingjie, YU Weidong, et al. Super-resolution Doppler beam sharpening imaging based on an iterative adaptive approach[J]. Remote Sensing Letters, 2016, 7(3): 259–268. doi: 10.1080/2150704X.2015.1128129.
[52]	ZHANG Yongchao, ZHANG Yin, HUANG Yulin, et al. Angular superresolution for scanning radar with improved regularized iterative adaptive approach[J]. IEEE Geoscience and Remote Sensing Letters, 2016, 13(6): 846–850. doi: 10.1109/LGRS.2016.2550491.
[53]	朱晗归, 冯为可, 冯存前, 等. 机载雷达深度展开空时自适应处理方法[J]. 雷达学报, 2022, 11(4): 676–691. doi: 10.12000/JR22051. ZHU Hangui, FENG Weike, FENG Cunqian, et al. Deep unfolding based space-time adaptive processing method for airborne radar[J]. Journal of Radars, 2022, 11(4): 676–691. doi: 10.12000/JR22051.