Clutter Suppression Technology Based Space-time Adaptive ANM-ADMM-Net for Bistatic SAR
-
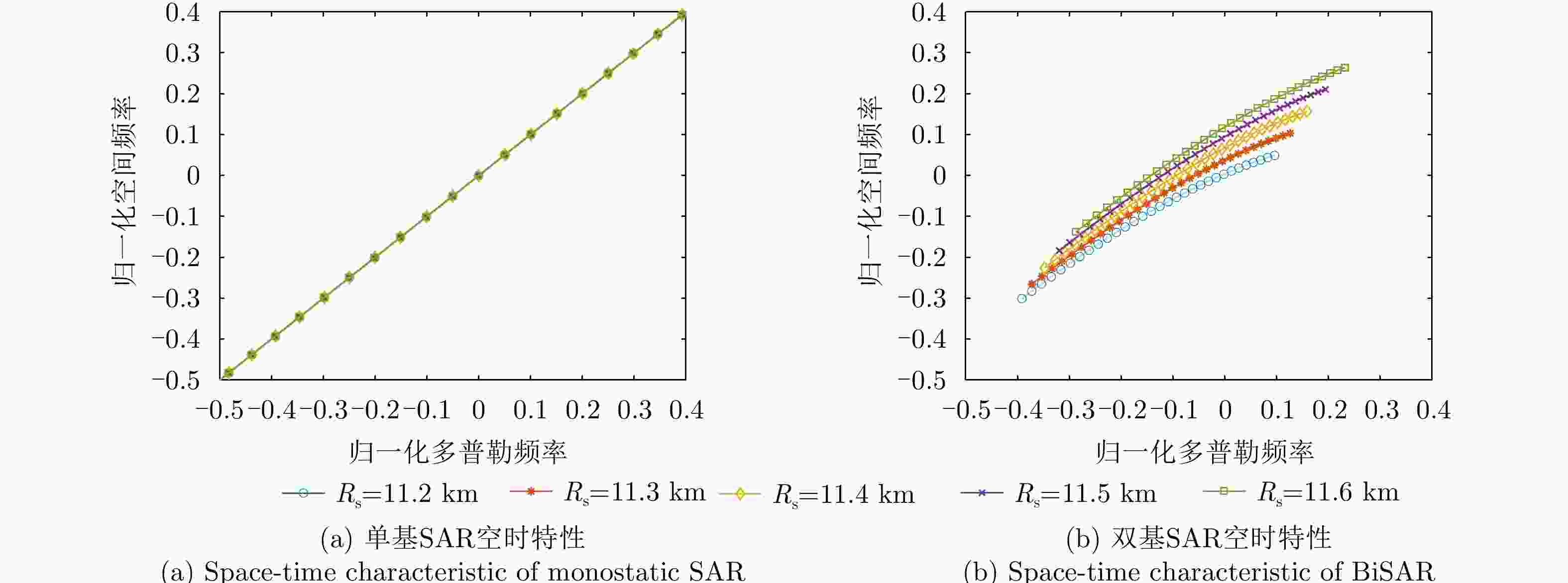
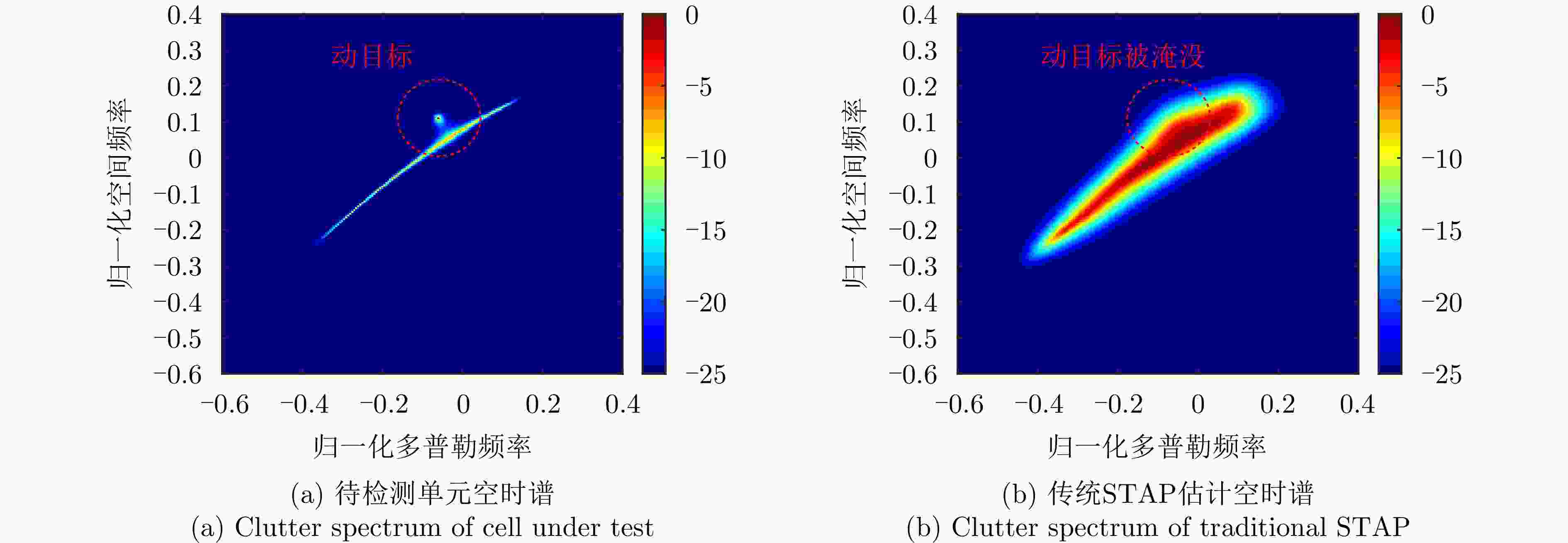
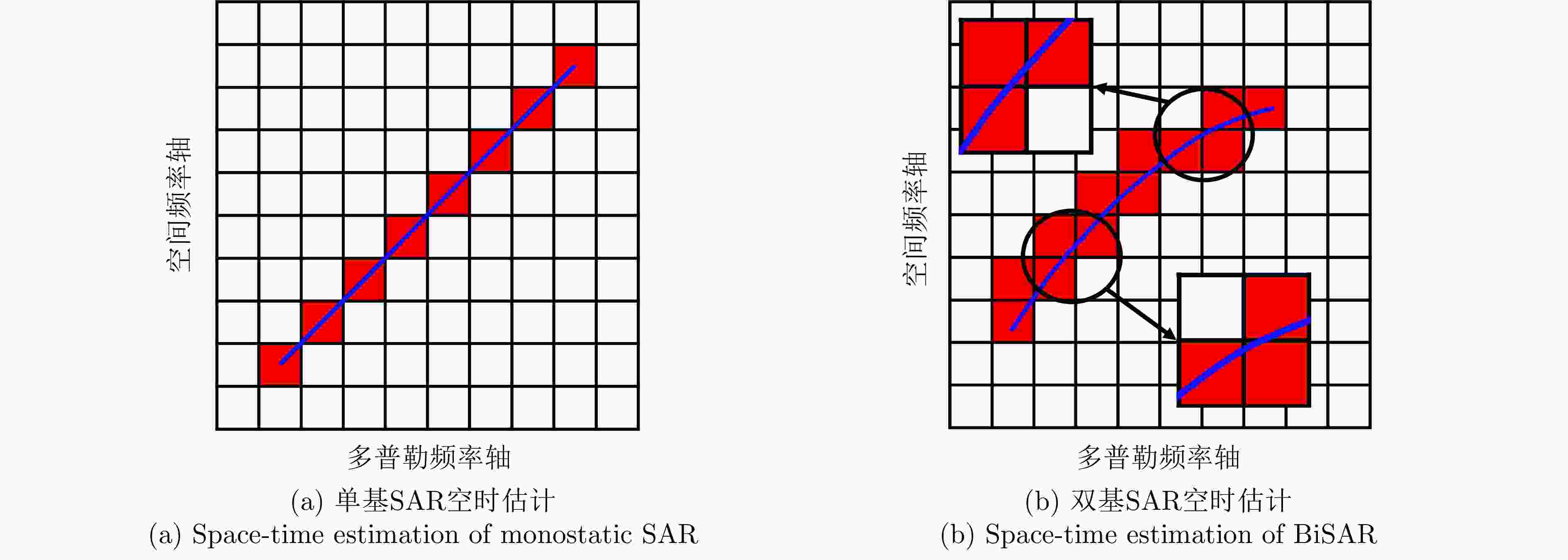
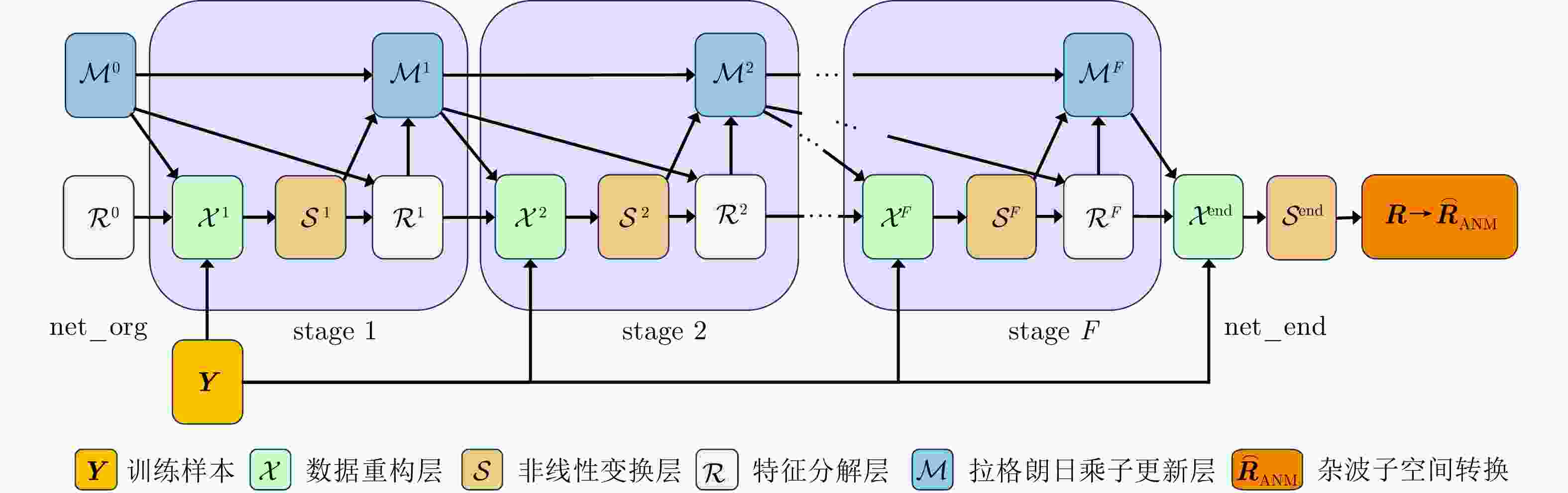
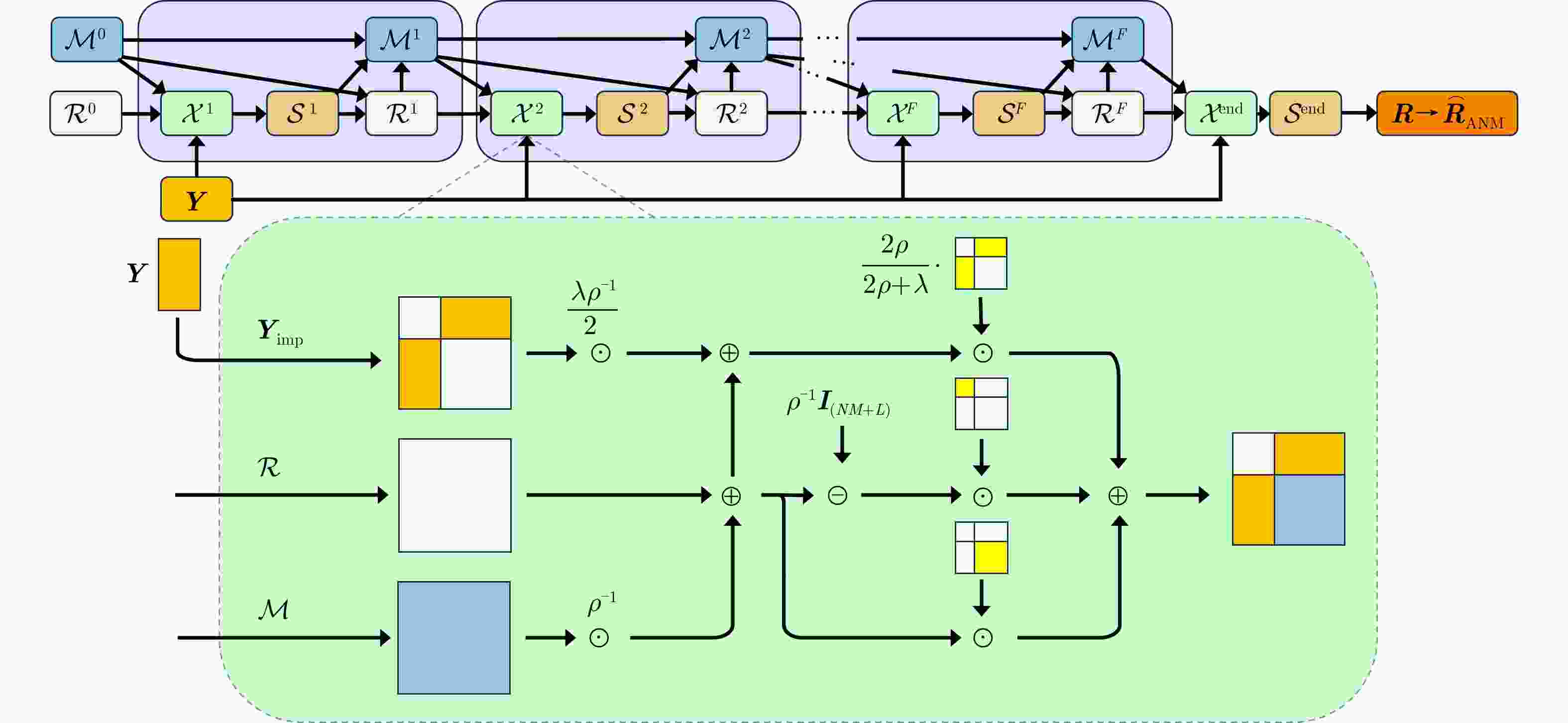
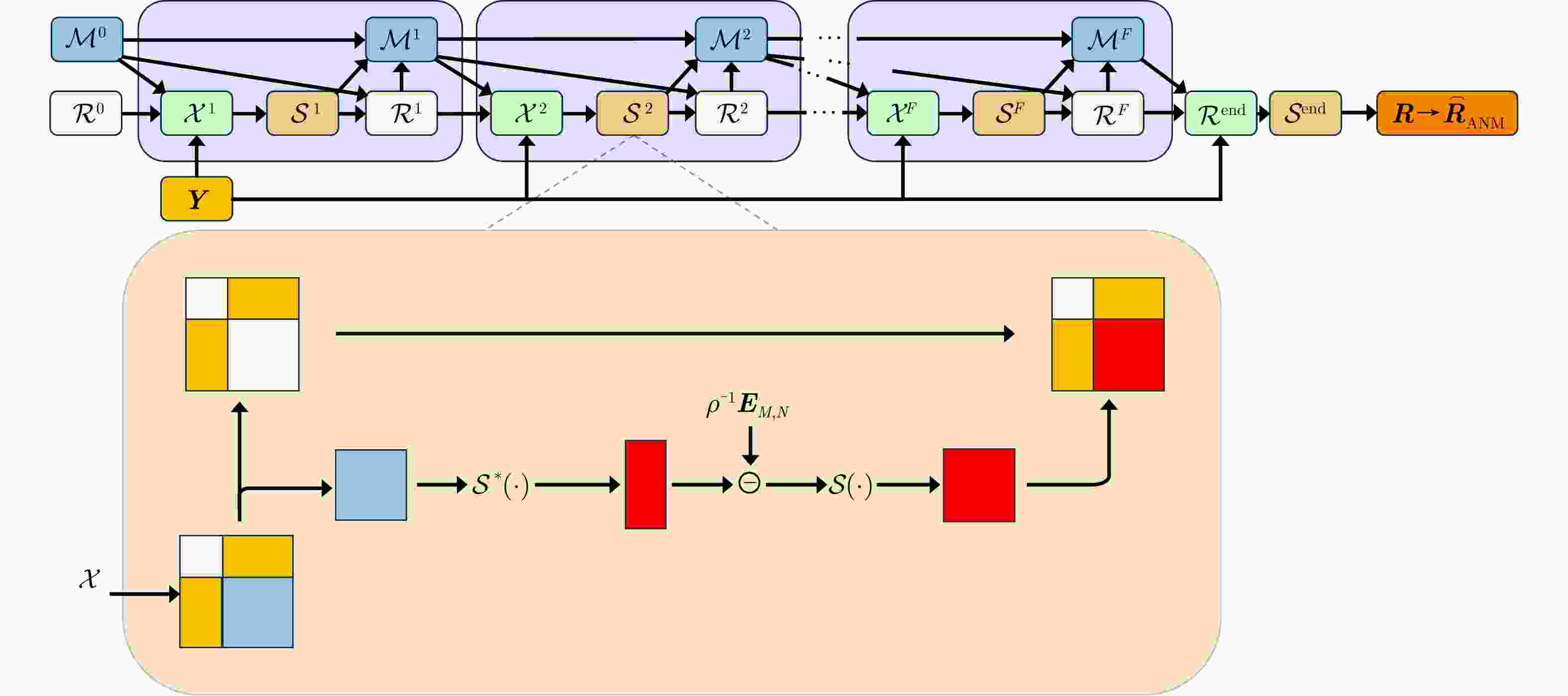
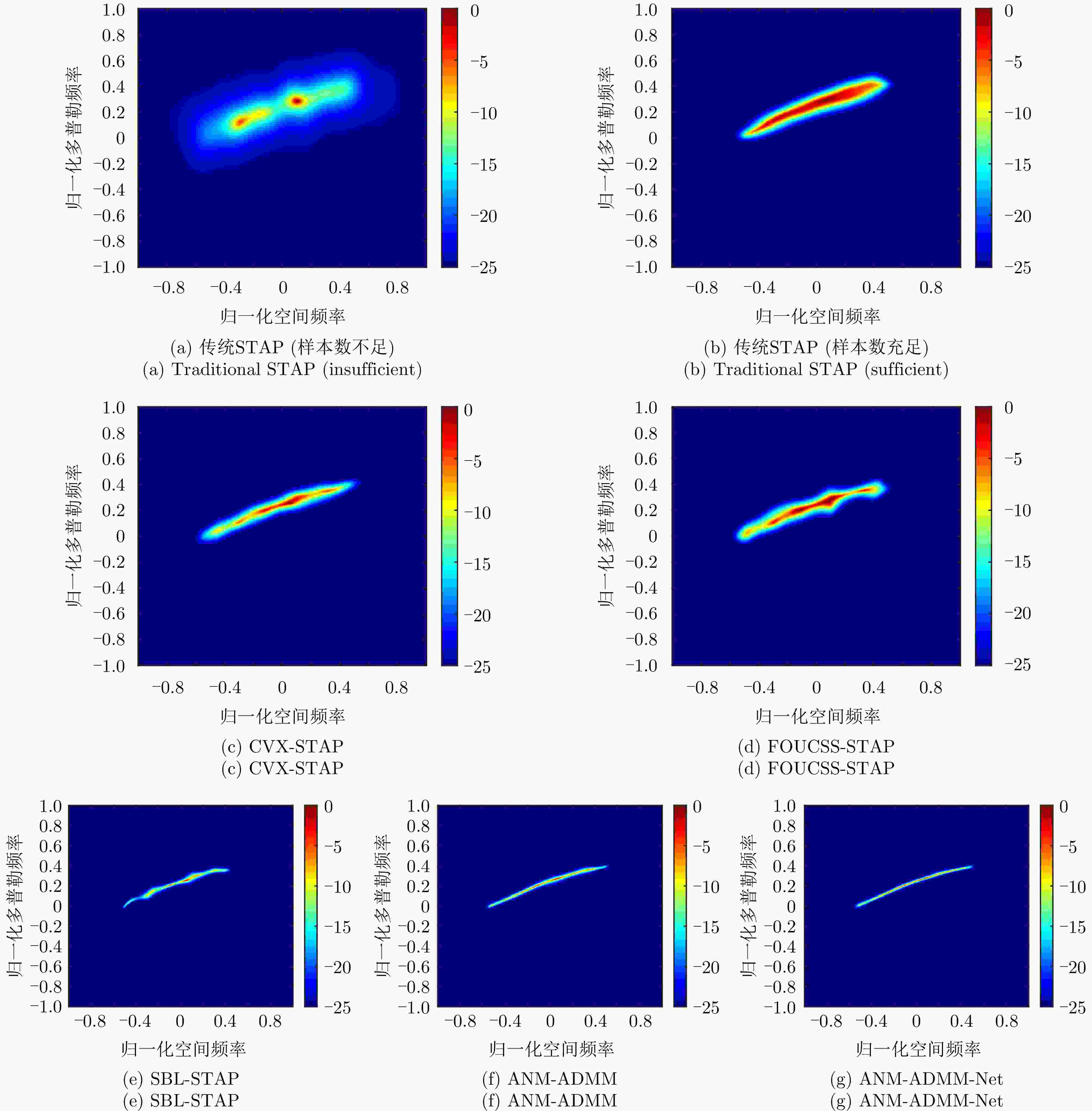
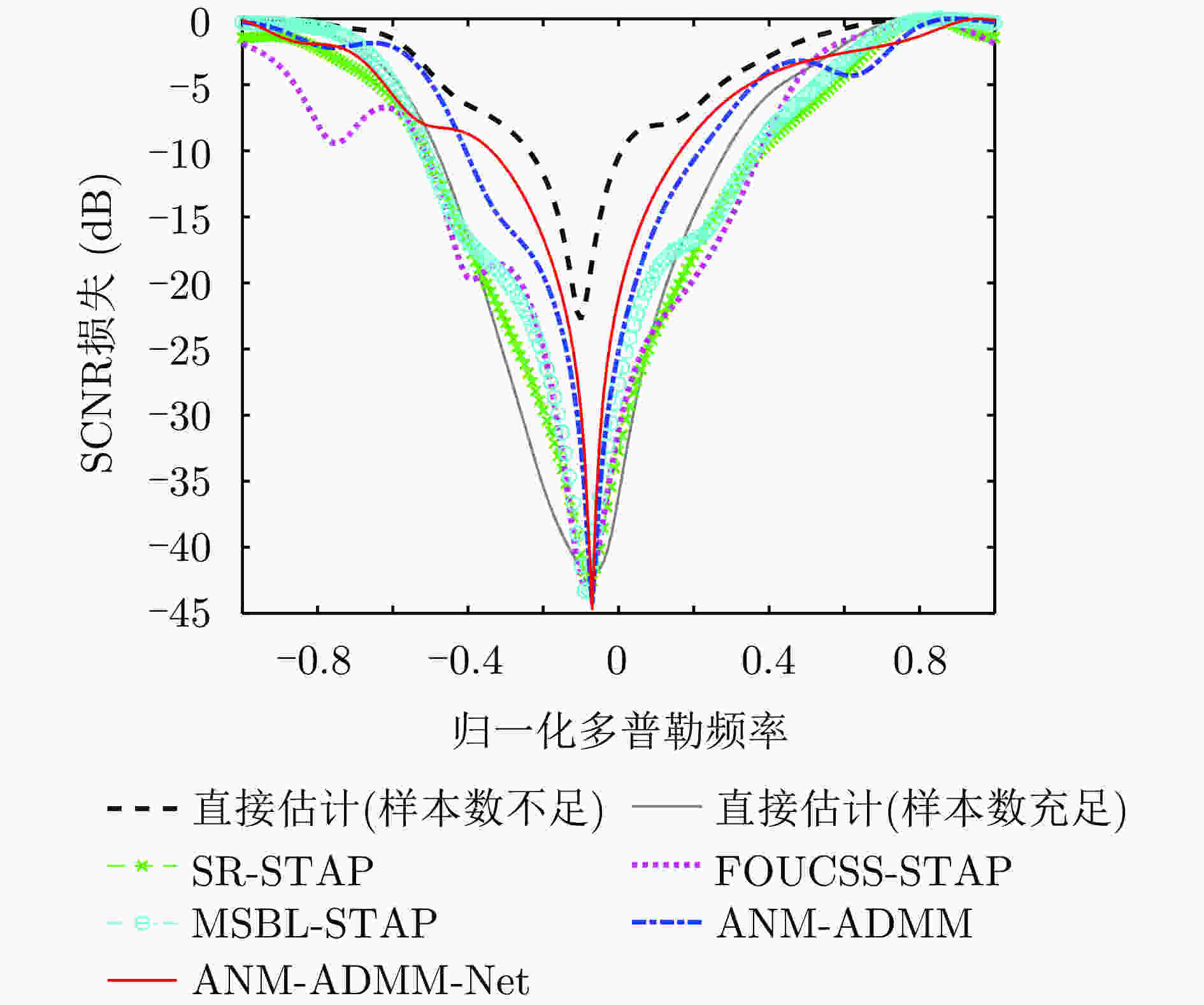
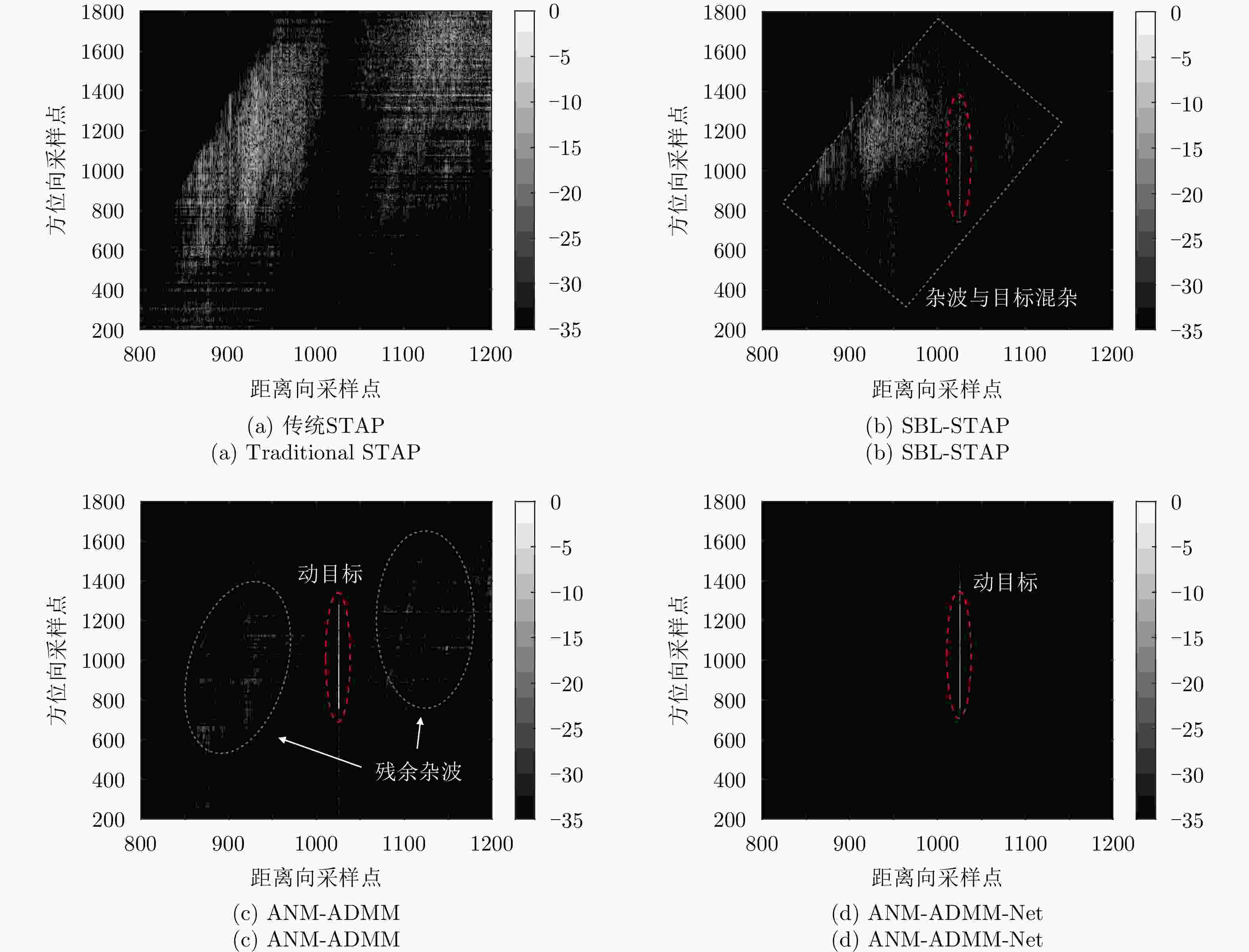
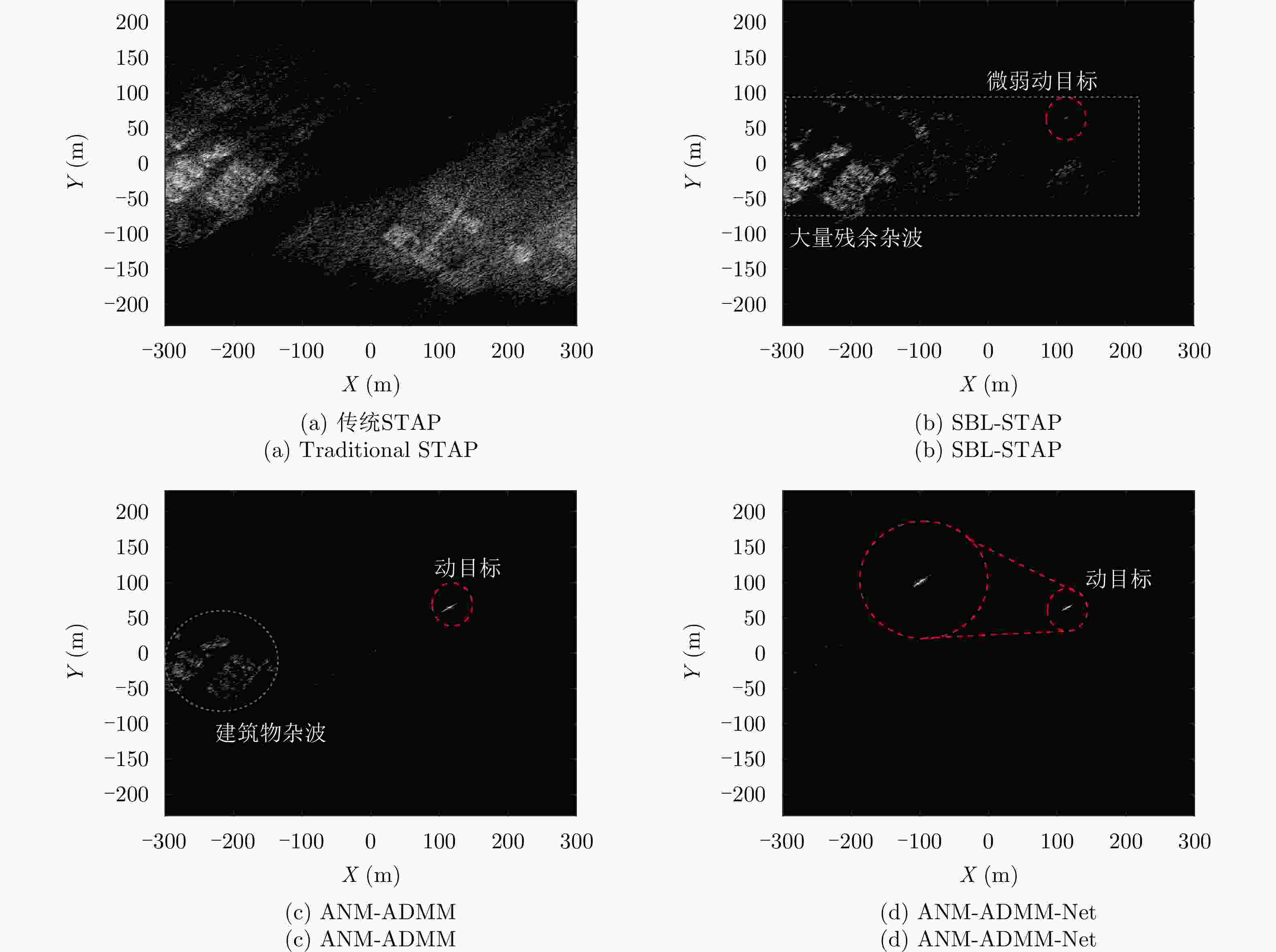
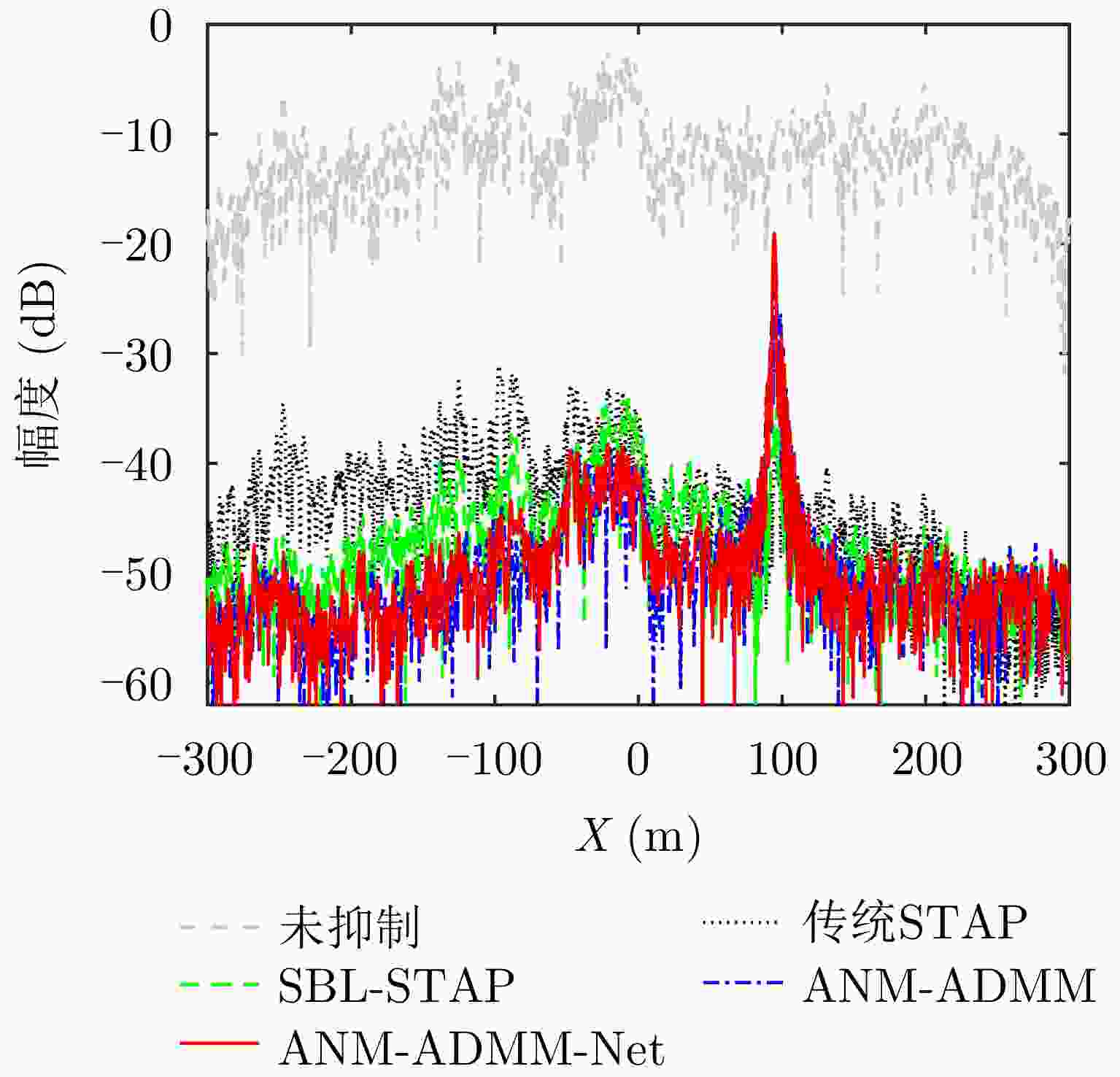
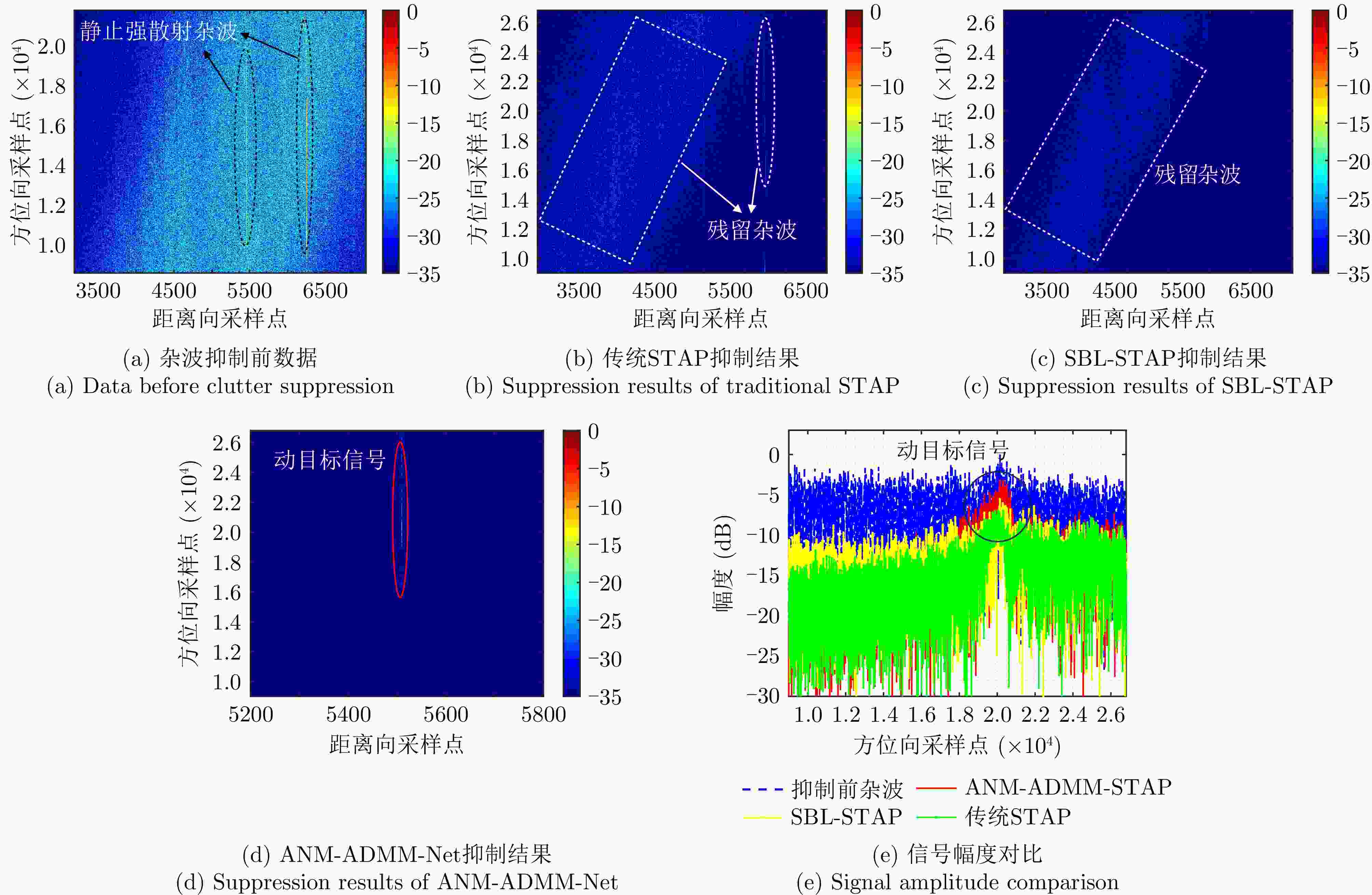
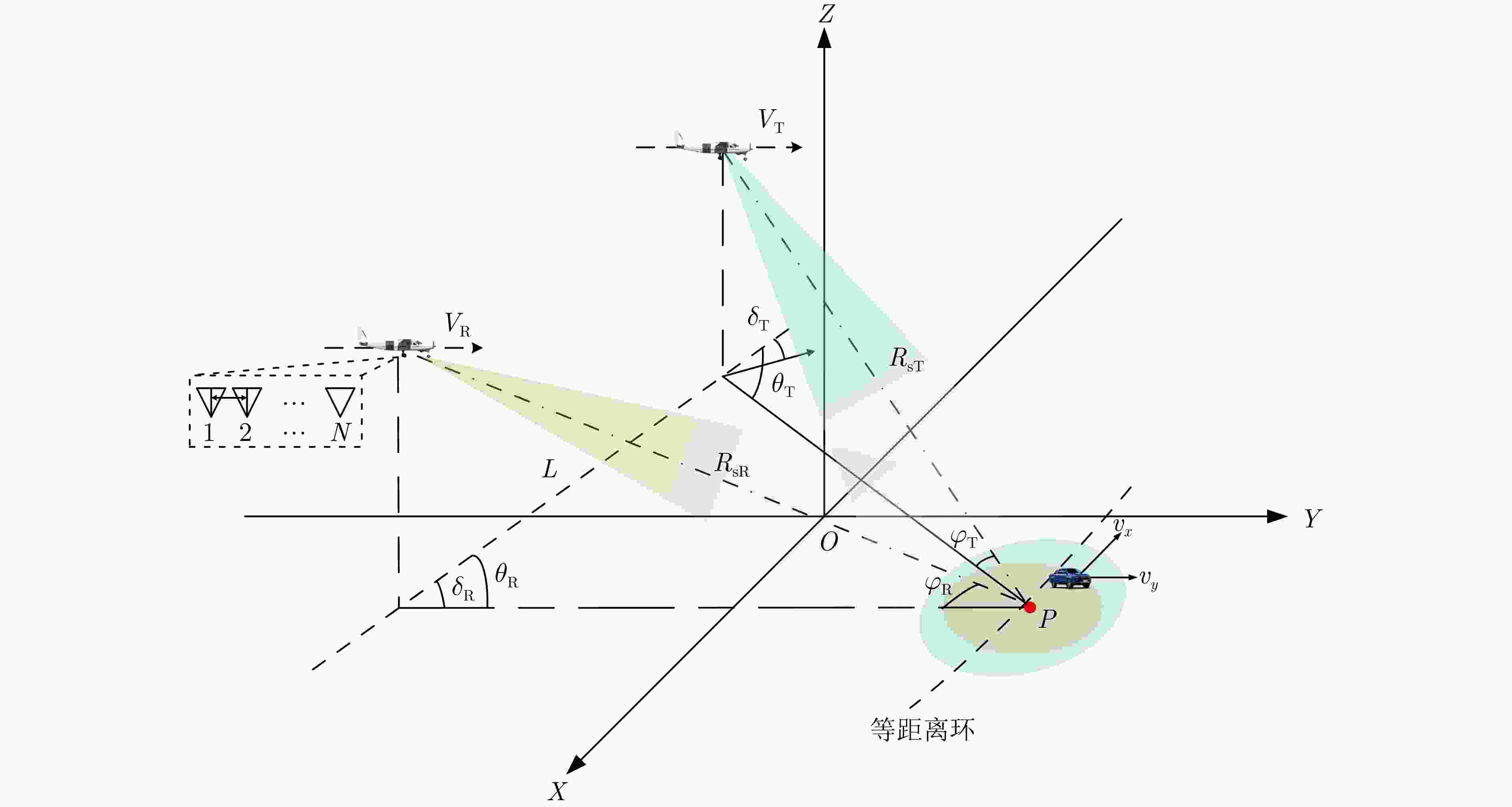
摘要: 双基合成孔径雷达(BiSAR)在实现对地面运动目标检测和成像时,需要抑制地面背景杂波。然而由于双基SAR收发分置的空间构型,会导致主瓣杂波出现严重的空时非平稳问题,从而恶化杂波抑制性能。基于稀疏恢复空时自适应处理方法(SR-STAP)虽然可以通过降低样本数量减少非平稳的影响,但是在处理过程中会出现字典离网问题,从而导致空时谱估计效果下降。并且大部分现有的典型SR-STAP方法虽然具有明确的数学关系和可解释性,但在针对复杂、多变场景时,也存在参数设置不恰当、运算复杂等问题。为解决上述一系列问题,该文提出了一种适用于双基SAR空时自适应杂波抑制处理的基于交替方向乘子法(ADMM)的复值神经网络ANM-ADMM-Net。首先,基于原子范数最小化(ANM)构建双基SAR连续空时域下杂波谱的稀疏恢复模型,克服传统离散字典模型下的离网问题;其次,采取ADMM对该双基SAR杂波谱稀疏恢复模型进行快速迭代求解;然后,根据迭代流程和数据流图进行网络化处理,将人工超参数迭代过程转换为网络可学习的ANM-ADMM-Net;再次,设置归一化均方根误差网络损失函数,并利用获取的数据集对网络模型进行训练;最后,利用训练后的ANM-ADMM-Net网络架构对双基SAR回波数据进行快速迭代处理,从而完成双基SAR杂波空时谱的精确估计和高效抑制。该文通过仿真试验和实测数据处理,表明该方法具有更好的杂波抑制性能和更加高效的运算效率。
-
关键词:
- 双基合成孔径雷达(BiSAR) /
- 稀疏恢复 /
- 空时处理 /
- 杂波抑制 /
- 复值神经网络
Abstract: Bistatic Synthetic Aperture Radar (BiSAR) needs to suppress ground background clutter when detecting and imaging ground moving targets. However, due to the spatial configuration of BiSAR, the clutter poses a serious space-time nonstationary problem, which deteriorates the clutter suppression performance. Although Space-Time Adaptive Processing based on Sparse Recovery (SR-STAP) can reduce the nonstationary problem by reducing the number of samples, the off-grid dictionary problem will occur during processing, resulting in a decrease in the space-time spectrum estimation effect. Although most of the typical SR-STAP methods have clear mathematical relations and interpretability, they also have some problems, such as improper parameter setting and complicated operation in complex and changeable scenes. To solve the aforementioned problems, a complex neural network based on the Alternating Direction Method of Multiplier (ADMM), is proposed for BiSAR space-time adaptive clutter suppression. First, a sparse recovery model of the continuous clutter space-time domain of BiSAR is constructed based on the Atomic Norm Minimization (ANM) to overcome the off-grid problem associated with the traditional discrete dictionary model. Second, ADMM is used to rapidly and iteratively solve the BiSAR clutter spectral sparse recovery model. Third according to the iterative and data flow diagrams, the artificial hyperparameter iterative process is transformed into ANM-ADMM-Net. Then, the normalized root-mean-square-error network loss function is set up and the network model is trained with the obtained data set. Finally, the trained ANM-ADMM-Net architecture is used to quickly process BiSAR echo data, and the space-time spectrum of BiSAR clutter is accurately estimated and efficiently restrained. The effectiveness of this approach is validated through simulations and airborne BiSAR clutter suppression experiments. -
表 1 不同算法的计算复杂度
Table 1. Computational complexity of different algorithms
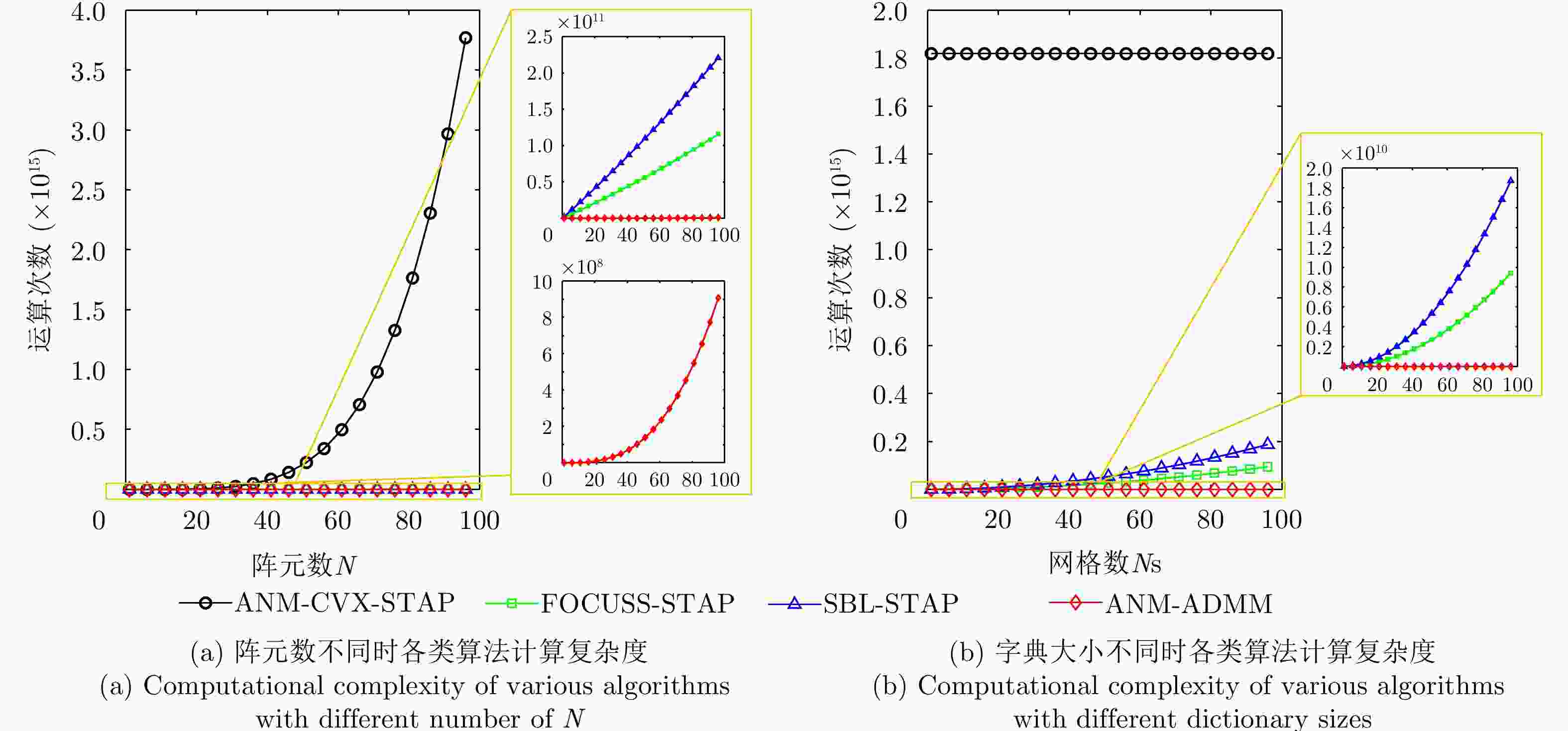
算法 计算复杂度 ANM-CVX-STAP $O({({L^2} + (2M - 1)(2N - 1) + MNL)^2}{(L + MN)^{2.5}})$ FOUCSS-STAP $O(NM{N_{\text{s}}}{M_{\text{d}}} + {(NM)^3} + 2{(NM)^2}{N_{\text{s}}}{M_{\text{d}}} + NM{({N_{\text{s}}}{M_{\text{d}}})^2})$ SBL-STAP $O(NM{N_{\text{s}}}{M_{\text{d}}} + {(NM)^3} + 3{(NM)^2}{N_{\text{s}}}{M_{\text{d}}} + 2NM{({N_{\text{s}}}{M_{\text{d}}})^2})$ ANM-ADMM $O({(MN + L)^3} + {(MN)^2} + 6MN + {L^2} + L)$ 表 2 算法运行时间对比(s)
Table 2. Run time of different algorithms (s)
算法 平均运行时间 ANM-CVX-STAP 32.7150 FOUCSS-STAP 5.3151 SBL-STAP 10.9429 ANM-ADMM 1.9462 表 3 双基SAR仿真参数
Table 3. Simulation parameters of BiSAR
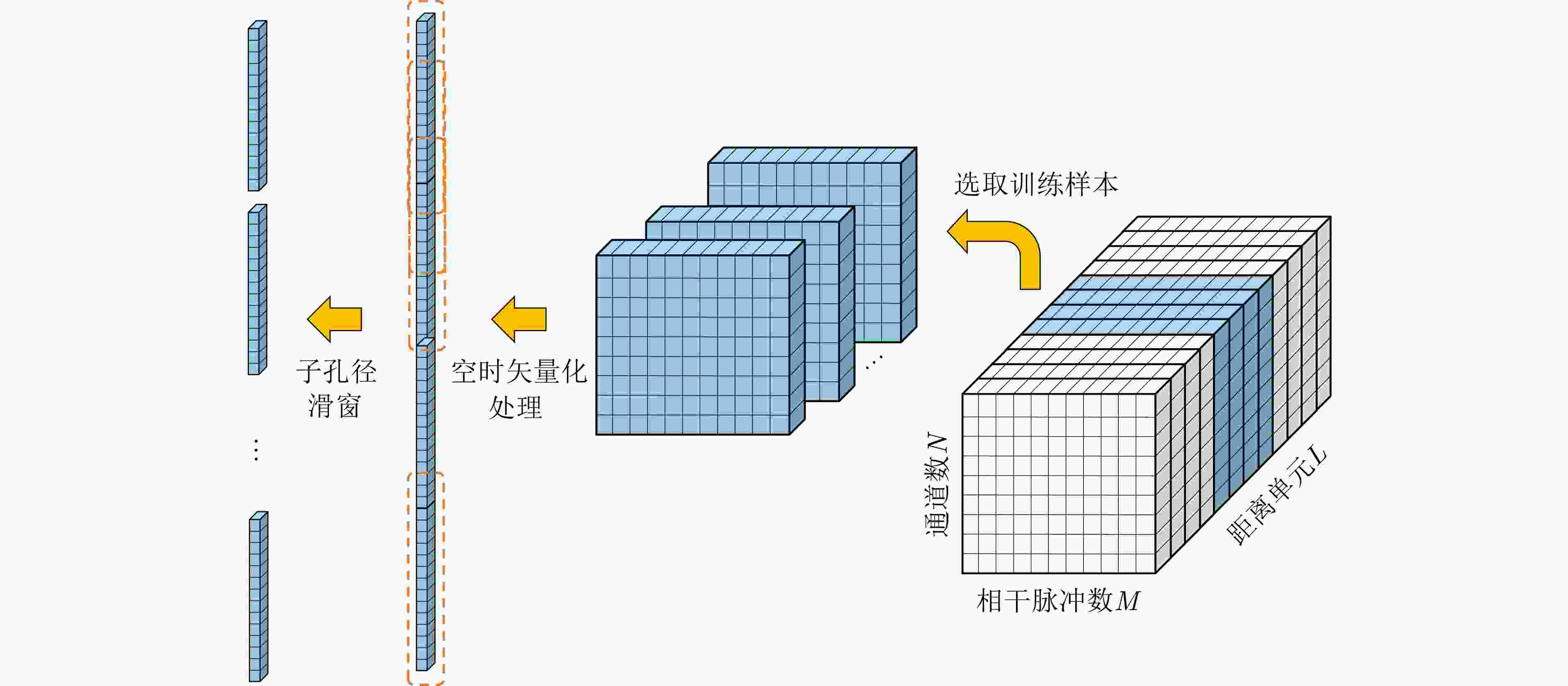
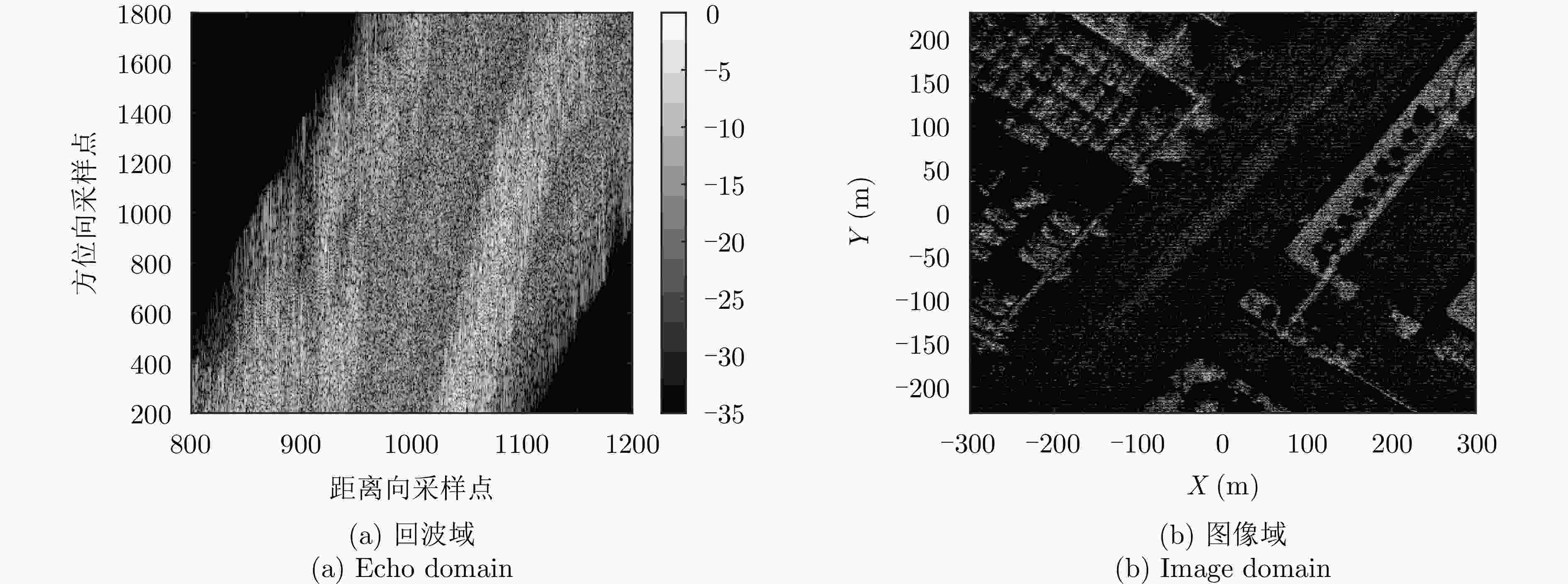
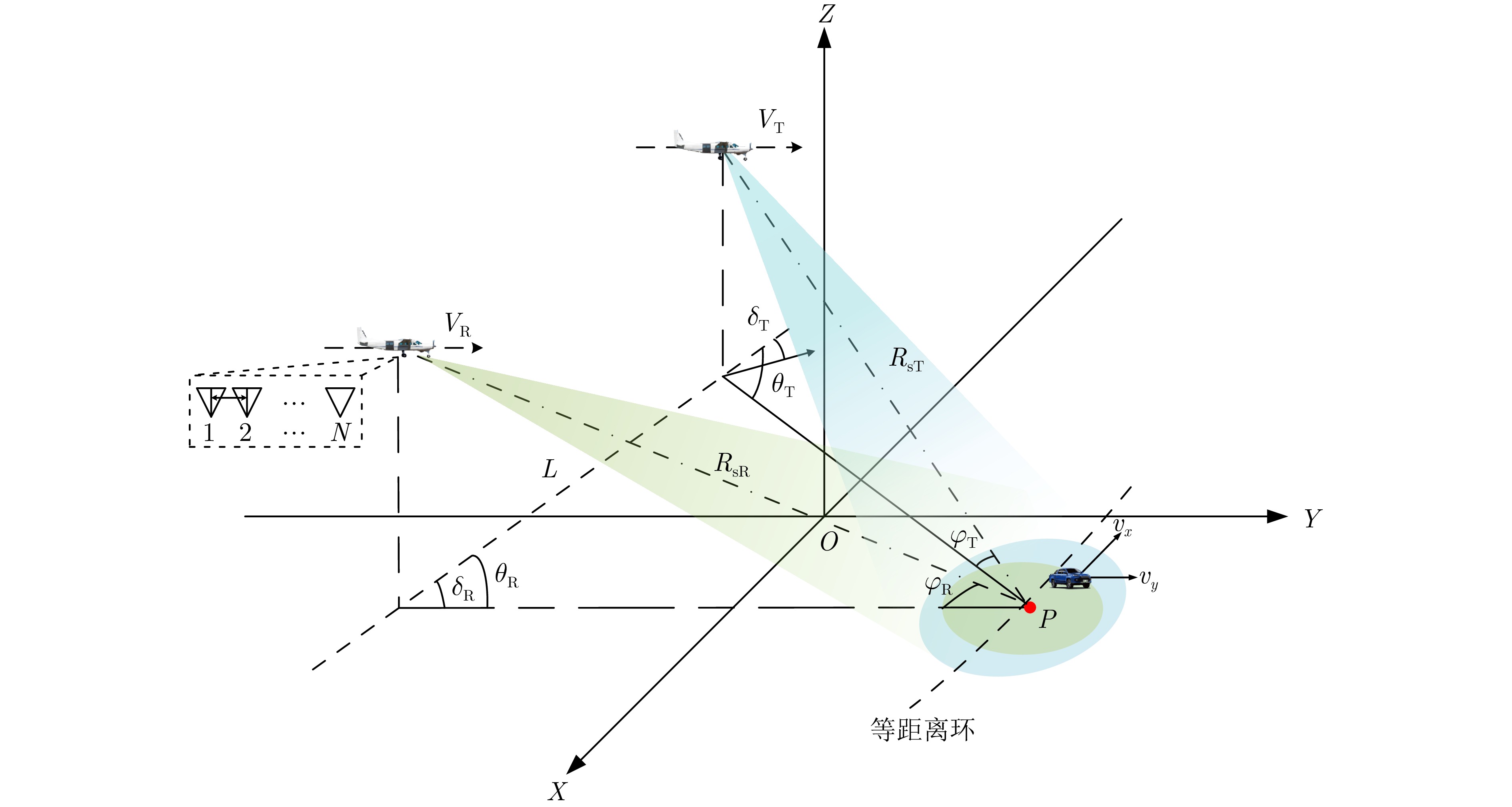
参数 数值 载频 10 GHz 信号带宽 150 MHz 脉冲重复频率 1000 Hz天线通道数 5 相干脉冲数 10 发射机初始位置 (– 5000 , –3000 ,4000 ) m接收机初始位置 (0, – 5000 ,3000 ) m发射机速度矢量 (0, 150, 0) m/s 接收机速度矢量 (0, 150, 0) m/s 运动目标初始位置 (0, 0, 0) m 运动目标速度矢量 (–4, 4, 0) m/s -
[1] ROBINSON P N. Synthetic array radar[J]. IEEE Potentials, 1997, 16(1): 8–11. doi: 10.1109/45.565604. [2] 杨建宇. 双基地合成孔径雷达技术[J]. 电子科技大学学报, 2016, 45(4): 482–501. doi: 10.3969/j.issn.1001-0548.2016.04.001.YANG Jianyu. Bistatic synthetic aperture radar technology[J]. Journal of University of Electronic Science and Technology of China, 2016, 45(4): 482–501. doi: 10.3969/j.issn.1001-0548.2016.04.001. [3] WILDEN H and BRENNER A R. The SAR/GMTI airborne radar PAMIR: Technology and performance[C]. IEEE MTT-S International Microwave Symposium, Anaheim, USA, 2010: 534–537. doi: 10.1109/MWSYM.2010.5518080. [4] LI Zhongyu, WU Junjie, HUANG Yulin, et al. Ground-moving target imaging and velocity estimation based on mismatched compression for bistatic forward-looking SAR[J]. IEEE Transactions on Geoscience and Remote Sensing, 2016, 54(6): 3277–3291. doi: 10.1109/TGRS.2016.2514494. [5] LI Junao, LI Zhongyu, YANG Qing, et al. Joint clutter suppression and moving target indication in 2-D azimuth rotated time domain for single-channel bistatic SAR[J]. IEEE Transactions on Geoscience and Remote Sensing, 2023, 61: 5202516. doi: 10.1109/TGRS.2023.3237553. [6] LI Zhongyu, WU Junjie, YANG Jianyu, et al. Bistatic SAR Clutter Suppression[M]. Singapore: Springer, 2022: 8–19. doi: 10.1007/978-981-19-0159-1. [7] 李中余. 双基地合成孔径雷达动目标检测与成像技术研究[D]. [博士论文], 电子科技大学, 2017: 11–59.LI Zhongyu. Research on bistatic SAR moving target detection and imaging technology[D]. [Ph.D. dissertation], University of Electronic Science and Technology of China, 2017: 11–59. [8] CHEN H C and MCGILLEM C D. Target motion compensation by spectrum shifting in synthetic aperture radar[J]. IEEE Transactions on Aerospace and Electronic Systems, 1992, 28(3): 895–901. doi: 10.1109/7.256313. [9] FIENUP J R. Detecting moving targets in SAR imagery by focusing[J]. IEEE Transactions on Aerospace and Electronic Systems, 2001, 37(3): 794–809. doi: 10.1109/7.953237. [10] MOREIRA J R and KEYDEL W. A new MTI-SAR approach using the reflectivity displacement method[J]. IEEE Transactions on Geoscience and Remote Sensing, 1995, 33(5): 1238–1244. doi: 10.1109/36.469488. [11] LIGHTSTONE L, FAUBERT D, and REMPEL G. Multiple phase centre DPCA for airborne radar[C]. IEEE National Radar Conference, Los Angeles, USA, 1991: 36–40. doi: 10.1109/NRC.1991.114720. [12] LI Zhongyu, LI Shanchuan, LIU Zhutian, et al. Bistatic forward-looking SAR MP-DPCA method for space-time extension clutter suppression[J]. IEEE Transactions on Geoscience and Remote Sensing, 2020, 58(9): 6565–6579. doi: 10.1109/TGRS.2020.2977982. [13] 谢文冲, 段克清, 王永良. 机载雷达空时自适应处理技术研究综述[J]. 雷达学报, 2017, 6(6): 575–586. doi: 10.12000/JR17073.XIE Wenchong, DUAN Keqing, and WANG Yongliang. Space time adaptive processing technique for airborne radar: An overview of its development and prospects[J]. Journal of Radars, 2017, 6(6): 575–586. doi: 10.12000/JR17073. [14] REED I S, MALLETT J D, and BRENNAN L E. Rapid convergence rate in adaptive arrays[J]. IEEE Transactions on Aerospace and Electronic Systems, 1974, AES-10(6): 853–863. doi: 10.1109/TAES.1974.307893. [15] KLEMM R. Comparison between monostatic and bistatic antenna configurations for STAP[J]. IEEE Transactions on Aerospace and Electronic Systems, 2000, 36(2): 596–608. doi: 10.1109/7.845248. [16] LIU Zhutian, YU Huaiqin, LI Zhongyu, et al. Non-stationary clutter suppression approach based on cascading cancellation for bistatic forward-looking SAR[C]. 2019 IEEE Radar Conference, Boston, USA, 2019: 1–5. doi: 10.1109/RADAR.2019.8835707. [17] LI Junao, LI Zhongyu, YANG Qing, et al. Efficient matrix sparse recovery STAP method based on Kronecker transform for BiSAR sea clutter suppression[J]. IEEE Transactions on Geoscience and Remote Sensing, 2024, 62: 5103218. doi: 10.1109/TGRS.2024.3362844. [18] 马泽强, 王希勤, 刘一民, 等. 基于稀疏恢复的空时二维自适应处理技术研究现状[J]. 雷达学报, 2014, 3(2): 217–228. doi: 10.3724/SP.J.1300.2014.14002.MA Zeqiang, WANG Xiqin, LIU Yimin, et al. An overview on sparse recovery-based STAP[J]. Journal of Radars, 2014, 3(2): 217–228. doi: 10.3724/SP.J.1300.2014.14002. [19] SUN Ke, ZHANG Hao, LI Gang, et al. A novel STAP algorithm using sparse recovery technique[C]. 2009 IEEE International Geoscience and Remote Sensing Symposium, Cape Town, South Africa, 2009: V-336–V-339. doi: 10.1109/IGARSS.2009.5417664. [20] TANG Gongguo, BHASKAR B N, SHAH P, et al. Compressed sensing off the grid[J]. IEEE Transactions on Information Theory, 2013, 59(11): 7465–7490. doi: 10.1109/TIT.2013.2277451. [21] YE Hongda, LI Zhongyu, LIU Zhutian, et al. Clutter-ridge matched SR-STAP technique for non-stationary clutter suppression[C]. 2020 IEEE Radar Conference, Florence, Italy, 2020: 1–4. doi: 10.1109/RadarConf2043947.2020.9266628. [22] DUAN Keqing, LIU Weijian, DUAN Guangqing, et al. Off-grid effects mitigation exploiting knowledge of the clutter ridge for sparse recovery STAP[J]. IET Radar, Sonar & Navigation, 2018, 12(5): 557–564. doi: 10.1049/iet-rsn.2017.0425. [23] LI Zhihui, ZHANG Yongshun, GE Qichao, et al. Off-grid STAP algorithm based on reduced-dimension local search orthogonal matching pursuit[C]. 2019 IEEE 4th International Conference on Signal and Image Processing, Wuxi, China, 2019: 187–191. doi: 10.1109/SIPROCESS.2019.8868509. [24] 段克清, 王泽涛, 谢文冲, 等. 一种基于联合稀疏恢复的空时自适应处理方法[J]. 雷达学报, 2014, 3(2): 229–234. doi: 10.3724/SP.J.1300.2014.13149.DUAN Keqing, WANG Zetao, XIE Wenchong, et al. A space-time adaptive processing algorithm based on joint sparse recovery[J]. Journal of Radars, 2014, 3(2): 229–234. doi: 10.3724/SP.J.1300.2014.13149. [25] HE Pengyuan, HE Shun, YANG Zhiwei, et al. An off-grid STAP algorithm based on local mesh splitting with bistatic radar system[J]. IEEE Signal Processing Letters, 2020, 27: 1355–1359. doi: 10.1109/LSP.2020.3010161. [26] LI Zhongyu, YE Hongda, LIU Zhutian, et al. Bistatic SAR clutter-ridge matched STAP method for nonstationary clutter suppression[J]. IEEE Transactions on Geoscience and Remote Sensing, 2022, 60: 5216914. doi: 10.1109/TGRS.2021.3125043. [27] FENG Weike, GUO Yiduo, ZHANG Yongshun, et al. Airborne radar space time adaptive processing based on atomic norm minimization[J]. Signal Processing, 2018, 148: 31–40. doi: 10.1016/j.sigpro.2018.02.008. [28] LI Zhongyue and WANG Tong. ADMM-based low-complexity off-grid space-time adaptive processing methods[J]. IEEE Access, 2020, 8: 206646–206658. doi: 10.1109/ACCESS.2020.3037652. [29] ZOU Bo, WANG Xin, FENG Weike, et al. DU-CG-STAP method based on sparse recovery and unsupervised learning for airborne radar clutter suppression[J]. Remote Sensing, 2022, 14(14): 3472. doi: 10.3390/rs14143472. [30] SU Hanning, BAO Qinglong, and CHEN Zengping. ADMM-net: A deep learning approach for parameter estimation of chirp signals under sub-nyquist sampling[J]. IEEE Access, 2020, 8: 75714–75727. doi: 10.1109/ACCESS.2020.2989507. [31] RICHARDS M A. The keystone transformation for correcting range migration in range-doppler processing[J]. Pulse, 2014, 1000(1). [32] LIU Zhutian, LI Zhongyu, YU Huaiqin, et al. Bistatic forward-looking SAR moving target detection method based on joint clutter cancellation in echo-image domain with three receiving channels[J]. Sensors, 2018, 18(11): 3835. doi: 10.3390/s18113835. -



 作者中心
作者中心 专家审稿
专家审稿 责编办公
责编办公 编辑办公
编辑办公
 下载:
下载: