-
摘要: 空间卫星目标的逆合成孔径雷达(ISAR)图像由离散的散射点构成,具有弱纹理、高动态、非连续的特性,造成传统算法对空间目标ISAR图像进行三维重建时,得到的点云结果稀疏,无法覆盖目标整体外形轮廓,进而导致难以精确提取目标结构、姿态参数。针对上述问题,并考虑到空间目标通常由特定模块化部件组成的特点,该文提出一种从空间目标ISAR图像中抽取参数化基元来表示其三维结构的方法。首先利用能量累积算法从ISAR图像中得到目标的稀疏点云,进而利用参数化基元对点云进行拟合,最后将基元投影至ISAR成像平面,并最大化与目标图像的相似度来优化基元参数,得到最优的目标三维基元表示。相比于传统点云三维重建,该方法能够获得对目标三维结构更完整的描述,且所得到的基元参数即代表目标的姿态及结构,可直接支撑后续的目标识别、分析研判等任务。仿真实验证明该方法能够根据ISAR序列图像,有效实现对空间目标的三维表示。
-
关键词:
- 三维重建 /
- 逆合成孔径雷达(ISAR) /
- 基元拟合 /
- 太空态势感知 /
- 姿态估计
Abstract: Inverse Synthetic Aperture Radar (ISAR) images of spacecraft are composed of discrete scatterers that exhibit weak texture, high dynamics, and discontinuity. These characteristics result in sparse point clouds obtained using traditional algorithms for the Three-Dimensional (3D) reconstruction of spacecraft ISAR images. Furthermore, using point clouds to comprehensively describe the complete shape of targets is difficult, which consequently hampers the accurate extraction of the structural and pose parameters of the target. To address this problem, considering that space targets usually have specific modular structures, this paper proposes a method for abstracting parametric structural primitives from space target ISAR images to represent their 3D structures. First, the energy accumulation algorithm is used to obtain the sparse point cloud of the target from ISAR images. Subsequently, the point cloud is fitted using parameterized primitives. Finally, primitives are projected onto the ISAR imaging plane and optimized by maximizing their similarity with the target image to obtain the optimal 3D representation of the target primitives. Compared with the traditional point cloud 3D reconstruction, this method can provide a more complete description of the three-dimensional structure of the target. Meanwhile, primitive parameters obtained using this method represent the attitude and structure of the target and can directly support subsequent tasks such as target recognition and analysis. Simulation experiments demonstrate that this method can effectively achieve the 3D abstraction of space targets based on ISAR sequential images. -
表 1 参数取值范围和含义
Table 1. The parameters and their meanings
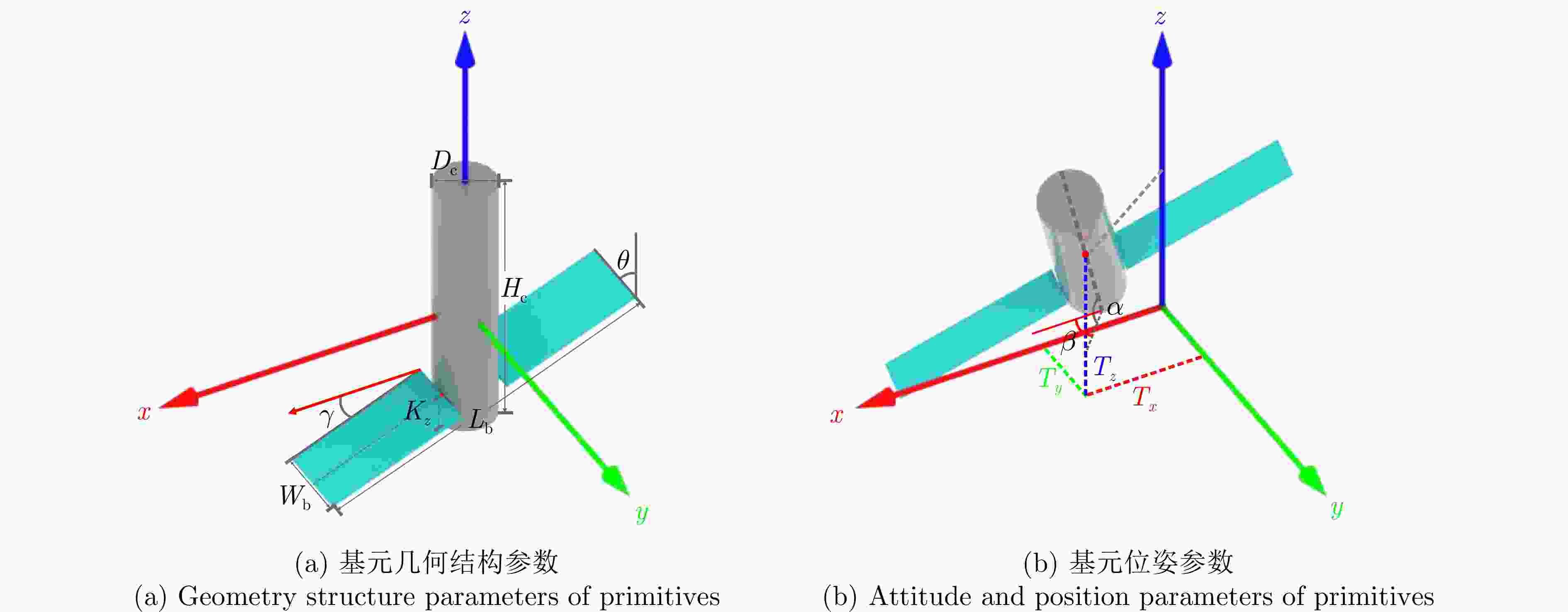
参数 含义 $ {D}_{\text{c}}\in \left(\text{0},\;\text{+}\infty \right) $ 舱体直径 $ {H}_{\text{c}}\in \left(\text{0},\;\text{+}\infty \right) $ 舱体长度 $ \alpha \in \left({-}\pi \text{/2},\;\pi \text{/2}\right) $ 目标俯仰角,即绕x轴的旋转角 $ \beta \in \left({-}\pi ,\;\pi \right) $ 目标偏航角,即绕y轴的旋转角 $ \gamma \in \left({-}\pi ,\;\pi \right) $ 目标滚转角,即绕z轴的旋转角(姿态旋转顺序为$\gamma - \alpha - \beta $) $ {T}_{x}\in \left({-}\infty ,\;\text{+}\infty \right) $ 沿x方向的相对平移 $ {T}_{y}\in \left({-}\infty ,\;\text{+}\infty \right) $ 沿y方向的相对平移 $ {T}_{z}\in \left({-}\infty ,\;\text{+}\infty \right) $ 沿z方向的相对平移 $ {L}_{\text{b}}\in \left(\text{0},\;\text{+}\infty \right) $ 帆板长度 $ {W}_{\text{b}}\in \left(\text{0},\;\text{+}\infty \right) $ 帆板宽度 $ \theta \in \left({-}\pi \text{/2},\;\pi \text{/2}\right) $ 帆板与舱体之间的夹角 $ {K}_{z}\in \left({-}{H}_{\text{c}}\text{/2},\;{H}_{\text{c}}\text{/2}\right) $ 帆板与主体的相对位置关系,即帆板沿舱体对称轴方向移动的距离 表 2 目标卫星轨道参数设置
Table 2. Target satellite orbit parameters settings
参数 数值 偏心率 1.721×10–4 近地点幅角(°) 14.191 轨道倾角(°) 98.7173 升交点赤经(°) 292.785 平均运动速率(°/s) 5.916×10–2 表 3 几何参数提取结果(m)
Table 3. Geometric parameters extraction results (m)
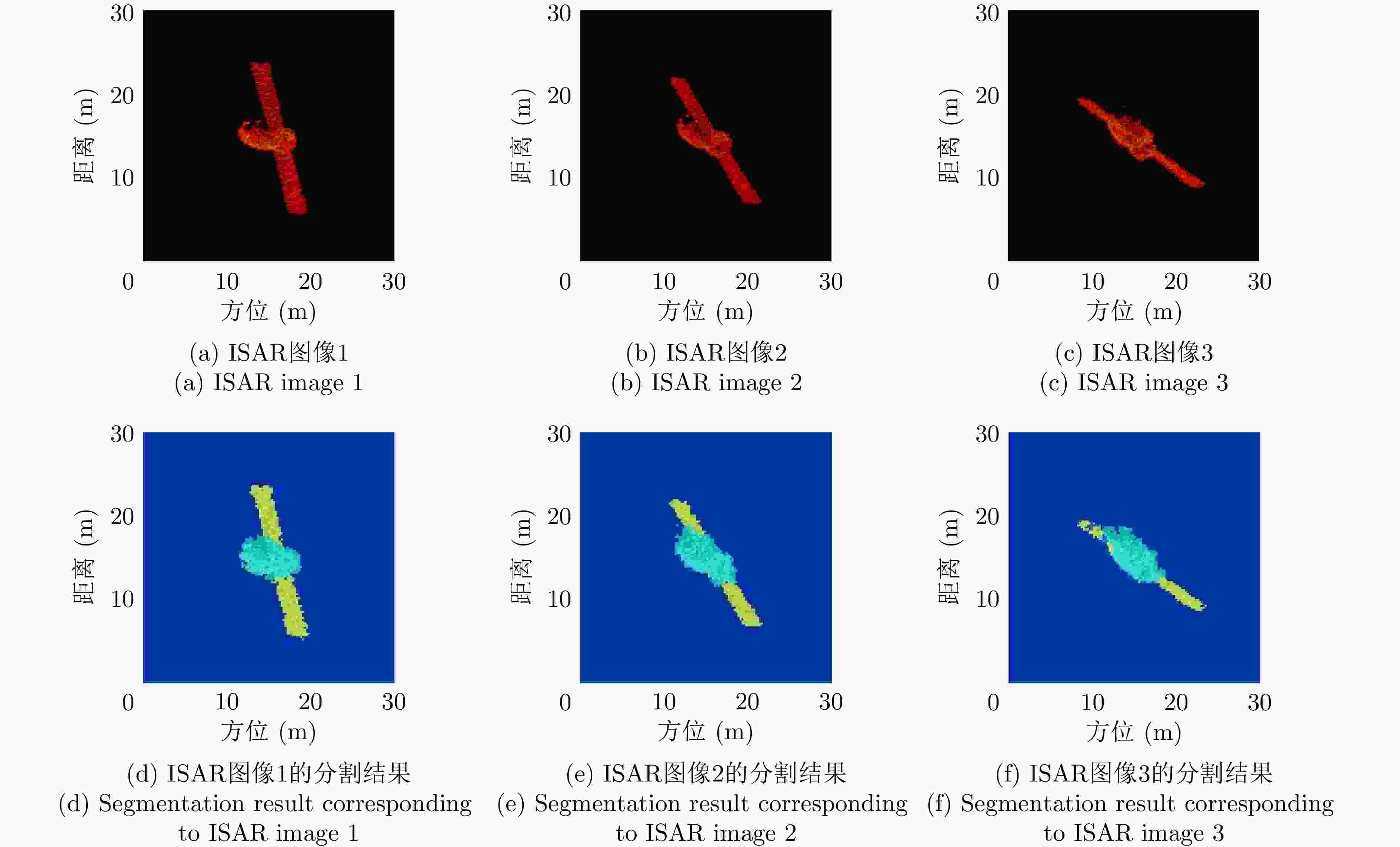
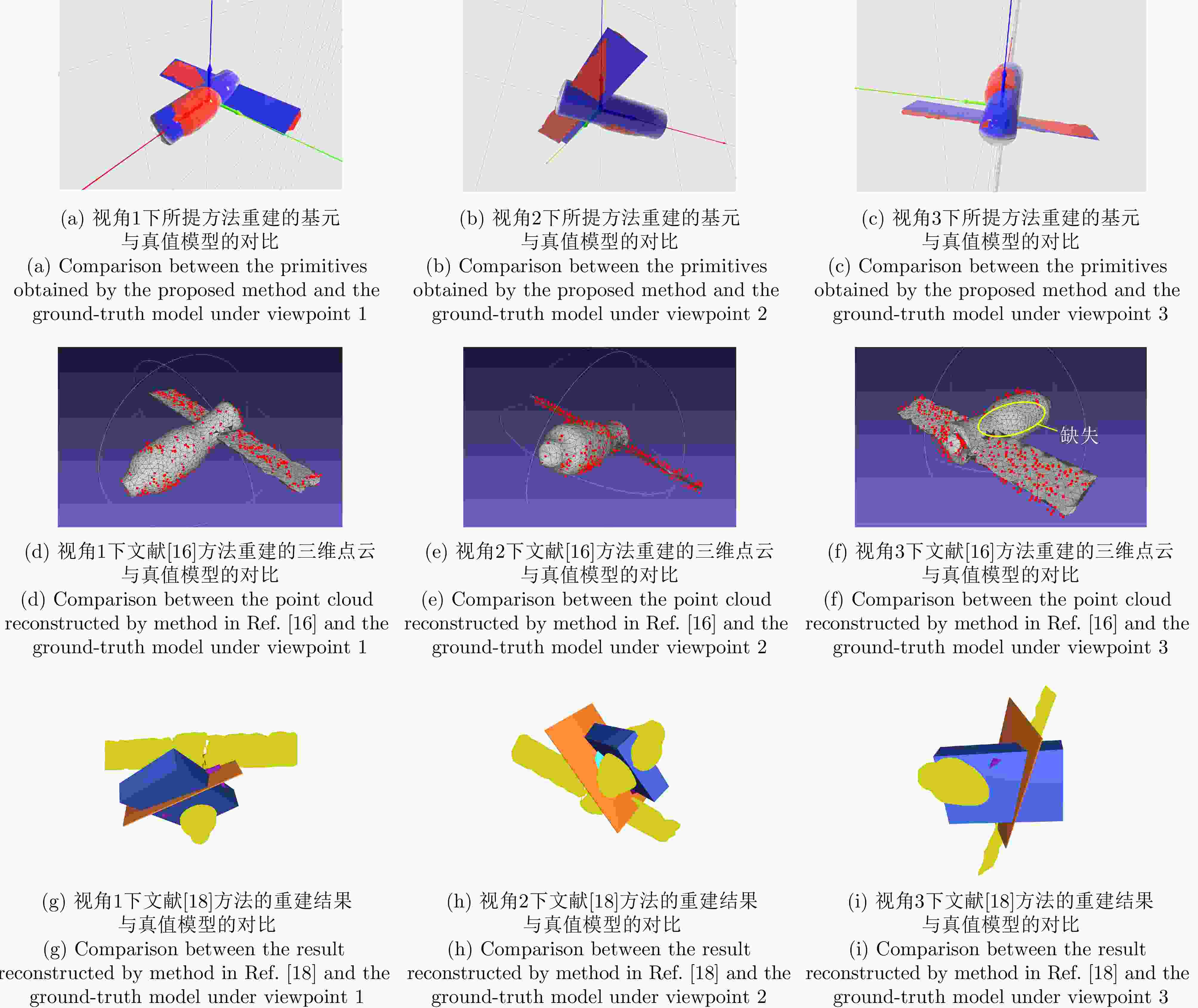
参数 PCA初始值 仅点云拟合 点云拟合+投影拟合 模型真值 主轴直径Dc 4.30 3.410 3.760 4.19(实验舱) 主轴长度Hc 12.97 10.696 11.712 11.95 帆板长度Lb 19.92 19.140 19.580 19.82 帆板宽度Wb 4.43 4.520 3.780 3.64 表 4 姿态参数提取结果(°)
Table 4. Attitude parameters extraction results (°)
参数 PCA初始值 仅点云拟合 点云拟合+投影拟合 模型真值 目标俯仰角α 90.05 83.09 91.05 90 目标偏航角β 86.74 88.36 88.22 90 目标滚转角γ 4.08 5.35 2.06 0 帆板倾角θ 18.74 22.51 21.42 20 表 5 平移参数提取结果(m)
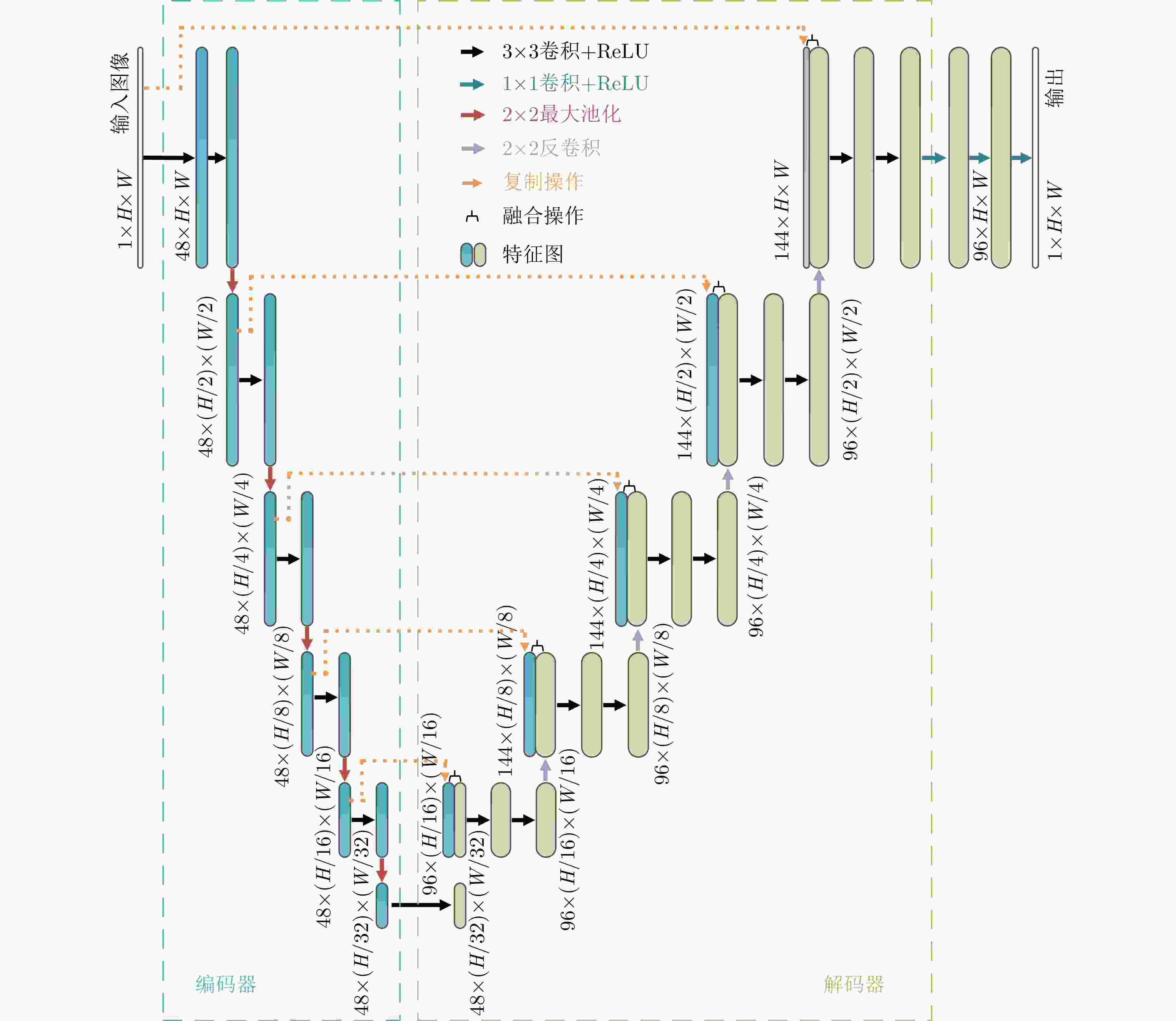
Table 5. Translation parameters extraction results (m)
参数 PCA初始值 仅点云拟合 点云拟合+投影拟合 模型真值 x方向位移Tx 0.62 0.88 1.38 1.79 y方向位移Ty –0.65 –0.44 –0.27 0 z方向位移Tz 0.07 –0.02 0.05 0 帆板位移Kz 2.21 2.21 2.01 1.78 表 6 平均参数误差
Table 6. Average parameter errors
参数 PCA初始值 仅点云拟合 点云拟合+投影拟合 εg (m) 1.64 1.42 0.89 εe (°) 6.07 5.59 2.92 εt (m) 1.63 1.01 0.50 IoU3D (ξt=3%lco) 0.62 2.21 0.92 -
[1] 田彪, 刘洋, 呼鹏江, 等. 宽带逆合成孔径雷达高分辨成像技术综述[J]. 雷达学报, 2020, 9(5): 765–802. doi: 10.12000/JR20060.TIAN Biao, LIU Yang, HU Pengjiang, et al. Review of high-resolution imaging techniques of wideband inverse synthetic aperture radar[J]. Journal of Radars, 2020, 9(5): 765–802. doi: 10.12000/JR20060. [2] 周叶剑, 马岩, 张磊, 等. 空间目标在轨状态雷达成像估计技术综述[J]. 雷达学报, 2021, 10(4): 607–621. doi: 10.12000/JR21086.ZHOU Yejian, MA Yan, ZHANG Lei, et al. Review of on-orbit state estimation of space targets with radar imagery[J]. Journal of Radars, 2021, 10(4): 607–621. doi: 10.12000/JR21086. [3] Fraunhofer FHR Lab. Space observation radar TIRA[EB/OL]. https://www.fhr.fraunhofer.de/en/the-institute/technical-equipment/Space-observation-radar-TIRA.html, 2020. [4] Fraunhofer FHR Lab. Monitoring the re-entry of the Chinese space station Tiangong-1 with TIRA[EB/OL]. https://www.fhr.fraunhofer.de/en/sections/Radar-for-Space-Situational-Awareness-RWL/monitoring-the-re-entry-of-the-chinese-space-station-tiangong-1-with-tira.html, 2018. [5] ZHOU Yejian, ZHANG Lei, CAO Yunhe, et al. Attitude estimation and geometry reconstruction of satellite targets based on ISAR image sequence interpretation[J]. IEEE Transactions on Aerospace and Electronic Systems, 2019, 55(4): 1698–1711. doi: 10.1109/TAES.2018.2875503. [6] ZHOU Yejian, ZHANG Lei, and CAO Yunhe. Dynamic estimation of spin spacecraft based on multiple-station ISAR images[J]. IEEE Transactions on Geoscience and Remote Sensing, 2020, 58(4): 2977–2989. doi: 10.1109/TGRS.2019.2959270. [7] ZHOU Yejian, ZHANG Lei, CAO Yunhe, et al. Optical-and-radar image fusion for dynamic estimation of spin satellites[J]. IEEE Transactions on Image Processing, 2020, 29: 2963–2976. doi: 10.1109/TIP.2019.2955248. [8] XIE Pengfei, ZHANG Lei, DU Chuan, et al. Space target attitude estimation from ISAR image sequences with key point extraction network[J]. IEEE Signal Processing Letters, 2021, 28: 1041–1045. doi: 10.1109/LSP.2021.3075606. [9] ZHOU Jianxiong, SHI Zhiguang, and FU Qiang. Three-dimensional scattering center extraction based on wide aperture data at a single elevation[J]. IEEE Transactions on Geoscience and Remote Sensing, 2015, 53(3): 1638–1655. doi: 10.1109/tgrs.2014.2346509. [10] 白雪茹. 空天目标逆合成孔径雷达成像新方法研究[D]. [博士论文], 西安电子科技大学, 2011.BAI Xueru. Study on new techniques for ISAR imaging of aerospace targets[D]. [Ph.D. dissertation], Xidian University, 2011. [11] FERRARA M, ARNOLD G, and STUFF M. Shape and motion reconstruction from 3D-to-1D orthographically projected data via object-image relations[J]. IEEE Transactions on Pattern Analysis and Machine Intelligence, 2009, 31(10): 1906–1912. doi: 10.1109/TPAMI.2008.294. [12] MCFADDEN F E. Three-dimensional reconstruction from ISAR sequences[C]. SPIE 4744, Sensor Technology and Data Visualization, Orlando, USA, 2002: 58–67. doi: 10.1117/12.488289. [13] LIU Lei, ZHOU Feng, BAI Xueru, et al. Joint cross-range scaling and 3D geometry reconstruction of ISAR targets based on factorization method[J]. IEEE Transactions on Image Processing, 2016, 25(4): 1740–1750. doi: 10.1109/TIP.2016.2526905. [14] WANG Canyu, JIANG Libing, LI Mengxi, et al. Slow-spinning spacecraft cross-range scaling and attitude estimation based on sequential ISAR images[J]. IEEE Transactions on Aerospace and Electronic Systems, 2023, 59(6): 7469–7485. doi: 10.1109/TAES.2023.3291337. [15] WANG Feng, XU Feng, and JIN Yaqiu. Three-dimensional reconstruction from a multiview sequence of sparse ISAR imaging of a space target[J]. IEEE Transactions on Geoscience and Remote Sensing, 2018, 56(2): 611–620. doi: 10.1109/TGRS.2017.2737988. [16] LIU Lei, ZHOU Zuobang, ZHOU Feng, et al. A new 3-D geometry reconstruction method of space target utilizing the scatterer energy accumulation of ISAR image sequence[J]. IEEE Transactions on Geoscience and Remote Sensing, 2020, 58(12): 8345–8357. doi: 10.1109/TGRS.2020.2986465. [17] PASCHALIDOU D, VAN GOOL L, and GEIGER A. Learning unsupervised hierarchical part decomposition of 3D objects from a single RGB image[C]. 2020 IEEE/CVF Conference on Computer Vision and Pattern Recognition, Seattle, USA, 2020: 1057–1067. doi: 10.1109/CVPR42600.2020.00114. [18] KLUGER F, ACKERMANN H, BRACHMANN E, et al. Cuboids revisited: Learning robust 3D shape fitting to single RGB images[C]. 2021 IEEE/CVF Conference on Computer Vision and Pattern Recognition, Nashville, USA, 2021: 13065–13074. doi: 10.1109/CVPR46437.2021.01287. [19] RONNEBERGER O, FISCHER P, and BROX T. U-Net: Convolutional networks for biomedical image segmentation[C]. 18th International Conference on Medical Image Computing and Computer-Assisted Intervention, Munich, Germany, 2015: 234–241. doi: 10.1007/978-3-319-24574-4_28. [20] QUADRELLI M B. Spacecraft dynamics and control: An introduction [bookshelf][J]. IEEE Control Systems Magazine, 2015, 35(2): 103–106. doi: 10.1109/MCS.2014.2385295. [21] BELLEKENS B, SPRUYT V, BERKVENS R, et al. A survey of rigid 3D pointcloud registration algorithms[C]. The Fourth International Conference on Ambient Computing, Applications, Services and Technologies, Rome, Italy, 2014: 8–13. [22] KINGMA D P and BA J. Adam: A method for stochastic optimization[C]. 3rd International Conference on Learning Representations, San Diego, USA, 2015: 13. [23] OTSU N. A threshold selection method from gray-level histograms[J]. IEEE Transactions on Systems, Man, and Cybernetics, 1979, 9(1): 62–66. doi: 10.1109/TSMC.1979.4310076. [24] BOAG A. A fast physical optics (FPO) algorithm for high frequency scattering[J]. IEEE Transactions on Antennas and Propagation, 2004, 52(1): 197–204. doi: 10.1109/tap.2003.822426. [25] 邹嘉玮, 何思远, 杨泽望, 等. 复杂目标雷达图像形成机理分析[J]. 科学技术与工程, 2022, 22(28): 12468–12475. doi: 10.3969/j.issn.1671-1815.2022.28.029.ZOU Jiawei, HE Siyuan, YANG Zewang, et al. Analysis of radar image formation mechanism of complex target[J]. Science Technology and Engineering, 2022, 22(28): 12468–12475. doi: 10.3969/j.issn.1671-1815.2022.28.029. [26] 董纯柱, 胡利平, 朱国庆, 等. 地面车辆目标高质量SAR图像快速仿真方法[J]. 雷达学报, 2015, 4(3): 351–360. doi: 10.12000/JR15057.DONG Chunzhu, HU Liping, ZHU Guoqing, et al. Efficient simulation method for high quality SAR images of complex ground vehicles[J]. Journal of Radars, 2015, 4(3): 351–360. doi: 10.12000/JR15057. [27] 崔闪, 李胜, 闫华. 一种基于HRRP的三维散射中心提取方法[J]. 系统仿真学报, 2018, 30(2): 443–451. doi: 10.16182/j.issn1004731x.joss.201802010.CUI Shan, LI Sheng, and YAN Hua. A method of 3D scattering center extraction based on multiple HRRP series[J]. Journal of System Simulation, 2018, 30(2): 443–451. doi: 10.16182/j.issn1004731x.joss.201802010. [28] 闫华, 张磊, 陆金文, 等. 任意多次散射机理的GTD散射中心模型频率依赖因子表达[J]. 雷达学报, 2021, 10(3): 370–381. doi: 10.12000/JR21005.YAN Hua, ZHANG Lei, LU Jinwen, et al. Frequency-dependent factor expression of the GTD scattering center model for the arbitrary multiple scattering mechanism[J]. Journal of Radars, 2021, 10(3): 370–381. doi: 10.12000/JR21005. -



 作者中心
作者中心 专家审稿
专家审稿 责编办公
责编办公 编辑办公
编辑办公

 下载:
下载: