针对回波数据异常时的雷达前视超分辨快速成像方法

李维新; 李明; 陈洪猛; 左磊; 王东; 杨磊; 辛东金

doi:10.12000/JR23209

针对回波数据异常时的雷达前视超分辨快速成像方法

DOI: 10.12000/JR23209

李维新¹,
李明²,
陈洪猛³,
左磊²,
王东¹,
杨磊¹,
辛东金^1, ,

1.
济南大学信息科学与工程学院济南 250022
2.
西安电子科技大学雷达信号处理国家重点实验室西安 710071
3.
北京无线电测量研究所北京 100854

基金项目: 山东省科技型中小企业创新能力提升工程(2023TSGC0332, 2023TSGC0141)

详细信息

作者简介:
李维新，博士，讲师，主要研究方向为雷达前视成像、雷达信号处理

李　明，博士，教授，主要研究方向为自适应信号处理、微弱目标检测、雷达图像处理

陈洪猛，博士，高级工程师，主要研究方向为空天基雷达总体设计、前斜视成像和运动目标检测

左　磊，博士，教授，主要研究方向为雷达协同探测、雷达对抗等

王　东，博士，副教授，主要研究方向无人机协同导航、边缘计算

杨　磊，博士，教授，主要研究方向为北斗/GNSS应用、被动雷达探测

辛东金，博士，讲师，主要研究方向为分布式信号处理、高速电路信号完整性设计

通讯作者:
辛东金 ise_xindj@ujn.edu.cn

责任主编：张永超 Corresponding Editor: ZHANG Yongchao
中图分类号: TN957
计量
- 文章访问数: 789
- HTML全文浏览量: 266
- PDF下载量: 156
- 被引次数: 0
出版历程
- 收稿日期: 2023-10-29
- 修回日期: 2024-01-12
- 网络出版日期: 2024-02-01
- 刊出日期: 2024-06-28

Fast Radar Forward-looking Super-resolution Imaging for Abnormal Echo Data

1.
School of Information Science and Engineering, University of Jinan, Jinan 250022, China
2.
National Laboratory of Radar Signal Processing, Xidian University, Xi’an 710071, China
3.
Beijing Institute of Radio Measurement, Beijing 100854, China

Funds: Innovation Capability Enhancement Program for Small and Medium-sized Technological Enterprises of Shandong Province (2023TSGC0332, 2023TSGC0141)

More Information

Corresponding author: XIN Dongjin, ise_xindj@ujn.edu.cn

摘要

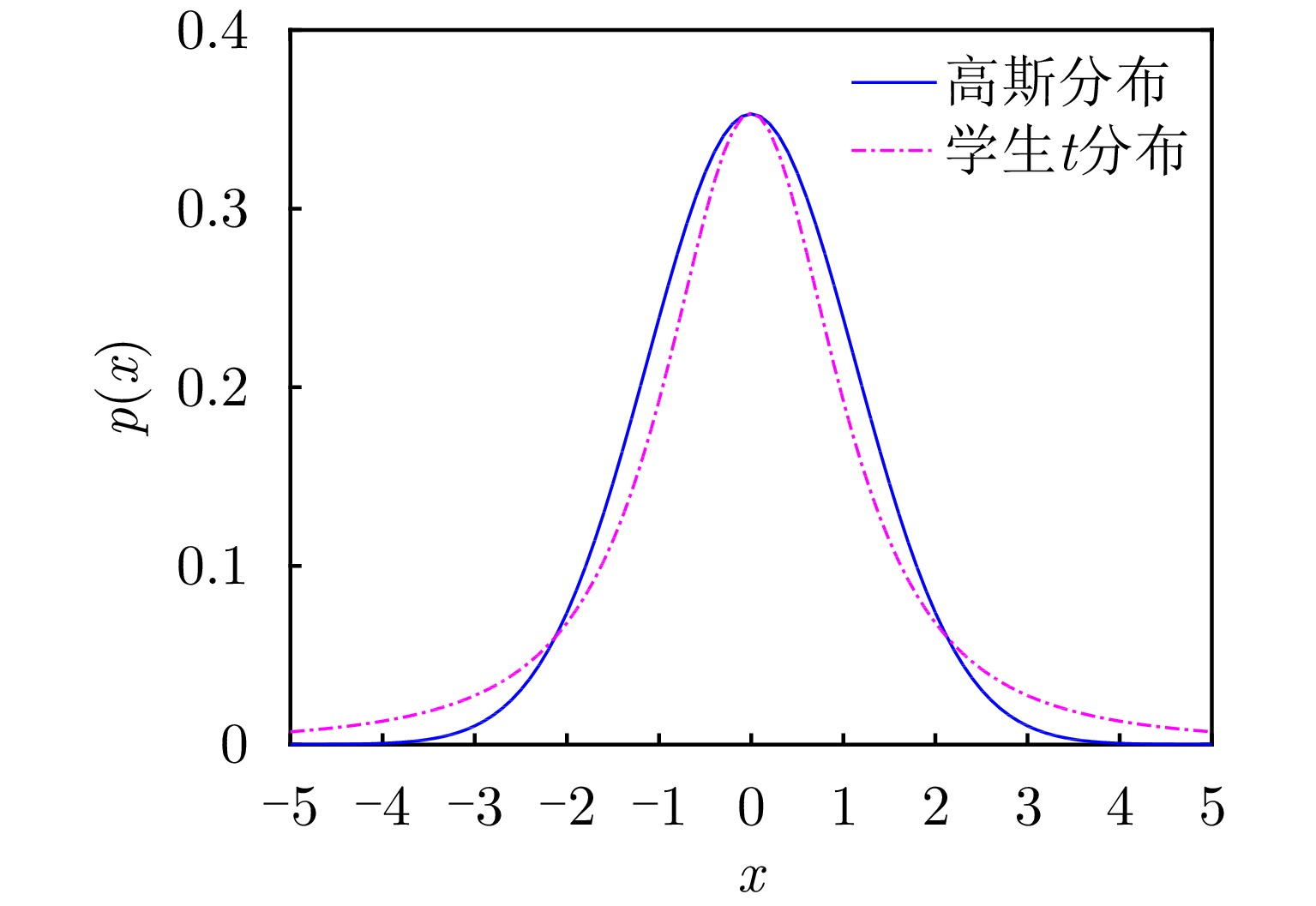
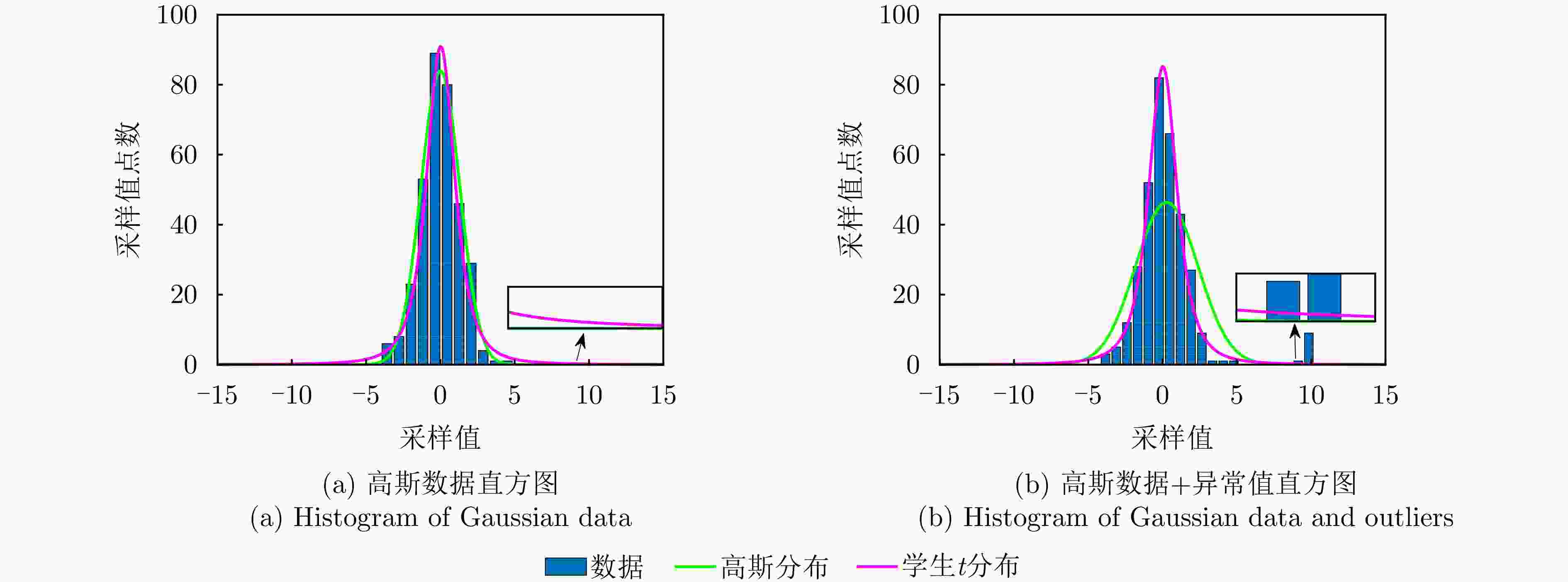
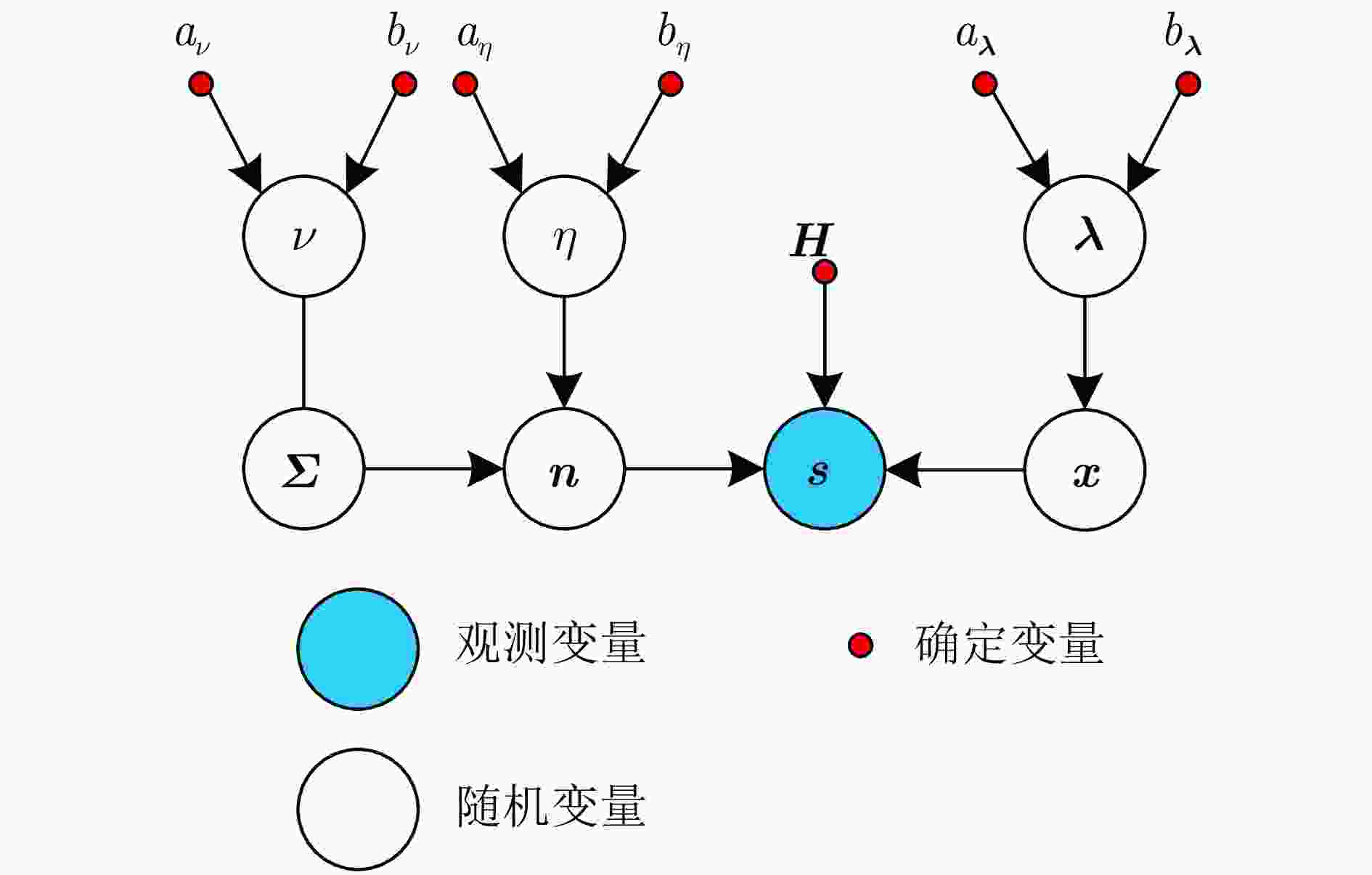
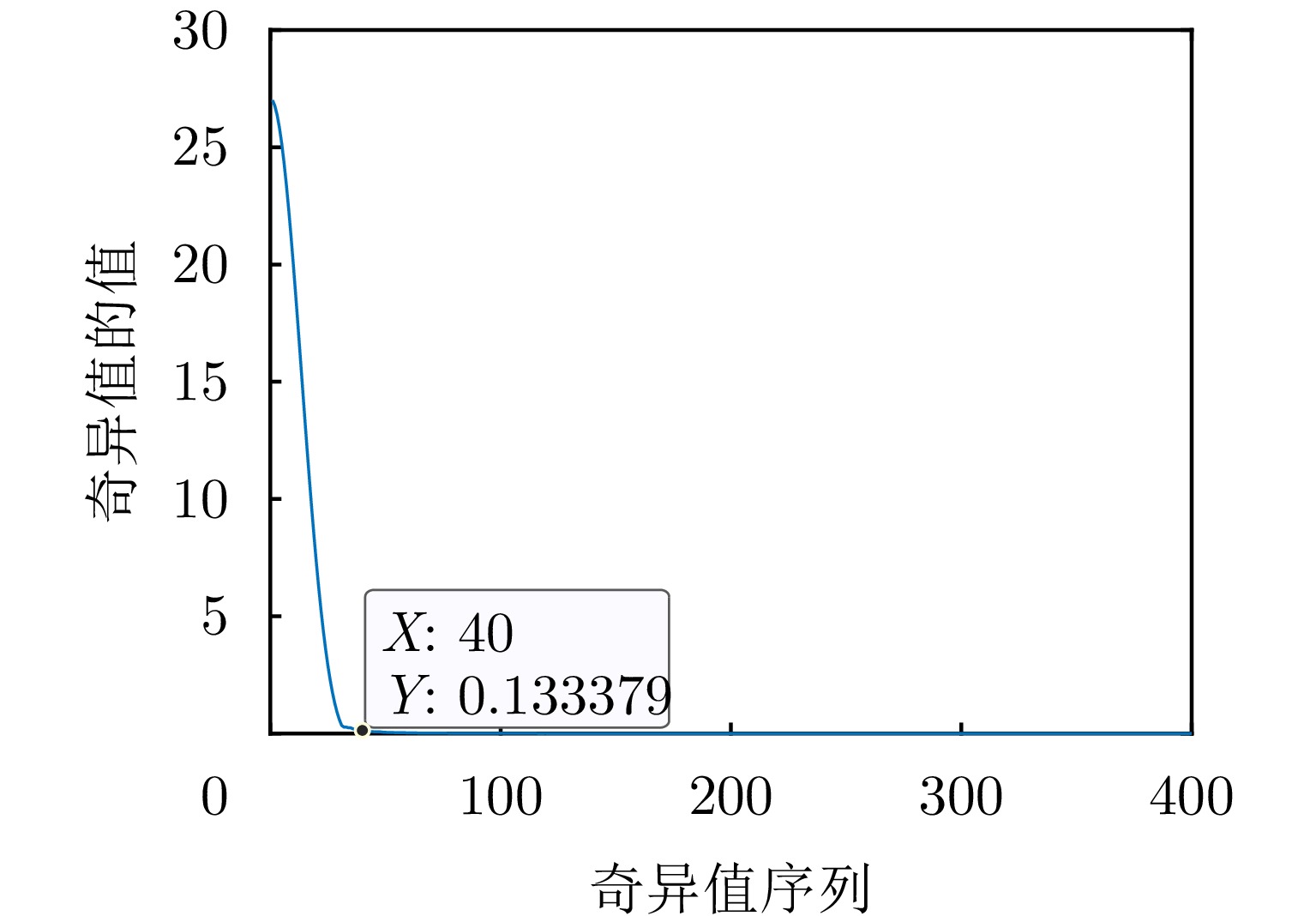
摘要: 机载扫描雷达前视成像可广泛应用于态势感知、自主导航和地形跟随。在雷达扫描过程中受到不经意的电磁脉冲干扰或设备性能异常等影响时，雷达回波数据出现异常值。已有的超分辨方法可以抑制回波中的异常值、提高角度分辨率，但没有考虑计算实时性问题。针对上述问题，该文提出了一种机载雷达超分辨方法实现回波数据异常时的快速前视成像。为了更好地拟合回波噪声，引入对异常值更加鲁棒的学生t分布，并采用期望最大化方法对成像参数进行估计。受截断奇异值分解方法的启发，将截断的酉矩阵引入目标散射系数的估计公式中。通过矩阵变换降低了求逆矩阵的尺寸，从而降低了参数估计的计算复杂度。仿真结果表明该文提出加速方法可以用更短的时间提高前视成像的角度分辨率，抑制回波数据中的异常值。
- 前视成像 /
- 超分辨 /
- 数据异常 /
- 矩阵变换
Abstract: Forward-looking imaging of airborne scanning radar is widely used in situation awareness, autonomous navigation and terrain following. When the radar is influenced by unintentional temporally sporadic electromagnetic interference or abnormal equipment performance, the echo signal contains outliers. Existing super-resolution methods can suppress outliers and improve azimuth resolution, but the real-time computing problem is not considered. In this study, we propose an airborne scanning radar super-resolution method to achieve fast forward-looking imaging when echo data are abnormal. First, we propose using the Student-t distribution to model noise. Then, the expectation-maximization method is used to estimate the parameters. Inspired by the truncated singular value decomposition method, we introduce the truncated unitary matrix into the estimation formula of the target scattering coefficient. Finally, the size of inverse matrix is reduced and the computational complexity of parameter estimation is reduced through matrix transformation. The simulation results show that the proposed method can improve the azimuth resolution of forward-looking imaging in a shorter time, and suppress outliers in echo data.
- Forward-looking imaging /
- Super-resolution /
- Abnormal echo data /
- Matrix transformation

HTML全文

图 1 扫描雷达几何示意图

Figure 1. Geometric model of scanning radar

下载: 全尺寸图片幻灯片

图 2 高斯分布和学生t分布的比较

Figure 2. Comparison of Gaussian distribution and student-t distribution

下载: 全尺寸图片幻灯片

图 3 直方图拟合曲线

Figure 3. Fitting curve of histogram distribution

下载: 全尺寸图片幻灯片

图 4 概率图模型

Figure 4. Probabilistic graphical model

下载: 全尺寸图片幻灯片

图 5 奇异值曲线

Figure 5. Singular value curve

下载: 全尺寸图片幻灯片

图 6 点目标仿真结果

Figure 6. Point target simulation results

下载: 全尺寸图片幻灯片

图 7 不同信噪比情况下的MSE曲线

Figure 7. MSE curves under different SNRs

下载: 全尺寸图片幻灯片

图 8 不同方位维度情况下的运行时间曲线

Figure 8. Time curves under different azimuth dimensions

下载: 全尺寸图片幻灯片

图 9 截断参数对MSE影响

Figure 9. Influence of truncated parameter on MSE

下载: 全尺寸图片幻灯片

图 10 截断参数对运行时间影响

Figure 10. Influence of truncated parameter on running time

下载: 全尺寸图片幻灯片

图 11 原始目标场景

Figure 11. Original target scene

下载: 全尺寸图片幻灯片

图 12 受电磁干扰时面目标仿真结果

Figure 12. Area target simulation results with electromagnetic interference

下载: 全尺寸图片幻灯片

图 13 设备性能异常时面目标仿真结果

Figure 13. Area target simulation results with abnormal equipment performance

下载: 全尺寸图片幻灯片

图 14 实测数据结果

Figure 14. Processed results of real data

下载: 全尺寸图片幻灯片

图 15 受电磁干扰时半实测数据仿真结果

Figure 15. Processed results of semi-real data with electromagnetic interference

下载: 全尺寸图片幻灯片

图 16 设备性能异常时半实测数据仿真结果

Figure 16. Processed results of semi-real data with abnormal equipment performance

下载: 全尺寸图片幻灯片

表 1 仿真系统参数

Table 1. System parameters of simulation

参数	数值	参数	数值
扫描速度$\left( {{{^ \circ } \mathord{\left/ {\vphantom {{^ \circ } {\text{s}}}} \right. } {\text{s}}}} \right)$	$50$	载波频率$ \left( {{\text{GHz}}} \right) $	$ 9.5 $
扫描范围$ \left( {^ \circ } \right) $	$ \pm 10$	信号带宽$ \left( {{\text{MHz}}} \right) $	$ 40 $
脉冲重复频率$\left( {{\text{Hz}}} \right)$	$1000$	平台速度$\left( {{{\text{m}} \mathord{\left/ {\vphantom {{\text{m}} {\text{s}}}} \right. } {\text{s}}}} \right)$	$30$
主瓣波束宽度$\left( {^ \circ } \right)$	3

下载: 导出CSV

表 2 面目标仿真系统参数

Table 2. System parameters of area target simulation

参数	数值	参数	数值
扫描速度$\left( {{{^ \circ } \mathord{\left/ {\vphantom {{^ \circ } {\text{s}}}} \right. } {\text{s}}}} \right)$	$50$	载波频率$ \left( {{\text{GHz}}} \right) $	$ 9.5 $
扫描范围$ \left( {^ \circ } \right) $	$ \pm 10$	信号带宽$ \left( {{\text{MHz}}} \right) $	$ 40 $
脉冲重复频率$\left( {{\text{Hz}}} \right)$	$1000$	平台速度$\left( {{{\text{m}} \mathord{\left/ {\vphantom {{\text{m}} {\text{s}}}} \right. } {\text{s}}}} \right)$	$30$
主瓣波束宽度$\left( {^ \circ } \right)$	5

下载: 导出CSV

表 3 受电磁干扰时面目标仿真的MSE和运行时间

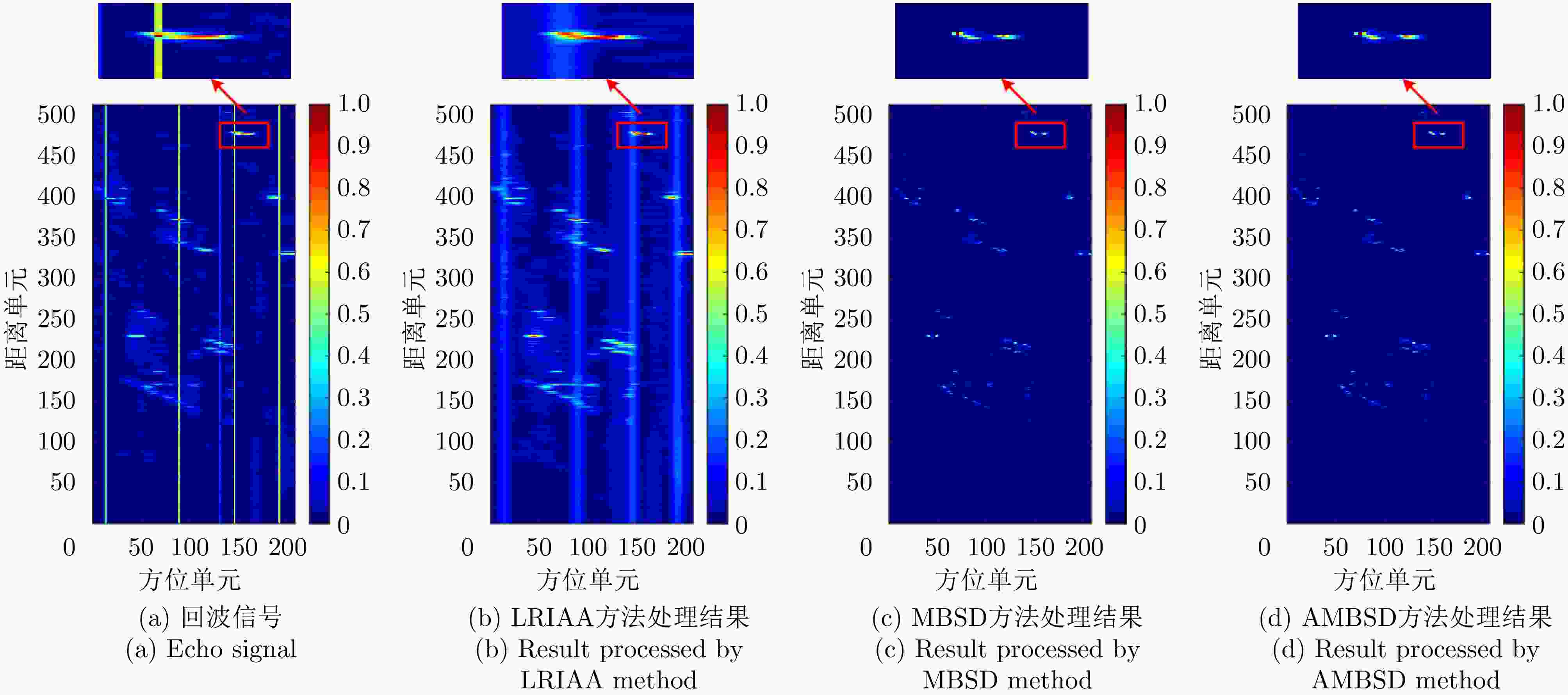
Table 3. MSE and running time of area target simulation with electromagnetic interference

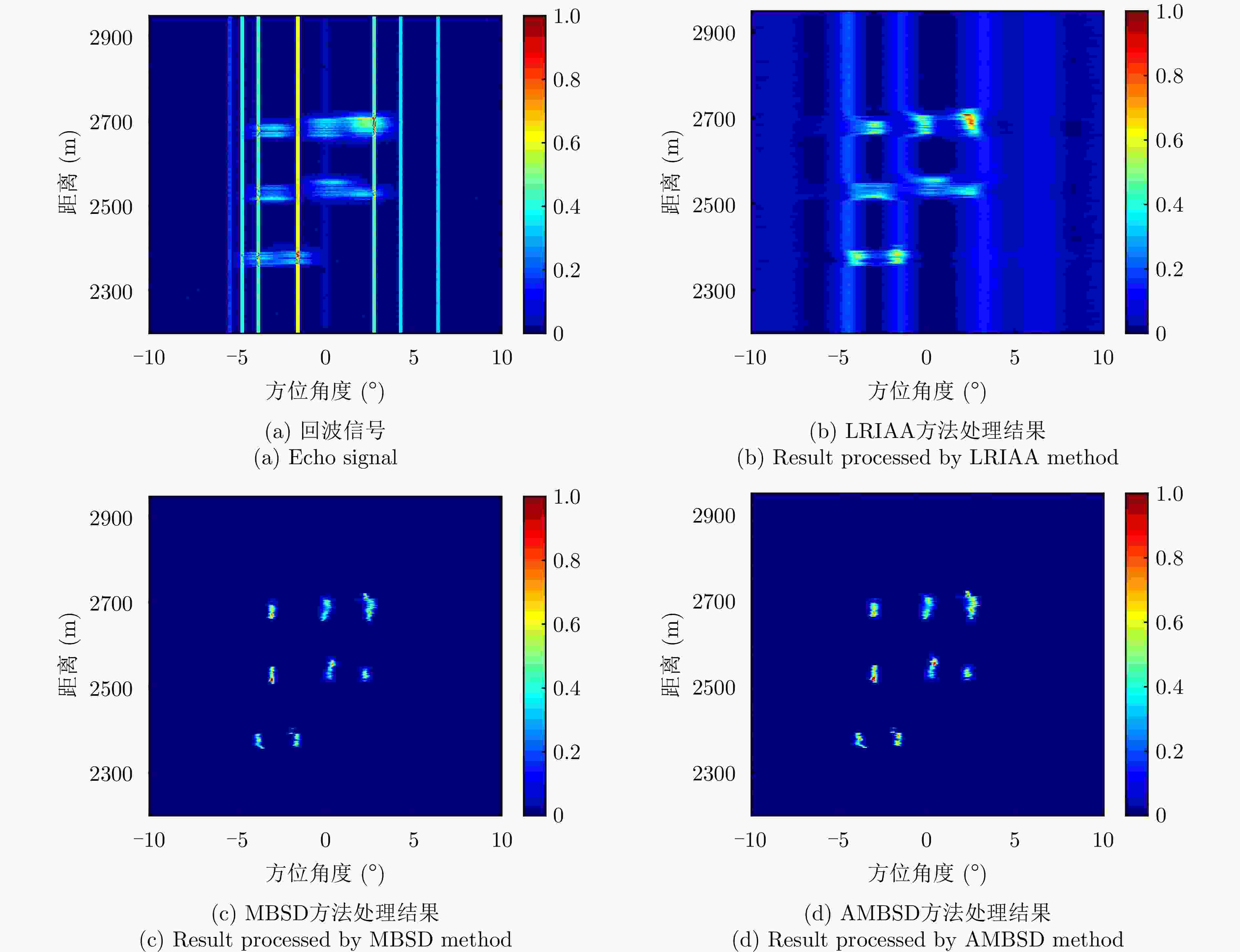
方法	MSE	运行时间(s)
LRIAA方法	6.15×10^–3	4.90
MBSD方法	0.65×10^–3	23.14
AMBSD方法	0.70×10^–3	3.82

下载: 导出CSV

表 4 设备性能异常时面目标仿真的MSE和运行时间

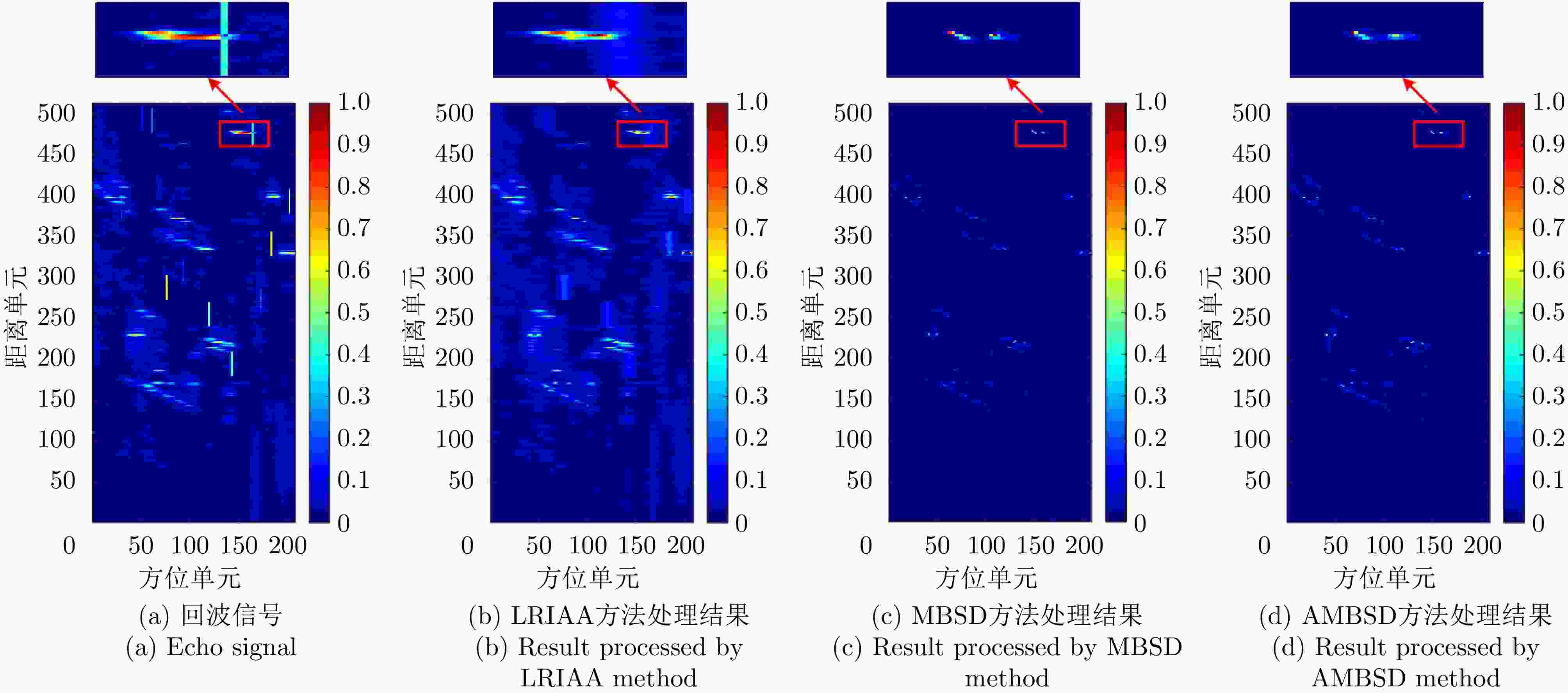
Table 4. MSE and running time of area target simulation with abnormal equipment performance

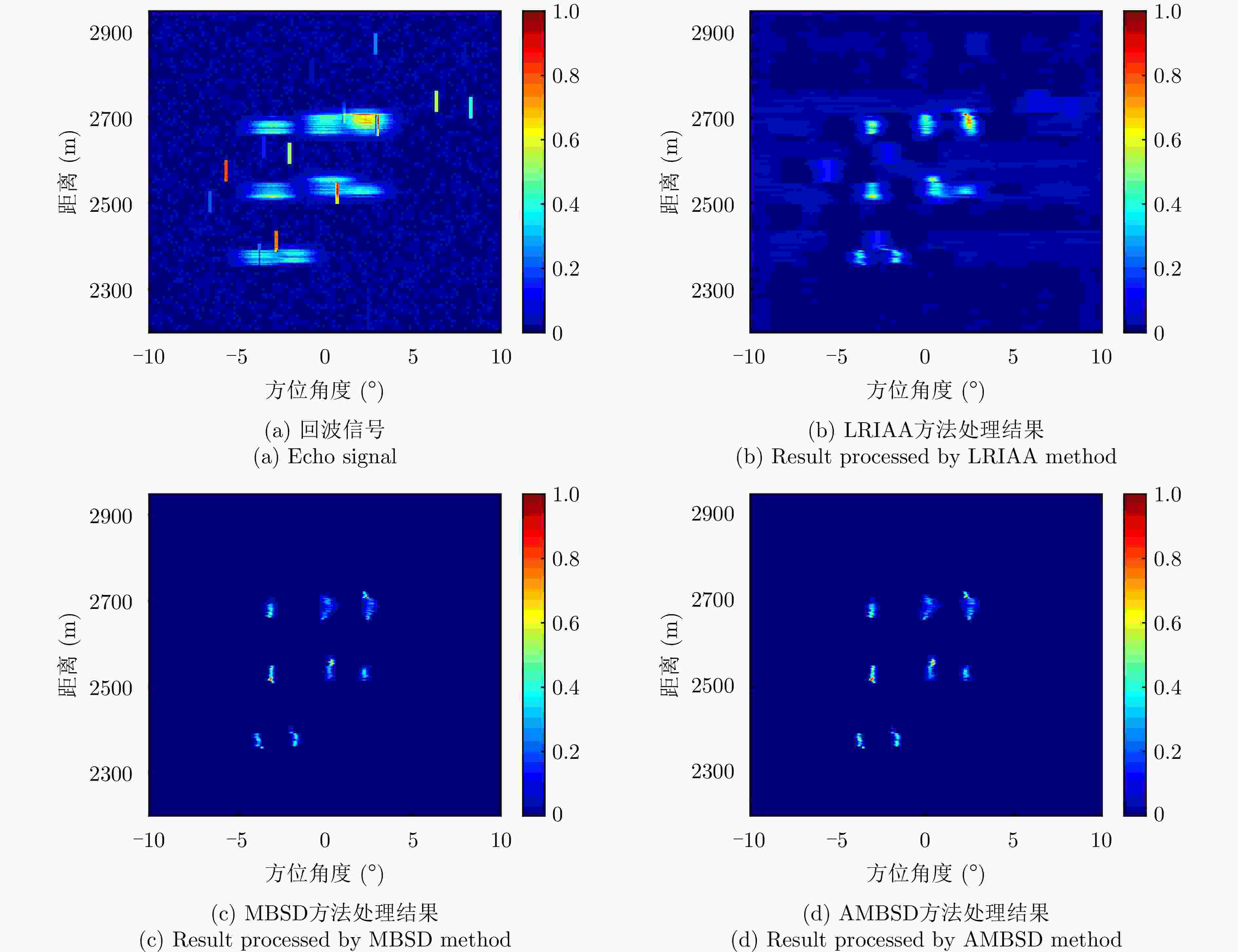
方法	MSE	运行时间(s)
LRIAA方法	1.09×10^–3	4.80
MBSD方法	0.80×10^–3	23.03
AMBSD方法	0.81×10^–3	3.90

下载: 导出CSV

表 5 半实测数据运行时间(s)

Table 5. Running time of semi-real data (s)

方法	受电磁干扰时运行时间	设备性能异常时运行时间
LRIAA方法	1.98	1.89
MBSD方法	4.57	4.58
AMBSD方法	1.18	1.19

下载: 导出CSV

参考文献(36)

[1]	STIMSON G W. Introduction to Airborne Radar[M]. 2nd ed. Mendham: SciTech Pub, 1998, 37–38.
[2]	李亚超, 王家东, 张廷豪, 等. 弹载雷达成像技术发展现状与趋势[J]. 雷达学报, 2022, 11(6): 943–973. doi: 10.12000/JR22119. LI Yachao, WANG Jiadong, ZHANG Tinghao, et al. Present situation and prospect of missile-borne radar imaging technology[J]. Journal of Radars, 2022, 11(6): 943–973. doi: 10.12000/JR22119.
[3]	樊晨阳, 贺思三, 郭乾. 雷达前视成像技术的研究现状[J]. 电光与控制, 2021, 28(9): 59–64. doi: 10.3969/j.issn.1671-637X.2021.09.013. FAN Chenyang, HE Sisan, and GUO Qian. Research status of radar forward-looking imaging technology[J]. Electronics Optics & Control, 2021, 28(9): 59–64. doi: 10.3969/j.issn.1671-637X.2021.09.013.
[4]	MEI Haiwen, LI Yachao, XING Mengdao, et al. A frequency-domain imaging algorithm for translational variant bistatic forward-looking SAR[J]. IEEE Transactions on Geoscience and Remote Sensing, 2020, 58(3): 1502–1515. doi: 10.1109/TGRS.2019.2943743.
[5]	LU Jingyue, ZHANG Lei, WEI Shaopeng, et al. Resolution enhancement for forwarding looking multi-channel SAR imagery with exploiting space-time sparsity[J]. IEEE Transactions on Geoscience and Remote Sensing, 2023, 61: 1–17. doi: 10.1109/TGRS.2022.3232392.
[6]	李悦丽, 马萌恩, 赵崇辉, 等. 基于单脉冲雷达和差通道多普勒估计的前视成像[J]. 雷达学报, 2021, 10(1): 131–142. doi: 10.12000/JR20111. LI Yueli, MA Meng’en, ZHAO Chonghui, et al. Forward-looking imaging via Doppler estimates of sum-difference measurements in scanning monopulse radar[J]. Journal of Radars, 2021, 10(1): 131–142. doi: 10.12000/JR20111.
[7]	毛德庆. 机载雷达扫描波束超分辨成像方法研究[D]. [博士论文], 电子科技大学, 2022. doi: 10.27005/d.cnki.gdzku.2022.004148. MAO Deqing. Research on scanning beam super-resolution imaging methods for airborne radar[D]. [Ph. D. dissertation], University of Electronic Science and Technology of China, 2022. doi: 10.27005/d.cnki.gdzku.2022.004148.
[8]	LI Weixin, LI Ming, ZUO Lei, et al. A computationally efficient airborne forward-looking super-resolution imaging method based on sparse Bayesian learning[J]. IEEE Transactions on Geoscience and Remote Sensing, 2023, 61: 5102613. doi: 10.1109/TGRS.2023.3260094.
[9]	唐军奎, 刘峥, 冉磊, 等. 基于稀疏和低秩先验的雷达前视超分辨成像方法[J]. 雷达学报, 2023, 12(2): 332–342. doi: 10.12000/JR22199. TANG Junkui, LIU Zheng, RAN Lei, et al. Radar forward-looking super-resolution imaging method based on sparse and low-rank priors[J]. Journal of Radars, 2023, 12(2): 332–342. doi: 10.12000/JR22199.
[10]	张启平. 雷达实孔径超分辨成像中的正则化方法研究[D]. [博士论文], 电子科技大学, 2021. doi: 10.27005/d.cnki.gdzku.2021.005078. ZHANG Qiping. Research on regularization method in radar real-aperture super-resolution imaging[D]. [Ph. D. dissertation], University of Electronic Science and Technology of China, 2021. doi: 10.27005/d.cnki.gdzku.2021.005078.
[11]	SHEA J D, VAN VEEN B D, and HAGNESS S C. A TSVD analysis of microwave inverse scattering for breast imaging[J]. IEEE Transactions on Biomedical Engineering, 2012, 59(4): 936–945. doi: 10.1109/TBME.2011.2176727.
[12]	TANG Junkui, LIU Zheng, RAN Lei, et al. Enhancing forward-looking image resolution: combining low-rank and sparsity priors[J]. IEEE Transactions on Geoscience and Remote Sensing, 2023, 61: 5100812. doi: 10.1109/TGRS.2023.3237332.
[13]	LI Wenchao, ZHANG Wentao, ZHANG Qiping, et al. Simultaneous super-resolution and target detection of forward-looking scanning radar via low-rank and sparsity constrained method[J]. IEEE Transactions on Geoscience and Remote Sensing, 2020, 58(10): 7085–7095. doi: 10.1109/TGRS.2020.2979508.
[14]	ZHANG Yin, TUO Xingyu, HUANG Yulin, et al. A TV forward-looking super-resolution imaging method based on TSVD strategy for scanning radar[J]. IEEE Transactions on Geoscience and Remote Sensing, 2020, 58(7): 4517–4528. doi: 10.1109/TGRS.2019.2958085.
[15]	GAMBARDELLA A and MIGLIACCIO M. On the superresolution of microwave scanning radiometer measurements[J]. IEEE Geoscience and Remote Sensing Letters, 2008, 5(4): 796–800. doi: 10.1109/LGRS.2008.2006285.
[16]	ZHANG Yongchao, JAKOBSSON A, ZHANG Yin, et al. Wideband sparse reconstruction for scanning radar[J]. IEEE Transactions on Geoscience and Remote Sensing, 2018, 56(10): 6055–6068. doi: 10.1109/tgrs.2018.2830100.
[17]	LI Yueli, LIU Jianguo, JIANG Xiaoqing, et al. Angular superresol for signal model in coherent scanning radars[J]. IEEE Transactions on Aerospace and Electronic Systems, 2019, 55(6): 3103–3116. doi: 10.1109/TAES.2019.2900133.
[18]	杨志伟, 贺顺, 廖桂生. 机载单通道雷达实波束扫描的前视探测[J]. 航空学报, 2012, 33(12): 2240–2245. YANG Zhiwei, HE Shun, and LIAO Guisheng. Forward-looking detection for airborne single-channel radar with beam scanning[J]. Acta Aeronautica et Astronautica Sinica, 2012, 33(12): 2240–2245.
[19]	ZHANG Yongchao, ZHANG Yin, LI Wenchao, et al. Angular superresolution for real beam radar with iterative adaptive approach[C]. 2013 IEEE International Geoscience and Remote Sensing Symposium, Melbourne, Australia, 2013: 3100–3103. doi: 10.1109/IGARSS.2013.6723482.
[20]	ZHANG Yongchao, LI Wenchao, ZHANG Yin, et al. A fast iterative adaptive approach for scanning radar angular superresolution[J]. IEEE Journal of Selected Topics in Applied Earth Observations and Remote Sensing, 2015, 8(11): 5336–5345. doi: 10.1109/JSTARS.2015.2449090.
[21]	ZHANG Yongchao, ZHANG Yin, HUANG Yulin, et al. Angular superresolution for scanning radar with improved regularized iterative adaptive approach[J]. IEEE Geoscience and Remote Sensing Letters, 2016, 13(6): 846–850. doi: 10.1109/lgrs.2016.2550491.
[22]	CHEN Hongmeng, GAO Wenquan, WANG Pei, et al. Sparse superresolution imaging for airborne forward-looking radar with multiple frames space[C]. IGARSS 2022 - 2022 IEEE International Geoscience and Remote Sensing Symposium, Kuala Lumpur, Malaysia, 2022: 1816–1819. doi: 10.1109/IGARSS46834.2022.9884278.
[23]	ZHANG Gang, LIANG Yi, CHEN Shuxuan, et al. Super-resolution forward-looking imaging method for manoeuvering platform with optimised dictionary and extended sparsity adaptive matching pursuit[J]. IET Radar, Sonar & Navigation, 2022, 16(5): 912–923. doi: 10.1049/rsn2.12229.
[24]	LIU Qingping, CHENG Yongqiang, CAO Kaicheng, et al. Radar forward-looking imaging for complex targets based on sparse representation with dictionary learning[J]. IEEE Geoscience and Remote Sensing Letters, 2022, 19: 4026605. doi: 10.1109/LGRS.2022.3200393.
[25]	CHEN Hongmeng, LI Yachao, GAO Wenquan, et al. Bayesian forward-looking superresolution imaging using Doppler deconvolution in expanded beam space for high-speed platform[J]. IEEE Transactions on Geoscience and Remote Sensing, 2022, 60: 5105113. doi: 10.1109/TGRS.2021.3107717.
[26]	陈洪猛, 李明, 王泽玉, 等. 基于多帧数据联合处理的机载单通道雷达贝叶斯前视成像[J]. 电子与信息学报, 2015, 37(10): 2328–2334. doi: 10.11999/JEIT150153. CHEN Hongmeng, LI Ming, WANG Zeyu, et al. Bayesian forward-looking imaging for airborne single-channel radar based on combined multiple frames data[J]. Journal of Electronics & Information Technology, 2015, 37(10): 2328–2334. doi: 10.11999/JEIT150153.
[27]	ZHANG Qiping, ZHANG Yin, HUANG Yulin, et al. TV-sparse super-resolution method for radar forward-looking imaging[J]. IEEE Transactions on Geoscience and Remote Sensing, 2020, 58(9): 6534–6549. doi: 10.1109/TGRS.2020.2977719.
[28]	TUO Xingyu, ZHANG Yin, HUANG Yulin, et al. Fast sparse-TSVD super-resolution method of real aperture radar forward-looking imaging[J]. IEEE Transactions on Geoscience and Remote Sensing, 2021, 59(8): 6609–6620. doi: 10.1109/TGRS.2020.3027053.
[29]	TUO Xingyu, MAO Deqing, ZHANG Yin, et al. Two-step dimension reduction strategy for real aperture radar fast super-resolution imaging[J]. IEEE Geoscience and Remote Sensing Letters, 2022, 19: 4025505. doi: 10.1109/LGRS.2022.3188704.
[30]	ZHANG Yongchao, LUO Jiawei, ZHANG Yongwei, et al. Resolution enhancement for large-scale real beam mapping based on adaptive low-rank approximation[J]. IEEE Transactions on Geoscience and Remote Sensing, 2022, 60: 5116921. doi: 10.1109/TGRS.2022.3202073.
[31]	ZHANG Yongchao, ZHANG Yin, LI Wenchao, et al. Super-resolution surface mapping for scanning radar: Inverse filtering based on the fast iterative adaptive approach[J]. IEEE Transactions on Geoscience and Remote Sensing, 2018, 56(1): 127–144. doi: 10.1109/TGRS.2017.2743263.
[32]	LI Jie, ZHANG Yongchao, ZHANG Yin, et al. Low-rank approximation-based super-resolution imaging for airborne forward-looking radar[C]. 2020 IEEE Radar Conference, Florence, Italy. 2020: 1–4. doi: 10.1109/RadarConf2043947.2020.9266355.
[33]	TUO Xingyu, MAO Deqing, ZHANG Yin, et al. Sparse target batch-processing framework for scanning radar superresolution imaging[J]. IEEE Geoscience and Remote Sensing Letters, 2023, 20: 3503905. doi: 10.1109/LGRS.2023.3274910.
[34]	MAO Deqing, ZHANG Yongchao, ZHANG Yin, et al. An efficient anti-interference imaging technology for marine radar[J]. IEEE Transactions on Geoscience and Remote Sensing, 2022, 60: 5101413. doi: 10.1109/TGRS.2021.3068787.
[35]	LI Weixin, LI Ming, ZUO Lei, et al. Real aperture radar forward-looking imaging based on variational Bayesian in presence of outliers[J]. IEEE Transactions on Geoscience and Remote Sensing, 2022, 60: 5117113. doi: 10.1109/TGRS.2022.3203807.
[36]	BISHOP C M. Pattern Recognition and Machine Learning[M]. New York: Springer, 2006: 102−105.