1.   引言

随着电子攻防对抗技术的迅速发展，雷达面临着日益复杂的电磁干扰环境。噪声压制式干扰是最常用的有源电子干扰类型之一，对雷达目标探测造成了极大的威胁^[1]。频率捷变技术发挥了雷达在电子对抗中波形主动对抗优势，具有优异的电子反对抗(Electronic Counter-Counter Measures, ECCM)性能^[2]，是对抗噪声压制式干扰的有效手段。然而，传统的频率捷变雷达多采用固定或随机的载频跳变序列^[3]，不能根据目标与电磁环境对载频序列进行优化，从而限制了频率捷变雷达在噪声压制干扰环境下的抗干扰能力^[4]。

为了应对不同的干扰策略，如何设计智能的频率捷变策略以提高雷达的检测和抗干扰性能已经成为国内外学者越来越关注的问题^[5]。传统的雷达频率捷变设计问题被描述为一个确定性的优化问题^[6]，该类方法需要估计干扰和目标特性，以确定雷达的最优发射参数^[7,8]。然而，在电子战场景下的噪声干扰通常是动态变化的，实时估计电磁环境参数对于资源有限的雷达通常是不切实际的。为了提高雷达对环境的适应能力，强化学习^[9]被引入雷达抗干扰技术中。Selvi等人^[10]将认知雷达与通信共存问题建模为一个马尔可夫决策问题，并采用策略迭代法^[11]解决该优化问题。Thornton等人^[12]将深度强化学习引入雷达抗干扰中，实验结果表明，在雷达与通信共存场景中，DQN (Deep Q-Network)算法^[13]表现出更好的抗干扰性能。Ailiya等人^[14]提出了一种基于强化学习的载频和脉宽选取方案，以增强抗干扰性能。Li等人^[15]设计了一种基于近端策略优化(Proximal Policy Optimization, PPO)算法^[16]的子脉冲捷变方法，该方法通过发射诱导子脉冲欺骗干扰机并保护真实的探测信号，从而提高雷达抗干扰性能。尽管基于强化学习的频率捷变方法获得了较好的抗干扰性能，但仍存在以下缺点：(1)基于强化学习的频率捷变方法需要进行离线训练。强化学习的样本效率是低下的^[17]，需要经过大量交互样本才能学习到较好的抗干扰策略，因此，将强化学习应用于雷达抗干扰中通常需要大量的离线探索来学习有效的频率捷变策略，而这在雷达抗干扰场景往往是不切实际的。(2)基于强化学习的频率捷变方法缺乏理论保证。基于强化学习的频率捷变方法将雷达与干扰环境的交互过程建模为马尔可夫决策过程，但干扰环境通常是一个时变的随机过程，其马尔可夫性质无法保证保持不变。此外，马尔可夫决策过程隐含着决策者的行为会影响环境的未来状态^[18]。然而，在一些随机干扰场景中，干扰环境的状态可能与雷达的发射频率独立，此时，马尔可夫决策过程的假设将不再成立。

为避免强化学习在雷达抗干扰决策应用中出现的问题，多臂赌博机^[19](Multi-Armed Bandit, MAB)决策模型被引入雷达系统中。MAB算法是在线学习算法的一个重要分支^[20]，由于其简单性和理论上的性能保证，已经在无线信道选择^[21,22]、动态频谱接入^[23,24]等领域展现出巨大的应用前景。目前，MAB在雷达中的应用还处于起步阶段，文献[25]基于组合式MAB算法设计了信道信噪比未知的MIMO雷达收发单元子集选择问题，该方法可以有效地用于求解MIMO雷达收发单元子集选择问题。文献[26]基于置信区间上界(Upper Confidence Bound, UCB)^[27]算法设计了一种相控阵雷达目标搜索策略，该方法可以提高发现目标的概率。文献[28]基于汤普森采样(Thompson Sampling, TS)^[29]和EXP3 (Exponential weights for Exploration and Exploitation)^[30]算法设计了雷达波形选择方法，有效提升了雷达的检测和跟踪性能。文献[31]基于折扣汤普森采样算法设计了一种非平稳环境下频率捷变雷达发射策略，提高了雷达在非平稳环境中的检测性能。上述研究表明了MAB算法在雷达在线决策问题上具有巨大的潜力。

然而，现有的MAB算法存在一定的局限性：一方面，TS类和UCB类算法对干扰策略极为敏感，在面对动态干扰场景时，学习性能不理想；另一方面，EXP3类算法在面对静态干扰场景时，由于收敛速度较慢，而选择大量的次优频率通道，导致学习性能降低。在实际应用中，由于无法提前获取敌方的干扰策略，此时使用其中一类算法可能会造成较大的性能损失。

因此，如何在没有干扰环境先验信息的条件下，设计一种适用于任意干扰策略的频率捷变雷达在线决策方法是一个重要且具有挑战性的问题。为了解决这个问题，本文根据干扰策略的特征，将雷达所面临的干扰场景分为3类，针对3类干扰场景下的干扰策略特征，提出一种基于MAB的频率捷变雷达在线决策方法。该方法在没有探测环境先验知识和离线训练的情况下仍能实现优异的学习性能，且在3类干扰场景中均具有理论上的遗憾性能保证，在提升频率捷变雷达探测和抗干扰性能方面具有重要的应用前景。

2.   问题描述

2.1   雷达检测模型

在噪声压制式干扰存在的情况下，雷达接收到的信号由目标信号、压制式干扰信号和噪声信号3部分构成^[32]。根据雷达方程^[33]，对于一个点目标回波信号的功率 ${y_{{\mathrm{s}}}}$ 为

其中， ${P_{{\mathrm{t}}}}$ 为雷达发射功率，G为发射天线增益， $\lambda$ 为雷达发射信号波长， $\sigma$ 为目标的散射截面积(Radar Cross Section, RCS)， ${L_{{\mathrm{s}}}}$ 为雷达系统损耗，R为雷达与目标之间的距离。

雷达的接收机内部噪声 ${y_{\rm n}}$ 为

其中， ${\mathrm{k}} = 1.38 \times {10^{ - 23}}\;{\mathrm{J}}/{\mathrm{K}}$ 为玻尔兹曼常数， ${{\mathrm{T}}_0}$ 为标准室温，一般取290 K， ${B_{\rm n}}$ 为接收机带宽， ${F_{\rm n}}$ 为接收机的噪声系数。

根据干扰方程^[34]，雷达接收到来自干扰机发射的干扰信号功率 ${y_{\mathrm{J}}}$ 为

其中， ${P_{\mathrm{J}}}$ 为干扰机的发射功率， ${\lambda _{\mathrm{j}}}$ 为干扰信号波长， $G(\theta )$ 为雷达在干扰机主瓣方向上的天线增益， ${G_{\mathrm{J}}}$ 为干扰机天线增益， ${\gamma _{\mathrm{J}}}$ 为极化失配损失， ${L_{\mathrm{J}}}$ 为干扰系统损耗， ${R_{\mathrm{j}}}$ 为雷达与干扰机之间的距离， $B_{\mathrm{J}}^{\mathrm{T}}$ 表示干扰机的发射带宽， $B_{\mathrm{J}}^{\mathrm{R}}$ 表示雷达接收机接收到的干扰信号带宽。

此时，雷达对目标的检测概率 ${P_{\mathrm{d}}}$ 可近似为^[33]

其中， ${\mathrm{erfc}}(z) = {2\pi}^{-1/2}\displaystyle\int_z^\infty {{{\mathrm{e}}^{ - {v^2}}}{\mathrm{d}}v}$ 为余误差函数， ${P_{{\mathrm{fa}}}}$ 为雷达的虚警概率， ${\mathrm{SINR}} = {{{{{y}}_{{\mathrm{s}}}}}}/({{{{{y}}_{\rm n}}{\text{ + }}{{{y}}_{\mathrm{J}}}}})$ 为雷达接收机关于目标的信干噪比。

2.2   频率捷变雷达MAB问题描述

将频率捷变雷达的跳频带宽分为互不重叠的N个频率通道。令 $\mathcal{F}=\left\{f_{1}, f_{2}, \cdots, f_{N}\right\}$ 表示雷达可用载频集，其中， ${f_i} = {f_0} + (i - 1) \cdot B$ , $i \in \{ 1,2,\cdots,N\}$ ， ${f_0}$ 为雷达初始载频，B为雷达发射信号带宽，频率捷变雷达在每个脉冲重复周期内可从N个可用载频内中任选一个作为雷达的发射载频。假设雷达的发射功率不变，则在第t个脉冲重复周期内，雷达的发射参数可用向量 ${\boldsymbol{A}}(t) = [{a_1}(t){\text{ }}{a_2}(t){\text{ }} \cdots {\text{ }}{a_{N}}(t)]$ 表示，其中， ${a_i}(t) \in \{ 0,1\}$ 为二元变量，用于表示雷达是否选择第i个频率通道用于探测。图1为雷达发射频率通道选择示意图，其中 $N = 10$ , ${\boldsymbol{A}} = [0{\text{ }}1{\text{ }}0{\text{ }}0{\text{ }}0{\text{ }}0{\text{ }}0{\text{ }}0{\text{ }}0{\text{ }}0]$ ，代表雷达选择第2个频率通道来发射。

图  1  雷达发射频率通道选择示意图

Figure  1.  Radar transmission frequency channel selection schematic

下载: 全尺寸图片 幻灯片

研究频率捷变雷达在线决策的目标是最大化雷达的探测性能，本文将检测概率作为频率捷变雷达MAB问题的奖励值。在其他参数一定时，每个频率通道的检测概率由该频率通道的目标的RCS值和干扰能量共同决定，考虑到频率捷变雷达通常不具有对整个跳频带宽信号频谱的同时感知能力，且在对抗中雷达难以提前获取目标的RCS值，在每次探测中，奖励值应只对发射频率通道的检测概率进行计算，不应对整个跳频带宽进行频谱感知。另一方面，在压制式干扰存在的情况下，目标信号可能被压制干扰淹没，导致雷达无法检测到目标，从而无法利用式(4)计算检测概率。因此本文设计了如下的奖励函数：

其中， ${g_{t}}({f_i})$ 代表第t个脉冲重复周期雷达选择第i个频率通道获得的收益值； ${c_{t}} \in \{ 0,1\}$ 为二元变量，用于表示第t个脉冲重复周期的回波信号中是否检测出目标信号； ${\text{SIN}}{{\text{R}}_{t}}({f_i})$ 表示第t个脉冲重复周期雷达接收到回波信号的信干噪比。

频率捷变雷达MAB问题可描述如下：在第t个脉冲重复周期，雷达根据跳频策略 ${\pi _{t}}$ 从可用载频集 $\mathcal{F}$ 中选择一个载频 ${f_i}$ 作为雷达的发射载频，接收回波信号并计算当前频率通道的收益值 ${g_{t}}({f_i})$ ，根据收益值选择下一脉冲重复周期雷达的跳频策略 ${\pi _{t + 1}}$ 。频率捷变雷达MAB问题一个基本挑战是解决探索与开发之间的权衡^[35]，即在利用过去获得最高收益的动作与探索未来可能获得更高收益的新动作之间取得平衡。MAB算法的性能用遗憾值 $R(t)$ 衡量^[19]，遗憾值 $R(t)$ 定义为在t个脉冲重复周期内，MAB算法计算出的跳频策略与使用最优固定频率通道之间的累计增益差值：

其中， ${g_{s}}({f_i})$ 表示第i个频率通道在第s个脉冲重复周期的收益值， ${g_{s}}({\pi _{s}})$ 表示雷达在应用策略 ${\pi _{s}}$ 时在第s个脉冲重复周期的收益值。由于收益值 ${g_{t}}$ 和策略 ${\pi _{t}}$ 通常是随机的，遗憾值 $R(t)$ 是一个随机变量，本文采用期望遗憾值衡量本文的算法性能：

由式(5)可知，收益值 ${g_{t}} \in [0,1]$ 为有界函数，令损失值 ${l_{t}} = 1 - {g_{t}}$ ，可以将收益值 ${g_{t}}$ 转换为损失值 ${l_{t}}$ ，期望遗憾值 $\bar R(t)$ 也可以写为损失值的形式：

2.3   噪声压制式干扰场景分类

与频率捷变雷达发射模型相似，干扰机的发射通道选择可用向量 ${\boldsymbol{J}}(t) = [{j_1}(t){\text{ }}{j_2}(t){\text{ }} \cdots {\text{ }}{j_N}(t)]$ 表示，其中， ${j_i}(t) \in \{ 0,1\} ,i = 1,2, \cdots ,N$ 为二元变量，用于表示干扰机是否选择干扰第i个频率通道。同时，假设干扰机在每个频率通道内的干扰功率用向量 ${{\boldsymbol{P}}_{\rm{j}}}(t) = [{p_{\rm j,1}}(t){\text{ }}{p_{\rm j,2}}(t){\text{ }} \cdots {\text{ }}{p_{{\mathrm{j}},N}}(t)]$ 表示，其中， ${p_{{\mathrm{j}},i}}(t) \in [0,{P_{\mathrm{j}}}^{\max }],i = 1,2, \cdots ,N$ ， ${P_{{\mathrm{j}}}^{\max}}$ 为干扰机最大发射功率。则在第t个脉冲重复周期内，干扰机的发射策略可表示为

其中， $\circ$ 表示Hadamard积。

一般而言，压制式干扰通常根据干扰带宽和干扰信号的中心频率分为瞄准式、阻塞式和扫频式3种干扰策略。然而，一方面，该分类方法仅关注干扰机的干扰通道选择策略 ${\boldsymbol{J}}(t)$ ，未考虑干扰功率变化对雷达跳频策略造成的影响；另一方面，该分类方法不能全面地描述干扰机的干扰策略，实际干扰机可以根据雷达的发射策略，对上述的基本形式进行组合，如多点频瞄准式干扰、分段阻塞式干扰等。

因此，本文从干扰策略的角度出发，根据干扰机的发射策略 ${\boldsymbol{I}}(t)$ 是否随时间改变以及干扰机是否根据雷达的发射策略实施针对性的干扰，对干扰场景进行分类。

本文将雷达所面临的噪声压制式干扰场景分为以下3类：

(1) 静态干扰场景

在静态干扰场景中，干扰机的干扰策略 ${\boldsymbol{I}}(t)$ 不随时间改变。由于干扰机在每个频率通道内的干扰功率不随时间改变，因此，每个通道的损失值 ${l_{t}}({f_i})$ 仅由干扰功率和目标RCS决定且不随时间改变，即 ${l_{t}}({f_i})$ 服从一个只依赖于通道 ${f_i}$ ，而不依赖于时间t的独立随机分布。此时，干扰环境满足随机性MAB问题的假设，常用的求解算法为UCB算法和TS算法，在随机性MAB问题中具有 $\ln (t)$ 阶的遗憾值上界。

在该类干扰场景下，使用 $\mu ({f_i}) = \mathbb{E}\left[ {{l_{t}}({f_i})} \right]$ 表示第i个频率通道的期望损失，若频率通道 ${f^*}$ 满足

则称 ${f^*}$ 为最优频率通道，否则称为次优频率通道。对于每个频率通道， $\varDelta ({f_i}) = \mu ({f_i}) - \mu ({f^*})$ 为频率通道损失期望差， ${\varDelta _{\min }} = \mathop {\min }\limits_{{f_i}:\varDelta ({f_i}) > 0} \{ \varDelta ({f_i})\}$ 为最小频率通道损失期望差。

令 ${N_{t}}({f_i})$ 表示前t轮交互中，第i个频率通道被雷达选择的次数，则静态干扰场景下的期望遗憾值也可写为

值得注意的是，无干扰的探测环境也可视为静态干扰场景的一种特例，此时，各频率通道内的期望损失值仅受目标RCS影响。

(2) 非自适应干扰场景

与静态干扰场景不同，在非自适应干扰场景下，干扰机的干扰策略 ${\boldsymbol{I}}(t)$ 随时间变化，即被干扰频率通道以及干扰功率都可能随着时间变化。在非自适应干扰场景下，可假设干扰机是一个非自适应的干扰机，即干扰机的干扰策略不会对雷达发射策略做出反应，是一种简单的攻击模型。

由于每个频率通道的损失值 ${l_{t}}({f_i})$ 受干扰机的干扰策略影响，每个通道的损失值 ${l_{t}}({f_i})$ 不只依赖于通道 ${f_i}$ ，还与时间t有关。此时，干扰环境满足对抗性MAB问题的假设，常用的求解算法为EXP3算法，在对抗性MAB问题中具有 $\sqrt t$ 阶的遗憾值上界。

(3) 自适应干扰场景

与非自适应干扰场景不同的是，我们假设干扰机是一个自适应干扰机，即干扰机可以观测到雷达的发射策略，并针对性地设计干扰策略，此时，每个通道的损失值 ${l_{t}}({f_i})$ 与雷达的前 $t - 1$ 个发射频率通道选择有关。与非自适应干扰场景相比，自适应干扰场景对频率捷变雷达具有更大的威胁。

文献[36]表明，对于具有无限记忆内存的自适应干扰机，它可以模仿并执行与雷达相同的学习算法，并设置与雷达频率通道选择概率相同的策略对雷达进行干扰，这将导致遗憾值随时间t线性增长。因此，本文考虑一个介于非自适应干扰机和无限记忆内存的自适应干扰机之间干扰模型：m-内存的自适应干扰机模型^[36]，该模型下干扰机仅会记录m个雷达最新的发射频点，并依赖于这些观测值对雷达进行干扰。

图2给出了噪声压制干扰场景的示意图，其中，红色为雷达的发射频率通道，蓝色为干扰机的干扰频率通道，紫色代表雷达发射频率通道与干扰机干扰通道重合。其中，无干扰环境可以看作静态干扰场景的一种特例。

图  2  噪声压制式干扰场景示意图

Figure  2.  Noise suppression jamming scene schematic

下载: 全尺寸图片 幻灯片

3.   基于MAB的频率捷变雷达在线决策算法

3.1   算法描述

如2.3节所述，根据干扰策略的特征，雷达所面临的噪声压制式干扰场景可分为3类。在静态干扰场景中每个频率通道的损失值服从一个不随时间改变的随机过程，这满足随机性MAB问题的假设；而在非自适应干扰场景和自适应干扰场景中，由于干扰策略不断变化，每个频率通道状态被敌方干扰机任意控制，这满足对抗性MAB问题的假设。随机性MAB问题和对抗性MAB问题是MAB问题的两种主要形式^[37]，由于两种问题的损失值确定形式不同，因此分析方法和性能结果存在明显差异。经典的EXP3算法、UCB算法和TS算法均只能在其中一种MAB问题上保证最优的遗憾性能。而在实际场景中，无法提前判断雷达所面临的干扰环境属于哪一种干扰场景，此时采用其中一种问题假设可能导致学习性能不佳。

本节中，我们将基于EXP3++算法^[38]，设计一种频率捷变雷达在线决策方法，该方法引入参数 ${\varepsilon _{t}}$ 对每个频率通道的选择概率进行单独的调整，提高了静态干扰场景下选择最优频率通道的概率；同时，该方法的频率通道选择策略为指数分布和参数 ${\varepsilon _{t}}$ 组合构成的分布，使得具有在非自适应干扰场景和自适应干扰场景下均具有良好的学习性能。本文将该算法命名为RAFA-EXP3++ (Radar Adaptive Frequency Agility based on EXP3++)算法，具体的流程如算法1所示。

1  RAFA-EXP3++算法

1.  RAFA-EXP3++ algorithm

初始化：频率通道数N， $\forall {f_i} \in \mathcal{F}$，初始损失估计值 ${\tilde L_0}({f_i}) = 0$，权重 ${w_0}({f_i}) = 1$，损失期望差估计值 ${\hat \varDelta _0}({f_i})$=1
对于每一个脉冲重复周期 $t = 1,2, \cdots ,T$
1. 设置参数： ${\beta _{t}} = \dfrac{1}{2}\sqrt {\dfrac{{\ln N}}{{tN}}}$; ${\eta _{t}} = 2{\beta _{t}}$; $c = 20$；
$\forall {f_i} \in \mathcal{F}$： ${\xi _{t}}({f_i}) = \dfrac{{c{{(\ln t)}^2}}}{{t{{\hat \varDelta }_{t - 1}}{{({f_i})}^2}}}$; ${\varepsilon _{t}}({f_i}) = \min \left\{ \dfrac{1}{{2N}},{\beta _{t}},{\xi _{t}}({f_i})\right\}$
2. $\forall {f_i} \in \mathcal{F}$，计算各频率通道选择概率 ${p_{t}}({f_i})$：
${p_{t}}({f_i}) = \left(1 - \displaystyle\sum\limits_{j = 1}^N {{\varepsilon _{t}}({f_j})} \right)\dfrac{{{w_{t - 1}}({f_i})}}{{\displaystyle\sum\limits_{j = 1}^N {{w_{t - 1}}({f_j})} }} + {\varepsilon _{t}}({f_i})$ 　　　　　　　　　　　　　　　　　　　　　　　　　 (11)
3. 依概率 ${p_{t}}$从可用频率通道集 $\mathcal{F}$中选择发射频率通道 ${f_a}$，接收回波信号并利用式(5)计算损失值 ${l_{t}}({f_a})$。
4. $\forall {f_i} \in \mathcal{F}$，更新各频率通道权重值 ${w_{t}}({f_i})$和损失期望差估计值 ${\hat \varDelta _{t}}({f_i})$：
${\tilde{L}}_{t}({f}_{i})=\left\{\begin{array}{cc}{\tilde{L}}_{t-1}({f}_{i})+\dfrac{{l}_{t}({f}_{i})}{{p}_{t}({f}_{i})},& 当{f}_{i}={f}_{a}时\\ {\tilde{L}}_{t-1}({f}_{i}),& 当{f}_{i}\ne {f}_{a}时\end{array} \right.$ 　　　　　　　　　　　　　　　　　　　　　　　　　　(12)
${w_{t}}({f_i}) = \exp \left( - {\eta _{t}}{\tilde L_{t}}({f_i})\right)$ 　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　 　 (13)
${\hat \varDelta _{t}}({f_i}) = \min \left\{ {1,\dfrac{1}{t}\left( {{{\tilde L}_{t}}({f_i}) - \mathop {\min }\limits_{{f_j} \in \mathcal{F}} {{\tilde L}_{t}}({f_j})} \right)} \right\}$ 　　　　　　　　　　　　　　　　　　　　　 　　　　　 (14)

下载: 导出CSV 

| 显示表格

3.2   遗憾性能分析

在本节，将分析该算法在上述3类干扰场景中的遗憾性能。

(1) 静态干扰场景下遗憾性能分析

在静态干扰场景中，由于干扰机的干扰策略不随时间改变，每个频率通道内的期望损失 $\mu ({f_i})$ 保持不变，满足随机MAB问题的假设。令 ${t^*}$ 为满足 ${t^*} \ge ({{{c^2}N\ln {{({t^ * })}^4}}})/{{\ln N}}$ 的最小整数， ${t^*}({f_i}) = \max \{ {t^*},\left\lceil {{{\mathrm{e}}^{1/\varDelta {{(a)}^2}}}} \right\rceil \}$ ，由文献[38]中的定理3可知，当 ${\eta _{t}} \ge {\beta _{t}}$ 时，EXP3++算法的遗憾值满足：

由于本文所提方法中 ${\eta _{t}} = 2{\beta _{t}}$ ，因此，在静态干扰场景中，本文所提方法的遗憾值满足式(15)，为 ${(\ln t)^3}$ 阶的遗憾值上界。

值得注意的是，当 $\varDelta ({f_j})$ 较小时，会导致次优频率通道的选择次数增加，由式(10)可知，在静态干扰场景下会造成较大的遗憾值。

(2) 非自适应干扰场景下遗憾性能分析

在非自适应干扰场景中，由于干扰机的干扰策略随时间改变，每个通道的损失值受干扰机的干扰策略影响，满足对抗MAB问题的假设。参考文献[38]中定理1的证明过程，可以获得如下的遗憾值上界：

由 ${\varepsilon _{t}}({f_i}) = \min\left\{ \dfrac{1}{{2N}},{\beta _{t}},{\xi _{t}}({f_i})\right\}$ 可知，

注意到 $\displaystyle\sum\nolimits_{t = 1}^n {\frac{1}{{\sqrt t }}} \le 2\sqrt n$ ，将 ${\eta _{t}} = 2{\beta _{t}} = \sqrt {{{\ln N}}/({{tN})}}$ 代入式(17)后可得到如下的遗憾值上界：

由式(18)可以看出，在非自适应干扰场景下，本文所提方法具有 $\sqrt t$ 阶的遗憾值上界，与EXP3算法相同，因此，本文所提方法在非自适应干扰场景下可获得与EXP3算法相近的学习性能。

(3) 自适应干扰场景下遗憾性能分析

如前文所述，对于一个无限内存的自适应干扰机，任何MAB算法都无法令遗憾值随时间t次线性增长。在自适应干扰场景中，考虑一个m-内存的自适应干扰机，根据文献[36]中的定理2可知，通过将整个时间t分为大小为 $\tau$ 的连续且不相交的批次进行处理，并利用该小批次受到的平均损失来反馈给RAFA-EXP3++，则当 $\tau = {(5\sqrt {N\ln N} )^{ - {1}/{3}}}{t^{{1}/{3}}}$ 时，本文所提方法的遗憾值上界为

对比式(19)和式(18)可以看出，自适应干扰场景的算法遗憾值更高，说明自适应干扰场景将对雷达造成更大的威胁。

4.   仿真结果及分析

4.1   参数设置

在本节将利用仿真实验验证2.3节的3类压制干扰场景下所提频率捷变雷达在线决策方法的性能。所有实验均重复进行10次，每次仿真的脉冲数为 ${\text{1}}{{\text{0}}^{\text{5}}}$ 个。所有实验结果均与随机捷变策略(Random)、 $\varepsilon {\text{-}} {\mathrm{Greedy}}$ 算法^[9]、UCB1算法^[27]，EXP3算法^[30]以及文献[31]中的CDTS算法进行比较。其中，随机捷变策略指雷达均匀随机地选择发射频率通道，该策略是频率捷变雷达的常用策略。 $\varepsilon {\text{-}} {\mathrm{Greedy}}$ 算法中探索率设置为0.1。UCB1算法是随机性MAB问题中的常用算法，仿真实验的雷达参数见表1。

表  1  仿真实验雷达参数

Table  1.  Radar parameters of simulation experiment

参数	数值
工作频段	Ku频段
信号带宽B	40 MHz
频率通道数N	30
脉冲重复周期 ${T_{\mathrm{r}}}$	20 μs
发射功率 ${P_{t}}$	1000 W
发射天线增益G	40 dB
雷达系统损耗 ${L_{s}}$	4 dB
接收机带宽 ${B_{\rm n}}$	40 MHz
接收机噪声系数 ${F_{\rm n}}$	3 dB
虚警率 ${P_{{\mathrm{fa}}}}$	${10^{ - 4}}$
目标的径向距离R	10 km

下载: 导出CSV 

| 显示表格

目标的RCS对电磁波频率的变化极为敏感。不失一般性，假设目标的RCS是起伏的，起伏模型为Swerling II型，在各频率通道内的RCS均值如表2所示。其中， $U(a,b)$ 表示服从在a到b之间均匀分布。

表  2  仿真实验中目标RCS均值(m²)

Table  2.  The mean RCS of target in the simulation experiment (m²)

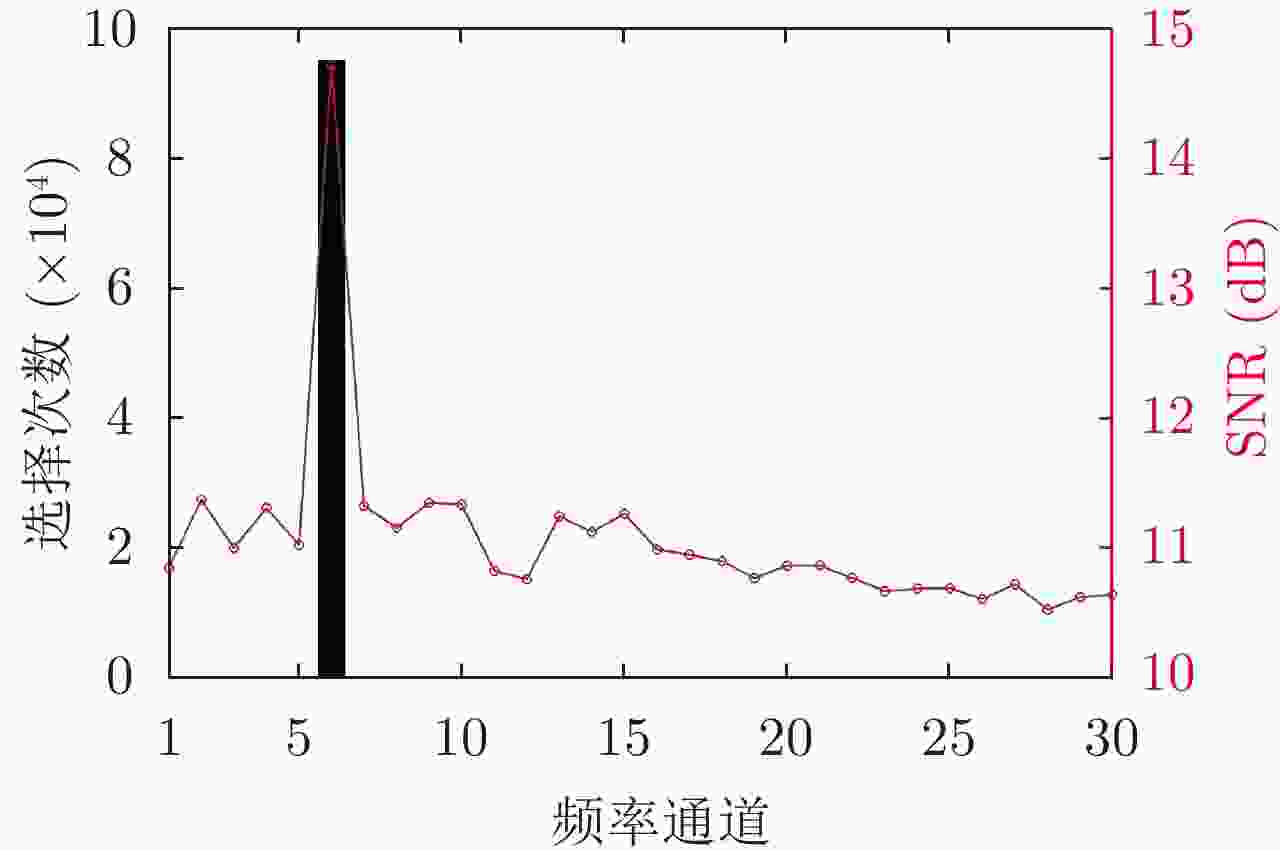
频率通道	RCS均值
1～5	$U(8.5,9.5)$
6	$14$
7～15	$U(8.5,10.0)$
16～30	$U(9.0,9.5)$

下载: 导出CSV 

| 显示表格

表3给出干扰机的部分仿真参数，其他参数在仿真实验部分给出。

表  3  仿真实验干扰机部分参数

Table  3.  Jammer parameters of simulation experiment

参数	数值
干扰机发射总功率 ${P_{\mathrm{J}}}$	800 W
干扰机天线增益 ${G_{\mathrm{J}}}$	10 dB
雷达在干扰方向增益 $G(\theta )$	20 dB
极化失配损失 ${\gamma _{\mathrm{J}}}$	0.5
干扰系统损耗 ${L_{\mathrm{J}}}$	5 dB
与雷达的径向距离 ${R_{\mathrm{J}}}$	15 km

下载: 导出CSV 

| 显示表格

4.2   静态干扰场景仿真结果及分析

为了验证本文提出的算法在静态干扰场景下的性能，在本节设计了无干扰以及固定干扰策略两种干扰场景。

首先验证无干扰场景下本文所提方法的性能。从图3可以看出约有95%的发射信号选择了SNR最高的频率通道，有效避免了由于选择次优频率通道而降低雷达探测性能的问题。图4为各算法的性能对比图，其中，实线代表10次重复实验的平均值，阴影部分为平均值 $\pm$ 标准差后的边界范围。从图中可以看出，随机捷变策略的性能最差，这是由于随机策略为均匀随机选择各频率通道，而不是选择收益最大的频率通道，因此在无干扰场景中检测性能较差。本文所提方法在无干扰场景下具有较低的遗憾值，与UCB1算法和CDTS算法的性能相近，与EXP3算法相比遗憾值降低90%。可以看出，在无干扰场景下本文所提方法优于EXP3算法和随机捷变策略。

图  3  无干扰环境下频率通道选择次数与SNR

Figure  3.  Frequency channel selection times and SNR in the no jamming environment

下载: 全尺寸图片 幻灯片

图  4  无干扰环境下所提算法的性能对比图

Figure  4.  Comparison plots of the performance of the proposed algorithm in no jamming environment

下载: 全尺寸图片 幻灯片

下面验证固定干扰策略的干扰场景下本文所提方法的性能。假设干扰机的干扰策略为干扰SNR最高的5个频率通道，且不随时间改变。从图5可以看出，约有15%的发射信号选择了SINR最高的频率通道4，同时，由于频率通道4与频率通道15的SINR相近，因此约13%的发射信号选择了频率通道1。对于受到干扰的频率通道，选择概率均在0.1%以下，可以有效避开干扰。从图6可以看出，本文所提方法在固定干扰策略的干扰场景下仍具有较低的遗憾值，与UCB1算法和CDTS算法性能相近，与EXP3算法相比遗憾值降低约50%。可以看出，在无干扰场景下本文所提方法优于EXP3算法和随机捷变策略。

图  5  固定干扰策略环境下频率通道选择次数与SINR

Figure  5.  Frequency channel selection times and SINR in the fixed jamming strategy environment

下载: 全尺寸图片 幻灯片

图  6  固定干扰策略场景下所提算法的性能对比图

Figure  6.  Comparison plots of the performance of the proposed algorithm in fixed jamming strategy environment

下载: 全尺寸图片 幻灯片

从本节仿真实验结果可以看出，本文所提方法与随机性MAB问题中常用的UCB1算法性能相近，优于随机捷变策略以及EXP3算法，与理论分析相同。我们注意到，与无干扰环境相比，固定干扰策略环境下本算法的累计遗憾值有所提高，这是因为当频率通道损失期望差 $\varDelta$ 变小时，选择次优频率通道的次数会增加，导致遗憾值变大，与理论分析相符合。由于最优频率通道与次优频率通道的期望奖励值相近，因此，增加选择次优频率通道的次数不会大幅降低雷达的探测性能。

4.3   非自适应干扰场景仿真结果及分析

在本节将验证本文所提方法在非自适应干扰场景中的性能，干扰场景设置如下。假设非自适应干扰场景中存在一扫频式干扰机和阻塞式干扰机。当雷达探测过程开始时，阻塞式干扰机开始对雷达工作全频段进行阻塞式干扰，此时干扰环境的SINR如图7所示。0.1 s之后扫频式干扰机开启，并以固定的干扰功率扫描雷达的工作频段，扫频式干扰机的干扰策略参数如表4所示，其他参数见表3。可以看出，无论扫频式干扰机还是阻塞式干扰机，其干扰策略都与雷达的频率通道选择策略无关。

图  7  阻塞式压制干扰下的SINR

Figure  7.  SINR under blocking suppression jamming

下载: 全尺寸图片 幻灯片

表  4  扫频式干扰参数设置

Table  4.  Parameter setting of sweeping frequency jamming

参数	数值
扫频带宽	1.2 GHz
干扰带宽	200 MHz
跳频带宽	200 MHz
扫频周期	120 μs

下载: 导出CSV 

| 显示表格

表5统计了在该场景下的雷达检测到目标的次数。图8展示了非自适应干扰场景下所提算法的性能对比，可以看出，UCB1算法和CDTS算法仅与随机捷变策略的性能相当，这说明了随机性MAB问题假设下提出的算法并不能很好地应用于对抗性MAB问题中。同时，我们注意到UCB1算法和CDTS算法的方差较大，在非自适应干扰场景中存在着不稳定的缺点。而本文所提方法具有与EXP3算法相近的遗憾和收益性能，且算法的方差较小。如表5所示，本文方法与EXP3算法检测到目标的概率达到73%， $\varepsilon {\text{-}} {\mathrm{Greedy}}$ 算法达到67%，而CDTS算法和UCB1算法仅与随机捷变策略的性能相当，仅在55%左右。可以看出，本文方法可以在非自适应干扰场景中有效提升雷达的探测性能。

表  5  非自适应干扰场景中检测到目标的次数

Table  5.  The number of detected targets in non-adaptive jamming scene

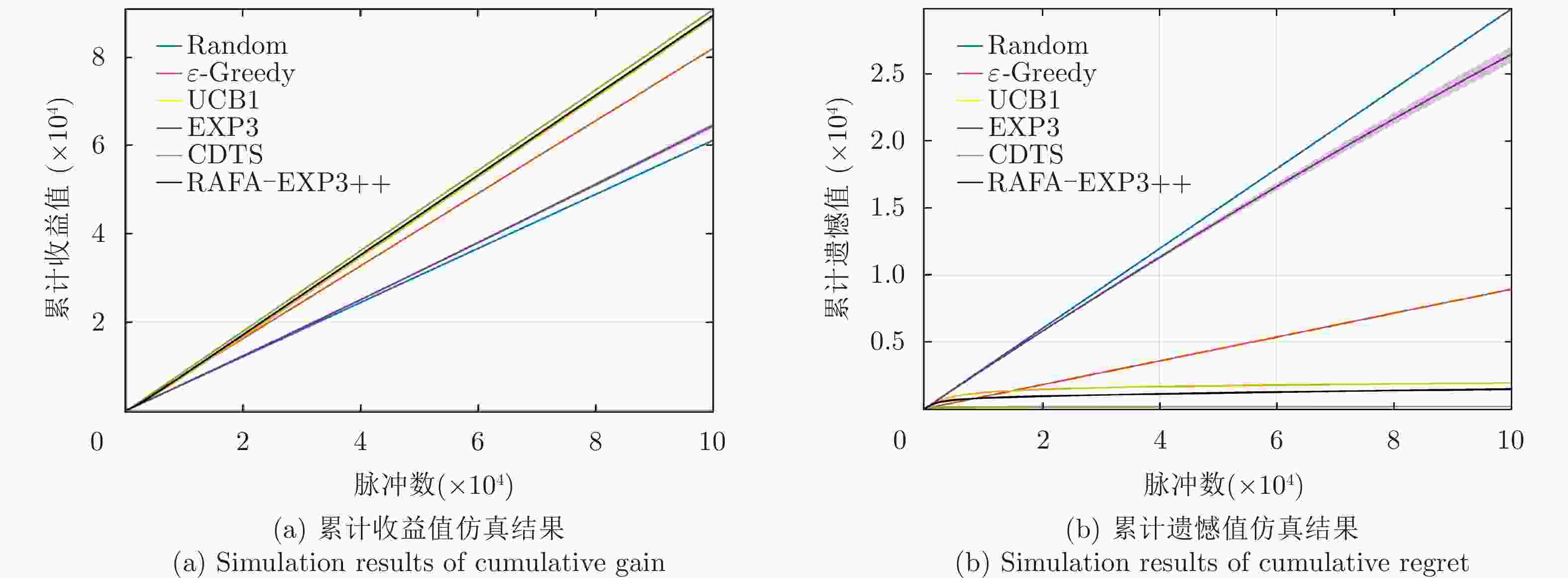
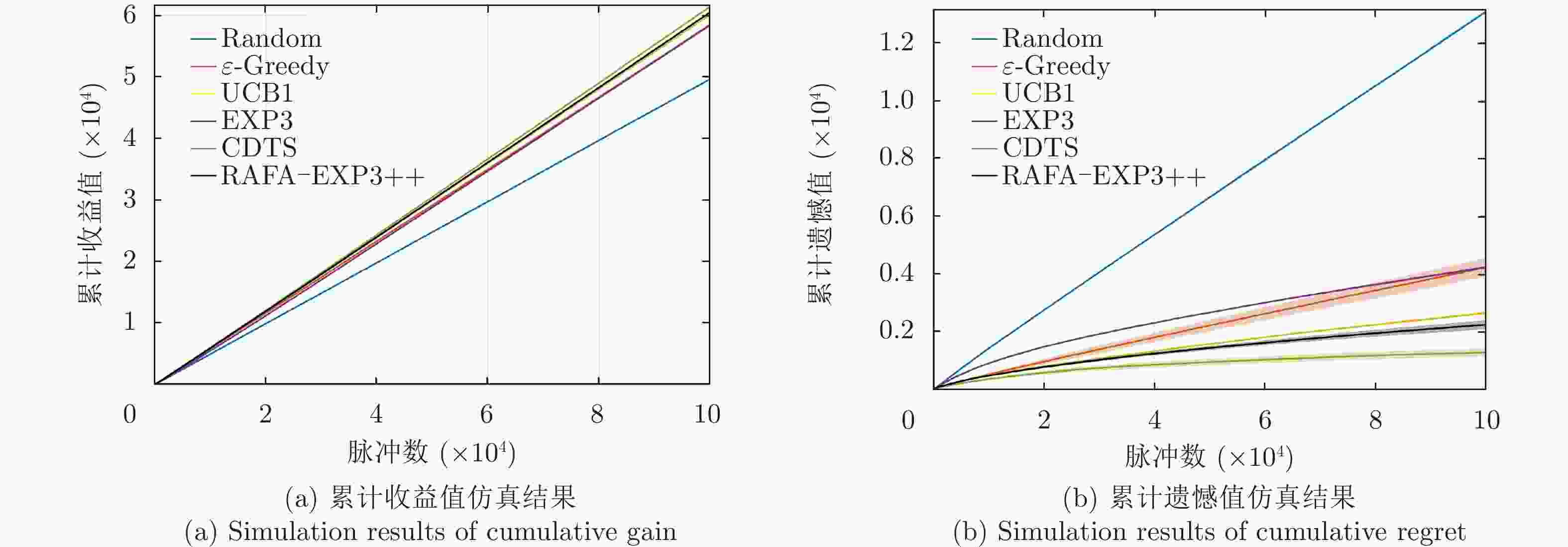
算法名称	次数
Random	53965
$\varepsilon {\text{-}} {\mathrm{Greedy}}$	66838
UCB1	55951
EXP3	72825
CDTS	55345
RAFA-EXP3++	72837

下载: 导出CSV 

| 显示表格

图  8  非自适应干扰场景中所提算法的性能对比图

Figure  8.  Comparison plots of the performance of the proposed algorithm in non-adaptive jamming scene

下载: 全尺寸图片 幻灯片

4.4   自适应干扰场景仿真结果及分析

本节将验证本文所提方法在自适应干扰场景中的性能，干扰场景设置如下。假设初始时自适应干扰场景中存在一自适应干扰机和阻塞式干扰机。其中，阻塞式干扰机的参数与4.3节相同，0.1 s后自适应干扰机开启工作。如前文所述，本文考虑以1-记忆的自适应干扰机，即干扰信号的中心频率为雷达的前一个发射频率，假设干扰机的干扰带宽为200 MHz，其他参数见表3，可以看出，干扰机的干扰策略与雷达的发射策略有关。

如图9所示，本文所提方法仍可以获得与EXP3算法相近的遗憾和收益性能，优于UCB1算法和CDTS算法。对比图8(a)与图9(a)可以看出，UCB1算法的收益性能下降最大，这是因为由UCB1算法计算出的发射策略为确定性策略，即在每次频率通道选择时，UCB1算法会计算出唯一的发射频率通道。而CDTS算法、EXP3算法以及本文所提方法计算出的发射策略为随机策略，在每次频率通道选择时，算法并不会指定唯一的频率通道，而是给出每个频率通道的选择概率，然后依概率选择当前的发射频率通道，这样可以提高自适应干扰机对雷达发射频率通道的预测难度，从而提高雷达对抗性能。我们注意到，相较于非自适应干扰场景，虽然干扰机的干扰功率和干扰带宽都相同，但由于干扰机的干扰策略与雷达发射策略相关，算法的性能会大幅下降，这与理论分析一致。

图  9  自适应干扰场景下所提算法的性能对比图

Figure  9.  Comparison plots of the performance of the proposed algorithm in adaptive jamming scene

下载: 全尺寸图片 幻灯片

表6统计了在该场景下的雷达探测到目标的次数，本文所提方法和EXP3算法检测到目标的概率约为55%，随机捷变策略约为54%，CDTS算法约为33%，UCB1算法和 $\varepsilon {\text{-}} {\mathrm{Greedy}}$ 算法均在30%以下。由式(11)可知，本文所提方法中各频率通道的选择概率与该频率通道的权重值呈正相关，由式(13)可知各频率通道的权重值为各频率通道累计损失估计值的负指数，对于累计损失值越小的频率通道，权重值越高，具有更大的被选择概率。因此，虽然本文所提方法与随机捷变策略所检测到目标的次数相近，但本文所提方法会以更大概率选择到高SINR的频率通道，可以提升雷达目标识别、跟踪等功能的性能，故本文所提方法可以提升雷达在自适应干扰场景下的性能。

表  6  自适应干扰场景下检测到目标的次数

Table  6.  The number of detected targets in adaptive jamming scene

算法名称	次数
Random	54048
$\varepsilon {\text{-}} {\mathrm{Greedy}}$	27423
UCB 1	16265
EXP3	55135
CDTS	33723
RAFA-EXP3++	55170

下载: 导出CSV 

| 显示表格

5.   结语

针对噪声压制干扰背景下的频率捷变雷达探测问题，本文提出一种基于多臂赌博机的频率捷变雷达在线决策方法。本文根据干扰机的策略特征，将压制干扰场景分为静态干扰场景、非自适应干扰场景以及自适应干扰场景，以雷达检测概率为奖励函数，设计了RAFA-EXP3++算法。理论分析和仿真结果表明，与随机捷变策略和经典方法相比，本文所提的方法具有更强的灵活性，可适应全部3类干扰场景；且在静态干扰场景中，本文所提方法可以获得与UCB1相近的性能，在非自适应干扰场景和自适应干扰场景中，可以获得与EXP3算法相近的性能。综上，本文所提方法无需干扰环境的先验信息和离线训练过程，可以满足雷达在噪声压制式干扰场景下的在线频率捷变需求，在多种干扰场景下均能够有效提升频率捷变雷达的抗干扰和目标检测性能。