Matrix Completion-based Range-Doppler Spectrum Estimation for Random Stepped-frequency Radars
-
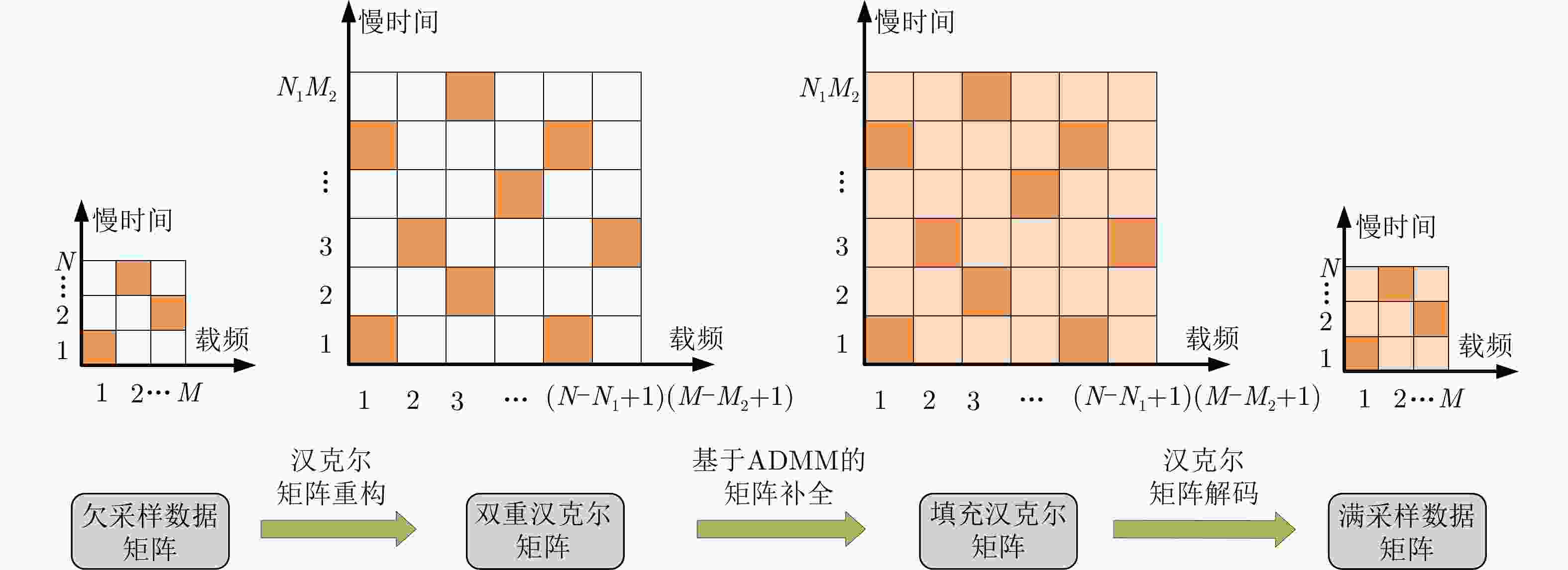
摘要: 随机步进频雷达通过合成大带宽,能在较低硬件复杂度下获得距离高分辨效果,同时由于其每个脉冲的载频随机捷变,因而具有强的抗干扰、电磁兼容能力,在复杂电磁环境高精度探测领域具有重要的应用价值。然而,由于其波形在时频域稀疏的感知形式,造成回波相参信息有所缺失,因而传统匹配滤波方法在估计高分辨距离-多普勒时会演化为欠定估计,导致估计谱中产生起伏高旁瓣,严重影响探测性能。为此,该文提出一种基于Hankel重构矩阵填充的随机步进频雷达高分辨距离-多普勒谱低旁瓣稀疏恢复方法。该方法采用低秩矩阵填充思想补全波形在时频域稀疏感知时造成的缺失采样,恢复目标连续相参信息,可以有效解决欠定估计问题。文章首先构建了随机步进频雷达的慢时间-载频(时-频)回波欠采样数据矩阵;然后,重构待恢复数据矩阵为双重Hankel型,并分析证明了矩阵满足低秩先验特性;最后,利用ADMM算法补全未采样时频数据,恢复相参信息,保证了高分辨距离-多普勒谱低旁瓣稀疏恢复。仿真和实测试验证明了该文所提方法的有效性和优越性。Abstract: Random Stepped Frequency (RSF) radars can achieve high-range resolution with relatively low hardware complexity by synthesizing a wide bandwidth. Moreover, because of the random frequency agility of each pulse, the radars possess robust anti-interference and electromagnetic compatibility capabilities, rendering them invaluable for high-precision detection in complex electromagnetic environments. However, the inherent sparsity sensing of the radar waveform in the time-frequency domain, causes a lack of echo coherence information, leading to an underdetermined estimation of the traditional matched filter, which results in fluctuating high side lobes in the estimation spectrum and adversely deteriorating detection performance. This paper proposes a sparse recovery method based on Hankel matrix completion for the high-resolution range-Doppler spectrum of the RSF radars. Using the low-rank matrix completion concept, this method fills in the missing samples caused by sparse sensing for RSF radars, thereby restoring continuous coherence information and effectively addressing the underdetermined estimation issue. First, an undersampled data matrix of a single coarse-resolution range for RSF radar is constructed. Subsequently, the time-frequency data matrix is reconstructed into a double Hankel form, and its low-rank prior characteristics are analyzed and proven. Finally, the Alternating Direction Method of Multipliers (ADMM) algorithm is applied to restore the unsampled time-frequency data, ensuring sparse recovery of the high-resolution range-Doppler spectrum with low sidelobes. Simulations and real tests demonstrate the effectiveness and superiority of the proposed method.
-
1 基于ADMM的Hankel变换矩阵填充算法
1. Matrix completion algorithm combined with Hankel transformation based on ADMM
输入:时频欠采样矩阵Y,载频编码${{U}_{n}}$ 输出:时频满采样恢复矩阵$ \hat{\boldsymbol{\varDelta}} $ 1. 对时频欠采样矩阵Hankel变换得到$ {{\boldsymbol{Y}}_{\rm H}} $ 2. ADMM矩阵填充: (a) 初始化:$ {\left( {{{\hat{\boldsymbol{\varDelta}} }_{\rm H}}} \right)_1} = {{\boldsymbol{W}}_1} = {{\boldsymbol{Y}}_{\rm H}} $, Z = 0,迭代次数K,惩罚
因子$ \beta $,步长因子$ \rho $(b) for k = 1 to K do i. 更新$ {\hat{\boldsymbol{\varDelta}} _{\rm H}} $:$ {\left( {{{\hat{\boldsymbol{\varDelta}} }_{\rm H}}} \right)_{k + 1}} = {D_{\textstyle\frac{1}{\beta }}}\left({{\boldsymbol{W}}_k} - \dfrac{1}{\beta }{{\boldsymbol{Z}}_k}\right) $ ii. 更新W:$ {{\boldsymbol{W}}_{k + 1}} = {\left( {{{\hat{\boldsymbol{\varDelta}} }_{\rm H}}} \right)_{k + 1}} + \dfrac{1}{\beta }({{\boldsymbol{A}}^{\rm H}}{\boldsymbol{B}} + {{\boldsymbol{Z}}_k}) $ 保持原有观测采样数据不变,即: $ {{\boldsymbol{W}}_{k + 1}} = {P_{\varOmega \notin {\varOmega _{\rm H}}}}\left( {{{\boldsymbol{W}}_{k + 1}}} \right) + {P_{\varOmega \in {\varOmega _{\rm H}}}}\left( {{{\boldsymbol{Y}}_{\rm H}}} \right) $ iii. 更新Z:$ {{\boldsymbol{Z}}_{k + 1}} = {{\boldsymbol{Z}}_k} + \beta \left( {{{\left( {{{\hat{\boldsymbol{\varDelta}} }_{\rm H}}} \right)}_{k + 1}} - {{\boldsymbol{W}}_{k + 1}}} \right) $ iv. 更新$ \beta $:$ {\beta _{k + 1}} = \rho {\beta _k} $ (c) end 3. 对$ {\left( {{{\hat{\boldsymbol{\varDelta}} }_{\rm H}}} \right)_K} $进行Hankel逆变换得到$ \hat{\boldsymbol{\varDelta}} $ 表 1 仿真参数
Table 1. Simulation parameters
参数 数值 中心频率${{f}_0}$ 93 GHz 最小步进带宽$\Delta $f 18.75 MHz 脉冲重复时间T 25 μs 脉冲个数N 64 捷变频点数M 64 载频编码$ {{U}}_{{n}} $ 随机均匀分布 二维FFT处理时窗函数 Hamming窗 表 2 运行时间对比结果(s)
Table 2. Runtimes comparison (s)
栅格点数 所提方法 压缩感知 栅格点数 所提方法 压缩感知 64×64 5.6 23.6 256×256 5.7 412.6 128×128 5.6 90.5 320×320 5.7 810.9 192×192 5.7 187.1 表 3 雷达波形参数
Table 3. Waveform parameters of the test radar
参数 数值 中心频率${{f}_0}$ 93.31 GHz 最小步进带宽$\Delta $f 18.75 MHz 脉冲重复时间T 25.8 μs 捷变频点数M 64 脉冲个数N 64 调频带宽B 25 MHz 脉冲宽度Tp 2 μs 载频编码$ {{U}}_{{n}} $ 随机均匀分布 -
[1] PANDA S S S, PANIGRAHI T, PARNE S R, et al. Recent advances and future directions of microwave photonic radars: A review[J]. IEEE Sensors Journal, 2021, 21(19): 21144–21158. doi: 10.1109/JSEN.2021.3099533. [2] 向寅, 张凯, 胡程. 基于NUFFT的调频步进频高分辨成像与目标识别算法[J]. 雷达学报, 2015, 4(6): 639–647. doi: 10.12000/JR15083.XIANG Yin, ZHANG Kai, and HU Cheng. A NUFFT based step-frequency Chirp signal high resolution imaging algorithm and target recognition algorithm[J]. Journal of Radars, 2015, 4(6): 639–647. doi: 10.12000/JR15083. [3] AL-HOURANI A, EVANS R J, MORAN B, et al. Efficient range-Doppler processing for random stepped frequency radar in automotive applications[C]. IEEE 85th Vehicular Technology Conference, Sydney, Australia, 2017: 1–7. doi: 10.1109/VTCSpring.2017.8108414. [4] SAPONARA S, GRECO M S, and GINI F. Radar-on-chip/in-package in autonomous driving vehicles and intelligent transport systems: Opportunities and challenges[J]. IEEE Signal Processing Magazine, 2019, 36(5): 71–84. doi: 10.1109/MSP.2019.2909074. [5] JIANG Yuan, WANG Yanhua, LI Yang, et al. Eigenvalue-based ground target detection in high-resolution range profiles[J]. IET Radar, Sonar & Navigation, 2020, 14(11): 1747–1756. doi: 10.1049/iet-rsn.2020.0002. [6] AXELSSON S R J. Analysis of random step frequency radar and comparison with experiments[J]. IEEE Transactions on Geoscience and Remote Sensing, 2007, 45(4): 890–904. doi: 10.1109/TGRS.2006.888865. [7] HUANG Tianyao, LIU Yimin, LI Gang, et al. Randomized stepped frequency ISAR imaging[C]. IEEE International Radar Conference, Atlanta, USA, 2012: 553–557. doi: 10.1109/RADAR.2012.6212202. [8] WEHNER D R. High Resolution Radar[M]. Norwood, MA, Artech House, 1987. [9] LIU Yimin, MENG Huadong, LI Gang, et al. Range-velocity estimation of multiple targets in randomised stepped-frequency radar[J]. Electronics Letters, 2008, 44(17): 1032–1034. doi: 10.1049/el:20081608. [10] ACKROYD M H and GHANI F. Optimum mismatched filters for sidelobe suppression[J]. IEEE Transactions on Aerospace and Electronic Systems, 1973, AES-9(2): 214–218. doi: 10.1109/TAES.1973.309769. [11] DAVIS R M, FANTE R L, and PERRY R P. Phase-coded waveforms for radar[J]. IEEE Transactions on Aerospace and Electronic Systems, 2007, 43(1): 401–408. doi: 10.1109/TAES.2007.357142. [12] KAJENSKI P J. Mismatch filter design via convex optimization[J]. IEEE Transactions on Aerospace and Electronic Systems, 2016, 52(4): 1587–1591. doi: 10.1109/TAES.2016.140556. [13] LIU Shuai, CAO Yunhe, YEO T S, et al. Range sidelobe suppression for randomized stepped-frequency chirp radar[J]. IEEE Transactions on Aerospace and Electronic Systems, 2021, 57(6): 3874–3885. doi: 10.1109/TAES.2021.3082670. [14] LIAO Zhikun, HU Jiemin, LU Dawei, et al. Motion analysis and compensation method for random stepped frequency radar using the pseudorandom code[J]. IEEE Access, 2018, 6: 57643–57654. doi: 10.1109/ACCESS.2018.2873784. [15] LIAO Zhikun, LU Dawei, HU Jiemin, et al. Waveform design for random stepped frequency radar to estimate object velocity[J]. Electronics Letters, 2018, 54(14): 894–896. doi: 10.1049/el.2018.1033. [16] QUAN Yinghui, LI Yachao, HU Wen, et al. FM sequence optimisation of chaotic-based random stepped frequency signal in through-the-wall radar[J]. IET Signal Processing, 2017, 11(7): 830–837. doi: 10.1049/iet-spr.2015.0565. [17] HUANG Tianyao, LIU Yimin, XU Xingyu, et al. Analysis of frequency agile radar via compressed sensing[J]. IEEE Transactions on Signal Processing, 2018, 66(23): 6228–6240. doi: 10.1109/TSP.2018.2876301. [18] YOON Y S, HONG Yunseog, and KIM S. Simple strategies to build random compressive sensing matrices in step-frequency radars[J]. IEEE Geoscience and Remote Sensing Letters, 2018, 15(9): 1357–1361. doi: 10.1109/LGRS.2018.2841189. [19] HUANG Tianyao, LIU Yimin, MENG Huadong, et al. Cognitive random stepped frequency radar with sparse recovery[J]. IEEE Transactions on Aerospace and Electronic Systems, 2014, 50(2): 858–870. doi: 10.1109/TAES.2013.120443. [20] QUAN Yinghui, LI Yachao, WU Yaojun, et al. Moving target detection for frequency agility radar by sparse reconstruction[J]. Review of Scientific Instruments, 2016, 87(9): 094703. doi: 10.1063/1.4962700. [21] CHI Yuejie, SCHARF L L, PEZESHKI A, et al. Sensitivity to basis mismatch in compressed sensing[J]. IEEE Transactions on Signal Processing, 2011, 59(5): 2182–2195. doi: 10.1109/TSP.2011.2112650. [22] WANG Mou, WEI Shunjun, SHI Jun, et al. CSR-Net: A novel complex-valued network for fast and precise 3-D microwave sparse reconstruction[J]. IEEE Journal of Selected Topics in Applied Earth Observations and Remote Sensing, 2020, 13: 4476–4492. doi: 10.1109/JSTARS.2020.3014696. [23] CANDES E J and TAO T. The power of convex relaxation: Near-optimal matrix completion[J]. IEEE Transactions on Information Theory, 2010, 56(5): 2053–2080. doi: 10.1109/TIT.2010.2044061. [24] 马宇欣, 海宇, 李中余, 等. 稀疏轨迹毫米波雷达三维高分辨成像算法[J]. 雷达学报, 2023, 12(5): 1000–1013. doi: 10.12000/JR23001.MA Yuxin, HAI Yu, LI Zhongyu, et al. 3D high-resolution imaging algorithm with sparse trajectory for millimeter-wave radar[J]. Journal of Radars, 2023, 12(5): 1000–1013. doi: 10.12000/JR23001. [25] SUN Shunqiao and ZHANG Y D. 4D automotive radar sensing for autonomous vehicles: A sparsity-oriented approach[J]. IEEE Journal of Selected Topics in Signal Processing, 2021, 15(4): 879–891. doi: 10.1109/JSTSP.2021.3079626. [26] SUN Shunqiao, BAJWA W U, and PETROPULU A P. MIMO-MC radar: A MIMO radar approach based on matrix completion[J]. IEEE Transactions on Aerospace and Electronic Systems, 2015, 51(3): 1839–1852. doi: 10.1109/TAES.2015.140452. [27] HU Xiaowei, TONG Ningning, WANG Jianye, et al. Matrix completion-based MIMO radar imaging with sparse planar array[J]. Signal Processing, 2017, 131: 49–57. doi: 10.1016/j.sigpro.2016.07.034. [28] ZHANG Yilong, LI Yuehua, CHEN Jianfei, et al. Sparse millimeter-wave InSAR imaging approach based on MC[J]. IEEE Geoscience and Remote Sensing Letters, 2018, 15(5): 714–718. doi: 10.1109/LGRS.2018.2810234. [29] HU Xueyao, LI Yang, LU Man, et al. A multi-carrier-frequency random-transmission Chirp sequence for TDM MIMO automotive radar[J]. IEEE Transactions on Vehicular Technology, 2019, 68(4): 3672–3685. doi: 10.1109/TVT.2019.2900357. [30] LIANG Can, LI Yang, HU Xueyao, et al. Coherent-on-Receive synthesis using dominant scatterer in millimeter-wave distributed coherent aperture radar[J]. Remote Sensing, 2023, 15(6): 1505. doi: 10.3390/rs15061505. [31] STRANG G. Introduction to Linear Algebra[M]. 6th ed. Wellesley, USA: Wellesley-Cambridge Press, 2022. [32] HORN R A and JOHNSON C R. Matrix Analysis[M]. Cambridge, UK: Cambridge University Press, 1985. doi: 10.1017/CBO9780511810817. [33] YE Hailiang, LI Hong, CAO Feilong, et al. A hybrid truncated norm regularization method for matrix completion[J]. IEEE Transactions on Image Processing, 2019, 28(10): 5171–5186. doi: 10.1109/TIP.2019.2918733. [34] HU Yao, ZHANG Debing, YE Jieping, et al. Fast and accurate matrix completion via truncated nuclear norm regularization[J]. IEEE Transactions on Pattern Analysis and Machine Intelligence, 2013, 35(9): 2117–2130. doi: 10.1109/TPAMI.2012.271. [35] CAI Jianfeng, CANDÈS E J, and SHEN Zuowei. A singular value thresholding algorithm for matrix completion[J]. SIAM Journal on Optimization, 2010, 20(4): 1956–1982. doi: 10.1137/080738970. [36] 邓理康, 张双辉, 张弛, 等. 一种基于多维交替方向乘子法的多输入多输出逆合成孔径雷达成像方法[J]. 雷达学报, 2021, 10(3): 416–431. doi: 10.12000/JR20132.DENG Likang, ZHANG Shuanghui, ZHANG Chi, et al. A multiple-input multiple-output inverse synthetic aperture radar imaging method based on multidimensional alternating direction method of multipliers[J]. Journal of Radars, 2021, 10(3): 416–431. doi: 10.12000/JR20132. [37] 范文, 蔚保国, 陈镜, 等. 基于波形优化和天线位置选择的MIMO雷达波束扫描算法研究[J]. 雷达学报, 2022, 11(4): 530–542. doi: 10.12000/JR22135.FAN Wen, YU Baoguo, CHEN Jing, et al. Joint waveform optimization and antenna position selection for MIMO radar beam scanning[J]. Journal of Radars, 2022, 11(4): 530–542. doi: 10.12000/JR22135. [38] OH T H, MATSUSHITA Y, TAI Y W, et al. Fast randomized singular value thresholding for low-rank optimization[J]. IEEE Transactions on Pattern Analysis and Machine Intelligence, 2018, 40(2): 376–391. doi: 10.1109/TPAMI.2017.2677440. [39] CHEN Yuxin and CHI Yuejie. Robust spectral compressed sensing via structured matrix completion[J]. IEEE Transactions on Information Theory, 2014, 60(10): 6576–6601. doi: 10.1109/TIT.2014.2343623. [40] GRANT M, BOYD S, and YE Yinyu. MATLAB software for disciplined convex programming[EB/OL]. https://web.stanford.edu/~boyd/papers/disc_cvx_prog.html, 2006. -



 作者中心
作者中心 专家审稿
专家审稿 责编办公
责编办公 编辑办公
编辑办公
 下载:
下载: