1.   引言

前视高分辨成像技术包括双基地前视成像、单基地超分辨前视成像技术以及单脉冲前视成像技术，近年来受到研究人员的广泛关注^[1−3]。其中，单脉冲前视成像(Monopulse Forward-looking Imaging)技术具有系统复杂度低、对航迹无特殊要求的优点，是一种实际可行的前视成像方法，已在机载、弹载雷达前视成像中得到了应用^[4−7]。但是，单脉冲前视成像技术需要克服单脉冲测角无法区分同分辨单元内多个目标的问题，因此，考虑首先在多普勒域基于目标的多普勒差异实现多目标分离，然后对主瓣内落入每个多普勒单元中的目标进行幅度估计，再通过比幅单脉冲测角提高对目标的方位分辨能力。基于多普勒差异分辨多目标的思想最早用于多普勒波束锐化(Doppler Beam Sharpen, DBS)技术^[8,9]，应用于前视成像时需要克服多普勒差异迅速下降带来的目标频率估计精度下降问题。为此，研究人员基于APES (Amplitude and Phase EStimation)、调频Z变换(Chirp-Z Transform, CZT)和旁瓣对消等算法研究了通过多普勒精估计提高单脉冲前视成像质量的方法^[10,11]，取得了成效。但是，当强点目标的旁瓣泄露到邻近多普勒单元时，会产生假目标或掩盖弱目标，对前视图像的质量造成不良影响。

目标的多普勒频率估计是一个常规的信号参数估计问题，已有大量成熟的研究成果，但是运用于前视成像中需要克服样本量小、目标个数未知等实际困难。现代谱估计方法按照是否对数据的总体分布进行假设分为参数模型法和非参数模型法两类，参数模型法将频率估计问题转化为模型参数求解问题，主要模型有自回归(Autoregressive, AR)模型、动平均(Moving Average, MA)模型和自回归动平均(Autoregressive Moving Average, ARMA)模型3种，这些模型有效提高了频率分辨率，运算速度较快，但其性能受到模型阶数及参数选取的限制，而成像具有场景未知和散射点多的特点，会导致模型阶数不确定、运算量激增等问题，因此以上模型难以适应高分辨率成像应用需求。较为典型的非参数模型法有多信号分类法(Multiple Signal Characterization, MUSIC)和子空间旋转不变法(Estimation of Signal Parameters via Rotational Invariance Techniques, ESPRIT)，其中：MUSIC^[12]算法在减小均方根估计误差方面取得了极大的进步，实现了真正意义上的超分辨信号参数估计^[13]，ESPRIT^[14]算法虽然估计误差大于MUSIC算法，但具有不需要进行谱峰搜索的优势，在现代信号处理中也得到了广泛的应用。但是，MUSIC算法和ESPRIT算法依赖于奇异值分解(Singular Value Decomposition, SVD)或数据协方差矩阵的反演，对样本量需求大，计算成本高，难以处理成像问题。在雷达成像领域，凸优化方法和CZT算法是两种常见改善谱估计精度的非参数化方法。当大范围的空域内只存在少数目标时，回波信号具有稀疏性，空间谱估计问题可以利用凸优化方法进行求解^[2,15]，在小样本情况下实现超分辨谱估计，不足之处是要求场景满足稀疏条件；CZT将频谱精确细化到源信号的窄带范围，然后搜索局部最大值，有效提高了频率分辨率，减少了幅度估计误差^[16,17]，已被应用于单脉冲前视成像。但是，CZT算法并没有对频谱泄露量进行处理，对弱目标的估计必然存在较大的误差。此外，大部分频率估计算法都将目标的数量作为已知条件，而雷达成像场景中的目标数量很难预知。

基于阵列模型的波束形成算法是一种传统的空间谱估计方法，具有复杂度低、计算效率高的优点，但是当存在由相邻源或强源引起的旁瓣泄露问题时，尤其在样本量较少时，到达角(Direction of Arrival, DOA)估计性能急剧下降，无法精确估计多点源参数^[18]，这与多普勒频率估计问题存在相似性。对此，研究人员采用了分段、加窗、插值、平均等方法^[18−21]来抑制由旁瓣泄露导致的参数估计误差。其中Ye等人^[22]提出的快速空间谱估计方法通过结合插值策略和泄露减法来解决频谱泄露问题，该方法能够利用单快拍数据实现准确和无偏的非稀疏多点目标到达角估计，经过不断的发展完善，形成了快速迭代插值波束形成(Fast Iterative Interpolated Beamforming, FIIB)算法^[23−25]。将FIIB算法与信息论准则结合，可以进一步解决目标个数估计的问题^[26]。本文引入FIIB算法解决前视成像中多普勒频率估计的问题，采用具有模型阶数估计(Model Order Estimation, MOE)能力的FIIB算法实现对主瓣内目标数量和多普勒频率的精确估计，并基于估计结果重建和差通道多普勒估计，实现单脉冲前视成像。论文首先介绍了基于单脉冲雷达和差通道多普勒估计的前视成像原理，然后给出了FIIB算法原理，通过数值分析展示了该算法对目标个数和多普勒频率估计的能力，最后通过仿真实验和实测数据验证了算法用于单脉冲前视成像的可行性。

2.   基于单脉冲雷达和差通道多普勒估计的前视成像原理

如图1所示，搭载雷达的平台以匀速v飞行，天线波束以角速度$\omega$均匀地扫描前视场景，同时以脉冲重复频率${F_{\text{R}}}$向每个方位发射线性调频信号并接收回波，总扫描脉冲数为${N_{\text{S}}}$。经过解调和距离压缩后，对于参考距离${R_0}$，方位角${\theta _0}$处的点目标P，回波信号的复包络可表示为

图  1  机载雷达前视成像几何示意图

Figure  1.  Geometry for forward-looking imaging of a scanning radar

下载: 全尺寸图片 幻灯片

其中，$\hat t$为快时间，${t_m}$为慢时间，B为发射信号带宽，${f_{\text{c}}}$为发射信号中心频率，$A(\theta )$为天线方向图，$\theta ({t_m})$为天线波束中心的指向，$\sigma({R}_{0},{\theta }_{0})$为目标的雷达截面积(Radar Cross Section, RCS)，$R({t_m})$为目标的距离。由于平台的运动，不同脉冲目标的距离发生变化，天线对目标的方位调制也随波束指向变化而变化，对式(1)做距离向傅里叶变换得到回波在距离频域的表达式：

其中，${\varphi _0}$表示目标的俯仰角，$\lambda$表示中心频率对应的波长。令${f_{\text{d}}} = 2v\cos {\theta _0}\cos {\varphi _0}/\lambda$表示目标的多普勒频率，指数项第2部分说明多普勒频率与距离频率存在耦合关系，采用Keystone变换完成距离走动校正，即用${t_m} = {t'_m}{f_{\text{c}}}/({f_{\text{c}}} + {f_r})$进行变量替换解耦合，则有

对于窄带雷达，满足${f_r} \ll {f_{\text{c}}}$, ${{{f_{\text{c}}}}}/({{{f_{\text{c}}} + {f_r}}}) \simeq 1$, $A(t'_m) \approx A({t_m})$，再进行傅里叶逆变换，得到

说明距离走动校正后，目标P的位置位于${R_0}$，而不同方位时刻目标的角度调制取决于天线波束指向与目标的方位角之差，目标的相位变化取决于平台运动和目标的方位角和俯仰角。

如图1所示，距离门${R_0}$内可能存在多个目标，每发射一个脉冲信号，天线波束覆盖范围内的目标均会产生回波，若将距离门${R_0}$对应的方位波束覆盖范围划分为K个网格，脉压后方位向的回波信号可以视为天线波束对网格内目标RCS角度调制后的叠加，即

由于目标位于同一距离门，可认为目标的俯仰角近似相同均为${\varphi _{\mathrm{0c}}}$。假设天线波束中心指向${\theta _{\text{c}}}$附近时，相参雷达接收了N个脉冲的回波信号，若满足$N \ll K$，说明天线扫描角度的变化很小可以忽略，$\theta (t'_m) \approx {\theta _{\text{c}}}$，提取出常数因子，回波近似为

其中，$\alpha = \sin {\text{c}}[ {B( {\hat t \;-\; {{2{R_0}}}/{{\text{c}}}} )} ]\;\exp \{ { \;-\; {\text{j}}{{4\pi {R_0}}}/{\lambda }} \}$, ${f_{\text{d}}}({\theta _i}) = {{2v}}\cos {\theta _i}\cos {\varphi _{\mathrm{0}}} /{{{\lambda _{\text{c}}}}}$为不同角度的多普勒频率。

设雷达的方位向3 dB波束宽度为${\theta _{3\;{\text{dB}}}}$，波束沿方位向扫描的间隔为${\delta _{\mathrm{a}}}$，$K = {\theta _{3\;{\text{dB}}}}/{\delta _{\mathrm{a}}}$是天线波束宽度内包含的角度网格数，将天线方向图离散化后定义为

当N 较小的时候，忽略天线扫描角度调制的变化，每个脉冲的天线矢量都相同，N个脉冲构成的天线观测矩阵近似为

而位于同一距离门的K个网格内的RCS分布可表示为

N个连续脉冲的方位复信号矢量可表示为${\boldsymbol{y}} = {\left[ {{y_0}{\text{ }}{y_1}{\text{ }} \cdots {\text{ }}{y_{N - 1}}} \right]^{\text{T}}}$，对静止平台，其每一个样本都近似相同，但是考虑到平台的运动后，将多普勒频率引起的相位变化因子引入观测矩阵，对位于距离${R_0}$处，不同方位角${\theta _i}$的目标构造相位调制矢量：

对距离门${R_0}$内目标RCS分布进行观测时增加了多普勒效应带来的相位调制矩阵：

样本间将存在差异，假设噪声为均值为0，方差为${\sigma ^2}$的加性高斯复白噪声，考虑噪声的影响，方位向回波模型可重写为

其中

$\odot$表示哈达玛积(Hadamard product)。式(13)说明当$N \ll K$时，基于天线方向图的角度调制差异很小，难以用来区分不同角度的目标，但是只要平台运动引起的多普勒差异足够大，也是可以分辨多目标的，这正是DBS成像的机理。而对于单脉冲雷达，由于增加了一个天线，其和差通道角度调制差异可以用来对目标的角度进行准确测量，分别将和差天线波束的方向图表示为

参考式(8)构造N个脉冲的天线观测矩阵${{\boldsymbol{H}}}_{\Sigma}, {{\boldsymbol{H}}}_{\Delta }\in {{\mathbb{C}}}_{{}^{N\times K}}$，方位和、差通道复信号矢量可表示为${{\boldsymbol{y}}_\Sigma } = {\left[ {{y_{\Sigma 1}},{y_{\Sigma 2}}, \cdots ,{y_{\Sigma N}}} \right]^{\text{T}}}$, ${{\boldsymbol{y}}_\Delta } = \left[ {{y_{\Delta 1}},{y_{\Delta 2}}, \cdots , {y_{\Delta N}}} \right]^{\text{T}} \in {\mathbb{C}_{N \times 1}}$，表示为矩阵形式：

其中，${\boldsymbol{{A}}}_{\Sigma },\;{{\boldsymbol{A}}}_{\Delta }\in {{\mathbb{C}}}_{N\times K}$为和差天线方向图对地面观测构成的感知矩阵，${{\boldsymbol{n}}}_{\Sigma },\;{{\boldsymbol{n}}}_{\Delta }\in {{\mathbb{C}}}_{N\times 1}$为和差通道噪声矢量。由于$N \ll K$，式(15)是一个欠定方程组，通过解方程组无法获得3 dB波束宽度唯一的RCS分布。

单脉冲雷达和差通道多普勒估计前视成像结合了单脉冲测角技术和DBS技术，首先将前视方向一次扫描接收到的所有${N_{\text{S}}}$个回波进行解调后，完成脉冲压缩和距离走动校正；然后将回波均匀分帧，每帧N个脉冲回波，将N个脉冲回波组成的相参脉冲串变换到多普勒域，利用不同点目标之间多普勒频移的差异实现方位向上目标的分离，缓解了单脉冲测角角度模糊的问题；然后，对和差通道进行多普勒频率的精确估计，并使用杂波锁定^[27]算法估计位于3 dB波束宽度内的目标；接着，利用多普勒频率估计值进行和差比幅测角，得到不同点目标的方位角信息，进而完成本帧的目标定位和能量投影；最后，所有帧的数据完成投影后，得到前视图像。

在对每帧信号进行测角和投影之前，需要对和差通道复信号矢量进行多普勒估计，假设同一距离门内连续N个均匀采样值构成的一维导向矢量${{\boldsymbol{a}}_{\mathrm{D}}} \equiv {\left[ {1{\text{ }}{{\text{e}}^{ - {\text{j}}\omega }}{\text{ }} \cdots {\text{ }}{{\text{e}}^{ - {{{\mathrm{j}}({{N}}-1)}}\omega }}} \right]^{\text{T}}}$，其中$\omega \in [0,2\pi )$为多普勒频率，则多普勒采样间隔${\omega _n} = 2\pi n/N$。定义${{\boldsymbol{A}}_{\mathrm{D}}} \,\equiv\, \left[ {{{\boldsymbol{a}}_{\mathrm{D}}}{\text{(}}{\omega _0}){\text{ }}{{\boldsymbol{a}}_{\mathrm{D}}}{\text{(}}{\omega _1}){\text{ }} \cdots {\text{ }}{{\boldsymbol{a}}_{\mathrm{D}}}({\omega _{N - 1}})} \right] \,\in\, {\mathbb{C}_{N \times N}}$为$n = 0,1, \cdots ,N - 1$方位向离散傅里叶变换(Discrete Fourier Transform, DFT)的傅里叶基矩阵，则和差通道信号的多普勒估计可表示为

DFT是可以用快速傅里叶(Fast Fourier Transform, FFT)实现的线性算子，${{\boldsymbol{e}}_\Sigma }$, ${{\boldsymbol{e}}_\Delta }$仍然为均值为0的复高斯白噪声，当$N \ll K$时，忽略方位角不同的目标在相参处理时间内的天线方向图加权值的变化，即${{\boldsymbol{A}}_\Sigma }$和${{\boldsymbol{A}}_\Delta }$在N个脉冲范围内可以近似看作定值，因此多普勒处理后的和差通道值仍然可以通过比幅测角来获得目标的方位角信息。

点目标P对应的多普勒中心频率为

雷达和通道天线3 dB波束宽度对应的多普勒带宽为

由$\Delta {f_{\text{d}}}/({F_{\text{R}}}/N)$可确定天线3 dB波束宽度覆盖区域内目标RCS的多普勒分布范围，然后基于和差通道多普勒频率估计的结果进行单脉冲测角得到目标的精确方位角。假设3 dB波束宽度内有M个多普勒分辨单元，则依次取出每个单元的和差通道多普勒估计值${{\boldsymbol{Y}}_\Delta }({\omega _m})$和${{\boldsymbol{Y}}_\Sigma }({\omega _m})$，计算和差通道复比^[28]

其中，$\mathrm{Re}[\cdot]$表示取信号的实部，$\mathrm{Im}[\cdot]$表示取信号的虚部，$\mathrm{sgn}(\cdot)$表示符号函数，由${\varepsilon _m}$在雷达鉴角曲线上查找得到目标偏离轴线的角度${\theta _{\mathrm{e}}}$，即可得到真实的目标方位角：

在文献[11]中，为了获得更精确的多普勒估计值，提出了基于CZT的和差通道多普勒估计方法，该方法有效提高了在前斜视向对目标多普勒值估计的精度，从而提高了图像质量，但是，CZT算法对每个可能存在目标的多普勒单元都进行了估计，且没有对泄露量进行处理，当邻近单元存在强目标时，强目标的旁瓣会泄露到邻近多普勒单元，造成假目标或掩盖弱目标，从而导致估计误差。为此，本文引入FIIB算法解决这一问题。

3.   FIIB算法原理

3.1   信号建模

在相参多普勒处理中，将同分辨单元内L个点目标的多普勒回波信号建模为L个复指数信号与噪声之和：

回波信号由L个复指数分量叠加而成，其中${A_l}$为复振幅，${f_l}$为归一化频率(${f_l} \in [0,1)$), $w(n)$为均值为0，方差为${\sigma ^2}$的加性高斯复白噪声，N为方位向的样本点数，此时假设目标数量是已知量，即信号模型阶数已知为L。

3.2   FIIB算法

FIIB算法利用迭代和插值相减策略，可有效抑制旁瓣泄露，实现目标空间谱等参数的精确估计^[24]。本文将该算法用于多普勒频率的快速精确估计，通过减去邻近目标的泄露量消除点目标估计的偏差，解决强点目标旁瓣引起的假目标或目标遮蔽问题。FIIB仅需一次FFT计算和少量傅里叶系数插值即可实现非稀疏条件下点目标多普勒频率和复振幅的准确估计，参数估计的误差在迭代过程中减小，每个迭代周期内算法按照幅度从大到小依次估计所有点目标。算法流程如算法1所示。

1  FIIB算法估计多普勒频率流程^[18]

1.  Flowchart of Doppler frequency estimation based on FIIB algorithm^[18]

初始化：
令 ${\hat f_l} = 0$, ${\hat A_l} = 0$, $l = 1,2, \cdots ,L$
设 $q = 0$
${\boldsymbol{X}} = {\text{FFT}}({\boldsymbol{x}},N)$
迭代(Q次)：
对于 $l = 1,2, \cdots ,L$
IF $q = 1$(粗估计)：
$\tilde X(k) = X(k) - \displaystyle\sum \limits_{i = 1,i \ne l}^L {\hat A_i}{\hat S_i}(k),k = 0,1, \cdots ,N - 1$ (i)
${\hat m_l} =\arg \mathop{\max}\limits_{0 \le k \le N - 1 } {\left| {\tilde X(k)} \right|^2}$ 　　　　　　　　　 (ii)
${\hat f_l} = \dfrac{1}{N}{\hat m_l}$ 　　　　　　　　　　　　　　　　　 (iii)
END IF
(精估计): 　　　　${\tilde X_p}({\hat f_l}) = {X_p}({\hat f_l}) - \displaystyle\sum \limits_{i = 1,i \ne l}^L {\hat A_i}{\hat S_i} \left( {{{\hat f}_l} + \dfrac{p}{N}} \right),p = \pm \dfrac{1}{2}$ 　(iv)
其中， ${X_p}({\hat f_l}) = X\left( {{{\hat f}_l} + \dfrac{p}{N}} \right)$ 　　　　　　　　　(v)
$\delta = \dfrac{1}{2}{{\mathrm{Re}}} \left[ {\dfrac{{{{\tilde X}_{0.5}}({{\hat f}_l}) + {{\tilde X}_{ - 0.5}}({{\hat f}_l})}}{{{{\tilde X}_{0.5}}({{\hat f}_l}) - {{\tilde X}_{ - 0.5}}({{\hat f}_l})}}} \right]$ 　　　　　　　(vi)
${\hat f_l} \leftarrow {\hat f_l} + \dfrac{\delta }{N}$ 　　　　　　　　　　　　　　　　(vii)
${\hat A_l} = \dfrac{1}{N} \left\{ {\displaystyle\sum \limits_{k = 0}^{N - 1} x(k){{\text{e}}^{ - {\text{j}}{\textstyle\frac{{2\pi }}{N}}k{{\hat f}_l}}} - \displaystyle\sum \limits_{i = 1,i \ne l}^L {{\hat A}_i}{{\hat S}_i}({{\hat f}_l})} \right\}$ (viii)
$q \leftarrow q + 1$
输出: $\left\{ {{{\hat f}_l},{{\hat A}_l}} \right\},l = 1,2, \cdots ,L$

下载: 导出CSV 

| 显示表格

在前视成像中，假设此时多普勒域目标个数已知为L，FIIB算法首先将回波信号变换到多普勒域，然后将多点目标估计等效为L个单点目标估计，按照幅度强弱依次从回波中提取单点目标进行估计。

每一个多普勒点目标的估计可以分为粗估计和精估计，粗估计仅在第1次迭代中执行。对于第l个多普勒目标，首先将前$l - 1$个已估计的单点目标信号从多普勒域中减去，得到抑制了已估计分量的信号$\tilde X(n)$，其中，${\hat S_i}(k) = {\hat S_i}(f){|_{f = (k/N)}}$, ${\hat S_i}(f)$为第i个频率估计量${\hat f_i}$对应的DFT系数矢量，$\hat{[\cdot]}$表示参量的估计值：

然后在$\tilde X(n)$中找到功率最大的谱线${\hat m_l}$，对应的频率值即为多普勒频率的粗估计值。

在多点目标的情况下，若插值函数在迭代时具有合适的收敛性，则将插值策略与迭代-泄露减法思想结合就可能消除偏差并得到准确的多普勒估计。文献[18]证明了FIIB算法经过迭代最终能收敛到与真实频率值重合的不动点，即实现无偏估计。步骤(iv)计算了偏离频率${\hat f_l}$(即多普勒频率估计值)p个多普勒单元的DFT系数${\tilde X_p}({\hat f_l})$，计算过程中同样减去了其他已估计频率点目标在该点的泄露量。计算方法如式(23)所示：

接着利用无泄露DFT系数${\tilde X_p}({\hat f_l})$进行插值分析来估计谱偏移量^[29]。设第l个多普勒点目标的真实频率与粗估计获得的最大功率谱线相距$\delta$，其中$\delta \in \left[ { - 0.5,0.5} \right]$，则多普勒频率偏移量为$\delta /N$，第$q + 1$次迭代的频谱估计结果为

此时，与真实多普勒频率相距p的插值DFT系数${X_p}({f_l})$表示为

其中，${W_p}({f_l})$为噪声信号在${f_l} + p/N$处的FFT值，设式(25)中与p无关的系数为b，令$p = \pm 0.5$，则${X_{0.5}}({f_l})$, ${X_{ - 0.5}}({f_l})$可化简为

令$\beta = ( {X_{0.5}}({f_l}) + {X_{ - 0.5}}( {f_l} ))/ ( {X_{0.5}}({f_l}) - {X_{ - 0.5}} ({f_l}))$， 代入式(26)可得

Aboutanios等人^[29]证明，当N足够大时，$\beta$可表示为

继续展开和化简可得

可知$\beta$的实部是偏移量$\delta$的带噪声估计，由于噪声是均值为0的高斯复白噪声，取$\delta = {{\mathrm{Re}}} \left[ \beta \right]/2$, $\beta = ({X_{0.5}}({f_l}) + {X_{ - 0.5}}({f_l}))/({X_{0.5}}({f_l}) - {X_{ - 0.5}}({f_l}))$。

最后根据偏移量修正第l个多普勒目标的频率，然后在该频率处减去其他多普勒目标的泄露得到复振幅估计值。按照幅度从强到弱依次提取出每个多普勒目标进行估计后，算法对每个多普勒目标的参数完成了一轮更新，总体的估计结果得到了改进，新的结果重新进入下一轮迭代直至结束。

3.3   基于信息论准则的目标个数估计方法

在FIIB算法及大多数频率估计算法中，通常要求目标的数量是已知的，而在实际应用中，目标的数量往往不是先验信息。尤其在成像问题中，散射点个数是未知的，但对于由大量散射点组成的扩展目标，进行目标个数估计的运算负荷非常庞大。因此，传统基于多普勒估计的单脉冲前视成像不进行目标个数估计，而是假设每个多普勒单元中都有目标，虽然能够避免计算负荷，但此时弱点目标的估计值反映的不一定是目标的真实值，反而可能是临近单元强目标泄露量的估计结果，会掩盖弱目标引入误差。而FIIB作为一种能够抑制能量泄露的快速频率估计算法，结合信息论准则解决目标个数估计问题，不会造成过大的运算负荷。根据信息论准则，使负对数似然函数与惩罚项构成的代价函数取得最小值的L即为目标个数的估计值$\hat L$，代价函数$C(L)$定义如下：

其中，$p(L)$为防止因为系数过大而让模型变复杂的惩罚项，$p(L)$为自由度k的系数，k与点目标的数量L相关， Akaike定义了第1个惩罚项^[30]${p_{{\text{AIC}}}}(L)$：

对于每一个可能的目标个数L, ($L \in \left[ {1,{L_{\max }}} \right]$)，首先使用FIIB算法对多普勒点目标进行估计并记录频率和复振幅估计值，然后根据信息论准则计算对应的代价函数${C_{{\text{ITC}}}}(L)$，本文选择以${p_{{\text{AIC}}}}(L)$为惩罚项的代价函数${C_{{\text{AIC}}}}(L)$。最后在所有代价函数计算值$\{ {C_{{\text{ITC}}}}(L)\}$中选择最小代价对应的L作为多普勒目标个数的估计值$\hat L$，同时返回其对应的频率和复振幅估计值$\{ {\hat A_l},{\hat f_l}\} _l^{\hat L}$。

以下推导基于AIC准则的代价函数，AIC准则的似然函数可以表示为^[26]

则其对数似然函数为

代入噪声的最大似然估计可得

加入惩罚项，且忽略常数项，代价函数可简化为

每个多普勒点目标位置由3个自由参数决定，即幅度、频率、相位，则在多普勒频率估计算法中自由度$k = 3L$。将信息论准则和FIIB算法相结合，可得到具有多普勒目标个数估计能力的FIIB算法^[26]，具体流程如算法2所示。

2  具有目标个数估计功能的FIIB算法

2.  The FIIB algorithm with model order estimation

初始化：
设 ${L_{\max }}$, Q
循环:
对于 $L = 1,2, \cdots ,{L_{\max }}$
$\left\{ {{{\hat f}_l},{A_l}} \right\}_{l = 1}^L = {\text{FIIB(}}{\boldsymbol{x}},L,Q)$
计算 ${C_{{\text{ITC}}}}(L)$
结束
取: $\hat{L}=\mathrm{arg}\mathop{ \mathrm{max}}\limits_{L=1,2,\cdots, {L}_{\mathrm{max}} }\{{C}_{\text{ITC}}(L)\}$
输出: $\hat L,\{ {\hat f_l},{\hat A_l}\} ,l = 1,2, \cdots ,\hat L$

下载: 导出CSV 

| 显示表格

4.   数值仿真与分析

本节首先针对强点目标泄露、相邻点目标泄露和多点目标3种情况仿真，仿真结果展示了FIIB算法的性能和应用场景，然后讨论了频率间隔和迭代次数的关系。其中，所有算法均进行了蒙特卡罗仿真，仿真次数为200次，用于对比的CZT算法假设每个多普勒单元都有目标，通过细化每个单元的频谱和搜索局部最大值得到更精细的频率估计值，本节中的CZT结果仅展示了点目标附近单元的估计结果。

4.1   强点目标泄露影响分析

为分析每个因素的单独影响，首先对两个功率相差20 dB的点目标进行仿真，具体仿真参数如表1所示，信号方位向采样长度N为64，两个点目标的多普勒频率间隔$\Delta f = 2/N$，功率之比${W_1}/{W_2} = 20\;{\text{dB}}$，设可能的最大目标数为5，迭代次数为10，回波叠加高斯白噪声，信噪比为20 dB。

表  1  点目标仿真参数

Table  1.  Simulation parameters of point targets

参数	数值		参数	数值
频率值${f_1}$	0.2687		信号长度N	64
复振幅${A_1}$	5.0000+3.0000j		迭代次数Q	10
频率值${f_2}$	0.3000		设定最大目标数${L_{\max}}$	5
复振幅${A_2}$	0.5000–0.3000j		信噪比$\rho$ (dB)	20

下载: 导出CSV 

| 显示表格

仿真结果如图2所示，其中，黑色实线为回波FFT结果，红色圆圈及对应虚线指示了目标的真实频率和幅度值，蓝色菱形框为CZT算法参数估计结果，绿色“×”字为FIIB算法参数估计结果。仿真结果显示，目标功率相差20 dB时，回波信号FFT的结果几乎与频率分量${f_1}$单独FFT的结果相同，这是由于幅度较大的频率分量会产生较大的旁瓣，${f_1}$产生的旁瓣盖过了${f_2}$的主瓣，因此回波信号在频域只显示出单峰，幅度较小的分量被淹没。通过频谱细化和最大值检索，CZT算法对幅度较大的频率分量进行了较好的估计，但无法分辨出幅度较小的频率分量。同时，由于在每个多普勒单元都进行了频谱细化和最大值搜索，CZT得到了多个点目标的频率和参数估计结果。相比之下，FIIB算法不仅准确地估计出了目标个数，且估计误差很小，估计结果基本与真值吻合，FIIB对于${f_1}$和${f_2}$估计的均方根误差分别为${\text{RMSE(}}{f_1}) = {\text{7}}{\text{.4774}} \times {10^{ - 5}}$, ${\text{RMSE}}({f_2}) = 7.{\text{6681}} \times {10^{ - 4}}$。仿真结果表明：在强点目标存在的情况下，FIIB能够通过插值-泄露减法的策略，有效解决强点目标旁瓣覆盖弱点目标的问题，从而准确地分辨出较小的频率，给出正确的频率、复振幅估计结果。

图  2  强点目标仿真结果(${W_1}/{W_2} = 20\;{\text{dB}}$)

Figure  2.  Simulation result of strong point targets (${W_1}/{W_2} = 20\;{\text{dB}}$)

下载: 全尺寸图片 幻灯片

估计的具体数值如表2所示。

表  2  强点目标参数估计结果(${\boldsymbol{W}}_{\bf{1}}/{\boldsymbol{W}}_{\bf{2}}$=20 dB)

Table  2.  Estimation result of strong point targets (W₁/W₂=20 dB)

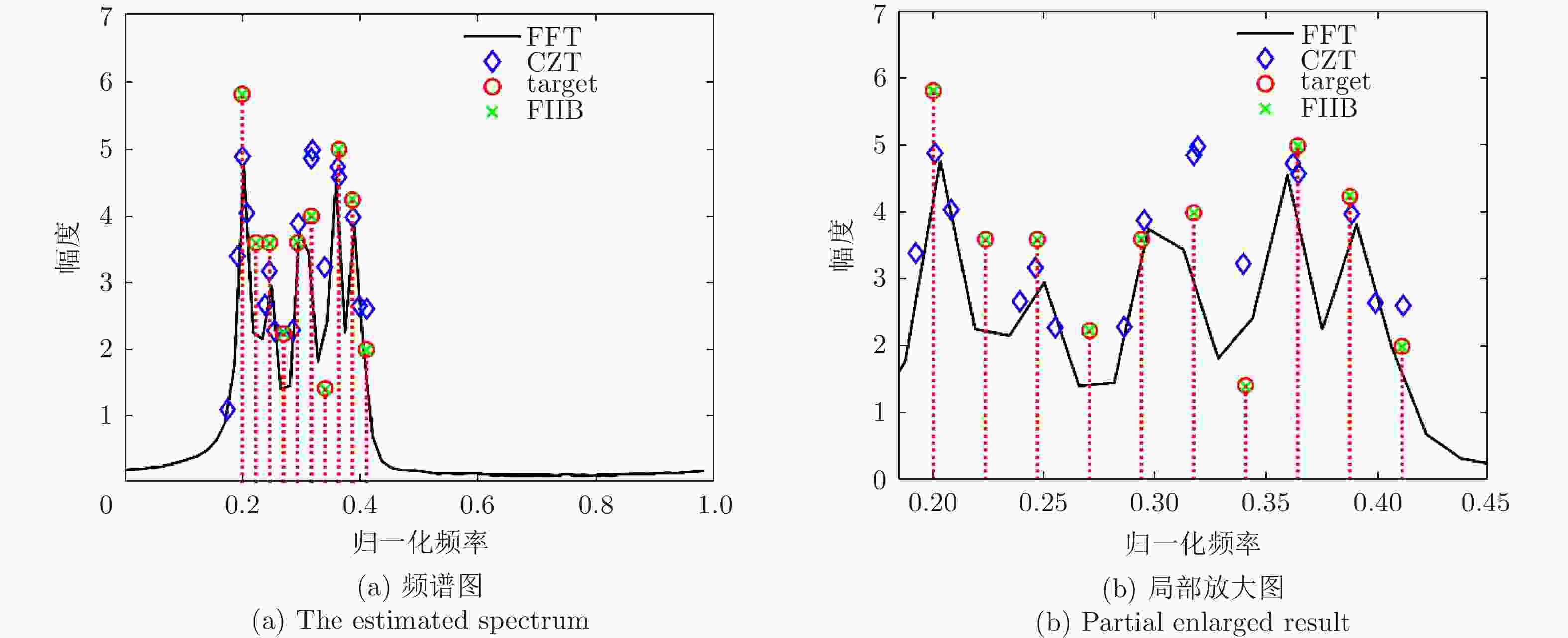
参数	方法	目标1	目标2	假目标	假目标	假目标	假目标
频率	True	0.2687	0.3000	/	/	/	/
	FIIB	0.2687	0.3000	/	/	/	/
	CZT	0.2689	0.2737	0.2578	0.2912	0.3063	0.3232
	FFT	0.2656	/	/	/	/	/
复振幅	True	5.0000+3.0000j	0.5000–0.3000j	/	/	/	/
	FIIB	4.9906+3.0169j	0.4905–0.3066j	/	/	/	/
	CZT	4.9230+3.1262j	4.6314–1.8004j	–1.8767+0.8188j	1.0581–0.5353	0.5413–0.8405j	0.3429–0.4851j
	FFT	2.2325+5.0000j	/	/	/	/	/

下载: 导出CSV 

| 显示表格

4.2   相邻点目标泄露影响分析

本节选择两个幅度相同的点目标进行仿真，其中，${f_1} = 0.2844$, ${A_2} = 5.0000 - 3.0000{\text{j}}$，其余仿真参数与表1相同，此时频率间隔$\Delta f = 1/N$。

仿真结果如图3所示，两个幅度相同的频率分量分布在相邻多普勒单元时，回波信号FFT结果出现双峰，这表明基于目标多普勒差异在多普勒域可实现多目标的分离。由于两个频率分量分布在相邻的多普勒单元，旁瓣泄露的影响较大，每个点目标都会受到另一个点目标的影响，此时FFT结果并不能很好地估计每个分量的复振幅，同时受点数限制，FFT频率估计的结果也较为粗糙。相比FFT，CZT算法的估计结果更为精确，但同时也存在和强点目标情况类似的估计出多个假目标的问题。FIIB算法准确地估计出了目标个数，对于${f_1}$和${f_2}$频率估计的均方根误差分别为${\text{RMSE(}}{f_1}) = 1.{\text{4210}} \times {10^{ - 4}}$, ${\text{RMSE(}}{f_2}) = 1.{\text{4885}} \times {10^{ - 4}}$。尽管均方根误差比强源情况低一个数量级，但精度仍然很高，这说明在频率分量位于相邻多普勒单元的情况下，FIIB能够通过插值-泄露减法有效消除相邻源的旁瓣泄露，得到准确的频率、复振幅估计结果。

图  3  相邻点目标仿真结果 ($\Delta f = 1/N$)

Figure  3.  Simulation result of neighboring point targets ($\Delta f = 1/N$)

下载: 全尺寸图片 幻灯片

具体数据如表3所示。

表  3  相邻点目标参数估计结果(${\boldsymbol{\Delta}} {\boldsymbol{f}} = {\bf{1}}/{\boldsymbol{N}}$)

Table  3.  Estimation result of neighboring point targets (${\boldsymbol{\Delta}} {\boldsymbol{f}} = {\bf{1}}/{\boldsymbol{N}}$)

参数	方法	目标1	目标2	假目标	假目标	假目标	假目标
频率	True	0.2844	0.3000	/	/	/	/
	FIIB	0.2844	0.3000	/	/	/	/
	CZT	0.2828	0.3021	0.3049	0.2734	0.3227	0.2550
	FFT	0.2813	0.2969	/	/	/	/
复振幅	True	5.0000+3.0000j	5.0000–3.0000j	/	/	/	/
	FIIB	4.9852+3.0081j	4.9980–3.0238j	/	/	/	/
	CZT	4.1085+4.3364j	4.1257–4.3441j	1.5993–5.3751j	–1.9113+1.6013j	0.2152–1.7055j	–0.5516+0.9638j
	FFT	3.0812+5.0246j	4.9664–0.8527j	/	/	/	/

下载: 导出CSV 

| 显示表格

4.3   多点目标的参数估计

为验证FIIB算法对多目标频率和复振幅的估计能力，设定10个等间隔的频率分量，起始频率${f_1} = 0.2\;{\text{Hz}}$，频率间隔$\Delta f = 1.5/N = 0.234375$，复振幅的实部和虚部均为[–5,5]区间内随机选取的整数，设定最大目标数${L_{\max }} = 15$，方位向采样信号长度为64，回波叠加高斯白噪声，信噪比仍为20 dB，此时由于目标数量增加，迭代次数需要适当增大，本节中取迭代次数为30次。

仿真结果如图4所示，在多点源情况下，CZT算法的估计结果与真实值相差较大，这是由于CZT无法确定目标的个数，输出了较多的目标，且当点目标出现在估计单元的边缘时，算法会在相邻的两个估计单元各输出一个较大的估计值。而FIIB算法依然表现更优，能够在准确估计点目标个数的同时，输出准确的频率和幅度估计值，此时频率估计的平均均方根误差为$\overline {{\text{RMSE}}} = {\text{4}}{\text{.0244}} \times {10^{ - 4}}$。

图  4  多点目标仿真结果($L = 10$)

Figure  4.  Simulation result of multiple point targets ($L = 10$)

下载: 全尺寸图片 幻灯片

4.4   不同频率间隔目标参数估计结果与迭代次数的关系

当目标频率间隔大于多普勒单元长度时($\Delta f \ge 1/N$)，FIIB算法展示出优异的性能，特别是点目标功率差距较大(如20 dB)时，FIIB相较其他算法更具优势，经过2～5迭代即可收敛并得到理想的结果。本小节仿真分析当两个点目标位于同一多普勒频率单元时($\Delta f＜1/N$)，FIIB是否可以获得对频率和复振幅的精确估计。令目标间隔为$\Delta f = 0.5/N$，信噪比为30 dB，其他参数与5.2节相同。仿真结果如图5所示，当迭代次数$Q{\text{ = 5}}0$时，FIIB对频率的估计较为准确，频率估计的平均误差为0.7091%，但此时复振幅的估计值与真实值偏离较大。直到迭代次数$Q \ge 200$时，频率估计值和复振幅估计值都较为准确，对于$Q = 200$频率估计的平均均方根误差$\overline {{\text{RMSE}}} = 1.{\text{3524}} \times {10^{ - 5}}$。文献[18]分析表明，FIIB算法与目标个数估计算法结合后，总计算量为$O\left\{ {N{{\log }_2}N + Q\left[ {k + N{L_{\max }}({L_{\max }} + 1)} \right]} \right\}$，当Q过大时，计算量将剧增。此时，虽然理论上FIIB算法能收敛到克拉美罗下界CRB(${N^{-3/2}}$)的1.0147倍^[31]，但是对复振幅估计的精度已明显下降，难以应用于成像处理中。具体的仿真结果如表4所示，当两个频率分量位于一个多普勒单元且幅度相等时，频率估计值确实最终能够达到收敛，但是迭代运算量较大。

图  5  不同迭代次数下同多普勒单元内两个目标的FIIB仿真结果

Figure  5.  Simulation results of FIIB for two targets situated in a Doppler bin by different iterations

下载: 全尺寸图片 幻灯片

表  4  不同迭代次数下同多普勒单元内两个目标的FIIB参数估计结果

Table  4.  Estimation result of FIIB for two targets situated in a Doppler bin by different iterations

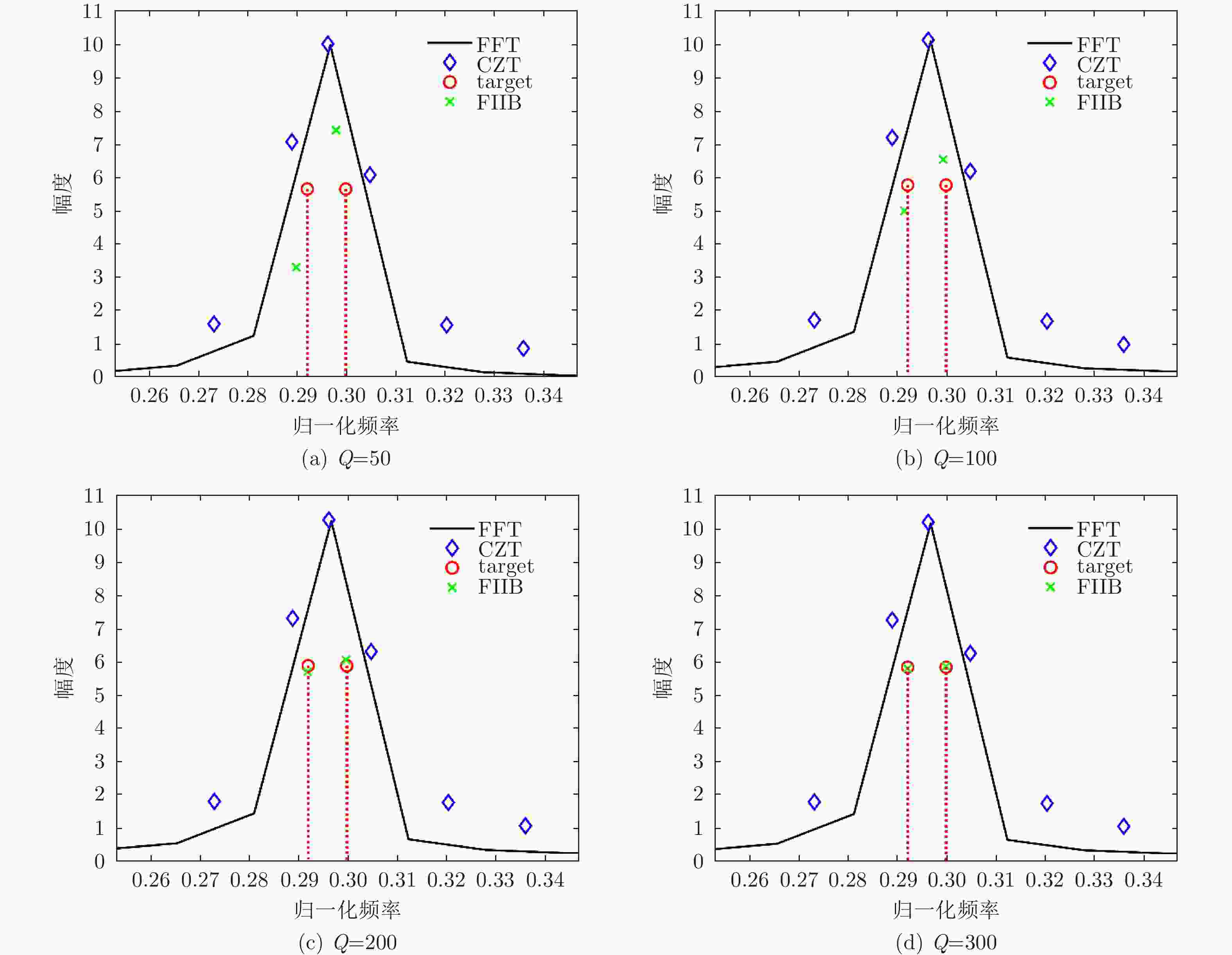
迭代次数Q	${f_1}$	${f_2}$	${A_1}$	${A_2}$
50	0.2899	0.2980	2.4221+2.4827j	7.3413–2.0001j
100	0.2915	0.2994	4.0880+2.9784j	5.9220–2.9249j
200	0.2920	0.2999	4.7896+2.9998j	5.2107–2.9917j
300	0.2922	0.3000	4.9617+2.9887j	5.0442–2.9834j
(真实值)	0.2922	0.3000	5.0000+3.0000j	5.0000–3.0000j

下载: 导出CSV 

| 显示表格

5.   雷达成像仿真与分析

在雷达成像处理中，多普勒频率的估计精度直接影响成像质量，数值分析表明FIIB能很好地适应同一波束内存在不满足稀疏条件的多个点目标的场景，并在旁瓣泄露的条件下给出精确的频率估计，因此将FIIB算法引入单脉冲前视成像改善成像质量。本节主要对比了分别使用传统单脉冲测角、CZT和FIIB这3种方法进行多普勒重建的结果，完成了单脉冲前视成像的仿真实验，最后用实测数据对仿真的结论进行验证。

5.1   点目标阵列仿真

仿真所用雷达系统参数如表5所示。位于机载平台上的雷达随平台以$v = 100\;{\text{m/s}}$的速度匀速飞行，发射信号中心频率${f_{\text{c}}}$为18 GHz，带宽为50 MHz，脉宽为1 μs。脉冲重复频率PRF=2000 Hz，天线波束的扫描范围为${{ - 15}}^\circ$～${\text{15}}^\circ$，扫描速度为30°/s。在地面上以[0, 1700] m为中心设置3×21目标点阵，点目标强度为1，方位向、距离向间隔均为30 m。脉压后回波的${\text{SNR}} = 20{\text{ dB}}$、噪声服从均值为0，方差为${\sigma ^{\text{2}}}$的复正态分布。

表  5  前视扫描成像实验仿真参数

Table  5.  Simulation parameters of a forward-looking scanning radar

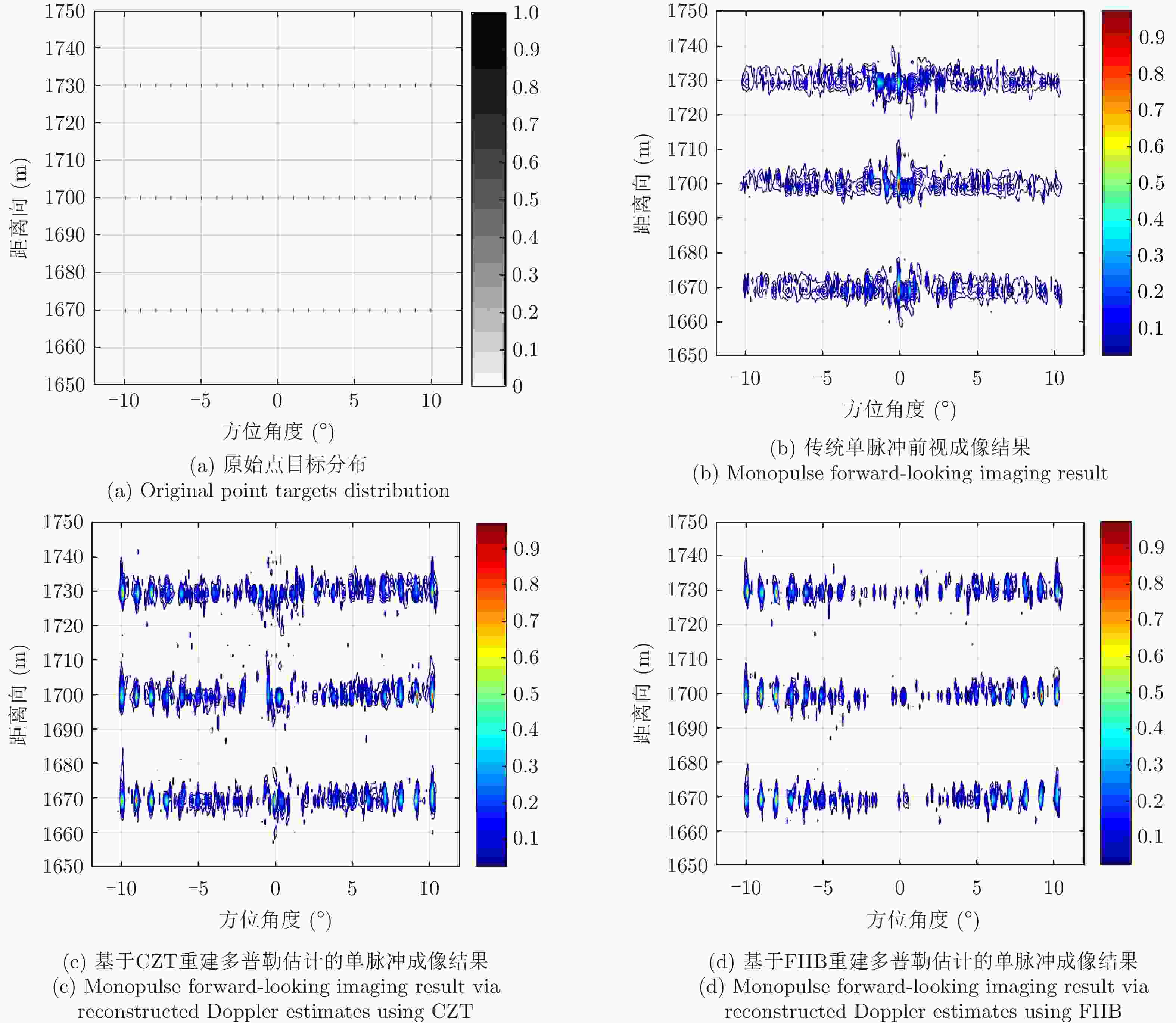
参数	数值		参数	数值
平台飞行速度(m/s)	100		场景中心地距(m)	1700
雷达中心频率(GHz)	18		距离×方位分辨单元 (m×m)	3×3
信号带宽(MHz)	50		和通道3 dB波束宽度(°)	5
信号脉宽(μs)	1		波束扫描范围(°)	–15～15
脉冲重复频率PRF (Hz)	2000		天线扫描速度(°/s)	30

下载: 导出CSV 

| 显示表格

对一个如图6(a)所示的3×21的点阵模拟产生回波，回波信号经过预处理和运动补偿后，分别采用传统单脉冲成像方法、基于CZT重建多普勒估计的单脉冲成像方法及基于FIIB重建多普勒估计的单脉冲成像方法进行处理，并绘制等高线图，结果如图6(b)—图6(d)所示。尽管FIIB算法能够实现对频率间隔较小的点目标的分辨并最终达到收敛，但此时对信噪比、迭代次数的要求较严格，因此在实际应用过程中，综合考虑计算时长和估计精度，令最大目标个数${L_{\max }}$为主瓣内多普勒单元的个数，然后利用FIIB算法对和通道的目标真实个数及其参数进行估计，基于估计结果求得和差通道对应的CZT值后再进行单脉冲测角。若目标分布过于密集，可根据实际情况进一步增大最大目标个数的设置值，同时迭代次数也需相应提高。

图  6  点阵目标单脉冲前视成像效果对比

Figure  6.  Comparison of forward-looking imaging performance

下载: 全尺寸图片 幻灯片

图6(b)中的点目标在距离向上得到有效的分离，但由于传统单脉冲前视成像无法对同一分辨单元内的多个目标进行分辨，因此成像结果在方位向上混叠。图6(c)、图6(d)显示在距离向上单脉冲成像使位于不同距离门的点目标得到了有效分离，图6(c)在方位向上位于左右两侧的点目标得到了分离，且左右两侧点目标在前斜视方向上的方位分布范围较小，这说明基于CZT算法进行多普勒估计可以解决同一分辨单元内多目标分辨的问题，但同时成像结果中也存在一些投影不理想造成的假目标；图6(d)中前斜视方向上位于左右两侧的点目标在方位向上同样得到了有效分离，且由于FIIB对目标个数进行了准确估计，有效消除了旁瓣的影响，点目标在方位向上的分布范围相比CZT明显缩小，背景杂波也明显减少。

为进一步对比方位向上的目标分辨情况，分别沿方位向截取图6(c)、图6(d)中距离向1700 m处的21个点目标绘制如图7所示的归一化剖面图，图中红色圆圈及虚线指示了点目标的真实角度，蓝色虚线代表基于CZT的单脉冲成像目标归一化方位向剖面图，绿色实线为基于FIIB的单脉冲成像目标归一化方位向剖面图。图7表明在方位向$\pm 5^\circ$外两个方法均表现良好，目标位置与真实位置基本重合，且目标的波束锐化程度较好、幅度较为均匀。同时，FIIB算法的大部分峰值都比CZT方法更高，旁瓣相对CZT更少更低，这说明FIIB方法目标投影能量更为集中，对旁瓣的抑制效果明显，且能准确地分辨目标的个数。此外，由于重建多普勒估计的单脉冲前视成像在正前视区域具有一定的局限性，CZT和FIIB算法在飞行方向的正前方及两侧$\pm 5^\circ$范围内仍存在盲区，仅当方位向波束主瓣内只存在一个强反射点目标时，算法能实现对目标的准确估计。同时，如果同波束内出现关于鼻锥向左右对称的目标，由于多普勒频率相同，也会因为“左右模糊”落入同一多普勒单元而无法区分，单脉冲测角失效。

图  7  距离向1700 m处目标方位向剖面图

Figure  7.  Azimuthal contour plots for point targets at the range cell 1700 m

下载: 全尺寸图片 幻灯片

5.2   场景仿真

本节通过场景仿真验证引入FIIB算法重建扩展目标的可行性。场景仿真的目标更为密集，点源不再满足稀疏条件，此时成像算法的计算量普遍增大。同时相邻点目标多普勒频率差距减小，在频域落入同一个多普勒单元，FIIB需进行多次迭代实现对复振幅的准确估计，为兼顾估计精度及计算量，仿真时选择$Q = {\text{1}}0$，采用FIIB对输出的目标个数、频率值进行估计，然后将对应单元的CZT值作为复振幅估计值实现方位角估计，完成能量投影。原始场景如图8(a)所示，采用了一幅经过降采样处理的Ku波段SAR图像，地面目标以[0,1700] m为中心，最大方位角为$17.9^\circ$，雷达扫描范围为${{ - 20}}^\circ$～$20^\circ$，其余参数与表5相同。利用图8(a)作为原始场景进行仿真，即可得到场景仿真的回波数据，依次利用3种成像方法处理回波，结果如图8(b)—图8(d)所示。

图  8  仿真场景前视成像效果对比

Figure  8.  Comparison of simulation results in forward-looking imaging

下载: 全尺寸图片 幻灯片

图8(b)为传统单脉冲前视成像结果，可以观察到当多个点目标位于同一波束内时，单脉冲测角技术得到的角度信息为所有目标的等效角度信息，无法在方位向上实现各目标的分离，此时产生测角错误，致使图像在方位向上模糊严重。图8(c)为基于CZT重建多普勒估计的单脉冲前视成像结果，此时DBS技术的引入缓解了同波束内多目标带来的测角严重模糊问题，DBS通过机载雷达与场景目标间相对运动产生的多普勒频差将同一波束内的不同目标分离，CZT算法对多普勒频率进行了更为精细的估计，使得场景轮廓重建更为清晰，目标分布范围更小。图8(d)为基于FIIB重建多普勒估计的单脉冲成像结果，FIIB对非稀疏场景具有良好的适应性，有效获取了目标的数量，抑制了相邻目标产生的旁瓣，消除了不同多普勒频率之间的相互影响，因此基于FIIB的成像结果相比于基于CZT的成像结果点目标分布范围减小，场景轮廓更为清晰。非稀疏场景仿真结果表明，基于FIIB重建多普勒估计的单脉冲成像能实现对扩展目标的前视高分辨成像。

为定量评估成像效果，采用均方误差(${\text{MSE}}$)及对比度(C)^[32]两个指标进行结果分析，指标分别定义为

其中，$M,N$分别表示图像的长和宽，$\hat g(m,n), g(m,n)$为重建图像和原始图像在$(m,n)$处的像素值。MSE是衡量重建图像和原始图像间相似度的指标，C反映的是图像的纹理特征，C值越大，图像中的细节越明显。场景仿真定量对比结果如表6所示。

表  6  场景仿真不同方法的定量评价

Table  6.  Quantitative evaluation of different methods of scenario simulation

方法	MSE	C
传统单脉冲前视成像	$0.00663$	$51.4994$
基于CZT重建多普勒估计的单脉冲成像	$0.00394$	$52.3441$
基于FIIB重建多普勒估计的单脉冲成像	$0.00387$	$59.7068$

下载: 导出CSV 

| 显示表格

表6中的MSE计算结果表明，传统单脉冲前视成像算法与原始图像的差异最大，基于FIIB算法的重构结果略优于基于CZT算法的重构结果。对比度的计算结果显示，基于FIIB的单脉冲成像算法相比传统成像算法和基于CZT的成像算法具有明显优势，重构图像更好地显示出场景的纹理特征，这是由于FIIB有效地消除了旁瓣的影响且对目标个数实现了准确估计。

5.3   实测数据验证

图9为各方法对机载雷达实测数据处理结果，成像区域主要分为水面和陆地两部分，雷达的扫描范围为${{ - 21}}^\circ$～$38^\circ$，右侧小图为框选的两个区域对应的局部放大图，右上放大图为红色方框限定的水陆边界区域，右下放大图为黄色方框限定的水面区域。图9(a)实孔径成像结果显示，目标在方位向上的分布范围较大，轮廓模糊，且海杂波干扰严重影响了对海面目标成像的质量。图9(b)为单脉冲前视成像结果，目标的能量分布更为集中，但由于多目标测角模糊问题，单脉冲测角出现错误，无法准确区分同一分辨单元内多个目标，各目标的投影在方位向上重叠，边缘区域成像轮廓明显模糊。此外，单脉冲成像对于陆地目标成像效果改善并不明显，且孤立的海面目标分布范围较大。图9(c)为基于CZT重建多普勒估计的单脉冲成像结果，可以发现基于CZT的成像方法陆地目标的分布范围相比于传统单脉冲成像有所减小，成像结果更为清晰，水陆相接区域轮廓更为明显，但背景杂波影响仍存在。图9(d)为基于FIIB重建多普勒估计的单脉冲成像结果，可以观察到相比于CZT成像结果所有区域目标的分布范围都明显减少，背景杂波得到了有效抑制，水陆边界区域也出现了明显的分界线，这是由于FIIB准确估计了回波内点目标的个数并抑制了旁瓣泄露，更细节地展示出了场景的纹理特征。

图  9  实测数据前视成像效果对比

Figure  9.  Comparison of experimental results in forward-looking imaging

下载: 全尺寸图片 幻灯片

鉴于实测数据重构结果无真值图像进行对比，无法计算各方法的${\text{MSE}}$，故加入图像熵(${\text{ENT}}$)对成像结果进行定量评估，图像熵是衡量图像聚焦效果的指标，具体定义^[33]如式(38)所示：

其中，${p_{mn}}$为重建图像在$(m,n)$处的像素值$\hat g(m,n)$的概率，${p_{mn}}$计算方法如式(39)所示：

实测数据定量对比结果如表7所示，结果说明相比其他方法，本文所提方法能有效解决旁瓣泄露的问题，对杂波抑制效果明显，因此聚焦性能最优，具有最小的图像熵。同时也注意到单脉冲成像算法存在一定的能量损失，这是由于在成像过程中测角时相当于对目标的能量进行了筛选，因此实孔径图像颜色较亮，与背景差异明显，对比度最大。而在3种采用单脉冲成像的算法中，基于FIIB方法的重构图像的对比度明显优于传统单脉冲算法和基于CZT算法的重构图像，这是由于FIIB算法考虑了旁瓣泄露，对目标的数量进行了准确估计，同时有效抑制了杂波，因此对比度更大，图像更为清晰，边缘轮廓明显。

表  7  实测数据不同方法的定量评价

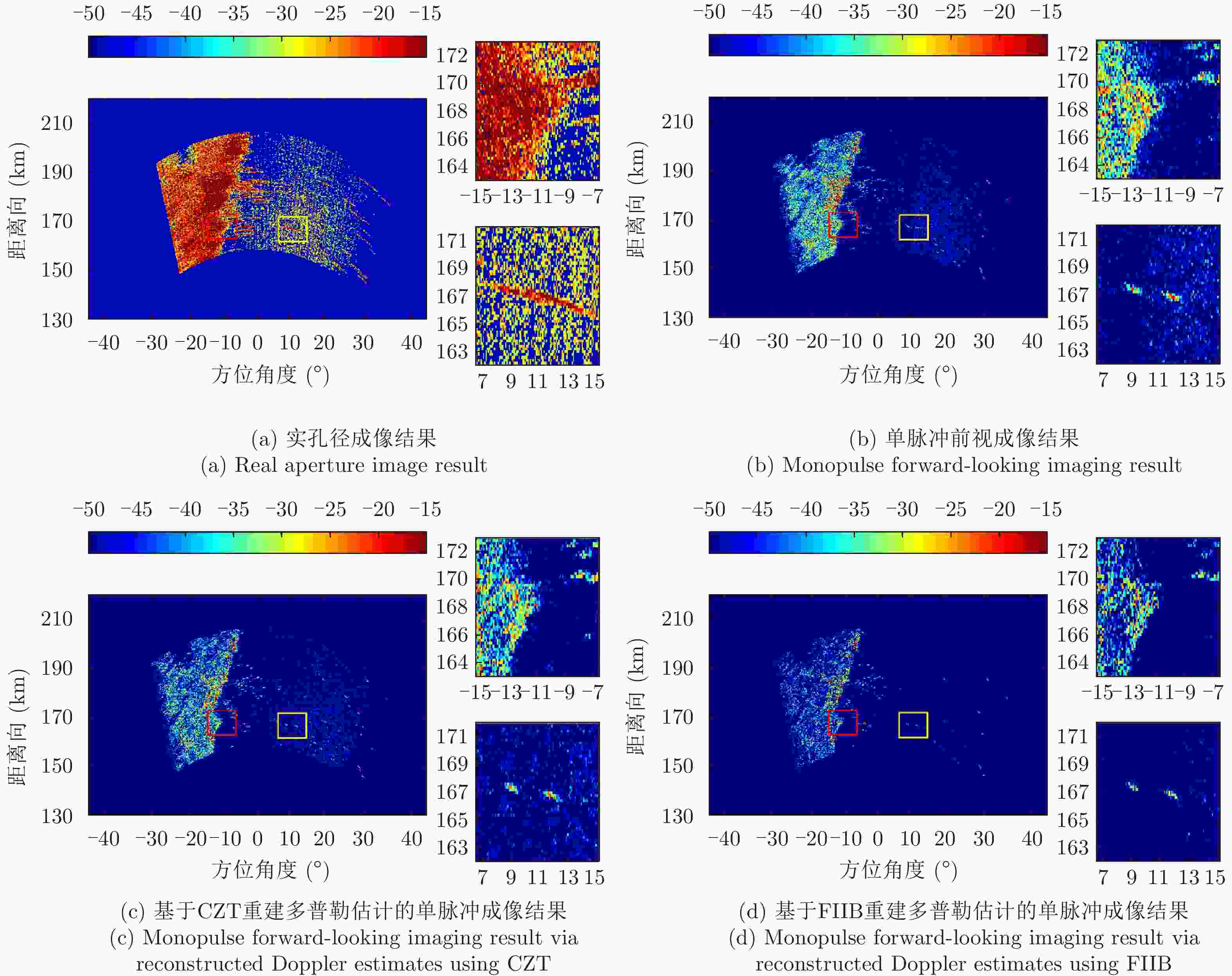
Table  7.  Quantitative evaluation of different methods of real data

方法	${\text{ENT}}$	C
实孔径图像	$4.2660$	$411.9599$
传统单脉冲前视成像	${\text{3}}{\text{.6825}}$	$213.4888$
基于CZT重建多普勒估计的单脉冲成像	$3.5228$	$233.1903$
基于FIIB重建多普勒估计的单脉冲成像	$2.9651$	$292.8872$

下载: 导出CSV 

| 显示表格

6.   结语

在雷达前视成像中，多普勒信息的处理对分离方位向目标至关重要，其中，多普勒频率和幅度的准确估计可有效提高目标定位的精度及成像质量。针对雷达前视成像中旁瓣泄露及主瓣内点目标个数估计的问题，本文引入了一种具有目标个数估计功能的快速迭代插值波束形成方法，实现了对回波信号中频率分量个数、频率值和复振幅值的精确估计。仿真和实测数据表明，FIIB能有效抑制杂波，提升单脉冲前视成像的清晰度，相比于基于CZT的成像算法具有优越性。但是，对位于同一个多普勒单元内的多个目标，FIIB算法无法有效分离，因此在鼻锥向两侧$\pm 5^\circ$范围内仍存在盲区，仅当波束主瓣内只存在一个强反射点目标时，能实现对目标的准确估计，未来将在此基础上进一步探究解决途径。

致谢 由衷感谢编辑和各位审稿专家对本文提出的宝贵建议，在本文投稿过程中，王雪松教授对文章提出了重要修改意见和建议，特此致谢！