基于复数域深度强化学习的多干扰场景雷达抗干扰方法

解烽; 刘环宇; 胡锡坤; 钟平; 李君宝

doi:10.12000/JR23139

基于复数域深度强化学习的多干扰场景雷达抗干扰方法

DOI: 10.12000/JR23139

1.
哈尔滨工业大学计算学部信息对抗技术研究所哈尔滨 150080
2.
国防科技大学电子科学学院长沙 410073

基金项目: 国家自然科学基金(62271166)，哈尔滨工业大学医工理交叉基金(IR2021104)

详细信息

作者简介:
解　烽，博士生，主要研究方向为雷达抗干扰技术、深度强化学习

刘环宇，讲师，主要研究方向为强化学习、目标识别检测和无人机控制

胡锡坤，助理研究员，主要研究方向为遥感图像处理和深度学习

钟　平，研究员，主要研究方向为智能目标识别

李君宝，教授，主要研究方向为机器学习算法、嵌入式智能系统、图像处理

通讯作者:
刘环宇 liuhuanyu@hit.edu.cn

责任主编：全英汇 Corresponding Editor: QUAN Yinghui
中图分类号: TN974
计量
- 文章访问数: 1154
- HTML全文浏览量: 835
- PDF下载量: 443
- 被引次数: 0
出版历程
- 收稿日期: 2023-07-31
- 修回日期: 2023-10-19
- 网络出版日期: 2023-11-09
- 刊出日期: 2023-12-28

A Radar Anti-jamming Method under Multi-jamming Scenarios Based on Deep Reinforcement Learning in Complex Domains

1.
Information Countermeasure Technique Institute, Faculty of Computing, Harbin Institute of Technology, Harbin 150080, China
2.
College of Electronic Science and Technology, National University of Defense Technology, Changsha 410073, China

Funds: The National Natural Science Foundation of China (62271166), Interdisciplinary Research Foundation of HIT (IR2021104)

More Information

Corresponding author: LIU Huanyu, liuhuanyu@hit.edu.cn

摘要

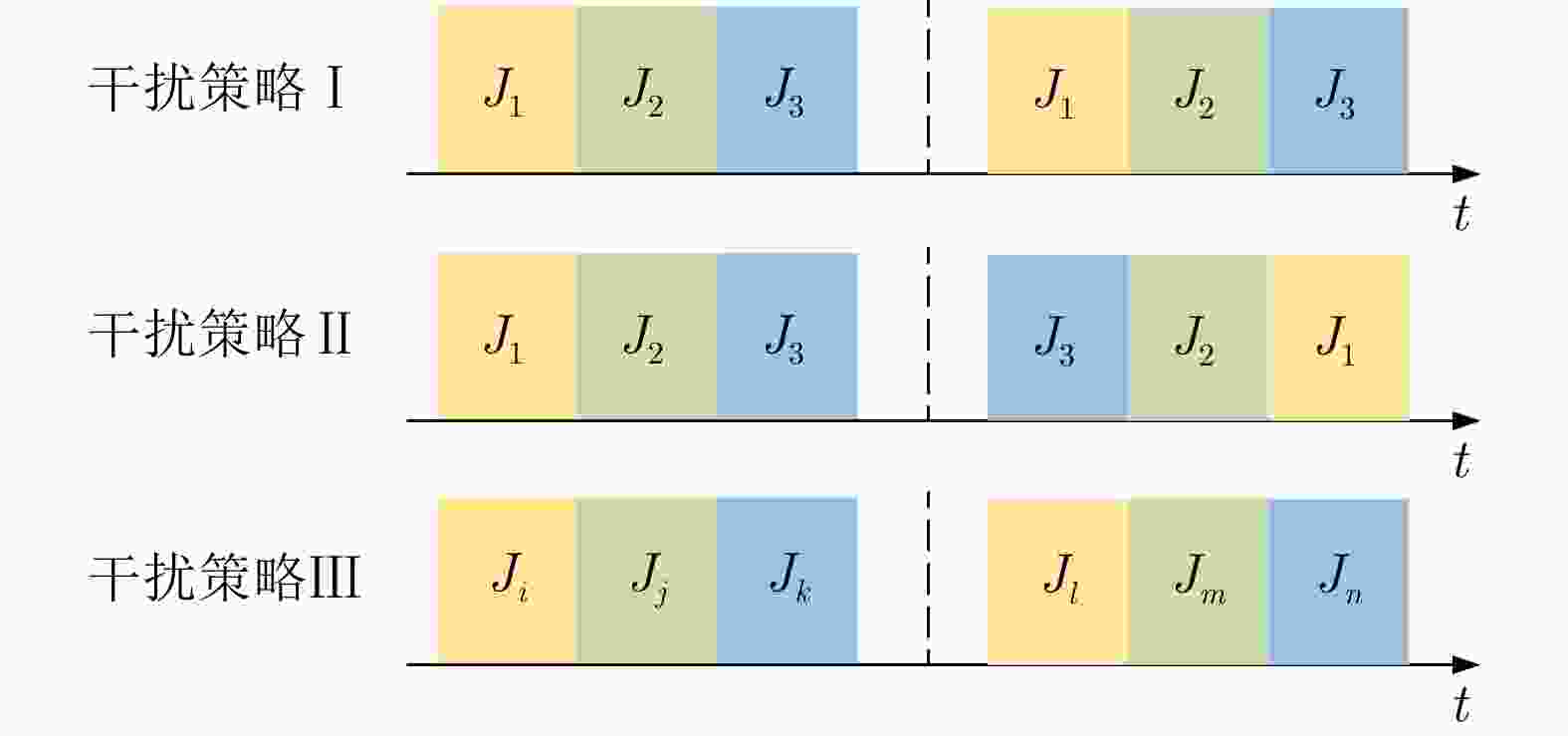
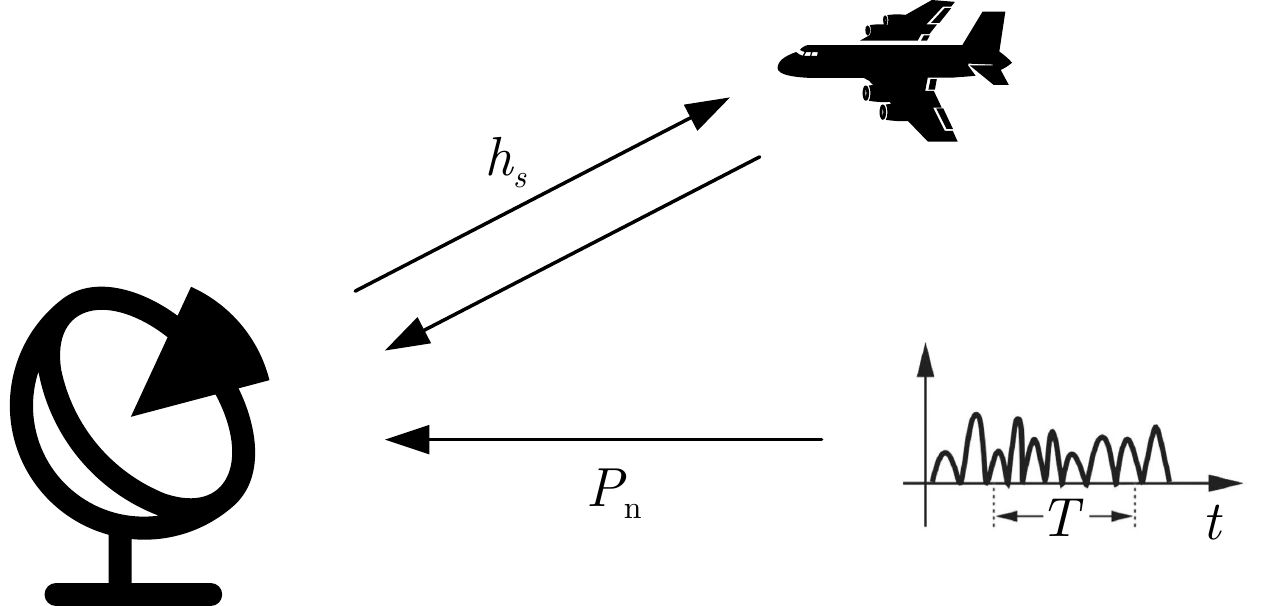
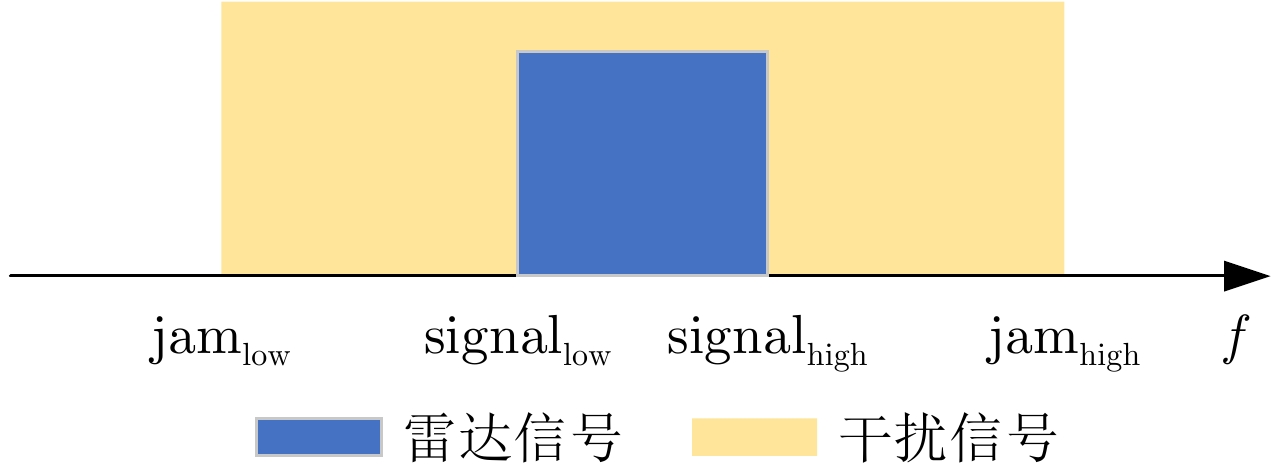
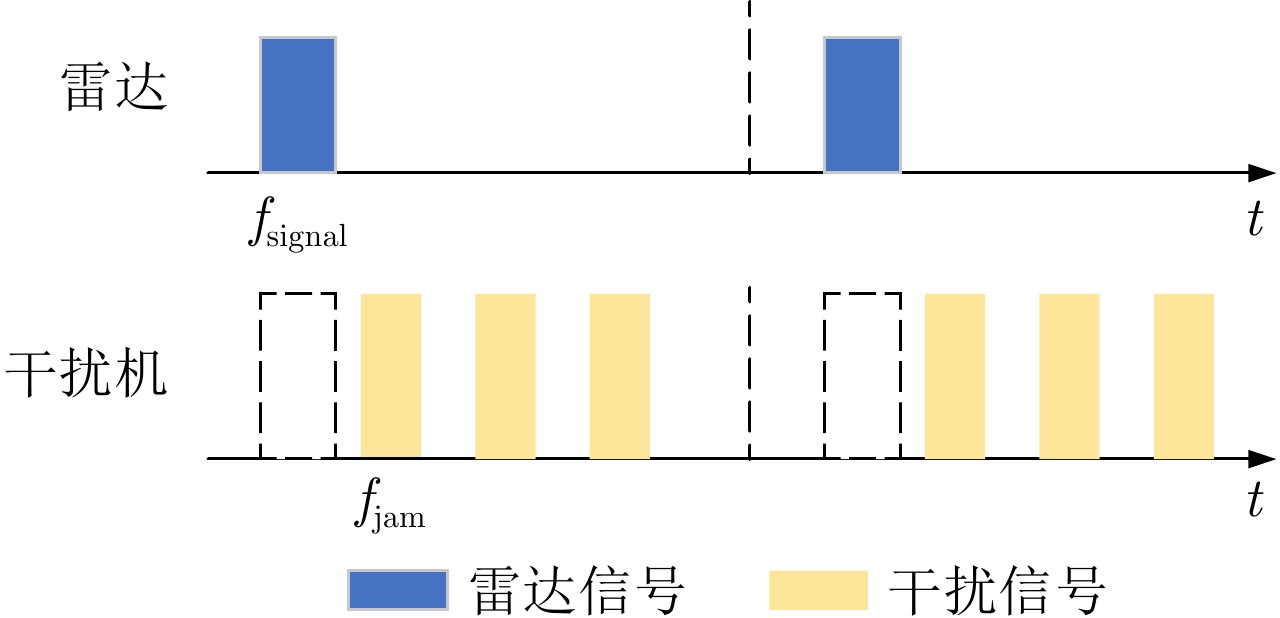
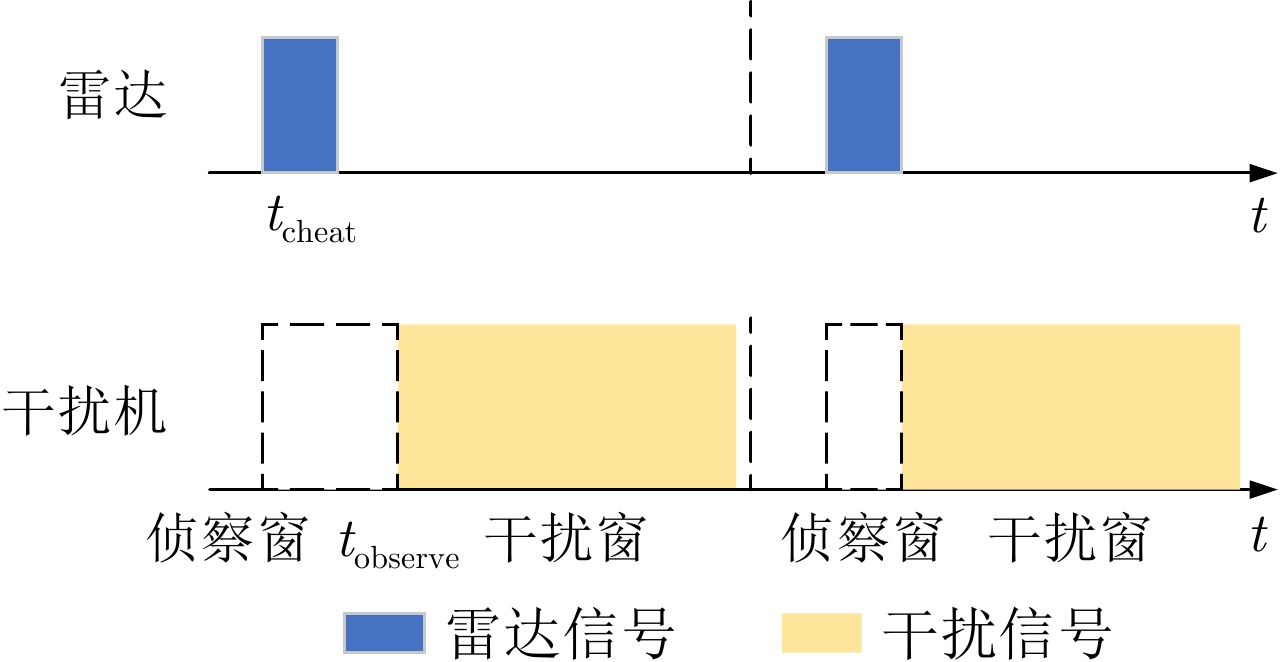
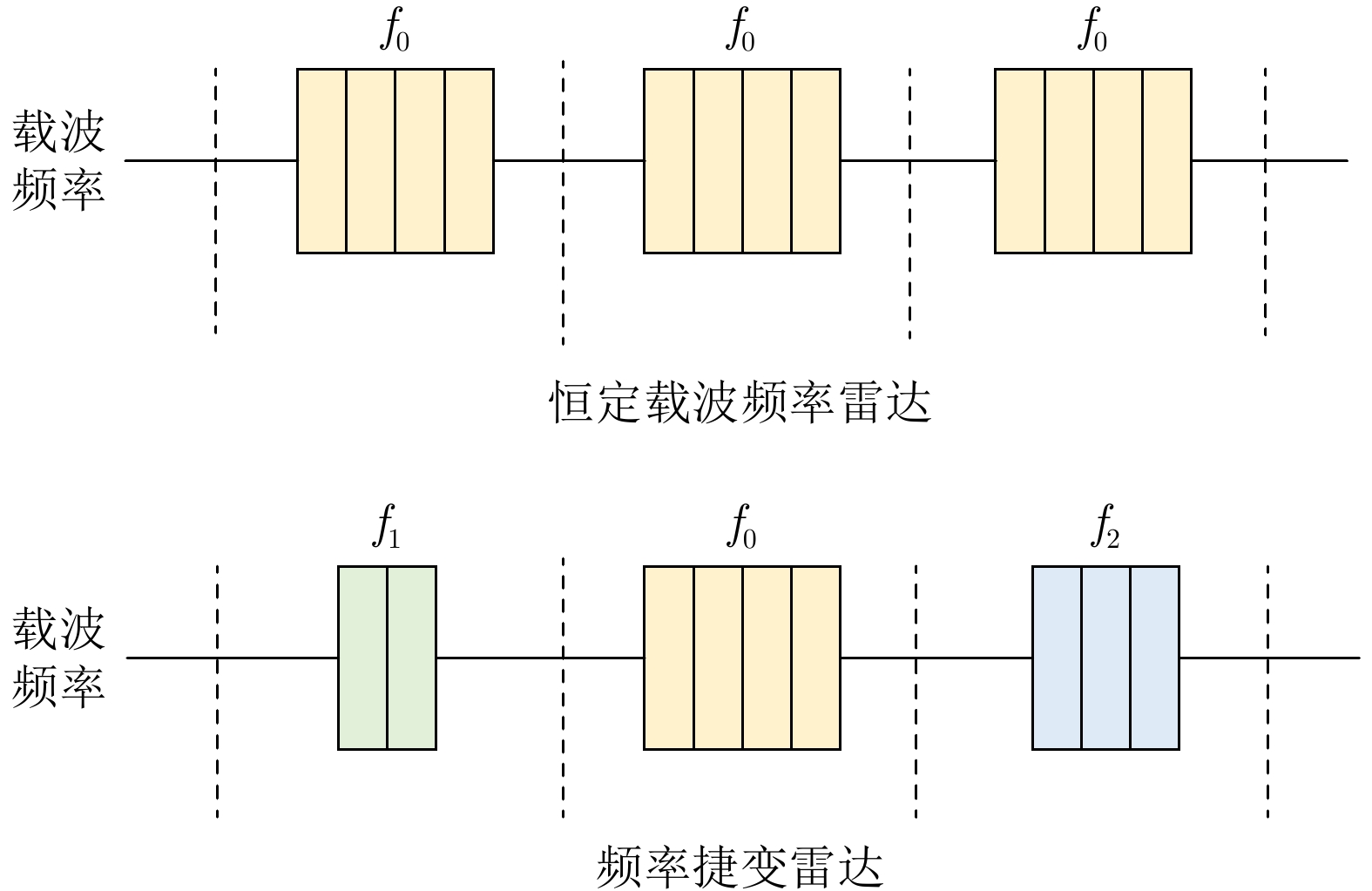
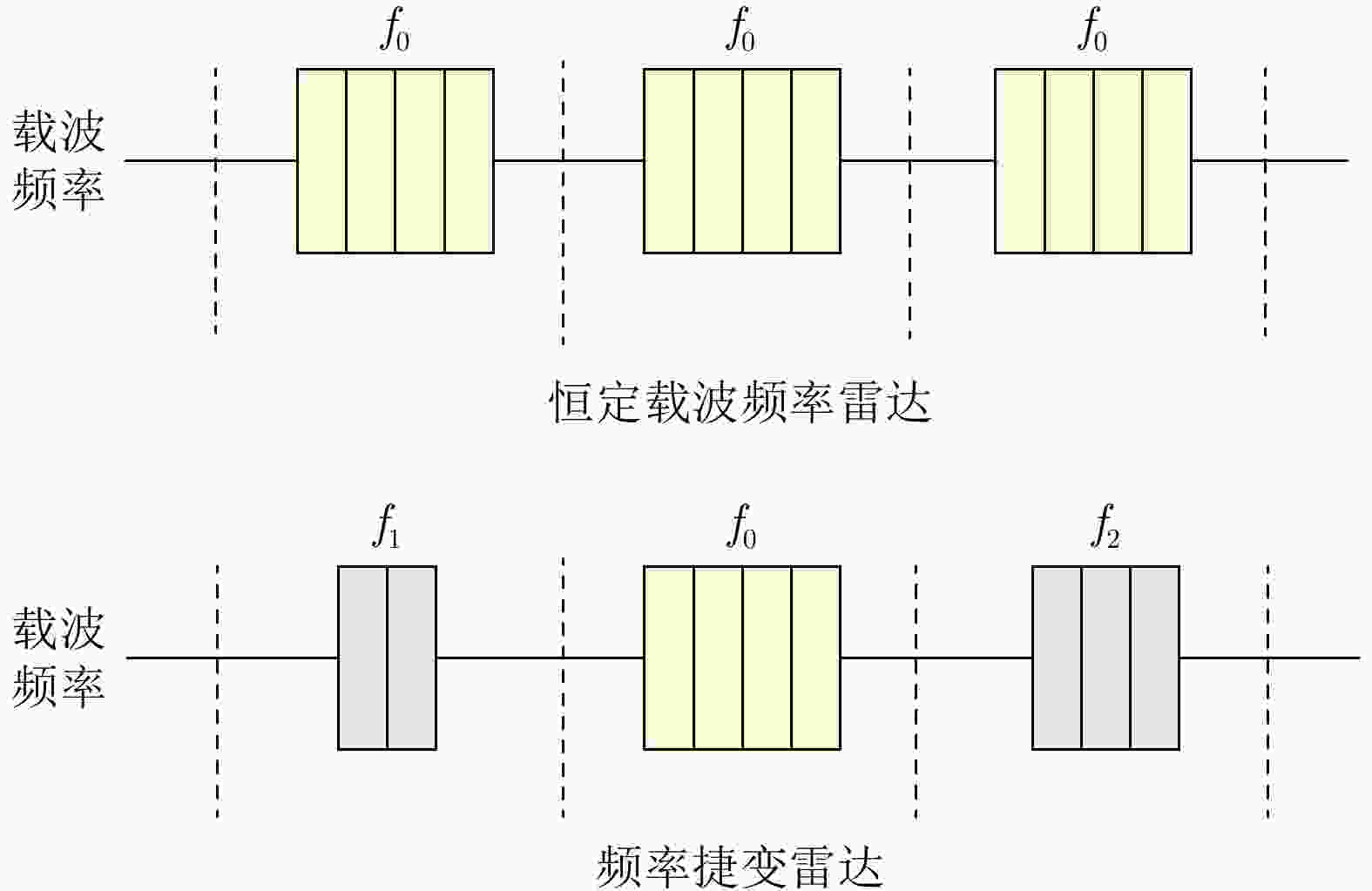
摘要: 在现代电子战中，雷达面临的干扰环境比以前更加复杂，机载干扰机会根据突袭任务与突袭阶段的不同而改变其干扰方式。近年来，基于强化学习的雷达抗干扰方法在单一干扰对抗场景下取得了一定进展，但在实际复杂多干扰场景下的研究仍有不足。为了解决该问题，本文提出了一种基于复数域深度强化学习的多干扰场景雷达抗干扰方法以优化频率捷变雷达的抗干扰策略。首先，针对突袭任务的阶段性特点建立了噪声瞄准干扰、距离假目标欺骗干扰与密集假目标转发干扰3种干扰模型，并设计了3种干扰顺序策略来模拟实际干扰场景。其次，针对多干扰场景模型，构建了一种融合信干噪比与目标航迹完整性的强化学习奖励函数，并针对干扰信号的复数域特征，提出了一种基于复数域深度强化学习的多干扰场景雷达抗干扰方法。最后，基于3种干扰顺序策略设计了雷达抗干扰仿真实验，结果表明，所提方法能够有效解决雷达面临的时序条件下复杂多干扰场景的主瓣干扰问题，与两种经典深度强化学习算法相比该方法抗干扰决策性能大幅提高，平均决策时间降低至405.3 ms。
- 复数域 /
- 深度强化学习 /
- 主瓣干扰 /
- 序贯干扰 /
- 频率捷变雷达
Abstract: In modern electronic warfare, the jamming environment of radar is more complex than ever. The airborne jammer adapts its jamming method based on diverse raid missions and stages. Recently, the reinforcement learning–based radar anti-jamming method has made some progress in the confrontation scenario of single jamming; however, the gap with respect to actual complex multi-jamming scenarios is large. To address this issue, this paper proposes a multi-jamming scenario radar anti-jamming method based on deep reinforcement learning in the complex domain to optimize the anti-jamming strategy of frequency agile radar. First, according to the stage characteristics of the raid mission, noise spot jamming, range deception jamming , and dense false target forwarding jamming models are established. The three jamming sequence strategies were designed to simulate actual jamming scenarios. Second, a reinforcement learning reward function that integrates the signal-to-noise ratio and target trajectory integrity is constructed for the multi-jamming scenario model. Thus, a multi-jamming scenario radar anti-jamming method based on deep reinforcement learning in a complex domain is proposed, which is based on the complex domain characteristics of the jamming signal. Finally, radar anti-jamming simulation experiments are performed based on the three jamming sequence strategies. The results show that the proposed method can effectively deal with the main-lobe jamming problem of complex multi-jamming scenarios under time-sequence conditions. Moreover, the average decision-making accuracy was improved, and the average decision-making time was reduced to 405.3 ms compared with the two classical reinforcement learning algorithms.
- Complex domain /
- Deep Reinforcement Learning (DRL) /
- Main-lobe jamming /
- Sequential jamming /
- Frequency agile radar

HTML全文

1. 引言

成像雷达因其稳定性及高分辨率的优势，在军事侦查和民用勘测领域得到广泛应用。其中，成像体制以合成孔径雷达(Synthetic Aperture Radar, SAR)为代表^[1,2]；但传统SAR成像技术和多普勒波束锐化技术(Doppler Beam Sharpening, DBS)受限于成像机理，无法满足正前视区域成像的需求；对于斜视SAR和侧视SAR的成像模式，其应用均存在一定的局限性^[3]。此外，SAR成像性能在积累时间、波束分辨瑞利限、信噪比等因素的制约下，对抗复杂电磁环境的应用性能受到极大挑战。

涡旋电磁波成像雷达采用一种新型成像体制，其波前相位受轨道角动量(Orbital Angular Momentum, OAM)调制^[4,5]，从而形成特定的相位分布，理论上可以生成无数种正交的调制模式，使得涡旋电磁波在数学处理上更为简便，可以提升成像分辨率、算法效率等性能。针对电磁涡旋雷达应用，学者开展了实孔径成像、SAR以及ISAR (Inverse Synthetic Aperture Radar)等一系列研究^[6−8]，并且在典型前视雷达成像应用中，展示出优异性能^[9]。

在涡旋雷达成像算法方面，2013年郭桂蓉等人^[10]对电磁涡旋雷达成像的机理与可行性方面进行了研究，为涡旋波在雷达成像感知领域的应用奠定了基础。2018年前后，学者结合SAR体制对单一模态下的二维成像^[11]与多模态三维合成孔径成像^[12]等开展了系列研究，研究结果表明，电磁涡旋可以用于SAR成像且成像效果优于平面波。2019年，Fang等人^[13]改进了对传统的Chirp Scaling算法，实现了电磁涡旋波合成孔径雷达成像，Bu等人^[14]将涡旋电磁波与合成孔径雷达干涉(Interferometric Synthetic Aperture Radar, InSAR)测量技术相结合对目标进行了三维成像。2020年，袁航等人^[15]将涡旋电磁波应用于对人体步态的识别，建立了人体目标的涡旋电磁波雷达回波模型。2022年，学者对涡旋雷达高分辨技术进行研究^[16]，力求突破现有的成像分辨率限制，实现涡旋电磁波的高精度成像。

在前视雷达成像应用中，较大视场角下的前视三维成像算法的研究尚未成熟，电磁涡旋雷达成像的研究仍处于起步阶段。为了解决在较大视场角的场景精确成像的问题，本文采用分时独立发射的多模态涡旋电磁波扫描方式，从前视雷达成像场景与均匀圆阵的几何构型出发构建了涡旋回波信号模型；在原有后向投影(Back Projection, BP)算法的基础上添加了对较大视场角的多普勒网格与贝塞尔幅度补偿，并利用目标涡旋方位角与OAM模态的对偶关系，获取目标方位-俯仰信息。在得到的成像结果下定义了信号处理增益，并计算了信号处理增益随俯仰角变化的趋势，对于实际场景要求的俯仰角，信号处理增益的最大衰减不超过–1.8 dB，算法将分布在各个模态的能量利用起来，有较好的成像性能。最后对涡旋雷达的前视场景的距离-俯仰-方位三维成像进行了仿真与实测分析，算法在实测场景也有较好的表现。并对输出信噪比与信号处理增益进行分析。

2. 成像几何模型

电磁涡旋场是一种由多个激励源组合形成的场，可以通过如多点、线、面激励源等多种方式来生成。均匀圆阵(Uniform Circular Array, UCA)体制利用多通道相控方法实现不同波束模式的调控，系统具有较强的灵活性和可变性；它可同时激励多种模态的涡旋波，因此成为电磁涡旋雷达系统的理想方案之一。所示的前视涡旋雷达的成像模型中，电磁涡旋成像的方位角分辨力来源于多模态涡旋波的差异性空域相位调制，距离向分辨力则基于信号带宽。不失一般性的以目标区域为参考系，以平台的初始位置为坐标原点建立直角坐标系O-XYZ，平台沿X轴移动，移动速度为 ${v_\eta }$ ，成像区域在雷达移动方向的前侧方。

图 1 涡旋雷达前视成像几何模型

Figure 1. Geometry of vortex radar forward-looking imaging

下载: 全尺寸图片幻灯片

放大的细节，在UCA本地坐标系下的目标各参数定义如所示。在慢时间 $\eta$ 时刻，以平台当前位置( ${x_\eta }$ , 0, 0)为原点建立直角坐标系O'-XYZ则UCA所在平面为YO'Z平面， ${N}$ 个发射天线均匀地分布在圆心为O'，半径为 ${r_a}$ 的圆周上，接收天线位于为YO'Z平面的原点 ${{O}}'$ ，目标到接收天线的距离定义为目标的斜距 ${r_m}$ ；目标的俯仰角 ${\theta _m}$ 定义为斜距与X轴之间的夹角；目标方位角 ${\varphi _m}$ 定义为斜距在YO'Z平面上的投影与Y轴正方向的夹角。

图 2 涡旋雷达前视成像坐标系

Figure 2. The coordinate system of vortex radar forward-looking imaging

下载: 全尺寸图片幻灯片

3. 回波信号建模

本文的发射信号采用如所示的分时多模态方式，每个发射阵元的时域波形根据当前模态增加初相调制。其中，每一个模态的脉冲持续时间均为 ${T_{\mathrm{p}}}$ ，雷达在一个周期内顺次发射 ${{{N}}_\alpha }$ 个模态的涡旋波，总积累时长 ${{T}} = {{{N}}_\alpha }{{{K}}_n}{T_{\mathrm{p}}}$ 。

图 3 分时多模态发射模式示意图

Figure 3. Procedure of time division multiple modes

下载: 全尺寸图片幻灯片

分时多模态对系统的要求较低，能够很好地兼容传统的SAR雷达系统，与基于波形分集实现OAM解调的同时多模态的发射机制^[17]相比，它能够快速地进行大空域的扫描，在一个周期内获取更多的空域信息。由于各个模态的信号在时间上的独立性，无需OAM解调即可分离多模态的信号，加快了算法的处理速度，更适用成像范围大，少快拍实时成像的机载或者弹载雷达场景。但无论哪一种波形发射方式，其目的是获取不同模态维的信息，本文后续所提出的成像方法仍然适用。

均匀圆阵列的每一个阵元发射带宽为B、调频率为K，幅度相同的线性调频信号。每一个阵元的方位角 ${\phi _n} = {\text{2}}\pi {{\left( {n - 1} \right)} \mathord{\left/ {\vphantom {{\left( {n - 1} \right)} {\text{N}}}} \right. } {{N}}},n = 1,2, \cdots ,{{N}}$ ，N为阵元个数。为了在远场合成模态为 $\alpha$ 的涡旋波，需要对阵元施加不同的相移。第n个阵元的发射信号为

${S_n}\left( {\alpha ,t} \right) = p\left( t \right) \cdot \exp \left( {{\text{j}}\alpha {\phi _n}} \right),n = 1,2, \cdots ,{{N}}$

(1)

其中，t为快时间变量。 $p\left( t \right)$ 为线性调频波包络，具体表达式为

$p(t) = {\text{rect}}\left( {{\frac{t} {T_{\mathrm{p}}}}} \right) \cdot \exp \bigr( {{\text{j}}\pi {{K}} \cdot {t^2}} \bigr)$

(2)

根据图1、的前视成像几何模型与UCA阵元位置关系，在YO'Z平面上第n个阵元的矢量向量为 ${{\boldsymbol{r}}_n} = {r_a} \left( {{\hat {\boldsymbol{y}}}}\cos {\phi _n} + {{\hat {\boldsymbol{z}}}}\sin {\phi _n} \right)$ ，其中 ${{\hat {\boldsymbol{y}}}},{{\hat {\boldsymbol{z}}}}$ 为Y轴与Z轴的单位向量， ${r_a}$ 为UCA阵元半径，远场目标 ${P_m}\left( {{r_m},{\theta _m},{\varphi _m}} \right)$ 的场点矢径 ${{\boldsymbol{r}}_m}$ 的单位向量为 ${{{\hat {\boldsymbol{r}}}}_m} = {{\hat {\boldsymbol{y}}}}{ \sin}{\theta _m}{\text{cos}}{\varphi _m} + {{\hat {\boldsymbol{z}}}}{ }{\text{sin}}{\theta _m} {\text{sin}}{\varphi _m} + {{\hat {\boldsymbol{x}}}}{ }{\text{cos}}{\theta _m}$ ，则第n个发射阵元到目标的实际距离为 $\left| {{{\boldsymbol{r}}_m} - {{\boldsymbol{r}}_n}} \right|$ ，目标到接收阵元的距离为 $\left| {{{\boldsymbol{r}}_m}} \right| = {r_m}$ ，在此双程作用下，接收阵元处的脉冲回波信号为

$\begin{split} {S_{{\text{nr}}}}\left( {\alpha ,t} \right) = \;&\sum\limits_{n = 1}^{{N}} {\sigma _m} \cdot p\left( {t - {\tau _m}} \right)\cdot \exp \left( {{\text{j}}\alpha {\phi _n}} \right)\\ \;& \cdot \exp \left[ {{\text{j}}2\pi {f_{\mathrm{d}}}\left( {t - {\tau _m}} \right)} \right] \\ & \cdot \exp \left[ { - {\text{j}}k\left( {{r_m} + \left| {{{\boldsymbol{r}}_m} - {{\boldsymbol{r}}_n}} \right|} \right)} \right] \end{split}$

(3)

其中， ${\sigma _m}$ 为后向散射系数， ${\tau _m} = 2{{{r_m}} \mathord{\left/ {\vphantom {{{r_m}} {\text{c}}}} \right. } {\text{c}}}$ ，c为光速， $\exp \left[ { - {\text{j}}k\left( {{r_m} + \left| {{{\boldsymbol{r}}_m} - {{\boldsymbol{r}}_n}} \right|} \right)} \right]$ 为传播相位，k为信号的波数， $k = {{2\pi } \mathord{\left/ {\vphantom {{2\pi } \lambda }} \right. } \lambda }$ 为信号的波数， $\lambda$ 为信号波长， $f_{\mathrm{c}}$ 为信号载频， ${f_{\mathrm{d}}}$ 为多普勒频移，在远场条件下可用 ${r_m} + \left| {{{\boldsymbol{r}}_m} - {{\boldsymbol{r}}_n}} \right| \approx 2{r_m} - {{{\hat {\boldsymbol{r}}}}_m} \cdot {{\boldsymbol{r}}_n} = 2{r_m} - {r_a}\sin {\theta _m} \cdot\cos \left( {{\varphi _m} - {\phi _n}} \right)$ 对传播相位作近似，则式(3)可近似为

$\begin{split} {S_{{\text{nr}}}}\left( {\alpha ,t} \right) =\;& {\sigma _m} \cdot p\left( {t - {\tau _m}} \right) \cdot \exp \left[ {{\text{j2}}\pi {f_{\mathrm{d}}}\left( {t - {\tau _m}} \right)} \right]\\ & \cdot \sum\limits_{n = 1}^{{N}} {\left\{ {\exp \left( {{\text{j}}\alpha {\phi _n}} \right) \cdot \exp \left( { - {\text{j2}}k{r_m}} \right)} \right.} \\ & \left. { \cdot \exp \left[ {{\text{j}}k \cdot {r_a}{\text{sin}}{\theta _m}{\text{cos}}\left( {{\varphi _m} - {\phi _n}} \right)} \right]} \right\} \end{split}$

(4)

当阵元数量N足够多时，式(4)中的求和可近似使用积分替换，可改写为

$\begin{split} \;&{S_{{\text{nr}}}}\left( {\alpha ,t} \right) \approx {\sigma _m} \cdot p\left( {t - {\tau _m}} \right) \cdot \exp \left[ {{\text{j2}}\pi {f_{\mathrm{d}}}\left( {t - {\tau _m}} \right)} \right] \\ \;& \qquad\qquad\;\; \cdot \exp \left( { - {\text{j2}}k{r_m}} \right) \cdot \frac{{{N}}}{{{\text{2}}\pi }}\int_0^{{\text{2}}\pi } {\exp \left( {{\text{j}}\alpha \phi } \right)} \\ \;& \qquad\qquad\;\; \cdot \exp \left[ {{\text{j}}k \cdot {r_a}{\text{sin}}{\theta _m}{\text{cos}}({\varphi _m} - \phi )} \right]{\mathrm{d}}\phi \\ \;& \qquad\;\;\, \mathop {\text{ = }}\limits^{{\varphi _m} - \varphi = \phi } {\sigma _m} \cdot p\left( {t - {\tau _m}} \right) \\ \;& \qquad\qquad\;\;\cdot \exp \left[ {{\text{j2}}\pi {f_{\mathrm{d}}}\left( {t - {\tau _m}} \right)} \right] \cdot \exp \left( { - {\text{j2}}k{r_m}} \right) \\ \;& \qquad\qquad\;\;\cdot \frac{{{N}}}{{{\text{2}}\pi }}\exp \left( {{\text{j}}\alpha {\varphi _m}} \right)\int_0^{{\text{2}}\pi } \exp \left( { - {\text{j}}\alpha \varphi } \right)\\ \;& \qquad\qquad\;\;\cdot \exp \left[ {{\text{j}}k \cdot {r_a}{\text{sin}}{\theta _m}{\text{cos}}\varphi } \right] {\mathrm{d}}\varphi {\text{ }} \\ & \qquad\quad\;\;\, = {{N}}{{\text{j}}^\alpha }{\sigma _m} \cdot p\left( {t - {\tau _m}} \right) \cdot \exp \left[ {{\text{j2}}\pi {f_{\mathrm{d}}}\left( {t - {\tau _m}} \right)} \right]\\ & \qquad\qquad\;\;\cdot \exp \left( { - {\text{j2}}k{r_m}} \right) \cdot \exp \left( {{\text{j}}\alpha {\varphi _m}} \right)\\ & \qquad\qquad\;\;\cdot {J_\alpha }\left( {k \cdot {r_a}{\text{sin}}{\theta _m}} \right)\\[-1pt] \end{split}$

(5)

其中， ${J_\alpha }\left( \cdot \right)$ 为 $\alpha$ 阶的第1类贝塞尔函数，式(5)利用了贝塞尔函数的积分形式^[18]的变换：

$\begin{split} {J_\alpha }\left( {k{r_a}{\text{sin}}{\theta _m}} \right) =\;& \frac{{{{\text{j}}^\alpha }}}{{{\text{2}}\pi }} \cdot \int_0^{{\text{2}}\pi } \exp \left( { - {\text{j}}k{r_a}{\text{sin}}{\theta _m}{\text{cos}}\varphi } \right) \\ & \cdot \exp \left( { - {\text{j}}\alpha \varphi } \right){\mathrm{d}}\varphi \\ =\;&\frac{{{{\left( { - 1} \right)}^\alpha }{{\text{j}}^\alpha }}}{{{\text{2}}\pi }} \cdot \int_0^{{\text{2}}\pi } \exp \left( {{\text{j}}k{r_a}{\text{sin}}{\theta _m}{\text{cos}}\varphi } \right) \\ & \cdot \exp \left( { - {\text{j}}\alpha \varphi } \right){\mathrm{d}}\varphi \\[-1pt] \end{split}$

(6)

考虑到成像场景下雷达与目标的相对运动，多个散射目标的斜距 ${r_m}$ 与俯仰角 ${\theta _m}$ ， $m = 1,2, \cdots ,{{M}}$ 随慢时间 $\eta$ 变化，可得到M点的复杂目标在成像过程中的回波表达式：

$\begin{split} {S_r}\left( {t,\alpha ,\eta } \right) =\;& {{N}}{{\text{j}}^\alpha } \cdot \sum\limits_{m = 1}^{{M}} \left\{ {\sigma _m}{J_\alpha }\left[ {k{r_a} \cdot \sin {\theta _m}\left( \eta \right)} \right]\right.\\ & \cdot \exp \left( {{\text{j}}\alpha {\varphi _m}} \right) \cdot \exp \left[ {{\text{j2}}\pi {f_{\mathrm{d}}}\left( {t - {\tau _m}} \right)} \right] \\ & \cdot \exp \left[ { - {\text{j2}}k{r_m}\left( \eta \right)} \right] \\ & \cdot {\text{rect}}\left[ {\frac{{t - {\text{2}}{r_m}\left( \eta \right)/{\mathrm{c}}}}{{{T_{\mathrm{p}}}}}} \right]\\ & \left.\cdot \exp \left[ {{\text{j}}\pi {{K}}{{\left( {t - 2{r_m}\left( \eta \right)/{\text{c}}} \right)}^2}} \right] \right\} \end{split}$

(7)

4. 成像处理算法

4.1 基于后向投影-距离多普勒的目标三维成像

成像处理目的是从距离-俯仰-方位多维度耦合的回波相位中分离出目标信息。本文所提出的整体算法流程如图4所示，首先基于匹配滤波方法实现距离压缩；其次，根据后向投影算法划分距离网格和俯仰网格，并在此基础上添加多普勒网格。然后，将网格在慢时间上投影的同时进行相位与幅度补偿，获得匹配的目标俯仰信息；最后对模态维做傅里叶变换获得目标的方位信息，在多普勒维非相干积累，获取更多离网目标信息，提升目标信噪比。

图 4 成像算法处理过程

Figure 4. Flowchart of the proposed imaging algorithm

下载: 全尺寸图片幻灯片

对式(7)的信号进行脉冲压缩后得到的回波表达式为

$\begin{split} {S_{{\text{rcomp}}}}\left( {t,\alpha ,\eta } \right) =\;& {{N}}{{\text{j}}^\alpha } \cdot \sum\limits_{m = 1}^{{M}} \left\{ {\sigma _m}{J_\alpha }\left[ {k{r_a} \cdot \sin {\theta _m}\left( \eta \right)} \right]\right.\\ & \cdot \exp \left( {{\text{j}}\alpha {\varphi _m}} \right) \cdot \exp \left[ { - {\text{j2}}k{r_m}\left( \eta \right)} \right] \\ & \left. \cdot {p_r}\left( \cdot \right) \right\} \\[-1pt] \end{split}$

(8)

其中， ${p_r}\left( \cdot \right)$ 为匹配滤波处理后的距离包络。

${p_r}\left( \cdot \right) = \left| {{K}} \right|{T_{\mathrm{p}}} \cdot {\text{sinc}}\left\{ \left| {{K}} \right|{T_{\mathrm{p}}} \cdot \left( t - 2{r_m}\left( \eta \right) - {{f_{\mathrm{d}}}} \mathord{\left/ {\vphantom {{{f_d}} {\text{K}}}} \right. } {{K}} \right) \right\}$

对于每一组模态-慢时间采样数据，反射波信号代表了该模态主副瓣照射范围内目标散射特性的总和，其中包含了目标距离单元、传播相位、当前模态的涡旋相位、雷达与目标相对运动与多普勒频移带来距离徙动相位。

BP算法首先将场景网格化，在慢时间采样点上，根据每个网格点的斜距，在回波信号中选取对应距离单元，计算网格点对应的相位因子进行相位补偿，最后将相位补偿后的信号叠加为网格点上的成像图。因此，BP算法本质上是针对所有网格点在时域上设计了相应的匹配滤波器，可有效解决回波信号相位中空域多维度难以解耦的问题，但是，在较大视场角的情况下，由于BP网络的划分限制，低密度的网络会大量丢失离网目标的信息，高密度的网络会大大增加算法的运算量，如何在不添加网络数量的情况获取更多目标信息，成为少快拍大空域成像急需解决的问题。

本文将多普勒偏移与BP算法相结合，在BP算法中根据已知的相对速度信息添加多普勒网格，补偿多普勒频率变化在距离与俯仰角网格变换时带来的距离偏移；并考虑到少快拍成像场景的算法运算量问题，对BP-RD网络的投影计算过程进行线性替代。无论图3中的分时多模态发射模式还是基于波形分集的同时多模态体制，均可基于BP-RD算法对于多维耦合的相位信息进行精确补偿后实现目标点聚焦。接下来对BP-RD成像算法的实现流程进行详细介绍。

(1) 成像场景网格化

当平台位于起始点O时，将成像场景划分为三维 $\left( {{R_g},{\theta _g},{\varphi _g}} \right)$ 网格，如所示。距离网格沿雷达视线方向延伸；以雷达视线与Y轴夹角增大方向划分方位角网格 ${\varphi _g}$ ，最大可划分范围为– $\pi$ ～ $\pi$ ；以雷达视线与X轴夹角增加方向划分俯仰角网格 ${\theta _g}$ ，最大可划分范围为0～ $\pi$ /2。最后在已经划分好的距离维与俯仰维上添加多普勒网格 ${D_g}$ ，具体计算方式见式(9)。在实际应用中可以根据前视雷达参数以及具体成像需求缩小网格划分范围，加快运算速度，降低运算量。

图 5 三维成像网络

Figure 5. Gridding the imaging scenario

下载: 全尺寸图片幻灯片

(2) 俯仰角变换与计算距离多普勒延迟

根据图6所示的雷达运动轨迹与场景网格之间的几何关系，在当前航迹采样点，将起始点网络变换迭代到真实距离和俯仰角网格上。网络的变换表达式为

图 6 网络变换关系示意图

Figure 6. The grid projection of range and elevation

下载: 全尺寸图片幻灯片

$\left\{ \begin{gathered} {R_\eta }\left( {{R_g},{\theta _g}} \right) = \sqrt {R_g^2 - 2{R_g}{x_\eta }\cos {\theta _g} + x_\eta ^2} \\ {\theta _\eta }\left( {{R_g},{\theta _g}} \right) = \arccos \left( {{{{R_g}\cos {\theta _g}} \mathord{\left/ {\vphantom {{{R_g}\cos {\theta _g}} {{R_\eta }}}} \right. } {{R_\eta }}}} \right) \\ {D_g}\left( {{R_g},{\theta _g}} \right) = {{{v_\eta }{\text{c}} \cdot \cos \left[ {{\theta _\eta }\left( {{R_g},{\theta _g}} \right)} \right]} \mathord{\left/ {\vphantom {{{v_\eta }{\text{c}} \cdot \cos \left[ {{\theta _\eta }\left( {{R_g},{\theta _g}} \right)} \right]} {\lambda {\text{K}}}}} \right. } ({\lambda {{K}}}}) \end{gathered} \right.$

(9)

其中， ${v_\eta }$ 为平台速度， ${x_\eta } = \displaystyle\int {{v_\eta }{\mathrm{d}}\eta }$ 为整个航迹位置采样点的位置X轴坐标。在前视雷达少快拍的成像条件下， ${x_\eta } \ll {R_g}$ ，对 ${R_g}$ 和 ${\theta _g}$ 在 ${{{x_\eta }} \mathord{\left/ {\vphantom {{{x_\eta }} {{R_g}}}} \right. } {{R_g}}} \to 0$ 处进行一阶泰勒展开：

$\left\{ \begin{aligned} & {R_\eta }\left( {{R_g},{\theta _g}} \right) = {R_g} \cdot \sqrt {1 - 2 \cdot \frac{{{x_\eta }}}{{{R_g}}}\cos {\theta _g} + {{\left( {\frac{{{x_\eta }}}{{{R_g}}}} \right)}^2}} = {R_g} - \cos {\theta _g} \cdot {x_\eta } \\ & {\theta _\eta }\left( {{R_g},{\theta _g}} \right) = \arccos \left( {\sqrt {\frac{{{{\cos }^2}{\theta _g}}}{{\sqrt {1 - 2 \cdot \dfrac{{{x_\eta }}}{{{R_g}}}\cos {\theta _g} + {{\left( {\dfrac{{{x_\eta }}}{{{R_g}}}} \right)}^2}} }}} } \right) = {\theta _g} - \frac{{{{\cos }^2}{\theta _g}}}{{2\sin {\theta _g}}} \cdot \frac{{{x_\eta }}}{{{R_g}}} \end{aligned} \right.$

(10)

(3) 贝塞尔幅度调制与传播相位补偿

由式(8)可知，贝塞尔函数将目标的俯仰维信息与不同模态的涡旋波束方位图耦合，导致了不同俯仰角的信息在模态维信号幅度谱上受贝塞尔函数的调制；影响了目标方位角与OAM模态的对称关系，使得信号在方位向成像时的脉冲旁瓣被抬高，甚至产生栅瓣干扰。对此，需要在BP-RD算法中对贝塞尔函数进行补偿，抑制栅瓣，尽可能地消除贝塞尔函数对后续累积的影响。本文采用的正负整数模态的发射模式下，贝塞尔函数在模态维上呈现如式(11)的对称性质^[9]：

${J}_{-\alpha }(\theta )=\left\{\begin{aligned} & -{J}_{\alpha }\left(\theta \right),\text{ }\alpha 为奇数\\ & {J}_{\alpha }\left(\theta \right),\text{ }\alpha 为偶数 \end{aligned} \right.$

(11)

因此，在对奇数阶模态的信号进行累加时会出现幅值相消的现象。由于BP算法类比于匹配滤波器的特性，当补偿因子与输入信号为复共轭时，输出信噪比达到最大。采用共轭式(11)不仅可以消除贝塞尔函数在模态维上幅值相消的现象，同时取得最大的信噪比。

${H_\alpha } = {\left( { - j} \right)^\alpha } \cdot {J_\alpha }\left( {k{r_a}{\text{sin}}{\theta _\eta }} \right) \cdot \exp \left[ {{\mathrm{j}}4\pi {f_{\mathrm{c}}}{R_\eta }\left( {{R_g},{\theta _g}} \right)/{\mathrm{c}}} \right]$

(12)

(4) 模态维傅里叶变换与多普勒非相干叠加

由于涡旋目标方位角 ${\varphi _m}$ 和OAM模态数 $\alpha$ 之间的对偶关系，经典谱估计方法即可得到目标的方位向轮廓。将每个网格中投影的回波与补偿因子 ${H_\alpha }$ 相乘，消除距离和相位偏移的影响后，在模态维傅里叶变换，在多普勒维进行非相干叠加，得到式(13)中对目标区域的成像结果。对于没有目标散射点分布的网格点，叠加后能量值较小。在对具有目标散射点分布的网格上的回波叠加时，可以累积能量，产生图像峰值。

$\begin{split} \delta \left( {{R_g},{\theta _g},{\varphi _g}} \right) = \;& \sum\limits_f \left| {{\mathrm{fft}}_\eta }\left\{ {{\mathrm{fft}}_\alpha }\left\{ {S_{{\text{rcomp}}}}\bigr[ {2\left( {{R_\eta } + {D_\eta }} \right)}/ {\mathrm{c}}, \right.\right.\right. \\ & \left.\left.\left.\alpha ,\eta \bigr] \cdot {H_\alpha } \right\} \right\} \right| ^2\\[-1pt] \end{split}$

(13)

其中，f为多普勒频率，根据帕塞瓦尔定理，得到最终的信号表达式：

$\begin{split} \delta \left( {{R_g},{\theta _g},{\varphi _g}} \right) =\;& \sum\limits_\eta \left| {{\mathrm{fft}}_\alpha }\left\{ {S_{{\text{rcomp}}}}\bigr[ {2\left( {{R_\eta } + {D_\eta }} \right)}/ {\mathrm{c}},\right.\right. \\ & \left.\left. \alpha ,\eta \bigr] \cdot {H_\alpha } \right\} \right| ^2\\[-1pt] \end{split}$

(14)

4.2 成像性能分析

在对成像性能分析之前，有必要先对阵列合成效果进行分析。中的仿真参数设置为：UCA半径12 $\lambda$ ，模态范围为[–34, 34]，目标俯仰角分别设为0.10 $\pi$ 与0.17 $\pi$ 。

图 7 阵元合成效果图

Figure 7. Rendering of array synthesis

下载: 全尺寸图片幻灯片

由可见，在低仰角、低模态的情况下，少量阵元也能有很好的拟合效果，但是随着俯仰角与模态数的增加，所需要的阵元个数也增加；在前视雷达的应用场景下，64阵元能得到不失真的最大模态范围为[–31, 31]，对应的俯仰角为0.15 $\pi$ ，满足前视空域的要求。本文后续基于64阵元合成涡旋波对成像性能进行分析。

$64$ 阵元合成的涡旋波如所示，仿真参数为阵元半径12 $\lambda$ ，模态范围[–34, 34]，如所示随着俯仰角的增加，能量越发分散于各个模态之中，俯仰角在0～0.15 $\pi$ 增大时，系统的峰值响应逐步减小，0.15 $\pi$ 达到最低–13 dB。在0.15 $\pi$ 后由于涡旋波的失真，高模态破坏了贝塞尔函数的调制关系，峰值响应位置偏移，峰值响应值增大。以0.16 $\pi$ 为例，在、中当俯仰角为0.16 $\pi$ 时贝塞尔函数的峰值响应点应位于±34模态，但阵元合成信号在模态上的峰值响应位于±31模态，且峰值响应值提高了4 dB。因此，在高模态存在失真，且高俯仰角峰值响应最大变化量为–13 dB的幅度调制下，有必要验证算法能否得到较高的信号处理增益，获得好的成像性能。表1列举了目标在不同俯仰位置下，信号处理增益的变化，图9以俯仰角为0时的信号处理增益为基准对信号处理增益进行归一化。为尽量贴近真实环境，本文添加接收机噪声，并计算多模态的信噪比作为输入信噪比。

图 8 贝塞尔函数幅度调制影响

Figure 8. Amplitude modulation of Bessel functions

下载: 全尺寸图片幻灯片

${\text{SN}}{{\text{R}}_{{\text{in}}}} = 10\lg \left( {\frac{{{P_r}}}{{{{{N}}_\alpha } \cdot {P_{{N_0}}}}}} \right)$

(15)

其中， ${P_r}$ 为多模态的无噪声的回波信号总功率， ${P_{{N_0}}}$ 为接收机噪声， ${{{N}}_\alpha }$ 为发射的涡旋波模态个数。

设在无目标的环境下的噪声信号的成像图幅值为 ${\delta _{{\text{noise}}}}$ ，有目标情况下输入雷达的成像图幅值为 ${\delta _{{\text{tar}}}}$ 。取 ${\delta _{{\text{tar}}}}$ 在3 dB主瓣宽度上的信号为 ${\delta _{{\text{3 dB}}}}$ ，该区域可被认为是目标的多模态成像的响应，则输出信噪比可以被定义为

${\text{SN}}{{\text{R}}_{{\text{out}}}} = 10\lg \left( {\frac{{\displaystyle\sum {\delta _{{\text{3 dB}}}}}}{{\displaystyle\sum {\delta _{{\text{noise}}}}}}} \right)$

(16)

在此基础上，信号处理增益G是指在经过信号处理后，使信号增强的同时，抑制输入噪声能力的大小，定义为

$G{\text{ = SN}}{{\text{R}}_{{\text{out}}}}-{\text{SN}}{{\text{R}}_{{\text{in}}}}$

(17)

表 1 不同俯仰位置下信号处理增益变化

Table 1. Signal processing gain of different elevation

俯仰角θ (rad)	有效模态	输入信噪比(dB)	输出信噪比(dB)	归一化信号处理增益(dB)
0	[0]	12.4140	52.3270	39.9130
0.01 $\pi$	[–2, 2]	12.4140	52.3231	39.9091
0.02 $\pi$	[–4, 4]	12.4140	52.3115	39.8975
0.03 $\pi$	[–6, 6]	12.4140	52.2922	39.8782
0.04 $\pi$	[–8, 8]	12.4140	52.2653	39.8513
0.05 $\pi$	[–10, 10]	12.4140	52.2307	39.8167
0.06 $\pi$	[–12, 12]	12.4140	52.1887	39.7747
0.07 $\pi$	[–14, 14]	12.4140	52.1393	39.7253
0.08 $\pi$	[–16, 16]	12.4140	52.0826	39.6686
0.09 $\pi$	[–18, 18]	12.4140	52.0188	39.6048
0.10 $\pi$	[–20, 20]	12.4140	51.9482	39.5342
0.11 $\pi$	[–23, 23]	12.4133	51.8693	51.4341
0.12 $\pi$	[–25, 25]	12.4010	51.7580	39.3570
0.13 $\pi$	[–27, 27]	12.2969	51.4341	39.1372
0.14 $\pi$	[–28, 28]	11.9384	50.5159	38.5775
0.15 $\pi$	[–30, 30]	11.7014	49.8458	38.1444
0.16 $\pi$	[–32, 32]	12.2512	51.0137	38.7625
0.17 $\pi$	[–34, 34]	12.2907	50.9907	38.7001

下载: 导出CSV

| 显示表格

图 9 归一化信号处理增益变化图(以俯仰角θ=0为参考点进行归一化)

Figure 9. Signal processing gain curves with different elevation (based on zero angle, normalized signal processing gain)

下载: 全尺寸图片幻灯片

从与可以看出，在多模态覆盖的目标区域内，低俯仰角处有效模态数较少，但是各模态对应的幅度方向图增益值高；高俯仰角的情况则与之相反；当俯仰角在[0, 0.15 $\pi$ ]变化时，进行累加处理后，归一化的等效增益(模态增益+累加处理增益)随着俯仰角的增大呈下降趋势，其最大损失为–1.77 dB。俯仰角为0.16 $\pi$ 与0.17 $\pi$ 时出现了输入信噪比与输出信噪比上升的现象。在中，俯仰角为0.16 $\pi$ 与0.17 $\pi$ 时，零模态响应不变，高模态的峰值响应变大，导致式(15)中多模态无噪声的回波信号功率 ${P_r}$ 增大，累加后的 ${\delta _{{\text{3 dB}}}}$ 功率随之增大，而噪声信号与其成像图 ${\delta _{{\text{noise}}}}$ 功率变化较小，导致了输入、输出信噪比的增大。在Ka波段，UCA半径为12 $\lambda$ 的情况下，俯仰角27°处的归一化增益不低于–1.8 dB，算法能将分布在各个模态的能量利用起来，系统在所需俯仰角范围上具有较高的稳定性，有较好的成像性能。

4.3 对比分析

为了定量分析成像性能，将本文提出的成像方法与先前学者提出的成像方法进行对比分析。单个散射点(300.5 m, 0.12 $\pi$ rad, 0.19 $\pi$ rad) 的三维剖面图如图10所示，图10(a)为BP-FFT与BP-FFT(H_p) 方法结果对比图，图10(b)为BP-FFT与 BP-RD-FFT方法结果对比图，图10(c)为FFT与Burg方法结果对比图。特别的，为区分FFT与Burg两种方法，此小节中BP-RD-FFT代指为4.1节提出的BP-RD成像方法。

图 10 三维点目标成像结果对比图

Figure 10. Three-dimensional profiles of the target imaging results

下载: 全尺寸图片幻灯片

图 13 目标2不同维度的成像结果(

$\theta =0.15\mathrm{\pi }$ )

Figure 13. Point target 2 imaging results in different dimensions (

$\theta =0.15\mathrm{\pi }$ )

下载: 全尺寸图片幻灯片

首先考虑未添加多普勒网格的情况， BP-FFT方法最终的成像图为 $\delta \left( {{R_g},{\theta _g},{\varphi _g}} \right) = \displaystyle\sum\nolimits_\eta {{\mathrm{fft}}_\alpha } \cdot\left\{ {{S_{{\text{rcomp}}}}\left[ {{{2{R_\eta }} \mathord{\left/ {\vphantom {{2{R_\eta }} {{\mathrm{c}},\alpha ,\eta }}} \right. } {{\mathrm{c}},\alpha ,\eta }}} \right] \cdot {H_\alpha }} \right\}$ ，BP-FFT(H_p)方法参考了文献[19]提出的一种相位补偿方法：

${H_{\mathrm{p}}} \;= \left\{ \begin{gathered} - {\left( { - {\text{j}}} \right)^\alpha },{J_\alpha }\left( {k{r_a}{\text{sin}}{\theta _\eta }} \right) < 0 \\ {\left( { - {\text{j}}} \right)^\alpha },{J_\alpha }\left( {k{r_a}{\text{sin}}{\theta _\eta }} \right) > 0 \\ \end{gathered} \right.$

该方法考虑了贝塞尔函数的正负号带来的影响，BP-FFT方法对俯仰维的副瓣电平改善幅度较小，说明贝塞尔函数幅度补偿对成像性能的提升没有帮助。在添加多普勒网格后，图10(b)中BP-RD-FFT方法相比于BP-FFT方法在距离以及俯仰维上缩窄了主瓣宽度，减低了副瓣电平，说明多普勒网格的添加能够较好地提升成像性能。同时，可以采用超分辨算法进一步提升成像性能。相比于传统的谱分析方法，基于AR模型的Burg方法能够降低副瓣电平并得到更高的分辨率^[20]，图10(c)中BP-Burg与BP-RD-Burg分别为改进后的BP-FFT与 BP-RD-FFT方法，可以观察到Burg方法在俯仰维与方位维上较大地改善了成像效果，其根本原因在于方位维的分辨率取决于模态个数，Burg通过外推实现了方位维的高分辨处理，但同时超分辨方法会带来额外的计算量，在实际运用中应该综合考虑成像性能与时效性来选取不同的方法。

在实际应用中，无论机载平台还是弹载平台，成像算法都需要适应高速平台与目标相对运动的场景，除了成像性能上的提升，本文所提出算法可以有效解决速度估计不准时，无法正确聚焦成像的问题，在中心速度200 m/s，速度偏差绝对值≤25 m/s的情况下，对上述5种方法在不同的估计误差下进行仿真，得到了聚焦偏差随速度估计误差的变化结果，如图11(a)、图11(b)所示。根据仿真结果，未添加多普勒网格的方法在较高的估计误差下聚焦结果较差，俯仰维的最大偏差接近20°，方位维的最大偏差接近90°。添加了多普勒网格的BP-RD-FFT与BP-RD-Burg方法在俯仰维与方位维的聚焦偏差远远小于其他方法，俯仰维最大偏差值小于1°，在方位维也大大改善了速度估计误差对成像的影响，验证了所提算法相比其他算法的性能优势。

图 11 不同速度偏差-聚焦成像偏差曲线

Figure 11. Imaging bias with different velocity bias

下载: 全尺寸图片幻灯片

5. 实验与分析

5.1 仿真实验

通过多模态连续等幅扫描波束、脉冲压缩、BP-RD成像处理，对目标进行距离-方位-俯仰三维成像仿真，仿真参数设置如表2所示。

表 2 仿真参数

Table 2. Simulation parameters

参数	数值
目标1的 $R - \theta - \varphi$ 坐标(m, rad, rad)	(300, 0.10 $\pi$ , 0.055 $\pi$ )
目标2的 $R - \theta - \varphi$ 坐标(m, rad, rad)	(300, 0.15 $\pi$ , 0.055 $\pi$ )
雷达UCA阵元数量N (个)	64
UCA半径 ${r_a}$ (m)	0.09
信号载频 ${f_{\mathrm{c}}}$ (GHz)	35
信号脉冲周期 ${T_{\mathrm{p}}}$ ( $\text{μ}\text{s}$ )	0.54
带宽B (MHz)	300
OAM范围	[–30, 30]

下载: 导出CSV

| 显示表格

在如所示的参数设置下，3个维度均有良好的成像分辨率。与中能清晰地观察到目标1与目标2对焦到正确位置的成像图峰值，算法有着很好的聚焦效果。并在此基础上对多个点目标进行成像，设置俯仰角分别为[0 $\pi$ , 0.04 $\pi$ , 0.08 $\pi$ , 0.12 $\pi$ , 0.15 $\pi$ ]的5个目标一同成像，算法对多目标的处理结果如图14所示，在方位-俯仰剖面图中，受到多目标的旁瓣影响，随着俯仰角的增大，个别目标的峰值响应增加，但整体上仍呈衰减趋势，且衰减量小于–1.5 dB，验证了信号处理增益的变化。对成像结果平滑处理后提取峰值位置即可得到目标的三维信息。

图 12 目标1不同维度的成像结果(

$\theta =0.1\mathrm{\pi }$ )

Figure 12. Point target 1 imaging results in different dimensions (

$\theta =0.1\mathrm{\pi }$ )

下载: 全尺寸图片幻灯片

图 14 多目标不同维度的成像结果

Figure 14. Multi-object imaging results

下载: 全尺寸图片幻灯片

5.2 实测数据分析

在微波暗室中模拟雷达的成像场景(图15)，飞机模型位于微波暗室的中央，放置在白色泡沐支架上，模型呈水平姿态，机翼部分稍有倾斜。涡旋波雷达采用UCA体制，具有16个发射阵元，单接收阵元位于均匀圆阵中心，对准了飞机模型的机身部分，模型整体位于雷达的多模态波束范围之内；理论上，在测试体制下的最大不失真俯仰角为10°，此时机翼部分位于视场边缘。对飞机的回波数据进行了分析，具体的环境参数如表3所示。

图 15 飞机目标实验场景照片

Figure 15. The scene of aircraft target experiment

下载: 全尺寸图片幻灯片

表 3 实测参数

Table 3. Experimental parameters

参数	数值
飞机模型中心位置(m)	4.5
飞机模型在XYZ上的跨度(m)	(1.5, 0.08, 1.15)
阵元数量N (个)	16
UCA半径 ${r_a}$ (m)	0.0615
信号载频 ${f_{\mathrm{c}}}$ (GHz)	35.025
信号脉冲周期 ${T_{\mathrm{p}}}$ ( $\text{μ}\text{s}$ )	0.54
带宽B (MHz)	300
OAM范围	[–7, 7]

下载: 导出CSV

| 显示表格

给出了一个周期内的不同模态值的信号脉压结果，模态值 $\alpha$ =0时发射阵元的相位调制量为零，此时发射的信号为线性调频波，其脉压后回波信号峰值的时延量对应着目标的距离向信息，与飞机摆放位置相吻合；贝塞尔函数幅度调制导致了不同模态的信号在距离向上的峰值幅度不同；飞机在距离向上的跨度决定了不同模态高于背景杂波的主瓣范围。

图 16 实测数据在不同模态下的脉压结果

Figure 16. Pulse pressure results of measured data with different modes

下载: 全尺寸图片幻灯片

图17、图18为最终的成像结果。实际测量中，受到模型大小与发射阵元数量的限制，在模型跨越距离单元较多的X轴和Z轴上，整体有较好的成像表现，在跨度较小的Y轴上出现了旁瓣增大，成像结果模糊的现象，导致了机身机尾等RCS较小的地方，成像效果较差，飞机头部以及机翼等RCS较强的部分在成像图中呈现较高的主瓣，有较好的成像效果。

图 17 飞机目标的三维成像图

Figure 17. Three-dimensional image of the aircraft target

下载: 全尺寸图片幻灯片

图 18 飞机目标三维成像的二维切面图

Figure 18. Aircraft target imaging results in different dimensions

下载: 全尺寸图片幻灯片

6. 结语

本文将涡旋电磁波与前视雷达成像相结合，建立了基于均匀圆阵多发单收体制的电磁涡旋前视雷达成像模型，提出了分时多模态扫描的空域成像体制，添加了多普勒网格并在幅度与相位补偿方面改进了BP成像算法，实现了对目标三维位置的准确的匹配，并通过仿真和实测验证了算法的成像性能。所提方法适用于分时多模态扫描、同时多模态收发等不同的电磁涡旋雷达体制。基于点目标成像结果，验证了在多模态涡旋波覆盖的较大视场范围内，目标回波的归一化等效增益在低俯仰角与高俯仰角处相当，在给出的示例中，视场角覆盖范围为±27°时，最大俯仰角处的等效增益相比0°不低于–1.8 dB。所提算法在飞机目标成像上得到了验证，成像结果可精确重构复杂目标的三维结构。在后续研究中，将根据前视雷达的具体应用场景，利用涡旋电磁波引入的多模态特性，通过分数阶模态扫描方式，从而进一步消除贝塞尔函数对成像性能的影响。

图 1 频率捷变雷达模型

Figure 1. Frequency agile radar model

下载: 全尺寸图片幻灯片

图 2 噪声瞄准干扰仿真图

Figure 2. Simulation diagram of noise spot jamming

下载: 全尺寸图片幻灯片

图 3 距离假目标欺骗干扰仿真图

Figure 3. Simulation diagram of distance false-target deception jamming

下载: 全尺寸图片幻灯片

图 4 密集假目标转发干扰仿真图

Figure 4. Simulation diagram of dense false-target repeater jamming

下载: 全尺寸图片幻灯片

图 5 3种干扰策略顺序

Figure 5. Order of three jamming strategies

下载: 全尺寸图片幻灯片

图 6 FA雷达与干扰机

Figure 6. FA radar and target jammer

下载: 全尺寸图片幻灯片

图 7 噪声瞄准干扰频域图

Figure 7. Frequency domain of noise spot jamming

下载: 全尺寸图片幻灯片

图 8 距离假目标欺骗干扰时域图

Figure 8. Time domain of distance false-target deception jamming

下载: 全尺寸图片幻灯片

图 9 密集假目标转发干扰时域图

Figure 9. Time domain of dense false-target repeater jamming

下载: 全尺寸图片幻灯片

图 10 基于复数域深度强化学习的多干扰场景雷达抗干扰网络

Figure 10. Deep RL based radar anti-jamming network under multi-jamming scenes in complex domain

下载: 全尺寸图片幻灯片

图 11 复数域特征提取网络

Figure 11. Complex domain feature extraction network

下载: 全尺寸图片幻灯片

图 12 深度确定性策略梯度网络

Figure 12. Deep deterministic policy gradient network

下载: 全尺寸图片幻灯片

图 13 态势预测过程损失值

Figure 13. Loss value of situation awareness process

下载: 全尺寸图片幻灯片

图 14 态势预测过程准确率

Figure 14. Accuracy value of situation awareness process

下载: 全尺寸图片幻灯片

图 15 3种干扰类型下不同强化学习算法的决策性能

Figure 15. Decision performance of different RL algorithms under three types of interference

下载: 全尺寸图片幻灯片

图 16 DRL-ANCD网络对于3种干扰类型的抗干扰行为决策

Figure 16. Anti-jamming decisions of DRL-ANCD networks for three interference

下载: 全尺寸图片幻灯片

图 17 3种干扰策略下不同强化学习算法的决策性能

Figure 17. Decision performance of different RL algorithms under three interference strategies

下载: 全尺寸图片幻灯片

图 18 干扰策略Ⅰ下DRL-ANCD网络的抗干扰行为

Figure 18. Anti-jamming behaviors of DRL-ANCD networks under interference strategy I

下载: 全尺寸图片幻灯片

图 19 干扰策略Ⅱ下DRL-ANCD网络的抗干扰行为

Figure 19. Anti-jamming behaviors of DRL-ANCD networks under interference strategy Ⅱ

下载: 全尺寸图片幻灯片

图 20 干扰策略Ⅲ下DRL-ANCD网络的抗干扰行为

Figure 20. Anti-jamming behaviors of DRL-ANCD networks under interference strategy Ⅲ

下载: 全尺寸图片幻灯片

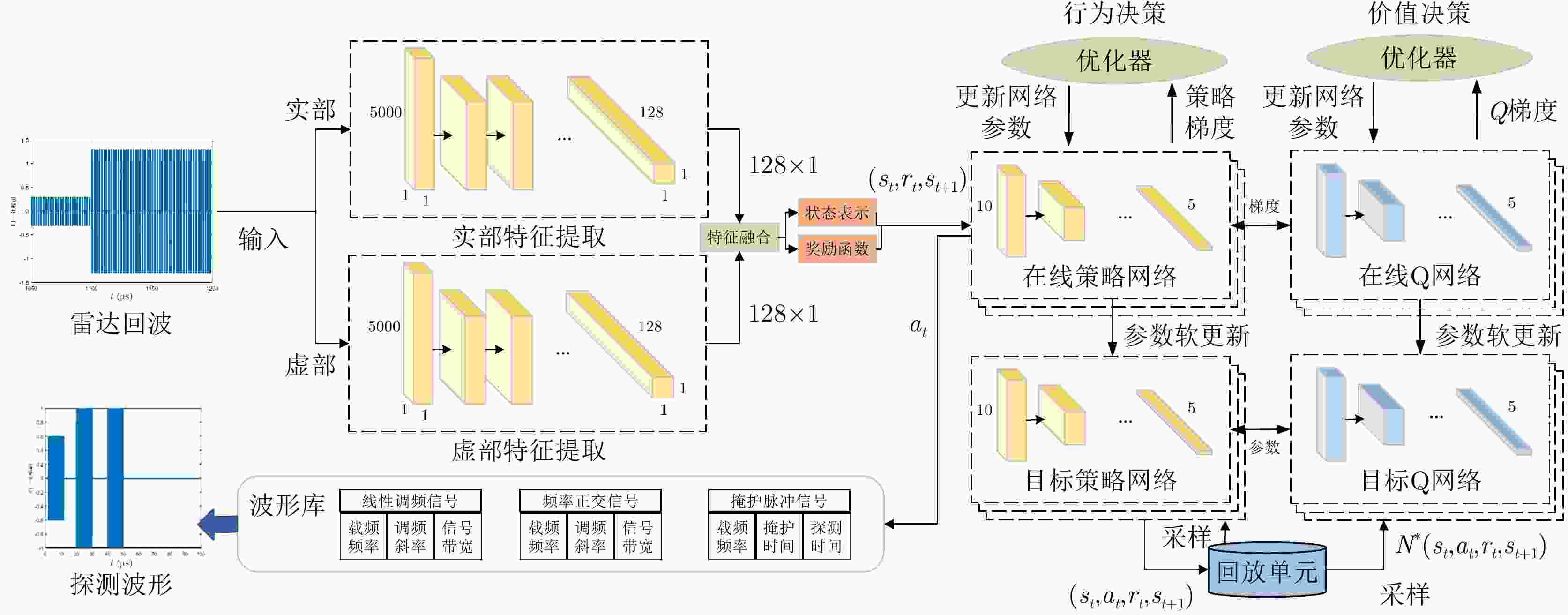
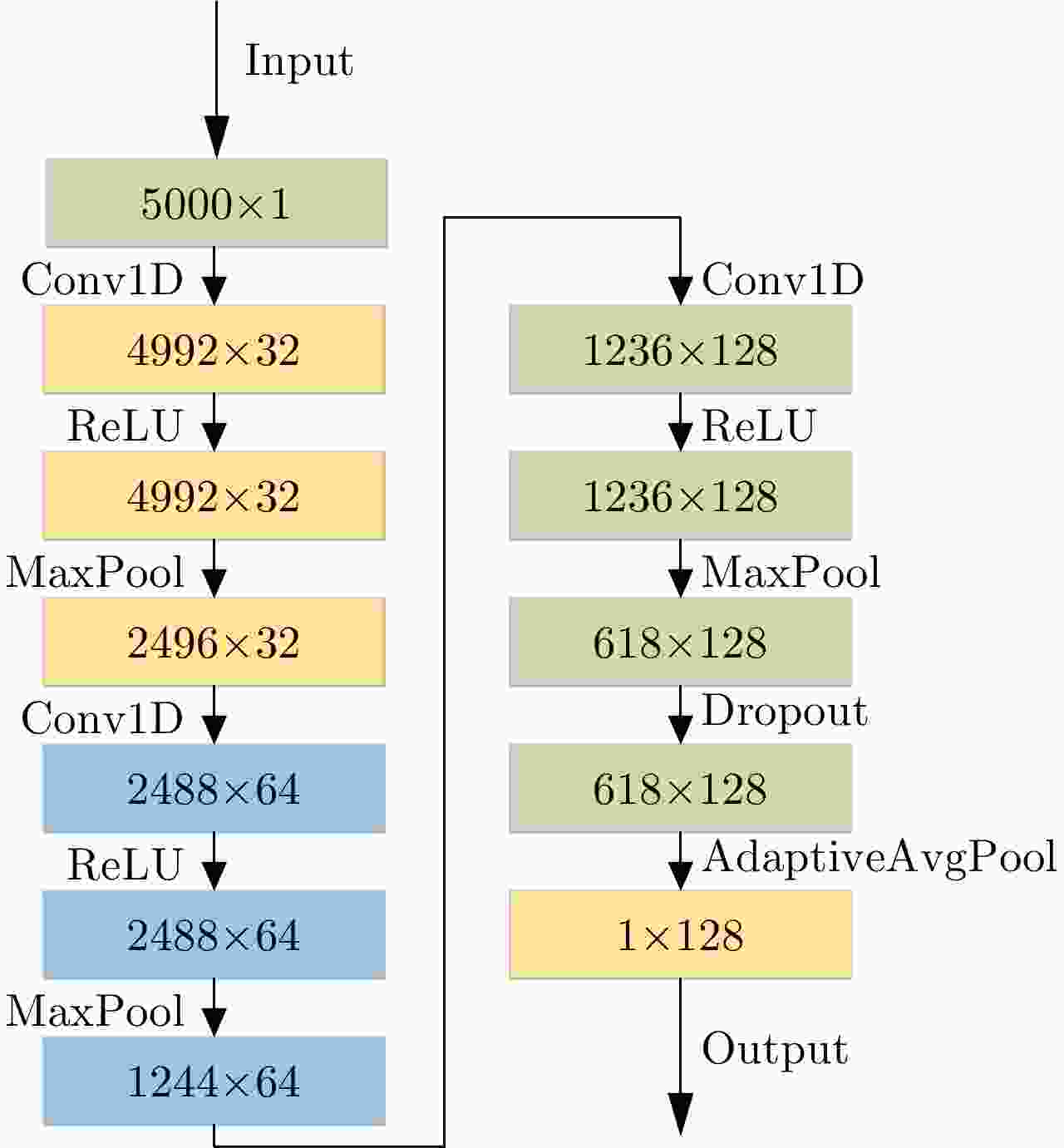
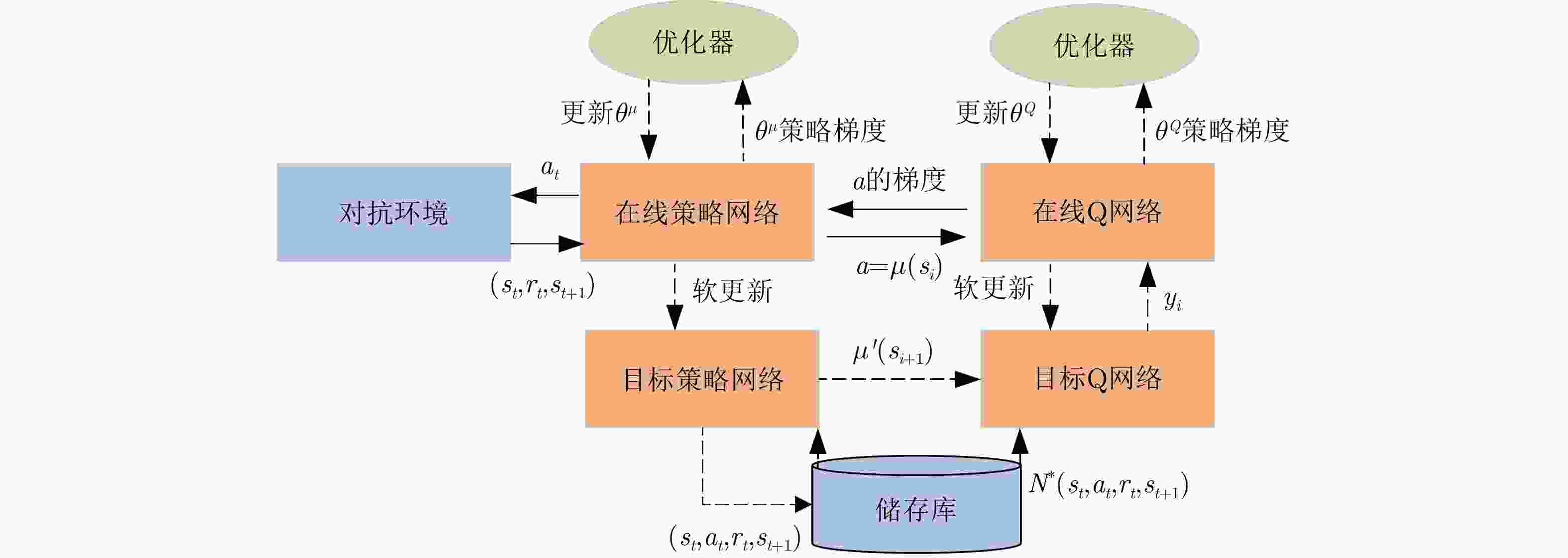
1 深度确定性策略梯度算法

1. Deep deterministic policy gradient algorithm

1. 使用权重 ${\theta ^Q}$ 和 ${\theta ^\mu }$ 随机初始化Q网络参数 $Q\left( {s,a\mid {\theta ^Q}} \right)$ 和策略　网络参数 $\mu \left( {s\mid {\theta ^\mu }} \right)$
2. 使用初始化目标网络
3. 使用权重 ${\theta ^{Q'}} \leftarrow {\theta ^Q}$ , ${\theta ^{\mu '}} \leftarrow {\theta ^\mu }$ 初始化目标网络 $Q'$ 和 $\mu '$
4. 初始化经验池R
5. for episode=1, 2, ···, ${{M}}$ ，执行：
6. 　为行动探索初始化一个随机过程 ${{N}}$
7. 　获得一个初始化观察状态 ${s_1}$
8. 　for ${{t}} = 1,2,\cdots,T$ ，执行：
9. 　　根据当前策略与探索噪声选择行动 ${a_t}$
10. 　执行动作 ${a_t}$ ,获得奖励 ${r_t}$ 与新的状态 ${s_{t + 1}}$
11. 　将样本 $\left( {{s_t},{a_t},{r_t},{s_{t + 1}}} \right)$ 存储至经验池R
12. 　从R中随机采样出N个样本 $\left( {{s_i},{a_i},{r_i},{s_{i + 1}}} \right)$
13. 　设置 ${y_i} = {r_i} + \gamma Q'\left( {{s_{i + 1}},\mu '\left( {{s_{i + 1}}\mid {\theta ^{\mu '}}} \right)\mid {\theta ^{Q'}}} \right)$
14. 　使用损失函数L更新Q网络参数
15. 　使用采样样本的策略梯度更新行为策略
16. 　更新目标网络参数：
${\theta }^{{Q}^{\prime }}\leftarrow \tau {\theta }^{Q}+\left(1-\tau \right){\theta }^{{Q}^{\prime }}$
${\theta ^{\mu '}} \leftarrow \tau {\theta ^\mu } + \left( {1 - \tau } \right){\theta ^{\mu '}}$
17. 　 end for
18. end for

下载: 导出CSV

表 1 雷达发射信号仿真参数表

Table 1. Radar transmit signal simulation parameters

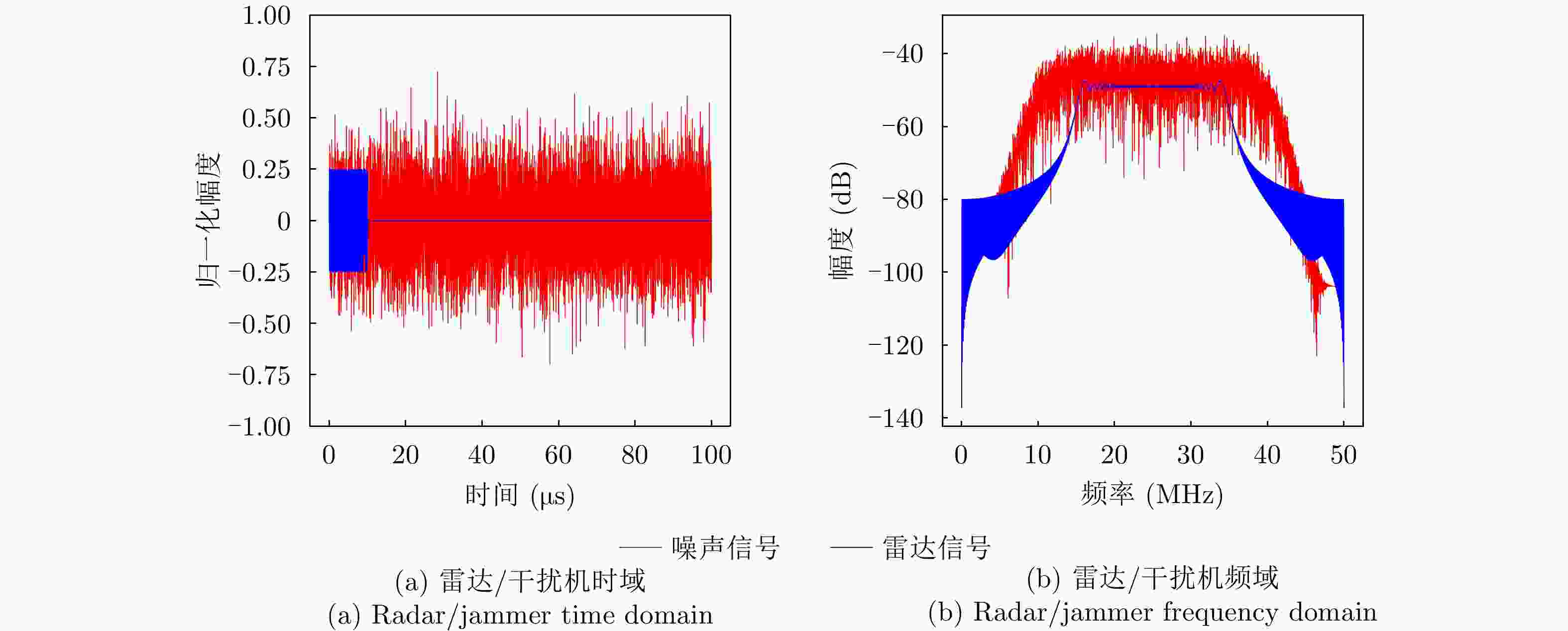
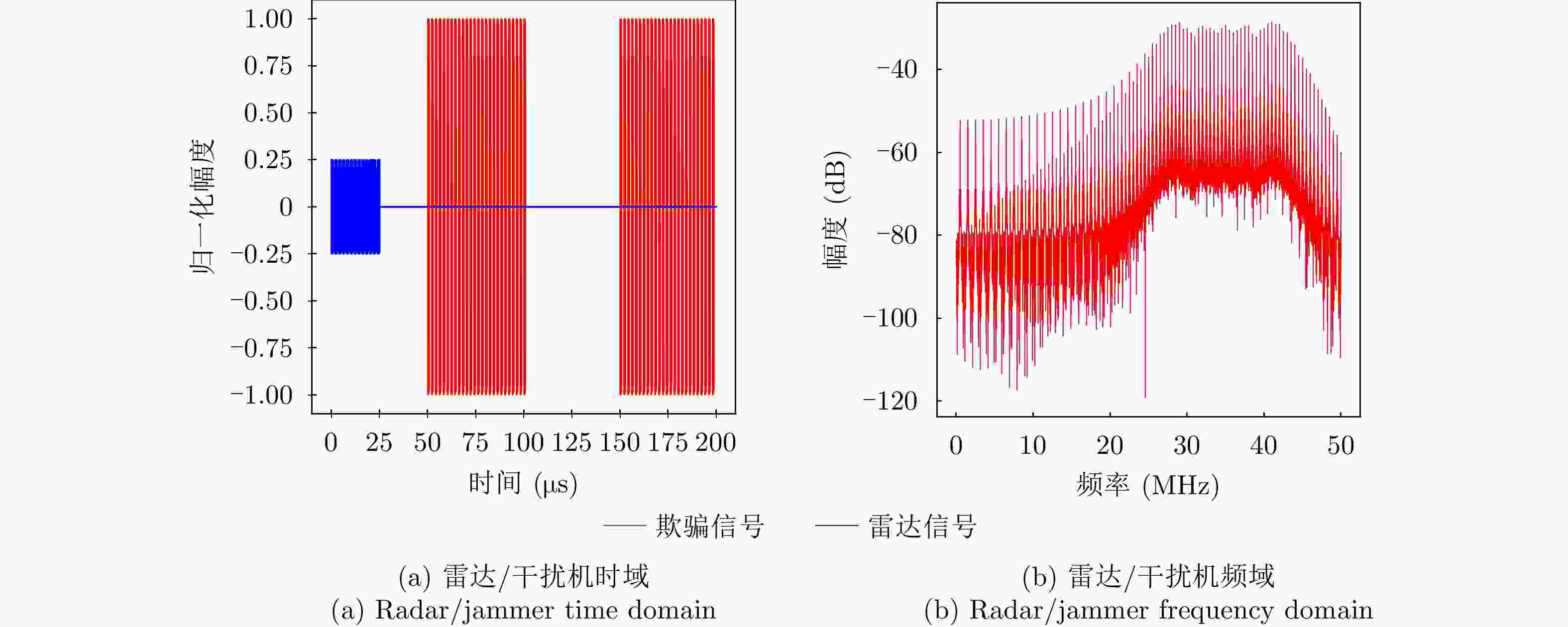
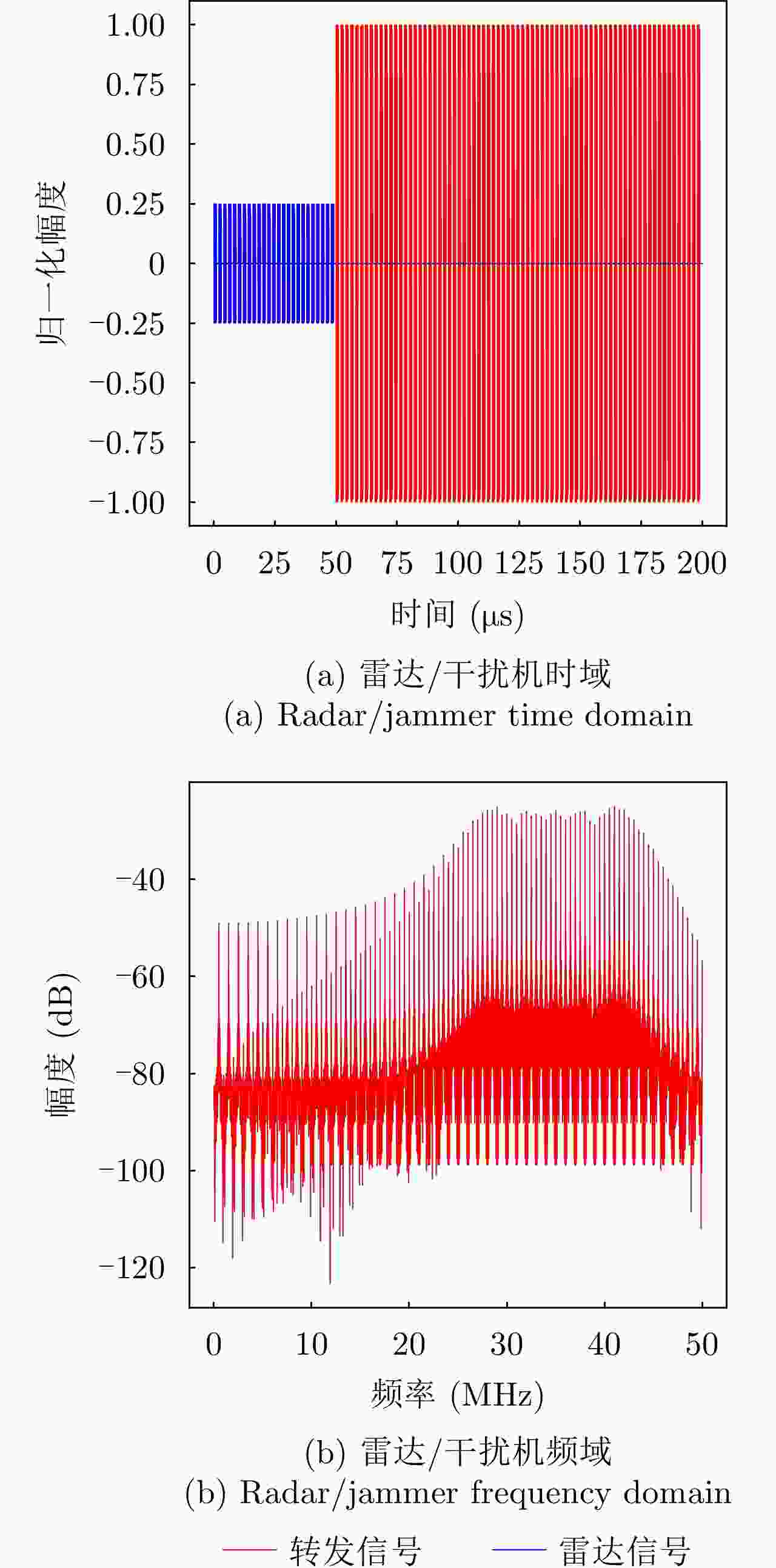
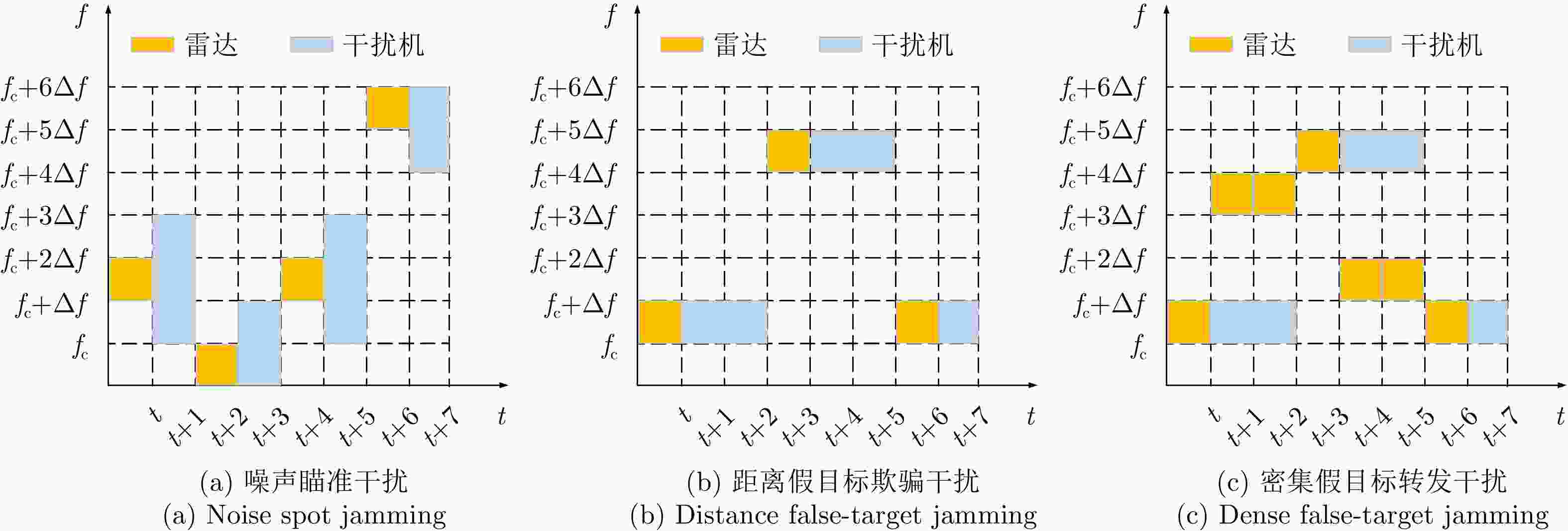
参数类型	数值
信号类型	LFM
采样频率 ${f_{\rm{s}}}$ (MHz)	100
脉冲宽度 ${T_{\rm{p}}}$ (μs)	10
脉冲重复周期 ${T_{\rm{r}}}$ (μs)	50
下变频后的中频频率 ${f_I}$ (MHz)	25
调频斜率k (Hz/s)	2×10¹²
带宽B (MHz)	20

下载: 导出CSV

表 2 3种干扰类型下的态势预测性能

Table 2. Posture prediction performance under 3 interference types

干扰类型	总体区间	步进	识别时间(ms)	识别精度(%)
噪声瞄准干扰	[3～4 GHz]	1 MHz	96	98.6
距离假目标欺骗干扰	[3～4 GHz]	1 MHz	132	97.4
密集假目标转发干扰	[1～1000 μs]	1 μs	144	94.4

下载: 导出CSV

表 3 算法参数设置

Table 3. Algorithm parameters setting

参数	PPO	TD3	DRL-ANCD
Q网络学习率	10^–3	10^–3	10^–3
策略网络学习率	10^–3	10^–3	10^–3
优化器	Adam	Adam	Adam
目标网络更新率	10^–3	5×10^–3	5×10^–3
批输入	128	128	128
折扣系数	0.99	0.99	0.99
奖励缩放	1.0	1.0	1.0
PPO裁剪参数	0.2	None	None

下载: 导出CSV

表 4 单一干扰类型下3种强化学习算法抗干扰性能

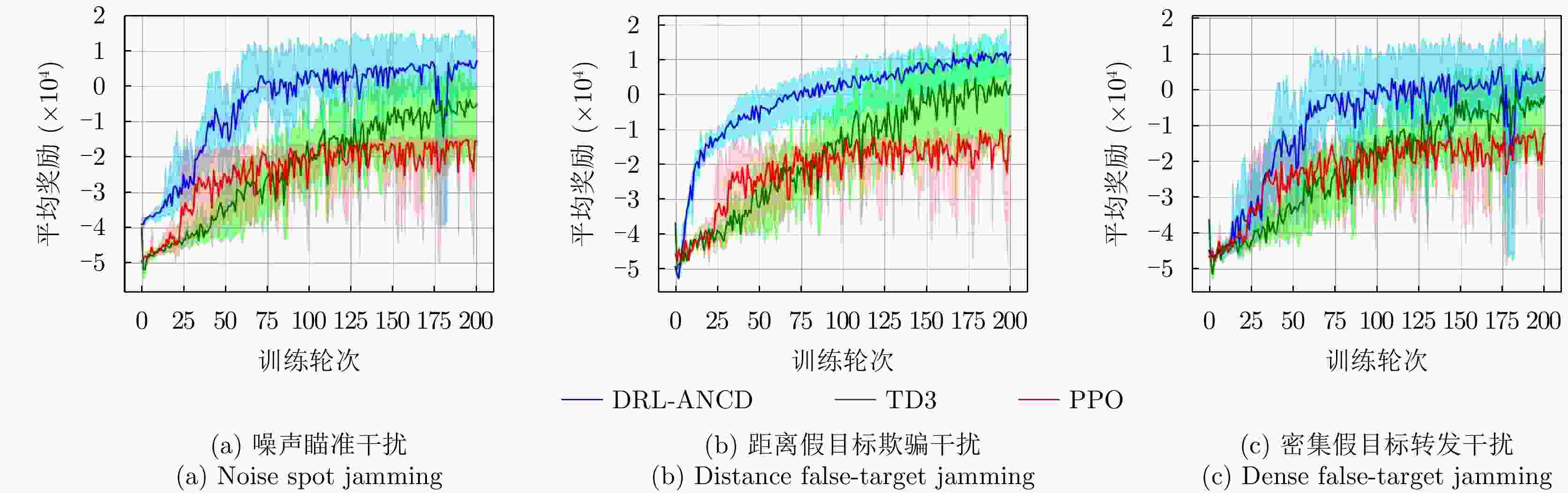
Table 4. Performance of 3 RL algorithms for a single jamming type

干扰类型	算法名称	平均奖励	决策时间(ms)
噪声瞄准干扰	PPO	–215	188
	TD3	–51	333
	DRL-ANCD	53	244
距离假目标欺骗干扰	PPO	–168	168
	TD3	–25	225
	DRL-ANCD	94	203
密集假目标转发干扰	PPO	–156	269
	TD3	–45	340
	DRL-ANCD	24	289

下载: 导出CSV

表 5 在线网络参数

Table 5. Online net parameters

网络	网络层	输入	输出	激活
策略网络	MLP1	State	256	ReLU
	MLP2	256	256	ReLU
	MLP3	256	128	ReLU
	MLP4	128	1	None
Q网络	MLP1	State+action	256	ReLU
	MLP2	Action+256	256	ReLU
	MLP3	256	128	ReLU
	MLP4	128	1	None

下载: 导出CSV

表 6 多干扰策略下3种强化学习算法抗干扰性能

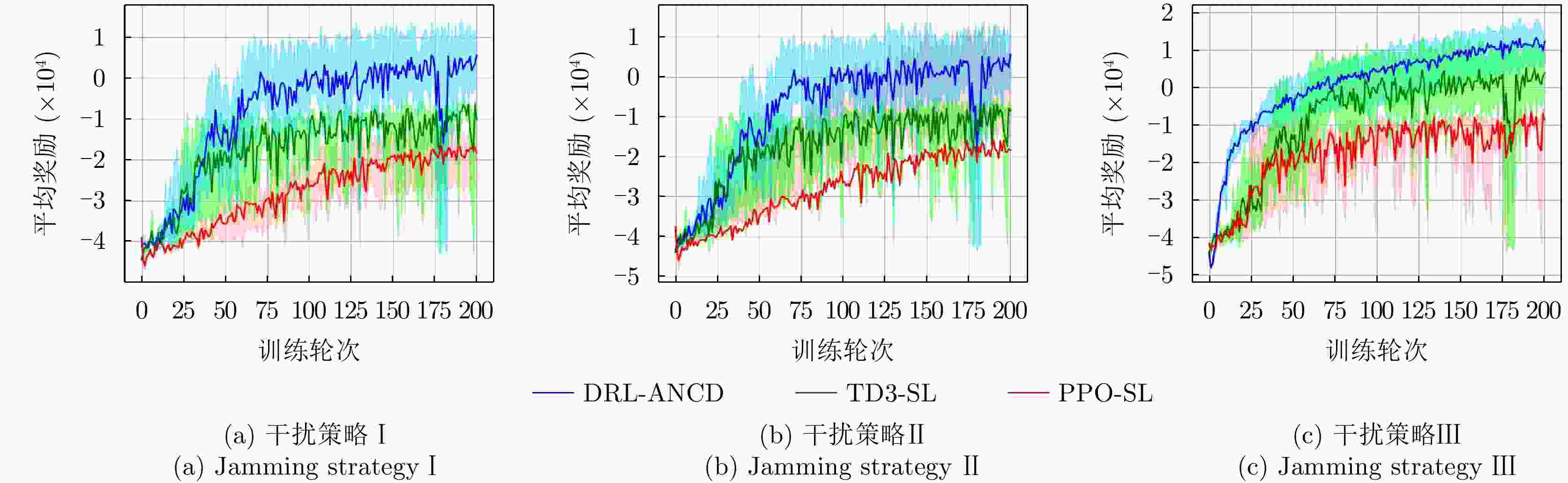
Table 6. Performance of 3 RL algorithms for a multi-jamming strategies

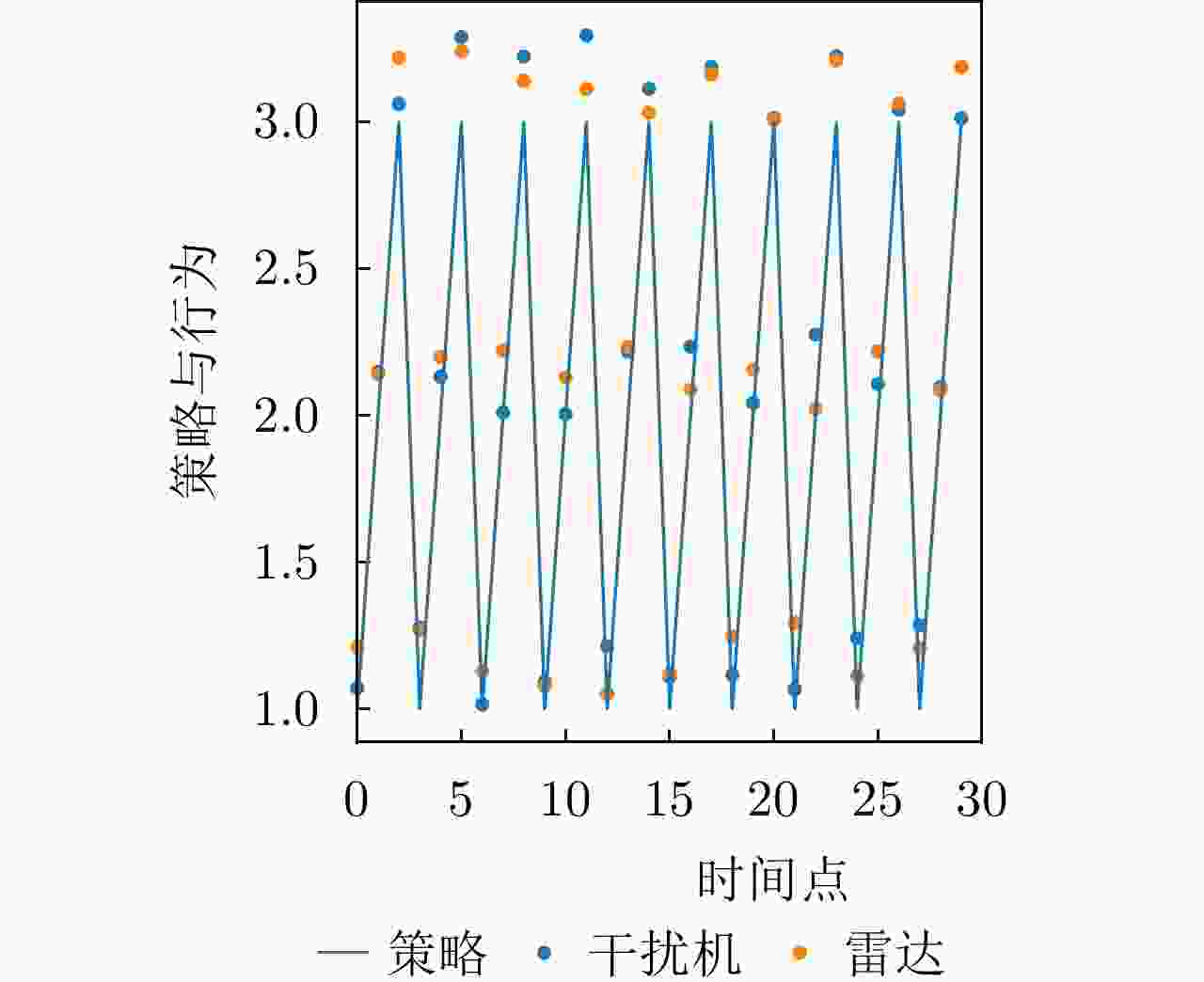
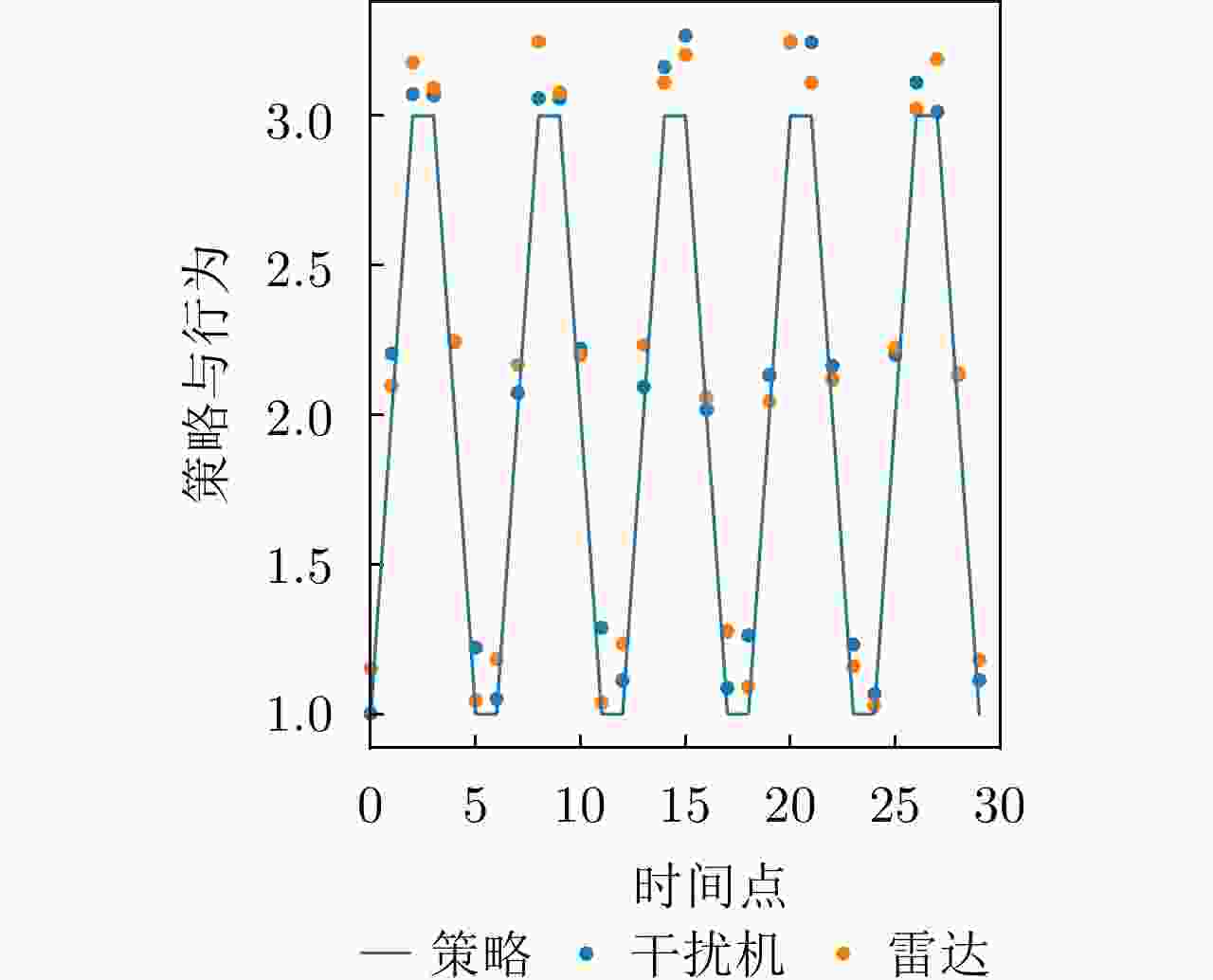
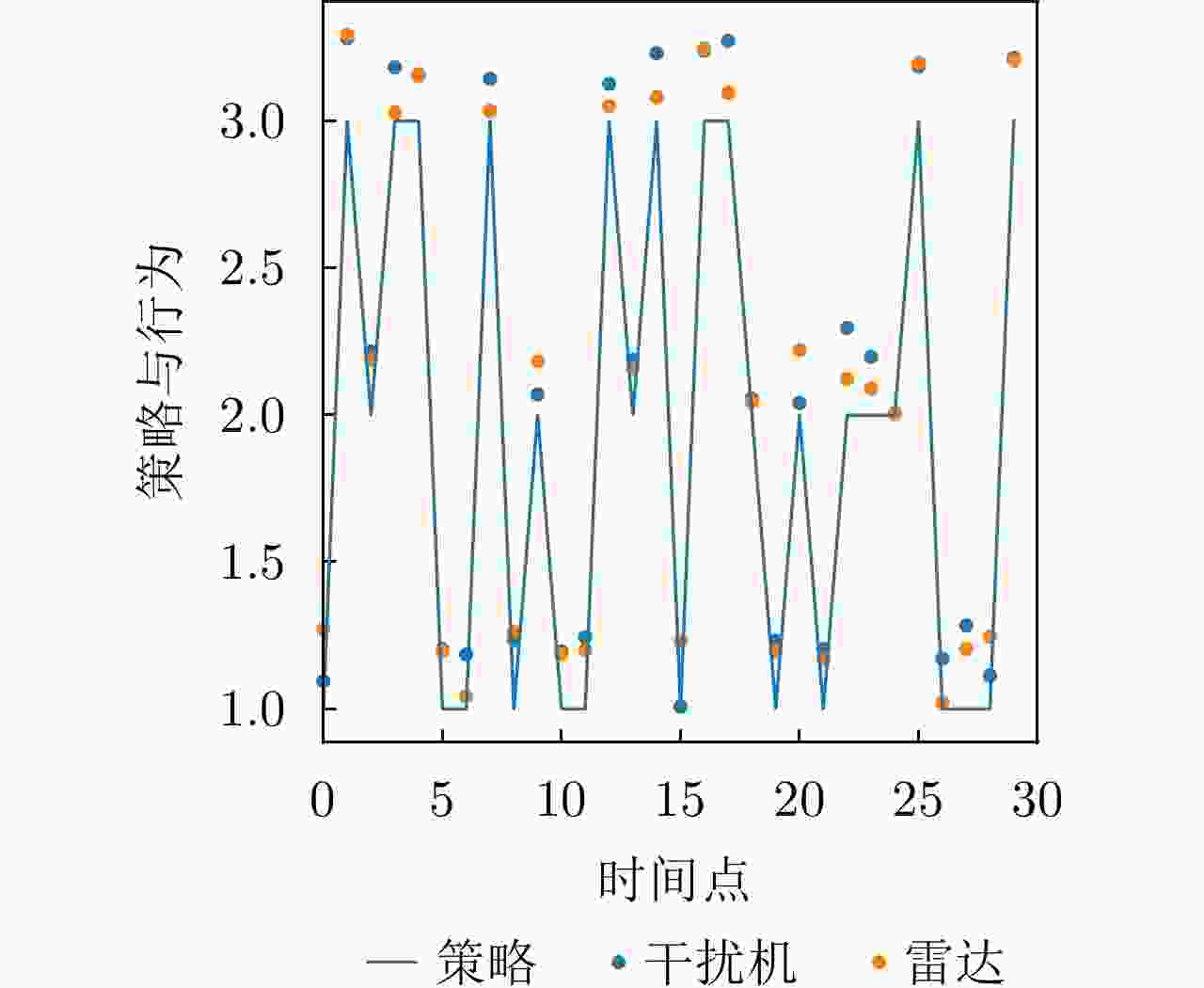
干扰策略	算法名称	对抗奖励	决策时间(ms)
干扰策略Ⅰ	PPO-SL	–202	356
	TD3-SL	–125	443
	DRL-ANCD	3	402
干扰策略Ⅱ	PPO-SL	–221	375
	TD3-SL	–122	429
	DRL-ANCD	14	392
干扰策略Ⅲ	PPO-SL	–124	386
	TD3-SL	25	463
	DRL-ANCD	107	422

下载: 导出CSV

参考文献(30)

[1]	KOGON S M, HOLDER E J, and WILLIAMS D B. Mainbeam jammer suppression using multipath returns[C]. Conference Record of the Thirty-First Asilomar Conference on Signals, Systems and Computers, Pacific Grove, USA, 1997: 279–283.
[2]	GRECO M, GINI F, and FARINA A. Radar detection and classification of jamming signals belonging to a cone class[J]. IEEE Transactions on Signal Processing, 2008, 56(5): 1984–1993. doi: 10.1109/TSP.2007.909326
[3]	NERI F. Introduction to Electronic Defense Systems[M]. SciTech Publishing, Raleigh, NC, 2006.
[4]	李宇环, 岳显昌, 张兰. 基于压缩感知的时域抗射频干扰方法[J]. 科学技术与工程, 2020, 20(7): 2767–2772. doi: 10.3969/j.issn.671-1815.2020.07.035 LI Yuhuan, YUE Xianchang, and ZHANG Lan. Time-domain radio frequency interference suppression method based on compressed sensing[J]. Science Technology and Engineering, 2020, 20(7): 2767–2772. doi: 10.3969/j.issn.671-1815.2020.07.035
[5]	杜思予, 刘智星, 吴耀君, 等. 基于SVM的捷变频雷达密集转发干扰智能抑制方法[J]. 雷达学报, 2023, 12(1): 173–185. doi: 10.12000/JR22065 DU Siyu, LIU Zhixing, WU Yaojun, et al. Dense-repeated jamming suppression algorithm based on the support vector machine for frequency agility radar[J]. Journal of Radars, 2023, 12(1): 173–185. doi: 10.12000/JR22065
[6]	董淑仙, 吴耀君, 方文, 等. 频率捷变雷达联合模糊C均值抗间歇采样干扰[J]. 雷达学报, 2022, 11(2): 289–300. doi: 10.12000/JR21205 DONG Shuxian, WU Yaojun, FANG Wen, et al. Anti-interrupted sampling repeater jamming method based on frequency-agile radar joint fuzzy C-means[J]. Journal of Radars, 2022, 11(2): 289–300. doi: 10.12000/JR21205
[7]	施龙飞, 任博, 马佳智, 等. 雷达极化抗干扰技术进展[J]. 现代雷达, 2016, 38(4): 1–7, 29. SHI Longfei, REN Bo, MA Jiazhi, et al. Recent developments of radar anti-interference techniques with polarimetry[J]. Modern Radar, 2016, 38(4): 1–7, 29.
[8]	陈新竹. 多功能数字阵列雷达空域抗有源干扰方法研究[D]. [博士论文], 上海交通大学, 2022. CHEN Xinzhu. Research on spatial jamming cancellation in mutifunction digital array radar[D]. [Ph.D. dissertation], Shanghai Jiao Tong University, 2022.
[9]	刘智星, 杜思予, 吴耀君, 等. 脉间-脉内捷变频雷达抗间歇采样干扰方法[J]. 雷达学报, 2022, 11(2): 301–312. doi: 10.12000/JR22001 LIU Zhixing, DU Siyu, WU Yaojun, et al. Anti-interrupted sampling repeater jamming method for interpulse and intrapulse frequency-agile radar[J]. Journal of Radars, 2022, 11(2): 301–312. doi: 10.12000/JR22001
[10]	LECUN Y, BENGIO Y, and HINTON G. Deep learning[J]. Nature, 2015, 521(7553): 436–444. doi: 10.1038/nature14539
[11]	李彦冬, 郝宗波, 雷航. 卷积神经网络研究综述[J]. 计算机应用, 2016, 36(9): 2508–2515, 2565. LI Yandong, HAO Zongbo, and LEI Hang. Survey of convolutional neural network[J]. Journal of Computer Applications, 2016, 36(9): 2508–2515, 2565.
[12]	刘全, 翟建伟, 章宗长, 等. 深度强化学习综述[J]. 计算机学报, 2018, 41(1): 1–27. doi: 10.11897/SP.J.1016.2018.00001 LIU Quan, ZHAI Jianwei, ZHANG Zongzhang, et al. A survey on deep reinforcement learning[J]. Chinese Journal of Computers, 2018, 41(1): 1–27. doi: 10.11897/SP.J.1016.2018.00001
[13]	刘朝阳, 穆朝絮, 孙长银. 深度强化学习算法与应用研究现状综述[J]. 智能科学与技术学报, 2020, 2(4): 312–326. doi: 10.11959/j.issn.2096-6652.202034 LIU Zhaoyang, MU Chaoxu, and SUN Changyin. An overview on algorithms and applications of deep reinforcement learning[J]. Chinese Journal of Intelligent Science and Technology, 2020, 2(4): 312–326. doi: 10.11959/j.issn.2096-6652.202034
[14]	DAYAN P and DAW N D. Decision theory, reinforcement learning, and the brain[J]. Cognitive, Affective, & Behavioral Neuroscience, 2008, 8(4): 429–453. doi: 10.3758/CABN.8.4.429
[15]	CAROTENUTO V, DE MAIO A, ORLANDO D, et al. Adaptive radar detection using two sets of training data[J]. IEEE Transactions on Signal Processing, 2018, 66(7): 1791–1801. doi: 10.1109/TSP.2017.2778684
[16]	汪浩, 王峰. 强化学习算法在雷达智能抗干扰中的应用[J]. 现代雷达, 2020, 42(3): 40–44, 48. WANG Hao and WANG Feng. Application of reinforcement learning algorithms in anti-jamming of intelligent radar[J]. Modern Radar, 2020, 42(3): 40–44, 48.
[17]	XING Qiang, ZHU Weigang, and JIA Xin. Research on method of intelligent radar confrontation based on reinforcement learning[C]. 2017 2nd IEEE International Conference on Computational Intelligence and Applications (ICCIA), Beijing, China, 2017: 471–475.
[18]	LI Kang, JIU Bo, LIU Hongwei, et al. Reinforcement learning based anti-jamming frequency hopping strategies design for cognitive radar[C]. 2018 IEEE International Conference on Signal Processing, Communications and Computing (ICSPCC), Qingdao, China, 2018: 1–5.
[19]	LI Kang, JIU Bo, and LIU Hongwei. Deep Q-network based anti-jamming strategy design for frequency agile radar[C]. 2019 International Radar Conference (RADAR), Toulon, France, 2019: 1–5.
[20]	WANG Shanshan, LIU Zheng, XIE Rong, et al. Reinforcement learning for compressed-sensing based frequency agile radar in the presence of active interference[J]. Remote Sensing, 2022, 14(4): 968. doi: 10.3390/rs14040968
[21]	LI Xinzhi and DONG Shengbo. Research on efficient reinforcement learning for adaptive frequency-agility radar[J]. Sensors, 2021, 21(23): 7931. doi: 10.3390/s21237931
[22]	崔国龙, 余显祥, 魏文强, 等. 认知智能雷达抗干扰技术综述与展望[J]. 雷达学报, 2022, 11(6): 974–1002. doi: 10.12000/JR22191 CUI Guolong, YU Xianxiang, WEI Wenqiang, et al. An overview of antijamming methods and future works on cognitive intelligent radar[J]. Journal of Radars, 2022, 11(6): 974–1002. doi: 10.12000/JR22191
[23]	WATERS W M and LINDE G J. Frequency-agile radar signal processing[J]. IEEE Transactions on Aerospace and Electronic Systems, 1979, AES-15(3): 459–464. doi: 10.1109/TAES.1979.308841
[24]	李尔康. 基于干扰认知的雷达反干扰波形设计与实现[D]. [硕士论文], 电子科技大学, 2022. LI Erkang. Design and implementation of radar anti-jamming waveform based on jamming cognition[D]. [Master dissertation], University of Electronic Science and Technology of China, 2022.
[25]	张昭建, 谢军伟, 杨春晓, 等. 掩护脉冲信号抗转发式欺骗干扰性能分析[J]. 弹箭与制导学报, 2016, 36(4): 149–152, 156. ZHANG Zhaojian, XIE Junwei, YANG Chunxiao, et al. Performance analysis of screening pulse signal confronts to deception jamming[J]. Journal of Projectiles, Rockets, Missiles and Guidance, 2016, 36(4): 149–152, 156.
[26]	李研. 雷达抗干扰波形设计及仿真分析[D]. [硕士论文], 西安电子科技大学, 2022. LI Yan. Radar anti-jamming waveform design and simulation analysis[D]. [Master dissertation], Xidian University, 2022.
[27]	温鹏飞. 基于雷达数据的目标航迹识别和聚类研究[D]. [硕士论文], 合肥工业大学, 2020. WANG Pengfei. Research on track recognition and clustering based on radar data[D]. [Master dissertation], Hefei University of Technology, 2020.
[28]	MNIH V, KAVUKCUOGLU K, SILVER D, et al. Human-level control through deep reinforcement learning[J]. Nature, 2015, 518(7540): 529–533. doi: 10.1038/nature14236
[29]	SCHULMAN J, WOLSKI F, DHARIWAL P, et al. Proximal policy optimization algorithms[EB/OL]. https://arxiv.org/abs/1707.06347, 2017.
[30]	FUJIMOTO S, HOOF H, and MEGER D. Addressing function approximation error in actor-critic methods[C]. 35th International Conference on Machine Learning, Stockholm, Sweden, 2018: 1587–1596.

施引文献

资源附件(0)

访问统计

图(20) / 表(7)

计量

文章访问数: 1154
HTML全文浏览量: 835
PDF下载量: 443
被引次数: 0

1. 引言
2. 成像几何模型
3. 回波信号建模
4. 成像处理算法
4.1 基于后向投影-距离多普勒的目标三维成像
4.2 成像性能分析
4.3 对比分析
5. 实验与分析
5.1 仿真实验
5.2 实测数据分析
6. 结语

基于复数域深度强化学习的多干扰场景雷达抗干扰方法

DOI: 10.12000/JR23139

通讯作者:
刘环宇 liuhuanyu@hit.edu.cn

计量

A Radar Anti-jamming Method under Multi-jamming Scenarios Based on Deep Reinforcement Learning in Complex Domains

Corresponding author: LIU Huanyu, liuhuanyu@hit.edu.cn

1. 引言

2. 成像几何模型

3. 回波信号建模

4. 成像处理算法

4.1 基于后向投影-距离多普勒的目标三维成像

4.2 成像性能分析

4.3 对比分析

5. 实验与分析

5.1 仿真实验

5.2 实测数据分析

6. 结语

计量

目录

1. 引言

2. 成像几何模型

3. 回波信号建模

4. 成像处理算法

4.1 基于后向投影-距离多普勒的目标三维成像

4.2 成像性能分析

4.3 对比分析

5. 实验与分析

5.1 仿真实验

5.2 实测数据分析

6. 结语

期刊介绍

联系我们

基于复数域深度强化学习的多干扰场景雷达抗干扰方法

DOI: 10.12000/JR23139

通讯作者: 刘环宇 liuhuanyu@hit.edu.cn

计量

出版历程

A Radar Anti-jamming Method under Multi-jamming Scenarios Based on Deep Reinforcement Learning in Complex Domains

Corresponding author: LIU Huanyu, liuhuanyu@hit.edu.cn

1. 引言

2. 成像几何模型

3. 回波信号建模

4. 成像处理算法

4.1 基于后向投影-距离多普勒的目标三维成像

4.2 成像性能分析

4.3 对比分析

5. 实验与分析

5.1 仿真实验

5.2 实测数据分析

6. 结语

计量

出版历程

目录

1. 引言

2. 成像几何模型

3. 回波信号建模

4. 成像处理算法

4.1 基于后向投影-距离多普勒的目标三维成像

4.2 成像性能分析

4.3 对比分析

5. 实验与分析

5.1 仿真实验

5.2 实测数据分析

6. 结语

期刊介绍

联系我们

通讯作者:
刘环宇 liuhuanyu@hit.edu.cn