Three-dimensional Micro-motion Parameters Extraction of Translational Rotating Targets Based on Vortex Electromagnetic Wave Radar
-
摘要: 与传统平面电磁波雷达相比,涡旋电磁波雷达能同时观测到目标投影到雷达径向和垂直于径向平面的微动分量,可为目标识别提供更多信息。当前关于涡旋电磁波雷达微多普勒效应的研究尚处于起步阶段,初步实现了对旋转目标的三维微动参数的提取,但均未考虑目标平动的影响。因此,该文研究了涡旋电磁波雷达中平动旋转目标的微多普勒效应,推导了平动旋转目标的角多普勒性质,提出了基于1/4微动周期多普勒频移曲线的三维微动参数提取方法,获得了目标旋转频率、旋转半径、旋转矢量和平动速度矢量等参数。仿真验证了角多普勒性质的正确性和参数提取方法的有效性。Abstract: Compared with traditional Electromagnetic (EM) wave radars, vortex EM wave radars can simultaneously observe the micro-motion components projected onto the radar’s radial and perpendicular planes, providing more information for target recognition. The current research on the micro-Doppler effect of vortex EM wave radar is still in its infancy, and the extraction of three-dimensional micro-motion parameters of rotating targets has been preliminarily achieved. However, the impact of target translation was not considered. Therefore, the micro-Doppler effect of translational rotating targets in vortex EM wave radar is studied in this paper. The angular Doppler properties of translational rotating targets are derived, and a three-dimensional micro-motion parameter extraction method based on the 1/4 micro-motion period Doppler frequency shift curve is proposed. Estimation of parameters such as target rotation frequency, rotation radius, rotation vector and translational velocity vector is achieved. The correctness of angular Doppler properties and the effectiveness of parameter extraction method are verified by simulations.
-
1. 引言
合成孔径雷达(Synthetic Aperture Radar, SAR)是一种主动式微波遥感成像系统,具有全天时、全天候的观测能力。随着SAR成像技术的不断发展,SAR自动目标识别(Automatic Target Recognition, ATR)成为SAR图像智能解译的一个重要组成部分。SAR ATR主要由3个阶段组成:检测、鉴别和分类[1]。近年来,随着深度学习的快速发展,SAR ATR领域也涌现了很多基于深度学习的优秀算法[2,3]。
然而,目前将深度学习应用于SAR ATR领域主要面临两方面的问题:一是深度神经网络往往需要大量标注数据才能有效提取目标特征,但SAR样本标注难度大、成本高,标注数量严重不足,很难达到和自然图像领域相当的标注样本量级;二是深度学习方法一直以来被视为“黑盒模型”,内部工作机理不透明,缺乏可解释性,难以为SAR ATR提供可靠的、可信任的应用服务。
针对SAR目标识别中标注样本不足的问题,Chen等人[2]提出了全卷积网络(All-Convolutional Networks, A-ConvNets),使用卷积层代替全连接层,减少了需要训练的参数,有效缓解了直接使用SAR数据训练CNN容易导致过拟合的情况,在MSTAR数据集上取得了很好的分类效果。Pan等人[4]提出了一种基于度量学习(Metric learning)的孪生网络(Siamese network),以样本对的形式输入训练图像,显著增加了训练数据量。但这些方法仍然不能完全摆脱对标注样本的依赖。
为此,已有研究者尝试利用仿真的SAR图像样本来支撑真实样本的分类任务。关于SAR图像仿真技术的研究已有很多,其中经典方法是建立物体的3D模型,结合电磁计算和计算机图形学方法,得到SAR仿真图像[5]。随着SAR仿真技术的发展,对于某些目标而言,仿真图像与实际图像可以达到目视难以分辨的程度。然而,利用仿真图像训练的神经网络很难直接对真实图像精确分类,文献[6]和文献[7]都指出SAR仿真图像与实测图像属于非同源图像,在背景纹理、目标结构等方面不可避免地存在一定差异,其实验结果也表明仿真图像难以直接支撑零标注样本下的真实图像分类任务。目前已有一些在小样本或零样本情况下提升仿真辅助SAR目标分类性能的相关研究。文献[8]首次探讨了结合仿真图像进行迁移学习实现真实SAR目标分类的可行性,其结果表明,当真实样本标注数量不足时,利用仿真数据进行预训练可以有效加快模型收敛。Zhang等人[9]提出了一种双流深度网络结构,通过利用方位角、幅度和相位信息等SAR领域知识进行数据增强,提升小样本情况下SAR目标识别的性能。这些研究表明,在小样本情况下,SAR仿真样本可以为实测SAR目标分类任务提供可用信息,但未对零样本情况下的仿真辅助SAR目标分类的效果进行验证。Song等人[6]提出了一种非必要因素抑制的方法,对仿真图像和真实图像进行非极大值抑制、风格调整和分割这一系列预处理后输入神经网络,实现了仿真辅助的零样本SAR目标识别。然而,其实验中只是将MSTAR数据集中10类目标之一T72目标图像替换为仿真图像,这对仿真图像支撑真实图像分类效果的验证是有限的。
笔者认为,为提高仿真辅助SAR图像分类的性能,需要找到一种可以有效拉近仿真图像和真实图像特征分布距离的方法以实现特征迁移。如何解决不同来源数据之间的特征迁移问题,是域自适应(Domain Adaptation)方法的研究内容。无监督域适应(Unsupervised Domain Adaptation, UDA)方法可以实现从带标注源域(Source domain)数据集到无标注目标域(Target domain)数据集上的信息迁移,找到不同域之间通用的分类特征提取方法。现有的UDA方法主要可分为4种[10]:(1)基于领域分布差异的方法[11-14];(2)基于对抗学习的方法[15-19];(3)基于重构的方法[20,21];(4)基于样本生成的方法[22]。
目前已有一些将域自适应方法应用到SAR目标识别领域的研究[23-26]。Huang等人[23]从迁移什么、迁移到哪、如何迁移3方面展开探讨,提出了一种结合多源数据的域适应传递方法。Wang等人[24]提出了一个结合域对抗训练和元学习(Meta-learning)的模型,使用大量仿真数据预训练网络后再使用少量带标签真实数据微调网络,实现了跨域和跨任务的迁移学习。Zhang等人[25]提出了一种基于对抗学习的多级无监督域适应方法,用以解决多波段SAR图像分类问题。Xu等人[26]提出的基于判别适应正则化的迁移学习方法D-ARTL实现了由自动识别系统AIS信息到SAR图像域舰船分类任务的知识迁移。
上述研究表明,域适应的方法在SAR遥感领域有很好的应用前景,但这些研究更多地关注了不同域之间的特征迁移是否成功,对域适应前后模型提取特征的变化分析不足。
为此,本文针对利用SAR仿真样本来实现无须实测标注样本的SAR目标分类问题开展研究,提出了一个集成域对抗训练和距离度量的神经网络模型;同时,对模型进行了可解释性分析,结合逐层相关性传播(Layer-wise Relevance Propagation, LRP)[27]和对比层关联传播(Contrastive Layer-wise Relevance Propagation, CLRP)[28]分析了域适应前后模型决策依据的变化。实验表明,本文方法能够显著提升仿真辅助SAR目标分类的准确率,可解释性分析的结果证明本文方法通过修正模型关注区域来提升仿真辅助SAR图像分类的性能,具有一定的合理性。本文的主要贡献可以概括如下:
(1) 提出了一种新的基于无监督域适应的仿真辅助SAR目标分类的网络框架,不同于以往的利用仿真数据进行数据增强或网络预训练工作的方法[6-8],本文方法不需要人为设计复杂的图像预处理过程,而是通过网络学习来提升域混淆程度、缩小仿真样本和实测样本的域差异,在完全不使用实测数据类别标签的情况下实现了较高精度的仿真辅助SAR目标分类,为当下SAR样本标注少、目标识别难的问题提供了新的解决思路;
(2) 本文通过LRP, CLRP等神经网络可解释性方法定位同类目标仿真和实测SAR图像中导致网络做出不同决策的区域,分析了域适应前后模型决策依据的变化,从可解释性角度分析了本文方法提升仿真辅助SAR目标分类性能的原因,可以为仿真方法的优化调整提供思路。
本文的其余部分内容安排如下:第2节介绍了本文提出的基于无监督域适应的仿真辅助SAR图像分类方法;第3节介绍了本文采用的可解释性方法;第4节给出了实验数据、实验结果以及详细的解释分析;第5节进行总结与展望。
2. 无监督域适应的仿真辅助SAR目标分类
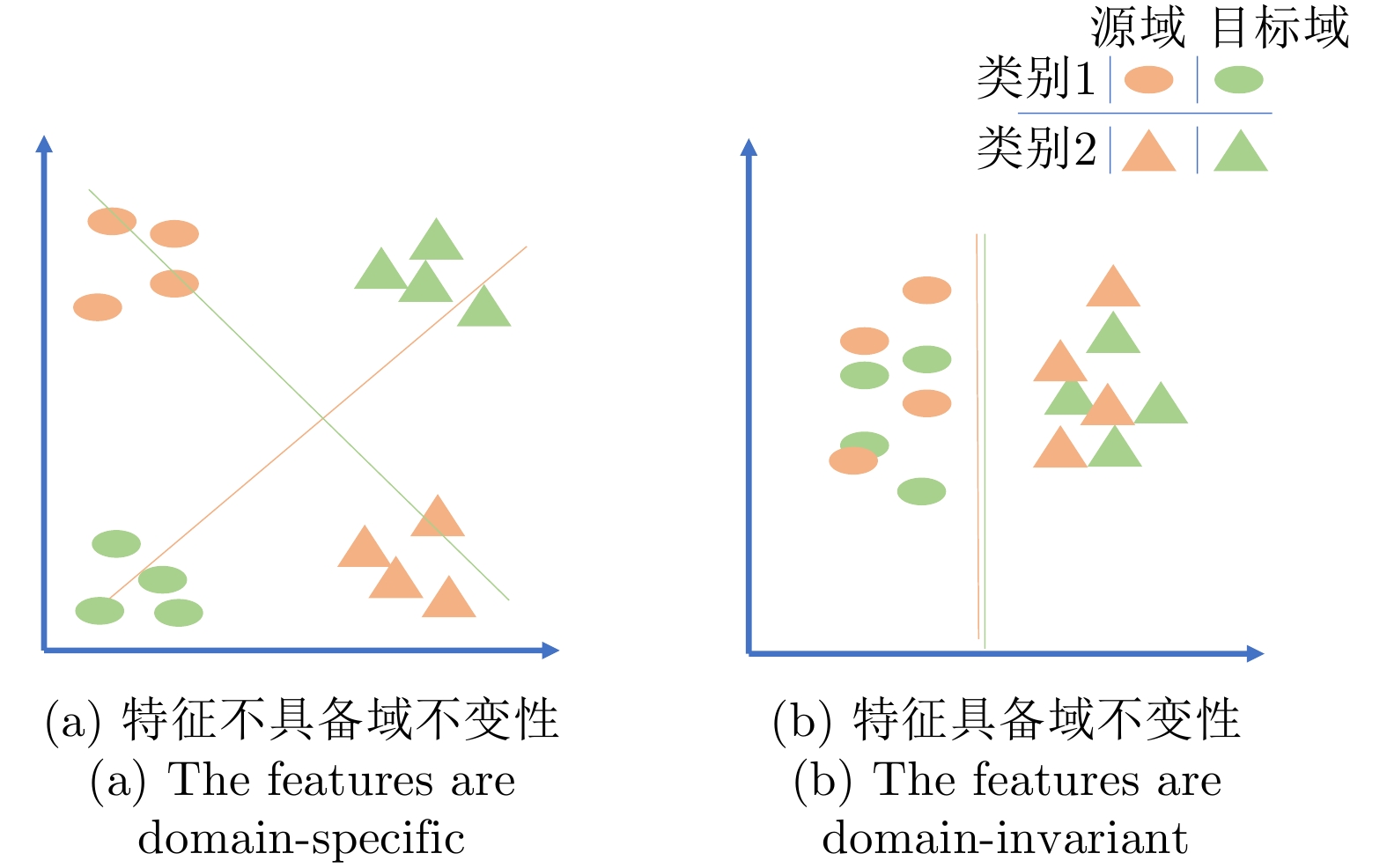
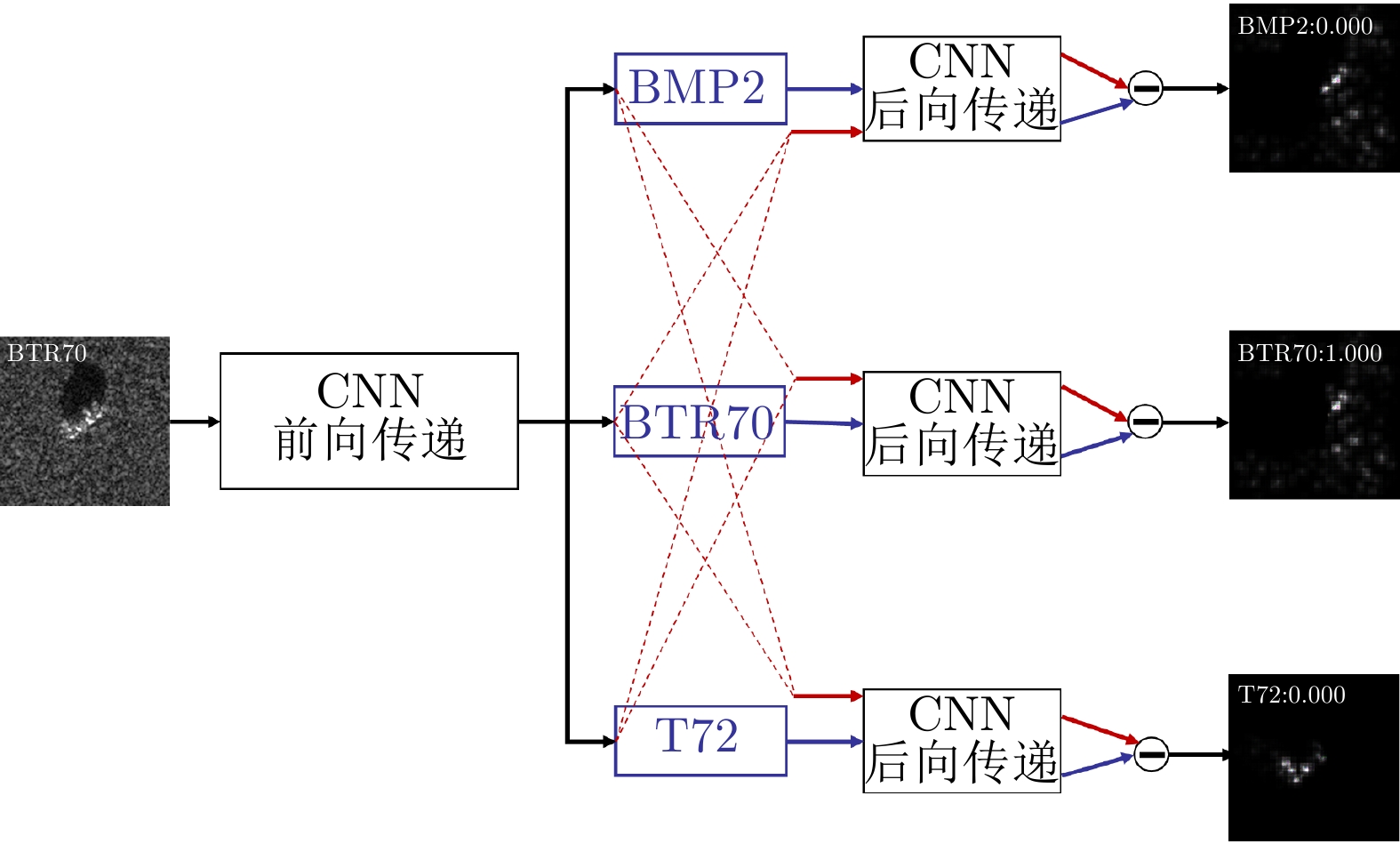
如图1所示,当网络提取到的特征越是局限于特定的域,就越难找到两个域可共用的分类边界;而当提取到的特征越能体现不同域间的共性,就越易于找到可共用的分类边界。为了使特征提取器提取到域不变特征且尽量缩小域间差异,本文提出了一种集成域对抗训练和域差异度量多核最大均值差异(Multi-Kernel Maximum Mean Discrepancy, MK-MMD)[29]的模型。其中,域对抗训练是指特征提取器和域判别器之间的对抗训练,域判别器通过最小化域分类损失来提升域判别能力,特征提取器则致力于学习可以“欺骗”域判别器的特征提取方法,以提取到域不变特征。域对抗训练虽然可以促进域混淆,但是不能保证拉近不同域样本在分类器隐藏层中的特征差异,为此本文方法在模型中添加域差异度量器,使用MK-MMD进行域差异计算,并以此为优化目标训练模型。2.1节对所提模型框架和网络结构进行介绍,2.2节给出了模型优化目标。
2.1 模型框架和网络结构
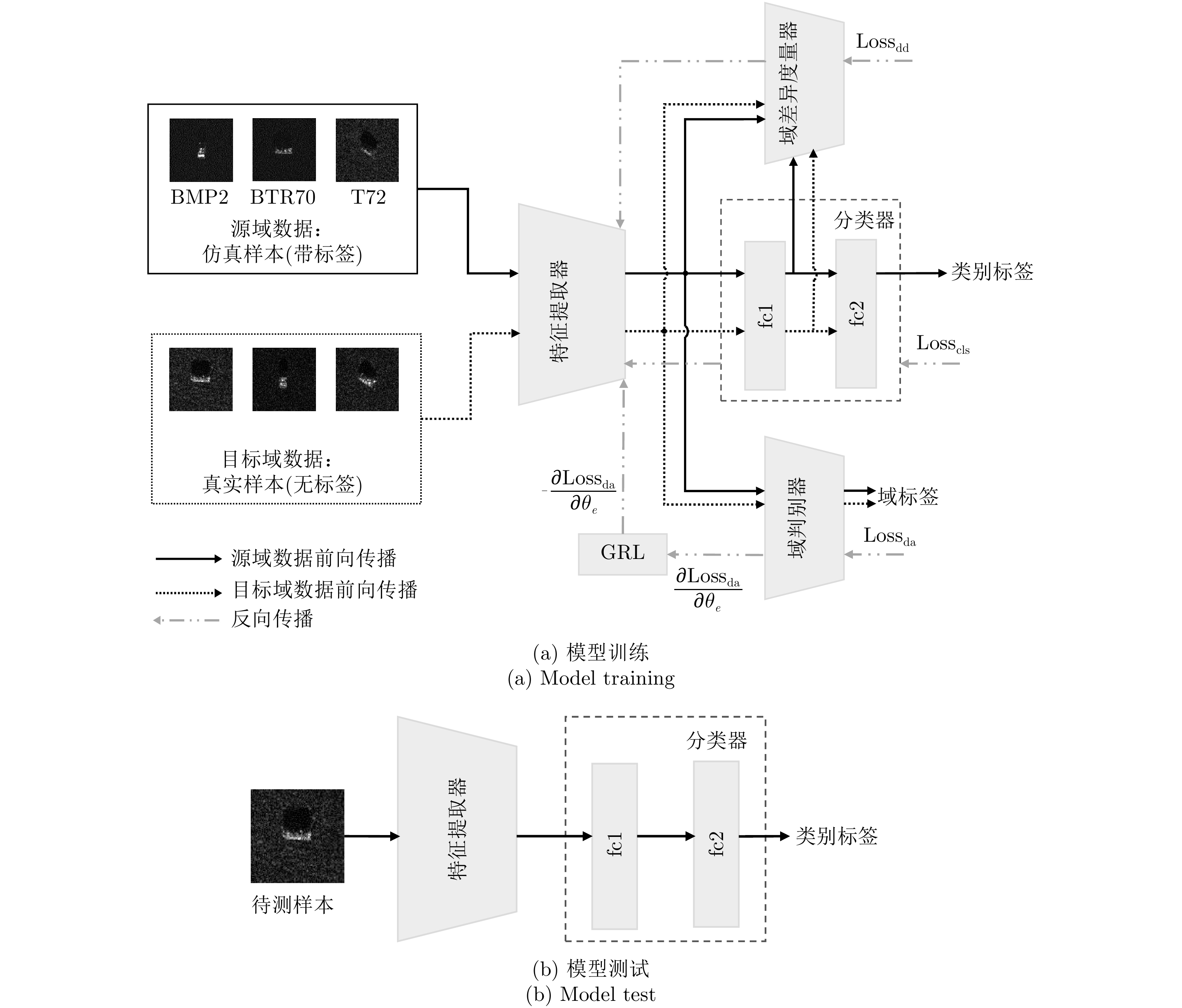
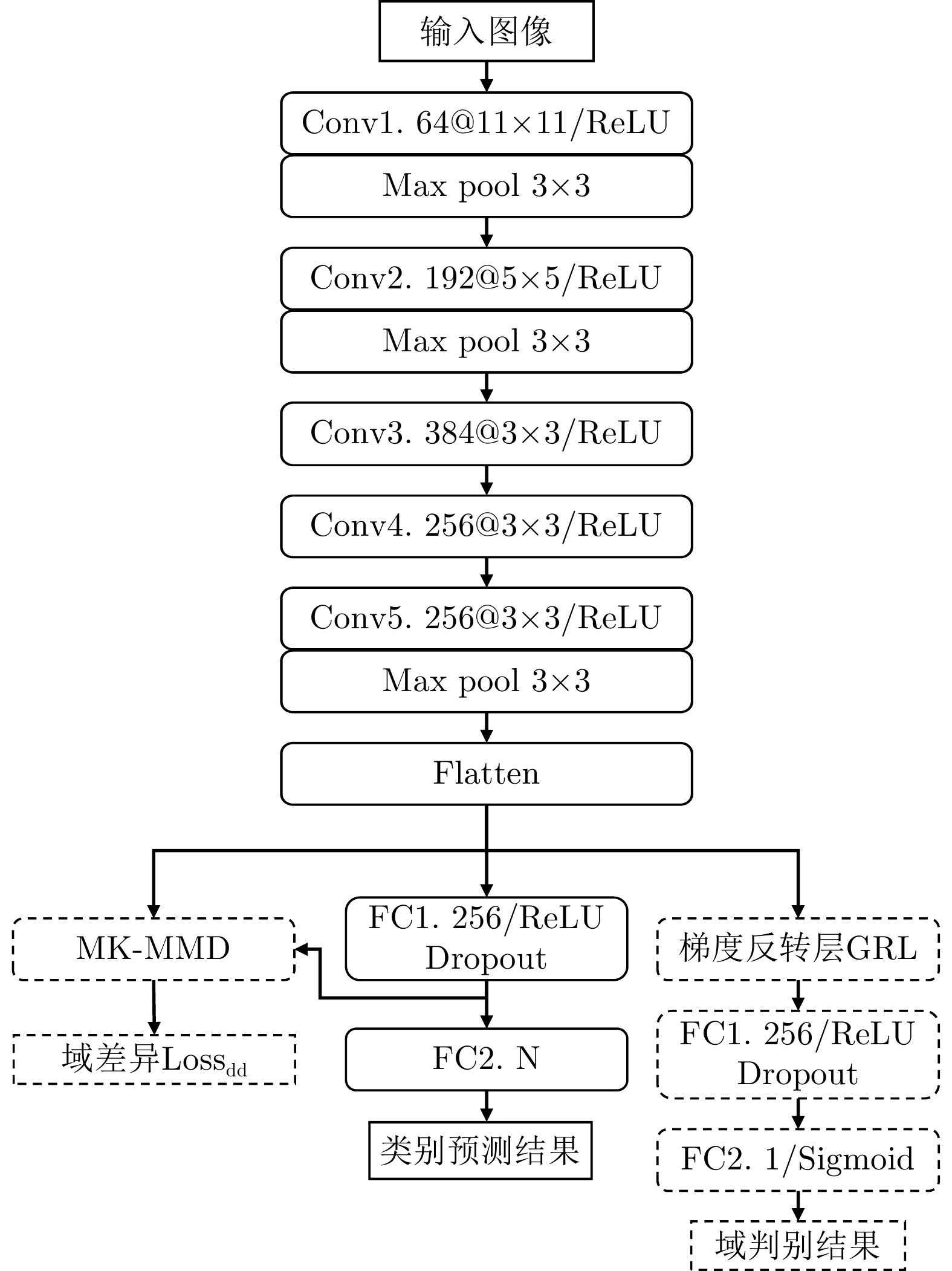
如图2所示,本文提出的网络模型可分为4个部分:特征提取器、目标分类器、域判别器和域差异度量器。本文方法使用带标签的仿真数据(即源域S)训练得到可以对仿真数据准确分类的特征提取器和分类器;同时利用无标签的实测样本(即目标域T)同仿真样本一起进行域对抗训练,帮助特征提取器提取到域不变特征,并结合MK-MMD度量进一步缩小仿真数据特征和真实数据特征在网络隐层中的差异;完成训练后,由特征提取器和分类器最终实现对实测样本的分类。图3给出了本文所提方法的网络结构参数,其中虚线所示结构仅在训练过程中激活,考虑到仿真SAR图像直接训练网络容易导致过拟合,特征提取器的网络层数不宜过多,因此参考了AlexNet[30]的卷积层设计,分类器和域判别器由两个全连接层组成。
在网络训练过程中,源域S为网络模型提供带标签仿真样本
Ds={(xsi,ysi)ni=1} ,其中xsi 为源域的第i 个样本,ysi 为该样本的类别标签,ysi∈{1,2,⋯,N} ,N代表类别数目;目标域T提供无标签实测样本Dt={(xti)mi=1} 。同时每个训练样本带有域标签di ,当样本来自源域即xi∼Ds 时,di=0 ;当xi∼Dt 时,di=1 。对于每个输入样本x ,特征提取器计算得到其特征向量f ,分类器对f 进行类别预测得到ˆy ,域判别器对f 进行域判别得到ˆd 。对于来自不同域的样本xs 和xt ,域差异度量器计算二者在全连接层fc1, fc2处的MK-MMD,作为域差异优化目标。使用θe ,θc 和θd 分别代表特征提取器、分类器和域判别器的参数,Ge(⋅) ,Gc(⋅) ,Gd(⋅) 表示对应的映射函数,则有特征向量f=Ge(x;θe) ,类别预测结果ˆy=Gc(f;θc) ,域预测结果ˆd=Gd(f;θd) 。训练时,将仿真数据和真实数据同时输入到网络模型。首先,基于仿真数据的标签真值
ysi 和分类器预测输出ˆysi 计算得到Losscls ,以此优化分类器和特征提取器。其次,引入梯度反转层(Gradient Reversal Layer, GRL)[15]实现特征提取器和域判别器之间的对抗训练,以使特征提取器提取到域不变特征。最后,使用MK-MMD在分类器全连接层(fc1, fc2)处计算每层输入特征的域差异(记为Lossdd ),以更好地拉近网络深层处不同域样本特征的距离。此处Losscls ,Lossdd 以及域对抗训练的优化目标Lossda 将在2.2节给出说明。2.2 优化目标
本文所提模型的整体优化目标可分为3部分:一是源域样本分类损失
Losscls 最小化,保证特征提取器和分类器可以实现源域样本的精确分类;二是域对抗训练损失Lossda 最小化,以实现域混淆,使特征提取器提取到域不变特征;三是域差异Lossdd 最小化,进一步缩小不同域样本在网络隐层中的特征距离。下面分别给出计算公式。源域样本分类损失
Losscls 的计算方法如式(1)所示。Losscls=1nn∑i=1di=0Jy(Gc(Ge(xi;θe);θc),yi) (1) 其中,
n 是源域训练样本总数量,Jy(⋅) 为softmax交叉熵损失函数,Ge(⋅) 和Gc(⋅) 分别代表特征提取器和分类器的映射函数,θe 和θc 分别为特征提取器和分类器的参数,yi 为样本类别标签。本文方法借助GRL实现域对抗训练,文献[15]最早将生成对抗网络(Generative Adversarial Network, GAN)[31]中对抗学习的思想引入到域适应任务中,通过GRL实现特征提取器和域判别器之间的博弈训练,之后的很多域适应模型都使用了这一结构[32,33]。GRL不影响网络训练的前向传播过程,只是在反向传播的过程中将后一层的梯度乘以一个负常数(
−λ ),完成梯度反转后再传递给前一层,这样使得在训练过程中域判别器致力于分辨特征来自源域还是目标域,特征提取器则致力于提取到可以骗过域判别器的特征,通过二者之间的对抗训练使特征提取器提取到域不变的特征。域对抗训练损失Lossda 根据式(2)计算得来,域对抗训练的目标则可表示为minθe,θdLossda 。Lossda=1qq∑i=1Jd(Gd(GRLλ(Ge(xi;θe));θd),di) (2) 其中,
q 是源域和目标域的训练样本总数量,Jd(⋅) 是二元交叉熵损失函数,Ge(⋅) 和Gd(⋅) 分别代表特征提取器和域判别器的映射函数,GRLλ(⋅) 代表梯度反转层的映射函数,θe 和θd 分别为特征提取器和域判别器的参数,di 为样本域标签。为进一步缩小域间样本特征差异,本文方法使用基于MK-MMD的域差异度量器计算分类器中每个全连接层输入特征的域差异。MMD是一种常用的度量不同域数据分布差异的方法,简单来说,就是将源域S和目标域T中数据的特征表示映射到再生核希尔伯特空间(Reproducing Kernel Hilbert Space, RKHS)中后,计算二者均值的距离。深度域混淆(Deep Domain Confusion, DDC)方法[11]最早将MMD引入到神经网络中,将源域特征和目标域特征之间的MMD作为域混淆度量加入到网络的目标函数当中。但DDC只对网络中的一层进行域适配,且只采用单核计算MMD,适配程度不够。为此,深度适配网络(Deep Adaptation Network, DAN)[12]对网络的多层进行适配,且引入了表征能力更强的MK-MMD,其为MMD的多核版本,表现出了比DDC更好的减小域差异的能力。受此启发,本文设计的域差异度量器使用MK-MMD对分类器中两个全连接层的输入同时进行域差异计算。本文的多层MK-MMD域差异
Lossdd 计算方法如式(3)所示。Lossdd=l=l2∑l=l1d2k(Dls,Dlt) (3) 其中,
l1 和l2 表示域差异度量器对应的网络层起止位置,Dl∗ 表示输入在第l 层的隐层表示,dk(Ds,Dt) 表示源域分布和目标域分布在RKHS中均值的距离,其定义如式(4)所示。d2k(Ds,Dt)=||Es[ϕ(xs)]−Et[ϕ(xt)]||2Hk=Es⟨ϕ(xs),ϕ(x′s)⟩Hk+Et⟨ϕ(xt),ϕ(x′t)⟩Hk−2Es,t⟨ϕ(xs),ϕ(xt)⟩Hk (4) 其中,
E∗[⋅] 代表对应分布D∗ 的数学期望,x∗ 和x′∗ 独立同分布,xs∼Ds ,xt∼Dt ,Hk 表示与核k 相关的RKHS,ϕ(⋅) 表示与核k 相关的特征映射,有k(x,y)=⟨ϕ(x),ϕ(y)⟩Hk 。核k 为U 个高斯核{ku} 的凸组合,如式(5)所示。k(x,y)=U∑u=1wuku(x,y), s.t. U∑u=1wu=1, wu>0 ∀u (5) 其中,
{wu} 的相关约束是为了保证生成的多核k 是特有的,本文方法中U=5 。使用核k 后式(4)的经验估计如式(6)所示。d2k(Ds,Dt)=1n2n∑i,j=1k(xsi,xsj)+1m2m∑i,j=1k(xti,xtj)−2mnn,m∑i,j=1k(xsi,xtj) (6) 其中,
n 为源域训练样本数量,m 为目标域训练样本数量。3. 深度学习的可解释性方法
本文针对SAR目标分类网络的可解释性研究,采用了LRP系列可解释性方法作为工具。相比于一些其他可解释性方法[34,35],LRP可以生成像素级的解释,能够更精细地刻画输入图像中影响决策的区域。SAR图像中目标和背景干扰大多以离散散射点的形式呈现,目标和背景之间、不同类别的目标之间可分性不强,使用LRP这种像素级解释的方法更利于分析。为便于对后文实验结果的理解,本节结合第2节提出的网络模型,简单介绍LRP和CLRP方法的原理和应用。
3.1 LRP方法
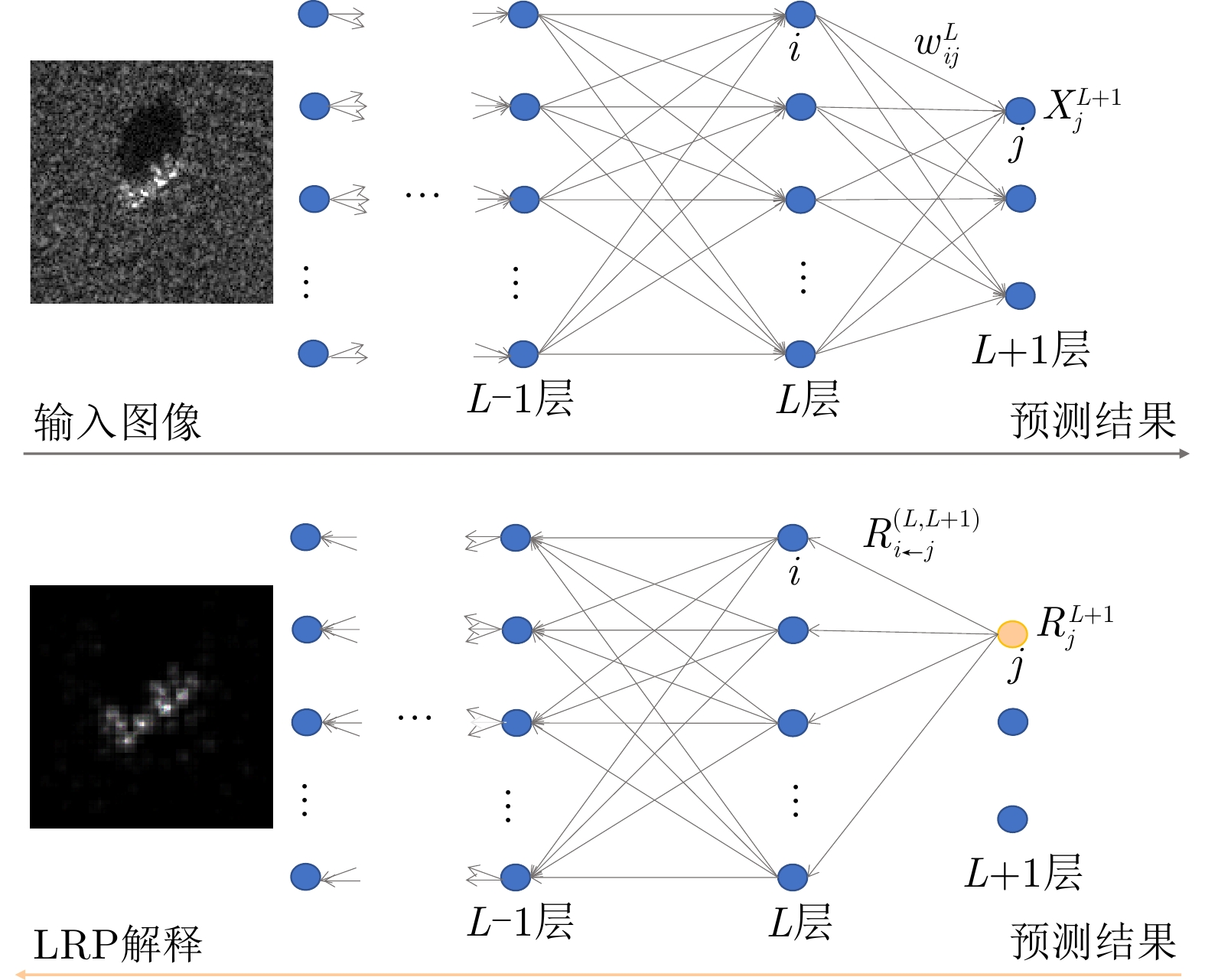
图4给出了一个简单的神经网络中前向传播过程和LRP后向传播过程,在神经网络中,第
L+1 层第j 个神经元的输出可以表示为XL+1j= ϕ(∑i(wLijXLi+bLi)) ,其中ϕ 代表神经元的激活函数,wLij 是连接神经元i 到神经元j 的权重,bLi 是对应的偏差。为了识别每个输入像素点的相关性,LRP将softmax归一化之前的激活值从指定神经元逐层传播回输入空间。RL+1j 表示第L+1 层第j 个神经元的相关性,它可以分解到第L层的全部神经元上,如式(7)所示。第L层第i 个神经元的相关性RLi 可以理解为第L+1层全部神经元的相关性分解后再求和,见式(8)。LRP的传播规则由整流神经元网络的深度泰勒分解推导得来[36]。实际应用中,R(L,L+1)i←j 常用的计算规则有两种:z+−rule 和zβ−rule ,如式(9)和式(10)所示。RL+1j=∑i∈(L)R(L,L+1)i→j (7) RLi=∑j∈(L+1)R(L,L+1)i←j (8) z+−rule:R(L,L+1)i←j=∑jxiw+ij∑i′xi′w+i′jRL+1j (9) zβ−rule:R(L,L+1)i←j=∑jxiwij−liw+ij−hiw−ij∑i′(xi′w+i′j−li′w+i′j−hi′w−i′j)RL+1j (10) 其中,
w+ij=wij∗1wij>0 ,w−ij=wij∗1wij<0 ,[l,h] 是激活值xi 对应的区域。3.2 CLRP方法
文献[28]指出,LRP生成的解释仅特定于实例,却不具备类别区分性,也即对于不同的类别,LRP生成的解释几乎是相同的。产生这一情况的原因,是LRP在解释的过程中使用了相同的特定于实例的结构信息(Instance-Specific Structure Information, ISSInfo),主要是指神经网络中的ReLU和池化操作。这使得前文中提到的
RL+1j= max(0,XLWLj+bLj) 只在最后一层成立,在其他层均不满足这一条件。换言之,对于不同的类别i , LRP的反向传递过程是类似的,接收到非零相关性的神经元也相同,只是绝对值可能不相等。因此,无论选择哪个类别对应的得分进行反向传播,接收到非零相关性的神经元始终保持不变,这使得LRP生成的解释独立于类别信息。CLRP通过构建虚拟类以剔除LRP生成的解释中与目标类别不相关的信息,进而生成具备类别区分性的解释。图5给出了使用CLRP解释网络的基本流程,其中红色路径表示与目标类别无关的LRP解释,蓝色路径表示对目标类别直接进行LRP解释得到的信息。定义与第
j 类相关的神经元nj 描述了一个视觉概念O ,nj 通过权重W={W1,W2,⋯, WL−1,WLj} 与输入形成连接,其中WL 表示连接第L –1层和第L层的权重,WLj 表示连接第L–1层和第L层中第j 个神经元的权重。对于输入样本X,LRP将神经网络得分Snj 映射回输入空间,得到相关向量R=fLRP(X,W,Snj) 。使用对偶虚拟概念ˉO 描述与O 相反的视觉信息,文献[28]给出了两种对ˉO 建模的方法:一是选择除与O 对应类之外的其余所有类,也即ˉO 对应的权重表示为ˉW={W1,W2,⋯, WL−1,WL{−j}} ,其中WL{−j} 表示连接第L –1层和第L层除神经元j 外的权重;二是对权重WLj 求反直接构建一个虚拟类,即ˉW={W1,W2,⋯,WL−1,−1∗WLj} 。ˉO 的相关性可由式(11)计算得到,那么CLRP生成的解释如式(12)所示。Rdual=fLRP(X,ˉW,Snj) (11) RCLRP=max(0,(R−Rdual)) (12) 相比于LRP, CLRP更适用于分析一张图像中存在多个不同类别目标或待分类目标结构相似的情况,但是LRP生成的解释在语义上更完整,更利于理解。考虑到SAR图像中不同目标相似性较高,目视上难以区分,本文在进行模型可解释性分析时,将以CLRP解释为主、以LRP解释为辅。在解释时,主要关注图2(b)所示的网络模型的分类过程,也即主要关注特征提取器和分类器两部分。首先使用LRP分析网络模型在分类过程中更关注哪些区域,分析网络模型决策依据的语义意义;然后利用CLRP进一步生成具有类别区分性的解释,结合域适应前的错分样本分析域适应后网络模型分类性能提升的可能原因。
4. 实验结果与分析
4.1 实验数据与实验设置
实验中使用的仿真数据(即源域数据)由东南大学毫米波国家重点实验室提供,利用该实验室自研软件通过目标电磁建模和散射计算的方式生成。仿真数据包括3类目标:BMP2, BTR70, T72。为保证仿真样本的多样性,仿真数据包括2个俯仰角(15°, 17°)和3种背景:(1)仿真软件自动生成的草地背景;(2)参考光学图像手动设置参数生成的草地背景;(3)参考光学图像手动设置参数生成的沙地背景。图6给出了3类目标的光学图像及典型方位角和俯仰角下的仿真与真实图像。每类目标在每个背景下每隔0.5°方位角生成一张仿真图像,仿真数据集共有12978张图像,按4:1划分仿真训练集和测试集。
以移动与静止目标获取识别(Moving and Stationary Target Acquisition and Recognition, MSTAR)数据集作为实验的目标域数据,MSTAR数据集通常分为标准工作条件(Standard Operating Condition, SOC)和扩展工作条件(Extended Operating Condition, EOC)两类。其中SOC指训练集和测试集的数据成像条件相似;EOC指训练集和测试集的数据成像条件存在一定差异,一般又可分为3类情况,第1类为大俯仰角情况,如训练集数据成像俯仰角为17°,测试集为30°,记为EOC-1;第2类指车辆配置不同,即车辆上某些部件的增加和拆除,如T72移除车上的油罐,记为EOC-2;第3类指车辆版本和功能不同,如原始车辆变化为运输车、侦察车等,记为EOC-3。实验用到的全部数据集大小见表1,其中目标域数据集的SOC数据集、EOC测试集见表2—表5。
表 1 数据集Table 1. Dataset数据集 目标类别 俯仰角 数量 源域(仿真)训练集 BMP2 17°, 15° 3462 BTR70 17°, 15° 3462 T72 17°, 15° 3462 源域(仿真)测试集 BMP2 17°, 15° 864 BTR70 17°, 15° 864 T72 17°, 15° 864 目标域(真实)训练集 BMP2 17° 233 BTR70 17° 233 T72 17° 233 目标域(真实)测试集
(SOC和EOC)BMP2 15°, 17° 1052 BTR70 15° 196 T72 15°, 17°, 30° 5906 表 2 SOC数据集Table 2. SOC dataset目标类别 目标型号 训练集 测试集 俯仰角 数量 俯仰角 数量 BMP2 9563 17° 233 15° 195 BTR70 C71 17° 233 15° 196 T72 132 17° 233 15° 196 表 3 EOC-1测试集(大俯仰角)Table 3. EOC-1 test set (large depression variation)目标类别 目标型号 俯仰角 数量 T72 A64 30° 288 表 4 EOC-2测试集(配置变化)Table 4. EOC-2 test set (configuration variant)目标类别 目标型号 俯仰角 数量 T72 S7 15°, 17° 419 A32 15°, 17° 572 A62 15°, 17° 573 A63 15°, 17° 573 A64 15°, 17° 573 表 5 EOC-3测试集(版本变化)Table 5. EOC-3 test set (version variant)目标类别 目标型号 俯仰角 数量 BMP2 9566 15°, 17° 428 C21 15°, 17° 429 812 15°, 17° 426 A04 15°, 17° 573 T72 A05 15°, 17° 573 A07 15°, 17° 573 A10 15°, 17° 567 实验中,通过在一个批次(batch)的训练中交替执行
minθe,θc(Losscls+γ∗Lossdd) (惩罚因子γ>0 )和minθe,θdLossda 以使模型各部分平滑收敛,具体的参数设置见表6,其中学习率随着训练轮次的增加逐渐减小,如式(13)所示。实验在Linux 3.10.0系统下基于Pytorch 1.4.0框架实现,硬件采用Intel(R) Xeon(R) Gold 5218R CPU @ 2.10GHz和NVIDIA Tesla V100S GPU。表 6 网络训练过程中参数设置Table 6. Parameters for the model training procedure名称 参数值 batch size 32 优化器 SGD 初始学习率lr0 0.01 GRL参数λ 1 惩罚因子γ 1 epoch 500 iteration/epoch 35 lr=lr0(1+10∗jepoch)0.75 (13) 其中,
lr0 为初始学习率,j 为当前的轮次数,epoch 为总的训练轮次数。4.2 消融实验
为验证所提方法的有效性,本文利用不同背景下的SAR仿真图像进行训练,在SOC数据集上进行测试,开展了消融实验,以比较MK-MMD多层自适应正则器和域对抗训练模块对模型分类性能的影响。消融实验的结果见表7。为避免单次训练的随机性,每组进行了3次实验,表7记录了3次实验结果的平均准确率及其标准差,其中仿真背景①、②、③对应4.1节提到的3种仿真背景,表格最后一行指的是同时使用3种背景下的仿真训练集图像。可以看出,本文方法对不同仿真背景SAR图像构成的源域训练集都能有效提升真实样本的分类精度,且除只使用仿真背景①图像的情况外,本文方法优于只使用多层MK-MMD自适应正则器或只采用域对抗训练的方法。对于在只使用仿真背景①图像时本文方法未能达到最好性能这一现象,笔者认为可能是由仿真软件自动生成的背景与目标所处的实际背景差异较大,直接由仿真背景①样本训练得到的模型对实测数据的分类性能较差,只有28.00%左右的准确率。对于本文实验中的3分类任务,仿真背景①图像似乎未能为该任务提供正信息,这可能导致训练过程中以MK-MMD为度量缩减域差异时,也拉近了不同域中不同类别样本的距离,进而导致分类准确率提升效果不好,甚至不如只使用域对抗训练方法的提升效果好。
表 7 结合不同背景仿真SAR图像的消融实验结果Table 7. Results of ablation experiments with simulation SAR images of different backgrounds仿真背景 方法 准确率(%) MK-MMD 域对抗训练 ① × × 28.00±1.39 × √ 47.53±1.39 √ × 35.48±0.52 √ √ 43.44±2.22 ② × × 73.20±1.38 × √ 77.40±2.18 √ × 85.20±1.19 √ √ 87.03±1.29 ③ × × 65.07±0.52 × √ 65.19±2.89 √ × 73.57±0.62 √ √ 77.29±1.58 全部应用 × × 74.79±1.35 × √ 83.99±1.19 √ × 85.85±2.33 √ √ 90.43±0.95 4.3 SOC实验与EOC实验
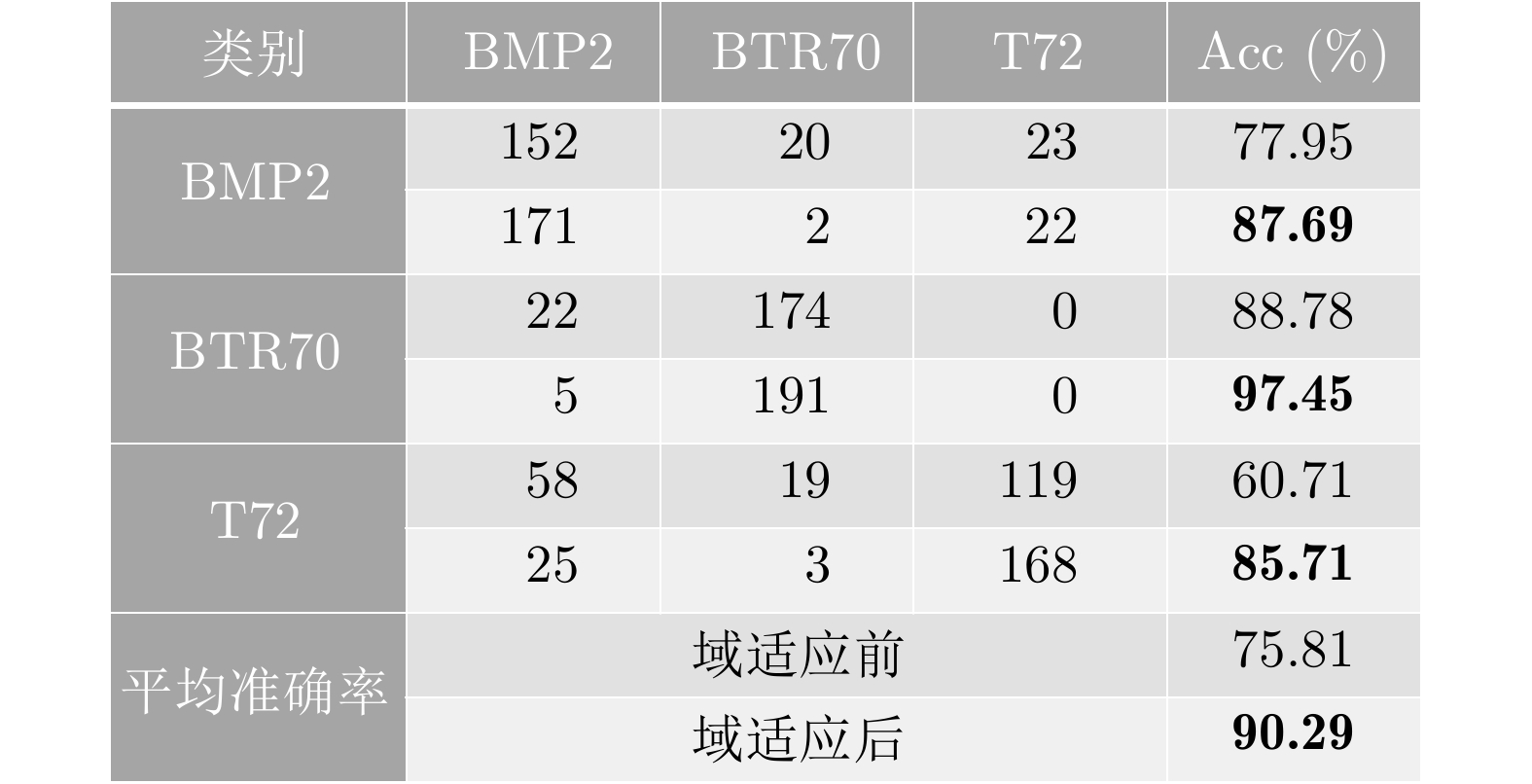
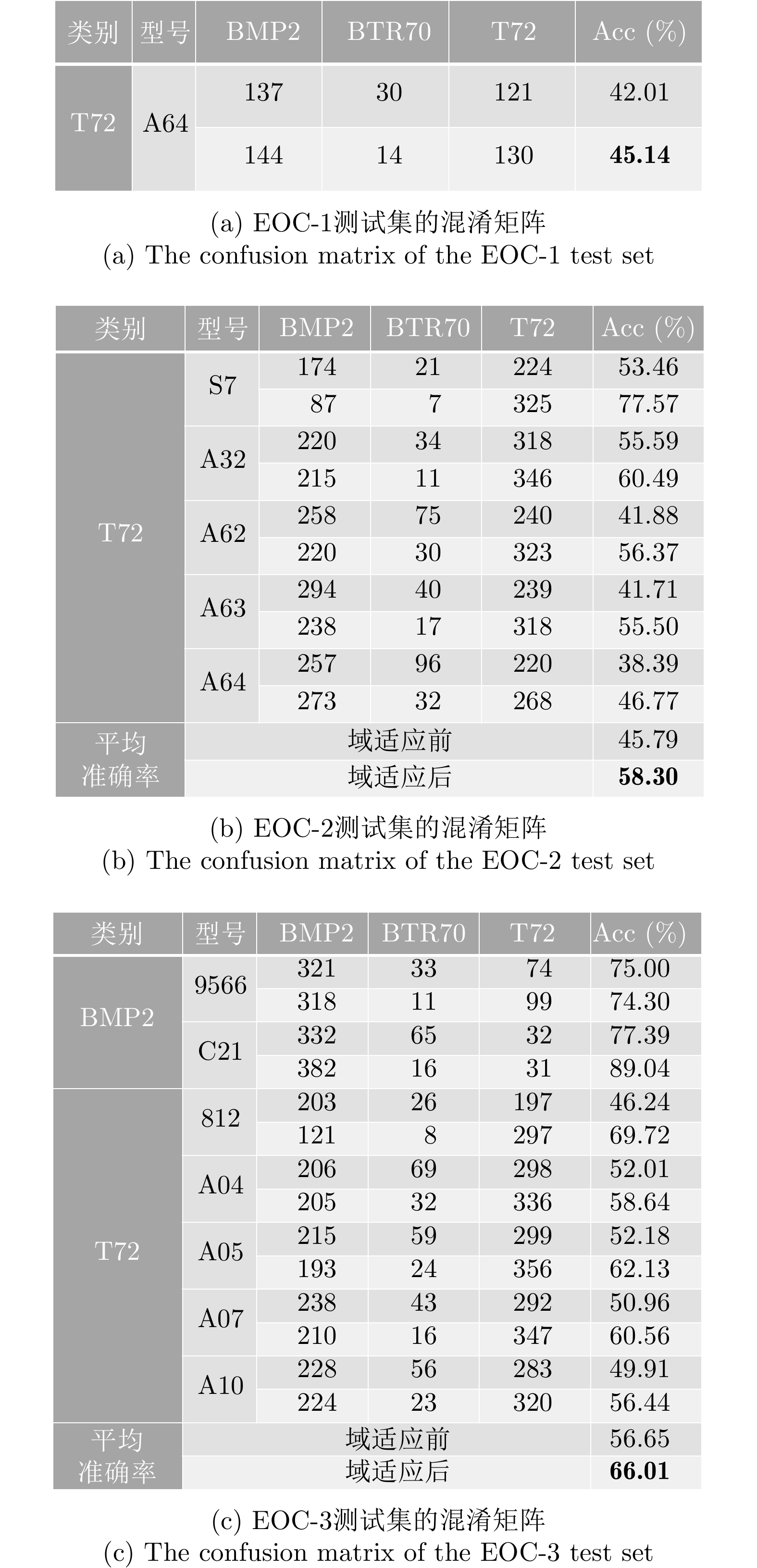
为深入评估模型的分类性能,本文在SOC和EOC测试集上进行了分类测试,图7,图8给出了利用本文所提方法进行域适应前后的混淆矩阵,其中深色行对应域适应前的识别结果,浅色行对应域适应后。实验结果表明,本文方法能显著提升模型在SOC和EOC数据上的分类准确率。
表8给出了使用不同仿真背景数据时,本文所提域适应方法和条件域对抗(Conditional Domain Adversarial Network, CDAN)[19]及深度子域对齐(Deep Subdomain Adaptation Network, DSAN)[14]在SOC测试集上的准确率对比。实验结果表明,针对不同仿真背景情况下的数据,本文方法都能较好地提升仿真辅助SAR目标分类的准确率,尤其在使用全部仿真背景数据时,本文方法分类准确率显著高于CDAN和DSAN方法。表明本文方法集成了域对抗训练和域差异度量两种域适应策略,比使用单一域适应策略的方法具有更好的域适配能力。
表 8 使用不同仿真背景数据时,各方法在SOC测试集上的分类准确率对比Table 8. Comparison of the classification accuracy on the SOC test set when using different methods with simulated data under different backgrounds4.4 模型可解释性分析
图9给出了使用t-SNE[37]对特征提取器提取到的仿真数据特征和真实数据特征降维可视化的结果,可见本文方法有效地拉近了仿真和真实SAR图像的特征分布。
为了对模型的决策机制有更深层次的理解,本文使用LRP和CLRP可视化了输入像素对模型决策结果的影响。实验过程中,参照文献[36]的设置,第1层卷积层应用
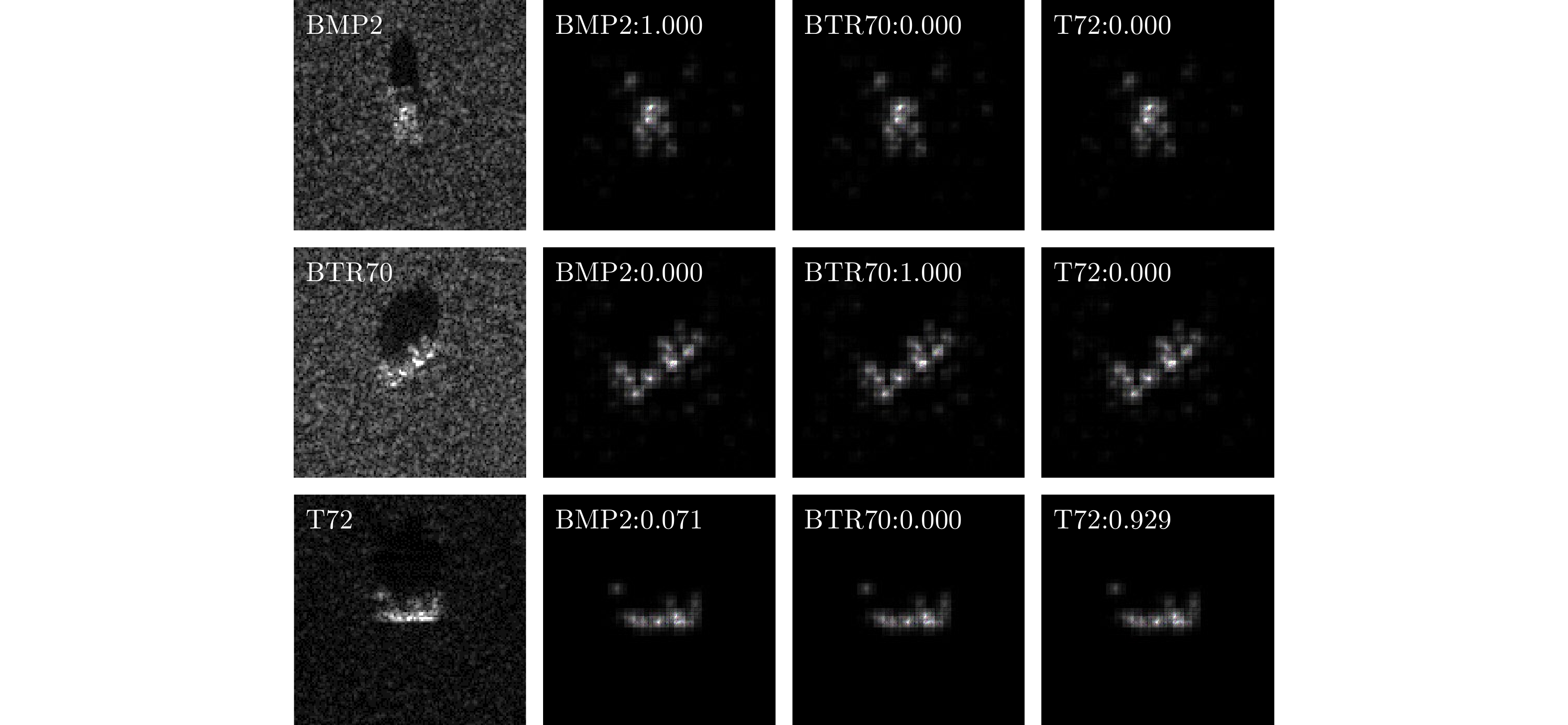
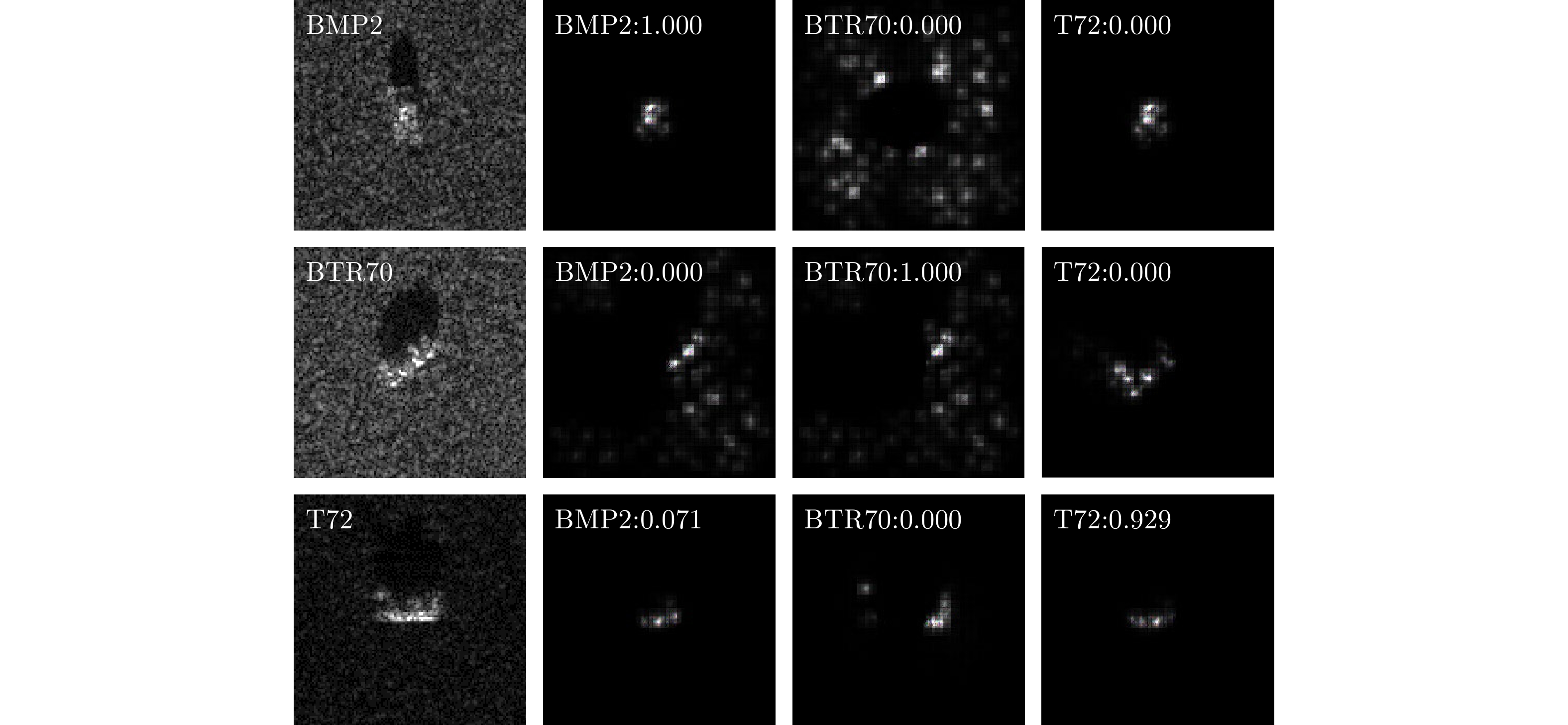
zβ−rule ,其余的卷积层和全连接层使用z+−rule 。对于最大池化层,将相关性系数重新分配到池化区域内值最大的神经元。相关性传播过程中,忽略偏差和标准化层。首先,在由真实数据训练得到的模型上对LRP和CLRP方法进行对比评估,结果如图10、图11所示。图中最左侧一列为输入图像,右侧3列依次为对应类别BMP2, BTR70, T72的解释,其中左上角标注了对应类别的预测得分。LRP生成的解释虽然不具备类别区分性,却能对影响网络决策的区域有一个语义上比较完整的表示,从LRP的解释结果可以看出,影响真实数据分类的关键在于SAR图像中强散射点的分布区域,而这些一般对应于目标中结构或装配复杂的地方,如炮筒、炮台等。CLRP的结果则更有助于理解模型“认为”不同目标之间的异同之处,从图11可以看出,模型认为BMP2和BTR70在背景上更加相似,而BMP2和T72在结构上更相似,这也与MSTAR提供的光学图像(图6)中反映出来的目标实际结构和所处背景中体现出来的信息一致。从结构上来说,BMP2和T72均为履带式车辆且装有圆形炮台和炮筒,BTR70为轮式运输车,没有装配火炮;从背景上来看,BMP2和BTR70目标所处的背景相近,而T72与之相异。
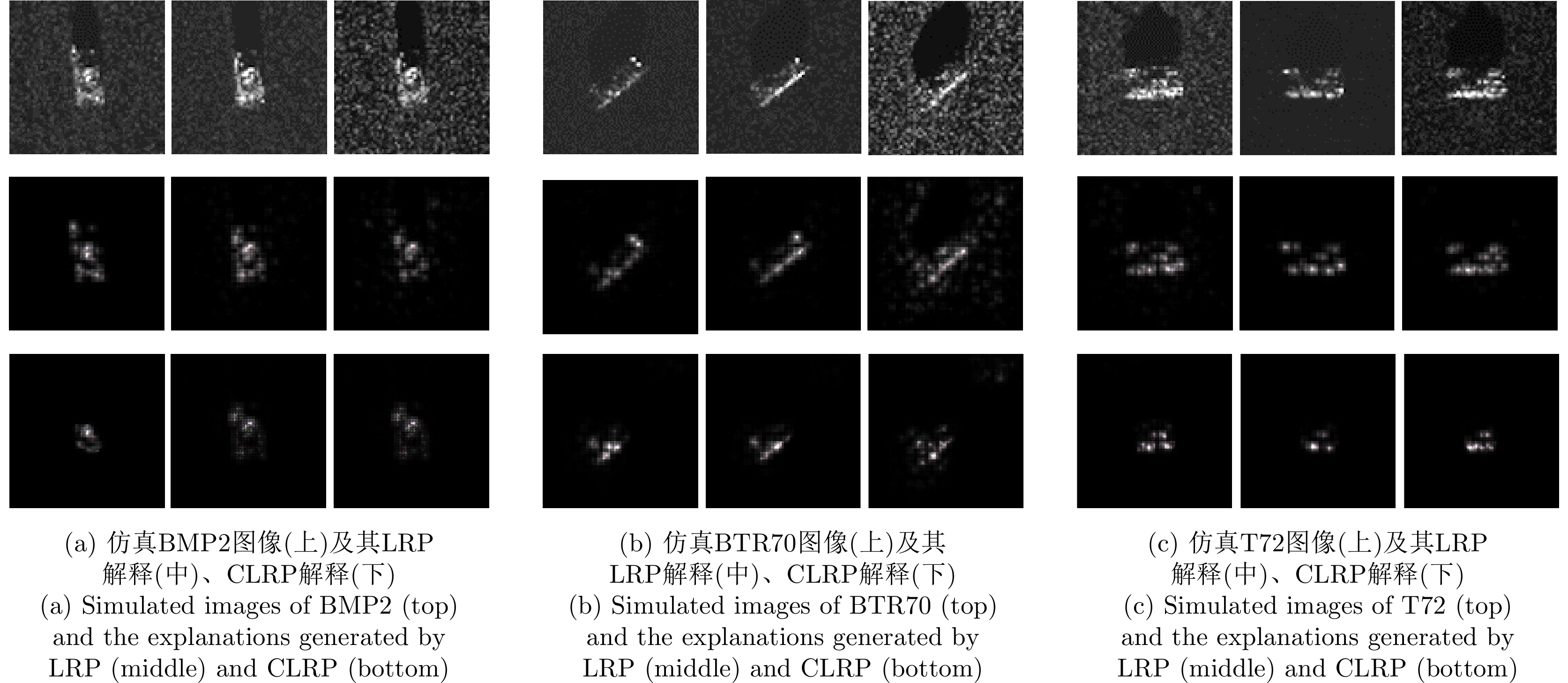
图12展示了仿真数据训练所得模型对不同背景下仿真图像的LRP解释及对应真值类别的CLRP解释,其中从左至右依次对应仿真背景①、②、③。可以看出,LRP和CLRP解释对于同一目标的不同图像关注区域大体一致,一定程度上可以证明这两种解释方法的有效性和鲁棒性。此外,从图12的解释结果中也可以看出仿真数据训练的模型也学习到了不同目标之间结构上的差异,较少关注背景区域。
前文提到,由于仿真图像和真实图像之间的域偏移,直接用仿真数据训练得到的模型对真实数据分类结果并不理想,本文尝试结合可解释性方法对仿真辅助真实数据分类任务中的域偏移问题给出一个具象的解释。图7所示的混淆矩阵中,在域适应前,T72的目标图像中有相当一部分被误判为BMP2。从这一现象出发,本文使用LRP和CLRP分析由仿真数据训练得到的模型(即域适应前的模型)对仿真和真实T72图像判断依据的异同,并结合CLRP进一步分析域适应前后模型对真实T72图像判断依据的变化。图13给出了域适应前的模型对仿真和真实图像的分类结果及对应的解释,其中CLRP-T72表示由CLRP分析得到的模型“认为”输入样本像T72的地方,CLRP可视化图像中左上方标注了对应类别的得分。图13用红色标注出了模型决策依据中存在较大差异的区域,图13(a)中这一区域大致对应T72目标的炮台结构,可以看出,在仿真图像中这一区域散射强度较大,而实测图像中散射较弱,仿真图像训练的网络模型在仿真图像上关注到了该区域特征,而应用到实测图像上则关注不到该区域特征,从而导致误判;图13(b)中差异较大的区域大致对应车头和车尾,实测图像中对应区域的散射强度高于仿真图像,对模型决策造成干扰,从而导致误判。
图14给出了域适应前后的模型对真实T72图像判断依据的变化,其中图14(a)对应域适应前后模型决策由错到对的T72样本,图14(b)则对应域适应后模型仍旧给出错误判断的样本。结合图13来看,图14(a)中域适应后的模型小范围修正了关注区域,提取到了炮台等区域的特征,给出了更准确的决策。但对于域适应后仍旧错分的样本,可能是域适应前的关注区域与应该关注的区域偏离较大,使得网络在域适应训练后对该样本的关注区域无法有效修正,反而引入了较多的背景区域,导致网络依然只能给出错误的判别结果。
5. 结束语
本文针对深度学习在SAR目标识别领域面临的标注样本少、标注样本难的问题,提出了一种集成域对抗训练和MK-MMD的无监督域适应方法,以充分利用仿真SAR图像可以快速生成且天然具备标签的优势,实现较高精度的仿真辅助的SAR目标分类。
同时,考虑到深度学习可解释性差、可信任程度不足等问题,本文使用可解释性方法LRP和CLRP对所提出的模型进行深入分析。结果表明,本文神经网络是通过修正模型关注区域来提升仿真辅助SAR图像分类的性能,具有一定的合理性。
但是,从可解释性分析的结果来看,模型并非对所有样本都找到了可靠的决策依据,且当仿真样本训练模型对真实数据直接分类效果较差时(如仿真背景①训练的模型),本文方法提升效果不明显,仍旧存在一定的局限性。未来的工作中,考虑从以下两方面继续优化本文方法:(1)本文方法虽然在MSTAR 3分类任务上表现出了不错的提升效果,但目前仿真目标类别较少,缺少在更多类别上的实验验证;(2)本文使用可解性方法分析了模型性能提升的原因,也找到了可能导致仿真和真实图像之间域偏移的目标主要结构,后续将考虑利用解释结果指导仿真方法调整和优化,并利用可解释性方法引导网络训练,帮助网络模型找到可靠的决策依据。
-
表 1 雷达和目标参数
Table 1. Parameters of radar and target
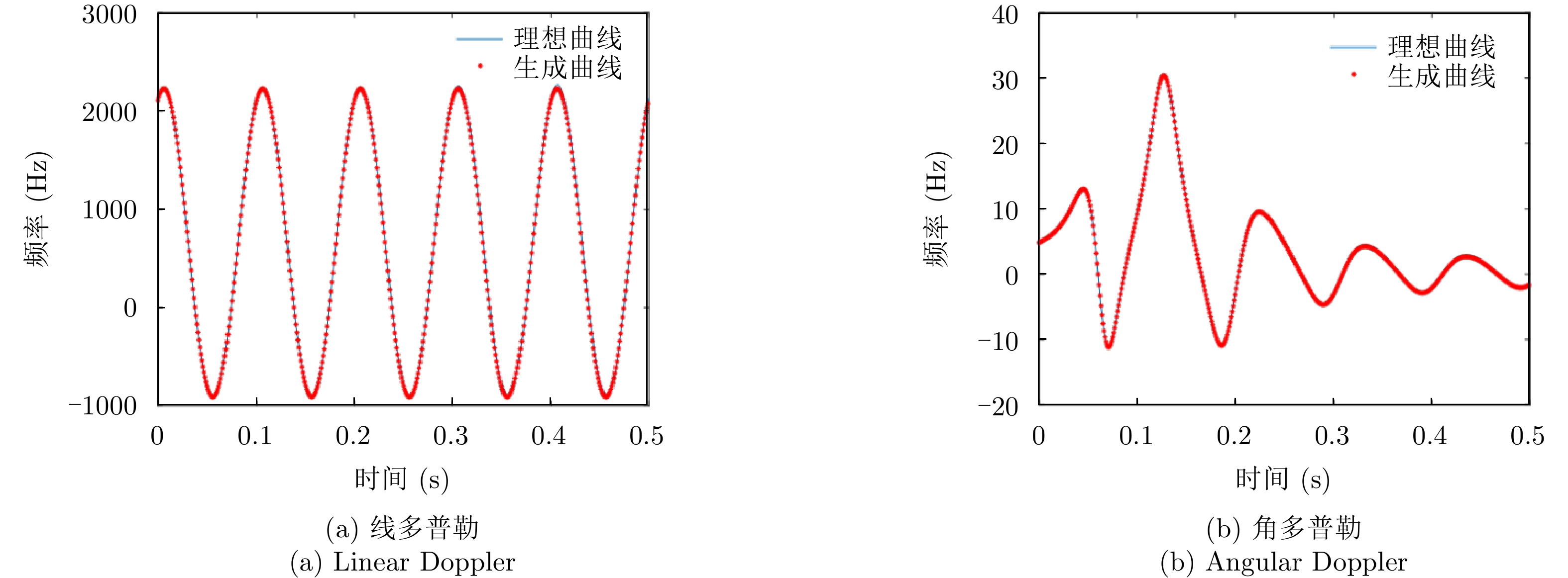
参数 数值 载频(GHz) 10 阵列半径(m) 1 模态数 4 旋转半径(m) 0.4 旋转频率(Hz) 10 欧拉角(rad) (1.0472,0.7854,0) 旋转矢量 (0.707,–0.612,0.353) 旋转中心(m) (0.8,1,100) 速度矢量(m/s) (–10, –5, 10) 表 2 选取点的时刻和角多普勒值
Table 2. The time and angular Doppler value of the selected point
序号 时刻(s) 角多普勒(Hz) 1 0 4.8271 2 0.0133 6.1418 3 0.0267 8.5308 4 0.0400 12.2020 5 0.0534 9.2937 6 0.0667 –9.3425 7 0.0800 –5.6511 8 0.0934 4.6931 表 3 求解过程的迭代误差
Table 3. Iterative error in the solving process
迭代次数 误差 学习率 1 2571.63 0.01 2 555.784 0.001 3 214.932 1 4 110.276 10 5 79.972 1 6 59.7386 0.1 7 15.365 0.01 8 9.63835 1 9 5.24274 0.1 10 0.994269 0.01 11 0.005036 0.001 12 5.25×10–7 0.0001 13 5.26×10–15 10–5 表 4 多元非线性方程组求解结果
Table 4. Solution results of multivariate nonlinear equations
参数 估计值 理想值 欧拉角(rad) (1.047,0.785) (1.0472,0.7854) 旋转半径相对大小(m) 0.631 0.4 旋转中心相对大小(m) (1.26,1.57) (0.8,1) 速度矢量相对大小(m/s) (–15.79, –7.89) (–10, –5) 表 5 完整周期频移曲线下的微动参数估计结果
Table 5. Estimation results of micro-motion parameters under complete periodic frequency shift curve
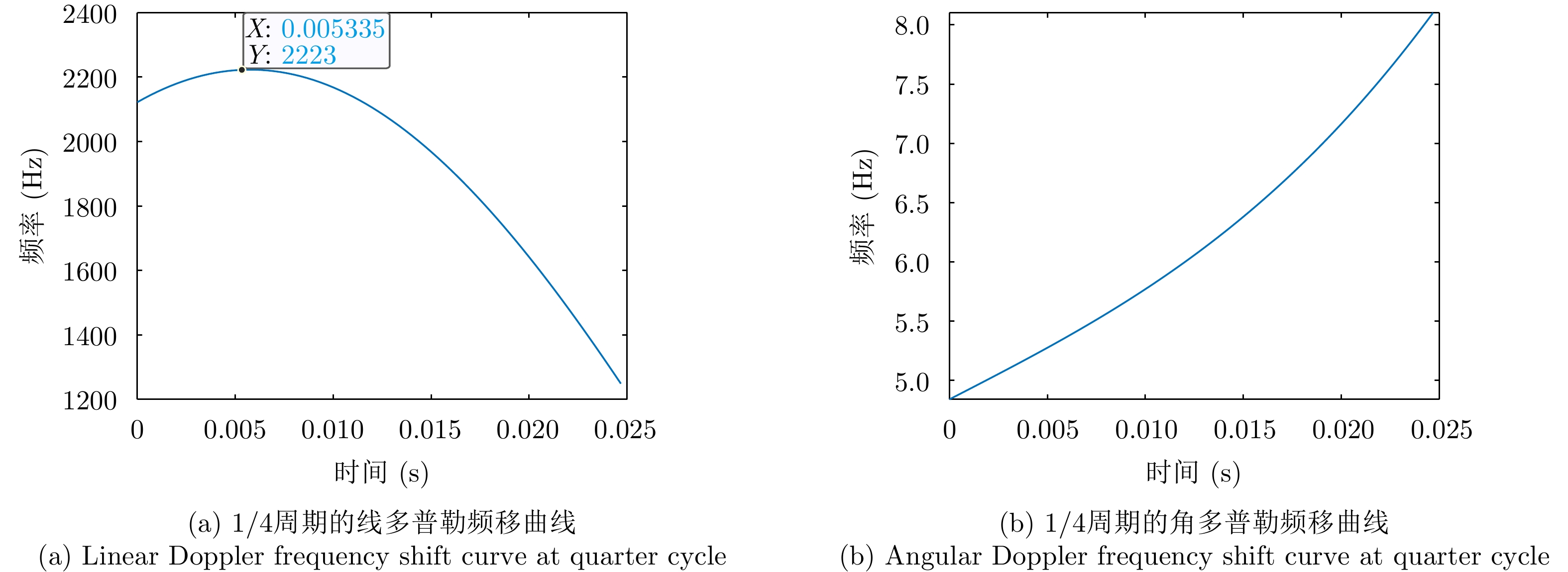
参数 估计值 理想值 误差 旋转矢量 (0.707,–0.612,0.353) (0.707,–0.612,0.353) 0.04% 旋转频率 9.944 Hz 10 Hz 0.56% 旋转半径 0.398 m 0.4 m 0.50% 旋转中心 (0.796,0.995) m (0.8,1) m 2.75% 速度矢量 (–9.953, –4.976) m/s (–10, –5) m/s 0.46% 表 6 选取1/4周期内8个点的时刻和角多普勒值
Table 6. Select the time and angular Doppler Values of 8 points within a quarter cycle
序号 时刻(s) 角多普勒(Hz) 1 0.0010 4.9123 2 0.0043 5.2019 3 0.0076 5.5134 4 0.0110 5.8640 5 0.0143 6.2706 6 0.0176 6.7500 7 0.0210 7.3187 8 0.0243 7.9918 表 7 1/4周期多元非线性方程组求解结果
Table 7. Solution results of multivariate nonlinear equations under 1/4 period
参数 估计值 理想值 欧拉角(rad) (1.047,0.785) (1.0472,0.7854) 旋转半径相对大小(m) 0.068 0.4 旋转中心相对大小(m) (0.136,0.171) (0.8,1) 速度矢量相对大小(m/s) (–1.709, –0.854) (–10, –5) 表 8 1/4周期频移曲线下的微动参数估计结果
Table 8. Estimation results of micro-motion parameters at quarter periodic frequency shift curve
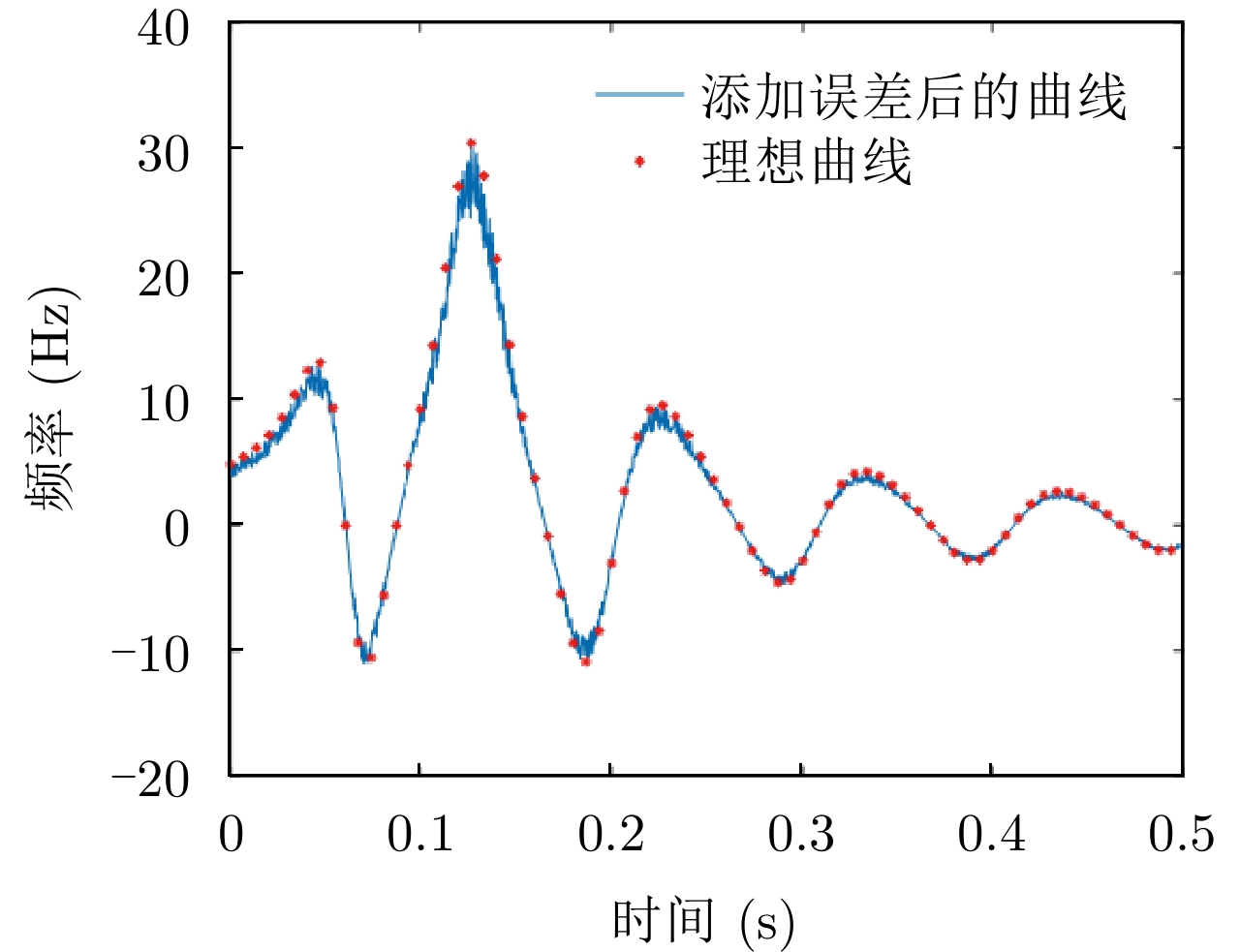
参数 估计值 理想值 误差 旋转矢量 (0.707,–0.612,0.353) m (0.707,–0.612,0.353) m 0.04% 旋转频率 9.944 Hz 10 Hz 0.56% 旋转半径 0.398 m 0.4 m 0.50% 旋转中心 (0.796,0.995) m (0.8,1) m 2.75% 速度矢量 (–9.953, –4.976) m/s (–10, –5) m/s 0.46% 表 9 添加误差后6个点的时刻和角多普勒值
Table 9. Time and angle Doppler values of 6 points after adding error
序号 时刻(s) 角多普勒(Hz) 误差(%) 1 0.0003 3.8878 19.93 2 0.0170 5.4510 18.01 3 0.0337 9.2341 11.79 4 0.0504 11.4651 1.48 5 0.0670 –8.7959 8.84 6 0.0837 –2.1743 11.49 表 10 添加误差后的微动参数估计结果
Table 10. Estimation results of micro-motion parameters after adding errors
参数 估计值 理想值 误差 旋转矢量 (0.760, –0.583, 0.271) m (0.707, –0.612, 0.353) m 12.36% 旋转频率 9.944 Hz 10 Hz 0.56% 旋转半径 0.389 m 0.4 m 2.62% 旋转中心 (0.71,1.02) m (0.8,1) m 6.36% 速度矢量 (–9.00, –6.02) m/s (–10, –5) m/s 15.18% -
[1] 陈小龙, 关键, 何友. 微多普勒理论在海面目标检测中的应用及展望[J]. 雷达学报, 2013, 2(1): 123–134. doi: 10.3724/SP.J.1300.2012.20102CHEN Xiaolong, GUAN Jian, and HE You. Applications and prospect of micro-motion theory in the detection of sea surface target[J]. Journal of Radars, 2013, 2(1): 123–134. doi: 10.3724/SP.J.1300.2012.20102 [2] LIU Yingxi, ZHANG Qun, LIU Zhidong, et al. An anti-jamming method against interrupted sampling repeater jamming based on compressed sensing[J]. Sensors, 2022, 22(6): 2239. doi: 10.3390/s22062239 [3] XIONG Shichao, NI Jiacheng, ZHANG Qun, et al. Ground moving target imaging for highly squint SAR by modified minimum entropy algorithm and spectrum rotation[J]. Remote Sensing, 2021, 13(21): 4373. doi: 10.3390/rs13214373 [4] WANG Haobo, LI Kaiming, LU Xiaofei, et al. ISAR resolution enhancement method exploiting generative adversarial network[J]. Remote Sensing, 2022, 14(5): 1291. doi: 10.3390/rs14051291 [5] 郭忠义, 汪彦哲, 王运来, 等. 涡旋电磁波旋转多普勒效应研究进展[J]. 雷达学报, 2021, 10(5): 725–739. doi: 10.12000/JR21109GUO Zhongyi, WANG Yanzhe, WANG Yunlai, et al. Research advances on the rotational Doppler effect of vortex electromagnetic waves[J]. Journal of Radars, 2021, 10(5): 725–739. doi: 10.12000/JR21109 [6] WANG Zhihao, LUO Ying, LI Kaiming, et al. Micro-Doppler parameters extraction of precession cone-shaped targets based on rotating antenna[J]. Remote Sensing, 2022, 14(11): 2549. doi: 10.3390/rs14112549 [7] WANG Zhihao, CHEN Yijun, YUAN Hang, et al. Real micro-Doppler parameters extraction of spinning targets based on rotating interference antenna[J]. Remote Sensing, 2022, 14(21): 5300. doi: 10.3390/rs14215300 [8] TIAN Xudong, BAI Xueru, and ZHOU Feng. Recognition of micro-motion space targets based on attention-augmented cross-modal feature fusion recognition network[J]. IEEE Transactions on Geoscience and Remote Sensing, 2023, 61: 5104909. doi: 10.1109/TGRS.2023.3275991 [9] ZHOU Xuening, BAI Xueru, WANG Li, et al. Robust ISAR target recognition based on ADRISAR-net[J]. IEEE Transactions on Aerospace and Electronic Systems, 2022, 58(6): 5494–5505. doi: 10.1109/TAES.2022.3174826 [10] BAI Xueru, HUI Ye, WANG Li, et al. Radar-based human gait recognition using dual-channel deep convolutional neural network[J]. IEEE Transactions on Geoscience and Remote Sensing, 2019, 57(12): 9767–9778. doi: 10.1109/TGRS.2019.2929096 [11] CHEN Xuebin, YE Chunmao, WANG Yong, et al. Unambiguous estimation of multidimensional parameters for space precession targets with wideband radar measurements[J]. IEEE Transactions on Geoscience and Remote Sensing, 2022, 60: 5112716. doi: 10.1109/TGRS.2022.3168326 [12] 张群, 胡健, 罗迎, 等. 微动目标雷达特征提取、成像与识别研究进展[J]. 雷达学报, 2018, 7(5): 531–547. doi: 10.12000/JR18049ZHANG Qun, HU Jian, LUO Ying, et al. Research progresses in radar feature extraction, imaging, and recognition of target with micro-motions[J]. Journal of Radars, 2018, 7(5): 531–547. doi: 10.12000/JR18049 [13] 罗迎, 龚逸帅, 陈怡君, 等. 基于跟踪脉冲的MIMO雷达多目标微动特征提取[J]. 雷达学报, 2018, 7(5): 575–584. doi: 10.12000/JR18035LUO Ying, GONG Yishuai, CHEN Yijun, et al. Multi-target micro-motion feature extraction based on tracking pulses in MIMO radar[J]. Journal of Radars, 2018, 7(5): 575–584. doi: 10.12000/JR18035 [14] XU Xuguang and FENG Cunqian. Micro-Doppler extraction of radar targets with translational motion based on spatial transformer network[J]. IEEE Signal Processing Letters, 2022, 29: 2348–2352. doi: 10.1109/LSP.2022.3217411 [15] GHALEB A, VIGNAUD L, and NICOLAS J M. Micro-Doppler analysis of pedestrians in ISAR imaging[C]. 2008 IEEE Radar Conference, Rome, Italy, 2008: 1–5. [16] YUAN Hang, CHEN YiJun, LUO Ying, et al. A resolution-improved imaging algorithm based on uniform circular array[J]. IEEE Antennas and Wireless Propagation Letters, 2022, 21(3): 461–465. doi: 10.1109/LAWP.2021.3135806 [17] LIU Kang, CHENG Yongqiang, LI Xiang, et al. Passive OAM-based radar imaging with single-in-multiple-out mode[J]. IEEE Microwave and Wireless Components Letters, 2018, 28(9): 840–842. doi: 10.1109/LMWC.2018.2852146 [18] LIU Kang, CHENG Yongqiang, GAO Yue, et al. Super-resolution radar imaging based on experimental OAM beams[J]. Applied Physics Letters, 2017, 110(16): 164102. doi: 10.1063/1.4981253 [19] LUO Ying, CHEN Yijun, ZHU Yongzhong, et al. Doppler effect and micro-Doppler effect of vortex-electromagnetic-wave-based radar[J]. IET Radar, Sonar & Navigation, 2020, 14(1): 2–9. doi: 10.1049/iet-rsn.2019.0124 [20] YUAN Hang, LUO Ying, CHEN Yijun, et al. Micro-motion parameter extraction of rotating target based on vortex electromagnetic wave radar[J]. IET Radar, Sonar & Navigation, 2021, 15(12): 1594–1606. doi: 10.1049/rsn2.12149 [21] WANG Yu, LIU Kang, LIU Hongyan, et al. Detection of rotational object in arbitrary position using vortex electromagnetic waves[J]. IEEE Sensors Journal, 2021, 21(4): 4989–4994. doi: 10.1109/JSEN.2020.3032665 [22] WU Zhenxiang, ZHOU Tong, LI Lei, et al. A new modified efficient Levenberg-Marquardt method for solving systems of nonlinear equations[J]. Mathematical Problems in Engineering, 2021, 2021: 5608195. doi: 10.1155/2021/5608195 期刊类型引用(3)
1. 闫莉,许高添,张廷豪. 基于改进混合坐标系的大斜视俯冲机动平台SAR快速时域成像算法. 电子学报. 2024(10): 3472-3481 .  百度学术
百度学术2. 刘裕洲,蔡天倚,李亚超,宋炫,王选琪,安培赟. 联合距离方位二维NCS的星弹双基前视SAR成像算法. 雷达学报. 2023(06): 1202-1214 .  本站查看
本站查看3. Yi Xiong,Buge Liang,Ning Wang,Jianlai Chen. Nonlinear Trajectory SAR Imaging Algorithms:Overview and Experimental Comparison. Journal of Beijing Institute of Technology. 2023(06): 653-669 .  必应学术
必应学术其他类型引用(3)
-



 作者中心
作者中心 专家审稿
专家审稿 责编办公
责编办公 编辑办公
编辑办公


 下载:
下载:


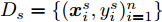
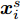
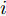
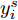
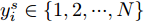
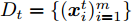

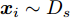

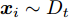
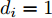
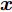
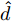
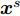
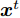
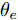
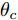
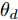
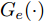

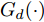
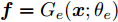

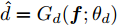
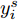
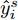
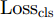
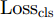
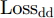
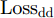
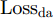
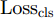
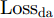
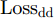
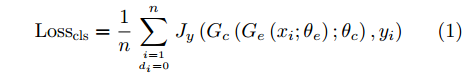
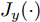
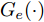
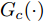
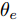
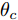
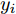
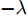
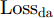
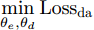
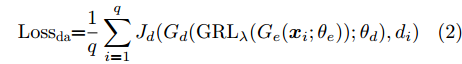

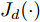
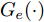
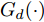
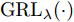
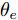
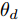
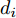
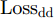
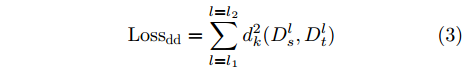
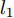
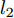
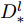

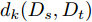
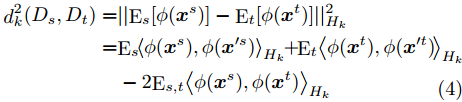
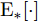
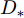
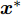
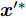
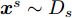
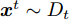
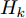
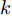

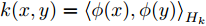
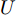
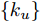
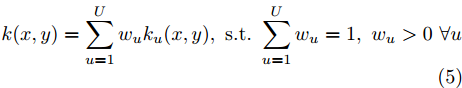
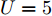
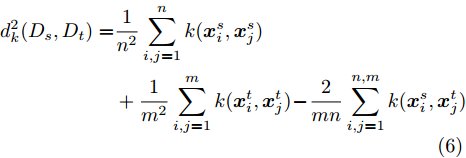
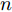

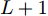

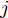
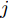
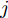
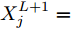

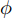
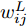
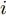
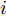


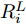

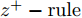
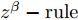



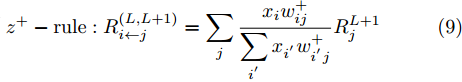
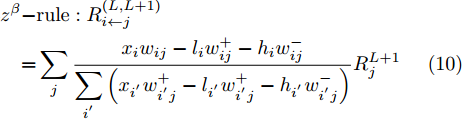
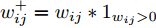
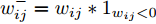
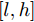
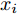
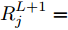
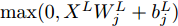
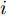
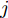
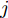
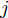
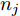
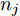



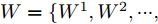
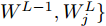

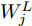

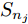
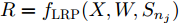
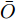
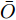
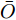
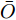
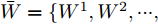

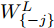
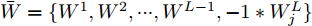

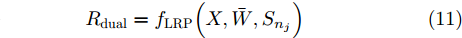
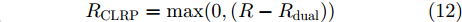

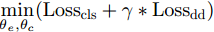
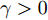
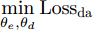
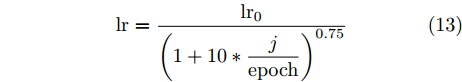
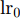
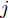




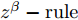
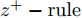





 下载:
下载:








 百度学术
百度学术