Three-dimensional Micro-motion Parameters Extraction of Translational Rotating Targets Based on Vortex Electromagnetic Wave Radar
-
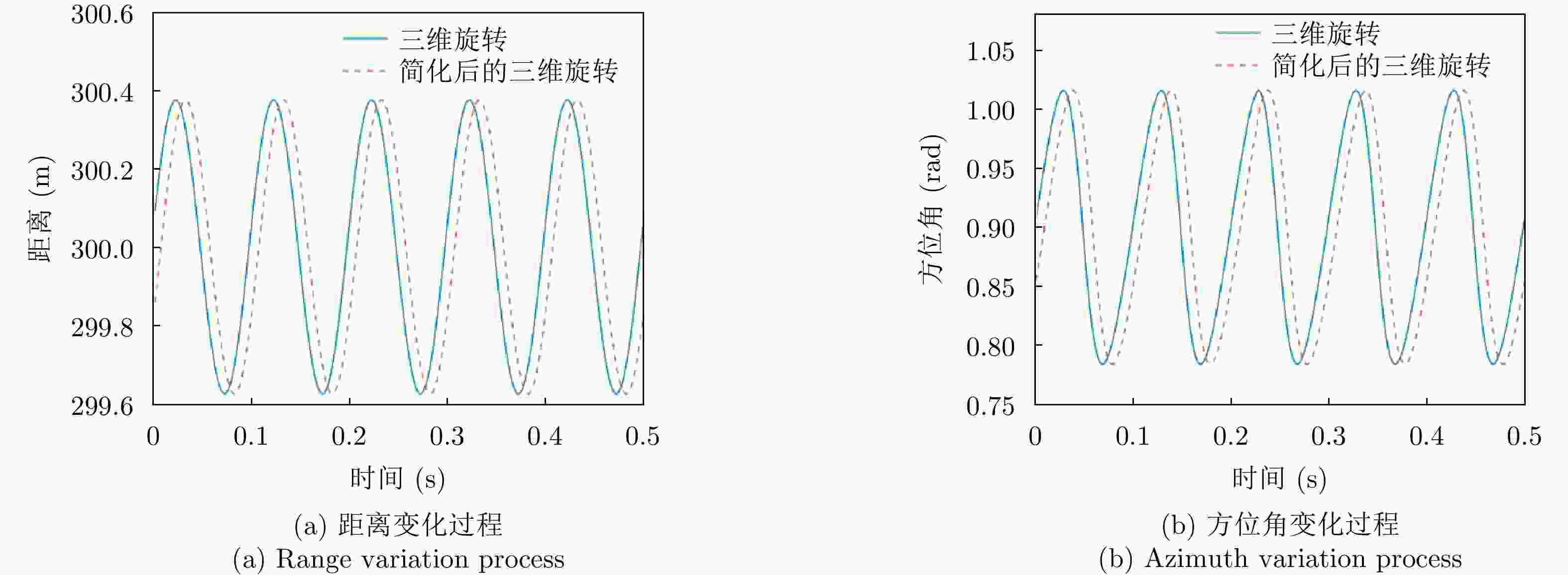
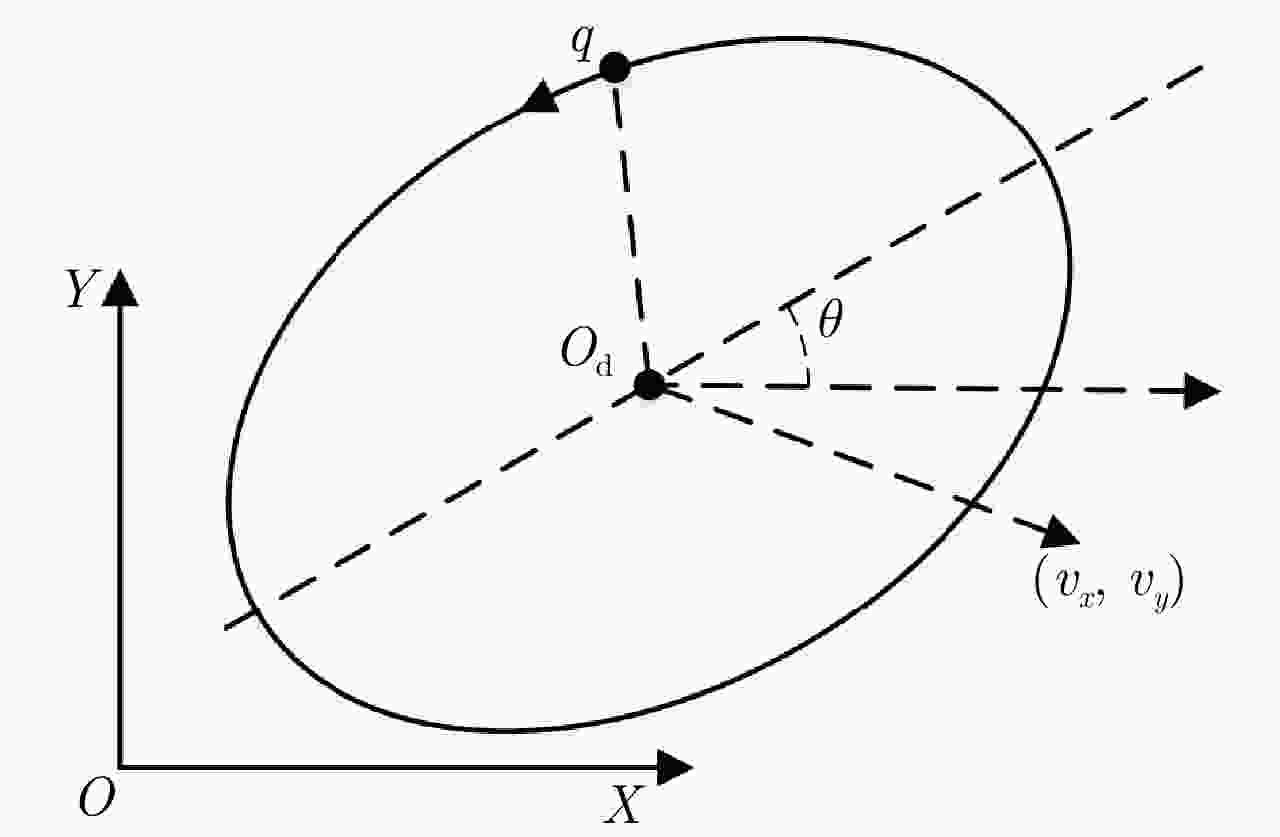
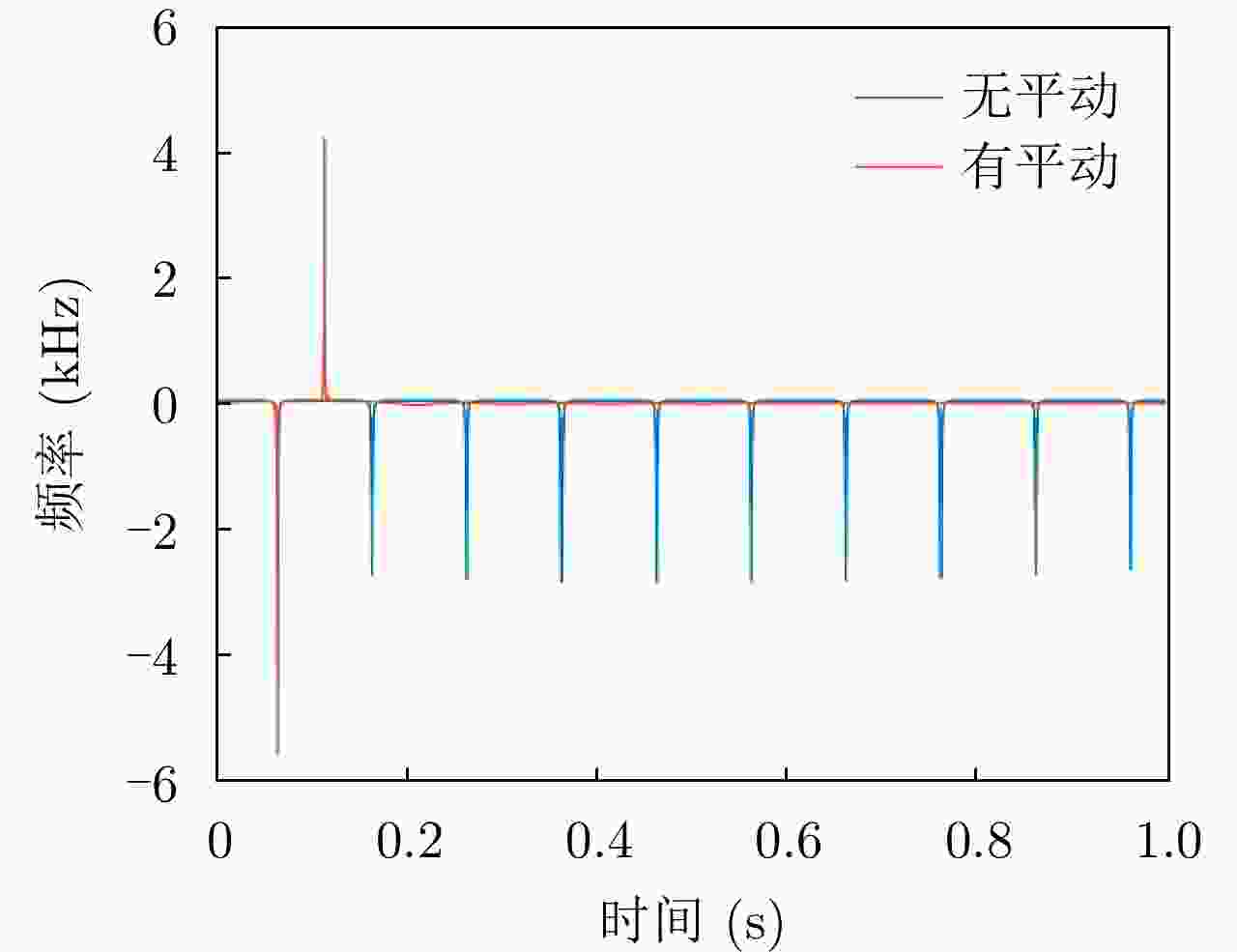
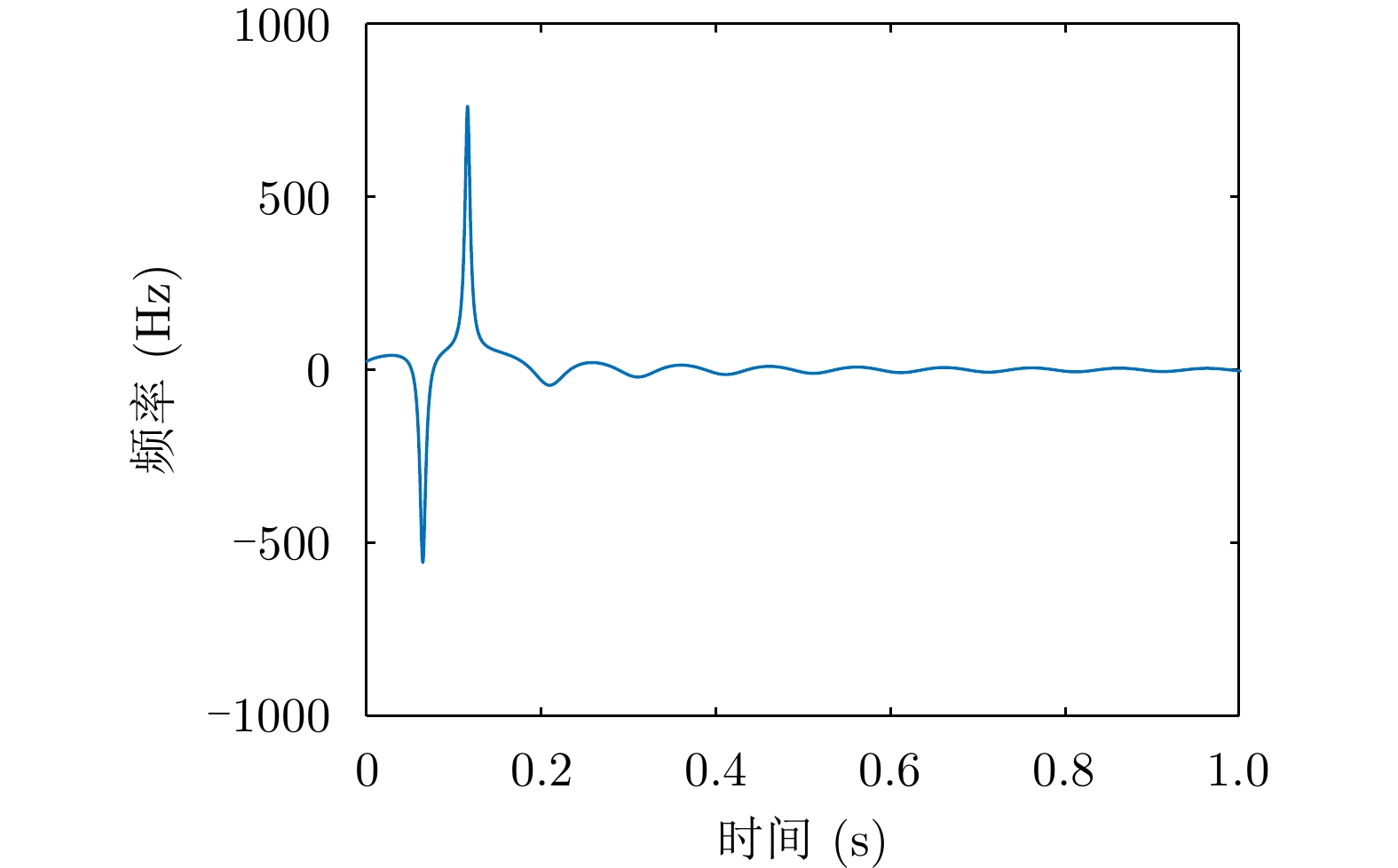
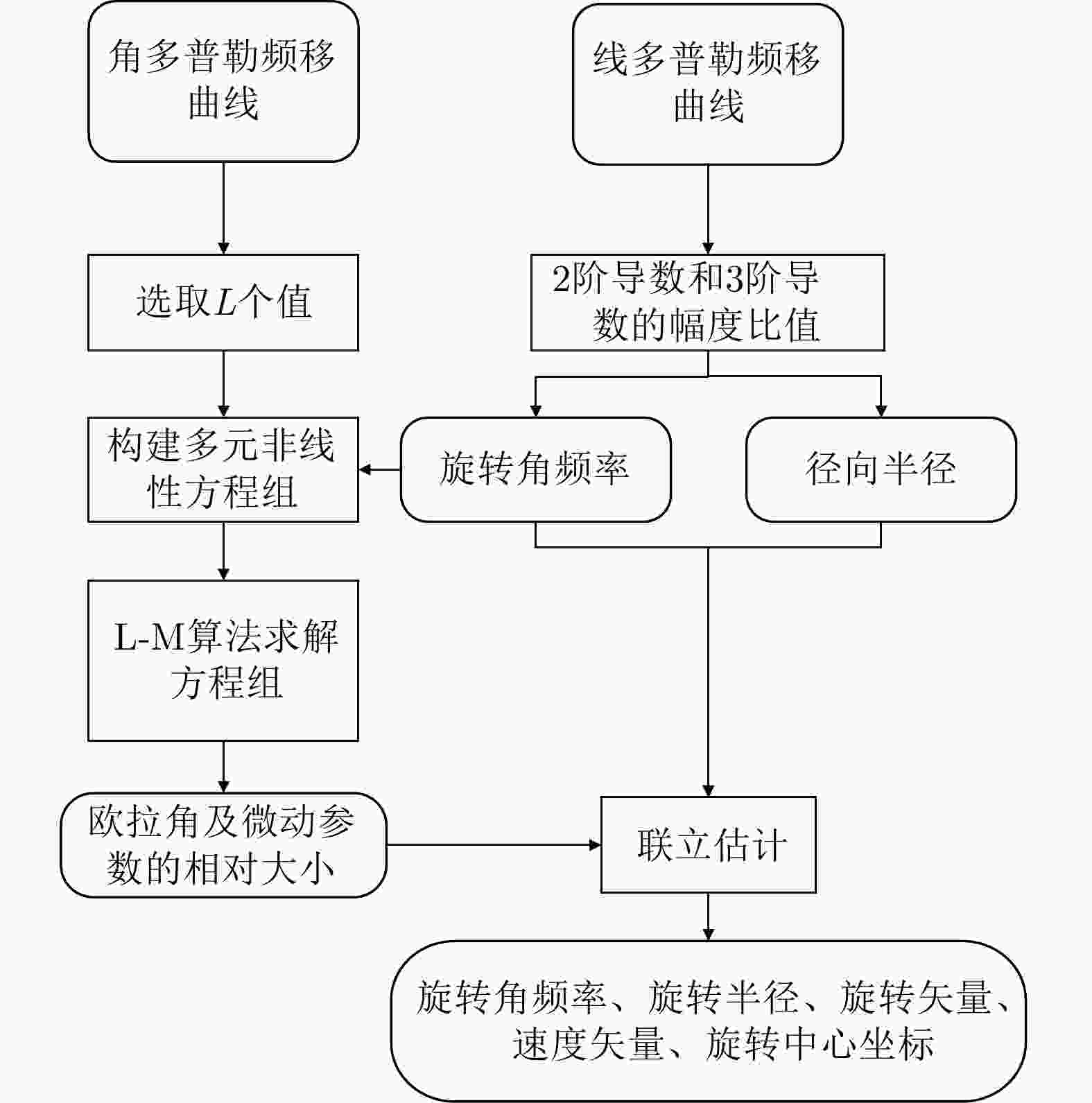
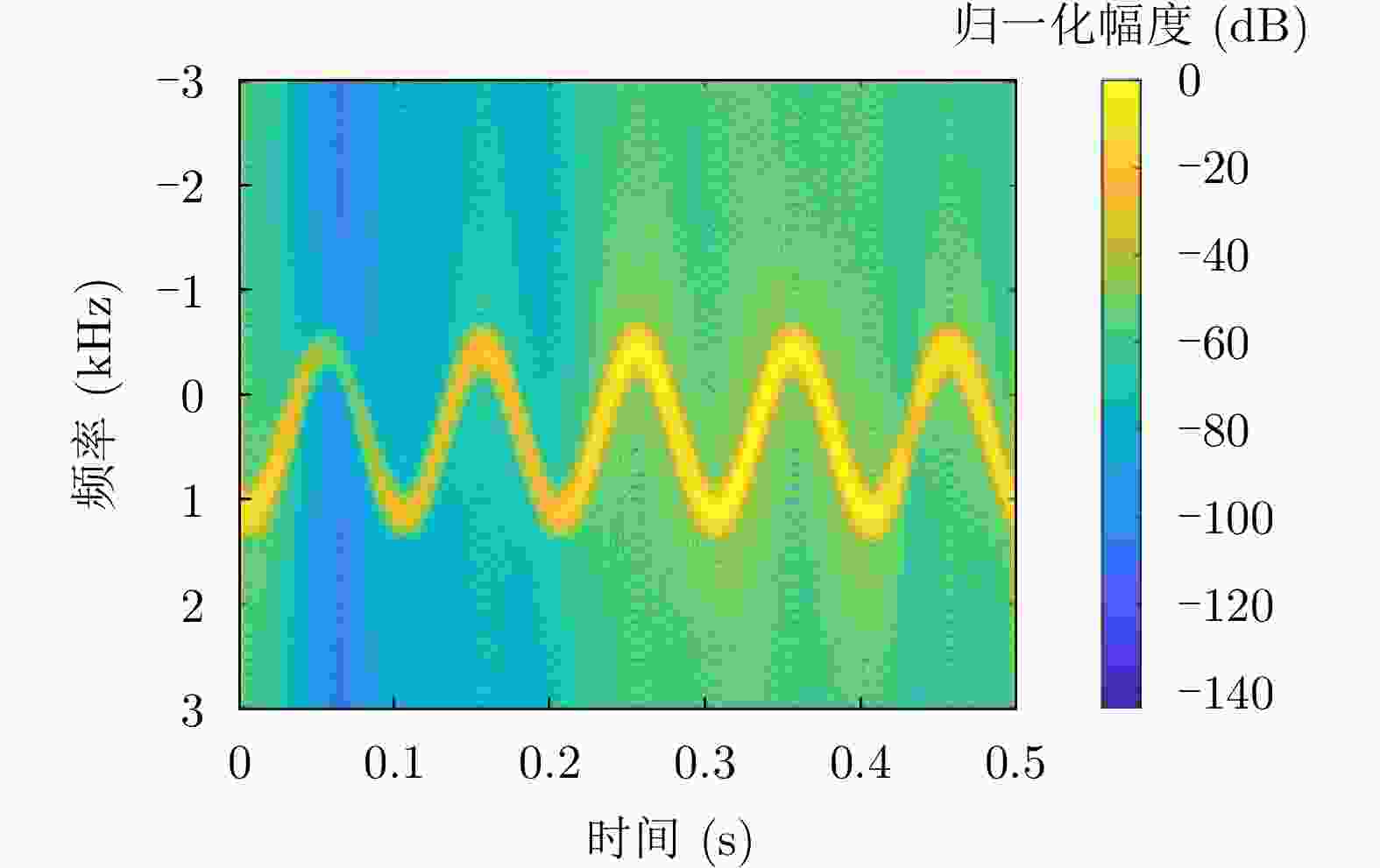
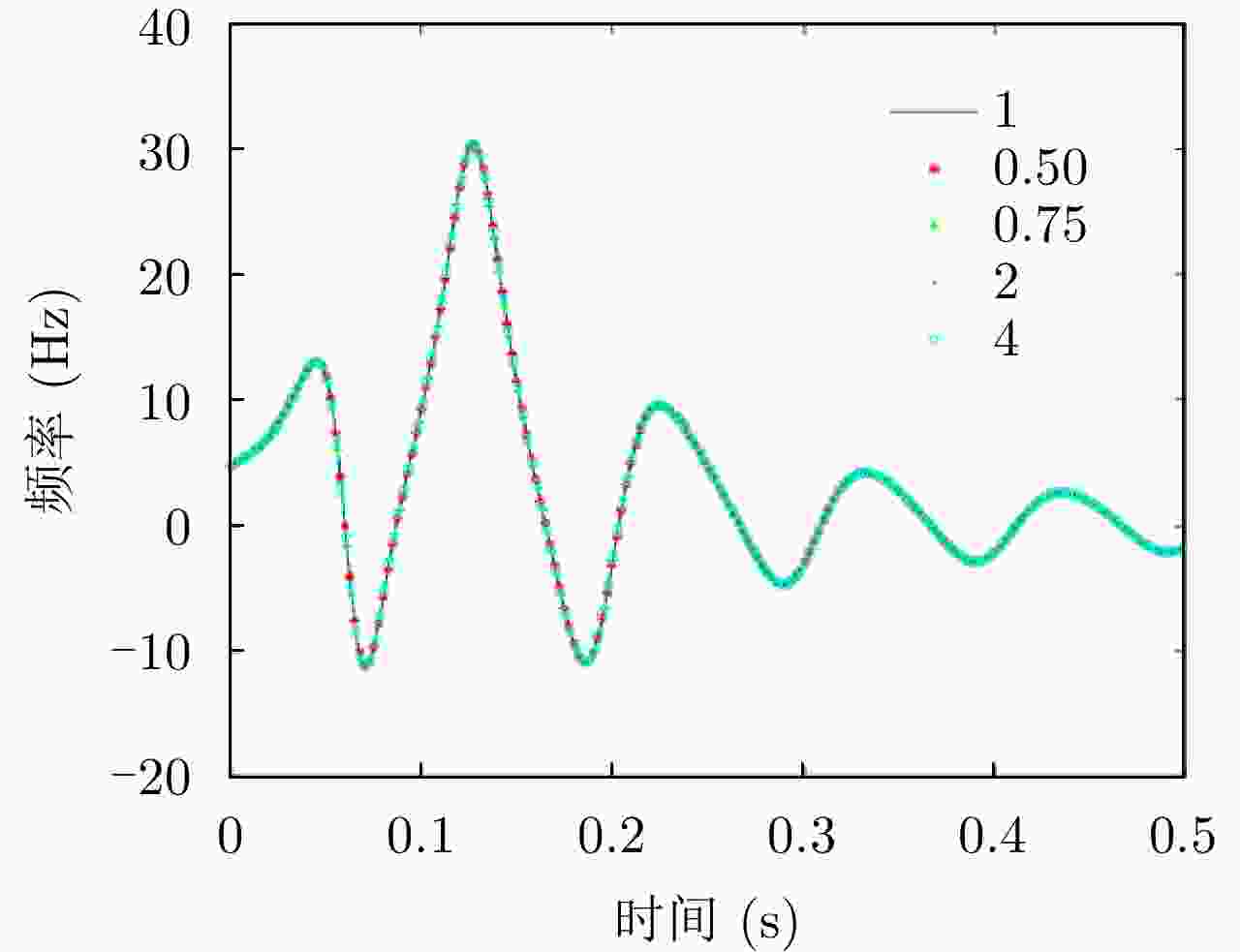
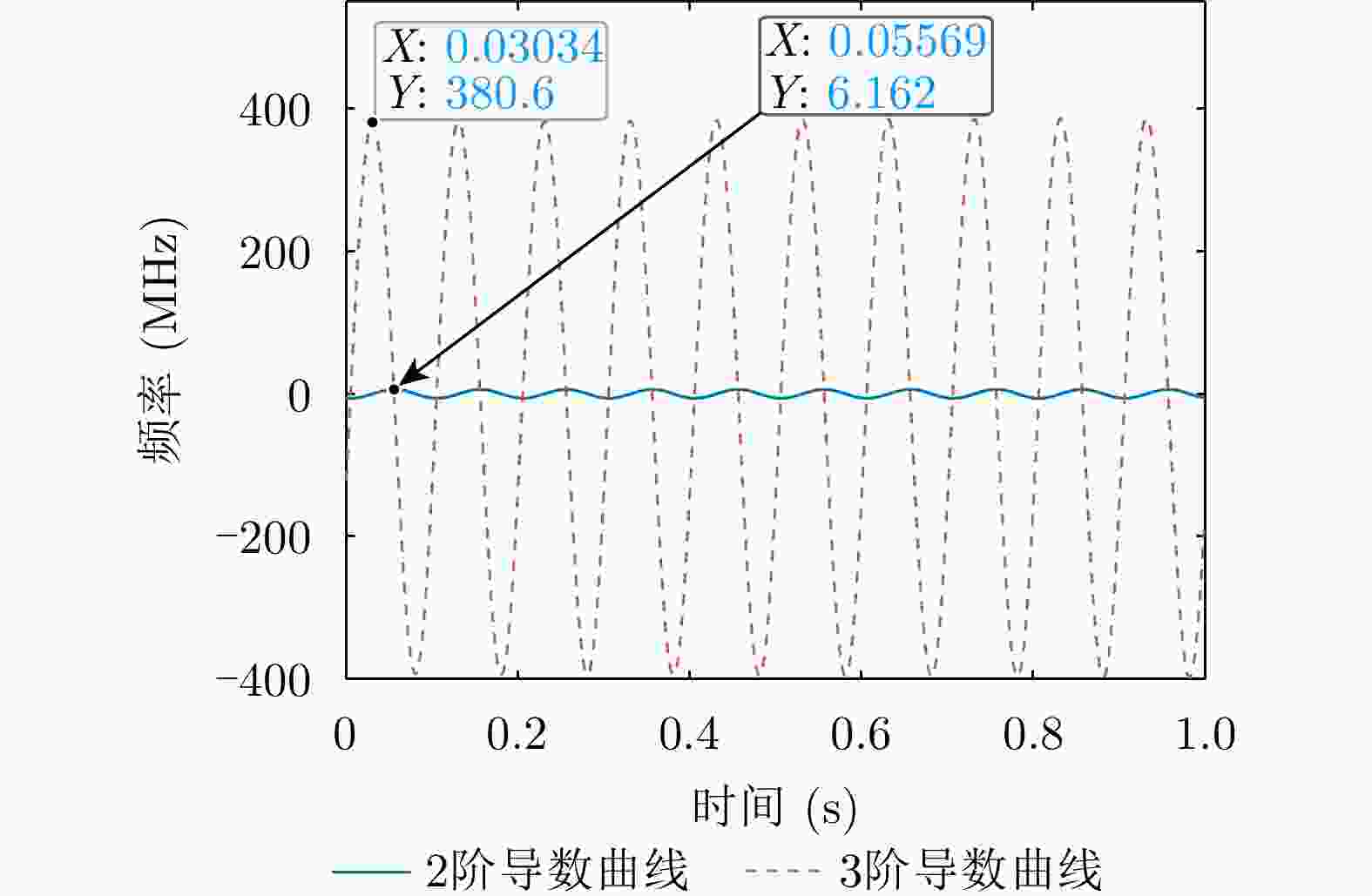
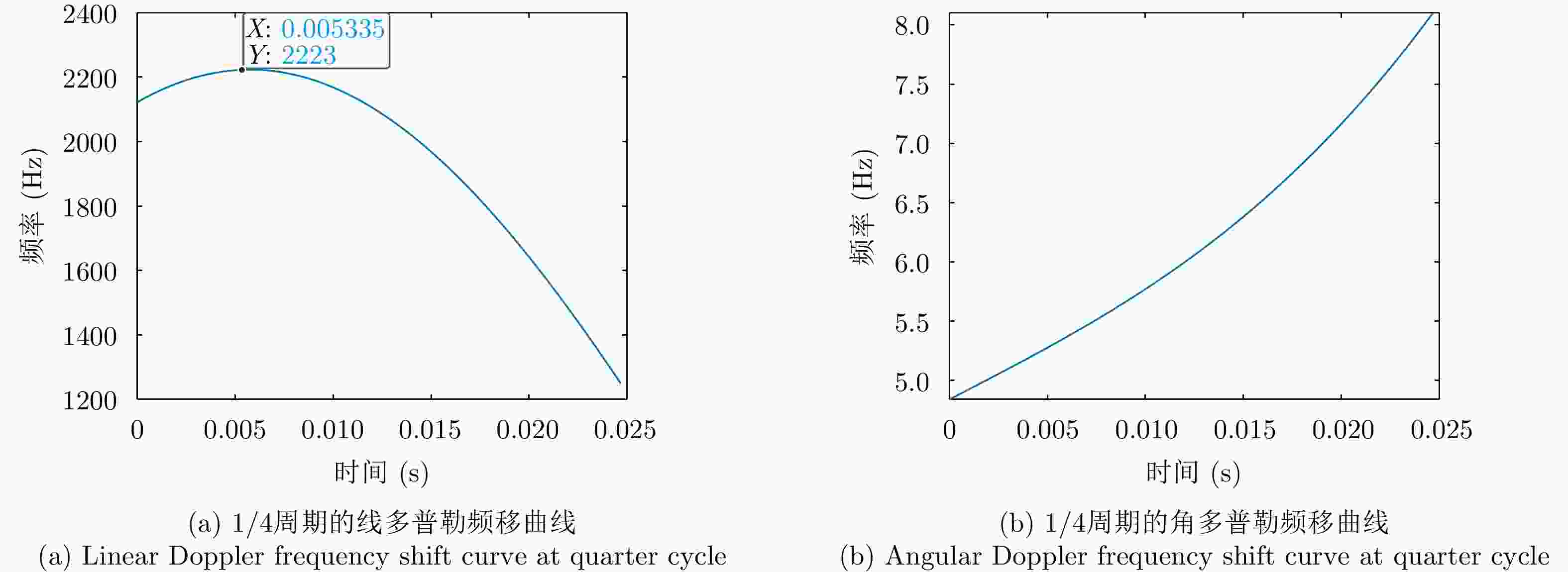
摘要: 与传统平面电磁波雷达相比,涡旋电磁波雷达能同时观测到目标投影到雷达径向和垂直于径向平面的微动分量,可为目标识别提供更多信息。当前关于涡旋电磁波雷达微多普勒效应的研究尚处于起步阶段,初步实现了对旋转目标的三维微动参数的提取,但均未考虑目标平动的影响。因此,该文研究了涡旋电磁波雷达中平动旋转目标的微多普勒效应,推导了平动旋转目标的角多普勒性质,提出了基于1/4微动周期多普勒频移曲线的三维微动参数提取方法,获得了目标旋转频率、旋转半径、旋转矢量和平动速度矢量等参数。仿真验证了角多普勒性质的正确性和参数提取方法的有效性。Abstract: Compared with traditional Electromagnetic (EM) wave radars, vortex EM wave radars can simultaneously observe the micro-motion components projected onto the radar’s radial and perpendicular planes, providing more information for target recognition. The current research on the micro-Doppler effect of vortex EM wave radar is still in its infancy, and the extraction of three-dimensional micro-motion parameters of rotating targets has been preliminarily achieved. However, the impact of target translation was not considered. Therefore, the micro-Doppler effect of translational rotating targets in vortex EM wave radar is studied in this paper. The angular Doppler properties of translational rotating targets are derived, and a three-dimensional micro-motion parameter extraction method based on the 1/4 micro-motion period Doppler frequency shift curve is proposed. Estimation of parameters such as target rotation frequency, rotation radius, rotation vector and translational velocity vector is achieved. The correctness of angular Doppler properties and the effectiveness of parameter extraction method are verified by simulations.
-
表 1 雷达和目标参数
Table 1. Parameters of radar and target
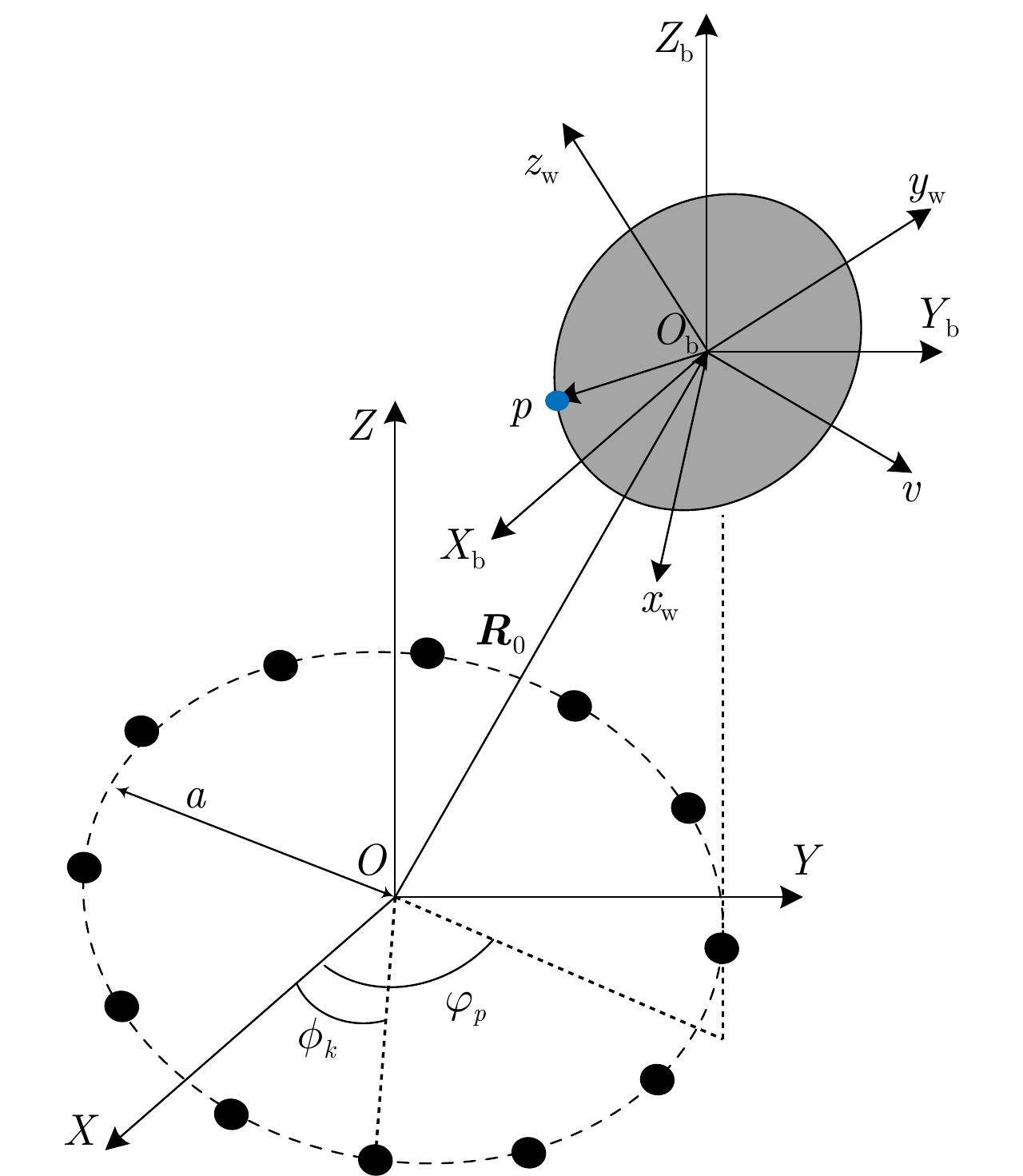
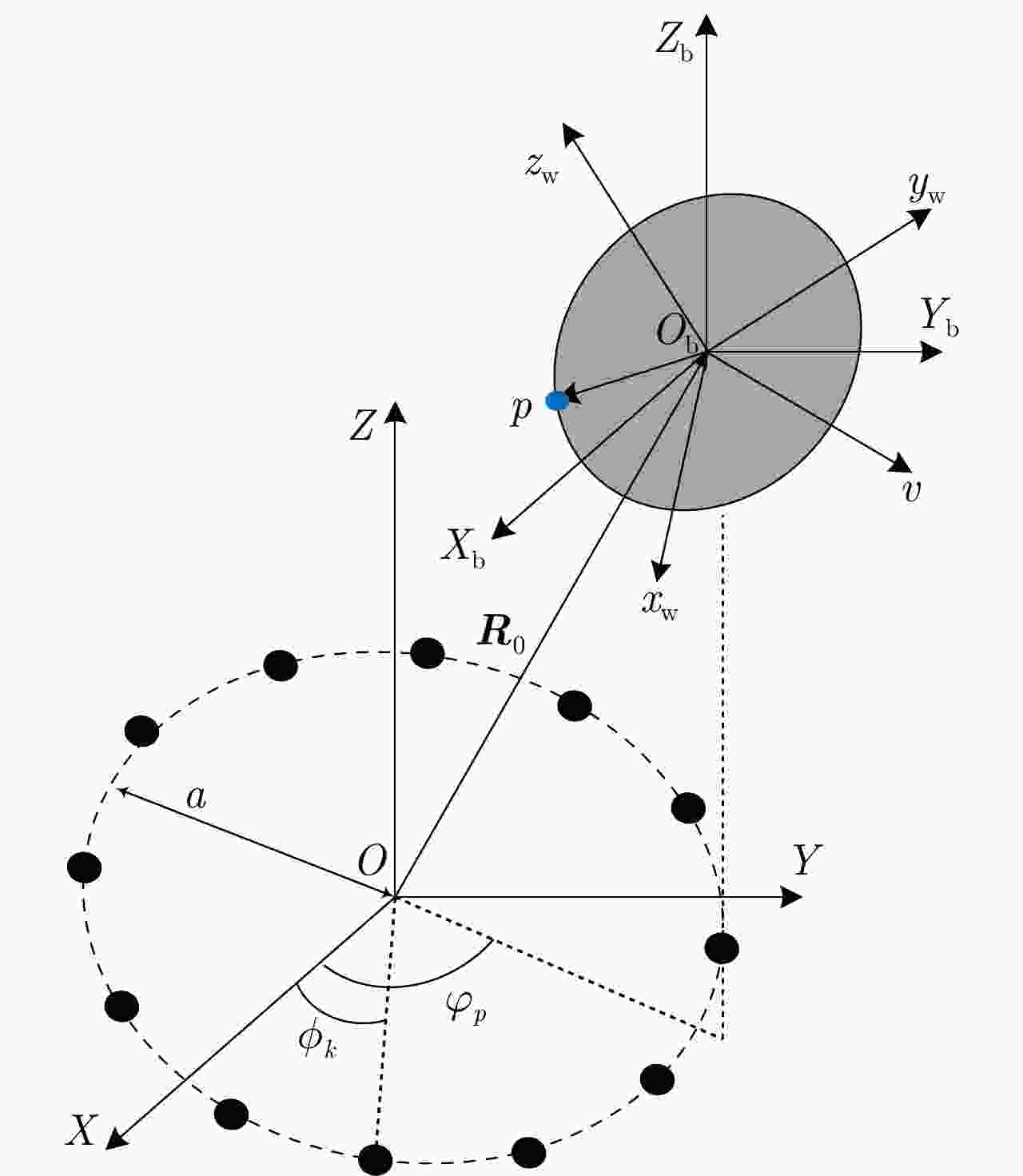
参数 数值 载频(GHz) 10 阵列半径(m) 1 模态数 4 旋转半径(m) 0.4 旋转频率(Hz) 10 欧拉角(rad) (1.0472,0.7854,0) 旋转矢量 (0.707,–0.612,0.353) 旋转中心(m) (0.8,1,100) 速度矢量(m/s) (–10, –5, 10) 表 2 选取点的时刻和角多普勒值
Table 2. The time and angular Doppler value of the selected point
序号 时刻(s) 角多普勒(Hz) 1 0 4.8271 2 0.0133 6.1418 3 0.0267 8.5308 4 0.0400 12.2020 5 0.0534 9.2937 6 0.0667 –9.3425 7 0.0800 –5.6511 8 0.0934 4.6931 表 3 求解过程的迭代误差
Table 3. Iterative error in the solving process
迭代次数 误差 学习率 1 2571.63 0.01 2 555.784 0.001 3 214.932 1 4 110.276 10 5 79.972 1 6 59.7386 0.1 7 15.365 0.01 8 9.63835 1 9 5.24274 0.1 10 0.994269 0.01 11 0.005036 0.001 12 5.25×10–7 0.0001 13 5.26×10–15 10–5 表 4 多元非线性方程组求解结果
Table 4. Solution results of multivariate nonlinear equations
参数 估计值 理想值 欧拉角(rad) (1.047,0.785) (1.0472,0.7854) 旋转半径相对大小(m) 0.631 0.4 旋转中心相对大小(m) (1.26,1.57) (0.8,1) 速度矢量相对大小(m/s) (–15.79, –7.89) (–10, –5) 表 5 完整周期频移曲线下的微动参数估计结果
Table 5. Estimation results of micro-motion parameters under complete periodic frequency shift curve
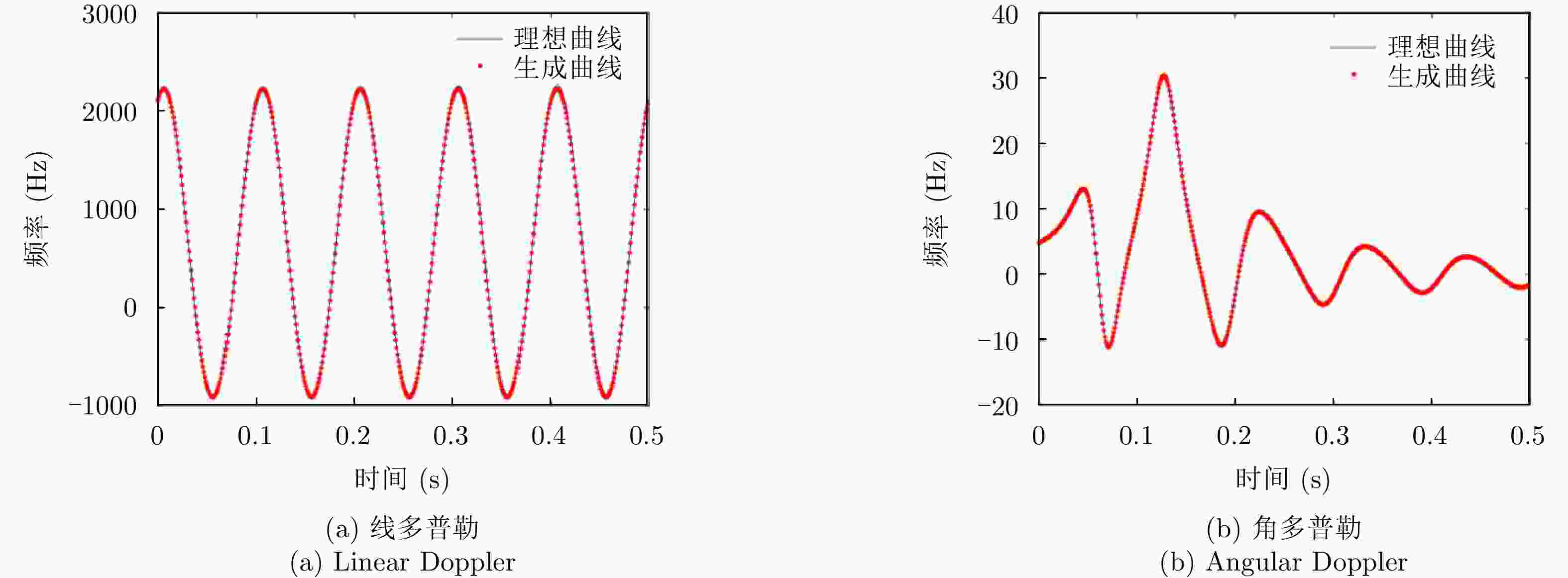
参数 估计值 理想值 误差 旋转矢量 (0.707,–0.612,0.353) (0.707,–0.612,0.353) 0.04% 旋转频率 9.944 Hz 10 Hz 0.56% 旋转半径 0.398 m 0.4 m 0.50% 旋转中心 (0.796,0.995) m (0.8,1) m 2.75% 速度矢量 (–9.953, –4.976) m/s (–10, –5) m/s 0.46% 表 6 选取1/4周期内8个点的时刻和角多普勒值
Table 6. Select the time and angular Doppler Values of 8 points within a quarter cycle
序号 时刻(s) 角多普勒(Hz) 1 0.0010 4.9123 2 0.0043 5.2019 3 0.0076 5.5134 4 0.0110 5.8640 5 0.0143 6.2706 6 0.0176 6.7500 7 0.0210 7.3187 8 0.0243 7.9918 表 7 1/4周期多元非线性方程组求解结果
Table 7. Solution results of multivariate nonlinear equations under 1/4 period
参数 估计值 理想值 欧拉角(rad) (1.047,0.785) (1.0472,0.7854) 旋转半径相对大小(m) 0.068 0.4 旋转中心相对大小(m) (0.136,0.171) (0.8,1) 速度矢量相对大小(m/s) (–1.709, –0.854) (–10, –5) 表 8 1/4周期频移曲线下的微动参数估计结果
Table 8. Estimation results of micro-motion parameters at quarter periodic frequency shift curve
参数 估计值 理想值 误差 旋转矢量 (0.707,–0.612,0.353) m (0.707,–0.612,0.353) m 0.04% 旋转频率 9.944 Hz 10 Hz 0.56% 旋转半径 0.398 m 0.4 m 0.50% 旋转中心 (0.796,0.995) m (0.8,1) m 2.75% 速度矢量 (–9.953, –4.976) m/s (–10, –5) m/s 0.46% 表 9 添加误差后6个点的时刻和角多普勒值
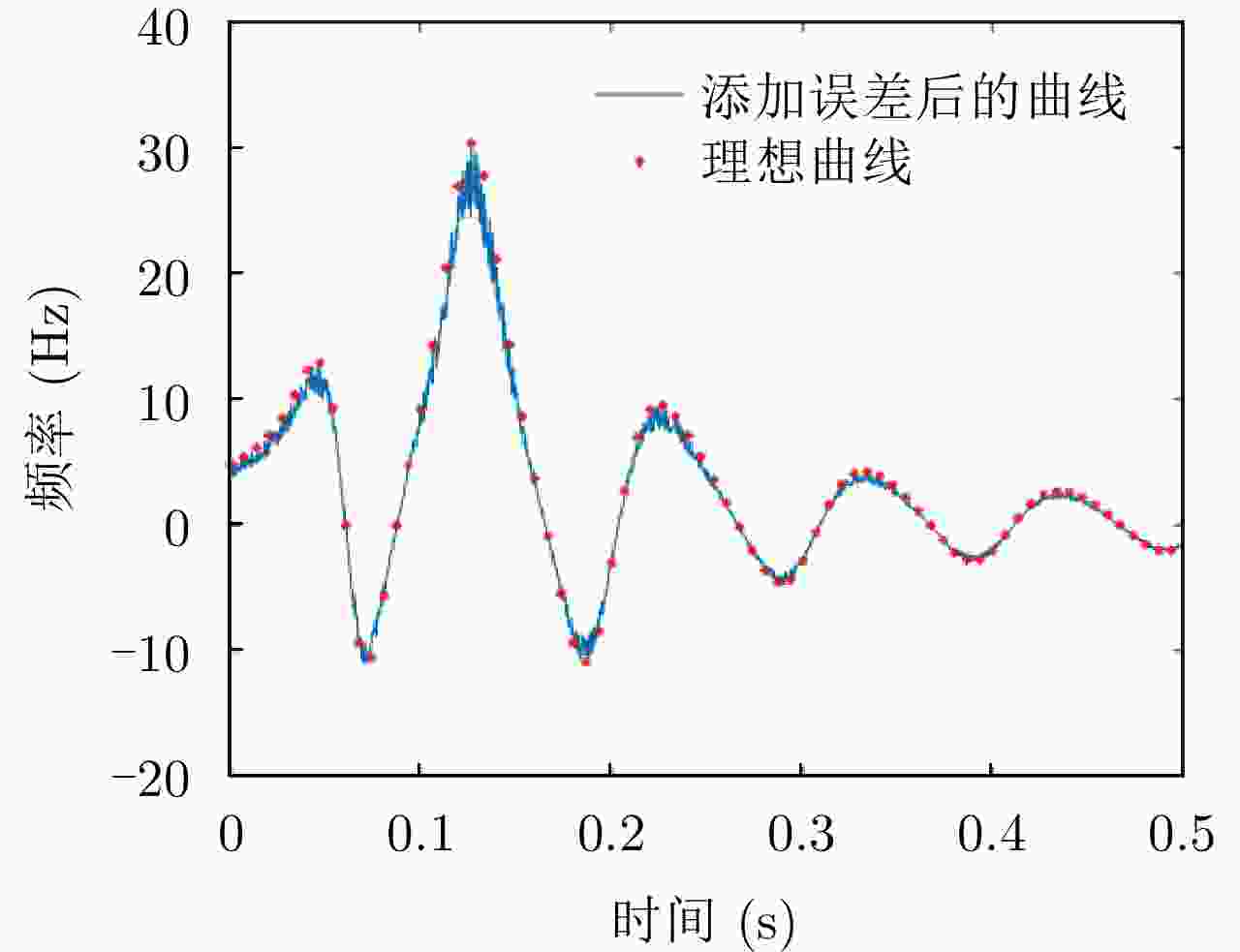
Table 9. Time and angle Doppler values of 6 points after adding error
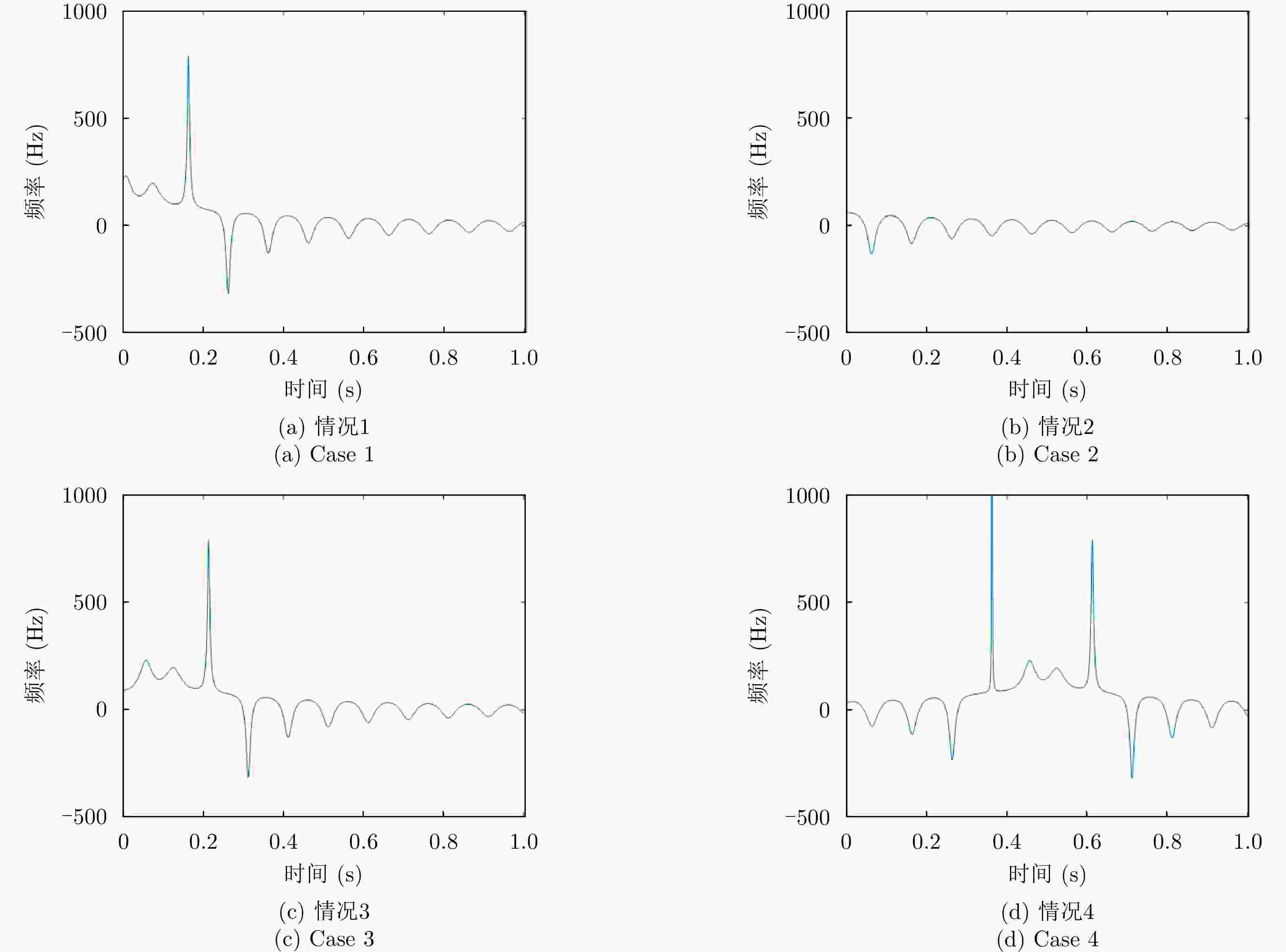
序号 时刻(s) 角多普勒(Hz) 误差(%) 1 0.0003 3.8878 19.93 2 0.0170 5.4510 18.01 3 0.0337 9.2341 11.79 4 0.0504 11.4651 1.48 5 0.0670 –8.7959 8.84 6 0.0837 –2.1743 11.49 表 10 添加误差后的微动参数估计结果
Table 10. Estimation results of micro-motion parameters after adding errors
参数 估计值 理想值 误差 旋转矢量 (0.760, –0.583, 0.271) m (0.707, –0.612, 0.353) m 12.36% 旋转频率 9.944 Hz 10 Hz 0.56% 旋转半径 0.389 m 0.4 m 2.62% 旋转中心 (0.71,1.02) m (0.8,1) m 6.36% 速度矢量 (–9.00, –6.02) m/s (–10, –5) m/s 15.18% -
[1] 陈小龙, 关键, 何友. 微多普勒理论在海面目标检测中的应用及展望[J]. 雷达学报, 2013, 2(1): 123–134. doi: 10.3724/SP.J.1300.2012.20102CHEN Xiaolong, GUAN Jian, and HE You. Applications and prospect of micro-motion theory in the detection of sea surface target[J]. Journal of Radars, 2013, 2(1): 123–134. doi: 10.3724/SP.J.1300.2012.20102 [2] LIU Yingxi, ZHANG Qun, LIU Zhidong, et al. An anti-jamming method against interrupted sampling repeater jamming based on compressed sensing[J]. Sensors, 2022, 22(6): 2239. doi: 10.3390/s22062239 [3] XIONG Shichao, NI Jiacheng, ZHANG Qun, et al. Ground moving target imaging for highly squint SAR by modified minimum entropy algorithm and spectrum rotation[J]. Remote Sensing, 2021, 13(21): 4373. doi: 10.3390/rs13214373 [4] WANG Haobo, LI Kaiming, LU Xiaofei, et al. ISAR resolution enhancement method exploiting generative adversarial network[J]. Remote Sensing, 2022, 14(5): 1291. doi: 10.3390/rs14051291 [5] 郭忠义, 汪彦哲, 王运来, 等. 涡旋电磁波旋转多普勒效应研究进展[J]. 雷达学报, 2021, 10(5): 725–739. doi: 10.12000/JR21109GUO Zhongyi, WANG Yanzhe, WANG Yunlai, et al. Research advances on the rotational Doppler effect of vortex electromagnetic waves[J]. Journal of Radars, 2021, 10(5): 725–739. doi: 10.12000/JR21109 [6] WANG Zhihao, LUO Ying, LI Kaiming, et al. Micro-Doppler parameters extraction of precession cone-shaped targets based on rotating antenna[J]. Remote Sensing, 2022, 14(11): 2549. doi: 10.3390/rs14112549 [7] WANG Zhihao, CHEN Yijun, YUAN Hang, et al. Real micro-Doppler parameters extraction of spinning targets based on rotating interference antenna[J]. Remote Sensing, 2022, 14(21): 5300. doi: 10.3390/rs14215300 [8] TIAN Xudong, BAI Xueru, and ZHOU Feng. Recognition of micro-motion space targets based on attention-augmented cross-modal feature fusion recognition network[J]. IEEE Transactions on Geoscience and Remote Sensing, 2023, 61: 5104909. doi: 10.1109/TGRS.2023.3275991 [9] ZHOU Xuening, BAI Xueru, WANG Li, et al. Robust ISAR target recognition based on ADRISAR-net[J]. IEEE Transactions on Aerospace and Electronic Systems, 2022, 58(6): 5494–5505. doi: 10.1109/TAES.2022.3174826 [10] BAI Xueru, HUI Ye, WANG Li, et al. Radar-based human gait recognition using dual-channel deep convolutional neural network[J]. IEEE Transactions on Geoscience and Remote Sensing, 2019, 57(12): 9767–9778. doi: 10.1109/TGRS.2019.2929096 [11] CHEN Xuebin, YE Chunmao, WANG Yong, et al. Unambiguous estimation of multidimensional parameters for space precession targets with wideband radar measurements[J]. IEEE Transactions on Geoscience and Remote Sensing, 2022, 60: 5112716. doi: 10.1109/TGRS.2022.3168326 [12] 张群, 胡健, 罗迎, 等. 微动目标雷达特征提取、成像与识别研究进展[J]. 雷达学报, 2018, 7(5): 531–547. doi: 10.12000/JR18049ZHANG Qun, HU Jian, LUO Ying, et al. Research progresses in radar feature extraction, imaging, and recognition of target with micro-motions[J]. Journal of Radars, 2018, 7(5): 531–547. doi: 10.12000/JR18049 [13] 罗迎, 龚逸帅, 陈怡君, 等. 基于跟踪脉冲的MIMO雷达多目标微动特征提取[J]. 雷达学报, 2018, 7(5): 575–584. doi: 10.12000/JR18035LUO Ying, GONG Yishuai, CHEN Yijun, et al. Multi-target micro-motion feature extraction based on tracking pulses in MIMO radar[J]. Journal of Radars, 2018, 7(5): 575–584. doi: 10.12000/JR18035 [14] XU Xuguang and FENG Cunqian. Micro-Doppler extraction of radar targets with translational motion based on spatial transformer network[J]. IEEE Signal Processing Letters, 2022, 29: 2348–2352. doi: 10.1109/LSP.2022.3217411 [15] GHALEB A, VIGNAUD L, and NICOLAS J M. Micro-Doppler analysis of pedestrians in ISAR imaging[C]. 2008 IEEE Radar Conference, Rome, Italy, 2008: 1–5. [16] YUAN Hang, CHEN YiJun, LUO Ying, et al. A resolution-improved imaging algorithm based on uniform circular array[J]. IEEE Antennas and Wireless Propagation Letters, 2022, 21(3): 461–465. doi: 10.1109/LAWP.2021.3135806 [17] LIU Kang, CHENG Yongqiang, LI Xiang, et al. Passive OAM-based radar imaging with single-in-multiple-out mode[J]. IEEE Microwave and Wireless Components Letters, 2018, 28(9): 840–842. doi: 10.1109/LMWC.2018.2852146 [18] LIU Kang, CHENG Yongqiang, GAO Yue, et al. Super-resolution radar imaging based on experimental OAM beams[J]. Applied Physics Letters, 2017, 110(16): 164102. doi: 10.1063/1.4981253 [19] LUO Ying, CHEN Yijun, ZHU Yongzhong, et al. Doppler effect and micro-Doppler effect of vortex-electromagnetic-wave-based radar[J]. IET Radar, Sonar & Navigation, 2020, 14(1): 2–9. doi: 10.1049/iet-rsn.2019.0124 [20] YUAN Hang, LUO Ying, CHEN Yijun, et al. Micro-motion parameter extraction of rotating target based on vortex electromagnetic wave radar[J]. IET Radar, Sonar & Navigation, 2021, 15(12): 1594–1606. doi: 10.1049/rsn2.12149 [21] WANG Yu, LIU Kang, LIU Hongyan, et al. Detection of rotational object in arbitrary position using vortex electromagnetic waves[J]. IEEE Sensors Journal, 2021, 21(4): 4989–4994. doi: 10.1109/JSEN.2020.3032665 [22] WU Zhenxiang, ZHOU Tong, LI Lei, et al. A new modified efficient Levenberg-Marquardt method for solving systems of nonlinear equations[J]. Mathematical Problems in Engineering, 2021, 2021: 5608195. doi: 10.1155/2021/5608195 -



 作者中心
作者中心 专家审稿
专家审稿 责编办公
责编办公 编辑办公
编辑办公
 下载:
下载: