作者中心
专家审稿
责编办公
编辑办公
Missing Covariance Matrix Recovery with the FDA-MIMO Radar Using Deep Learning Method
-
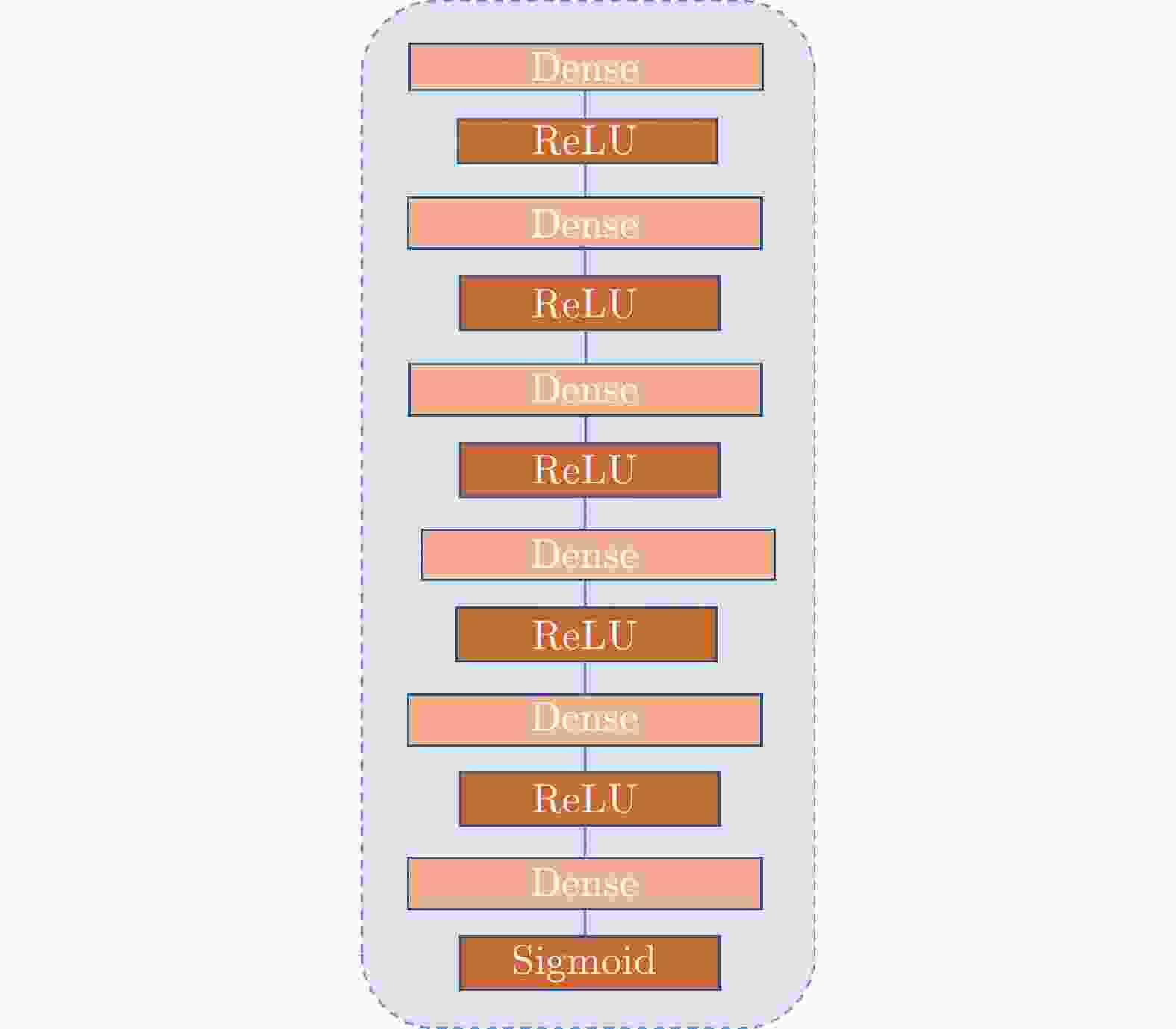
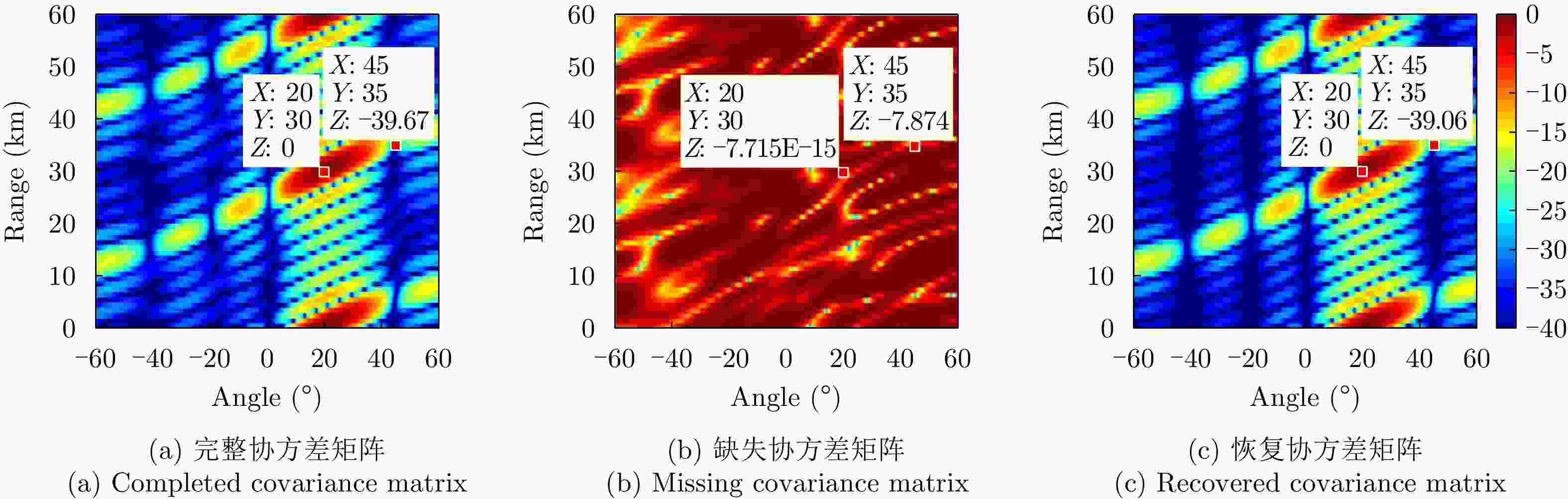
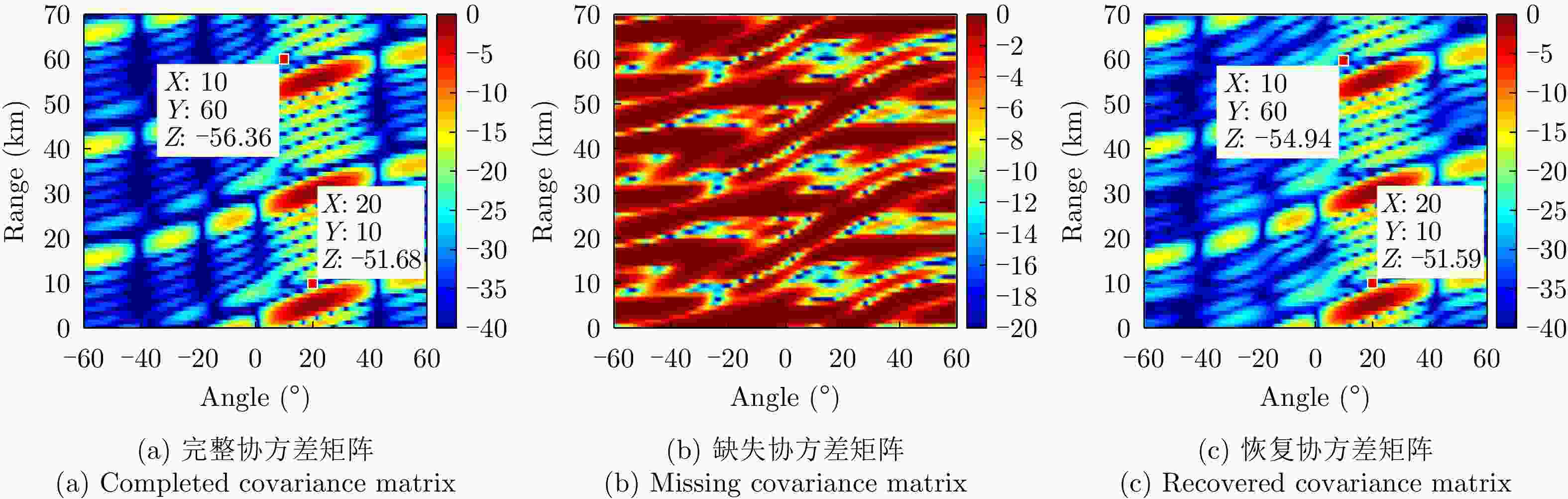
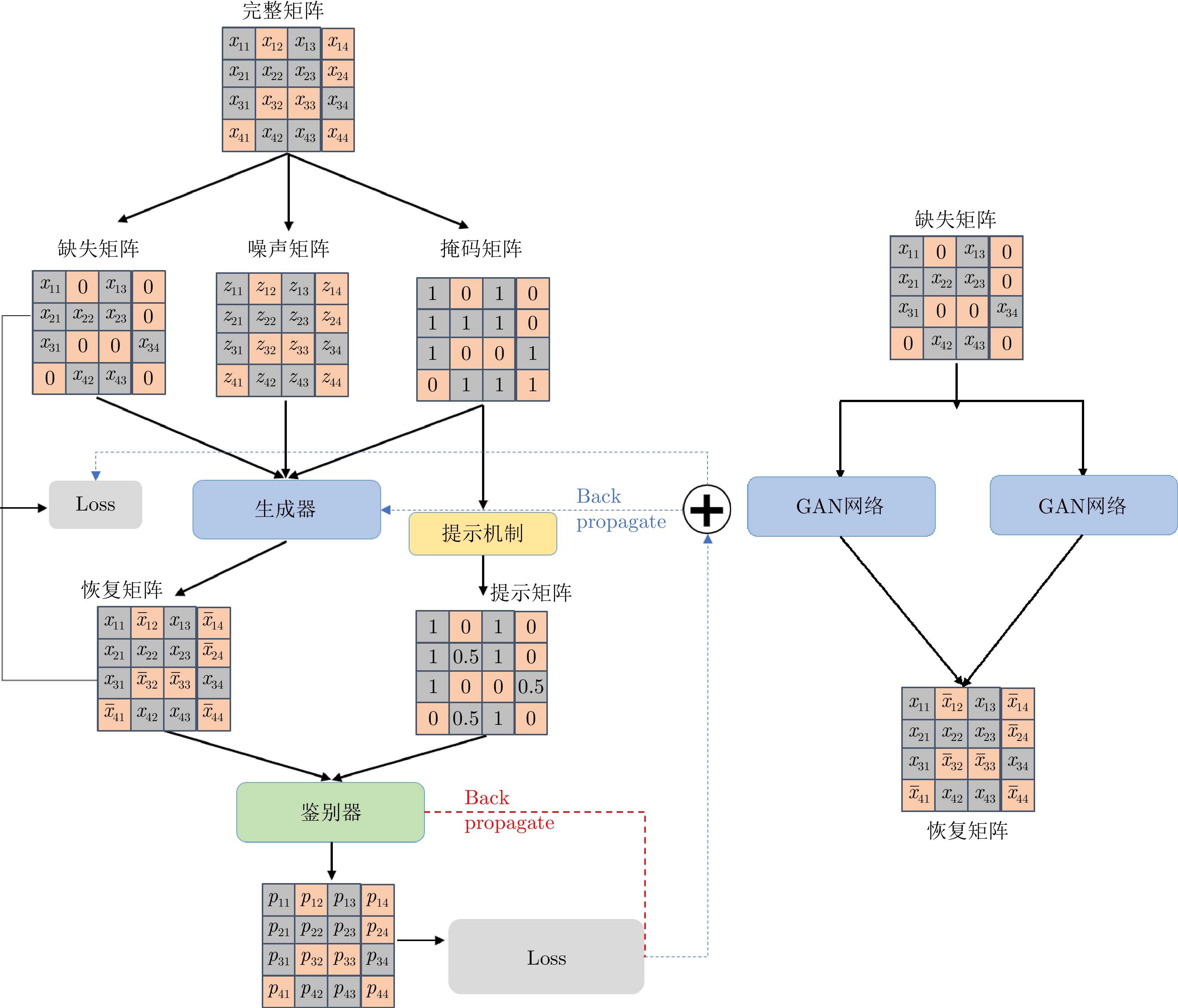
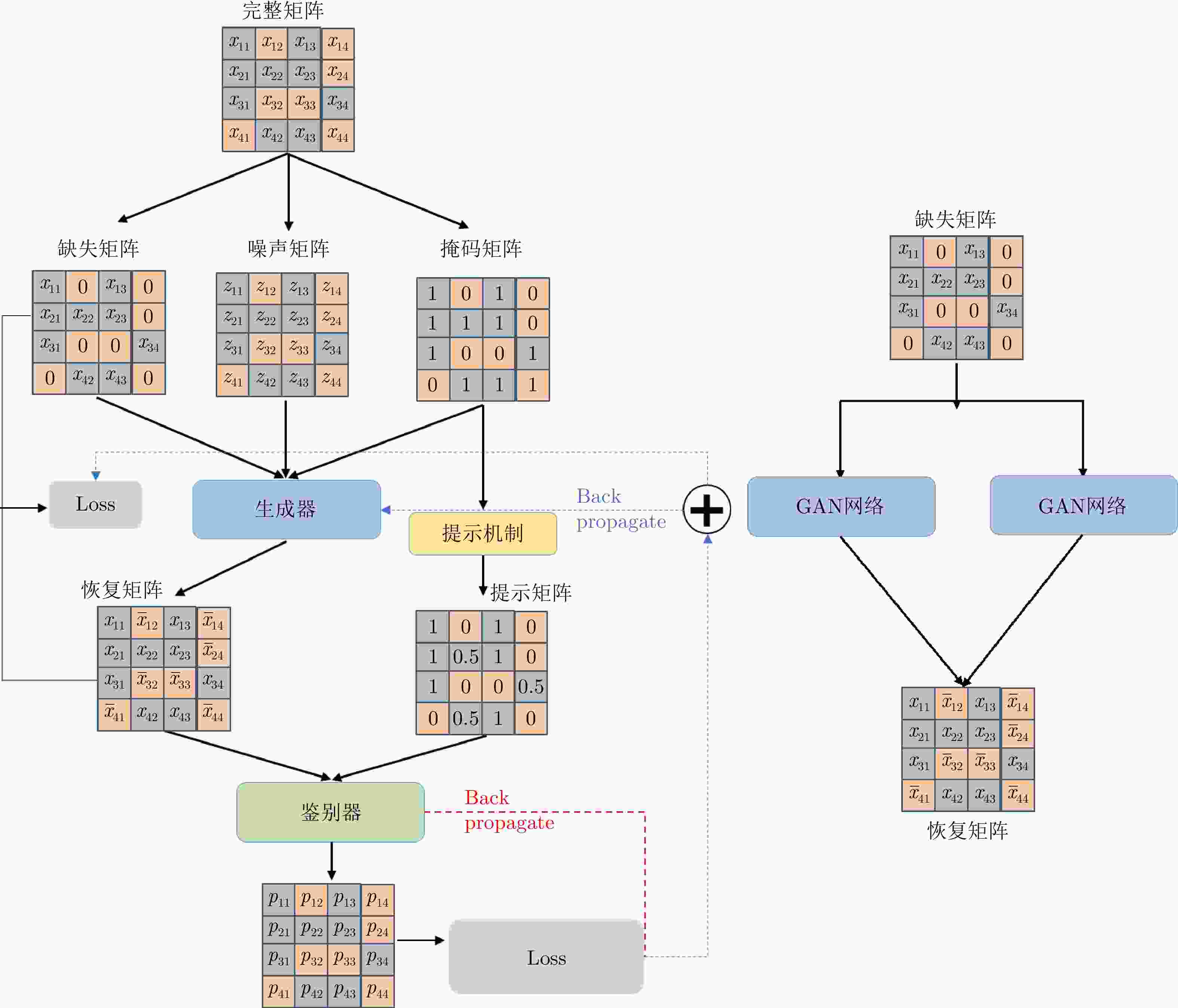
摘要: 频控阵-多输入多输出(FDA-MIMO)雷达通过波束形成技术实现抗干扰的研究已经十分丰富。然而，在实际工作中，受元器件老化和存储设备容量等硬件因素的影响，计算得到的信号协方差矩阵可能会出现数据缺失的情况。为了克服协方差矩阵数据缺失对波束形成算法性能的影响，该文提出了一种基于深度学习的FDA-MIMO雷达协方差矩阵数据恢复方法，并建立了协方差矩阵恢复-自适应波束形成的两阶段处理框架；提出了一种双通道生成对抗网络(GAN)来解决矩阵数据恢复问题，该网络主要由鉴别器(D)和生成器(G)两部分组成：生成器主要功能是输出完整的矩阵数据，鉴别器则是判别数据为真实数据还是填补数据。整个网络通过鉴别器和生成器之间相互对抗使生成器生成样本接近于真实数据的分布，从而实现对协方差矩阵缺失数据的恢复。此外，考虑到协方差矩阵数据为复数，分别构造两个独立的GAN网络以满足矩阵数据实部和虚部的训练。最后，数值实验结果表明，协方差矩阵真实数据与恢复后的数据平均均方根误差仅为0.01量级，验证了所提方法能够有效恢复协方差矩阵的缺失数据。
-
关键词:
- 数据恢复 /
- 生成对抗网络 /
- FDA-MIMO雷达 /
- 深度学习 /
- 波束形成
Abstract: The realization of anti-jamming technologies via beamforming for applications in Frequency-Diverse Arrays and Multiple-Input and Multiple-Output (FDA-MIMO) radar is a field that is undergoing intensive research. However, because of limitations in hardware systems, such as component aging and storage device capacity, the signal covariance matrix data computed by the receiver system may be missing. To mitigate the impact of the missing covariance matrix data on the performance of the beamforming algorithm, we have proposed a covariance matrix data recovery method for FDA-MIMO radar based on deep learning and constructed a two-stage framework based on missing covariance matrix recovery-adaptive beamforming. Furthermore, a learning framework based on this two-stage framework and the Generative Adversarial Network (GAN) is constructed, which is mainly composed of a discriminator (D) and a generator (G). G is primarily used to output complete matrix data, while D is used to judge whether this data is real or filled. The entire network closes the gap between the samples generated by G and the distribution of the real data via a confrontation between D and G, consequently leading to the missing data of the covariance matrix being recovered. In addition, considering that the covariance matrix data is complex, two independent networks are constructed to train the real and imaginary parts of the matrix data. Finally, the numerical experiment results reveal that the difference in the root square mean error levels between the real and recovery data is 0.01 in magnitude. -
图 3 协方差矩阵实部灰度图(单干扰源)
Figure 3. The grayscale image of the real part of covariance matrix (single interference)
图 4 协方差矩阵虚部灰度图(单干扰源)
Figure 4. The grayscale image of the imaginary part of covariance matrix (single interference)
图 5 矩阵恢复数据的RMSE在训练过程中的变化情况(不同损失率
$\varepsilon $ )Figure 5. RMSE performance versus training process (different
$ \varepsilon $ )
图 6 矩阵恢复数据的RMSE在训练过程中的变化情况(不同网络层数k)
Figure 6. RMSE performance versus training process (different k)
图 7 基于不同协方差矩阵的FDA-MIMO雷达波束方向图(多干扰源)
Figure 7. FDA-MIMO radar beampattern based on different covariance matrices (single interference)
图 8 协方差矩阵实部灰度图(多干扰源)
Figure 8. The grayscale image of the real part of covariance matrix (multiple interferences)
图 9 协方差矩阵虚部灰度图(多干扰源)
Figure 9. The grayscale image of the imaginary part of covariance matrix (multiple interferences)
图 10 基于不同协方差矩阵的FDA-MIMO雷达波束方向图(多干扰源)
Figure 10. FDA-MIMO radar beampattern based on different covariance matrices (multiple interferences)
算法1 双通道GAN伪代码 Alg. 1 Pseudocode of dual channels GAN network while 训练损失值未达到收敛条件 or 未达到预设的迭代次数 do 1 鉴别器训练(${ {\rm{D} }_1}$和${ {\rm{D} }_2}$分别为实部和虚部网络的鉴别器) 从训练数据集取出$ {J_{\text{D}}} $个样本作为一批量的数据$\left\{ {\left( { {\text{Re} }\left( {\tilde {\boldsymbol{x}}\left( j \right)} \right),{\boldsymbol{m} }\left( j \right)} \right)} \right\}_{j = 1}^{ {J_{\text{D} } } }$,$\left\{ {\left( { {\text{Im} }\left( {\tilde {\boldsymbol{x}}\left( j \right)} \right),{\boldsymbol{m} }\left( j \right)} \right)} \right\}_{j = 1}^{ {J_{\text{D} } } }$，并分别归一化处理。 随机采样$ {J_{\text{D}}} $个样本$\left\{ {{\boldsymbol{z}}\left( j \right)} \right\}_{j = 1}^{ {J_{\text{D} } } }$, $\left\{ {{\boldsymbol{b}}\left( j \right)} \right\}_{j = 1}^{ {J_{\text{D} } } }$，并分别归一化处理。 for $j = 1,2,\cdots,{J_{\text{D} } }$ do ${ {\rm{Re} } } \left( {\bar {\boldsymbol{x}}\left( j \right)} \right) \leftarrow {\text{G} }\left( { { {\rm{Re} } } \left( {\tilde {\boldsymbol{x}}\left( j \right)} \right),{\boldsymbol{m} }\left( j \right),{\boldsymbol{z} }\left( j \right)} \right)$, ${ {\rm{Im} } } \left( {\bar {\boldsymbol{x}}\left( j \right)} \right) \leftarrow {\text{G} }\left( { { {\rm{Im} } } \left( {\tilde {\boldsymbol{x}}\left( j \right)} \right),{\boldsymbol{m} }\left( j \right),{\boldsymbol{z} }\left( j \right)} \right)$ ${ {\rm{Re} } } \left( {\hat {\boldsymbol{x}}\left( j \right)} \right) \leftarrow {\boldsymbol{m} }\left( j \right) \odot { {\rm{Re} } } \left( {\tilde {\boldsymbol{x} } \left( j \right)} \right) + \left( {1 - {\boldsymbol{m} }\left( j \right)} \right) \odot { {\rm{Re} } } \left( {\bar {\boldsymbol{x}}\left( j \right)} \right)$, ${ {\rm{Im} } } \left( {\hat {\boldsymbol{x}}\left( j \right)} \right) \leftarrow {\boldsymbol{m} }\left( j \right) \odot { {\rm{Im} } } \left( {\tilde {\boldsymbol{x} }\left( j \right)} \right) + \left( {1 - {\boldsymbol{m} }\left( j \right)} \right) \odot { {\rm{Im} } } \left( {\bar {\boldsymbol{x}}\left( j \right)} \right)$ ${\boldsymbol{h} }\left( j \right) = {\boldsymbol{b} }\left( j \right) \odot {\boldsymbol{m} }\left( j \right) + 0.5\left( {1 - {\boldsymbol{b}}\left( j \right)} \right)$ end for 使用随机梯度下降(Stochastic Gradient Descent, SGD)算法, 分别更新$ {{\text{D}}_1} $和$ {{\text{D}}_2} $网络参数(固定$ {{\text{G}}_1} $和$ {{\text{G}}_2} $网络的参数)
${{\text{∇}} _{ { {\text{D} }_1} } } - \displaystyle\sum\limits_{j = 1}^{ {J_{\text{D} } } } { {\mathcal{L}_{\text{D} } }\left( { {\boldsymbol{m} }\left( j \right),{ {\text{D} }_1}\left( { {\text{Re} }\left( {\hat {\boldsymbol{x} }\left( j \right)} \right),{\boldsymbol{h} }\left( j \right)} \right),{\boldsymbol{b} }\left( j \right)} \right)}$${{\text{∇}} _{ { {\text{D} }_2} } } - \displaystyle\sum\limits_{j = 1}^{ {J_{\text{D} } } } { {\mathcal{L}_{\text{D} } }\left( { {\boldsymbol{m} }\left( j \right),{ {\text{D} }_2}\left( { {\text{Im} }\left( {\hat {\boldsymbol{x} }\left( j \right)} \right),{\boldsymbol{h} }\left( j \right)} \right),{\boldsymbol{b} }\left( j \right)} \right)}$ 2 生成器训练(${ {\rm{G} }_1}$和${ {\rm{G} }_2}$分别为实部和虚部网络的生成器) 从训练数据集取出$ {J_{\text{G}}} $个样本作为一批量的数据$\left\{ {\left( { {\text{Re} }\left( {\tilde {\boldsymbol{x}}\left( j \right)} \right),{\boldsymbol{m}}\left( j \right)} \right)} \right\}_{j = 1}^{ {J_{\text{G} } } }$,$\left\{ {\left( { {\text{Im} }\left( {\tilde {\boldsymbol{x}}\left( j \right)} \right),{\boldsymbol{m} }\left( j \right)} \right)} \right\}_{j = 1}^{ {J_{\text{G} } } }$ 随机采样$ {J_{\text{G}}} $个样本$\left\{ {{\boldsymbol{z}}\left( j \right)} \right\}_{j = 1}^{ {J_{\text{G} } } }$, $\left\{ {{\boldsymbol{b}}\left( j \right)} \right\}_{j = 1}^{ {J_{\text{G} } } }$ for $j = 1,2,\cdots,{J_{\rm{D}}}$ do ${\boldsymbol{h} }\left( j \right) = {\boldsymbol{b} }\left( j \right) \odot {\boldsymbol{m} }\left( j \right) + 0.5\left( {1 - {\boldsymbol{b}}\left( j \right)} \right)$ end for 使用SGD算法更新$ {{\text{G}}_1} $和$ {{\text{G}}_2} $网络(固定$ {{\text{D}}_1} $和$ {{\text{D}}_2} $网络参数)
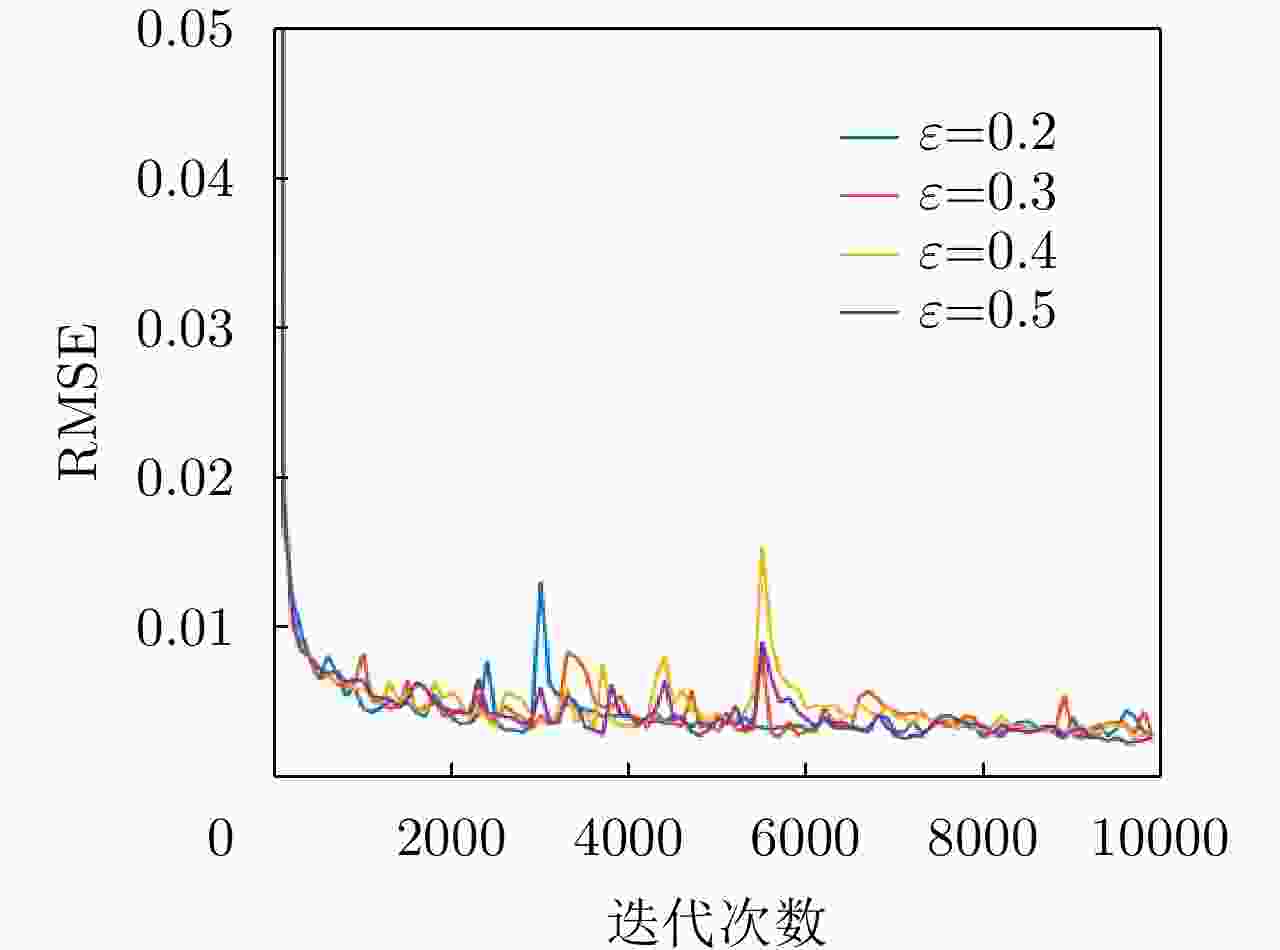
${{\text{∇}} _{ { {\text{G} }_1} } } - \displaystyle\sum\limits_{j = 1}^{ {J_{\text{G} } } } { {\mathcal{L}_{\text{G} } }\left( { {\boldsymbol{m} }\left( j \right),\hat {\boldsymbol{m} }\left( j \right),{\boldsymbol{b} }\left( j \right)} \right)} + \beta {\mathcal{L}_{\text{M} } }\left( { {\text{Re} }\left( {\hat {\boldsymbol{x} }\left( j \right)} \right),{\text{Re} }\left( {\tilde {\boldsymbol{x} }\left( j \right)} \right)} \right)$${{\text{∇}} _{ { {\text{G} }_2} } } - \displaystyle\sum\limits_{j = 1}^{ {J_{\text{G} } } } { {\mathcal{L}_{\text{G} } }\left( { {\boldsymbol{m} }\left( j \right),\hat {\boldsymbol{m} }\left( j \right),{\boldsymbol{b} }\left( j \right)} \right)} + \beta {\mathcal{L}_{\text{M} } }\left( { {\text{Im} }\left( {\hat {\boldsymbol{x} }\left( j \right)} \right),{\text{Im} }\left( {\tilde {\boldsymbol{x} }\left( j \right)} \right)} \right)$ end while 
下载: 导出CSV
表 1 测试集矩阵恢复数据的平均RMSE(不同损失率
${\boldsymbol{\varepsilon}} $ )Table 1. Average RMSE of the missing data recovery (different
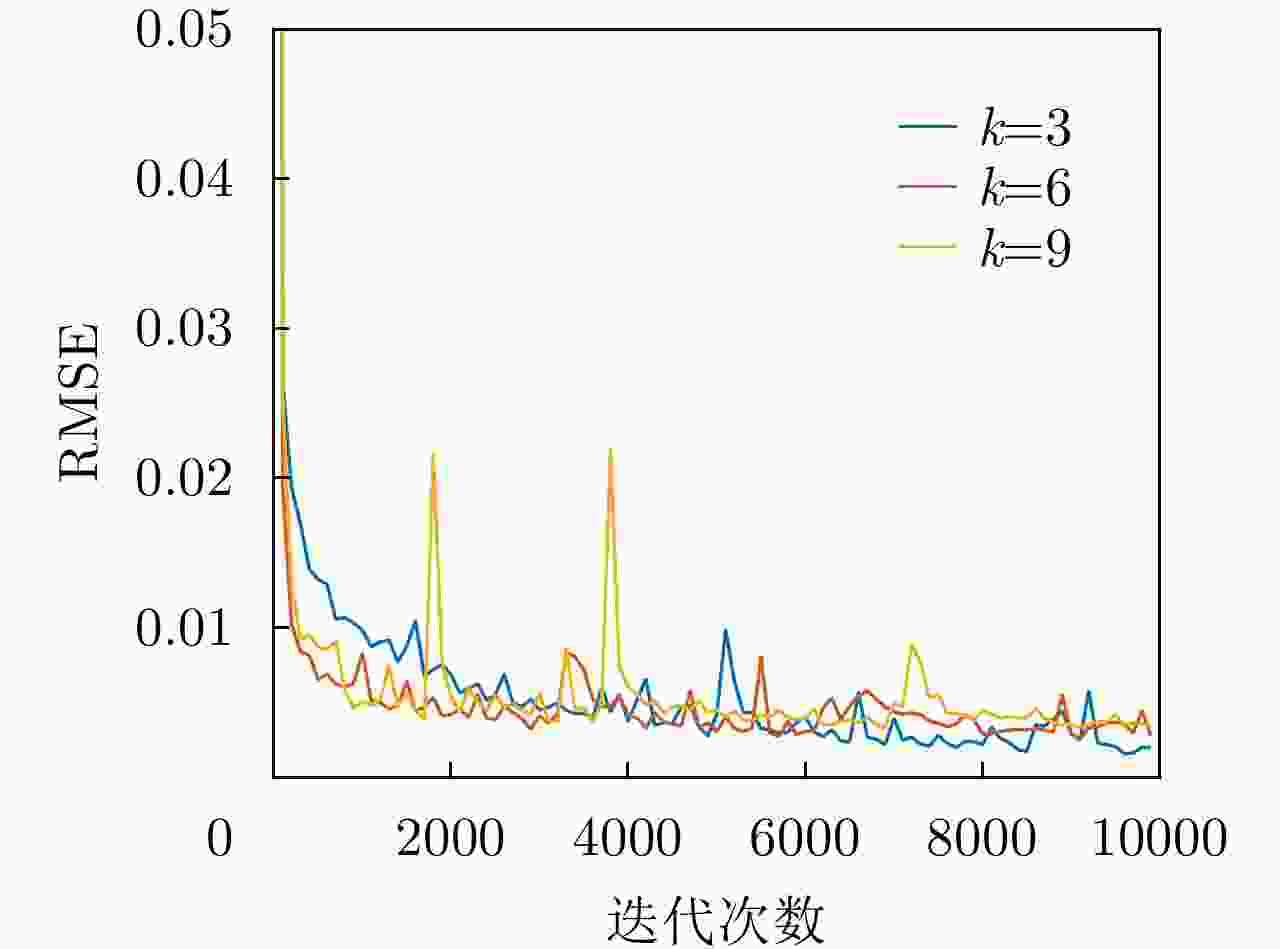
$ {\boldsymbol{\varepsilon}} $ )损失率 平均RMSE 损失率 平均RMSE $ \varepsilon = 0.2 $ 1.43E–02 $ \varepsilon = 0.4 $ 2.20E–02 $ \varepsilon = 0.3 $ 1.59E–02 $ \varepsilon = 0.5 $ 2.33E–02
下载: 导出CSV
表 2 测试集矩阵恢复数据的平均RMSE(不同网络层数k)
Table 2. Average RMSE of the missing data recovery (different k)
网络层数 平均RMSE 3 1.92E–02 6 1.59E–02 9 1.63E–02
下载: 导出CSV
表 3 测试集矩阵恢复数据的平均RMSE(不同方法)
Table 3. Average RMSE of the missing data recovery (different methods)
矩阵缺失数据恢复方法 平均RMSE EM 3.66E–02 随机森林 2.87E–02 降噪自编码器 3.08E–02 本文所提算法 1.59E–02
下载: 导出CSV
-
[1] WANG Wenqin. Overview of frequency diverse array in radar and navigation applications[J]. IET Radar, Sonar & Navigation, 2016, 10(6): 1001–1012. doi: 10.1049/iet-rsn.2015.0464 [2] ANTONIK P, WICKS M C, GRIFFITHS H D, et al. Frequency diverse array radars[C]. The 2006 IEEE Conference on Radar, Verona, USA, 2006: 215–217. [3] WICKS M C and ANTONIK P. Frequency diverse array with independent modulation of frequency, amplitude, and phase[P]. US, 7319427, 2008. [4] WANG Wenqin and SHAO Huaizong. Range-angle localization of targets by a double-pulse frequency diverse array radar[J]. IEEE Journal of Selected Topics in Signal Processing, 2014, 8(1): 106–114. doi: 10.1109/JSTSP.2013.2285528 [5] BASIT A, KHAN W, KHAN S, et al. Development of frequency diverse array radar technology: A review[J]. IET Radar, Sonar & Navigation, 2018, 12(2): 165–175. doi: 10.1049/iet-rsn.2017.0207 [6] SECMEN M, DEMIR S, HIZAL A, et al. Frequency diverse array antenna with periodic time modulated pattern in range and angle[C]. The 2007 IEEE Radar Conference, Waltham, USA, 2007: 427–430. [7] SAMMARTINO P F, BAKER C J, and GRIFFITHS H D. Frequency diverse MIMO techniques for Radar[J]. IEEE Transactions on Aerospace and Electronic Systems, 2013, 49(1): 201–222. doi: 10.1109/TAES.2013.6404099 [8] XU Jingwei, LIAO Guisheng, ZHU Shengqi, et al. Joint range and angle estimation using MIMO radar with frequency diverse array[J]. IEEE Transactions on Signal Processing, 2015, 63(13): 3396–3410. doi: 10.1109/TSP.2015.2422680 [9] LAN Lan, ROSAMILIA M, AUBRY A, et al. Single-snapshot angle and incremental range estimation for FDA-MIMO radar[J]. IEEE Transactions on Aerospace and Electronic Systems, 2021, 57(6): 3705–3718. doi: 10.1109/TAES.2021.3083591 [10] LAN Lan, LIAO Guisheng, XU Jingwei, et al. Transceive beamforming with accurate nulling in FDA-MIMO radar for imaging[J]. IEEE Transactions on Geoscience and Remote Sensing, 2020, 58(6): 4145–4159. doi: 10.1109/TGRS.2019.2961324 [11] XU Jingwei, LIAO Guisheng, ZHU Shengqi, et al. Deceptive jamming suppression with frequency diverse MIMO radar[J]. Signal Processing, 2015, 113: 9–17. doi: 10.1016/j.sigpro.2015.01.014 [12] LAN Lan, LIAO Guisheng, XU Jingwei, et al. Range-angle-dependent beamforming for FDA-MIMO radar using oblique projection[J]. Science China Information Sciences, 2022, 65(5): 152305. doi: 10.1007/s11432-020-3250-7 [13] WEN Cai, PENG Jinye, ZHOU Yan, et al. Enhanced three-dimensional joint domain localized STAP for airborne FDA-MIMO radar under dense false-target jamming scenario[J]. IEEE Sensors Journal, 2018, 18(10): 4154–4166. doi: 10.1109/JSEN.2018.2820905 [14] BASIT A, WANG Wenqin, NUSENU S Y, et al. Cognitive FDA-MIMO with channel uncertainty information for target tracking[J]. IEEE Transactions on Cognitive Communications and Networking, 2019, 5(4): 963–975. doi: 10.1109/TCCN.2019.2928799 [15] HUANG Bang, WANG Wenqin, BASIT A, et al. Bayesian detection in Gaussian clutter for FDA-MIMO Radar[J]. IEEE Transactions on Vehicular Technology, 2022, 71(3): 2655–2667. doi: 10.1109/TVT.2021.3139894 [16] LAN Lan, MARINO A, AUBRY A, et al. GLRT-based adaptive target detection in FDA-MIMO radar[J]. IEEE Transactions on Aerospace and Electronic Systems, 2021, 57(1): 597–613. doi: 10.1109/TAES.2020.3028485 [17] WANG Keyi, LIAO Guisheng, XU Jingwei, et al. Clutter rank analysis in airborne FDA-MIMO radar with range ambiguity[J]. IEEE Transactions on Aerospace and Electronic Systems, 2022, 58(2): 1416–1430. doi: 10.1109/TAES.2021.3122822 [18] WEN Cai, HUANG Yan, PENG Jinye, et al. Slow-time FDA-MIMO technique with application to STAP radar[J]. IEEE Transactions on Aerospace and Electronic Systems, 2022, 58(1): 74–95. doi: 10.1109/TAES.2021.3098100 [19] WEN Cai, TAO Mingliang, PENG Jinye, et al. Clutter suppression for airborne FDA-MIMO radar using multi-waveform adaptive processing and auxiliary channel STAP[J]. Signal Processing, 2019, 154: 280–293. doi: 10.1016/j.sigpro.2018.09.016 [20] WEN Cai, MA Changzheng, PENG Jinye, et al. Bistatic FDA-MIMO radar space-time adaptive processing[J]. Signal Processing, 2019, 163: 201–212. doi: 10.1016/j.sigpro.2019.05.025 [21] DING Zihang, XIE Junwei, WANG Bo, et al. Robust adaptive null broadening method based on FDA-MIMO radar[J]. IEEE Access, 2020, 8: 177976–177983. doi: 10.1109/ACCESS.2020.3025602 [22] WANG Yuzhuo and ZHU Shengqi. Main-beam range deceptive jamming suppression with simulated annealing FDA-MIMO radar[J]. IEEE Sensors Journal, 2020, 20(16): 9056–9070. doi: 10.1109/JSEN.2020.2982194 [23] JAMSHIDIAN M and BENTLER P M. ML estimation of mean and covariance structures with missing data using complete data routines[J]. Journal of Educational and Behavioral Statistics, 1999, 24(1): 21–24. doi: 10.3102/10769986024001021 [24] WU C F J. On the convergence properties of the EM algorithm[J]. The Annals of Statistics, 1983, 11(1): 95–103. doi: 10.1214/aos/1176346060 [25] AUBRY A, DE MAIO A, MARANO S, et al. Structured covariance matrix estimation with missing-(complex) data for radar applications via expectation-maximization[J]. IEEE Transactions on Signal Processing, 2021, 69: 5920–5934. doi: 10.1109/TSP.2021.3111587 [26] LOUNICI K. High-dimensional covariance matrix estimation with missing observations[J]. Bernoulli, 2014, 20(3): 1029–1058. doi: 10.3150/12-BEJ487 [27] HIPPERT-FERRER A, EL KORSO M N, BRELOY Y A, et al. Robust low-rank covariance matrix estimation with a general pattern of missing values[J]. Signal Processing, 2022, 195: 108460. doi: 10.1016/j.sigpro.2022.108460 [28] XU Danlei, DU Lan, LIU Hongwei, et al. Compressive sensing of stepped-frequency radar based on transfer learning[J]. IEEE Transactions on Signal Processing, 2015, 63(12): 3076–3087. doi: 10.1109/TSP.2015.2421473 [29] JI Yuanjie, WEN Cai, HUANG Yan, et al. Robust direction-of-arrival estimation approach using beamspace-based deep neural networks with array imperfections and element failure[J]. IET Radar, Sonar & Navigation, 2022, 16(11): 1761–1778. doi: 10.1049/rsn2.12295 [30] ZOOGHBY A H E, CHRISTODOULOU C G, and GEORGIOPOULOS M. Neural network-based adaptive beamforming for one- and two-dimensional antenna arrays[J]. IEEE Transactions on Antennas and Propagation, 1998, 46(12): 1891–1893. doi: 10.1109/8.743843 [31] SALLAM T, ABDEL-RAHMAN A B, ALGHONIEMY M, et al. A neural-network-based beamformer for phased array weather radar[J]. IEEE Transactions on Geoscience and Remote Sensing, 2016, 54(9): 5095–5104. doi: 10.1109/TGRS.2016.2554116 [32] ZHAO Zhonghui, ZHAO Huiling, WANG Zhaoping, et al. Radial basis function neural network optimal modeling for phase-only array pattern nulling[J]. IEEE Transactions on Antennas and Propagation, 2021, 69(11): 7971–7975. doi: 10.1109/TAP.2021.3083787 [33] SALLAM T and ATTIYA A M. Convolutional neural network for 2D adaptive beamforming of phased array antennas with robustness to array imperfections[J]. International Journal of Microwave and Wireless Technologies, 2021, 13(10): 1096–1102. doi: 10.1017/S1759078721001070 [34] TAN Ming, WANG Chunyang, and LI Zhihui. Correction analysis of frequency diverse array radar about time[J]. IEEE Transactions on Antennas and Propagation, 2021, 69(2): 834–847. doi: 10.1109/TAP.2020.3016508 [35] CAPON J. High-resolution frequency-wavenumber spectrum analysis[J]. Proceedings of the IEEE, 1969, 57(8): 1408–1418. doi: 10.1109/PROC.1969.7278 [36] YOON J, JORDON J, and VAN DER SCHAAR M. GAIN: Missing data imputation using generative adversarial nets[C]. The 35th International Conference on Machine Learning, Stockholm, Sweden, 2018: 5675–5684. [37] STEKHOVEN D J and BÜHLMANN P. MissForest-non-parametric missing value imputation for mixed-type data[J]. Bioinformatics, 2012, 28(1): 112–118. doi: 10.1093/bioinformatics/btr597 -
图(10) / 表(4)
计量
- 文章访问数: 988
- HTML全文浏览量: 551
- PDF下载量: 237
- 被引次数: 0
