-
摘要: 该文提出了一种针对合成孔径雷达(SAR)的单比特多模态干扰方法,干扰机在截获SAR信号后,将其与单频阈值比较后量化为单比特数据。与传统高精度采样量化生成高逼真度假目标的欺骗干扰方法相比,单比特量化仅保留了数据的符号信息,降低了采样数据的位宽,达到简化系统、提升效率、降低成本的目的。同时,基于单频阈值的单比特量化在截获SAR信号中引入了丰富的谐波分量,通过合理设计阈值的幅度、频率与相位参数,可以将单频阈值泛化为多种阈值。不同阈值可以有效利用不同特性的谐波,进而达到单目标欺骗干扰、多目标欺骗干扰、射频干扰和类噪声干扰等多种干扰模态单一对抗或协同对抗、多模态间捷变的灵巧干扰效果。通过仿真实验定量分析了不同干扰模态下的干扰性能,验证了所提方法的有效性。Abstract: This paper proposes a one-bit multi-modality jamming method against Synthetic Aperture Radar (SAR). After being intercepted by the jammer, the SAR signal is quantized to one-bit sampling data through comparison with the single-frequency threshold. Compared with the conventional deceptive jamming method that uses the high-precision samples of a SAR signal to generate false targets with high fidelity, one-bit quantization only preserves the symbolic information of the signal, which reduces the data width of the sampled data and consequently simplifies the system, improves efficiency, and reduces the cost. Meanwhile, abundant harmonic components have been introduced into intercepted SAR signals by one-bit quantization based on the Single-Frequency Threshold (SFT). The SFT can be generalized to various thresholds by reasonably designing the threshold parameters, including amplitude, frequency, and phase. Harmonics with different characteristics can be effectively used by purposely designed thresholds. Then, ingenious jamming is achieved, which can manifest a single modality or combine multiple jamming modalities among single-target deceptive jamming, multi-target deceptive jamming, radio-frequency jamming, and noise-like jamming and has modality agility. The performance of the proposed method under different jamming modes is quantitatively analyzed through simulation experiments, verifying its effectiveness.
-
表 1 剔除不同匹配度的谐波分量的参数组
Table 1. A parameter group that excludes harmonics components with different matching degrees
参数组 $ {F_{\text{s}}}/{B_{\text{r}}} $ $ {f_{\text{0}}}/{B_{\text{r}}} $ 1 1.00 – 2 4.00 0.66 3 6.00 2.73 4 11.00 3.04 5 14.00 3.77 表 2 机载SAR参数
Table 2. Airborne SAR parameters
参数名称 参数值 脉冲宽度 (μs) 10 信号带宽 (MHz) 150 SAR采样率 (MHz) 300 干扰机采样率 (MHz) 150 载频 (GHz) 9.4 场景中心斜距 (km) 10 天线孔径 (m) 2 载机速度 (m/s) 50 脉冲重复频率 (Hz) 100 表 3 不同干扰模态的参数
Table 3. Parameters of different jamming modes
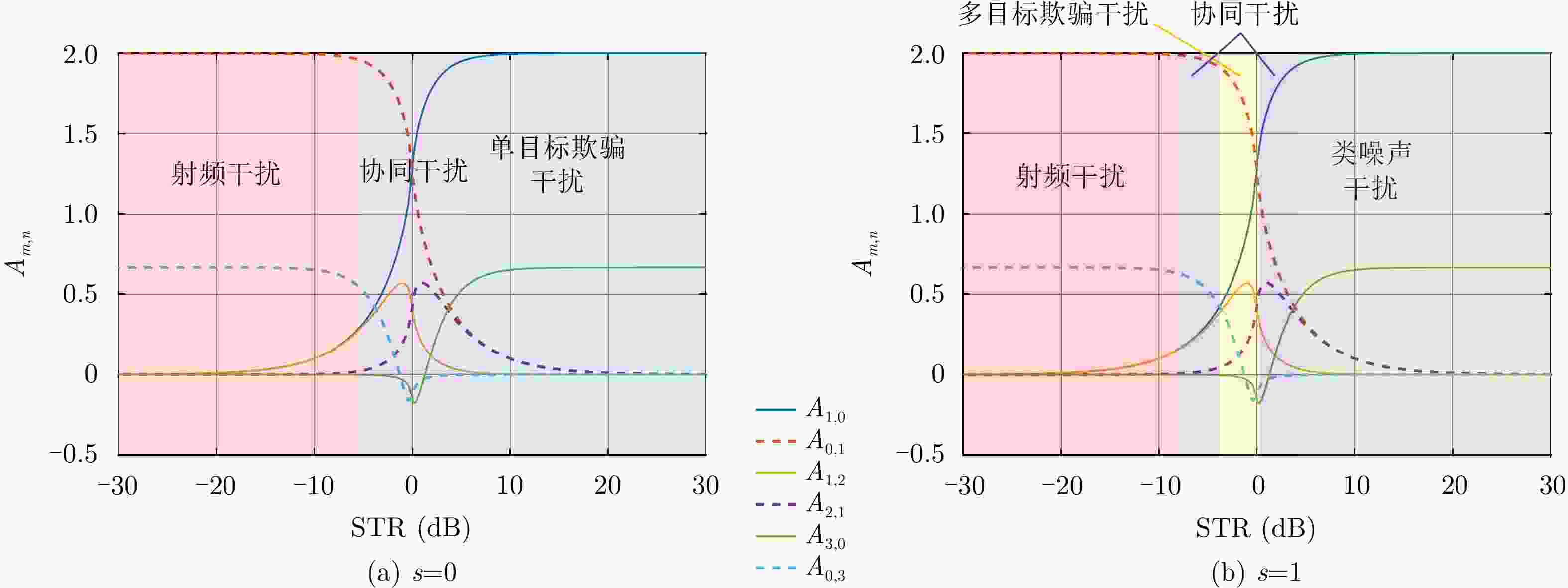
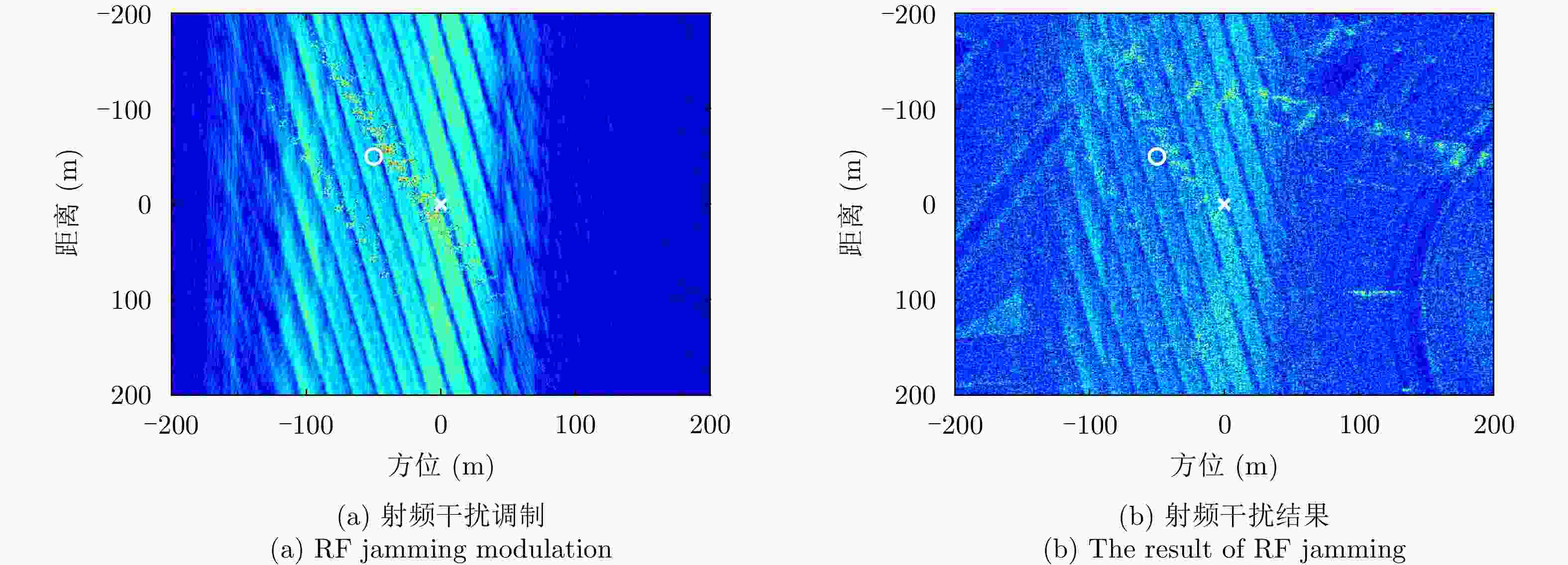
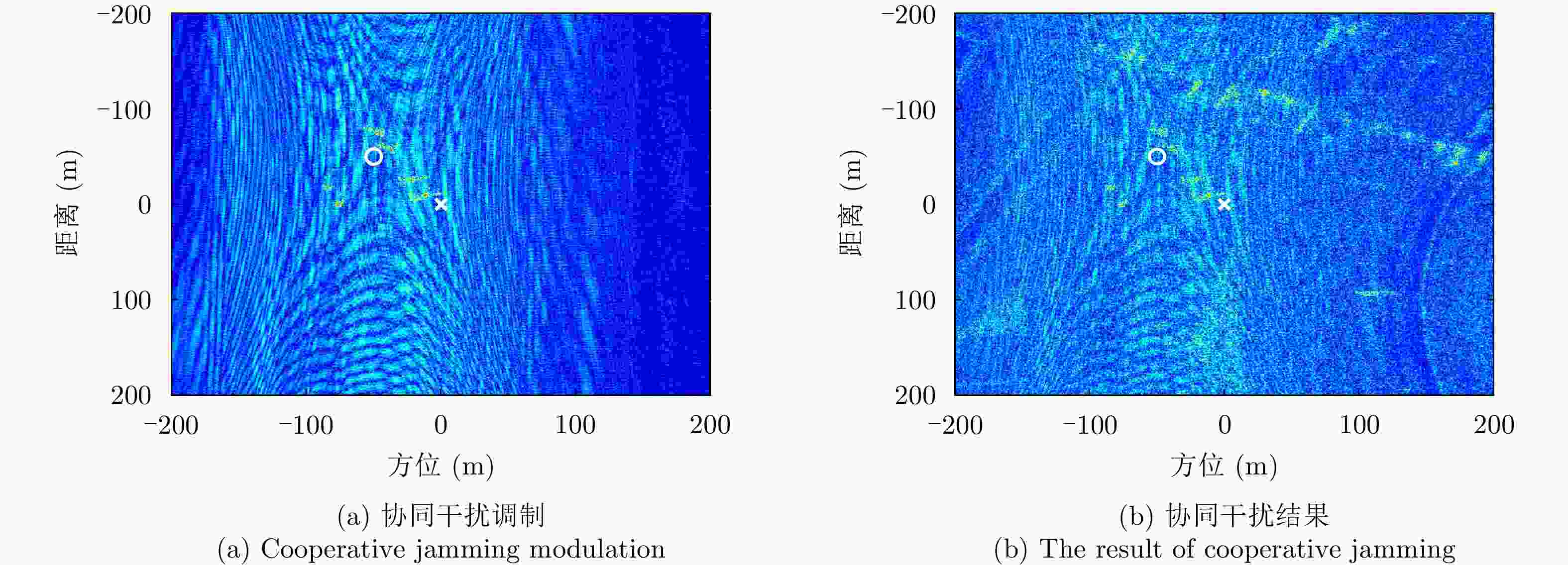
干扰模态 STR (dB) JSR (dB) 传统高精度欺骗 – 12.0 单目标欺骗 0 13.0 多目标欺骗 –0.8 16.5 多目标欺骗-射频压制协同 –6.0 19.0 射频干扰 –10.0 23.0 多目标欺骗-类噪声压制协同 1.6 21.8 类噪声干扰 10.0 23.0 表 4 不同干扰模态成像评估指标
Table 4. Imaging evaluation indicators of different jamming modes
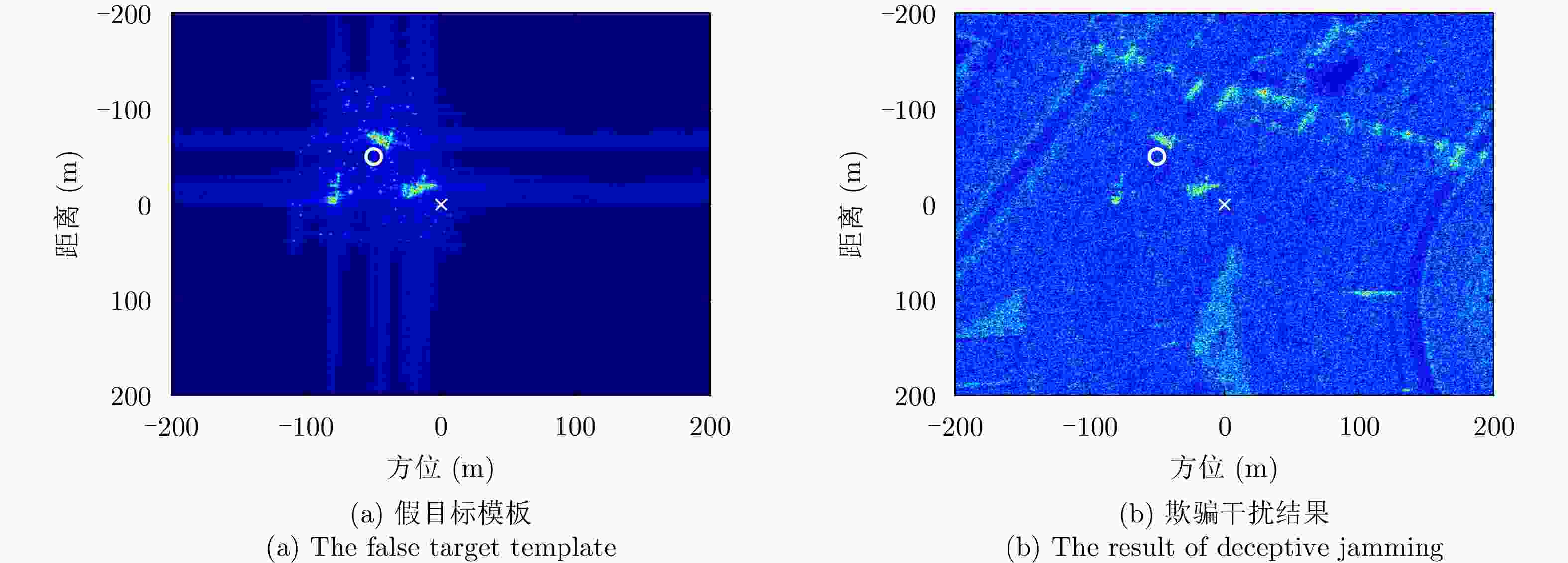
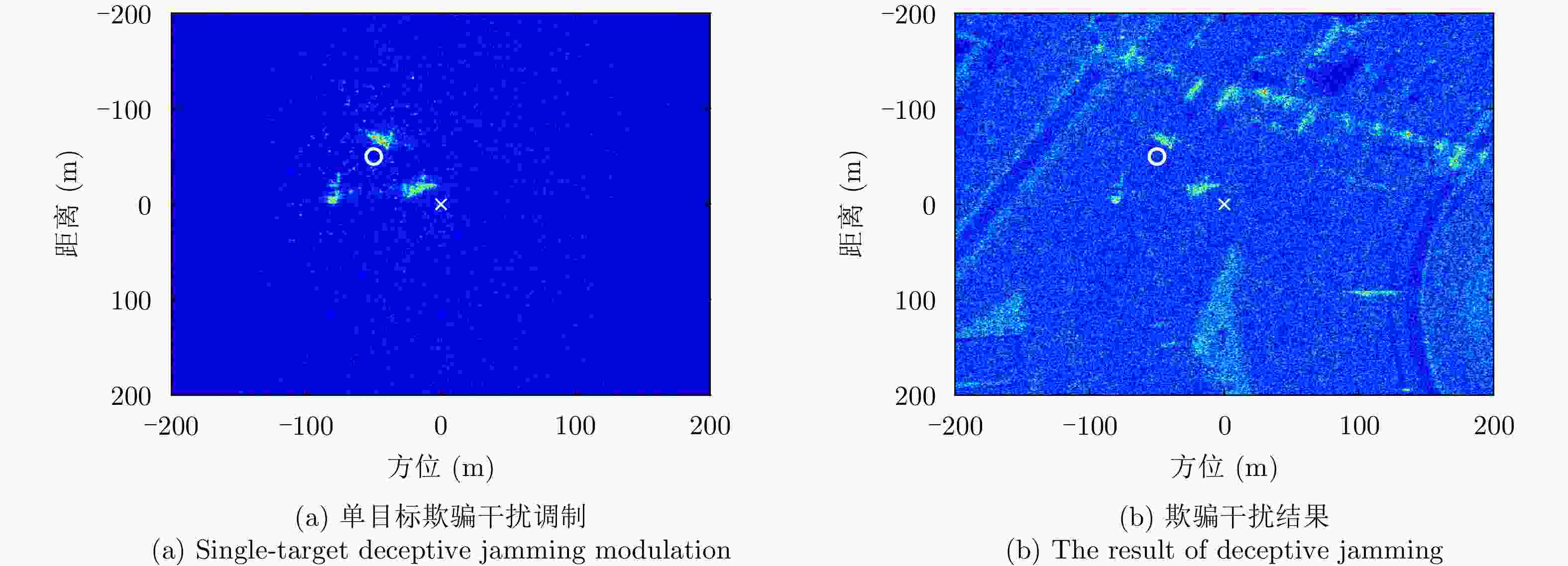
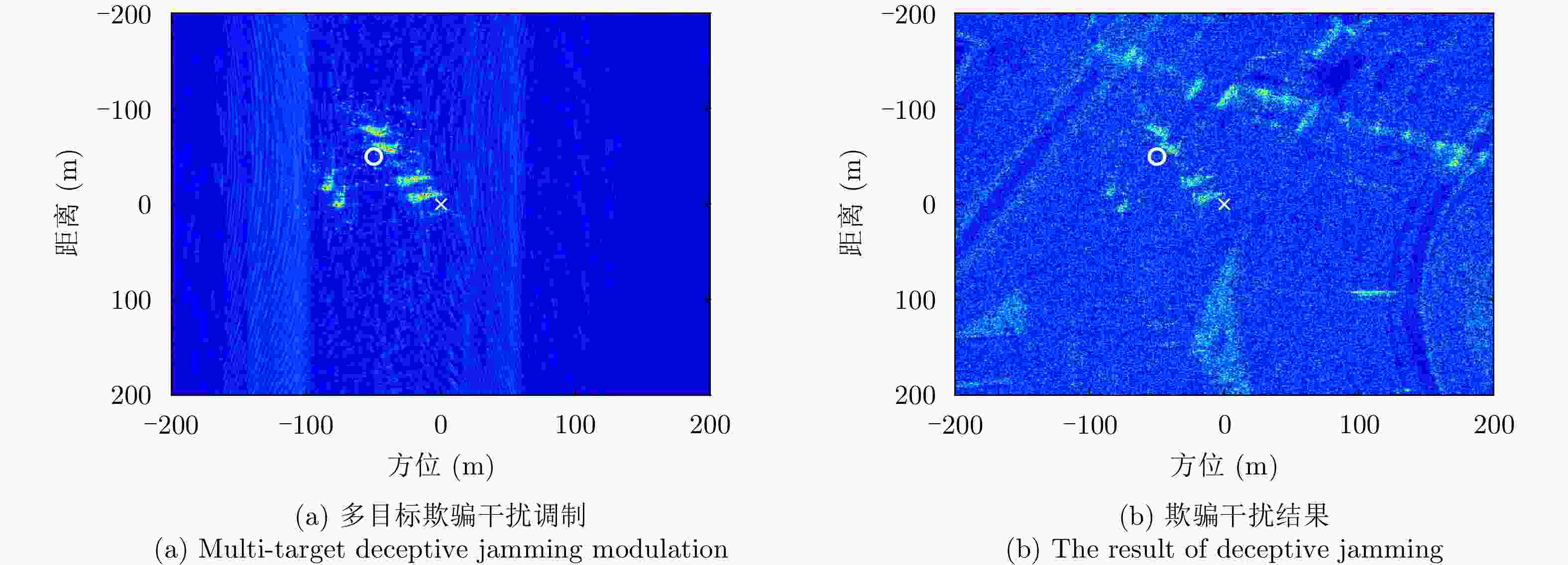
干扰类型 评估指标 SSIM PSNR (dB) ENL Entropy 传统欺骗干扰 – – 2.4762 5.1016 单目标欺骗干扰 0.9532 40.0326 2.5468 5.2031 多目标欺骗干扰 0.9318 36.1002 2.5584 5.2377 射频干扰 0.6718 24.6604 3.0406 5.7346 类噪声干扰 0.6924 28.4512 3.0288 5.5302 -
[1] 黄岩, 赵博, 陶明亮, 等. 合成孔径雷达抗干扰技术综述[J]. 雷达学报, 2020, 9(1): 86–106. doi: 10.12000/JR19113HUANG Yan, ZHAO Bo, TAO Mingliang, et al. Review of synthetic aperture radar interference suppression[J]. Journal of Radars, 2020, 9(1): 86–106. doi: 10.12000/JR19113 [2] 承德宝. 雷达原理[M]. 北京: 国防工业出版社, 2008: 371–416.CHENG Debao. Theory of Radar[M]. Beijing: National Defense Industry Press, 2008: 371–416. [3] 李永祯, 黄大通, 邢世其, 等. 合成孔径雷达干扰技术研究综述[J]. 雷达学报, 2020, 9(5): 753–764. doi: 10.12000/JR20087LI Yongzhen, HUANG Datong, XING Shiqi, et al. Review of synthetic aperture radar jamming technique[J]. Journal of Radars, 2020, 9(5): 753–764. doi: 10.12000/JR20087 [4] LIN Xiaohong, LIU Peiguo, and XUE Guoyi. Fast generation of SAR deceptive jamming signal based on inverse range Doppler algorithm[C]. IET International Radar Conference 2013, Xi’an, China, 2013: 1–4. [5] ZHAO Bo, HUANG Lei, ZHOU Feng, et al. Performance improvement of deception jamming against SAR based on minimum condition number[J]. IEEE Journal of Selected Topics in Applied Earth Observations and Remote Sensing, 2017, 10(3): 1039–1055. doi: 10.1109/JSTARS.2016.2614957 [6] TIAN Tian, ZHOU Feng, and ZHAO Bo. Multi-receiver deception jamming against synthetic aperture radar[C]. 2016 CIE International Conference on Radar (RADAR), Guangzhou, China, 2016: 1–4. [7] FAN Weiwei, ZHOU Feng, and TIAN Tian. A deceptive jamming template synthesis method for SAR using generative adversarial nets[C]. IGARSS 2020 - 2020 IEEE International Geoscience and Remote Sensing Symposium, Waikoloa, USA, 2020: 6926–6929. [8] CHANG Xin, DONG Chunxi, TANG Zhengzhao, et al. Mosaic scene deception jamming based on 2D separation modulation against SAR[J]. IET Radar, Sonar & Navigation, 2019, 13(2): 310–315. doi: 10.1049/iet-rsn.2018.5166 [9] 余檑. 基于阴影特征的SAR对抗方法研究[D]. [硕士论文], 电子科技大学, 2017: 16–18.YU Lei. Research of SAR countermeasures based on shadow feature[D]. [Master dissertation], University of Electronic Science and Technology of China, 2017: 16–18. [10] 孟智超, 卢景月, 张磊. 前视多通道SAR自适应鉴别抑制欺骗干扰[J]. 雷达学报, 2019, 8(1): 82–89. doi: 10.12000/JR18081MENG Zhichao, LU Jingyue, and ZHANG Lei. Forward-looking multi-channel SAR adaptive identification to suppress deception jamming[J]. Journal of Radars, 2019, 8(1): 82–89. doi: 10.12000/JR18081 [11] 曾铮, 张福博, 陈龙永, 等. 基于多输入多输出合成孔径雷达的二维混合基线抗欺骗干扰方法[J]. 雷达学报, 2019, 8(1): 90–99. doi: 10.12000/JR18118ZENG Zheng, ZHANG Fubo, CHEN Longyong, et al. A two-dimensional mixed baseline method based on MIMO-SAR for countering deceptive jamming[J]. Journal of Radars, 2019, 8(1): 90–99. doi: 10.12000/JR18118 [12] CAPPUCCINO G, COCORULLO G, CORSONELLO P, et al. Real-time processing of one-bit-coded SAR data[C]. The 8th Mediterranean Electrotechnical Conference on Industrial Applications in Power Systems, Computer Science and Telecommunications, Bari, Italy, 1996: 117–119. [13] SCHAEFER C, FISCHER C, and VOELKER M. One-bit digitization for DBF-SAR: Too good to be true[C]. 7th European Conference on Synthetic Aperture Radar, Friedrichshafen, Germany, 2008: 1–4. [14] OSSOWSKA A. One-bit quantization for synthetic aperture radar with DBF[C]. 7th European Conference on Synthetic Aperture Radar, Friedrichshafen, Germany, 2008: 1–4. [15] ZHAO Bo, HUANG Lei, LI Qiang, et al. 1-bit SAR imaging assisted with single-frequency threshold[C]. 2019 IEEE International Geoscience and Remote Sensing Symposium, Yokohama, Japan, 2019: 815–818. [16] ZHAO Bo, HUANG Lei, and BAO Weimin. One-bit SAR imaging based on single-frequency thresholds[J]. IEEE Transactions on Geoscience and Remote Sensing, 2019, 57(9): 7017–7032. doi: 10.1109/TGRS.2019.2910284 [17] ZHAO Bo, HUANG Lei, LI Jian, et al. Deceptive SAR jamming based on 1-bit sampling and time-varying thresholds[J]. IEEE Journal of Selected Topics in Applied Earth Observations and Remote Sensing, 2018, 11(3): 939–950. doi: 10.1109/JSTARS.2018.2793247 [18] ZHAO Bo, HUANG Lei, LI Bing, et al. One-bit splitting deceptive jamming against SAR[J]. Defence Technology, 2022, 18(10): 1760–1777. doi: 10.1016/j.dt.2021.09.018 [19] 王强. 对合成孔径雷达的弹射式干扰研究[J]. 电子科技, 2013, 26(4): 113–115, 123. doi: 10.16180/j.cnki.issn1007-7820.2013.04.024WANG Qiang. Research of jamming to SAR by rebound mode[J]. Electronic Science and Technology, 2013, 26(4): 113–115, 123. doi: 10.16180/j.cnki.issn1007-7820.2013.04.024 [20] 赵博, 杨军, 孙光才, 等. 一种虚假大场景SAR快速转发式欺骗干扰方法研究[J]. 电子与信息学报, 2012, 34(4): 963–968. doi: 10.3724/SP.J.1146.2011.0050ZHAO Bo, YANG Jun, SUN Guangcai, et al. A method of SAR fast repeater deception jamming for large false scene[J]. Journal of Electronics &Information Technology, 2012, 34(4): 963–968. doi: 10.3724/SP.J.1146.2011.0050 [21] 黄磊, 赵博. 基于多接收机等距直角分布的SAR欺骗干扰方法及系统[P]. 中国, 105467368B, 2017.HUANG Lei and ZHAO Bo. Multi-receiver equidistant rectangular distribution-based SAR deception jamming method and system[P]. CN, 105467368B, 2017. [22] ZHAO Bo, HUANG Lei, and JIN Benzhou. Strategy for SAR imaging quality improvement with low-precision sampled data[J]. IEEE Transactions on Geoscience and Remote Sensing, 2021, 59(4): 3150–3160. doi: 10.1109/TGRS.2020.3014300 [23] Synthetic aperture radar (SAR) imagery[EB/OL]. https://www.sandia.gov/radar/pathfinder-radar-isr-and-synthetic-aperture-radar-sar-systems/complex-data/. -



 作者中心
作者中心 专家审稿
专家审稿 责编办公
责编办公 编辑办公
编辑办公
 下载:
下载: