作者中心
专家审稿
责编办公
编辑办公
Self-supervised Learning Method for SAR Interference Suppression Based on Abnormal Texture Perception
-
摘要: 面对日渐复杂的电磁干扰环境，合成孔径雷达干扰抑制已成为亟须解决的难题。现有主流合成孔径雷达非参数/参数化干扰抑制方法，严重依赖干扰先验和强能量差异，存在计算复杂度高、信号损失严重等问题，难以满足对抗日益复杂的干扰的需求。针对上述问题，该文提出一种基于纹理异常感知的SAR自监督学习干扰抑制方法，利用正常雷达回波与干扰的时频域纹理差异性特征克服干扰先验的约束。首先，构建了一种干扰时频定位网络模型Location-Net，对雷达回波时频谱进行压缩重构，根据网络的重构误差对干扰进行时频定位；其次，针对干扰抑制损失问题，构建了一种信号修复神经网络模型Recovery-Net，实现对干扰抑制后回波信号损失修复。相比传统方法，所提方法克服对干扰先验的需求，可有效对抗多种复杂干扰类型，具备较强的泛化能力。基于仿真和实测数据的抗干扰处理结果，验证了所提方法对多种有源主瓣压制干扰的有效性，并通过与3种现有抗干扰方法进行对比，体现了该算法的优越性。最后，对比了所提神经网络与主流轻量化神经网络的复杂度差异，结果表明设计的两个神经网络计算复杂度更低，具备实时应用前景。Abstract: Facing the increasingly complex electromagnetic interference environment, Synthetic Aperture Radar (SAR) interference suppression has become an urgent problem to be solved. The existing mainstream synthetic aperture radar nonparametric/parametric interference suppression methods, which heavily rely on interference priori and strong energy difference, have serious problems such as high computational complexity and signal loss, and have difficulty in meeting the needs of countering increasingly complex interference. To solve the aforementioned problems, we propose an anti-interference method using self-supervised learning based on deep learning, which uses the time-frequency domain texture difference between normal radar echo and interference to overcome the constraint of using interference prior. First, we construct an interference location network model Location-Net, which compresses and reconstructs the time-frequency spectrum of the radar echo and locates the interference according to the network’s reconstruction error. Second, aiming at the signal loss caused by interference suppression, a signal recovery neural network model Recovery-Net is constructed to recover the echo signal after interference suppression. Compared with traditional methods, our method overcomes the need for interference prior, can effectively resist various complex interference types and has strong generalization ability. The anti-interference processing results based on simulation and measured data verify the effectiveness of the proposed method for various active main lobe suppression interference and show the superiority of the algorithm proposed here by comparing it with three existing anti-interference methods. Finally, comparing the complexity difference between the proposed and mainstream lightweight neural networks shows that the neural networks designed here have low computational complexity and real-time application prospects.
-
图 1 间歇采样转发/非均匀间歇采样转发/线性函数移频干扰的多域特性图
Figure 1. Multi-domain of interrupted-sampling and repeater jamming/heterogeneous interrupted-sampling and repeater jamming/linear function frequency shift jamming
图 2 干扰时频定位网络模型(Location-Net)
Figure 2. Interference time-frequency location network model (Location-Net)
图 4 基于自监督学习的干扰抑制流程
Figure 4. Interference suppression process based on self-supervised learning
图 5 本文方法处理各阶段时频域
Figure 5. Time-frequency of echo stage during processing by our method
图 8 现有方法抗干扰处理后回波时频域
Figure 8. Time-frequency of echo stage after processing by existing anti-jamming method
图 9 仿真干扰数据抗干扰成像结果对比
Figure 9. Comparison of imaging result of data with simulated interference after anti-jamming
图 10 实测相参压制干扰抗干扰时频域
Figure 10. Time-frequency spectrum of measured data with coherent suppression jamming after anti-jamming
图 11 实测相参压制干扰抗干扰成像结果
Figure 11. Imaging result of measured data with coherent suppression jamming after anti-jamming
图 12 实测相参运动多假目标干扰抗干扰时频域
Figure 12. Time-frequency spectrum of measured data with coherent motion and multi-false target interference after anti-jamming
图 13 实测相参运动假目标干扰抗干扰成像结果
Figure 13. Imaging result of measured data with coherent motion and multi-false target interference after anti-jamming
图 14 实测复合干扰抗干扰处理时频域
Figure 14. Time-frequency spectrum of measured data with complex interference after anti-jamming
图 15 实测组合式干扰抗干扰处理成像结果
Figure 15. Imaging result of measured data with complex interference after anti-jamming
表 1 干扰时频定位网络参数
Table 1. Interference time-frequency location network parameter list
类型 核/步长 补零个数 BN/激活 卷积 3×3×16/2 1 是/ReLU 卷积 3×3×32/2 1 是/ReLU 转置卷积 3×3×16/2 1 是/ReLU 转置卷积 3×3×2/2 1 – 
下载: 导出CSV
表 2 基于卷积层的信号修复网络参数
Table 2. Parameter list of signal recovery network based on convolution layers
核/步长 补零个数 BN/激活 5×5×8/(2,1) 0 是/ReLU 5×5×16/(2,1) 0 是/ReLU 5×5×24/1 0 是/ReLU 1×7×32/1 0 是/ReLU 1×7×32/1 0 是/ReLU 1×7×32/1 0 是/ReLU 1×1×2/1 0 –
下载: 导出CSV
表 3 加入仿真干扰的实测SAR回波参数
Table 3. Parameters of measured SAR echo with simulated jamming
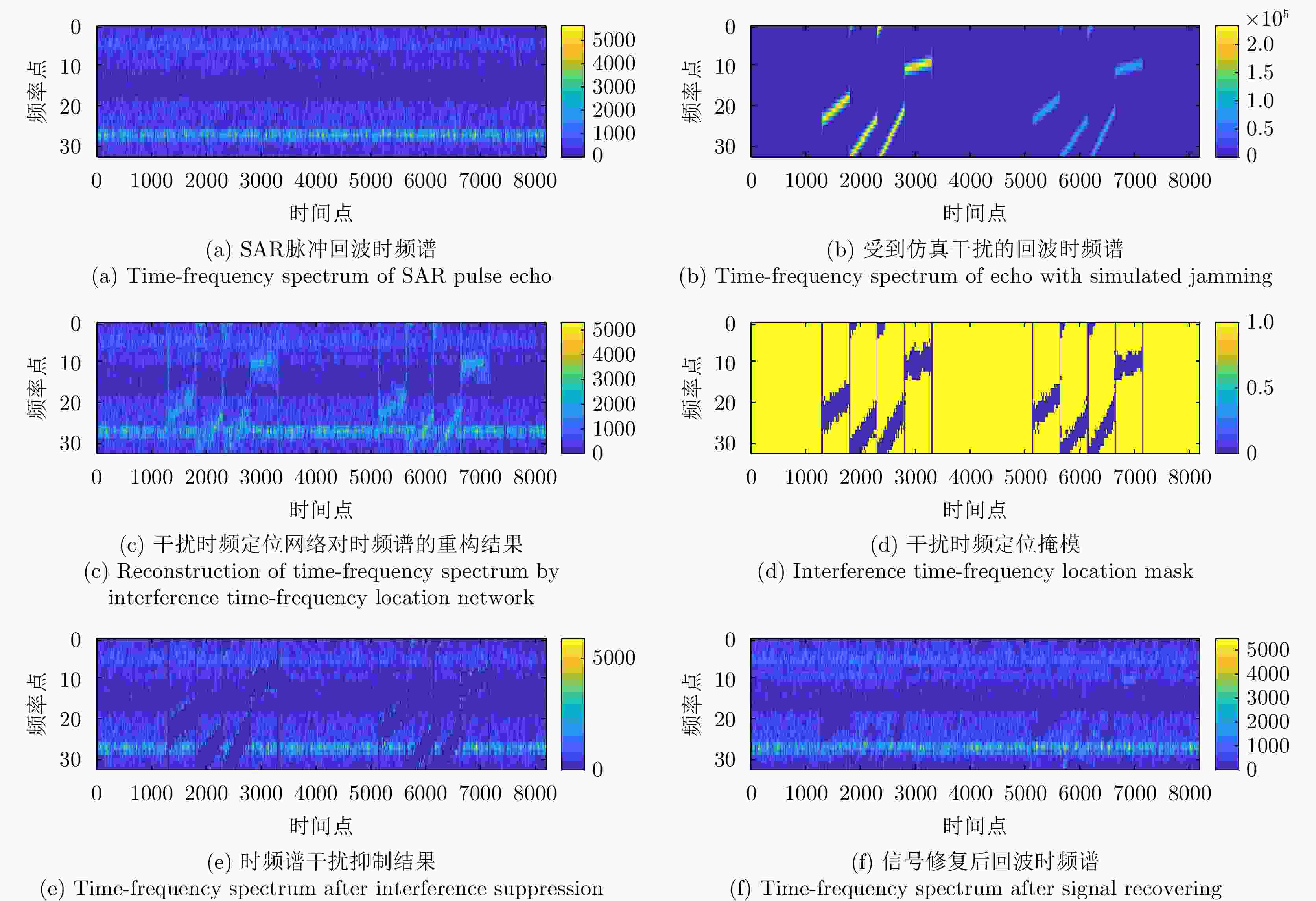
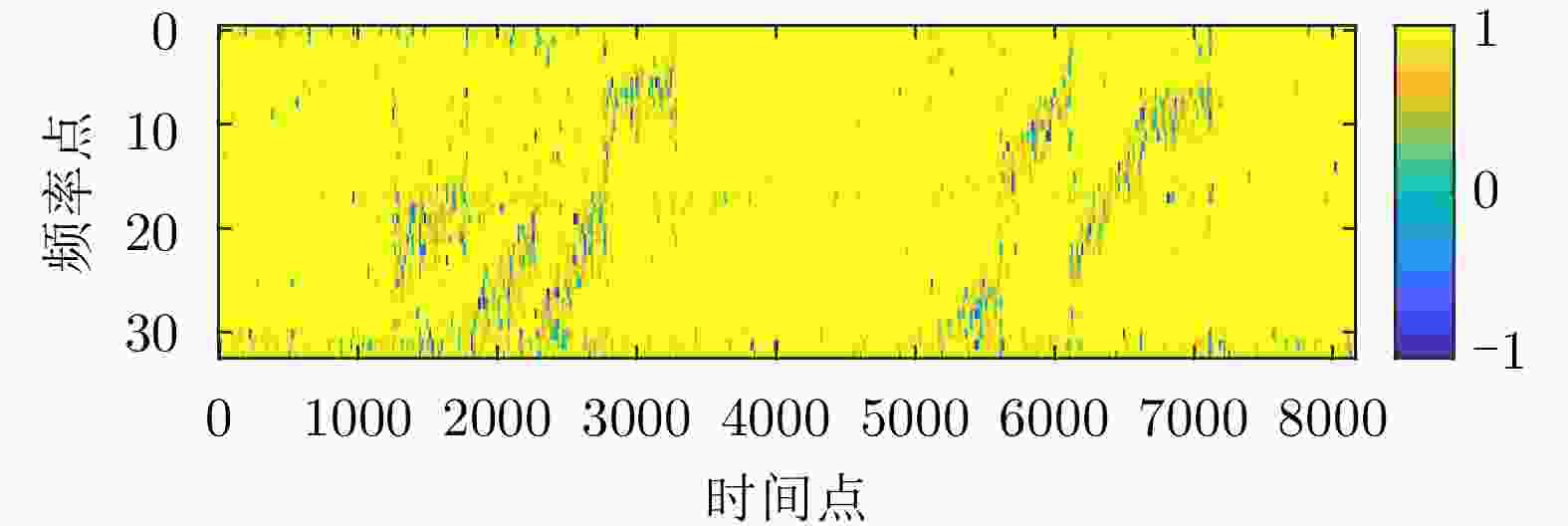
参数 数值 载频 Ku波段 带宽 50 MHz 采样频率 60 MHz 脉冲重复频率 800 Hz 平台运动速度 80 m/s
下载: 导出CSV
表 4 仿真干扰数据抗干扰评估
Table 4. Anti-jamming evaluation of data with simulate interference
方法 ISR (dB) SDR (dB) SSIM IALM 21.40 2.76 0.31 ESP 5.72 0.07 0.05 陷波滤波器 16.70 5.44 0.21 干扰抑制 18.95 11.18 0.77 信号修复 18.65 13.56 0.94
下载: 导出CSV
表 5 实测数据雷达参数
Table 5. Radar parameters of measured data
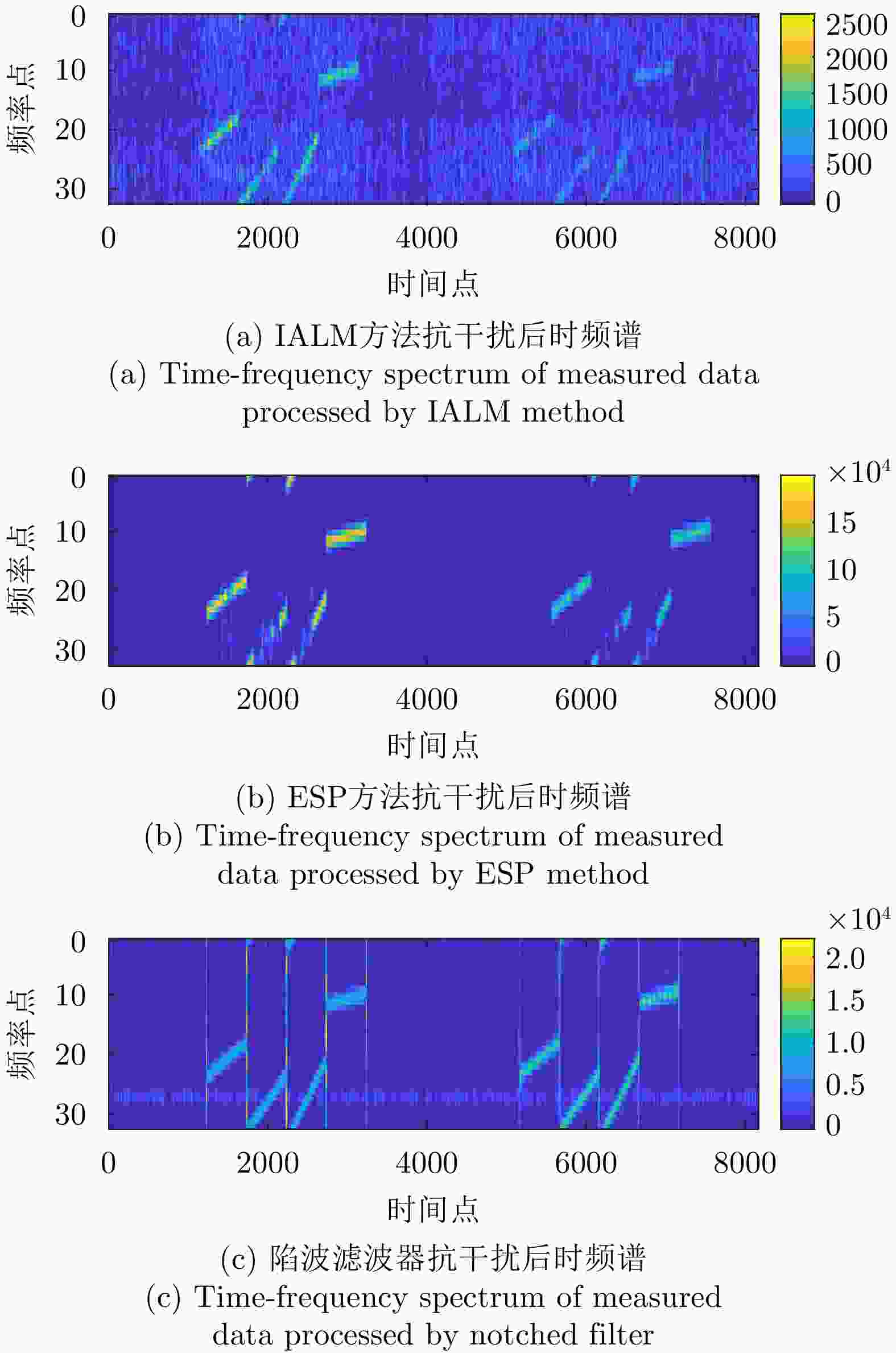
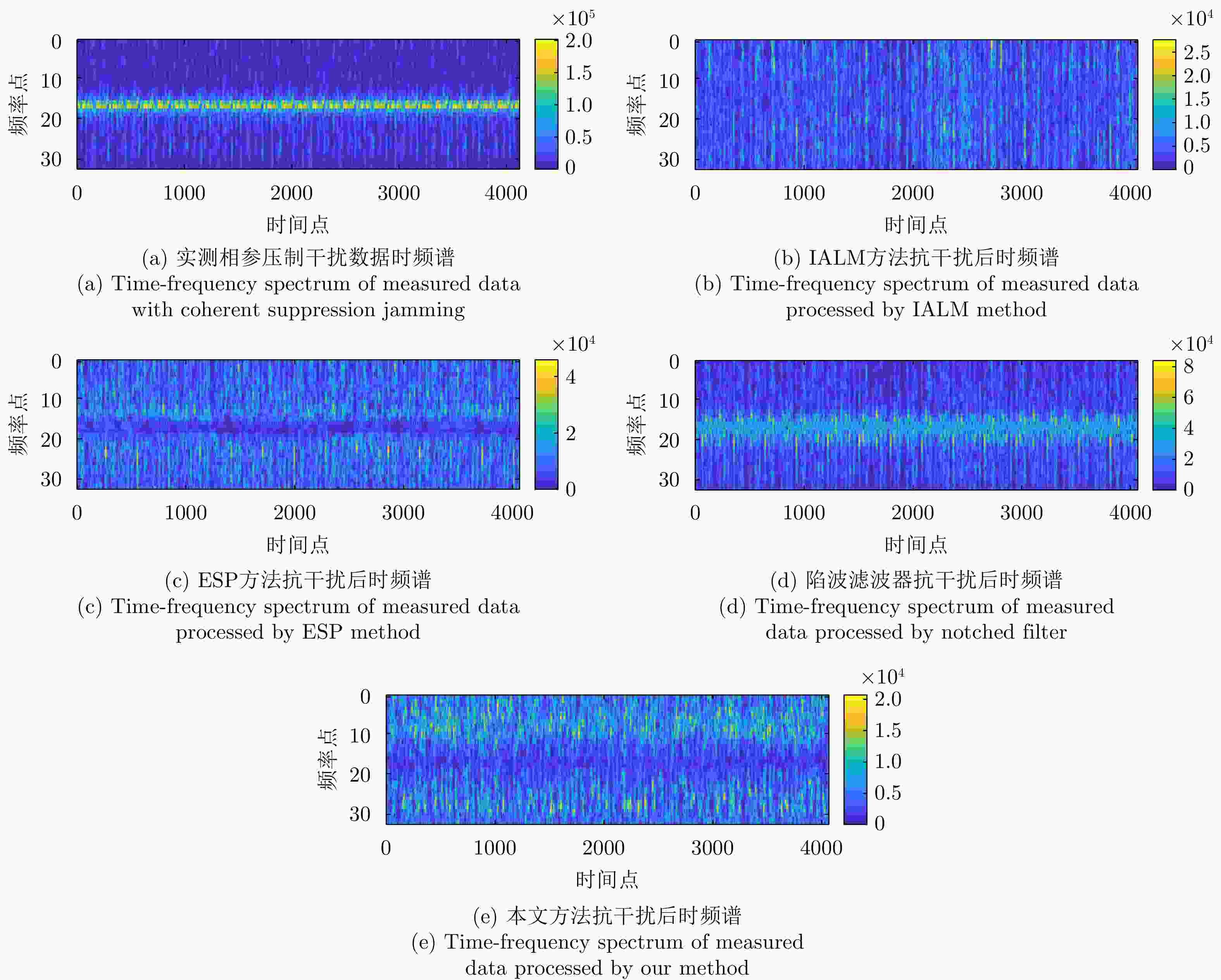
参数 数值 载频 Ku波段 带宽 100 MHz 采样频率 120 MHz 脉冲重复频率 600 Hz 平台速度 85 m/s
下载: 导出CSV
表 6 实测相参压制干扰数据抗干扰评估
Table 6. Anti-jamming evaluation of measured data with coherent suppression jamming
方法 ISR (dB) MNR (dB) IALM 14.72 –7.62 ESP 8.45 –8.17 陷波滤波器 13.33 –7.91 本文方法 18.72 –8.43
下载: 导出CSV
表 7 实测相参运动假目标干扰数据抗干扰评估
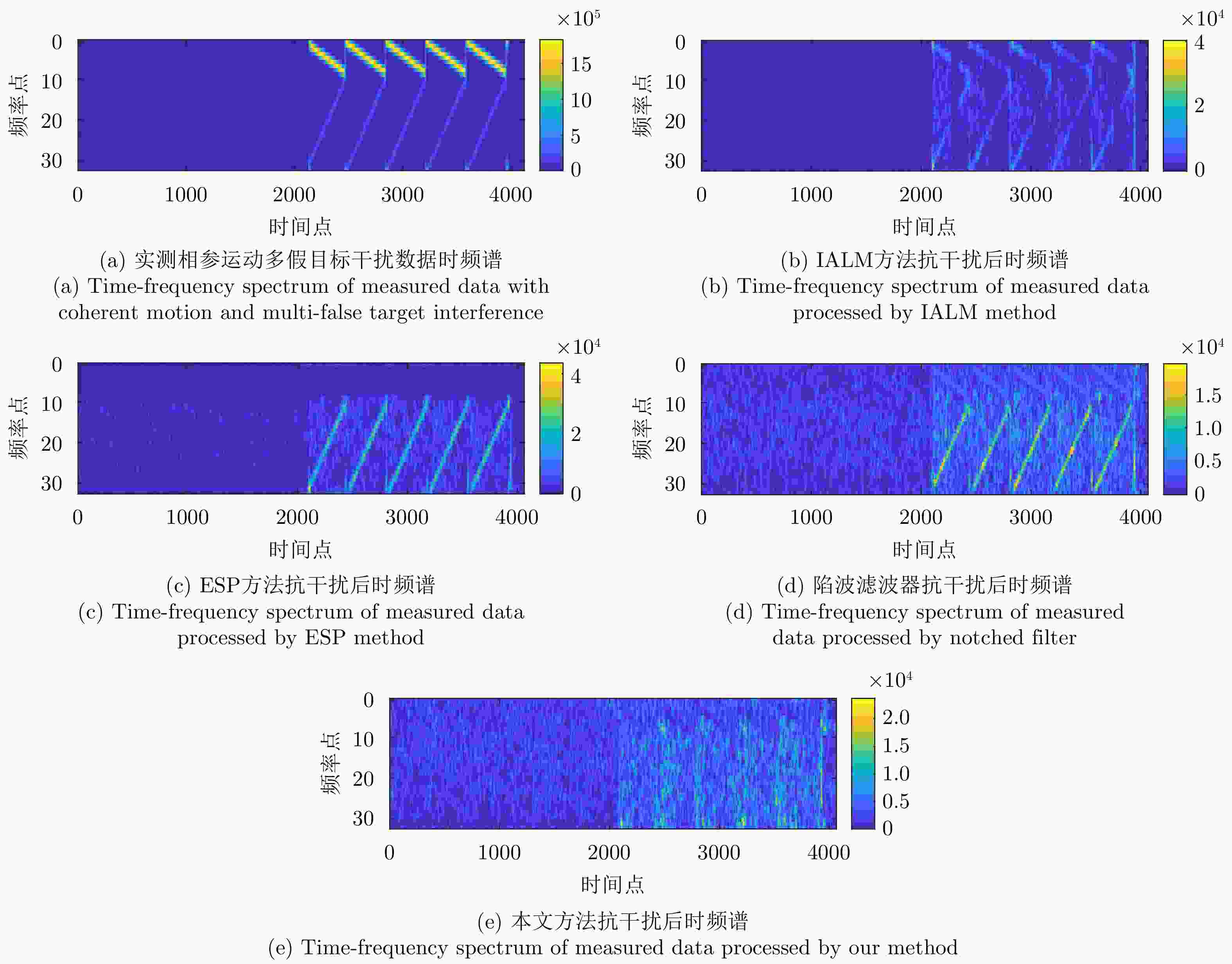
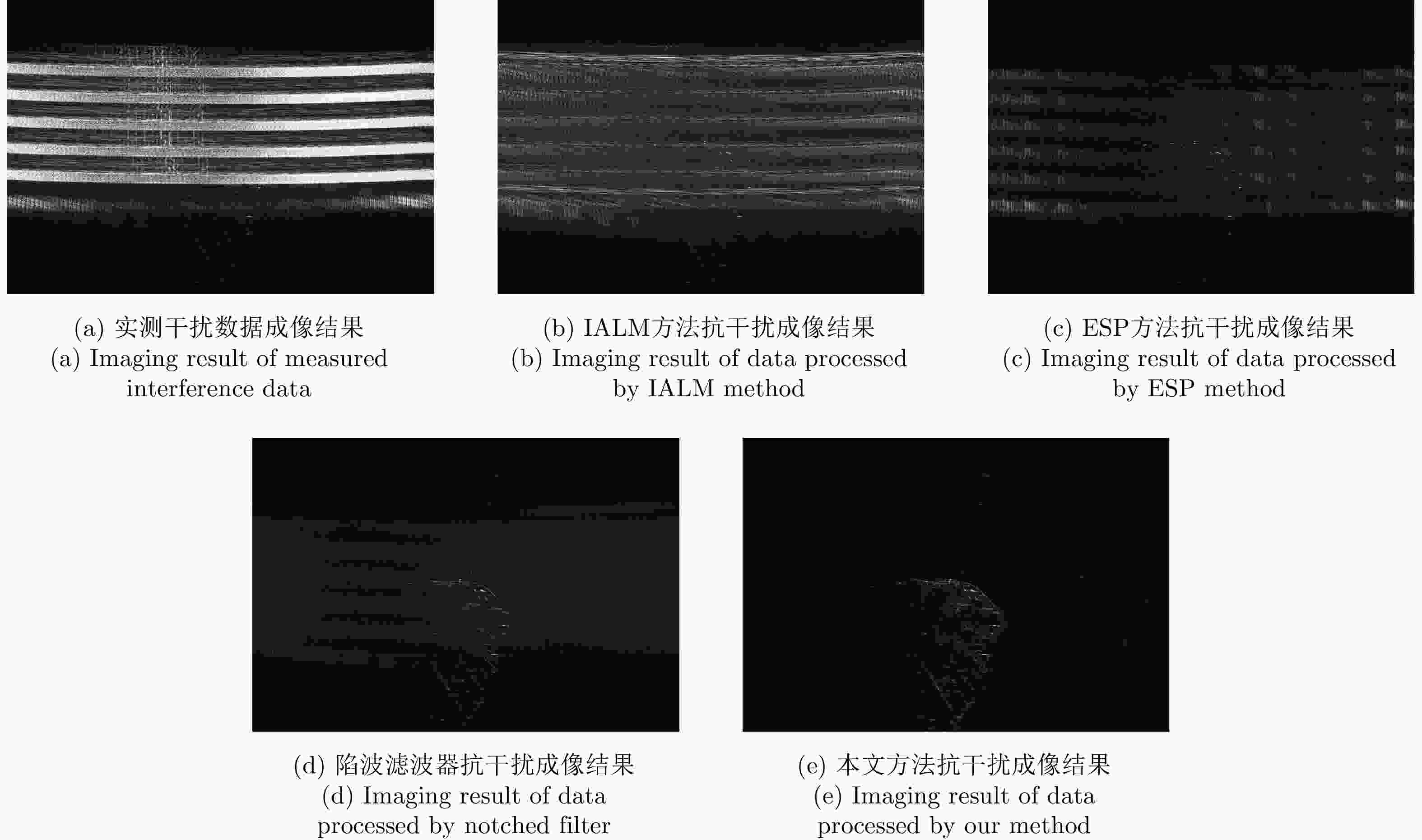
Table 7. Anti-jamming evaluation of measured data with coherent motion and multi-false target interference
方法 ISR (dB) MNR (dB) IALM 17.79 –10.83 ESP 15.09 –11.80 陷波滤波器 16.96 –9.58 本文方法 19.93 –7.85
下载: 导出CSV
表 8 实测组合式干扰数据抗干扰评估
Table 8. Anti-jamming evaluation of measured data with complex interference
方法 ISR (dB) MNR (dB) IALM 16.61 –12.41 ESP 14.48 –7.34 陷波滤波器 17.21 –8.21 本文方法 18.65 –8.43
下载: 导出CSV
表 9 神经网络模型复杂度对比
Table 9. Comparison of neural network complexity
模型 参数量 浮点运算量 内存访问量 MobileNet V2 3.5 M 209.6 M 110.6 M ShuffleNet V2 2.3 M 98.7 M 36.7 M IDN + IMN 136.6 M 53.8 G 2.1 G L-Net + R-Net 43330 76.0 M 14.1 M
下载: 导出CSV
-
[1] LENG Xiangguang, JI Kefeng, ZHOU Shilin, et al. Fast shape parameter estimation of the complex generalized Gaussian distribution in SAR images[J]. IEEE Geoscience and Remote Sensing Letters, 2020, 17(11): 1933–1937. doi: 10.1109/LGRS.2019.2960095 [2] HUANG Yan, ZHANG Lei, LI Jie, et al. Reweighted tensor factorization method for SAR narrowband and wideband interference mitigation using smoothing multiview tensor model[J]. IEEE Transactions on Geoscience and Remote Sensing, 2020, 58(5): 3298–3313. doi: 10.1109/TGRS.2019.2953069 [3] 李永祯, 黄大通, 邢世其, 等. 合成孔径雷达干扰技术研究综述[J]. 雷达学报, 2020, 9(5): 753–764. doi: 10.12000/JR20087LI Yongzhen, HUANG Datong, XING Shiqi, et al. A review of synthetic aperture radar jamming technique[J]. Journal of Radars, 2020, 9(5): 753–764. doi: 10.12000/JR20087 [4] 黄岩, 赵博, 陶明亮, 等. 合成孔径雷达抗干扰技术综述[J]. 雷达学报, 2020, 9(1): 86–106. doi: 10.12000/JR19113HUANG Yan, ZHAO Bo, TAO Mingliang, et al. Review of synthetic aperture radar interference suppression[J]. Journal of Radars, 2020, 9(1): 86–106. doi: 10.12000/JR19113 [5] MEYER F J, NICOLL J B, and DOULGERIS A P. Correction and characterization of radio frequency interference signatures in L-band synthetic aperture radar data[J]. IEEE Transactions on Geoscience and Remote Sensing, 2013, 51(10): 4961–4972. doi: 10.1109/TGRS.2013.2252469 [6] DAKOVIĆ M, THAYAPARAN T, DJUKANOVIĆ S, et al. Time-frequency-based non-stationary interference suppression for noise radar systems[J]. IET Radar, Sonar & Navigation, 2008, 2(4): 306–314. doi: 10.1049/iet-rsn:20070137 [7] ZHOU Feng, TAO Mingliang, BAI Xueru, et al. Narrow-band interference suppression for SAR based on independent component analysis[J]. IEEE Transactions on Geoscience and Remote Sensing, 2013, 51(10): 4952–4960. doi: 10.1109/TGRS.2013.2244605 [8] TAO Mingliang, ZHOU Feng, LIU Jianqiang, et al. Narrow-band interference mitigation for SAR using independent subspace analysis[J]. IEEE Transactions on Geoscience and Remote Sensing, 2014, 52(9): 5289–5301. doi: 10.1109/TGRS.2013.2287900 [9] TAO Mingliang, ZHOU Feng, and ZHANG Zijing. Wideband interference mitigation in high-resolution airborne synthetic aperture radar data[J]. IEEE Transactions on Geoscience and Remote Sensing, 2016, 54(1): 74–87. doi: 10.1109/TGRS.2015.2450754 [10] DJUKANOVIC S and POPOVIC V. A parametric method for multicomponent interference suppression in noise radars[J]. IEEE Transactions on Aerospace and Electronic Systems, 2012, 48(3): 2730–2738. doi: 10.1109/TAES.2012.6237624 [11] LIU Zhiling, LIAO Guisheng, and YANG Zhiwei. Time variant RFI suppression for SAR using iterative adaptive approach[J]. IEEE Geoscience and Remote Sensing Letters, 2013, 10(6): 1424–1428. doi: 10.1109/LGRS.2013.2259575 [12] YANG Zhiwei, DU Wentao, LIU Zhiling, et al. WBI suppression for SAR using iterative adaptive method[J]. IEEE Journal of Selected Topics in Applied Earth Observations and Remote Sensing, 2016, 9(3): 1008–1014. doi: 10.1109/JSTARS.2015.2470107 [13] JOY S, NGUYEN L H, and TRAN T D. Radio frequency interference suppression in ultra-wideband synthetic aperture radar using range-azimuth sparse and low-rank model[C]. 2016 IEEE Radar Conference, Philadelphia, USA, 2016: 1–4. [14] NGUYEN L H and TRAN T D. Efficient and robust RFI extraction via sparse recovery[J]. IEEE Journal of Selected Topics in Applied Earth Observations and Remote Sensing, 2016, 9(6): 2104–2117. doi: 10.1109/JSTARS.2016.2528884 [15] LIU Hongqing, LI Dong, ZHOU Yi, et al. Joint wideband interference suppression and SAR signal recovery based on sparse representations[J]. IEEE Geoscience and Remote Sensing Letters, 2017, 14(9): 1542–1546. doi: 10.1109/LGRS.2017.2721425 [16] WANG Yafeng, SUN Boye, and WANG Ning. Recognition of radar active-jamming through convolutional neural networks[J]. The Journal of Engineering, 2019, 2019(21): 7695–7697. doi: 10.1049/joe.2019.0659 [17] ZHAO Qingyuan, LIU Yang, CAI Linjie, et al. Research on electronic jamming identification based on CNN[C]. 2019 IEEE International Conference on Signal, Information and Data Processing (ICSIDP), Chongqing, China, 2019: 1–5. [18] LIN Junjie and FAN Xiaolei. Radar active jamming recognition based on recurrence plot and convolutional neural network[C]. 2021 IEEE 4th Advanced Information Management, Communicates, Electronic and Automation Control Conference (IMCEC), Chongqing, China, 2021: 1511–1515. [19] QIU Lei and FAN Yize. A radar jamming recognition method based on hybrid dilated convolution[C]. 2022 3rd International Conference on Computer Vision, Image and Deep Learning & International Conference on Computer Engineering and Applications (CVIDL & ICCEA), Changchun, China, 2022: 692–695. [20] FAN Weiwei, ZHOU Feng, RONG Pengshuai, et al. Interference mitigation for synthetic aperture radar using deep learning[C]. 2019 6th Asia-Pacific Conference on Synthetic Aperture Radar (APSAR), Xiamen, China, 2019: 1–6. [21] CHEN Shengyi, SHANGGUAN Wangyi, TAGHIA J, et al. Automotive radar interference mitigation based on a generative adversarial network[C]. 2020 IEEE Asia-Pacific Microwave Conference (APMC), Hong Kong, China, 2020: 728–730. [22] NAIR A A, RANGAMANI A, NGUYEN L H, et al. Spectral gap extrapolation and radio frequency interference suppression using 1D UNets[C]. 2021 IEEE Radar Conference, Atlanta, USA, 2021: 1–6. [23] MUN J, HA S, and LEE J. Automotive radar signal interference mitigation using RNN with self attention[C]. IEEE International Conference on Acoustics, Speech and Signal Processing, Barcelona, Spain, 2020: 3802–3806. [24] HASELMANN M, GRUBER D P, and TABATABAI P. Anomaly detection using deep learning based image completion[C]. 17th IEEE International Conference on Machine Learning and Applications (ICMLA), Orlando, USA, 2018: 1237–1242. [25] IOFFE S and SZEGEDY C. Batch normalization: Accelerating deep network training by reducing internal covariate shift[C]. 32nd International Conference on Machine Learning, Lille, France, 2015: 448–456. [26] KRIZHEVSKY A, SUTSKEVER I, and HINTON G E. ImageNet classification with deep convolutional neural networks[J]. Communications of the ACM, 2017, 60(6): 84–90. doi: 10.1145/3065386 [27] HE Kaiming, ZHANG Xiangyu, REN Shaoqing, et al. Deep residual learning for image recognition[C]. 2016 IEEE Conference on Computer Vision and Pattern Recognition (CVPR), Las Vegas, USA, 2016: 770–778. [28] SIMONYAN K and ZISSERMAN A. Very deep convolutional networks for large-scale image recognition[C]. 3rd International Conference on Learning Representations, San Diego, USA, 2015: 1–14. [29] WANG Zhou, BOVIK A C, SHEIKH H R, et al. Image quality assessment: From error visibility to structural similarity[J]. IEEE Transactions on Image Processing, 2004, 13(4): 600–612. doi: 10.1109/tip.2003.819861 [30] PASZKE A, GROSS S, MASSA F, et al. PyTorch: An imperative style, high-performance deep learning library[C]. 33rd International Conference on Neural Information Processing System, Vancouver, Canada, 2019: 8026–8037. [31] KINGMA D P and BA J. Adam: A method for stochastic optimization[C]. 3rd International Conference on Learning Representations (ICLR), San Diego, USA, 2015. [32] MOWLAEE P, SAEIDI R, CHRISTENSEN M G, et al. Subjective and objective quality assessment of single-channel speech separation algorithms[C]. 2012 IEEE International Conference on Acoustics, Speech and Signal Processing (ICASSP), Kyoto, Japan, 2012: 69–72. [33] 刘忠. 基于DRFM的线性调频脉冲压缩雷达干扰新技术[D]. [博士论文], 国防科学技术大学, 2006.LIU Zhong. Jamming technique for countering LFM pulse compression radar based on digital radio frequency memory[D]. [Ph. D. dissertation], National University of Defense Technology, 2006. [34] SANDLER M, HOWARD A, ZHU Menglong, et al. MobileNetV2: Inverted residuals and linear bottlenecks[C]. 2018 IEEE/CVF Conference on Computer Vision and Pattern Recognition, Salt Lake City, USA, 2018: 4510–4520. [35] MA Ningning, ZHANG Xiangyu, ZHENG Haitao, et al. ShuffleNet V2: Practical guidelines for efficient CNN architecture design[C]. 15th European Conference on Computer Vision (ECCV), Munich, Germany, 2018: 122–138. -
计量
- 文章访问数: 1342
- HTML全文浏览量: 601
- PDF下载量: 202
- 被引次数: 0
