基于频率分集阵列的多功能一体化波形设计与信号处理方法

兰岚; 廖桂生; 许京伟; 朱圣棋; 曾操; 张玉洪

doi:10.12000/JR22163

基于频率分集阵列的多功能一体化波形设计与信号处理方法

DOI: 10.12000/JR22163

1.
西安电子科技大学雷达信号处理国家级重点实验室西安 710071
2.
西安电子科技大学电子工程学院西安 710071

基金项目: 国家自然科学基金(62101402, 61931016, 62071344)，中国博士后科学基金(2021TQ0261, 2021M702547)，中国科协青年人才托举工程(2021QNRC001)，陕西省创新能力支持计划(2022TD-38)，声纳技术重点实验室基金(6142109KF212202)

详细信息

作者简介:
兰　岚，博士，副教授，主要研究方向为新体制雷达抗干扰、波形分集阵列雷达信号处理、目标检测与参数估计

廖桂生，博士，教授，主要研究方向为雷达系统技术与阵列处理、雷达稀疏成像处理等

许京伟，博士，副教授，主要研究方向为雷达系统建模、阵列信号处理、波形分集雷达(频率分集阵列和空时编码阵列)等

朱圣棋，博士，教授，主要研究方向为雷达运动目标检测、频率分集阵列、波形分集阵列雷达信号处理

曾　操，博士，教授，主要研究方向为新体制阵列信号处理、雷达运动目标检测

张玉洪，博士，教授，主要研究方向为阵列信号处理、微波遥感与成像、信号建模与仿真、波形分集技术等

通讯作者:
廖桂生 liaogs@xidian.edu.cn

责任主编：胡卫东 Corresponding Editor: HU Weidong
1¹值得注意的是，为了与相控阵形成对比，也有文献称FDA为频控阵^[3,5]，而本文统一使用“频率分集阵”。²广义上，发射阵元之间除了改变载频，引入波形、时延、相位调制也可得到依赖于距离和时间的方向图，即波形分集阵列^[8]。
中图分类号: TN957
计量
- 文章访问数: 1928
- HTML全文浏览量: 748
- PDF下载量: 285
- 被引次数: 0
出版历程
- 收稿日期: 2022-08-02
- 修回日期: 2022-10-05
- 网络出版日期: 2022-10-14
- 刊出日期: 2022-10-28

Waveform Design and Signal Processing Method of a Multifunctional Integrated System Based on a Frequency Diverse Array（in English）

1.
National Key Laboratory of Radar Signal Processing, Xidian University, Xi’an 710071, China
2.
School of Electronic Engineering, Xidian University, Xi’an 710071, China

Funds: The National Natural Science Foundation of China (62101402, 61931016, 62071344), China Postdoctoral Science Foundation (2021TQ0261, 2021M702547), Young Elite Scientists Sponsorship Program by CAST (2021QNRC001), The Science and Technology Innovation Team of Shaanxi Province (2022TD-38), Science and Technology on Sonar Laboratory (6142109KF212202)

More Information

Corresponding author: LIAO Guisheng, liaogs@xidian.edu.cn

摘要

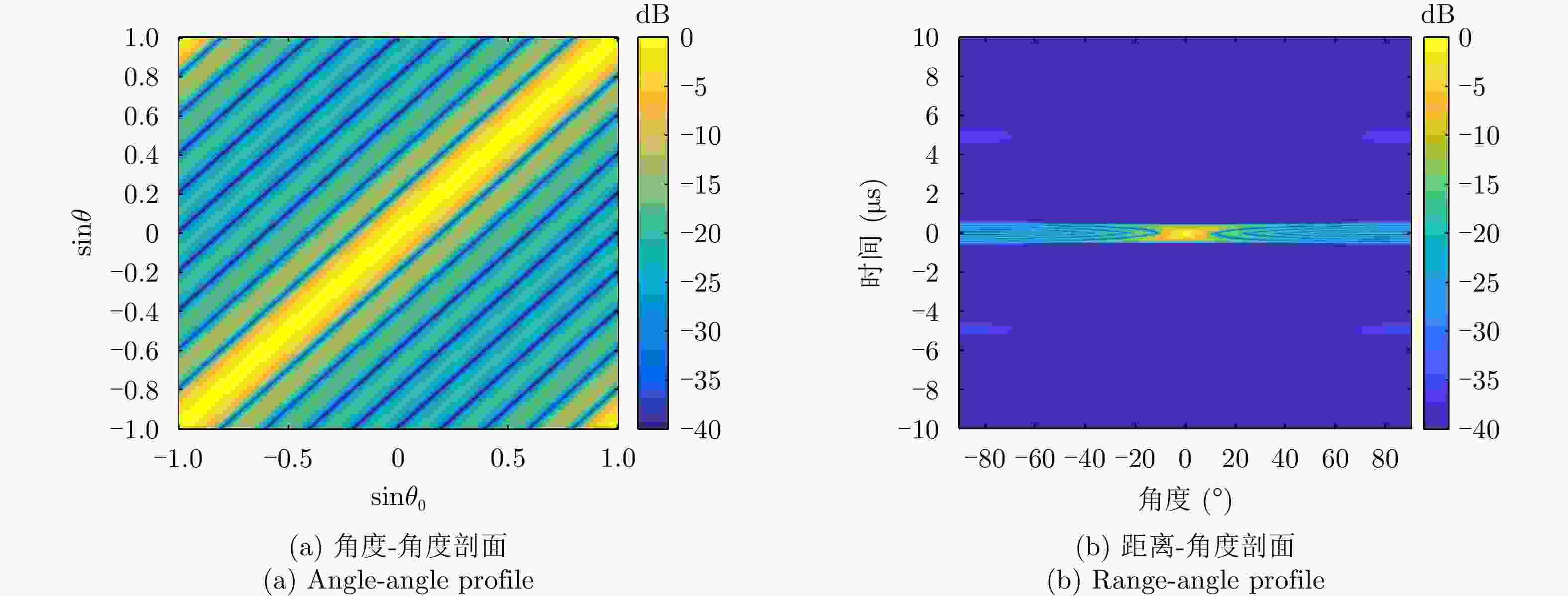
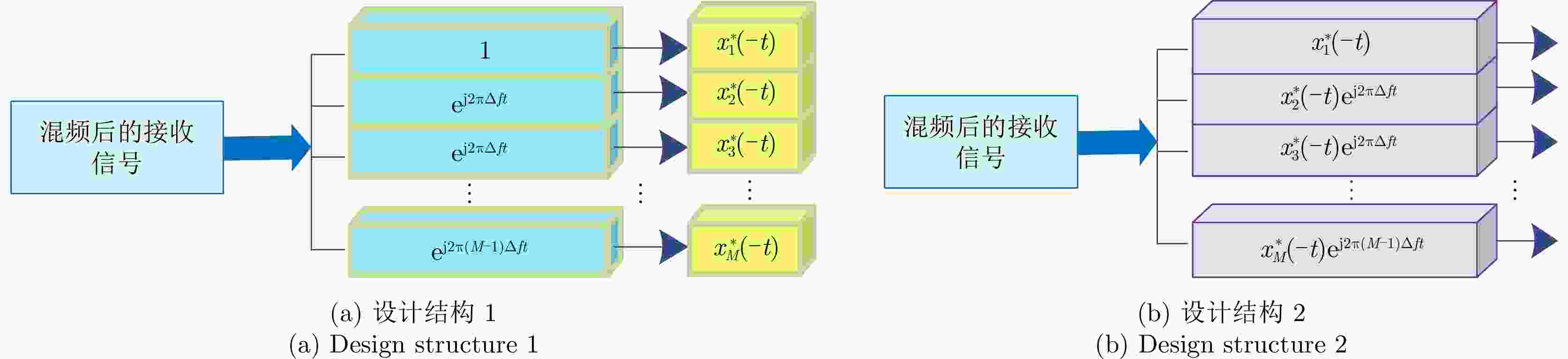
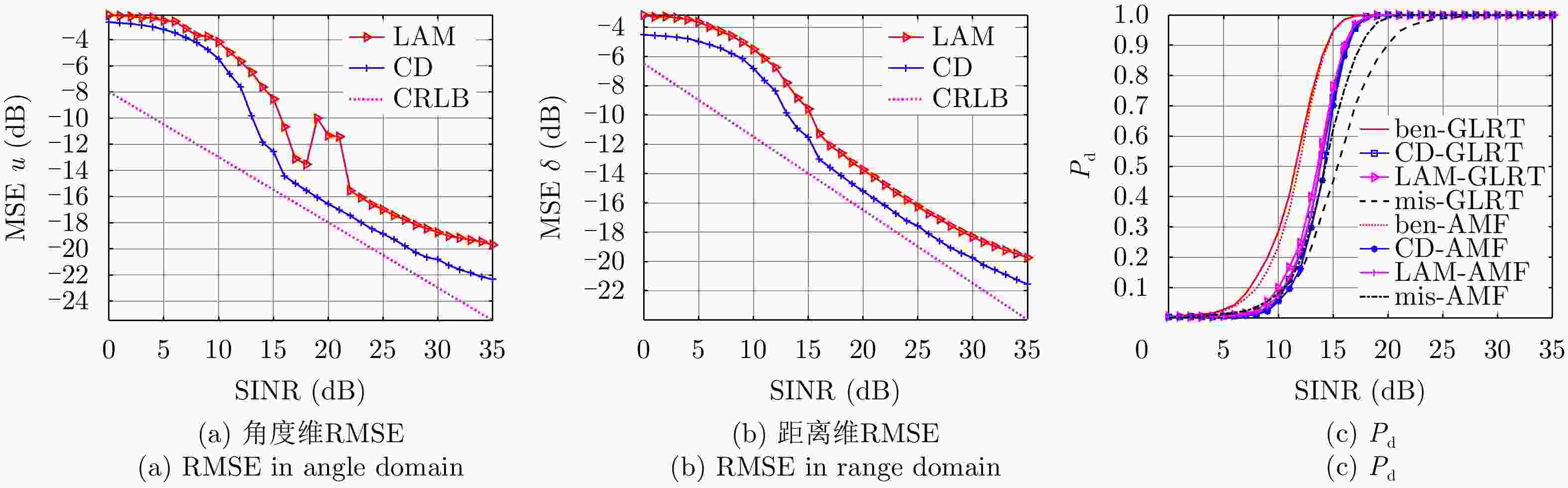
摘要: 频率分集阵(FDA)是在相控阵基础上的一次体制革新，其通过在发射天线阵元间进行频率步进，得到的发射方向图是角度、距离、时间的多维函数，显著提升了波束控制能力与信号处理维度，经过收发联合处理后，可应用于多维参数联合估计、主瓣欺骗式干扰抑制、模糊杂波抑制、高分宽幅成像等方面。该文从系统层面出发，研究基于FDA的多功能一体化波形设计与信号处理方法，重点对其在检测与估计一体化、解模糊与抗干扰一体化、合成孔径雷达(SAR)成像与动目标检测一体化的信号处理新方法进行综述、评述及研究，并对FDA多功能一体化系统的应用前景进行展望。
- 频率分集阵雷达 /
- 波形设计与信号处理 /
- 多维发射方向图 /
- 检测与估计一体化 /
- 解模糊与抗干扰一体化 /
- SAR成像与动目标检测一体化
Abstract: A Frequency Diverse Array (FDA), developed innovatively based on phased array radar, can obtain an angle-range-time-dependent multidimensional transmit beampattern by modulating frequencies across different transmit antenna elements, which considerably increases the beam control ability and signal processing dimension. After joint transmit-receive processing, an FDA can be applied to various areas, such as multidimensional parameter joint estimation, mainlobe deceptive jammer suppression, ambiguous clutter suppression, and high-resolution and wide-swath imaging. This study investigates the waveform design and signal processing method of a multifunctional integrated system based on an FDA from the system level, with emphasis on new signal processing methods for integrated detection and estimation, integrated ambiguity resolution and jammer suppression, as well as integrated Synthetic Aperture Radar (SAR) imaging and moving target detection. Moreover, the application prospects of FDA multifunctional integrated systems are provided.

HTML全文

图 1 FDA发展动态时间线

Figure 1. The dynamic timeline of FDA development

下载: 全尺寸图片幻灯片

图 2 FDA-MIMO雷达不同应用的关联

Figure 2. Relationships among different FDA-MIMO radar applications

下载: 全尺寸图片幻灯片

图 3 FDA多维模糊函数

Figure 3. Multi-dimensional ambiguity function of FDA

下载: 全尺寸图片幻灯片

图 4 相干FDA发射方向图空域覆盖性分析

Figure 4. Analysis on the spatial coverage of the transmit beampattern for coherent FDA

下载: 全尺寸图片幻灯片

图 5 相干FDA接收机基本结构

Figure 5. Basic structures of coherent FDA receiver

下载: 全尺寸图片幻灯片

图 6 FDA-MIMO雷达接收匹配滤波处理流程

Figure 6. Processing procedurse of receive matched filtering in FDA-MIMO radar

下载: 全尺寸图片幻灯片

图 7 FDA-MIMO雷达检测与估计一体化结果

Figure 7. Integrated detection and estimation results in FDA-MIMO radar

下载: 全尺寸图片幻灯片

图 8 FDA-MIMO雷达解距离模糊示意图

Figure 8. Principle of resolving the range ambiguity in FDA-MIMO radar

下载: 全尺寸图片幻灯片

图 9 假目标产生示意图

Figure 9. Generation of false targets

下载: 全尺寸图片幻灯片

图 10 基于波束形成的FDA-MIMO雷达抗主瓣欺骗式干扰方法

Figure 10. Mainlobe deceptive jammer suppression with beamforming in FDA-MIMO radar

下载: 全尺寸图片幻灯片

图 11 FDA-MIMO雷达基于稳健波束形成抗干扰方法输出SINR结果

Figure 11. Output SINR with robust beamforming for jammer suppression in FDA-MIMO radar

下载: 全尺寸图片幻灯片

图 12 频率分集系统抗干扰验证

Figure 12. Verification of jammer suppression with FDA system

下载: 全尺寸图片幻灯片

图 13 基于FDA-MIMO STAP雷达的一体化杂波与干扰抑制

Figure 13. Integrated clutter and jammer suppression in FDA-MIMO STAP radar

下载: 全尺寸图片幻灯片

图 14 频分正交LFM信号模型

Figure 14. Signal model of orthogonal frequency diverse LFM signal

下载: 全尺寸图片幻灯片

图 15 FDA-MIMO空时频局域化处理示意图

Figure 15. Diagram of space-time-frequency localized processing with FDA-MIMO

下载: 全尺寸图片幻灯片

图 16 FDA-MIMO降维处理器结果

Figure 16. Results on dimension reduction processor in FDA-MIMO

下载: 全尺寸图片幻灯片

图 17 基于多子带FDA的高分宽幅SAR成像处理流程

Figure 17. Procedure of HRWS SAR imaging based on multiple sub-band FDA

下载: 全尺寸图片幻灯片

图 18 子带FDA-HRWS成像结果

Figure 18. Imaging results of sub-band FDA-HRWS

下载: 全尺寸图片幻灯片

图 1 The dynamic timeline of FDA development

下载: 全尺寸图片幻灯片

图 2 Relationships among different FDA-MIMO radar applications

下载: 全尺寸图片幻灯片

图 3 Multi-dimensional ambiguity function of FDA

下载: 全尺寸图片幻灯片

图 4 Analysis on the spatial coverage of the transmit beampattern for coherent FDA

下载: 全尺寸图片幻灯片

图 5 Basic structures of coherent FDA receiver

下载: 全尺寸图片幻灯片

图 6 Processing procedurse of receive matched filtering in FDA-MIMO radar

下载: 全尺寸图片幻灯片

图 7 Integrated detection and estimation results in FDA-MIMO radar

下载: 全尺寸图片幻灯片

图 8 Principle of resolving the range ambiguity in FDA-MIMO radar

下载: 全尺寸图片幻灯片

图 9 Generation of false targets

下载: 全尺寸图片幻灯片

图 10 Mainlobe deceptive jammer suppression with beamforming in FDA-MIMO radar

下载: 全尺寸图片幻灯片

图 11 Output SINR with robust beamforming for jammer suppression in FDA-MIMO radar

下载: 全尺寸图片幻灯片

图 12 Verification of jammer suppression with FDA system

下载: 全尺寸图片幻灯片

图 13 Integrated clutter and jammer suppression in FDA-MIMO STAP radar

下载: 全尺寸图片幻灯片

图 14 Signal model of orthogonal frequency diverse LFM signal

下载: 全尺寸图片幻灯片

图 15 Diagram of space-time-frequency localized processing with FDA-MIMO

下载: 全尺寸图片幻灯片

图 16 Results on dimension reduction processor in FDA-MIMO

下载: 全尺寸图片幻灯片

图 17 Procedure of HRWS SAR imaging based on multiple sub-band FDA

下载: 全尺寸图片幻灯片

图 18 Imaging results of sub-band FDA-HRWS

下载: 全尺寸图片幻灯片

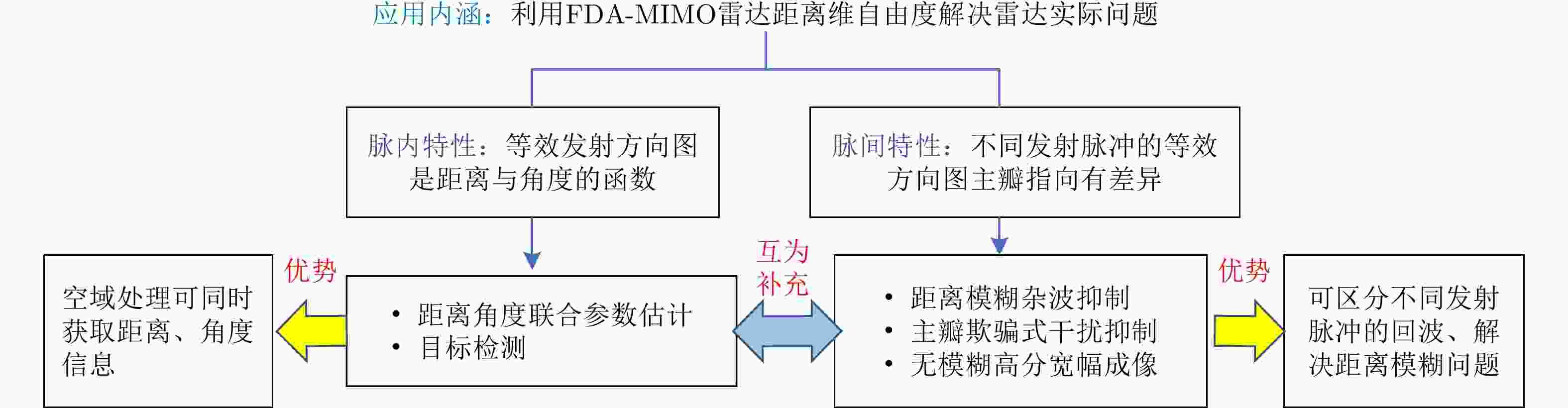
表 1 多功能FDA-MIMO优势及信号处理方法

Table 1. Advantages and signal processing methods of multifunctional FDA-MIMO

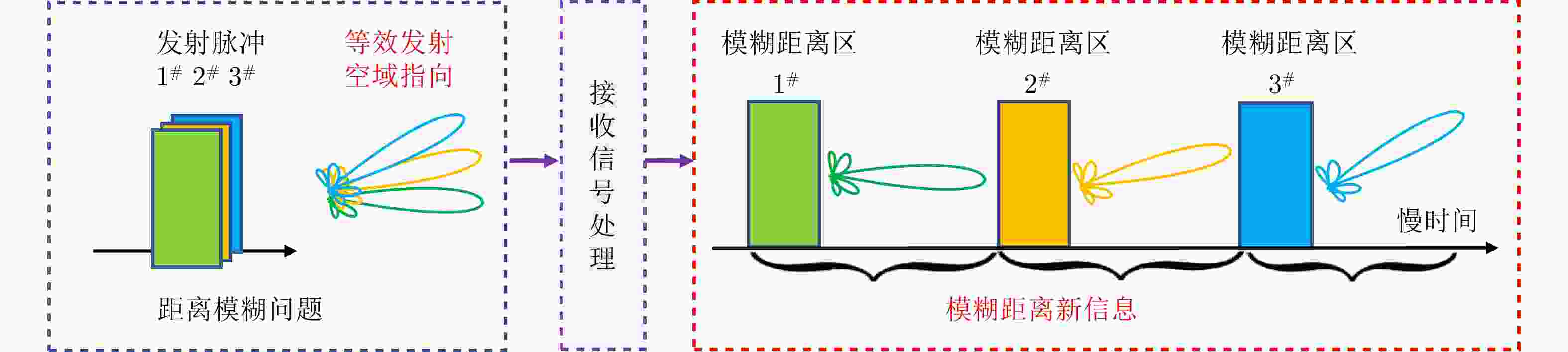
雷达功能任务	面临问题	FDA优势	具体方法
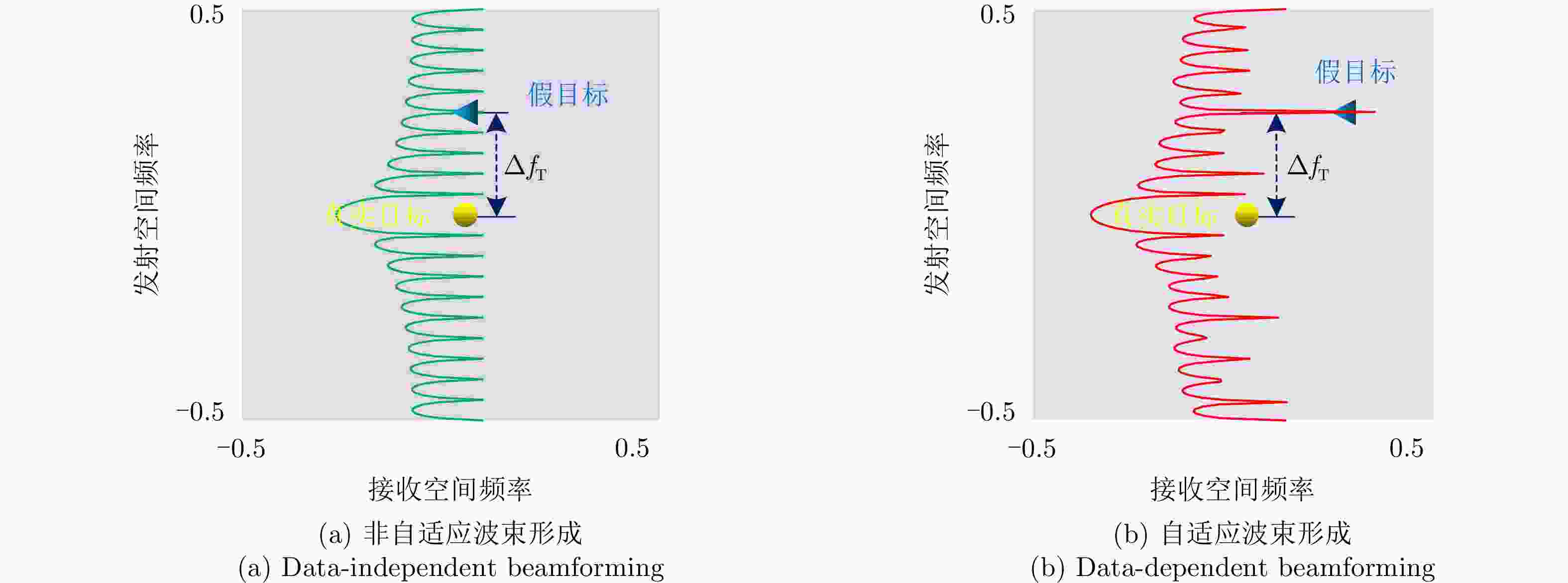
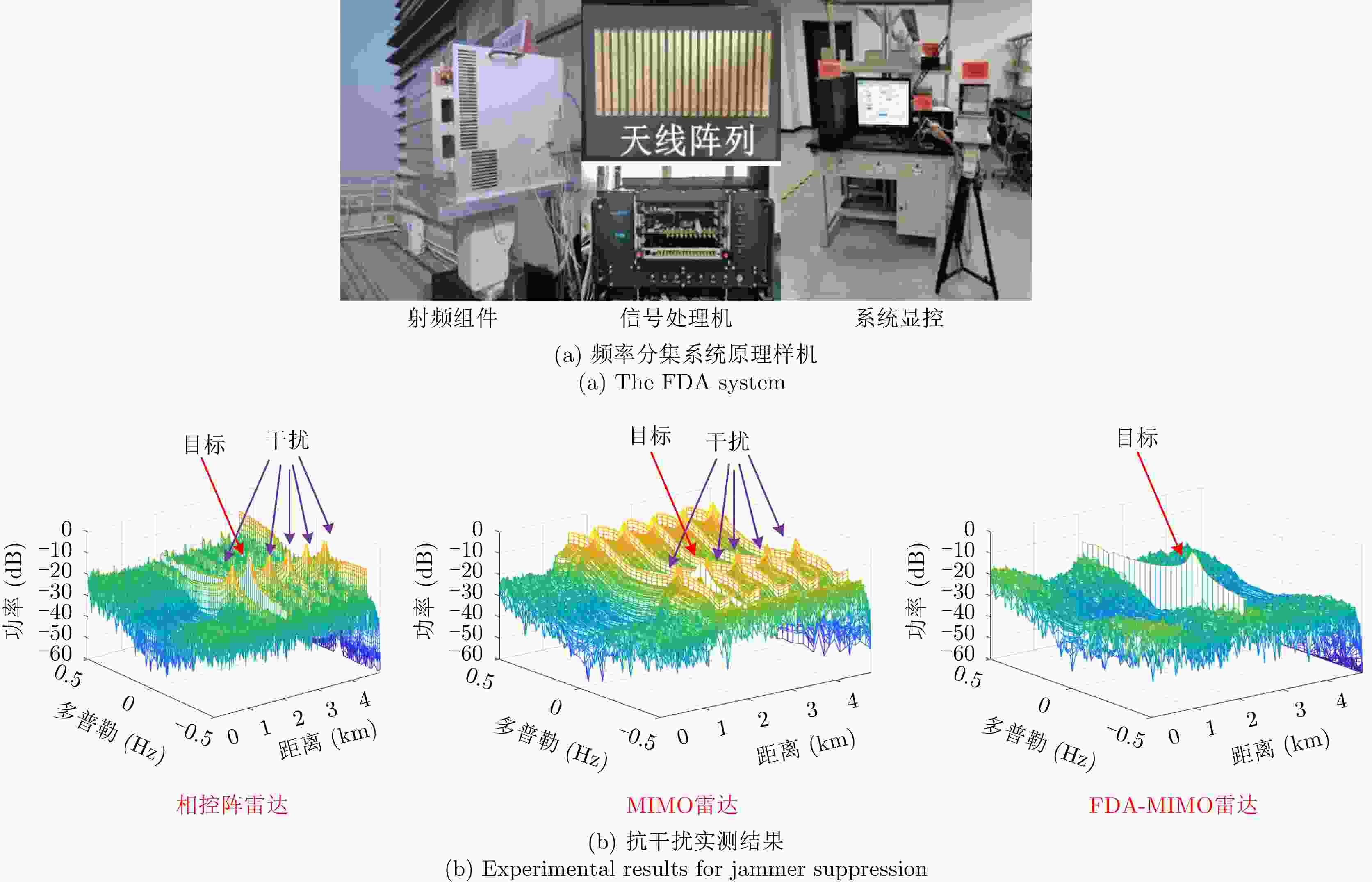
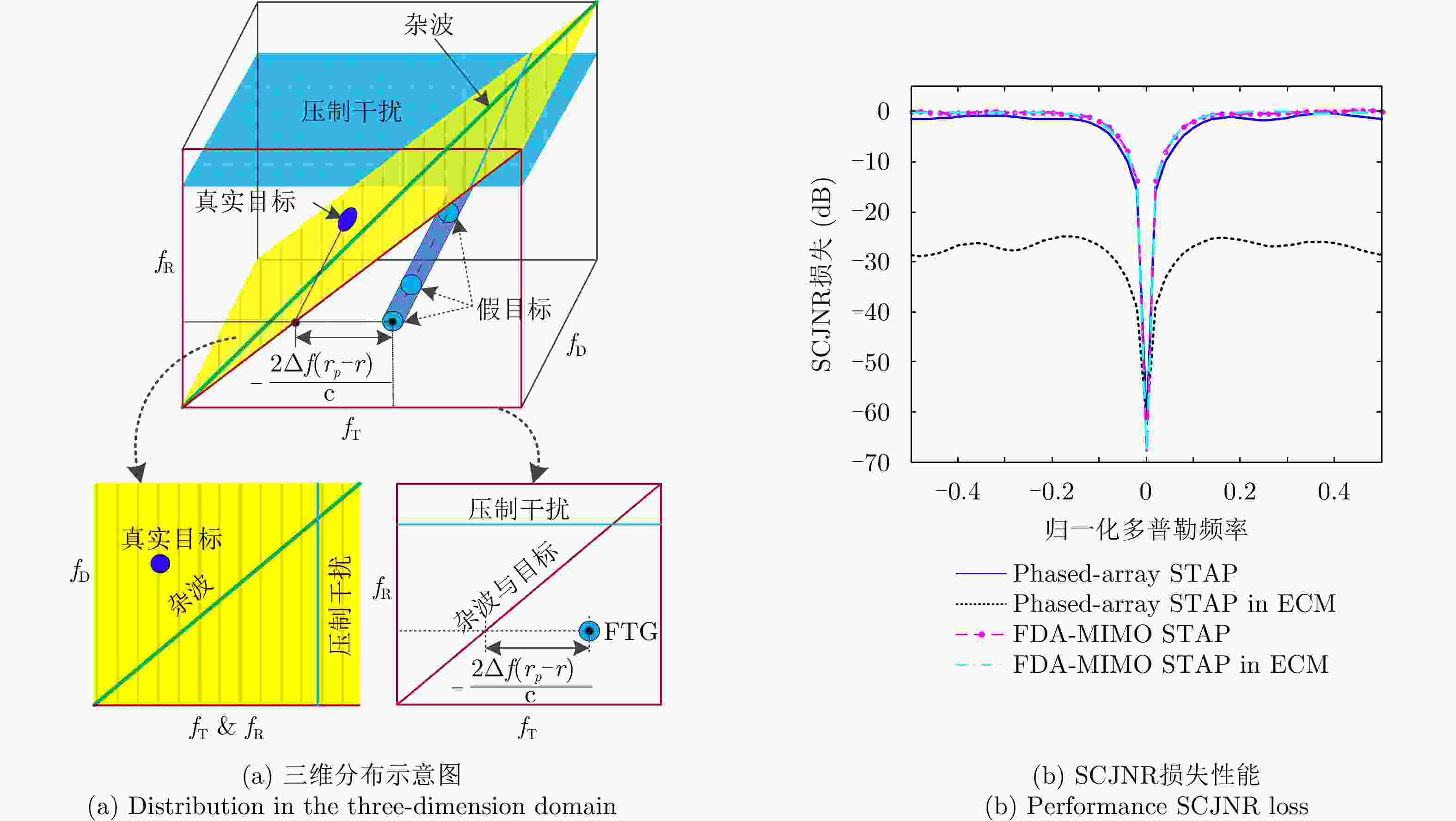
参数估计	中高重频带来的距离模糊问题严重	实现距离和角度的同步估计；能够估计距离模糊数	子空间(MUSIC, ESPRIT)方法、最大似然类方法、单脉冲法
杂波抑制		区分不同距离模糊区间对应的回波	二次距离补偿、STAP、空时距离三维自适应处理
高分宽幅成像		区分不同距离模糊区间对应的回波	距离相关补偿、发射通道与慢时间编码
目标检测	小样本、未知非均匀环境	提升未知非均匀环境下的检测性能	基于GLRT的自适应检测器设计
抗干扰	主瓣欺骗式干扰难以抑制	在联合收发二维平面对干扰进行置零	自适应波束形成、空间投影类、基于方向图设计抗干扰

下载: 导出CSV

表 1 Advantages and signal processing methods of multifunctional FDA-MIMO

Functions of radars	Problems	Advantages of FDA	Methods
Parameter estimation	Range ambiguity reduced by high pulse repetition frequency	Estimating joint range, angle, and range ambiguity number	Subspace-based methods (MUSIC and ESPRIT), ML, monopulse-based methods
Clutter suppression		Discriminating echoes corresponding to different range ambiguity regions	Secondary range compensation, STAP, space-time-range adaptive processing
HRWS-SAR imaging		Discriminating echoes corresponding to different range ambiguity regions	Range compensation, transmit channel and slow-time processing
Target detection	Insufficient samples, nonhomogeneous environment	Improving the detection performance in a nonhomogeneous environment	Design of adaptive detectors based on GLRT
Jammer suppression	Mainlobe deceptive jammers	Nulling the jammers in the joint transmit-receive spatial	Data-dependent beamforming, space projection, beampattern synthesis-based methods

下载: 导出CSV

参考文献(86)

[1]	WICKS M C. A brief history of waveform diversity[C]. 2009 IEEE Radar Conference, Pasadena, USA, 2009: 328–333.
[2]	ANTONIK P, WICKS M C, GRIFFITHS H D, et al. Multi-mission multi-mode waveform diversity[C]. 2006 IEEE Conference on Radar, Verona, USA, 2006: 580–582.
[3]	王文钦, 陈慧, 郑植, 等. 频控阵雷达技术及其应用研究进展[J]. 雷达学报, 2018, 7(2): 153–166. doi: 10.12000/JR18029. WANG Wenqin, CHEN Hui, ZHENG Zhi, et al. Advances on frequency diverse array radar and its applications[J]. Journal of Radars, 2018, 7(2): 153–166. doi: 10.12000/JR18029.
[4]	许京伟, 朱圣棋, 廖桂生, 等. 频率分集阵雷达技术探讨[J]. 雷达学报, 2018, 7(2): 167–182. doi: 10.12000/JR18023. XU Jingwei, ZHU Shengqi, LIAO Guisheng, et al. An overview of frequency diverse array radar technology[J]. Journal of Radars, 2018, 7(2): 167–182. doi: 10.12000/JR18023.
[5]	王文钦, 邵怀宗, 陈慧. 频控阵雷达: 概念、原理与应用[J]. 电子与信息学报, 2016, 38(4): 1000–1011. doi: 10.11999/JEIT151235. WANG Wenqin, SHAO Huaizong, and CHEN Hui. Frequency diverse array radar: Concept, principle and application[J]. Journal of Electronics&Information Technology, 2016, 38(4): 1000–1011. doi: 10.11999/JEIT151235.
[6]	XU Jingwei, LAN Lan, HE Xiongpeng, et al. System design and signal processing for frequency diverse array radar[J]. Journal of Beijing Institute of Technology, 2021, 30(1): 1–19. doi: 10.15918/j.jbit1004-0579.2021.004.
[7]	SAMMARTINO P F, BAKER C J, and GRIFFITHS H D. Frequency diverse MIMO techniques for radar[J]. IEEE Transactions on Aerospace and Electronic Systems, 2013, 49(1): 201–222. doi: 10.1109/TAES.2013.6404099.
[8]	LAN Lan, LIAO Guisheng, XU Jingwei, et al. Control and utilization of range-dependent beampattern with waveform diverse array radars[J]. Chinese Journal of Aeronautics, in press, 2022.
[9]	XU Jingwei, LIAO Guisheng, ZHU Shengqi, et al. Joint range and angle estimation using MIMO radar with frequency diverse array[J]. IEEE Transactions on Signal Processing, 2015, 63(13): 3396–3410. doi: 10.1109/TSP.2015.2422680.
[10]	LAN Lan, ROSAMILIA M, AUBRY A, et al. Single-snapshot angle and incremental range estimation for FDA-MIMO radar[J]. IEEE Transactions on Aerospace and Electronic Systems, 2021, 57(6): 3705–3718. doi: 10.1109/TAES.2021.3083591.
[11]	FENG Maoyuan, CUI Zhongma, YANG Yunxiu, et al. A reduced-dimension MUSIC algorithm for monostatic FDA-MIMO radar[J]. IEEE Communications Letters, 2021, 25(4): 1279–1282. doi: 10.1109/LCOMM.2020.3045440.
[12]	刘润东, 薛峰涛, 杨赟秀, 等. FDA-MIMO雷达实值降维求根MUSIC参数估计算法[J]. 现代雷达, 2022, 44(4): 31–37. doi: 10.16592/j.cnki.1004-7859.2022.04.005. LIU Rundong, XUE Fengtao, YANG Yunxiu, et al. Real-value reducing-dimension Root-MUSIC method in monostatic FDA-MIMO radar[J]. Modern Radar, 2022, 44(4): 31–37. doi: 10.16592/j.cnki.1004-7859.2022.04.005.
[13]	YAN Yisheng, CAI Jingye, and WANG Wenqin. Two-stage ESPRIT for unambiguous angle and range estimation in FDA-MIMO radar[J]. Digital Signal Process, 2019, 92: 151–165. doi: 10.1016/j.dsp.2019.06.002.
[14]	LI Binbin, BAI Weixiong, and ZHENG Guimei. Successive ESPRIT algorithm for joint DOA-range-polarization estimation with polarization sensitive FDA-MIMO radar[J]. IEEE Access, 2018, 6: 36376–36382. doi: 10.1109/ACCESS.2018.2844948.
[15]	GONG Shiqi, WANG Shuai, CHEN Sheng, et al. Time-invariant joint transmit and receive beampattern optimization for polarization-subarray based frequency diverse array radar[J]. IEEE Transactions on Signal Processing, 2018, 66(20): 5364–5379. doi: 10.1109/TSP.2018.2868041.
[16]	XIONG Jie, WANG Wenqin, and GAO Kuandong. FDA-MIMO radar range-angle estimation: CRLB, MSE, and resolution analysis[J]. IEEE Transactions on Aerospace and Electronic Systems, 2018, 54(1): 284–294. doi: 10.1109/TAES.2017.2756498.
[17]	LI Xingxing, WANG Dangwei, WANG Wenqin, et al. Range-angle localization of targets with planar frequency diverse subaperturing MIMO radar[J]. IEEE Access, 2018, 6: 12505–12517. doi: 10.1109/ACCESS.2018.2810139.
[18]	陈慧, 田湘, 李子豪, 等. 共形FDA-MIMO雷达降维目标参数估计研究[J]. 雷达学报, 2021, 10(6): 811–821. doi: 10.12000/JR21197. CHEN Hui, TIAN Xiang, LI Zihao, et al. Reduced-dimension target parameter estimation for conformal FDA-MIMO radar[J]. Journal of Radars, 2021, 10(6): 811–821. doi: 10.12000/JR21197.
[19]	MAO Zihuan, LIU Shengheng, ZHANG Y D, et al. Joint DOA-range estimation using space-frequency virtual difference coarray[J]. IEEE Transactions on Signal Processing, 2022, 70: 2576–2592. doi: 10.1109/TSP.2022.3173150.
[20]	TANG Wengen, JIANG Hong, and ZHANG Qi. Range-angle decoupling and estimation for FDA-MIMO radar via atomic norm minimization and accelerated proximal gradient[J]. IEEE Signal Processing Letters, 2020, 27: 366–370. doi: 10.1109/LSP.2020.2972470.
[21]	巩朋成, 刘刚, 黄禾, 等. 频控阵MIMO雷达中基于稀疏迭代的多维信息联合估计方法[J]. 雷达学报, 2018, 7(2): 194–201. doi: 10.12000/JR16121. GONG Pengcheng, LIU Gang, HUANG He, et al. Multidimensional parameter estimation method based on sparse iteration in FDA-MIMO radar[J]. Journal of Radars, 2018, 7(2): 194–201. doi: 10.12000/JR16121.
[22]	ZHU Yu, LIU Lei, LU Zheng, et al. Target detection performance analysis of FDA-MIMO radar[J]. IEEE Access, 2019, 7: 164276–164285. doi: 10.1109/ACCESS.2019.2943082.
[23]	LI Shengyuan, ZHANG Linrang, LIU Nan, et al. Adaptive detection with conic rejection to suppress deceptive jamming for frequency diverse MIMO radar[J]. Digital Signal Processing, 2017, 69: 32–40. doi: 10.1016/j.dsp.2017.06.008.
[24]	LI Shengyuan, ZHANG Linrang, LIU Nan, et al. Range-angle dependent detection for FDA-MIMO radar[C]. 2016 IEEE International Geoscience and Remote Sensing Symposium, Beijing, China, 2016: 6629–6632.
[25]	LAN Lan, MARINO A, AUBRY A, et al. GLRT-based adaptive target detection in FDA-MIMO radar[J]. IEEE Transactions on Aerospace and Electronic Systems, 2021, 57(1): 597–613. doi: 10.1109/TAES.2020.3028485.
[26]	GUI Ronghua, WANG Wenqin, FARINA A, et al. FDA radar with Doppler-spreading consideration: Mainlobe clutter suppression for blind-Doppler target detection[J]. Signal Processing, 2021, 179: 107773. doi: 10.1016/j.sigpro.2020.107773.
[27]	XU Ziting, HUANG Bang, and WANG Wenqin. Performance prediction of FDA-MIMO radar detector[C]. 2020 IEEE Radar Conference, Florence, Italy, 2020: 1–6.
[28]	CHEN Xiaolong, CHEN Baoxin, GUAN Jian, et al. Space-range-Doppler focus-based low-observable moving target detection using frequency diverse array MIMO radar[J]. IEEE Access, 2018, 6: 43892–43904. doi: 10.1109/access.2018.2863745.
[29]	XU Jingwei, LIAO Guisheng, ZHANG Yuhong, et al. An adaptive range-angle-Doppler processing approach for FDA-MIMO radar using three-dimensional localization[J]. IEEE Journal of Selected Topics in Signal Processing, 2017, 11(2): 309–320. doi: 10.1109/JSTSP.2016.2615269.
[30]	XU Jingwei, ZHU Shengqi, and LIAO Guisheng. Range ambiguous clutter suppression for airborne FDA-STAP radar[J]. IEEE Journal of Selected Topics in Signal Processing, 2015, 9(8): 1620–1631. doi: 10.1109/JSTSP.2015.2465353.
[31]	XU Jingwei, LIAO Guisheng, and SO H C. Space-time adaptive processing with vertical frequency diverse array for range-ambiguous clutter suppression[J]. IEEE Transactions on Geoscience and Remote Sensing, 2016, 54(9): 5352–5364. doi: 10.1109/TGRS.2016.2561308.
[32]	WEN Cai, TAO Mingliang, PENG Jinye, et al. Clutter suppression for airborne FDA-MIMO radar using multi-waveform adaptive processing and auxiliary channel STAP[J]. Signal Processing, 2019, 154: 280–293. doi: 10.1016/j.sigpro.2018.09.016.
[33]	WEN Cai, MA Changzheng, PENG Jinye, et al. Bistatic FDA-MIMO radar space-time adaptive processing[J]. Signal Processing, 2019, 163: 201–212. doi: 10.1016/j.sigpro.2019.05.025.
[34]	XU Jingwei, LIAO Guisheng, ZHU Shengqi, et al. Deceptive jamming suppression with frequency diverse MIMO radar[J]. Signal Processing, 2015, 113: 9–17. doi: 10.1016/j.sigpro.2015.01.014.
[35]	陈浩, 李荣锋, 戴凌燕, 等. 基于FVE法的FDA-MIMO雷达主瓣密集假目标干扰抑制[J]. 空军预警学院学报, 2018, 32(6): 397–401, 406. doi: 10.3969/j.issn.2095-5839.2018.06.002. CHEN Hao, LI Rongfeng, DAI Lingyan, et al. FDA-MIMO radar mainlobe dense false target jamming suppression based on feature vector eliminating[J]. Journal of Air Force Early Warning Academy, 2018, 32(6): 397–401, 406. doi: 10.3969/j.issn.2095-5839.2018.06.002.
[36]	张昭建, 谢军伟, 李欣, 等. 基于FDA-MIMO的距离欺骗干扰鉴别方法[J]. 北京航空航天大学学报, 2017, 43(4): 738–746. doi: 10.13700/j.bh.1001-5965.2016.0257. ZHANG Zhaojian, XIE Junwei, LI Xin, et al. Discrimination method of range deception jamming based on FDA-MIMO[J]. Journal of Beijing University of Aeronautics and Astronautics, 2017, 43(4): 738–746. doi: 10.13700/j.bh.1001-5965.2016.0257.
[37]	谭清莉, 张艺乐, 张伟, 等. FDA-MIMO雷达主瓣欺骗干扰对抗方法[J]. 雷达科学与技术, 2017, 15(6): 671–676. doi: 10.3969/j.issn.1672-2337.2017.06.017. TAN Qingli, ZHANG Yile, ZHANG Wei, et al. A method of mainlobe deception jamming countermeasure in FDA-MIMO radar[J]. Radar Science and Technology, 2017, 15(6): 671–676. doi: 10.3969/j.issn.1672-2337.2017.06.017.
[38]	GE Jiaang, XIE Junwei, and WANG Bo. A cognitive active anti-jamming method based on frequency diverse array radar phase center[J]. Digital Signal Processing, 2021, 109: 102915. doi: 10.1016/j.dsp.2020.102915.
[39]	兰岚, 廖桂生, 许京伟, 等. FDA-MIMO雷达主瓣距离欺骗式干扰抑制方法[J]. 系统工程与电子技术, 2018, 40(5): 997–1003. doi: 10.3969/j.issn.1001-506X.2018.05.06. LAN Lan, LIAO Guisheng, XU Jingwei, et al. Main-beam range deceptive jamming suppression approach with FDA-MIMO radar[J]. Systems Engineering and Electronics, 2018, 40(5): 997–1003. doi: 10.3969/j.issn.1001-506X.2018.05.06.
[40]	兰岚, 许京伟, 朱圣棋, 等. 波形分集阵列雷达抗干扰进展[J]. 系统工程与电子技术, 2021, 46(6): 1437–1451. doi: 10.12305/j.issn.1001-506X.2021.06.01. LAN Lan, XU Jingwei, ZHU Shengqi, et al. Advances in anti-jamming using waveform diverse array radar[J]. Systems Engineering and Electronics, 2021, 46(6): 1437–1451. doi: 10.12305/j.issn.1001-506X.2021.06.01.
[41]	LAN Lan, LIAO Guisheng, XU Jingwei, et al. Suppression approach to main-beam deceptive jamming in FDA-MIMO radar using nonhomogeneous sample detection[J]. IEEE Access, 2018, 6: 34582–34597. doi: 10.1109/access.2018.2850816.
[42]	WANG Yuzhuo and ZHU Shengqi. Main-beam range deceptive jamming suppression with simulated annealing FDA-MIMO radar[J]. IEEE Sensors Journal, 2020, 20(16): 9056–9070. doi: 10.1109/JSEN.2020.2982194.
[43]	许京伟, 廖桂生, 张玉洪, 等. 波形分集阵雷达抗欺骗式干扰技术[J]. 电子学报, 2019, 47(3): 545–551. doi: 10.3969/j.issn.0372-2112.2019.03.005. XU Jingwei, LIAO Guisheng, ZHANG Yuhong, et al. On anti-jamming technique with waveform diverse array radar[J]. Acta Electronica Sinica, 2019, 47(3): 545–551. doi: 10.3969/j.issn.0372-2112.2019.03.005.
[44]	LIU Qi, XU Jingwei, DING Zhi, et al. Target localization with jammer removal using frequency diverse array[J]. IEEE Transactions on Vehicular Technology, 2020, 69(10): 11685–11696. doi: 10.1109/TVT.2020.3016948.
[45]	LAN Lan, XU Jingwei, LIAO Guisheng, et al. Suppression of mainbeam deceptive jammer with FDA-MIMO radar[J]. IEEE Transactions on Vehicular Technology, 2020, 69(10): 11584–11598. doi: 10.1109/TVT.2020.3014689.
[46]	LAN Lan, LIAO Guisheng, XU Jingwei, et al. Mainlobe deceptive jammer suppression using element-pulse coding with MIMO radar[J]. Signal Processing, 2021, 182: 107955. doi: 10.1016/j.sigpro.2020.107955.
[47]	FAROOQ J, TEMPLE M A, and SAVILLE M A. Application of frequency diverse arrays to synthetic aperture radar imaging[C]. 2007 International Conference on Electromagnetics in Advanced Applications, Turin, Italy, 2007: 447–449.
[48]	FAROOQ J, TEMPLE M A, and SAVILLE M A. Exploiting frequency diverse array processing to improve SAR image resolution[C]. 2008 IEEE Radar Conference, Rome, Italy, 2008: 1–5.
[49]	WANG Wenqin, SO H C, and SHAO Huaizong. Nonuniform frequency diverse array for range-angle imaging of targets[J]. IEEE Sensors Journal, 2014, 14(8): 2469–2476.
[50]	WANG Chenghao, XU Jingwei, LIAO Guisheng, et al. A range ambiguity resolution approach for high-resolution and wide-swath SAR imaging using frequency diverse array[J]. IEEE Journal of Selected Topics in Signal Processing, 2017, 11(2): 336–346. doi: 10.1109/JSTSP.2016.2605064.
[51]	GUO Yifan, LIAO Guisheng, ZHANG Qingjun, et al. A robust radial velocity estimation method for FDA-SAR[J]. IEEE Geoscience and Remote Sensing Letters, 2020, 17(4): 646–650. doi: 10.1109/LGRS.2019.2929493.
[52]	WANG Hanbing, ZHANG Yuhong, XU Jingwei, et al. A novel range ambiguity resolving approach for high-resolution and wide-swath SAR imaging utilizing space-pulse phase coding[J]. Signal Processing, 2020, 168: 107323. doi: 10.1016/j.sigpro.2019.107323.
[53]	HE Xiongpeng, LIAO Guisheng, ZHU Shengqi, et al. Range-ambiguous clutter suppression for the SAR-GMTI system based on extended azimuth phase coding[J]. IEEE Transactions on Geoscience and Remote Sensing, 2020, 58(11): 8147–8162. doi: 10.1109/TGRS.2020.2987630.
[54]	NUSENU S Y, SHAO Huaizong, PAN Ye, et al. Dual-function radar-communication system design via sidelobe manipulation based on FDA butler matrix[J]. IEEE Antennas and Wireless Propagation Letters, 2019, 18(3): 452–456. doi: 10.1109/LAWP.2019.2894015.
[55]	JI Shilong, CHEN Hui, HU Quan, et al. A dual-function radar-communication system using FDA[C]. 2018 IEEE Radar Conference, Oklahoma, USA, 2018: 23–27.
[56]	BASIT A, WANG Wenqin, NUSENU S Y, et al. FDA based QSM for mmWave wireless communications: Frequency diverse transmitter and reduced complexity receiver[J]. IEEE Transactions on Wireless Communications, 2021, 20(7): 4571–4584. doi: 10.1109/TWC.2021.3060512.
[57]	NUSENU S Y and SHAO Huaizong. Green secure communication range-angle focusing quadrature spatial modulation using frequency modulated diverse retrodirective array for mmWave wireless communications[J]. IEEE Transactions on Vehicular Technology, 2019, 68(7): 6867–6877. doi: 10.1109/TVT.2019.2919921.
[58]	DING Y, ZHANG J, and FUSCO V. Frequency diverse array OFDM transmitter for secure wireless communication[J]. Electronics Letters, 2015, 51(17): 1374–1376. doi: 10.1049/el.2015.1491.
[59]	GUI Ronghua, ZHENG Zhi, and WANG Wenqin. Cognitive FDA radar transmit power allocation for target tracking in spectrally dense scenario[J]. Signal Processing, 2021, 183: 108006. doi: 10.1016/j.sigpro.2021.108006.
[60]	SUN Yan, ZHENG Zhi, WANG Wenqin, et al. DOA estimation and tracking for FDA-MIMO radar signal[J]. Digital Signal Processing, 2020, 106: 102858. doi: 10.1016/j.dsp.2020.102858.
[61]	WANG Yuxi, LI Wei, HUANG Guoce, et al. Time-invariant range-angle-dependent beampattern synthesis for FDA radar targets tracking[J]. IEEE Antennas and Wireless Propagation Letters, 2017, 16: 2375–2379. doi: 10.1109/LAWP.2017.2718580.
[62]	GUI Ronghua, WANG Wenqin, PAN Ye, et al. Cognitive target tracking via angle-range-Doppler estimation with transmit subaperturing FDA radar[J]. IEEE Journal of Selected Topics in Signal Processing, 2018, 12(1): 76–89. doi: 10.1109/JSTSP.2018.2793761.
[63]	巩朋成, 吴云韬. 基于ADMM改进的低截获FDA-MIMO雷达发射波束设计[J]. 通信学报, 2022, 43(4): 133–142. doi: 10.11959/j.issn.1000-436x.2022065. GONG Pengcheng and WU Yuntao. Improved transmit beamforming design based on ADMM for low probability of intercept of FDA-MIMO radar[J]. Journal on Communications, 2022, 43(4): 133–142. doi: 10.11959/j.issn.1000-436x.2022065.
[64]	WANG Liu, WANG Wenqin, GUAN Haoliang, et al. LPI property of FDA transmitted signal[J]. IEEE Transactions on Aerospace and Electronic Systems, 2021, 57(6): 3905–3915. doi: 10.1109/TAES.2021.3083402.
[65]	WANG Wenqin, DAI Miaomiao, and ZHENG Zhi. FDA radar ambiguity function characteristics analysis and optimization[J]. IEEE Transactions on Aerospace and Electronic Systems, 2018, 54(3): 1368–1380. doi: 10.1109/TAES.2017.2785598.
[66]	于雷, 何峰, 董臻, 等. 一种基于非线性调频信号和空域编码的FDA雷达波形设计方法[J]. 雷达学报, 2021, 10(6): 822–832. doi: 10.12000/JR21008. YU Lei, HE Feng, DONG Zhen, et al. A waveform design method based on nonlinear frequency modulation and space-coding for coherent frequency diverse array radar[J]. Journal of Radars, 2021, 10(6): 822–832. doi: 10.12000/JR21008.
[67]	FAN Wen, LIANG Junli, and LI Jian. Constant modulus MIMO radar waveform design with minimum peak sidelobe transmit beampattern[J]. IEEE Transactions on Signal Processing, 2018, 66(16): 4207–4222. doi: 10.1109/TSP.2018.2847636.
[68]	DE MAIO A, DE NICOLA S, HUANG Yongwei, et al. Code design to optimize radar detection performance under accuracy and similarity constraints[J]. IEEE Transactions on Signal Processing, 2008, 56(11): 5618–5629. doi: 10.1109/TSP.2008.929657.
[69]	YU Xianxiang, CUI Guolong, KONG Lingjiang, et al. Constrained waveform design for colocated MIMO radar with uncertain steering matrices[J]. IEEE Transactions on Aerospace and Electronic Systems, 2019, 55(1): 356–370. doi: 10.1109/TAES.2018.2852200.
[70]	HE Hao, STOICA P, and LI Jian. Designing unimodular sequence sets with good correlations—Including an application to MIMO radar[J]. IEEE Transactions on Signal Processing, 2009, 57(11): 4391–4405. doi: 10.1109/TSP.2009.2025108.
[71]	STOICA P, HE Hao, and LI Jian. Optimization of the receive filter and transmit sequence for active sensing[J]. IEEE Transactions on Signal Processing, 2012, 60(4): 1730–1740. doi: 10.1109/TSP.2011.2179652.
[72]	CUI Guolong, LI Hongbin, and RANGASWAMY M. MIMO radar waveform design with constant modulus and similarity constraints[J]. IEEE Transactions on Signal Processing, 2014, 62(2): 343–353. doi: 10.1109/TSP.2013.2288086.
[73]	CUI Guolong, YU Xianxiang, CAROTENUTO V, et al. Space-time transmit code and receive filter design for colocated MIMO radar[J]. IEEE Transactions on Signal Processing, 2017, 65(5): 1116–1129. doi: 10.1109/TSP.2016.2633242.
[74]	HERBERT S, HOPGOOD J R, and MULGREW B. MMSE adaptive waveform design for active sensing with applications to MIMO radar[J]. IEEE Transactions on Signal Processing, 2018, 66(5): 1361–1373. doi: 10.1109/tsp.2017.2786277.
[75]	MISHRA K V, ELDAR Y C, SHOSHAN E, et al. A cognitive sub-Nyquist MIMO radar prototype[J]. IEEE Transactions on Aerospace and Electronic Systems, 2020, 56(2): 937–955. doi: 10.1109/TAES.2019.2924163.
[76]	COHEN D, COHEN D, and ELDAR Y C. High resolution FDMA MIMO radar[J]. IEEE Transactions on Aerospace and Electronic Systems, 2020, 56(4): 2806–2822. doi: 10.1109/TAES.2019.2958193.
[77]	RABASTE O, SAVY L, CATTENOZ M, et al. Signal waveforms and range/angle coupling in coherent colocated MIMO radar[C]. 2013 International Conference on Radar, Adelaide, Australia, 2013: 157–162.
[78]	许京伟, 兰岚, 朱圣棋, 等. 相干频率分集阵雷达匹配滤波器设计[J]. 系统工程与电子技术, 2018, 40(8): 1720–1728. doi: 10.3969/j.issn.1001-506X.2018.08.08. XU Jingwei, LAN Lan, ZHU Shengqi, et al. Design of matched filter for coherent FDA radar[J]. Systems Engineering and Electronics, 2018, 40(8): 1720–1728. doi: 10.3969/j.issn.1001-506X.2018.08.08.
[79]	AUBRY A, DE MAIO A, MARANO S, et al. Single-pulse simultaneous target detection and angle estimation in a multichannel phased array radar[J]. IEEE Transactions on Signal Processing, 2020, 68: 6649–6664. doi: 10.1109/TSP.2020.3039883.
[80]	XU Jingwei, ZHANG Yuhong, LIAO Guisheng, et al. Resolving range ambiguity via multiple-input multiple-output radar with element-pulse coding[J]. IEEE Transactions on Signal Processing, 2020, 68: 2770–2783. doi: 10.1109/TSP.2020.2988371.
[81]	兰岚, 廖桂生, 许京伟, 等. FDA-MIMO雷达非自适应波束形成抗主瓣欺骗式干扰研究[J]. 信号处理, 2019, 35(6): 944–950. doi: 10.16798/j.issn.1003-0530.2019.06.002. LAN Lan, LIAO Guisheng, XU Jingwei, et al. Main-beam deceptive jamming suppression with non-adaptive beam-forming in FDA-MIMO radar[J]. Journal of Signal Processing, 2019, 35(6): 944–950. doi: 10.16798/j.issn.1003-0530.2019.06.002.
[82]	朱圣棋, 余昆, 许京伟, 等. 波形分集阵列新体制雷达研究进展与展望[J]. 雷达学报, 2021, 10(6): 795–810. doi: 10.12000/JR21188. ZHU Shengqi, YU Kun, XU Jingwei, et al. Research progress and prospect for the noval waveform diverse array radar[J]. Journal of Radars, 2021, 10(6): 795–810. doi: 10.12000/JR21188.
[83]	许京伟. 频率分集阵列雷达运动目标检测方法研究[D]. [博士论文], 西安电子科技大学, 2015. XU Jingwei. Study on moving target detection with frequency diverse array radar[D]. [Ph. D. dissertation], Xidian University, 2015.
[84]	ZHANG Mengdi, LIAO Guisheng, XU Jingwei, et al. High-resolution and wide-swath SAR imaging with sub-band frequency diverse array[J]. IEEE Transactions on Aerospace and Electronic Systems, in press, 2022.
[85]	金林. 智能化认知雷达综述[J]. 现代雷达, 2013, 35(11): 6–11. doi: 10.3969/j.issn.1004-7859.2013.11.002. JIN Lin. Overview of cognitive radar with intelligence[J]. Modern Radar, 2013, 35(11): 6–11. doi: 10.3969/j.issn.1004-7859.2013.11.002.
[86]	王晓海. 认知雷达系统技术发展综述[J]. 数字通信世界, 2018(S1): 40–43. WANG Xiaohai. An overview of cognitive radar system technology developments[J]. Digital Communication World, 2018(S1): 40–43.