Sea Clutter Spectral Parameters Prediction and Influence Factor Analysis Based on Deep Learning
-
摘要: 该文基于不同雷达参数和海洋环境参数条件下的岸基雷达海杂波实测数据,利用深度神经网络(DNN)建模技术,建立了从多个测量条件参数出发的海杂波多普勒谱参数预测模型,实现了独立于杂波数据、基于环境特征的海杂波谱特征认知,谱频移和展宽的预测精度达90%以上。基于该预测模型,该文提出了一种基于参数循环递减认知的多普勒谱影响因素分析方法,分析了不同测量参数对海杂波多普勒谱预测的影响,得到了谱参数随主要影响因素的变化规律,结果对基于多普勒特征的海面目标检测应用具有重要意义。Abstract: Using Deep Neural Network (DNN) modeling technology, a prediction model of Doppler spectral parameters of sea clutter based on multiple measurement conditions is established based on measured data of sea clutter from shore-based radar under different radar parameters and marine environmental parameters. The recognition of sea clutter spectral characteristics based on environmental characteristics and independent of clutter data is realized. The spectral frequency shift and broadening prediction accuracy are greater than 90%. Based on the prediction model, an analysis method of Doppler spectrum influence factors based on the parameter cycle decreasing cognition is proposed. The influence of different measurement parameters on the Doppler spectrum prediction of sea clutter is analyzed, and the change law of spectrum parameters with the main influence factors is obtained. The results are of great significance to the application of sea surface target detection based on Doppler characteristics.
-
Key words:
- Sea clutter /
- Doppler spectrum /
- Deep Neural Network (DNN) /
- Influence factors /
- Prediction model
-
1. 引言
受海洋气象和地理环境的影响,海面环境错综复杂,实现海上目标的精准探测具有极大的挑战性[1,2],这是由于当雷达对海面进行探测时,接收到的海面回波信号同时混杂着目标信号、噪声信号和海杂波信号。海杂波是指海面的雷达散射回波,是海面目标信号的重要“污染源”,研究海杂波特性对于海面目标检测具有重要的意义[3-5]。
海杂波的多普勒谱特性是指海表面单个距离门内连续相参时间序列信号自相关函数的傅里叶变换,谱参数包括多普勒频移与多普勒展宽。海杂波的谱特性能够反映海面能量特征和运动相位信息,在海杂波研究中有着不可替代的作用。1955年,Crombie[6]通过分析L波段雷达海杂波实测数据,开启了海杂波多普勒谱特性研究的先河。20世纪90年代,各国研究团体陆续开展了多项海杂波谱特性研究试验,建立了多种考虑散射机理的海杂波多普勒谱模型。例如,Lee等人[7]通过对多组实测数据的分析,提出了具有一定物理意义的Lee模型。Walker[8]利用造浪池数据,分析了海浪从产生到破碎全过程的多普勒变化特性,并建立了结合布拉格、白浪和破碎3种散射机制的Walker模型。Ward等人[3]借鉴了复合K分布幅度建模的思想,提出了利用两个高斯函数对谱形状进行描述的Ward模型。进入21世纪,澳大利亚国防科技部(DSTO)的Rosenberg等人[9,10]详细研究了海杂波谱特性在不同海洋环境和不同测量雷达下的详细变化,并提出了Rosenberg模型。中国电波传播研究所的Zhang等人[11]通过对海杂波实测数据的长期观测,对多普勒谱建模进行了深入的研究,并提出了时变多普勒谱模型。然而,上述模型都属于基于物理机理和经验数据的海杂波谱形状建模,解决的是谱线结构服从何种函数形式的问题,尚未实现从测量参数出发的海杂波谱形状和谱参数的预测。
近年来,人工智能、深度学习等新兴信息技术手段,被用于更加快速、智能化地研究各种海杂波特性[12],这给从海量的海杂波数据出发,解决海杂波多普勒谱特性预测的问题带来了曙光。McDonald等人[13]使用径向基神经网络(Radial Basis Function Neural Network, RBFNN)对包含噪声的海杂波混沌序列进行预测,并得到了较好的结果。Shen等人[14]使用后向传播神经网络(Back Propagation Neural Network, BPNN)对海杂波幅度进行了预测。Fernández等人[15]使用BPNN实现了对海杂波幅度分布参数的预测;2019年,Ma等人[16]用LSTM-NN对海杂波幅度均值和幅度分布参数进行预测;2021年,Shui等人[17]使用广义回归神经网络(General Regression Neural Network, GRNN)对UHF波段海杂波散射均值进行预测。可见,众多学者已经利用人工智能手段先后尝试解决了海杂波幅度均值和幅度分布特性的预测问题,然而在海杂波多普勒特性的智能化预测方面,尚未见相关研究报道。此外,现有的海杂波特性参数预测研究成果,测量覆盖的雷达参数和海洋环境参数范围有限,并且缺乏预测结果的影响因素分析。
本文基于黄海海域测量的大量Ku波段岸基雷达实测海杂波数据,利用深度学习网络建模技术,研究了从多个测量条件参数出发的海杂波多普勒谱参数预测方法,建立了谱频移和展宽的预测模型,并提出了一种基于参数循环递减认知的多普勒谱影响因素分析方法,首次实现了海杂波多普勒谱的多影响因素定量分析,得到了谱参数随主要影响因素的变化规律,对基于多普勒特征的海面目标检测应用具有重要意义。
2. 海杂波谱预测数据集构建
2.1 海杂波数据概况
本文基于中国电波传播研究所在黄海灵山岛海域测量的Ku波段岸基雷达海杂波数据开展海杂波谱参数预测方法研究。Ku波段雷达为全相参脉冲体制,可实现HH和VV极化、小擦地角(1°~10°)及多种海洋环境参数条件下的海杂波数据采集,雷达脉宽5~40 μs,脉冲重复频率(Pulse Repetition Freguency, PRF)为1 kHz或2 kHz。雷达架设高度约450 m,架设实况如图1所示。
海杂波数据测量的时间范围为2020年11月—2021年3月,雷达工作在凝视模式下,每一组数据包括一段20 s的海面固定区域的雷达连续观测回波,覆盖海况等级为1~3级。经过数据预处理和杂噪比分析,筛选出杂波区域明显的105363组数据。根据海情大小和极化方式的不同,数据集信息如表1所示。从数据总量上可以看出,2级海况下的数据最多,3级海况下的数据最少。此外,HH极化的海杂波数据比VV极化的海杂波数据更多;HH极化的2级海况数据占比比VV极化更多,3级海况数据占比比VV极化更少。
表 1 Ku波段海杂波数据集信息Table 1. Ku band sea clutter dataset information海情等级 HH极化(组) VV极化(组) 总数(组) 1 18675 16165 34840 2 28356 23726 52082 3 6942 11499 18441 合计 53973 51390 105363 2.2 谱预测训练数据集构建
在进行海杂波的谱参数智能化预测之前,需要先构建预测模型的数据集。数据集构建的具体步骤包括谱参数提取、环境参数匹配、数据筛选与清洗和归一化等。
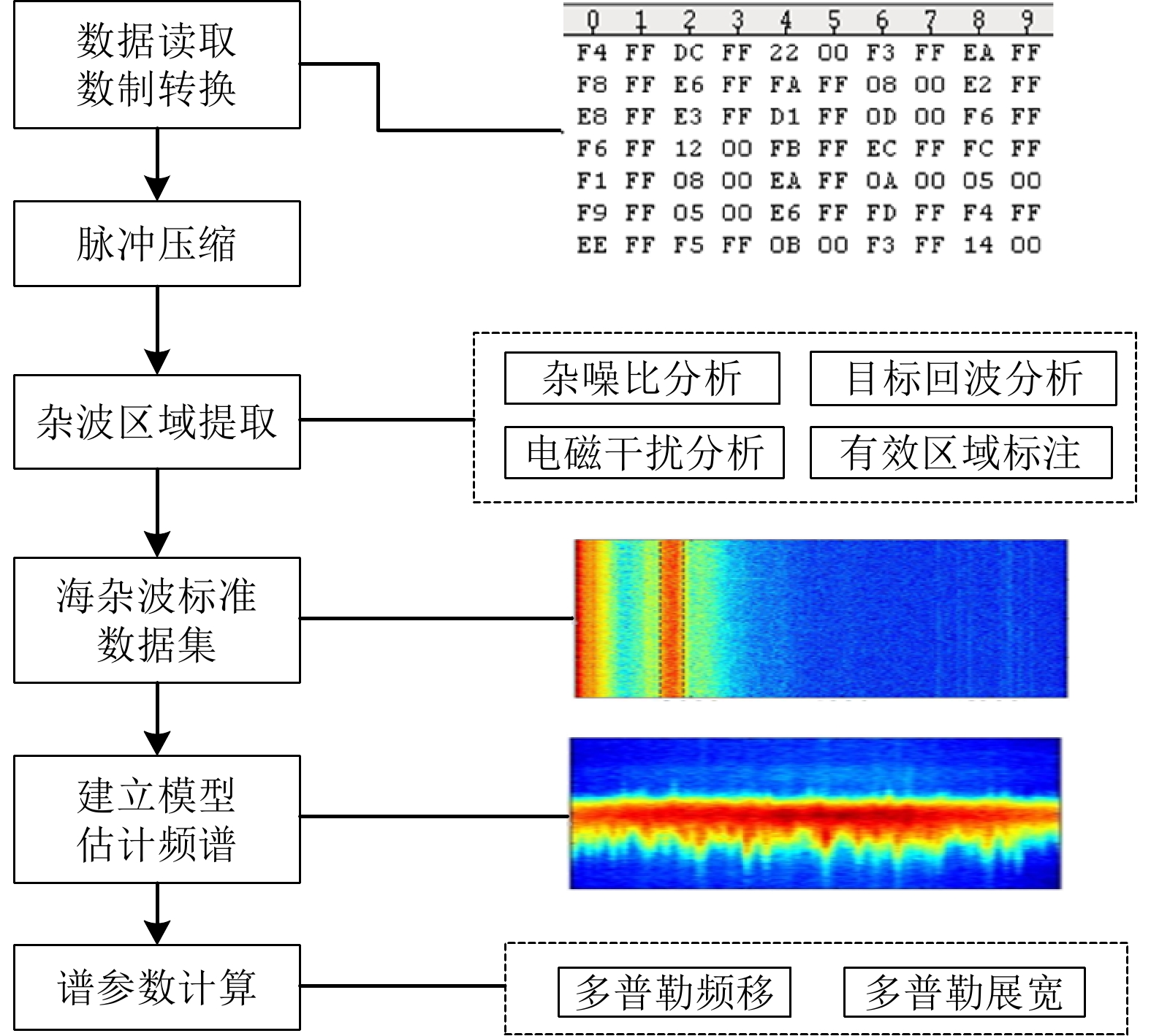
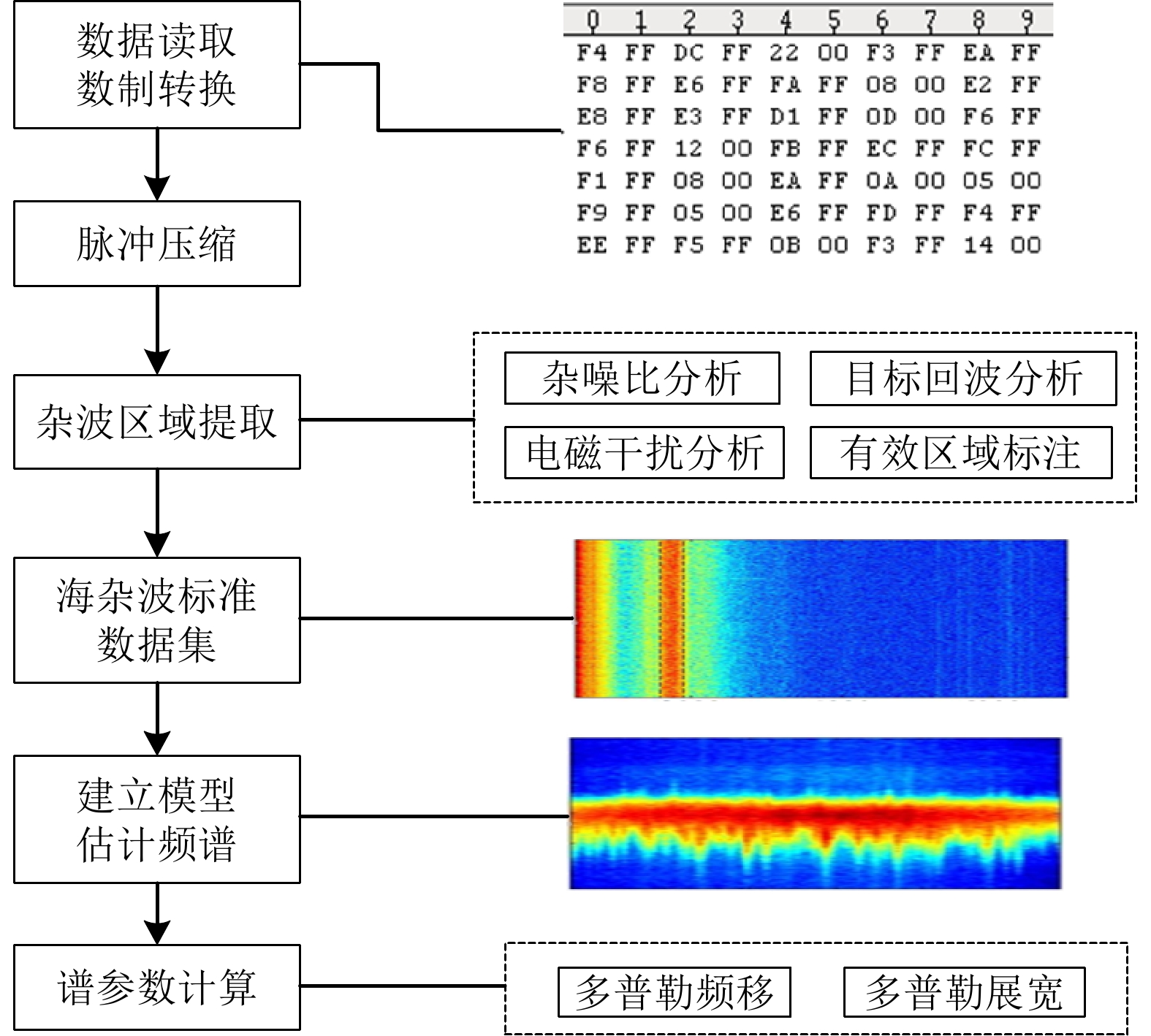
海杂波谱参数提取方法包含以下流程:首先对实测原始数据进行预处理,包括数制转换、脉冲压缩、有效杂波区域提取等,从而得到距离-脉冲幅值图;然后使用频谱估计方法,估计得到海杂波的多普勒谱;最后计算得到海杂波的多普勒频移和展宽。具体流程如图2所示。
本文选择Burg法[18]作为海杂波谱估计方法,该方法比起传统估计方法频率分辨率更好、适应性更强,比起其他现代谱估计方法的计算效率更高。根据Ku波段实测数据的参数情况,Burg法中的AR模型阶数取50,FFT点数取1024,采样频率设置为雷达的脉冲重复频率,取1 kHz或2 kHz。估计得到的多普勒谱表达式如式(1)所示:
SBu(f)=Ep|1+M∑m=1ˆame−j2πfm|2 (1) 式(1)中,
Ep 表示方差,SBu(f) 表示估计得到的海杂波功率谱密度。在得到多普勒谱曲线后,计算海杂波有效区域内每个距离门的多普勒频移
fd 和展宽Bw ,公式如下:fd=∫+∞−∞fSBu(f)df∫+∞−∞SBu(f)df (2) Bw=√∫+∞−∞(f−fd)2SBu(f)df∫+∞−∞SBu(f)df (3) 海杂波的测量条件参数是实现海杂波谱参数预测的输入数据,主要包括雷达测量参数和海洋环境参数。在海杂波测量过程中,Ku波段雷达固定照射频率,调整俯仰角和方向角实现对不同方向海域的探测。本文选取擦地角、极化方式和带宽3个雷达测量参数作为输入信息。海洋环境参数由浮标系统和风速计测量得到,其中浮标(波浪骑士DWR4)投放于海杂波测量区域,风速计架设于雷达位置附近,周围无遮挡。在浮标和风速计记录的多维参数中,筛选出7个海洋环境参数,包括海浪参数(有效浪高、浪向、浪周期)、海流参数(有效流速、流向)和海风参数(有效风速、风向),作为谱预测的输入信息。因此,用于海杂波多普勒谱参数预测的测量条件参数共计10个。
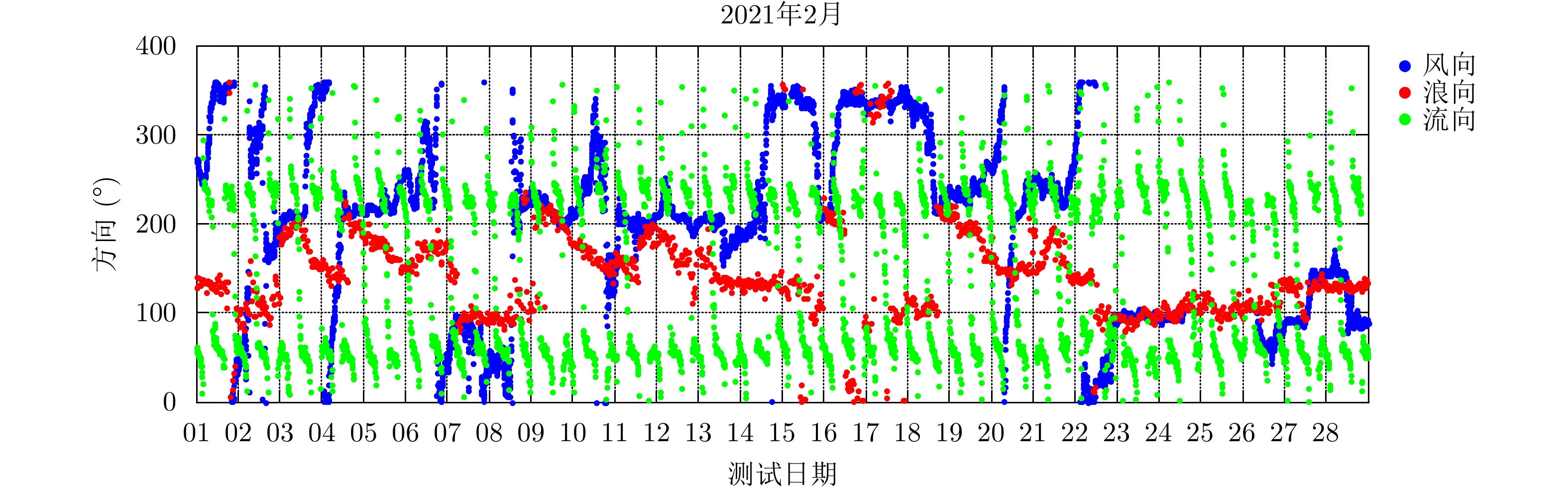
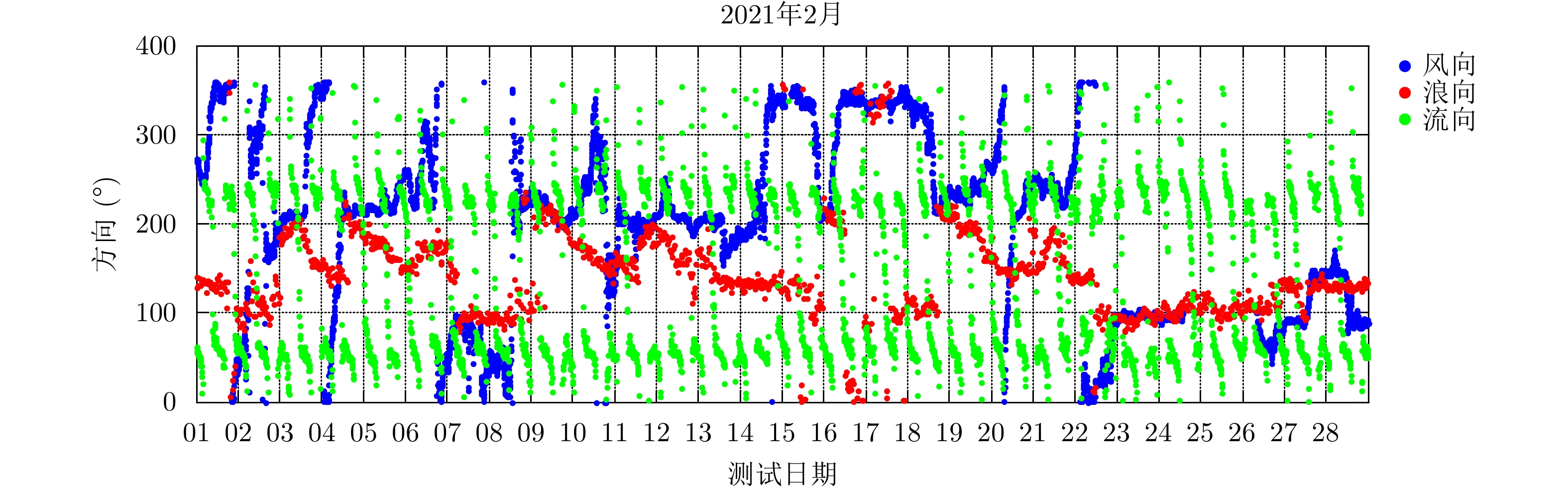
在海杂波的测量条件参数中,风浪流三者的方向存在密切的关联,若三者一致性程度很高,则这种强关联会影响海杂波多普勒谱影响因素的分析结果,若三者完全不相关,尤其是如果风向和浪向完全不吻合,则说明海面风对海浪的形成起的作用很小,风速意义不大。图3给出了2021年2月测量的风浪流方向的关系图。从图3可以看出,2月23日至2月26日,风向和浪向存在一定的关联性,说明这期间海浪充分发展; 2月14日至2月16日,风向和浪向偏差较大,说明这期间海浪发展程度很低。对流向而言,其与另外两种参数的一致性较低,这与海流形成的物理机理是一致的,不影响数据分析。总体而言,本文使用的风浪流数据存在一定的关联耦合性,也存在相当的独立性,满足海杂波影响因素分析对数据的需求。
为消除不同参数的量纲对谱预测准确度的影响,本文对10个测量条件参数进行归一化操作。在这里,归一化处理是指将输入数据统一限制在给定的范围内,从而加快模型训练过程中的收敛速度,同时提高训练的精度。对于数据的所有输入参数,都将归一化到区间[0, 1]内,其变换公式为
p′i=pi−piminpimax−pimin (4) 式(4)中,
pi 依次对应每个输入参数,p′i 表示归一化之后的输入参数。按照测量时间将测量条件参数与海杂波频移和展宽进行匹配,得到谱参数预测的训练数据集,形式如表2所示。
表 2 海杂波谱参数预测训练数据集组成形式Table 2. Composition of training data set for prediction of sea clutter spectral parameters参数 符号 输入 擦地角 θ 极化 Pol 带宽 B 有效浪高 Have 浪向 α 浪周期 T 流速 vf 流向 β 风速 vs 风向 γ 输出 频移 fd 展宽 Bw 3. 基于深度学习的海杂波谱参数预测
3.1 模型架构与参数设置
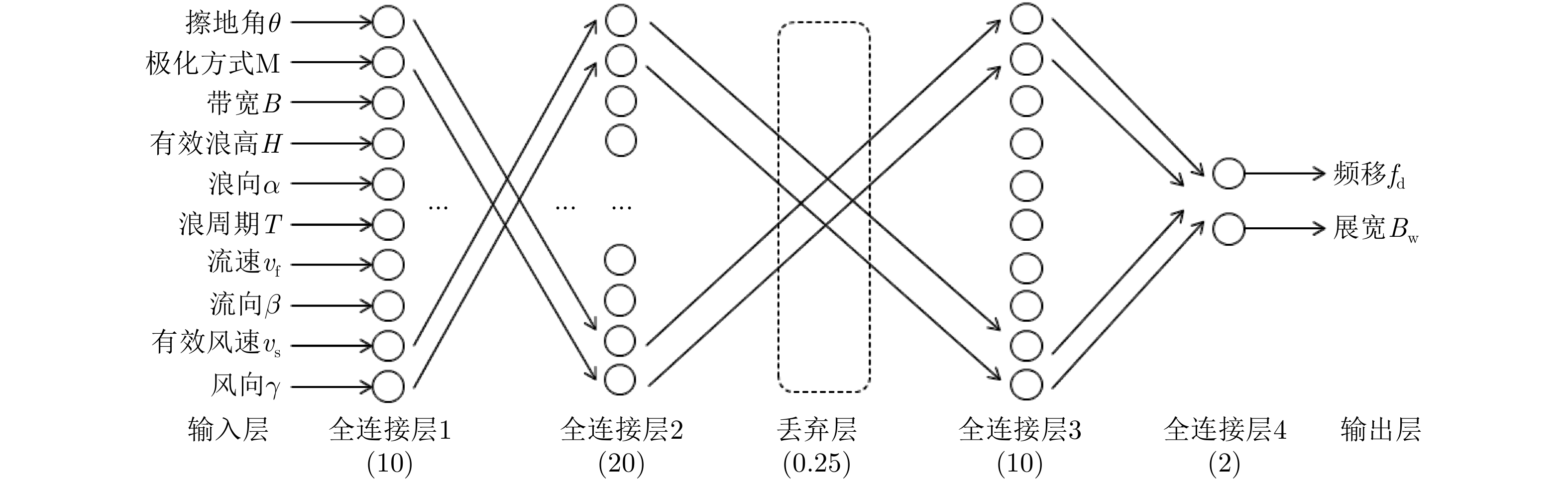
为了实现海杂波多普勒谱参数快速高效的智能化预测,本文基于上述Ku波段岸基海杂波数据集,利用深度神经网络(Deep Neural Network, DNN)建模技术,建立了从多个测量条件参数出发的海杂波多普勒谱参数网络预测模型,模型架构如图4所示。
经过试验数据的测试调优,本文提出使用一种5层的深度神经网络(DNN-5)建立预测模型。DNN-5是一种复合前馈神经网络,由4个全连接层和1个丢弃层组成,每个全连接层的神经元个数分别为10个、20个、10个和2个,而丢弃层进行随机丢弃,丢弃比例是25%。DNN-5网络及其输入-输出结构图如图5所示。
为了与提出的DNN-5网络模型预测效果相比较,论文另外采用了5种经典的回归预测模型,包括径向基函数神经网络(RBFNN)、反向传播神经网络(BPNN)、循环神经网络(RNN)、支持向量回归模型(SVR)和K-近邻回归模型(KNN)。不同网络的隐层函数与参数设置如表3所示,表3中的“改进Huber Loss”如式(5)所示,改进后的Huber Loss加快了小误差范围内模型的收敛速率。
表 3 不同网络的隐层参数设置Table 3. Hidden layer parameter settings of different networks模型名称 隐藏层数 激活函数 损失函数 优化函数 DNN-5 5 Leaky ReLU 改进
Huber LossAdam函数 BPNN 2 ReLU RBFNN 2 RBF RNN 4 ReLU SVR 无须训练 KNN L5(y,f(x))={12(y−f(x))2,|y−f(x)|≤55(y−|f(x)|−52)2,|y−f(x)|>5 (5) 本文中海杂波的谱参数预测基于Tensorflow v2.2平台进行,并使用单块Titan V GPU进行模型训练。对于每种网络模型的每一步训练,划分数据集比例为“训练集:验证集:测试集=3:1:1”。对数据随机打乱后,将输入参数归一化到区间[0, 1]。对于每种需要训练的网络模型,首先在学习率为0.001,batchsize为100的参数下训练500个epochs;再在学习率为0.0002,batchsize为100的参数下训练100个epochs。
在网络模型的评价指标方面,同时选用平均绝对误差(Mean Absolute Error, MAE)、均方根误差(Root Mean Squared Error, RMSE)和皮尔逊相关系数(Pearson Correlation Coefficient, PR),以上指标的计算公式如式(6)—式(8)所示,多普勒频移和谱宽的各项参数将分开计算。
MAE=1nn∑i=1|˜Yi−Yi| (6) RMSE=√1nn∑i=1(˜Yi−Yi)2 (7) PR=n∑i=1(Xi−ˉX)(Yi−ˉY)√n∑i=1(Xi−ˉX)2√n∑i=1(Yi−ˉY)2 (8) 其中,
˜Yi 代表多普勒参数的预测值,Yi 代表多普勒参数的实际值,n表示数据的总组数。为更为直观地评估模型预测精度,本文中提出一种新的评价参数“平均预测精度(用
η 表示)”,该参数能够反映谱参数预测模型的准确度,其表达式由式(9)给出。多普勒频移fd 和多普勒展宽Bw 平均预测精度也将分开计算。η=1−1nn∑i=1‖ (9) 3.2 预测结果分析
基于测试集数据,对海杂波谱参数预测模型的精度进行了测试。表4记录了6种不同模型下的4种预测指标。为了减小随机误差,每个模型均运行3遍,并将3次的结果取平均值填入表中。从表4可以看出,各个指标下评价结果体现出较高的一致性:对于多普勒频移的预测,DNN-5模型具有最好的效果,平均预测精度
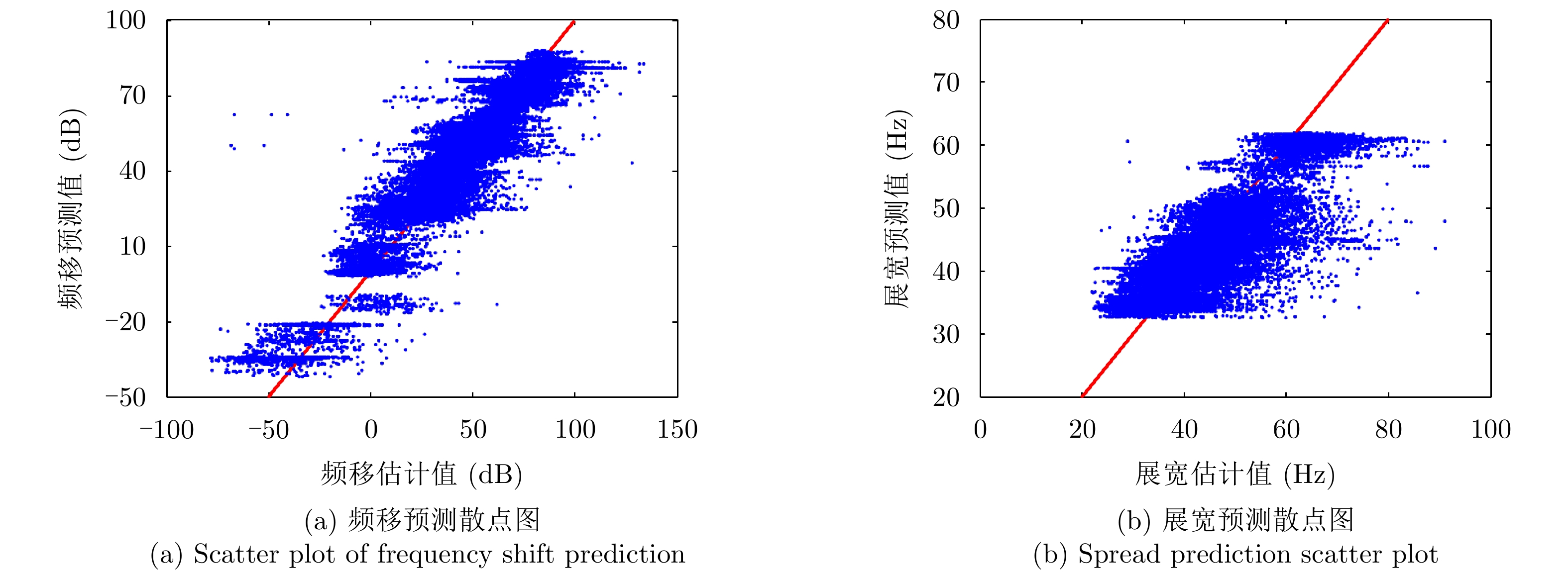
\eta 达91.3%,RBFNN和KNN其次,RNN, BPNN和SVR的预测效果较为一般。对于多普勒展宽的预测,DNN-5和RNN具有较好的预测效果,平均预测精度\eta 分别达95.3%和95.2%,RBFNN效果其次,BPNN, KNN和SVR模型的预测效果较为一般。通过5种经典回归预测模型的对比,可以发现DNN-5是效果最好的预测模型。表 4 各个模型的谱参数预测结果Table 4. Prediction results of spectral parameters of each model模型 MAE RMSE \eta PR {f_{\text{d}}} {B_{\text{w}}} {f_{\text{d}}} {B_{\text{w}}} {f_{\text{d}}} {B_{\text{w}}} {f_{\text{d}}} {B_{\text{w}}} SVR 17.46 5.10 22.37 6.78 0.815 0.892 0.749 0.780 KNN 9.87 5.06 12.63 6.69 0.889 0.911 0.926 0.792 DNN-5 8.50 4.58 11.57 6.16 0.913 0.953 0.941 0.827 BPNN 11.97 4.83 16.05 6.53 0.877 0.941 0.877 0.802 RBFNN 9.15 4.60 12.34 6.20 0.905 0.951 0.930 0.819 RNN 10.26 4.67 13.38 6.17 0.887 0.952 0.922 0.826 对于预测效果最好的谱参数预测模型DNN-5,画出其频移和谱宽的(真实值、预测值)的散点图如图6所示,图中蓝点代表每个谱参数样本的真实值和预测值的对应关系。当预测值完全等于真实值时,蓝点落在红色直线上,当预测值偏离真实值时,蓝点远离红色直线。相应的误差分布直方图如图7所示。从图6可以看出,DNN-5模型的预测散点非常靠近y=x直线,具有较好的预测效果;从图7可以看出,DNN-5模型的误差分布直方图也较为靠近中心0误差区域,误差分布较为合理。
4. 海杂波多普勒谱影响因素分析
4.1 基于循环递减认知的谱参数影响因素分析
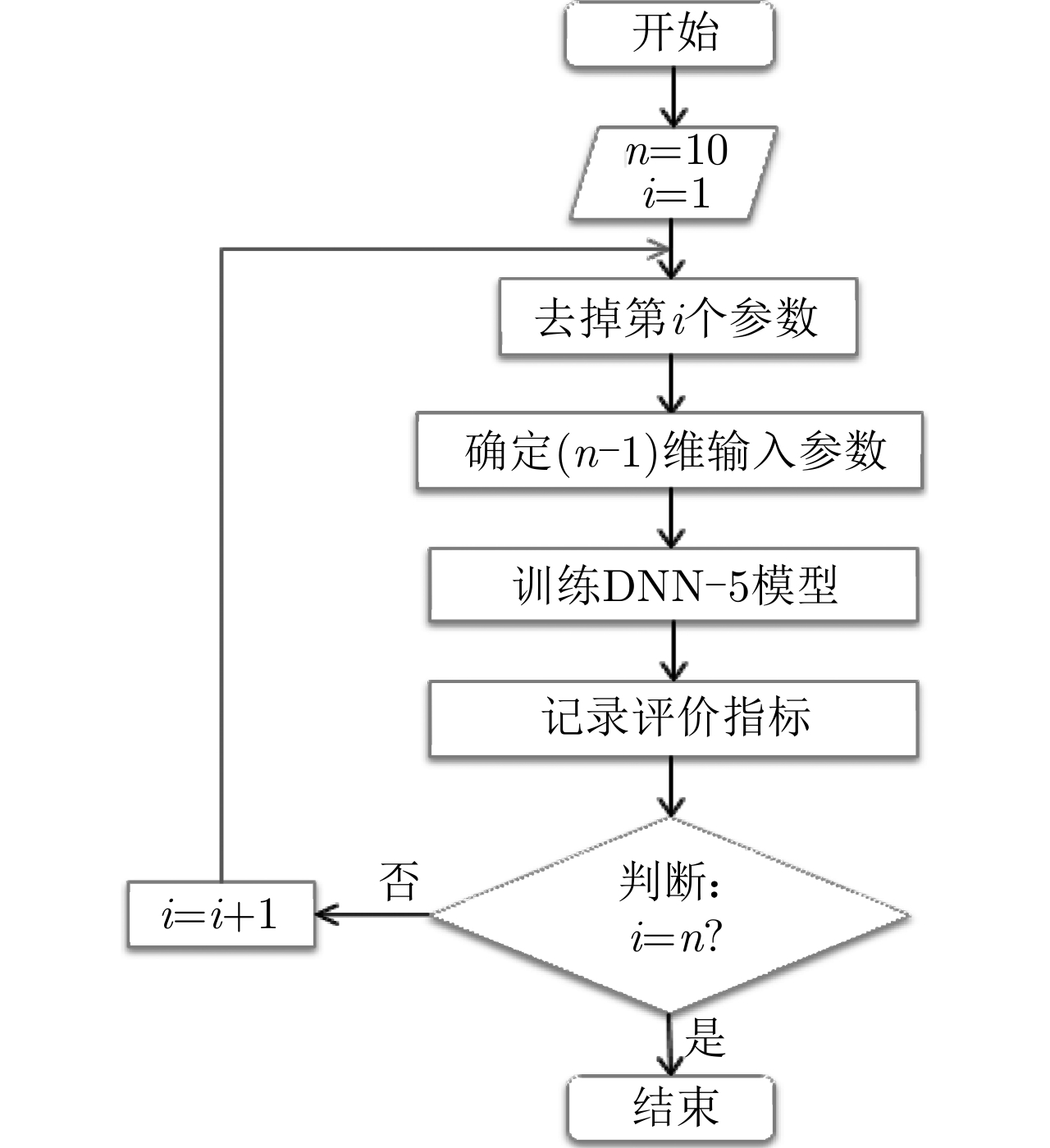
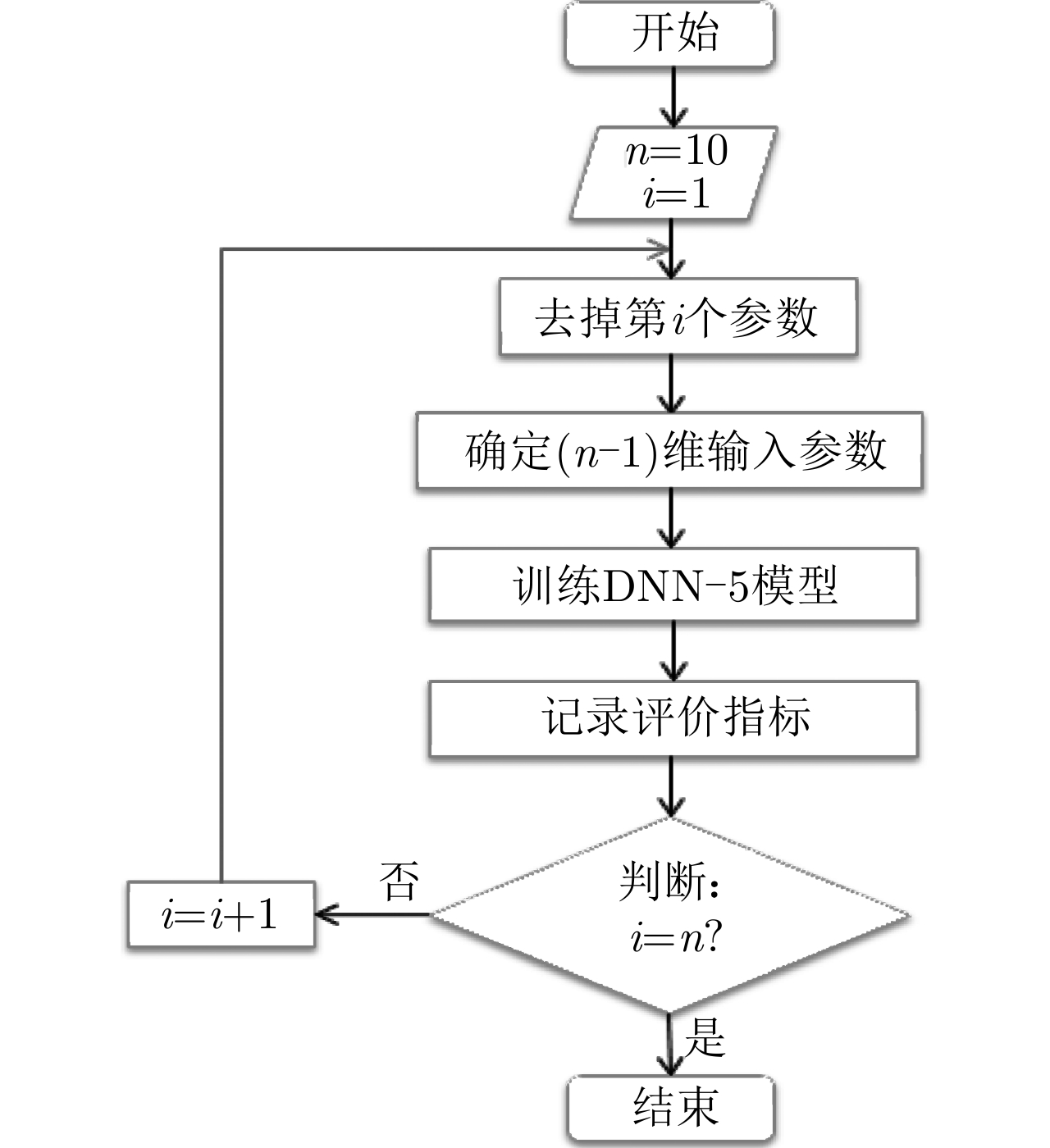
为了预测海杂波的多普勒频移和展宽,输入模型的10维参数包括三维雷达测量参数和7维海洋环境参数。为了确定每个输入参数对于预测结果的影响大小和变化关系,需要进行详细的参数影响分析。本文提出一种参数循环递减认知的谱影响参数分析方法,对预测影响因素的权重进行分析,分析方法如图8所示。在分析过程中,海杂波谱预测模型采用DNN-5模型,训练时的参数设置仍与3.1节相同,隐藏层的神经元数量则依据输入参数的情况进行等比例调整。
基于循环递减认知的网络影响参数分析步骤为:假设不同参数之间彼此相互独立,首先确定10维输入参数,每次抽取去掉一个参数,将9维输入参数输入DNN-5模型中,预测多普勒频移和展宽;记录模型的评价指标后,则继续抽取去掉另一个参数(上一次去掉的参数恢复,始终保持9个输入参数),直到10维输入参数均完成循环,每次记录的评价指标如表5所示。
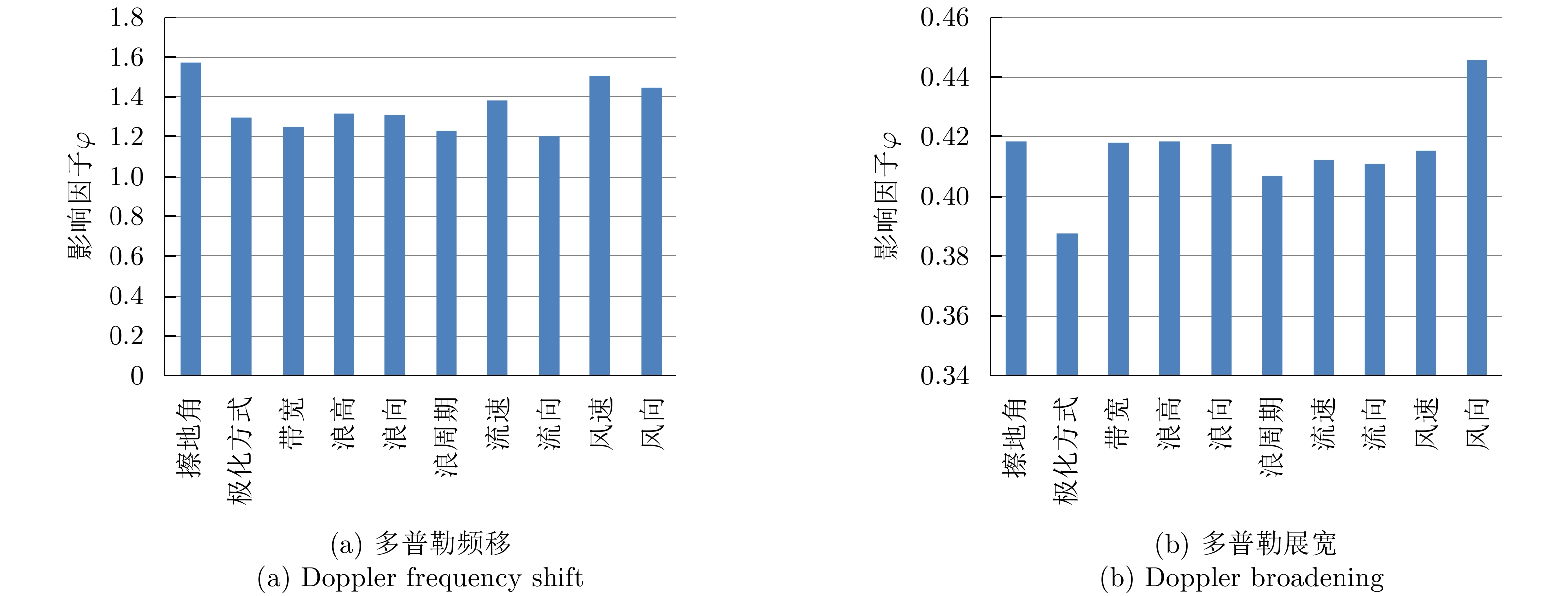
表 5 基于循环递减认知方法的DNN-5评价指标Table 5. Evaluation index of DNN-5 based on the cyclic decreasing cognition method去掉参数 多普勒频移 多普勒展宽 MAE RMSE PR η \varphi MAE RMSE PR η \varphi 擦地角 9.62 13.48 0.916 0.902 1.57 4.87 6.55 0.803 0.949 0.418 极化方式 9.02 12.20 0.937 0.907 1.29 4.77 6.39 0.828 0.950 0.387 带宽 8.90 12.03 0.942 0.909 1.25 4.93 6.62 0.824 0.947 0.418 浪高 9.17 12.23 0.942 0.906 1.31 4.94 6.60 0.823 0.947 0.418 浪向 9.15 12.25 0.943 0.906 1.31 4.91 6.59 0.818 0.947 0.417 浪周期 8.90 11.83 0.942 0.909 1.23 4.90 6.51 0.827 0.948 0.407 流速 9.30 12.56 0.937 0.904 1.38 4.90 6.57 0.824 0.948 0.412 流向 8.76 11.77 0.944 0.910 1.20 4.90 6.57 0.826 0.948 0.411 风速 9.63 13.11 0.931 0.900 1.51 4.86 6.62 0.817 0.948 0.415 风向 9.54 12.75 0.932 0.902 1.45 5.08 6.79 0.819 0.945 0.446 为了能更全面地根据评价指标对预测结果进行分析,本文定义参数影响因子
\varphi ,如式(9)所示。由于RMSE和MAE随预测效果的提升而减小,{\text{PR}} 和\eta 随预测效果的提升而增大,因而影响因子\varphi 随预测效果的提升而减小;\varphi 越大即表示在去掉某影响因素后的预测效果越差,即该因素对预测结果的影响越大。\varphi {\text{ = }}\frac{{{\text{RMSE}} \times {\text{MAE}}}}{{100{\text{PR}} \times \eta }} (10) 图9给出了各个输入参数对多普勒频移和谱宽预测的影响因子统计图。分析该统计图可以看出,对多普勒频移影响最大的因素依次为擦地角、风速和风向(均超过1.4),其余影响因素的影响因子对谱参数预测的影响相对较小。对多普勒展宽影响最大的因素为风向,对展宽影响最小的因素为极化方式,其余参数的影响因子大小较为接近。因而,将擦地角、风速和风向称作多普勒频移的主影响因素,将风向称作多普勒展宽的主影响因素。
4.2 海杂波多普勒谱参数变化规律分析
本文进一步分析了海杂波多普勒频移和展宽随主影响因素的变化趋势。考虑到实际物理意义,在多普勒频移随擦地角和风速的变化图中,频移取绝对值;而在多普勒频移和展宽随风向角的变化图中,频移不取绝对值,其中风向角表示风向与雷达探测方向的夹角。
为了便于观察参数变化规律,依据L-M (Levenberg-Marquardt)算法对散点图的整体变化趋势进行拟合。L-M算法是一种使用广泛的非线性最小二乘算法,是对牛顿迭代算法的改进,使用该算法对参数变化趋势进行拟合,运算效率出色,精确度也较高[19]。依据拟合的均方根误差(RMSE),本文在频移和擦地角的关系拟合中采用分式函数,在频移和风速的关系拟合中采用一阶多项式函数,而在频移/展宽与风向的关系拟合中采用二项三角函数。频移/谱宽随主影响因素变化的散点图分别如图10所示,其中蓝点代表不同参数条件下的实测谱参数样本,红色曲线表示拟合结果。
通过图10可以看出,海杂波频移和谱宽的样本方差相对较大,但红色拟合曲线随主影响因素的变化规律较明显,方差较大可能是由于海面未充分发展造成的,这通过图3给出的测量参数对应关系也可以反映出,不影响海杂波谱参数的变化规律分析。由图10(a)可以看出,随着擦地角的增大,多普勒频移绝对值呈逐渐减小的趋势,这是由于海浪速度在雷达视向的投影减小造成的。图中数据样本呈现柱状条形分布,是由于试验测量数据集中在某些擦地角,在部分擦地角处无数据。从图10(b)可以看出,随着风速增大,多普勒频移绝对值呈增大的趋势,说明海浪速度变大,与机理相符;在图10(c)中,多普勒频移受风向角的影响非常显著,在逆风情况下(风向角小于90°),显示为正向频移,在侧风情况下(风向角为90°附近)频移近似为0,在顺风情况下(风向角大于90°),显示为负向频移。值得注意的是,在一定的风向角情况下,多普勒频移可能同时出现正值样本和负值样本,这是由于风向角和浪向角未达到完全一致性,同一个浪向下可能对应多个不同风向的样本。从图10(d)可以看出,多普勒展宽随风向角近似呈现周期性变化,在风向角约为0°(逆风)、90°(正侧风)和180°(顺风)情况下,谱展宽相对较小,当风向角在0°~90°中间和90°~180°中间(斜侧风)情况下,谱展宽相对较大,该规律说明斜侧风条件下的海浪速度分量更多,海浪状态更为复杂,从而反映海浪运动速度的海杂波谱展宽更大。
5. 结语
本文基于岸基雷达海杂波实测数据,提出了一种基于DNN-5的海杂波谱参数预测方法,对多普勒频移和谱宽的预测精度分别达到了91.3%和95.3%。基于该预测模型,本文提出了一种基于参数循环递减认知的多普勒谱影响因素分析方法,对海杂波多普勒谱的影响因素展开了定性和定量分析,确定了多普勒频移的主影响因素(擦地角、风速和风向)和多普勒展宽的主影响因素(风向),并分析了频移和展宽参数随主影响因素的变化趋势。研究结果对基于海杂波频谱的目标检测算法设计和应用具有重要意义。
致谢 感谢各位编辑和读者的宝贵意见,感谢中国电波传播研究所提供的Ku波段雷达海杂波实测数据,感谢各位同事在研究过程中提供的慷慨援助。
-
表 1 Ku波段海杂波数据集信息
Table 1. Ku band sea clutter dataset information
海情等级 HH极化(组) VV极化(组) 总数(组) 1 18675 16165 34840 2 28356 23726 52082 3 6942 11499 18441 合计 53973 51390 105363 表 2 海杂波谱参数预测训练数据集组成形式
Table 2. Composition of training data set for prediction of sea clutter spectral parameters
参数 符号 输入 擦地角 \theta 极化 Pol 带宽 B 有效浪高 {H_{{\text{ave}}}} 浪向 \alpha 浪周期 T 流速 {v_{\text{f}}} 流向 \beta 风速 {v_{\rm{s}}} 风向 \gamma 输出 频移 {f_{\text{d}}} 展宽 {B_{\text{w}}} 表 3 不同网络的隐层参数设置
Table 3. Hidden layer parameter settings of different networks
模型名称 隐藏层数 激活函数 损失函数 优化函数 DNN-5 5 Leaky ReLU 改进
Huber LossAdam函数 BPNN 2 ReLU RBFNN 2 RBF RNN 4 ReLU SVR 无须训练 KNN 表 4 各个模型的谱参数预测结果
Table 4. Prediction results of spectral parameters of each model
模型 MAE RMSE \eta PR {f_{\text{d}}} {B_{\text{w}}} {f_{\text{d}}} {B_{\text{w}}} {f_{\text{d}}} {B_{\text{w}}} {f_{\text{d}}} {B_{\text{w}}} SVR 17.46 5.10 22.37 6.78 0.815 0.892 0.749 0.780 KNN 9.87 5.06 12.63 6.69 0.889 0.911 0.926 0.792 DNN-5 8.50 4.58 11.57 6.16 0.913 0.953 0.941 0.827 BPNN 11.97 4.83 16.05 6.53 0.877 0.941 0.877 0.802 RBFNN 9.15 4.60 12.34 6.20 0.905 0.951 0.930 0.819 RNN 10.26 4.67 13.38 6.17 0.887 0.952 0.922 0.826 表 5 基于循环递减认知方法的DNN-5评价指标
Table 5. Evaluation index of DNN-5 based on the cyclic decreasing cognition method
去掉参数 多普勒频移 多普勒展宽 MAE RMSE PR η \varphi MAE RMSE PR η \varphi 擦地角 9.62 13.48 0.916 0.902 1.57 4.87 6.55 0.803 0.949 0.418 极化方式 9.02 12.20 0.937 0.907 1.29 4.77 6.39 0.828 0.950 0.387 带宽 8.90 12.03 0.942 0.909 1.25 4.93 6.62 0.824 0.947 0.418 浪高 9.17 12.23 0.942 0.906 1.31 4.94 6.60 0.823 0.947 0.418 浪向 9.15 12.25 0.943 0.906 1.31 4.91 6.59 0.818 0.947 0.417 浪周期 8.90 11.83 0.942 0.909 1.23 4.90 6.51 0.827 0.948 0.407 流速 9.30 12.56 0.937 0.904 1.38 4.90 6.57 0.824 0.948 0.412 流向 8.76 11.77 0.944 0.910 1.20 4.90 6.57 0.826 0.948 0.411 风速 9.63 13.11 0.931 0.900 1.51 4.86 6.62 0.817 0.948 0.415 风向 9.54 12.75 0.932 0.902 1.45 5.08 6.79 0.819 0.945 0.446 -
[1] SHI Yanling, GUO Yaxing, YAO Tingting, et al. Sea-surface small floating target recurrence plots FAC classification based on CNN[J]. IEEE Transactions on Geoscience and Remote Sensing, 2022, 60: 5115713. doi: 10.1109/TGRS.2022.3192986 [2] QU Qizhe, WANG Yongliang, LIU Weijian, et al. A false alarm controllable detection method based on CNN for sea-surface small targets[J]. IEEE Geoscience and Remote Sensing Letters, 2022, 19: 4025705. doi: 10.1109/LGRS.2022.3190865 [3] WARD K D, TOUGH R J A, and WATTS S. Sea Clutter: Scattering, The K Distribution and Radar Performance[M]. 2nd ed. London: The Institution of Engineering and Technology, 2013: 129–142. [4] 李清亮, 尹志盈, 朱秀芹, 等. 雷达地海杂波测量与建模[M]. 北京: 国防工业出版社, 2017: 312–408.LI Qingliang, YIN Zhiying, ZHU Xiuqin, et al. Measurement and Modeling of Radar Clutter from Land and Sea[M]. Beijing: National Defense Industry Press, 2017: 312–408. [5] 丁昊, 董云龙, 刘宁波, 等. 海杂波特性认知研究进展与展望[J]. 雷达学报, 2016, 5(5): 499–516. doi: 10.12000/JR16069DING Hao, DONG Yunlong, LIU Ningbo, et al. Overview and prospects of research on sea clutter property cognition[J]. Journal of Radars, 2016, 5(5): 499–516. doi: 10.12000/JR16069 [6] CROMBIE D D. Doppler spectrum of sea echo at 13.56 Mc./s.[J]. Nature, 1955, 175(4459): 681–682. doi: 10.1038/175681a0 [7] LEE P H Y, BARTER J D, BEACH K L, et al. Power spectral lineshapes of microwave radiation backscattered from sea surfaces at small grazing angles[J]. IEE Proceedings-Radar, Sonar and Navigation, 1995, 142(5): 252–258. doi: 10.1049/ip-rsn:19952084 [8] WALKER D. Experimentally motivated model for low grazing angle radar Doppler spectra of the sea surface[J]. IEE Proceedings-Radar, Sonar and Navigation, 2000, 147(3): 114–120. doi: 10.1049/ip-rsn:20000386 [9] ROSENBERG L and STACY N J. Analysis of medium grazing angle X-band sea-clutter Doppler spectra[C]. 2008 IEEE Radar Conference, Rome, Italy, 2008: 1–6. [10] ROSENBERG L. Parametric modeling of sea clutter Doppler spectra[J]. IEEE Transactions on Geoscience and Remote Sensing, 2022, 60: 5105409. doi: 10.1109/TGRS.2021.3107950 [11] ZHANG Jinpeng, ZHANG Yushi, XU Xinyu, et al. Estimation of sea clutter inherent Doppler spectrum from shipborne S-band radar sea echo[J]. Chinese Physics B, 2020, 29(6): 068402. doi: 10.1088/1674-1056/ab888a [12] WEN Liwu, DING Jinshan, ZHONG Chao, et al. Modeling of correlated complex sea clutter using unsupervised phase retrieval[J]. IEEE Transactions on Geoscience and Remote Sensing, 2021, 59(1): 228–239. doi: 10.1109/TGRS.2020.2995892 [13] MCDONALD M K and CERUTTI-MAORI D. Clairvoyant radar sea clutter covariance matrix modelling[J]. IET Radar, Sonar & Navigation, 2017, 11(1): 154–160. doi: 10.1049/iet-rsn.2016.0103 [14] SHEN Yan and LI Guoqiang. The chaotic neural network is used to predict the sea clutter signal[C]. 2009 International Conference on Artificial Intelligence and Computational Intelligence, Shanghai, China, 2009: 25–30. [15] FERNÁNDEZ J R M and DE LA CONCEPCIÓN BACALLAO VIDAL J. Improved shape parameter estimation in K clutter with neural networks and deep learning[J]. International Journal of Interactive Multimedia and Artificial Intelligence, 2016, 3(7): 96–103. doi: 10.9781/ijimai.2016.3714 [16] MA Liwen, WU Jiaji, ZHANG Jinpeng, et al. Sea clutter amplitude prediction using a Long short-term memory neural network[J]. Remote Sensing, 2019, 11(23): 2826. doi: 10.3390/rs11232826 [17] SHUI Penglang, SHI Xiaofan, LI Xin, et al. GRNN-based predictors of UHF-band sea clutter reflectivity at low grazing angle[J]. IEEE Geoscience and Remote Sensing Letters, 2022, 19: 1502205. doi: 10.1109/LGRS.2021.3076842 [18] 张晓峰, 王莉, 殷国东, 等. Ku波段地海杂波极化特性实验与分析[J]. 电波科学学报, 2019, 34(6): 676–686. doi: 10.13443/j.cjors.2019043003ZHANG Xiaofeng, WANG Li, YIN Guodong, et al. The experiments and analysis of polarization characteristics of the ground and sea clutters at Ku band[J]. Chinese Journal of Radio Science, 2019, 34(6): 676–686. doi: 10.13443/j.cjors.2019043003 [19] MADSEN K, NIELSEN H B, and TINGLEFF O. Methods for Non-Linear Least Squares Problems[M]. 2nd ed. Lyngby: Informatics and Mathematical Modelling, Technical University of Denmark, 2004: 24–29. 期刊类型引用(4)
1. 张庆珍,曾昭赫,徐涛,曾鹏,张金鹏. 基于内点算法的海杂波幅度分布参数估计方法. 电波科学学报. 2025(01): 191-198 .  百度学术
百度学术2. 薛健,孙孟玲,潘美艳. 基于支持向量回归和分位数的雷达K分布海杂波形状参数估计方法. 电子与信息学报. 2024(04): 1399-1407 .  百度学术
百度学术3. 范一飞,王心宝,粟嘉,陶明亮,陈明,王伶. 基于智能学习的机载海杂波谱参数估计方法. 西北工业大学学报. 2024(03): 446-452 .  百度学术
百度学术4. 李清亮,张金鹏,张玉石. 海杂波测量与建模研究进展. 电波科学学报. 2023(04): 559-573 .  百度学术
百度学术其他类型引用(0)
-



 作者中心
作者中心 专家审稿
专家审稿 责编办公
责编办公 编辑办公
编辑办公


 下载:
下载:

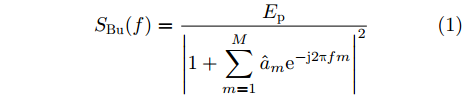
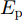
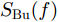
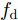
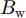
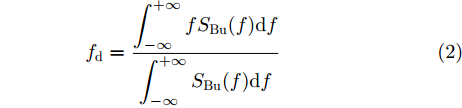
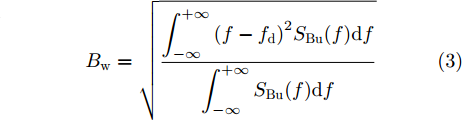

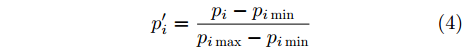
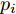
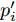



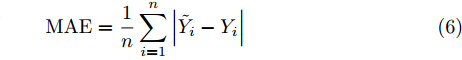
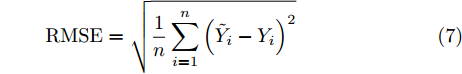
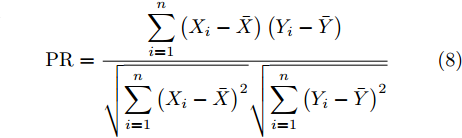
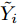
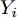
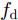
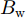
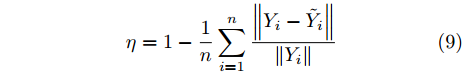




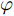
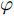
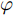
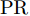
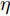
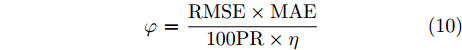



 下载:
下载:



 百度学术
百度学术