1.   引言

“蜂群”战术最早源于13世纪蒙古人的远征，他们模仿自然界里的蜂群组织方式执行军事侦察等任务，而蜂群无人机是由越南战争中的美军最先提出，用于越南复杂丛林的战术侦查。随着无人机自主能力的不断提高，智能“蜂群”技术成为科学研究的热点，具有智能化、集群化、自组织的特点，可以将复杂的功能或者任务分解到大量的无人机平台上。通过这些具有智能化能力的无人机，实现自主协同，完成动态变化环境中的复杂任务^[1]。这种由小型无人机组成的无人机蜂群有效利用无人机单个个体雷达反射面积小、不易被探测的特点，降低被对方探测的概率。同时，由多数无人机组成的蜂群可以借助数量优势和自组织的智能优势，实现饱和攻击和应对动态变化的环境和任务。蜂群技术的核心在于将大量无人机在开放体系架构下进行集成，借助人工智能基于有限信息通过蜂群自组织行为，协同完成特定任务。由于具有高灵活性、高机动性以及自组织性，蜂群技术在应对动态环境或者动态任务具有无可比拟的优势。为此，本文引入自组织蜂群的组网技术，开展基于蜂群无人机的无线电感知技术研究。

基于蜂群无人机的无线电感知技术，是在每个无人机上搭载一个全向感知天线，从而整体形成了构型可控的移动天线集群阵列。不同于以往的共形阵和相控阵，其整个阵列或部分阵列固定在特定的载体上。而无人机蜂群天线阵列是由众多的蜂群无人机形成一个移动的天线阵列，阵列元素之间的相对位置并不固定，具有柔性阵列特点^[2-5]。因此，这样的蜂群柔性阵列可以通过无人机平台的位置部署、蜂群的天线位置及波束权向量的联合优化，从而完成特定的感知、探测任务。文献[6,7]从给定的天线位置里挑选出尽可能少的天线，同时优化权向量，以最少的阵列天线完成探测任务。文献[8]基于粒子群优化算法进行天线坐标及权向量相位的优化，本质上想解决文献[6]中式(10)所描述的复杂约束的优化问题，最终将多约束的优化问题转换成了文献[8]中式(14)所描述的多目标优化问题。然而，加权系数很难设定，而且最终获得的解无法保证一定满足文献[8]中式(10)的约束。

基于以上考虑，本文首先根据无人机的运行速度以及下一感知时刻所要达到的波束指向，建立无人机位置及天线阵列权向量的联合优化数学模型。接着，应用Lawson准则简化复杂的目标函数，将天线坐标位置及权向量的两类优化变量简化为天线坐标位置的单类变量优化问题，并进一步转换为无约束的非线性优化问题。再引入辅助变量，进行约束和复杂目标函数的分离，通过交替方向乘子法完成联合优化，实现约束集和目标函数分离。

2.   问题描述及数学建模

考虑由N个无人机散布在空间中形成一个自组织蜂群，其在空间中的当前坐标位置为${{\boldsymbol{\tilde p}}_n} = {\left[ {{{\tilde x}_n}{\text{ }}{{\tilde y}_n}{\text{ }}{{\tilde z}_n}} \right]^{\rm{T}}}$, $n = 1, 2,\cdots ,N$。无人机在T时间内以速度${v_n}$匀速运动，经过T时间后的坐标位置${{\boldsymbol{p}}_n} = {\left[ {{x_n}{\text{ }}{y_n}{\text{ }}{z_n}} \right]^{\rm{T}}}$应该在以当前位置${{\boldsymbol{\tilde p}}_n}$为中心的球内：

T时间后，这N个天线构成的空间三维阵列对应俯仰角$\theta$和方位角$\phi$的导向矢量为

其中，${\boldsymbol{\kappa }} = {\left[ {\sin \theta \cos \phi {\text{ }}\sin \theta \sin \phi {\text{ }}\cos \theta } \right]^{\rm{T}}}$为波向量(Wave Vector, WV)。

令${\boldsymbol{w}} = {\left[ {{w_1}{\text{ }}{w_2}{\text{ }} \cdots {\text{ }}{w_N}} \right]^{\rm{T}}}$表示N个天线的权向量，在目标方向$({\theta _0},{\phi _0})$期望响应为1，而在干扰方向$({\theta _l},{\phi _l})$的期望响应为0，实现抑制干扰的目的，$l = 1,2 \cdots ,L$。除此之外，期望旁瓣越低越好，这里最小化峰值旁瓣电平(Peak Sidelobe Level, PSL)。基于以上考虑，构造如下波束赋形^[9-14]优化模型达到上述目的：

本文的主要任务为求解式(3)所描述的优化问题，确定权向量w和天线坐标位置$\left\{ {{{\boldsymbol{p}}_n}} \right\}_{n = 1}^N$，进而完成无人机蜂群自组织调整相应位置、权向量，实现波束指向及抗干扰任务。

3.   算法推导

3.1   基本算法

分析式(3)，由文献[15,16]不难发现：(1)导向矢量${\boldsymbol{a}}\left( {\theta ,\phi } \right)$的指数元素中包含天线坐标位置$\left\{ {{{\boldsymbol{p}}_n}} \right\}_{n = 1}^N$，且呈现出高度的非线性；(2)待优化的权向量w和导向矢量为内积关系，即${{\boldsymbol{w}}^{\rm{H}}}{\boldsymbol{a}}\left( {\theta ,\phi } \right)$，使得两类优化变量耦合在一起，难以共同优化；(3)由于目标函数和约束部分都存在内积项${{\boldsymbol{w}}^{\rm{H}}}{\boldsymbol{a}}\left( {\theta ,\phi } \right)$，使得目标函数和约束集高度耦合。

为解决上述难题，本文考虑解耦两类优化变量为单类优化变量：将权向量w表示为天线坐标位置$\left\{ {{{\boldsymbol{p}}_n}} \right\}_{n = 1}^N$的函数，消除权向量w。

Lawson近似为一种极大极小化近似策略^[17-19]，通过形成一系列加权最小二乘问题，获得极大极小化近似效果，已成功应用于FIR滤波器设计等领域。基于以上考虑，本文进行以下迭代算法设计。

步骤1　初始化旁瓣区域所有角度$\left( {\theta ,\phi } \right)$的Lawson权值${v_t}\left( {\theta ,\phi } \right)$为1，即${v_0}\left( {\theta ,\phi } \right) = 1,{\text{ }}\forall \left( {\theta ,\phi } \right) \in {\rm{Sidelobe}}$；迭代次数$t = 1$。

步骤2　采用权值对目标函数中的各项进行加权，形成如下优化问题：

步骤3　根据步骤1所获得的权向量${\boldsymbol{w}}(t + 1)$、天线坐标位置$\left\{ {{{\boldsymbol{p}}_n}(t + 1)} \right\}_{n = 1}^N$，计算Lawson近似加权系数：

步骤4　判断是否收敛；若收敛终止迭代，若未收敛，令$t = t + 1$，转步骤2。

尽管上述迭代算法将min-max准则变得简单，但步骤1所描述的问题依然是关于权向量w和天线坐标位置$\left\{ {{{\boldsymbol{p}}_n}} \right\}_{n = 1}^N$耦合的优化问题。但注意到假设天线坐标位置$\left\{ {{{\boldsymbol{p}}_n}} \right\}_{n = 1}^N$已知，式(4)退化为如下优化问题：

式中，

式(6)描述的问题类似于线性约束最小方差准则(Linear-Constraint Minimum-Variance, LCMV)问题，其解的闭合解析式为

将式(9)代入式(4)可得：

尽管式(10)中约束为凸集，但非线性目标函数相当复杂。考虑进行目标函数和约束集的分离，使得目标函数对应的子问题不存在约束，这样求解更为方便。为此引入辅助变量 ${{\boldsymbol{q}}_n}{\text{ = }}{{\boldsymbol{p}}_n},n = 1,2, \cdots ,N$，则式(10)可以转换为

基于式(11)，构造如下特殊的增广拉格朗日函数：

其中，${{\rho}} > 0$为用户自定义步长，${{\boldsymbol{\lambda}} _n}$为相应的拉格朗日乘子。不同于通常的拉格朗日函数，这里的拉格朗日函数引入乘子向量，仅将辅助变量对应的一致性约束${{\boldsymbol{q}}_n}{\text{ = }} {{\boldsymbol{p}}_n},n = 1,2 \cdots ,N$引入到目标函数中，而不是将所有的约束转移到目标函数中。

针对式(12)描述的增广拉格朗日函数求解，采用交替方向乘子法(Alternating Direction Method of Multipliers, ADMM)通过以下步骤A—步骤C迭代完成^[20-23]。在获得${{\boldsymbol{p}}_n},n = 1,2, \cdots ,N$后，结合式(9)，本质上解决了式(4)所描述的问题。

步骤A　基于给定的$\left\{ {{{\boldsymbol{q}}_n}(k),{{\boldsymbol{\lambda }}_n}(k)} \right\}_{n = 1}^N$，求解如下子问题确定$\left\{ {{{\boldsymbol{p}}_n}(k + 1)} \right\}_{n = 1}^N$：

去掉常数项并配方，式(13)等价为

式(14)呈现高度的非线性，这里考虑采用BFGS算法进行求解。BFGS算法是一种常用的拟牛顿方法，是由Broyden, Fletcher, Goldfarb, Shanno 4人分别提出的，故称为BFGS算法。具体操作为：在MATLAB中定义符号变量$\left\{ {{{\boldsymbol{p}}_n}} \right\}_{n = 1}^N$，然后采用定义法计算梯度以及Hessian矩阵，通过逆Hessian来确定移动的方向，并在所选方向上使用线搜索确定移动距离。本文采用MATLAB命令fminunc进行求解。

步骤B　基于给定的$\left\{ {{{\boldsymbol{p}}_n}(k + 1),{{\boldsymbol{\lambda }}_n}(k)} \right\}_{n = 1}^N$，求解如下子问题确定$\left\{ {{{\boldsymbol{q}}_n}(k + 1)} \right\}_{n = 1}^N$：

去掉常数项并配方，上述问题等价为

设${{{{\boldsymbol{\delta}}}_n} ={\boldsymbol{p}}_n(t+1) + \dfrac{{\boldsymbol{\lambda }}_n}{\rho} - {{{\boldsymbol{\tilde p}}}_n}}$可以得到闭合解析式：

步骤C　更新拉格朗日乘子：

重复步骤A—步骤C，直至收敛。

基于以上推导，算法可描述为

算法1　任务驱动的自组织蜂群柔性阵列波束赋形
Alg. 1 Task-driven flexible array beampattern synthesis for self-organized drone swarm
步骤1 　随机初始化无人机坐标位置$\left\{ { {{\boldsymbol{p}}_n}(0)} \right\}$；设定波束指向方 　　　　　向$({\theta _0},{\phi _0})$和干扰方向$({\theta _l},{\phi _l})$；初始化Lawson权值 　　　　　${v_t}\left( {\theta ,\phi } \right)$为1，即${v_0}\left( {\theta ,\phi } \right) = 1,{\text{ }}\forall \left( {\theta ,\phi } \right) \in {\rm {Sidelobe}}$；设 　　　　　外循环迭代变量为t；最大外循环次数${T_0}$；
步骤2 　随机初始化$\{ {{\boldsymbol{q}}_n}(0),{{\boldsymbol{\lambda }}_n}(0)\}$，设内循环迭代变量为k；最 　　　　 大内循环次数${K_0}$；根据式(9)计算权值矢量${{\boldsymbol{w}}_t}$；
步骤2.1　应用式(13)，式(14)确定$\left\{ {{{\boldsymbol{p}}_n}(k + 1)} \right\}_{n = 1}^N$；
步骤2.2　应用式(17)确定$\left\{ {{{\boldsymbol{q}}_n}(k + 1)} \right\}_{n = 1}^N$；
步骤2.3　应用式(18)更新拉格朗日乘子；
步骤2.4　重复步骤2.1—步骤2.3，直至达到最大迭代次 　　　　　　　　 数${K_0}$；
步骤3 　应用式(5)进行权值更新；
步骤4 　重复步骤2、步骤3，直至达到最大迭代次数${T_0}$。
输出：无人机权矢量${{\boldsymbol{w}}_t}$和坐标$\left\{ {{{\boldsymbol{p}}_n}(k)} \right\}$

下载: 导出CSV 

| 显示表格

3.2   扩展算法

实际探测过程中，在目标的准确角度未知的情况下，需要考虑宽主瓣设置。将目标的可能方向，即M个格点$\left\{ {({\theta _m},{\phi _m})} \right\}_{m = 1}^M$均当做主瓣区域；而旁瓣区域划分为S个格点：$\left\{ {({{\bar \theta }_s},{{\bar \phi }_s})} \right\}_{s = 1}^S$。为保持和上述模型一致，同时为了和其他角度有所区别，这里加波浪线$\left\{ {({{\tilde \theta }_l},{{\tilde \phi }_l})} \right\}_{l = 1}^L$表示零陷区域。

基于以上考虑，形成如下优化问题：

注意：式(19)中对主瓣施加了超“1”约束^[24]，即期望目标潜在的角度对应的主瓣电平均不小于1，这可能会导致主瓣区域的电平不平坦。如果需要考虑主瓣平坦，也可以替换该约束为双边约束$1 + \eta \ge {\left| {{{\boldsymbol{w}}^{\rm{H}}}{\boldsymbol{a}}({\theta _m},{\phi _m})} \right|^2} \ge 1 - \eta$^[25-28]，其中$\eta$为用户自定义的一个小于1的正常数。上述两种约束的差别在于：双边约束由于上下界限定更为严苛，消耗了更多的变量自由度，会以其他性能指标下降为代价(如峰值旁瓣电平)，但主瓣较为平坦，如文献[25,26]中相应部分的实验所示。双边约束的ADMM详细求解方法可以参考文献[25,26]，这里不再赘述。这里以超“1”约束为例进行描述。

引入辅助变量：

得到如下等价形式：

基于式(21)，构造如下特殊的增广拉格朗日函数：

式中，$\{ {\lambda _m},{\kappa _s}\}$为相应约束的拉格朗日乘子。然后基于ADMM设计如下迭代算法进行式(22)所描述的拉格朗日函数的求解。

步骤1　基于给定的$\{ {\boldsymbol{w}}(t),{{\boldsymbol{p}}_n}(t),{\lambda _m}(t),{\kappa _s}(t)\}$求解如下子问题，确定$\{ \varepsilon (t + 1),{u_m}(t + 1), {v_s}(t + 1)\}$：

式(23)可以分解为如下2个子问题(第1个可以通过cvx或者MATLAB命令qcqp求解；第2个子问题式(25)可以直接给出闭合解析式，参考式(16)：

步骤2　基于$\{ \varepsilon (t + 1),{u_m}(t + 1),{v_s}(t + 1),{\lambda _m}(t), {\kappa _s}(t)\}$，求解如下问题确定${\boldsymbol{w}}(t + 1),\,{{\boldsymbol{p}}_n}(t + 1)$：

进一步，可简化为如下形式：

式中，

注意：当${{\boldsymbol{p}}_n}(t + 1)$已知时，式(27)变成

构造拉格朗日函数

分别对权向量和拉格朗日乘子${\boldsymbol{w}},\left\{ {{\gamma _l}} \right\}$求导，可得：

式(32)，式(33)形成方程组：

则最优的w在获得解${\left[ {{{\boldsymbol{w}}^{\rm{T}}}{\text{ }}{\gamma _1} \cdots {\gamma _L}} \right]^{\rm{T}}}$的基础上，通过选择矩阵${\boldsymbol{S}} = \left[ {\begin{array}{*{20}{c}} {{{\boldsymbol{I}}_N}}&{{0_{N \times L}}} \end{array}} \right]$进行选择，取出前N个元素，即

将w代入式(30)的目标函数形成关于$\left\{ {{\boldsymbol{p}}_n}\right\}$的优化问题：

参照于式(10)—式(18)的求解方法求解获得${{\boldsymbol{p}}_n}$，再代入式(35)获得w。

步骤3　更新拉格朗日乘子：

基于以上推导，算法可描述为

算法2　目标方向不精确时的自组织蜂群柔性阵列波束赋形
Alg. 2 Flexible array beampattern synthesis for self-organized drone swarm with imprecise target direction
步骤1　初始化$\{ {\boldsymbol{w}}(0),{{\boldsymbol{p}}_n}(0),{\lambda _m}(0),{\kappa _s}(0)\}$；循环迭代变量t； 　　　　 最大循环次数${T_0}$；
步骤2　执行式(23)—式(25)获得$\{ \varepsilon (t + 1),{u_m}(t + 1),{v_s}(t + 1)\}$；
步骤3　执行式(26)—式(36)获得${\boldsymbol{w}}(t + 1),{{\boldsymbol{p}}_n}(t + 1)$；
步骤4　执行式(37)，式(38)进行拉格朗日乘子更新；
重复步骤2—步骤4，直至达到最大迭代次数${T_0}$。
输出：无人机权矢量${{\boldsymbol{w}}_t}$和坐标$\left\{ {{{\boldsymbol{p}}_n}(k)} \right\}$

下载: 导出CSV 

| 显示表格

4.   计算复杂度及收敛性分析

4.1   计算复杂度分析

本小节对算法1和算法2的计算复杂度进行简要分析，算法计算复杂度使用一次迭代中涉及的乘法总次数表示。

在算法1中，根据步骤2.1—步骤2.3，步骤2的复杂度为$O\left( {{N^2}} \right)$，步骤3的复杂度为$O\left( {2NS} \right)$，因此算法1总的计算复杂度为$O\left( {{N^2} + 2NS} \right)$。算法2中步骤2的复杂度为$O\left( {N\left( {M + S} \right)} \right)$，步骤3复杂度为$O\left( {{N^2} + N{{\left( {N + L} \right)}^2}} \right)$，步骤4复杂度$O\left( {N\left( {M + S} \right)} \right)$，因此算法2总的计算复杂度为$O\Bigr( 2N\left( {M + S} \right) + {N^2} + N{{\left( {N + L} \right)}^2} \Bigr)$。

4.2   收敛性分析

基本算法的Lawson收敛性中内循环实现了约束和目标函数的分离，且内循环为标准的ADMM算法，收敛证明同文献[29]附录B，这里不再赘述。内循环中，式(17)的求解步骤保证了所得的解满足约束${\left\| {{{\boldsymbol{p}}_n} - {{{\boldsymbol{\tilde p}}}_n}} \right\|^2} \le {v_n}T,n = 1,2 ,\cdots ,N$。而式(9)中权值w用${{\boldsymbol{p}}_n}$表示的消元思路，保证了所得的解一定满足约束${\text{ }}{{\boldsymbol{w}}^{\rm{H}}}{\boldsymbol{a}}({\theta _0},{\phi _0}) = 1,{{\boldsymbol{w}}^{\rm{H}}}{\boldsymbol{a}}({\theta _l},{\phi _l}) = 0,{\text{ }} l = 1, 2, \cdots ,L$。因此可得：所得的解一定满足式(3)中的约束，即所获得的解在式(3)所示问题的可行域内(实验部分的图1(c)主瓣及图1(g)零陷也证实了这一点)。值得注意，式(10)为高度非线性非凸优化问题，存在很多局部解，但是由于式(17)以及式(9)的特殊处理方式，即使不同初始化可能产生不同的解，但所有的解一定满足式(3)的约束

图  1  蜂群不调整位置时进行波束赋形结果

Figure  1.  Results of beamforming when the swarm does not adjust its position

下载: 全尺寸图片 幻灯片

此外，根据文献[17-19]，可得：

即经过Lawson加权迭代后，目标函数值随迭代次数呈下降趋势(实验部分的图1(c)的旁瓣又低又平也反映了Lawson最后达到了预期的min-max效果)。

扩展算法中为标准的ADMM算法，收敛性同文献[29]附录B，可得证明。

5.   仿真结果

本小节将通过仿真实验分析自组织蜂群柔性阵列波束赋形算法在不同情形下的赋形综合性能。首先，以仅优化权值和权值位置联合优化作为对比，以此说明天线位置移动对峰值旁瓣的影响，并且将所提算法与其他算法进行对比；其次，测试不同天线个数对峰值旁瓣的影响；然后，测试无人机距离范围约束对算法波束赋形的影响；最后，为验证算法稳定性，对目标方向以及初始化值的敏感程度做出测试。

5.1   蜂群自组织优化实验

蜂群系统最大的优势就是各无人机能通过灵活的自组织运动，以达到更好的探测效果。因此本实验先对比无人机位置移动展开测试，探究空间位置对波束赋形能力的影响。而后为验证算法的有效性，给出对比算法。

对于算法1，参数设置如下：在$x,y,z \in \left\{ {\left[ {0,10} \right] \times \left[ {0,10} \right] \times \left[ {0,10} \right]} \right\}$(单位为半波长)范围内随机初始化100个无人机的位置，如图1(a)所示。设置目标及两干扰对应方向分别为(0°, 0°), (–30°,–30°), (40°, 40°)，设置距离约束为${v_{\text{n}}}T = {\lambda}/{2}$，此处$\lambda$为半波长。在无人机位置给定情况下，求解式(40)仅优化权值向量问题。对于算法2，无人机位置初始化方式、距离约束设置与算法1相同，初始位置如图1(b)所示。假设目标俯仰角和方位角方向不确定，潜在的区域为$\theta ,\phi \in \left\{ {\left[ {{{ - }}{{10}^{\text{o}}},{{10}^{\text{o}}}} \right] \times \left[ {{{ - }}{{10}^{\text{o}}},{{10}^{\text{o}}}} \right]} \right\}$，以1°为间隔，主瓣区域划分为441个格点。设置两个干扰方向分别为(–30°, –30°), (40°, 40°)。在无人机位置给定情况下，求解式(41)仅优化权值向量问题。

求解式(39)所获得的波束图如图1(c)所示，此时最大峰值旁瓣为–16.85 dB，图1(e)为$\theta$方向和$\phi$方向切片结果，虚线部分框出了两方向–3 dB主瓣宽度，分别为11.4°, 11.0°，图1(g)为两干扰沿$\phi$方向的切片，两干扰方向的电平分别为–308.10 dB, –311.50 dB。求解式(41)所获得的波束图如图1(d)所示，此时最大峰值旁瓣为–11.42 dB，图1(f)为$\theta$方向和$\phi$方向切片结果，虚线部分框出了两方向–3 dB主瓣宽度，分别为30.2°, 27.8°，图1(h)为两干扰沿$\phi$方向的切片，两干扰方向的电平分别为–259.73 dB, –268.43 dB。

为了验证蜂群进行位置调整带来波束赋形的增益，执行算法1进行蜂群位置和权向量w的联合优化，所获得的蜂群位置如图2(a)所示，所获得的波束赋形结果如图2(c)所示；此时的最大峰值旁瓣电平为–23.13 dB，相比不进行蜂群位置调整的结果，峰值旁瓣降低了–6.28 dB；图2(e)为$\theta$方向和$\phi$方向切片结果，虚线部分框出了两方向–3 dB主瓣宽度，均为10.4°，相比图1(e)的结果减少了1.0°和0.6°；图2(g)为两干扰沿$\phi$方向的切片，两干扰方向的电平分别为–336.18 dB, –308.19 dB。由此可见，蜂群进行位置调整可以获得更佳的无人机坐标，有利于低旁瓣波束赋形。执行算法2进行蜂群位置和权向量w的联合优化，所获得的蜂群位置如图2(b)所示，所获得的波束赋形结果如图2(d)所示；结果证实此时的最大峰值旁瓣电平为–24.45 dB，低于不进行蜂群位置调整的–11.42 dB，峰值旁瓣降低了–13.03 dB；图2(f)为$\theta$方向和$\phi$方向切片结果，虚线部分框出了两方向–3 dB宽度，分别为32.1°, 25.6°；图2(h)为两干扰沿$\phi$方向的切片，两干扰方向的电平分别为–229.97 dB, –231.12 dB。由此可见，蜂群进行位置调整可以获得更佳的无人机坐标，有利于低旁瓣波束赋形。

图  2  蜂群位置和权向量联合优化结果

Figure  2.  Joint optimization results of swarm position and weight vector

下载: 全尺寸图片 幻灯片

由于遗传算法对可行解表示的广泛性，因此本文选用遗传算法和Lawson+遗传算法作为所提出算法的对比方法。遗传算法指所提出模型的权值和位置均由遗传算法搜索所得，Lawson+遗传算法指所提出模型的权值由Lawson迭代所得，位置由遗传算法搜索所得。两组实验的无人机初始位置、目标角度、干扰角度、距离约束参数设置同算法1，遗传算法迭代次数设置为30次。遗传算法和Lawson+遗传算法所得结果如图3所示。其中，图3(a)，图3(c)权值、位置均由遗传算法优化所得。可以看出，虽然遗传算法能解出此问题，但其效果较为一般，PSL在优化后仅为–12.06 dB。图3(b)，图3(d)为权值由Lawson迭代所得、位置由遗传算法搜索所得，其PSL值为–17.42 dB。可以看出，用Lawson近似+遗传算法所得结果要优于全部使用遗传所得结果。但这两种方法所得结果相较于上述联合优化后PSL值达到–23.13 dB而言，结果都较差，从而进一步证实所提出算法的优越性。

图  3  算法1的对比算法所得结果

Figure  3.  Comparison of the results of algorithm 1

下载: 全尺寸图片 幻灯片

5.2   天线个数的影响

阵元的个数往往对波束赋形能力有较大影响，因此本测试主要分析天线个数对本文所提算法影响。天线个数分别设置为50, 100, 150(其中设置100时结果如图2(c)所示)，天线随机取值范围同5.1小节。表1，表2给出了不同天线个数时，仅优化权向量、联合优化蜂群位置和权向量时的结果。从表1，表2可以看出，随着天线个数的增加，峰值旁瓣在降低；权值位置同时优化的结果优于仅优化权值的结果。

表  1  算法1天线个数变化时PSL对比

Table  1.  PSL comparison when the number of antennas changes in algorithm 1

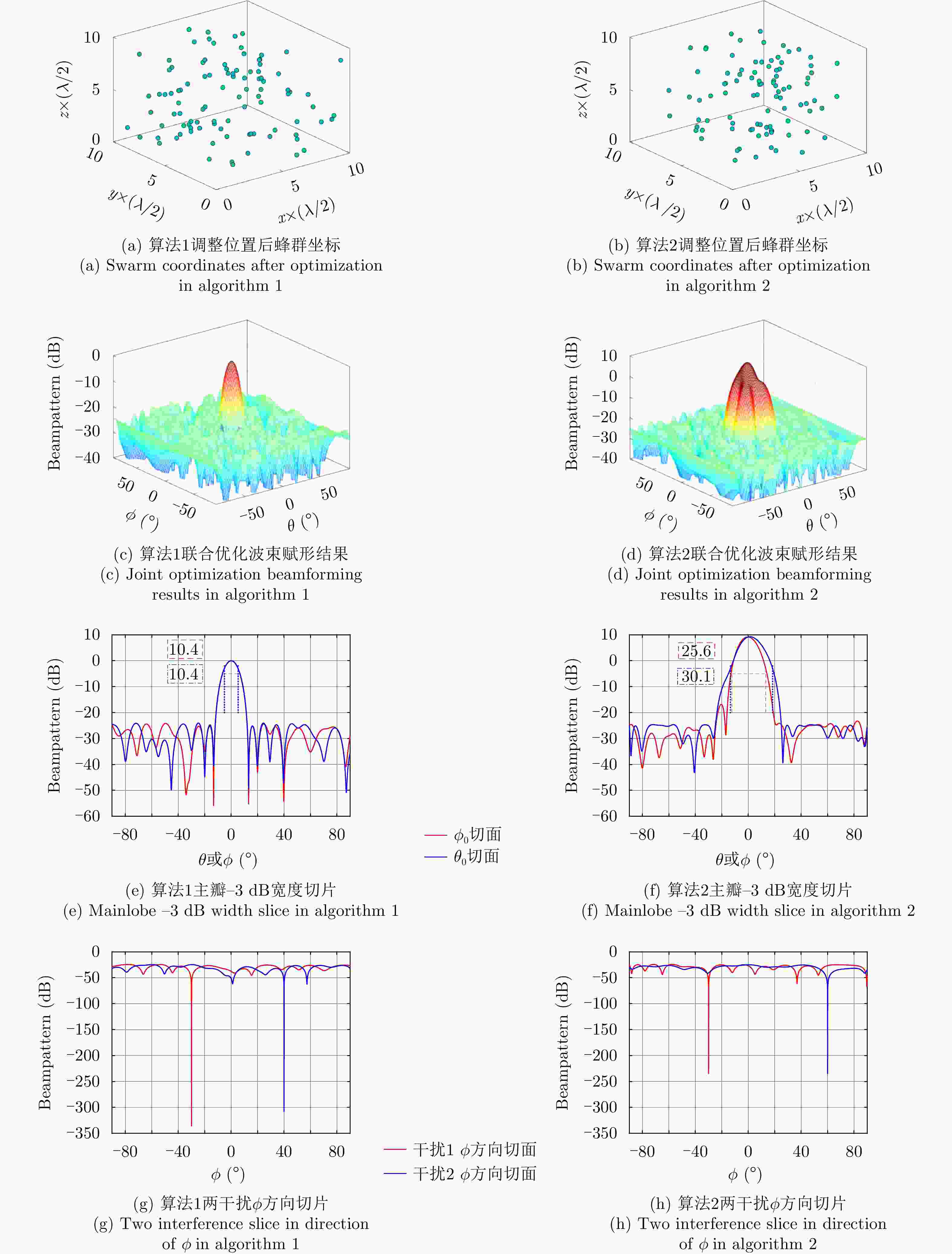
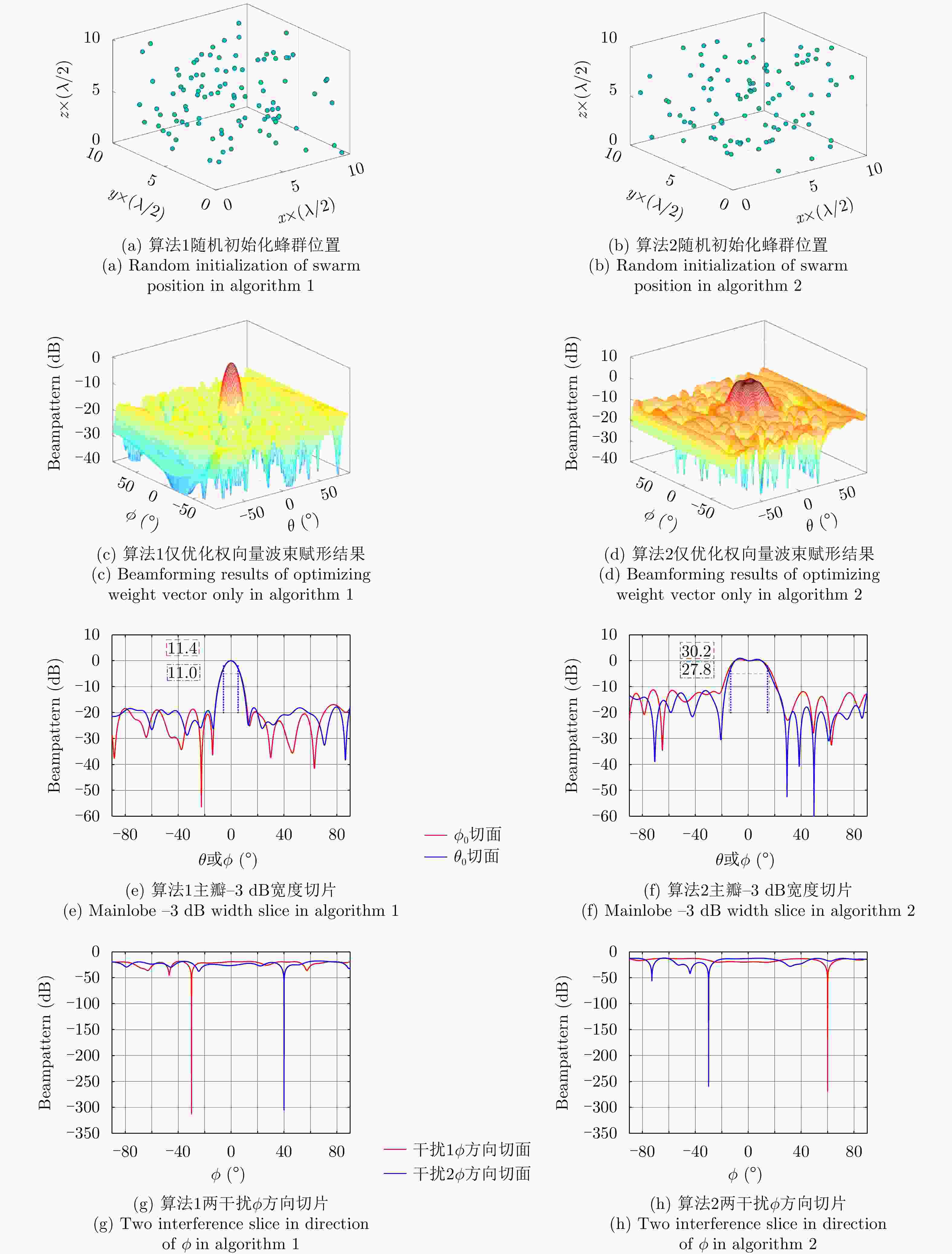
天线个数	仅优化权向量时的PSL (dB)	联合优化时的PSL (dB)
50	–13.27	–15.56
100	–16.33	–23.13
150	–20.50	–25.21

下载: 导出CSV 

| 显示表格

表  2  算法2天线个数变化时PSL对比

Table  2.  PSL comparison when the number of antennas changes in algorithm 2

天线个数	仅优化权向量时的PSL (dB)	联合优化时的PSL (dB)
50	–5.55	–15.82
100	–10.76	–24.45
150	–19.39	–28.04

下载: 导出CSV 

| 显示表格

5.3   距离约束范围

无人机的速度是有限的，因此在一定时间范围内其运动范围也是有限的。为了探究在何种情况下会获得更优的性能，本测试主要分析蜂群位置调整范围${v}_{n}T$对算法性能的影响。

天线个数仍为图1(a)所示的100个，当距离约束分别设置为$0.2 \times( {\lambda}/{2} )$, $0.5 \times ({\lambda}/{2})$, $1 \times ({\lambda}/{2})$, $2 \times ({\lambda}/{2})$, $5 \times({\lambda}/{2})$，分别求解算法1和算法2所获得的PSL如表3，表4所示。从表3，表4数据可以看出，PSL随着距离约束的变化呈现一定的规律变化。距离约束过小，无人机可移动空间位置小，此时PSL值偏大；距离约束大，无人机可移动空间大，PSL值会一定程度降低，但其存在上限，不能无限度降低，距离约束过大会导致性能的急剧恶化。这是因为，所提出算法是对无人机飞行的距离上限做出约束，初始迭代阶段运动距离过大导致部分无人机超出设定范围，超出半波长，无法有效优化，即使后期在向优化方向修正，也无法对其完全修正，从而导致其优化性能下降。从距离约束$2 \times ({\lambda}/{2})$和$5 \times ({\lambda}/{2})$两组实验的无人机空间位置可得到验证。因此距离约束应该选取在一个合适的值，考虑到本实验天线个数及其分散情况，距离约束为$1 \times ({\lambda}/{2})$较好。

表  3  算法1不同距离约束下PSL对比

Table  3.  Comparison of PSL under different distance constraints in algorithm 1

距离约束	PSL (dB)		距离约束	PSL (dB)
$0.2 \times \dfrac{\lambda}{2}$	–20.43		$2 \times \dfrac{\lambda}{2}$	–23.58
$0.5 \times \dfrac{\lambda}{2}$	–19.16		$5 \times \dfrac{\lambda}{2}$	–22.35
$1 \times \dfrac{\lambda}{2}$	–23.87

下载: 导出CSV 

| 显示表格

表  4  算法2不同距离约束下PSL对比

Table  4.  Comparison of PSL under different distance constraints in algorithm 2

距离约束	PSL (dB)		距离约束	PSL (dB)
$0.2 \times \dfrac{\lambda}{2}$	–14.65		$2 \times \dfrac{\lambda}{2}$	–17.27
$0.5 \times \dfrac{\lambda}{2}$	–21.34		$5 \times \dfrac{\lambda}{2}$	–11.73
$1 \times \dfrac{\lambda}{2}$	–24.45

下载: 导出CSV 

| 显示表格

5.4   鲁棒性测试

为测试所提出算法的鲁棒性，对目标指向和初始化值做出测试。由于扩展算法为基本算法的进一步拓展，因此此处仅对基本算法做出测试。

在上述实验中，目标角度均设置为(0°, 0°)，为测试提出算法对于目标区域的鲁棒性，下面给出对照实验。该实验除目标角度设置为(–30°, 30°)外，其余参数设置同5.1节，所得结果如图4(a)所示，易知即使目标所在角度改变，所提出算法仍具较好指向性。

图  4  算法1鲁棒性测试

Figure  4.  Robustness test of algorithm 1

下载: 全尺寸图片 幻灯片

为分析所提出算法对初始值的敏感性，此处增加不同初始化对算法结果的分析讨论，以此查看算法对初始值的敏感程度。共设置10组实验，其中每组目标角度、无人机初始范围、天线个数各组初始化参数不同，对比10组仅优化相位结果和相位位置联合优化结果。所得仿真结果如图4(b)所示，从图来看，所提出算法对于初始化值确实较为敏感，但对于高度非线性非凸优化问题而言，存在很多局部解，但经过式(23)与式(15)的特殊处理方式，即使不同初始化可能产生不同的解，但所有解一定满足式(3)的约束。

6.   结语

本文提出了两种自组织蜂群柔性阵列波束赋形算法，能够同时完成自组织调整蜂群位置与天线权向量、实现波束指向特定方向的任务。其中，第1种算法适用于目标方向确知的情况，而第2种算法适用于目标方向未知的情况。为了求解这两种算法形成的非线性、蜂群位置和权向量耦合优化数学优化问题，本文采用变量解耦及消元、约束和复杂目标函数分离等措施进行数值求解。最后的仿真结果表明了本文方法的有效性。未来将关注以下研究：除了规划无人机空间位置，还要进行路径的详细规划，包括避免飞行时发生碰撞^[30]。此外，未来将进一步研究柔性阵列校准算法^[31,32]以及鲁棒波束形成算法^[33]。