面向目标跟踪的机载组网雷达辐射参数与航迹规划联合优化算法

时晨光; 王奕杰; 代向荣; 周建江

doi:10.12000/JR22005

面向目标跟踪的机载组网雷达辐射参数与航迹规划联合优化算法

DOI: 10.12000/JR22005

南京航空航天大学雷达成像与微波光子技术教育部重点实验室南京 210016

基金项目: 国家自然科学基金(62271247, 61801212)，国家部委基金，航空科学基金(20200020052005, 20200020052002)，南京航空航天大学前瞻布局科研专项资金

详细信息

作者简介:
时晨光，博士，副教授，硕士生导师，研究方向为飞行器射频隐身技术、组网雷达协同感知、多传感器信息融合与管理等

王奕杰，硕士生，主要研究方向为飞行器射频隐身技术

代向荣，硕士生，主要研究方向为飞行器射频隐身技术

周建江，博士，教授，博士生导师，研究方向为隐身技术、雷达目标特性分析与特征控制等

通讯作者:
时晨光 scg_space@163.com

责任主编：易伟 Corresponding Editor: YI Wei
中图分类号: TN957
计量
- 文章访问数: 1112
- HTML全文浏览量: 677
- PDF下载量: 190
- 被引次数: 12
出版历程
- 收稿日期: 2022-01-07
- 修回日期: 2022-02-27
- 网络出版日期: 2022-03-21
- 刊出日期: 2022-10-28

Joint Transmit Resources and Trajectory Planning for Target Tracking in Airborne Radar Networks

Key Laboratory of Radar Imaging and Microwave Photonics, Ministry of Education, Nanjing University of Aeronautics and Astronautics, Nanjing 210016, China

Funds: The National Natural Science Foundation of China (62271247, 61801212), The National Ministries Foundation, The National Aerospace Science Foundation of China (20200020052005, 20200020052002), The Fund of Prospective Layout of Scientific Research for Nanjing University of Aeronautics and Astronautics

More Information

Corresponding author: SHI Chenguang, scg_space@163.com

摘要

摘要: 该文针对机载组网雷达，在单目标跟踪场景下，研究了雷达辐射参数与航迹规划联合优化问题。首先，推导了包含各雷达辐射功率、驻留时间、发射信号高斯脉冲长度和信号带宽等射频辐射参数以及各载机速度、朝向角等平台运动参数的贝叶斯克拉默-拉奥下界(BCRLB)表达式，以此作为表征目标跟踪精度的衡量指标；推导了含有各雷达辐射功率、驻留时间等射频辐射参数以及各载机速度、朝向角等平台运动参数的机载组网雷达被截获概率，以此作为表征机载组网雷达射频隐身性能的衡量指标。在此基础上，建立了面向目标跟踪的机载组网雷达辐射参数与航迹规划联合优化模型，以最小化机载组网雷达的目标估计误差BCRLB为优化目标，以满足给定的系统射频资源、载机机动能力和预先设定的被截获概率阈值为约束条件，对各载机飞行速度、朝向角以及各机载雷达辐射功率、驻留时间、发射信号高斯脉冲长度和信号带宽进行联合优化设计，以提升机载组网雷达的目标跟踪精度。最后，针对上述优化问题，结合粒子群算法，采用5步分解迭代算法进行求解。仿真结果表明，与现有算法相比，所提算法能够在满足一定射频隐身性能要求的条件下，有效提升机载组网雷达的目标跟踪精度。
- 辐射资源控制 /
- 航迹规划 /
- 机载组网雷达 /
- 射频隐身 /
- 目标跟踪
Abstract: This paper investigates the joint optimization problem of transmit resources and trajectory planning for target tracking in airborne radar networks. First, the analytical expression for the Bayesian Cramér-Rao Lower Bound (BCRLB) with the variables of the radar transmit power, dwell time, transmit signal Gaussian pulse length and signal bandwidth, and speed and heading angle of airborne nodes is derived and adopted as the metric function to evaluate the target tracking accuracy. In addition, the analytical expression of intercept probability with the variables of the radar transmit power, dwell time, and speed and heading angle of airborne nodes is also derived and utilized as the metric function to gauge the radio frequency stealth performance of the overall system. On this basis, a joint optimization model of transmit resources and trajectory planning for target tracking in airborne radar networks is established to jointly optimize the radar transmit power, dwell time, transmit signal Gaussian pulse length and signal bandwidth, and speed and heading angle of airborne nodes. This is done to minimize the target estimation error BCRLB under the constraints of given system resources, aircraft maneuvering and intercept probability threshold, thereby improving the target tracking accuracy of airborne radar network. Subsequently, a five-step decomposition iterative algorithm incorporating the particle swarm algorithm is used to solve the underlying optimization problem. The simulation results demonstrate that the target tracking accuracy of the proposed algorithm outperforms other existing approaches.
- Transmit resources control /
- Trajectory planning /
- Airborne radar network /
- Radio frequency stealth /
- Target tracking

HTML全文

1. 引言

探地雷达(Ground Penetrating Radar, GPR)是一种无损的利用电磁波传播来探测地下的地球物理方法，其已经在工程^[1]、考古^[2]、水文^[3]、地雷探测^[4]、极地及冰层探测^[5]、星球探测^[6]等领域有了广泛的应用。大部分传统的商业探地雷达只能测量共极化数据(VV)，而全极化探地雷达(Full-Polarimetric GPR, FP-GPR)不但可以获得共极化数据VV和HH，还可以获得交叉极化数据VH。目标体通过极化散射机制不同可以分为单次散射目标体、二次散射目标体和体散射目标体。目前FP-GPR数据处理大体可以分为两个方面，一种是极化分解方法，它是通过遥感极化分析手段结合FP-GPR数据进行处理。例如，Pauli分解技术结合偏移处理^[7]，H-α分解结合偏移处理^[8]，Freeman分解结合3D偏移成像^[9]。另一种就是数据融合方法，将VV, HH, VH 3种图像进行图像融合，使融合后图像具备VV, HH, VH的所有特点，再用传统探地雷达处理方法进行处理，得到分辨率更高更好的地下目标体图像。

图像融合是综合来自不同传感器的同一目标的图像信息，通过对多幅图像信息的提取和综合，从而获得对同一目标的准确全面可靠的图像描述^[10]。Daily等人^[11]首次将雷达图像和陆地卫星图像融合到一起并应用于地质探测上。最近20年，图像融合已经应用于智能机器人、医学、遥感等方面^[12-14]。例如，Ding等人^[15]提出了一种基于高斯过程模型的多传感器数据融合方法来进行复杂的表面测量；Wan等人^[16]提出一种鲁棒的主成分分析方法用于解决多焦点图像的融合问题。但是，在FP-GPR数据融合领域，目前常用的加权平均融合方法，会掩盖全极化的优点且无法确定准确适合的权值。因此，需要一种或几种能够保留全极化信息的数据融合方法，且可以适应不同极化散射机制的目标体。为此，本文选择了几种已经应用于图像融合领域的方法(主成分分析、拉普拉斯金字塔、多尺度小波变换)，结合FP-GPR数据，进行对比，选择适合不同极化散射机制目标体的方法。

主成分分析(Principal Component Analysis, PCA)是一种基于统计特征的多维正交线性变换方法，通常用于信号的特征提取和数据降维^[17]。PCA最初是Pearson^[18]在1901年提出的，并已广泛应用于人脸识别，网络入侵检测和图像降噪。例如，Safayani等人^[19]提出了扩展二维PCA来提高人脸识别的准确性和时间；Hadri等人^[20]将PCA和模糊PCA结合，可以保留来自网络流量数据的最相关信息；Qiu等人^[21]使用PCA来提取SAR图像目标分类中的特征。

拉普拉斯金字塔(Laplacian Pyramid, LP)是将原图像分解成不同空间分辨率的子图像，高分辨率子图像放到下面，低分辨率子图像放到上面，形成金字塔形^[22]。Burt等人^[23]提出的LP最早是用于图像的压缩处理，广泛应用于图像融合、图像检测等。例如，Mao等人^[24]提出了一种多方向联合平均的LP算法，用来加强融合图像边缘信息；Liang等人^[25]提出了由拉普拉斯锐化和LP组成的联合边缘检测器，加强了图像的边缘检测。

20世纪80年代发展起来的小波变换(Wavelet Transform, WT)技术，是一种图像的多分辨率多尺度分解^[26]，可以将信号分解为多个高频信号和1个低频信号，如今已经广泛应用于图像检测、数字视频水印、语音增强等方面。例如，Kumar等人^[27]用WT来分解高低频信号来进行图像边缘检测；Liu等人^[28]将离散WT与奇异值分解结合方法进行了改进，在数字视频水印的不可感知性与鲁棒性方面有了显著提高; Tasmaz^[29]利用双树复数WT对语音效果进行了增强。

本文在实验室中选择3个典型目标体获取其全极化探地雷达数据集，然后使用主成分分析、拉普拉斯金字塔、多尺度小波变换方法分别获得这3个典型目标体的融合图像，利用瞬时振幅为主、梯度为辅来比较加权平均融合和这3种融合的效果，并且找到适合未知散射机制目标体的方法。之后对冰裂缝进行实际数据测量，利用未知散射机制的融合方法与加权融合方法比较，最后得出结论。

2. 全极化探地雷达数据融合理论

平面波传播时，极化是指电场强度方向与入射面的关系。电场方向位于入射面中，为平行极化(H)；电场方向垂直于入射面，为垂直极化(V)。传统商用探地雷达是一种单极化探地雷达，它可以传输垂直极化的波形并接收相同的波形(获取VV数据)。全极化GPR将在发射H极化和V极化波形之间交替进行，同时接收H极化和V极化信号，从而获得VV, HH, VH和HV数据。由于在GPR系统中发射天线和接收天线的作用可以互换，所以VH数据等于HV数据。天线配置如图1所示，其中T表示发射天线，R表示接收天线。

图 1 全极化探地雷达系统中的天线配置

Figure 1. Antenna configurations used in a FP-GPR system

下载: 全尺寸图片幻灯片

为了进行全极化探地雷达数据融合，我们可以使用VV, HH和VH探地雷达系统作为不同的传感器来探测同一地下目标，获得VV, HH, VH数据集。这3个数据集就是做数据融合的基础。加权平均融合公式为

$F{\rm{ = }}{{{S}}_{{\rm{VV}}}}{\rm{ \times }}{Z_{{\rm{VV}}}}{\rm{ + }}{{{S}}_{{\rm{HH}}}}{\rm{ \times }}{Z_{{\rm{HH}}}}{\rm{ + }}{{{S}}_{{\rm{VH}}}}{\rm{ \times }}{Z_{{\rm{VH}}}}$

(1)

其中，S_VV, S_HH和S_VH是由FP-GPR获得的数据矩阵。Z_VV, Z_HH和Z_VH是平衡S_VV, S_HH, S_VH三者贡献的权重系数^[11]。

2.1 主成分分析数据融合

主成分分析可以将n维数据转换为m维数据，其中m维数据称为主成分。主成分可以代表原始数据，因为它具有最大的方差，代表着原始数据的大多数特征。因此，我们可以使用寻找主成分的方法来去除3个极化数据的多余相同部分，并融合不同部分。

为了对FP-GPR数据S = {S_VV, S_HH, S_VH}使用主成分分析，首先需要将S_VV, S_HH和S_VH3个矩阵转化为一个FP-GPR数据矩阵。全极化探地雷达PCA数据融合的步骤如下：

(1) 假设S_VV, S_HH和 S_VH矩阵维度都是M×N，而FP-GPR矩阵为X = [X_VV X_HH X_VH]。其中，X_VV, X_HH, X_VH分别是由S_VV, S_HH, S_VH转化而得的，3个长度为M×N的一维向量，比如X_VV是将S_VV的N列数据按2～N的顺序依次放到第1列数据下，使其变成一维向量。

(2) 计算数据X的均值，其中 $\bar {{X}}$ 是X的平均值

$\bar {{X}}{\rm{ = }}\frac{{\rm{1}}}{{\rm{3}}}{\rm{(}}{{{X}}_{{\rm{VV}}}}{\rm{ + }}{{{X}}_{{\rm{HH}}}}{\rm{ + }}{{{X}}_{{\rm{VH}}}}{\rm{)}}$

(2)

(3) 进行去均值，其中 $\tilde {{X}}$ 是FP-GPR数据X减去均值 $\bar{{X}}$ 的结果

$\tilde {{X}} = {{X}} - \bar {{X}},\;\tilde {{X}} = \left[ {{{{X}}_{{\rm{VV}}}} - \bar {{X}},\;{{{X}}_{{\rm{HH}}}} - \bar {{X}},{{{X}}_{{\rm{VH}}}} - \bar {{X}}} \right]$

(3)

(4) 构造数据矩阵 $\tilde {{X}}$ 的协方差矩阵V，其中T代表矩阵转置

${{V}} = \frac{1}{3}{\tilde {{X}}^{\rm{T}}}\tilde {{X}}$

(4)

(5) 协方差矩阵V进行特征值分解，求取特征值λ= {λ₁, λ₂, λ₃}和对应特征向量W= {W₁ W₂ W₃}

${{VW}} = \left[ {\begin{array}{*{20}{c}} {{\lambda _1}}&{}&{} \\ {}&{{\lambda _2}}&{} \\ {}&{}&{{\lambda _3}} \end{array}} \right]{{W}}$

(5)

(6) 选取最大特征值λ_max对应的特征向量W_max，主成分C 可以由W_max和 $\tilde {{X}}$ 相乘得到

${{C}} = \tilde {{X}}{{{W}}_{\max }}$

(6)

(7) C是一个长度为M×N 的一维向量，再将其重新转化成一个维度为M×N的矩阵F。F 就是数据融合后的FP-GPR矩阵。

2.2 拉普拉斯金字塔数据融合

图像的LP分解能够将原图像分解到各个不同的频带范围，这样数据融合就可以针对不同的分解层获得的不同频带，采用不同的融合规则，对VV, HH, VH图像分解获得的相同分解层进行融合，再对其进行图像重构，可以获得具备几个原图像的所有细节特点的融合图像。

下面以VV数据为例进行LP分解。

要建立图像的拉普拉斯金字塔首先要建立高斯金字塔，原VV图像为 ${{S}}_{\rm{0}}^{{\rm{VV}}}$ ，将其当做金字塔的底，则第L层图像 ${{S}}_{{L}}^{{\rm{VV}}}$ 可以由式(7)表示

$\begin{split} {{S}}_L^{{\rm{VV}}}(i,j) =\,& \mathop \sum \limits_{m = 1}^5 \mathop \sum \limits_{n = 1}^5 {{U}}\left( {m,n} \right)\\ & \cdot{{S}}_{L - 1}^{{\rm{VV}}}\left( {2i + m - 3,2j + n - 3} \right),\\ & 0< L \le Q,0 \le i < {M_L},0 \le j < {N_L} \end{split}$

(7)

其中， ${{S}}_{{{L - 1}}}^{{\rm{VV}}}$ 为第L–1层的图像，Q为高斯金字塔顶层的层号，M_L和N_L分别为第L层图像的行数和列数，U是具备低通性质的窗口，称为高斯模板。常用的高斯模板如式(8)所示

${{U}} = \left[ {\begin{array}{*{20}{c}} 1&4&6&4&1 \\ 4&{16}&{24}&{16}&4 \\ 6&{24}&{36}&{24}&6 \\ 4&{16}&{24}&{16}&4 \\ 1&4&6&4&1 \end{array}} \right]$

(8)

由此，VV可以转化为由 ${{S}}_{\rm{0}}^{{\rm{VV}}}$ , ${{S}}_{\rm{1}}^{{\rm{VV}}}$ , ···, ${{S}}_{{L}}^{{\rm{VV}}}$ 排列的高斯金字塔。

之后由高斯金字塔建立拉普拉斯金字塔，引入放大算子expand，将 ${{S}}_L^{{\rm{VV}}}$ 放大得到 ${{S}}_L^{{\rm{VV'}}}$ ,使其与 ${{S}}_{{{L - 1}}}^{{\rm{VV}}}$ 尺寸相同，放大算子如式(9)所示

$\left. \begin{aligned} & {{S}}_L^{{\rm{VV'}}}\left( {i,j} \right) = 4\mathop \sum \limits_{m = 1}^5 \mathop \sum \limits_{n = 1}^5 {{U}}(m,n)\\ & \quad\cdot {{S}}_L^{{\rm{VV}}}\left( {\frac{{i + m - 3}}{2},\frac{{j + n - 3}}{2}} \right),0 < L \le Q,\\ & \quad0 \le i < {M_{L - 1}},0 \le j < {N_{L - 1}}\\ & {{S}}_L^{{\rm{VV}}}\left( {\frac{{i + m - 3}}{2},\frac{{j + n - 3}}{2}} \right) \\ & \quad\quad= \left\{ \begin{aligned} & {{{S}}_L^{{\rm{VV}}}\left( {\dfrac{{i + m - 3}}{2},\dfrac{{j + n - 3}}{2}} \right),}\\ &\qquad\ \ {\dfrac{{i + m - 3}}{2},\dfrac{{j + n - 3}}{2}{\text{为整数}}}\\ & 0,\qquad {\text{其他}} \end{aligned} \right. \end{aligned} \right\}$

(9)

由于 ${{S}}_{{L}}^{{\rm{VV}}}$ 是 ${{S}}_{{{L - 1}}}^{{\rm{VV}}}$ 经过低通滤波和降采样之后得到的，而 ${{S}}_{{L}}^{{\rm{VV}}}$ 经过放大算子得到的 ${{S}}_{{L}}^{{\rm{VV'}}}$ , 虽然尺寸与 $S_{L - 1}^{{\rm{VV}}}$ 相同，但是细节信息却是少于 $S_{L - 1}^{{\rm{VV}}}$ ，所以如式(10)所示

$\left. \begin{aligned} & {{{P}}_L^{{\rm{VV}}} = {{S}}_L^{{\rm{VV}}} - {\rm{expand}}\left({{S}}_{L + 1}^{{\rm{VV}}}\right),\ 0 \le L < Q}\\ & {{{P}}_Q^{{\rm{VV}}} = {{S}}_Q^{{\rm{VV}}},\qquad\qquad\qquad\qquad\;\ L = Q} \end{aligned} \right\}$

(10)

${{P}}_L^{{\rm{VV}}}$ 为第L层的拉普拉斯金字塔图像。由此可以得到由 ${{P}}_{\rm{0}}^{{\rm{VV}}}$ , ${{P}}_1^{{\rm{VV}}}$ , ···, ${{P}}_L^{{\rm{VV}}}$ 组成的数据VV的拉普拉斯金字塔。

同理，可以得到HH与VH的拉普拉斯金字塔。对同一层级的用相同融合规则进行数据融合， ${{P}}_{{Q}}^{{\rm{VV}}}$ , ${{P}}_{{Q}}^{{\rm{HH}}}$ , ${{P}}_{{Q}}^{{\rm{VH}}}$ 都是低频成分，而其余的LP成分是高频信息。高频部分代表细节信息，低频部分代表轮廓信息，所以对于融合法则的选取是对对应处的每个像素点，低频部分平均处理，保留3种极化方式的目标体反射情况，高频部分则是选取最大值，取3幅图像中最能代表该目标体的细节部分，增加了融合图像的细节反射。最后得到融合图像的拉普拉斯金字塔 ${{P}}_{\rm{0}}^{\rm{F}}$ , ${{P}}_{\rm{1}}^{\rm{F}}$ , ···, ${{P}}_{{L}}^{\rm{F}}$ 。

在数据融合之后，进行图像重构，得到融合后的图像。由LP重建融合后的图像 ${{S}}_{\rm{0}}^{\rm{F}}$ ，从LP顶层开始逐层由上到下进行逆推式(10)，就可以得到重建的高斯金字塔。由式(11)表示，最后，一直代入得到 ${{S}}_{\rm{0}}^{\rm{F}}$ ，就是所得LP数据融合图像。

$\left. \begin{aligned} & {{{S}}_{L - 1}^{\rm{F}} = {{P}}_{L - 1}^{\rm{F}} + {\rm{expand}}\left({{S}}_L^{\rm{F}}\right),\ 0 \le L < Q}\\ & {{{P}}_Q^{\rm{F}} = {{S}}_Q^{\rm{F}},\qquad\qquad\qquad\qquad\quad\ L = Q} \end{aligned} \right\}$

(11)

2.3 多尺度小波变换数据融合

小波变换的多尺度特性，即在大尺度时，观察到图像的轮廓，在小尺度的空间里，则可以观察图像的细节^[26]。根据mallat快速算法^[26]，可以做二维WT，将VV, HH, VH进行图像分解，得到不同频带范围的图像，将对应频带的部分进行融合，再重构即可得到FP-GPR数据融合的结果。以VV为例，进行mallat小波变换方法分解，如式(12)所示

$\left. \begin{aligned} & {\bf{V}}{{\bf{V}}_{j + 1}}\left( {m,n} \right) = \mathop \sum \limits_{x,y} {h^*}\left( {x - 2m} \right){h^*}\left( {y - 2n} \right)\\ & \qquad\qquad\qquad\quad\cdot {\bf{V}}{{\bf{V}}_j}\left( {x,y} \right)\\ & {\bf{VV}}_{j + 1}^{{\rm{LH}}}\left( {m,n} \right) = \mathop \sum \limits_{x,y} {h^*}\left( {x - 2m} \right){g^*}\left( {y - 2n} \right)\\ & \qquad\qquad\qquad\quad\cdot{\bf{V}}{{\bf{V}}_j}\left( {x,y} \right)\\ & {\bf{VV}}_{j + 1}^{{\rm{HL}}}\left( {m,n} \right) = \mathop \sum \limits_{x,y} {g^*}\left( {x - 2m} \right){h^*}\left( {y - 2n} \right)\\ & \qquad\qquad\qquad\quad\cdot{\bf{V}}{{\bf{V}}_j}\left( {x,y} \right)\\ & {\bf{VV}}_{j + 1}^{{\rm{HH}}}\left( {m,n} \right) = \mathop \sum \limits_{x,y} {g^*}\left( {x - 2m} \right){g^*}\left( {y - 2n} \right)\\ & \qquad\qquad\qquad\quad\cdot{\bf{V}}{{\bf{V}}_j}\left( {x,y} \right) \end{aligned} \right\}$

(12)

其中，j表示小波分解的层数， ${\bf{VV}}_j$ 表示小波分解j层的原始近似图像，j=0时为原始图像。h和g 分别表示低通滤波器和高通滤波器，*表示共轭反转。 ${{V}}{{{V}}_{j + 1}}$ 为对 ${\bf{VV}}_j$ 在水平方向降采样后做低通滤波，再在垂直方向降采样后做低通滤波，代表着图像的低频部分，也是下一级的原始图像； ${\bf{VV}}_{j + 1}^{{\rm{LH}}}$ 为对 ${\bf{VV}}_j$ 数据先在水平方向降采样后做低通滤波，再在垂直方向降采样后做高通滤波，代表着图像在垂直方向的高频信息； ${\bf{VV}}_{j + 1}^{{\rm{HL}}}$ 为对 ${\bf{VV}}_j$ 数据先在水平方向降采样后做高通滤波，再在垂直方向降采样后做低通滤波，代表着图像在水平方向的高频信息； ${\bf{VV}}_{j + 1}^{{\rm{HH}}}$ 为对 ${\bf{VV}}_j$ 数据在水平方向降采样后做高通滤波，再在垂直方向降采样后做高通滤波，代表着图像对角线的高频信息。进行多层之后就是将图像的低频部分继续进行上述操作，最后分解J次之后，会得到关于VV的一个低频部分，和3J个高频部分。

之后与LP相似，对HH和VH进行相同层数的小波分解，取3组数据相同频带的分解部分进行融合，如 ${\bf{VV}}_{\rm{2}}^{{\rm{HL}}},{\bf{HH}}_{\rm{2}}^{{\rm{HL}}},{\bf{VH}}_{\rm{2}}^{{\rm{HL}}}$ 进行融合，不同部分不同规则进行融合，对高频部分取最大值，低频取平均值，得到融合图像，最后进行小波逆变换进行重构，如式(13)所示，最后一直推到 ${{F}}_0$ 即为数据融合后的结果。

$\begin{split} {{{F}}_j}\left( {x,y} \right) =\,& \mathop \sum \limits_{m,n} h\left( {x - 2m} \right)h\left( {y - 2n} \right){{{F}}_{j + 1}}\left( {m,n} \right) \\ &+ \mathop \sum \limits_{m,n} h\left( {x - 2m} \right)g\left( {y - 2n} \right){{F}}_{j + 1}^{{\rm{LH}}}\left( {m,n} \right)\\ & + \mathop \sum \limits_{m,n} g\left( {x - 2m} \right)h\left( {y - 2n} \right){{F}}_{j + 1}^{{\rm{HL}}}\left( {m,n} \right) \\ & + \mathop \sum \limits_{m,n} g\left( {x - 2m} \right)g\left( {y - 2n} \right){{F}}_{j + 1}^{{\rm{HH}}}\left( {m,n} \right) \end{split}$

(13)

3. 室内实验和讨论

为了检测3种FP-GPR数据融合方法的效果和对应3种极化散射机制地下目标体的成像效果，本文选取了3种典型的金属目标体，分别是对应单次散射的金属板，二次散射的金属二面角，体散射的金属多分支散射体，如图2所示。板的长宽分别是35 cm和20 cm。二面角是由两个摆成角度为90º的金属板构成的，在两个板的交际处具有最大的二次散射。多分支散射体的长度大约为40 cm。将这3种目标体分别埋进实验室的干沙中，深度分别为23 cm, 32 cm, 25 cm，并由实验室搭建的FP-GPR系统进行测量^[30]，如图3所示。测线共有99个测点，测点间距为1 cm，样本点数为1024个，选择的频带范围为800 MHz～4.5 GHz。

图 2 金属目标体

Figure 2. Metallic targets

下载: 全尺寸图片幻灯片

图 3 FP-GPR系统

Figure 3. FP-GPR system

下载: 全尺寸图片幻灯片

本文对FP-GPR数据进行预处理，用傅里叶逆变换将频率域数据转变为时间域，都进行去直达波处理。处理之后3种目标体图像如图4—图6所示。对于单散射目标体，如图4所示，VV极化和HH极化可以清晰反映出目标体的位置，而VH极化虽然较杂乱，但仍可以看到目标体的位置；对于二次散射目标体，如图5所示，VV极化可以清晰看到目标体的整体反射剖面形状，而HH极化更突出的是二次散射的位置，即二面角的交界处，VH极化更多体现的是目标体反射剖面的左侧；对于体散射目标体，如图6所示，VV极化和HH极化的目标体反射剖面不清晰，而VH极化可以更清晰看到目标体的反射情况。这表明需要数据融合，将3种极化的不同特点进行融合，还需要找到更适合不同极化散射机制的方法。

图 4 板的FP-GPR图像

Figure 4. FP-GPR image of plate

下载: 全尺寸图片幻灯片

图 5 二面角的FP-GPR图像

Figure 5. FP-GPR image of dihedral

下载: 全尺寸图片幻灯片

图 6 多分支散射体的FP-GPR图像

Figure 6. FP-GPR image of multi-branch scatterer

下载: 全尺寸图片幻灯片

最后，本文进行数据融合。将加权平均融合、PCA融合、LP融合和WT融合的适应性进行了比较，通过比较寻找更适应3种不同极化散射机制的方法。对于加权平均融合，为了方便对权值系数都选择了1做平均，而其余3种融合方法根据前面理论部分所述进行计算，LP和WT均选择分解4层。为了突出目标体位置，本文使用了偏移成像的方法来处理四种融合后图像，偏移公式^[4,9]如式(14)所示

$s(x,z) = \frac{1}{{2{{\pi }}}}\iint \frac{{\cos \theta }}{{{v_{{\rm{rms}}}}r}}\frac{\partial }{{\partial t}}{{{S}}_{\rm{F}}}(x,t){\rm{d}}x$

(14)

其中，v_rms表示均方根速度，r和t表示测点(x, 0)和图像点s(x, z)之间的距离和传播时间，θ表示传播方向与垂直方向夹角， ${{S}}_{\rm{F}}$ 表示融合后数据。本文使用瞬时振幅为主梯度为辅来判别这几种数据融合方法的效果，瞬时振幅由希尔伯特变换求得。瞬时振幅代表着整个图像中振幅的大小，可以突出异常体的位置。梯度公式由文献[10]中改变而得，如式(15)所示

$\begin{split} {{G}} =\,& \frac{1}{{(M - 1)(N - 1)}}\\ & \cdot\sqrt {\left({{\left(\frac{{\partial {{{S}}_{\rm{F}}}(x,z)}}{{\partial x}}\right)}^2} + {\left(\frac{{\partial {{{S}}_{\rm{F}}}(x,z)}}{{\partial z}}\right)^2}\right)\Bigr/2} \end{split}$

(15)

其中，M与N表示行数与列数， ${{S}}_{\rm{F}}$ 为融合图像的数值。梯度公式表示图像值与附近其他值差异性的大小，可以突出目标体处的异常。结果如图7—图15所示。为了方便比较，色标以及梯度和瞬时振幅里的垂向轴是相同的。在肉眼无法辨别峰值大小的时候，做了3种目标体瞬时振幅和梯度的最大值表格，如表1、表2所示。

图 7 板偏移后融合图像

Figure 7. Fusion images of plate after migration

下载: 全尺寸图片幻灯片

图 8 板偏移后融合瞬时振幅图

Figure 8. Fusion instantaneous amplitude images of plate after migration

下载: 全尺寸图片幻灯片

图 9 板偏移后融合梯度图

Figure 9. Fusion gradient images of plate after migration

下载: 全尺寸图片幻灯片

图 10 二面角偏移后融合图像

Figure 10. Fusion images of dihedral after migration

下载: 全尺寸图片幻灯片

图 11 二面角偏移后融合瞬时振幅图

Figure 11. Fusion instantaneous amplitude images of dihedral after migration

下载: 全尺寸图片幻灯片

图 12 二面角偏移后融合梯度图

Figure 12. Fusion gradient images of dihedral after migration

下载: 全尺寸图片幻灯片

图 13 多分支散射体偏移后融合图像

Figure 13. Fusion images of multi-branch scatterer after migration

下载: 全尺寸图片幻灯片

图 14 多分支散射体偏移后融合瞬时振幅图

Figure 14. Fusion instantaneous amplitude images of multi-branch scatterer after migration

下载: 全尺寸图片幻灯片

图 15 多分支散射体偏移后融合梯度图

Figure 15. Fusion gradient images of multi-branch scatterer after migration

下载: 全尺寸图片幻灯片

表 1 瞬时振幅最大值

Table 1. Max of instantaneous amplitude

目标体	加权平均	PCA	LP	WT
板	0.0066	0.0150	0.0134	0.0183
二面角	0.0031	0.0119	0.0094	0.0100
多分支散射体	3.0135×10^–4	8.707×10^-4	8.6279×10^–4	8.7215×10^–4

下载: 导出CSV

| 显示表格

表 2 梯度最大值

Table 2. Max of gradient

目标体	加权平均	PCA	LP	WT
板	8.8737×10^–9	2.0838×10^–8	1.9288×10^–9	9.5532×10^–8
二面角	9.0147×10^–9	1.6597×10^–8	3.5484×10^–8	6.0511×10^–8
多分支散射体	9.0209×10^–10	2.3254×10^–9	2.4932×10^–9	3.8864×10^–9

下载: 导出CSV

| 显示表格

对于单散射目标体，如图7所示，4种方法都可以体现出地下目标体的位置。因为在单次散射目标体中，VV在FP-GPR中占有主体地位，所以另3种融合方法在图像上与加权融合方法无明显区别。它们都能看到目标体的反射剖面，以及极化信息是单次散射。为了更进一步比较，以瞬时振幅为主梯度为辅的方法，如图8、图9所示，我们看到PCA融合和WT融合瞬时振幅较大，LP融合次之。在梯度中WT融合比PCA和LP融合的值大很多，所以单次散射目标体选择WT融合方法。

对于二次散射目标体，如图10所示，加权平均融合只有较弱的反射剖面，其它3种有较强剖面反射，在二面角交际处有更突出能量，这个位置体现着二次散射的位置即二面角的极化信息。进一步比较，选择瞬时振幅和梯度，如图11、图12所示，瞬时振幅中，在二次散射位置即交际处，PCA融合有单一最突出的峰值，LP融合是两个突出峰值，而WT融合是多个峰值导致信息较杂乱，而加权平均融合在交际处和图像两侧有较弱的幅值；在梯度图像中，加权平均融合、PCA融合和LP融合的梯度峰值在二次散射的位置均较小，而WT融合的梯度峰值形成多个峰值无法突出目标体。以瞬时振幅为主的原则，二次散射目标体选取PCA融合。

对于体散射目标体，如图13所示，加权平均融合的目标体反射剖面不清晰，是因为融合中VV和HH掩盖了只有VH可以清晰得到的反射信号，而其余3种方法都有明显反射剖面。进一步比较，选择瞬时振幅和梯度，如图14、图15，在瞬时振幅中，加权融合有几个较小峰值，无法突出目标体信息，而PCA融合和LP融合有两个突出位置的峰值，如表1所示，与WT融合的峰值大小近似，WT融合却有多个峰值突出，都体现体散射目标体的位置；在梯度图像中，加权融合最小，无法反映目标体位置；PCA融合与LP融合较大，可以反映目标体的位置，如表2所示LP融合的梯度值稍高于PCA融合；而WT融合信息较为杂乱，无法反映出目标体的有效信息。综上，体散射目标体选取LP融合方法。

对于未知散射机制的目标体，本文通过瞬时振幅选取在不同散射机制中表现的效果均较好的数据融合方法。单次散射目标体中，PCA融合和WT融合在目标体位置具备最大的瞬时振幅，LP融合次之；二次散射目标体中，PCA, LP和WT融合均在二次散射位置具有最大瞬时振幅，三者相比PCA融合具有唯一突出峰值；体散射目标体中，PCA与LP融合瞬时振幅能量大小相似，WT融合略低。综上，面对未知目标体时我们优先选择PCA融合。

4. 冰裂缝实验与讨论

在冰面上本文使用FP-GPR系统进行冰层裂缝探测如图16所示，得到冰层的FP-GPR数据，将其进行数据融合处理。测线垂直于冰裂缝摆放，位于测线中点处。测线共有101个测点，测点间距为1 cm，样本点数为1024个，选择的频带范围为1～4 GHz。进行预处理得到的FP-GPR图像如图17所示，由于天线馈电点过高，在天线内部传到冰表面有一定的距离，到8 ns处即为冰的表面。VV极化和HH极化在图像中间，即50 cm处均有反射双曲线，且由上至下能量逐渐衰减，这与冰裂缝存在位置吻合；且VH极化在50 cm处存在明显的相位断层，推断是由冰层裂缝引起的，本文需要数据融合的方法将3种不同极化方式进行融合，得到具备3种极化信息且分辨率更高的冰裂缝FP-GPR图像。

图 16 冰裂缝实验

Figure 16. Ice crack experiment

下载: 全尺寸图片幻灯片

图 17 冰裂缝FP-GPR数据图像

Figure 17. FP-GPR image of ice crack

下载: 全尺寸图片幻灯片

由于前文已经选择了PCA融合作为未知散射机制目标体的融合方法，所以本文对3种极化数据进行加权平均融合、PCA融合，并进行偏移成像处理。通过瞬时振幅和梯度进行对比，证明PCA融合的可靠性。为方便比较，图像色标均保持一致。结果如图18所示，PCA融合可以清晰得到冰裂缝的位置图像，在图像50 cm, 8 ns处有较为明显的能量集中，数据融合突出了冰裂缝具备最强反射的位置，且随着深度的增加能量逐渐衰减，比加权平均融合有更好的图像清晰度。由瞬时振幅图像可见，如图19所示，PCA融合在冰裂缝位置具备明显的峰值，且明显高于加权平均融合。同时比较梯度图像，如图20所示，PCA融合在冰裂缝位置有更高的梯度值。由此得出，在实际数据及未知散射机制的目标体上，PCA融合可得到很好的融合图像，比原始3种极化图像具备更突出的反射特征，强于加权融合方法。

图 18 冰裂缝偏移后融合图像

Figure 18. Fusion images of ice crack after migration

下载: 全尺寸图片幻灯片

图 19 冰裂缝偏移后融合瞬时振幅图

Figure 19. Fusion instantaneous amplitude images of ice crack after migration

下载: 全尺寸图片幻灯片

图 20 冰裂缝偏移后融合梯度图

Figure 20. Fusion gradient images of ice crack after migration

下载: 全尺寸图片幻灯片

5. 结论

本文将主成分分析、拉普拉斯金字塔和小波变换分别应用于全极化探地雷达数据融合中，均可以取得较好的融合效果，融合图像具备更清晰的几何图像特征。此外，引入了瞬时振幅和梯度对3种融合方法与已有的加权平均融合进行比较，得出了3种方法均强于加权平均融合，以及3种不同融合方法适应不同散射机制目标体的结论。对于已知散射机制目标体，WT融合更适合单散射目标体，PCA融合更适合二次散射目标体，LP融合更适合体散射目标体；对于未知散射机制目标体，选择了PCA融合。之后进行未知散射机制的冰裂缝实际数据采集，可以发现，PCA融合可以得到很好的实际数据融合图像，且强于加权平均融合方法。综上，融合方法集合了目标体的几何图像特征和不同的散射极化信息，可以得到更高分辨率的GPR图像。

图 1 载机运动模型示意图

Figure 1. Schematic diagram of the movement model of the carrier aircraft

下载: 全尺寸图片幻灯片

图 2 目标跟踪场景

Figure 2. Target tracking scene

下载: 全尺寸图片幻灯片

图 3 飞行速度优化结果

Figure 3. Flight speed optimization results

下载: 全尺寸图片幻灯片

图 4 飞行朝向角优化结果

Figure 4. Flight heading angle optimization results

下载: 全尺寸图片幻灯片

图 5 辐射功率优化结果

Figure 5. Transmit power optimization results

下载: 全尺寸图片幻灯片

图 6 驻留时间优化结果

Figure 6. Dwell time optimization results

下载: 全尺寸图片幻灯片

图 7 发射信号高斯脉冲长度优化结果

Figure 7. Transmit signal Gaussian pulse length optimization results

下载: 全尺寸图片幻灯片

图 8 发射信号带宽优化结果

Figure 8. Transmit signal bandwidth optimization results

下载: 全尺寸图片幻灯片

图 9 ARMSE对比结果

Figure 9. Comparison results of ARMSE

下载: 全尺寸图片幻灯片

图 10 不同被截获概率阈值的RMSE对比结果

Figure 10. Comparison results of RMSE with different intercept probability thresholds

下载: 全尺寸图片幻灯片

表 1 粒子群算法求解模型(23)

Table 1. Particle swarm algorithm to solve the model (23)

　步骤1：初始化

$Q$ 个粒子的初始位置和速度，初始位置代表各载
　　　　机飞行速度和朝向角；定义权重系数

$\zeta$ ，常数

${c_1}$ 和

${c_2}$ ，最
　　　　大迭代次数

${L_{\max }}$ ；

　步骤2：根据机载组网雷达辐射参数与各载机飞行参数之间的关
　　　　系，在满足约束条件

${p_{n,k} } \le {p_{ {\text{th} } } },\forall n$ 情况下，计算每个粒
　　　　子当前位置下的最优雷达辐射参数；
　步骤3：根据优化目标

$\mathbb{F}\left( {{\boldsymbol{X}}_{\left. k \right|k - 1}^{ {\text{tgt} } }{{,} }{{\boldsymbol{P}}_{ {\text{t} },k} }{{,} }{{\boldsymbol{T}}_{ {\text{d} },k} } } \right){\text{ } }$ 计算粒子适应度；

　步骤4：更新全局最优粒子和个体最优粒子：
　步骤5：根据式(28)更新粒子的速度与位置；

　步骤6：检验结束条件，若结果收敛或达到最大迭代次数，则迭
　　　　代结束，输出全局最优粒子；否则令

$l = l + 1$ ，转入步
　　　　骤2，继续迭代循环。

下载: 导出CSV

表 2 机载组网雷达参数设置

Table 2. Parameter setting of airborne radar network

参数	数值	参数	数值
${G_{\text{t}}}$	$36\;{\text{dB} }$	${B_{\text{r}}}$	$1\;{\text{MHz} }$
${G_{\text{r}}}$	$35\;{\text{dB} }$	${F_{\text{r}}}$	$3\;{\text{dB}}$
${G_{{\text{RP}}}}$	$45$	${f_{\text{c}}}$	$12\;{\text{GHz}}$
${\bar P _{\min } }$	$0$	${\bar P _{\max }}$	$5\;{\text{kW}}$
${\bar \theta _{\max } }$	${15^ \circ }$	$k$	$1.38 \times {10^{ - 23}}{{\text{J}} \mathord{\left/ {\vphantom {{\text{J}} {\text{K}}}} \right. } {\text{K}}}$
${\bar v _{\min } }$	$0.1\;{ { {\text{km} } } / {\text{s} } }$	${\bar v _{\max }}$	$0.4\;{ { {\text{km} } } / {\text{s} } }$
${T_{\text{r}}}$	$5 \times {10^{ - 4} }\;{\text{s} }$	${\bar T _{\max }}$	$2.5 \times {10^{ - 2} }\;{\text{s} }$

下载: 导出CSV

表 3 截获接收机参数设置

Table 3. Parameter setting of intercept receiver

参数	数值	参数	数值
$p'_{{\rm{fa} } }$	${10^{ - 8}}$	${G_{{\text{IP}}}}$	$2$
${F_{\text{I}}}$	$6\;{\text{dB} }$	${T_{\text{I}}}$	$2\;{\text{s} }$
${G_{\text{I}}}$	$10\;{\text{dB} }$	${B_{\text{I}}}$	$40\;{\text{GHz} }$

下载: 导出CSV

表 4 机载组网雷达初始状态

Table 4. The initial state of airborne radar network

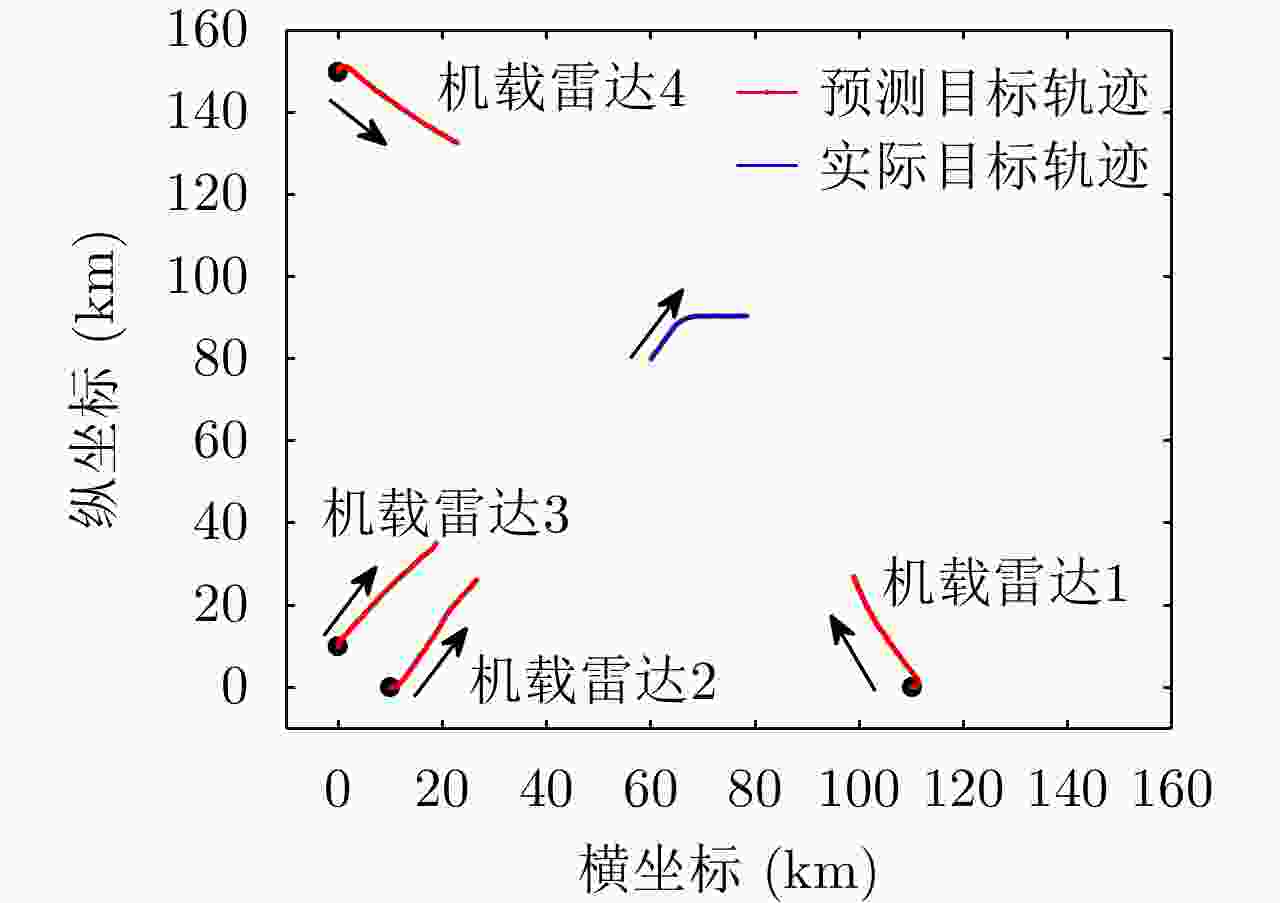
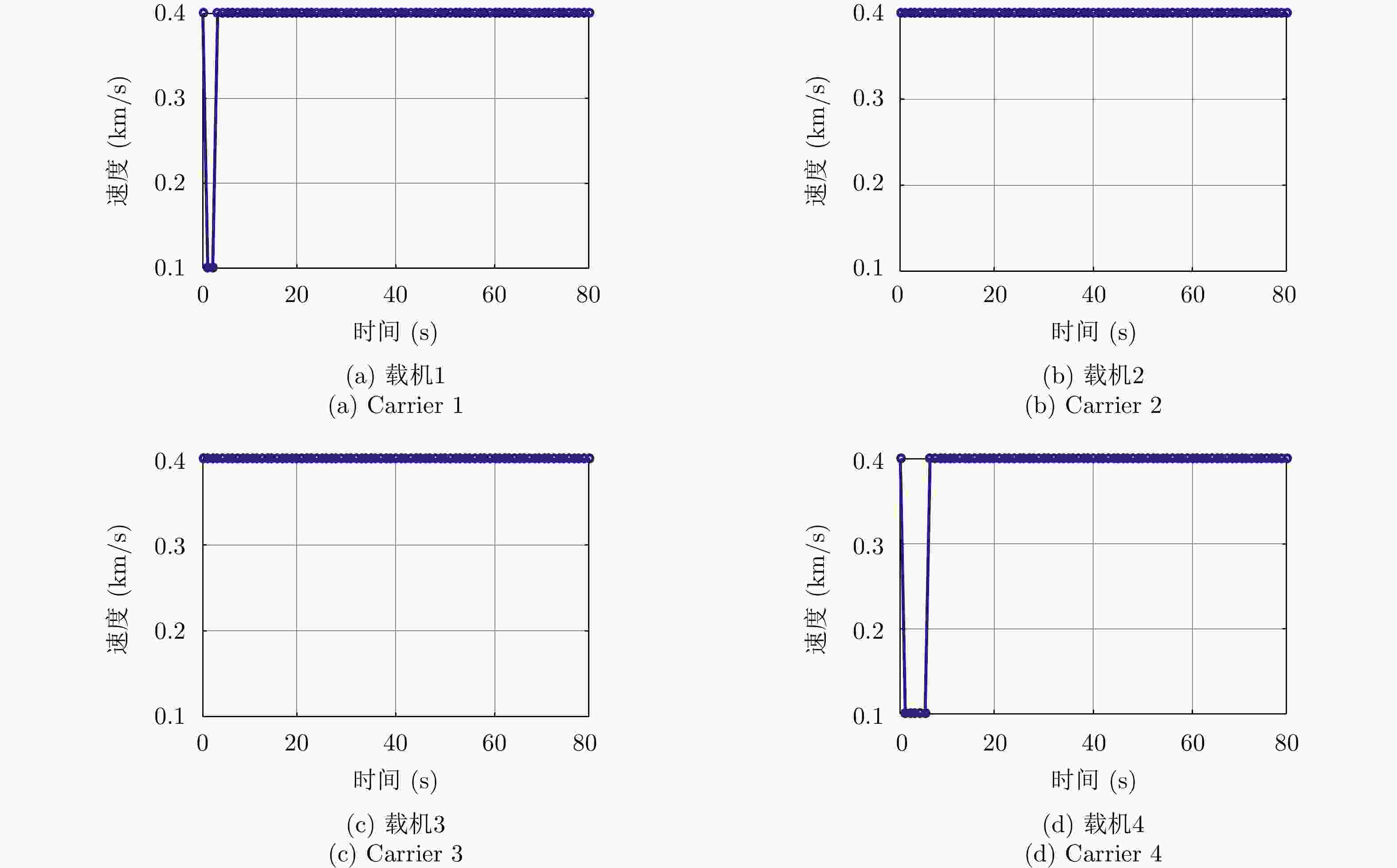
雷达编号	初始位置(km)	初始速度(km/s)	初始朝向角(°)
机载雷达1	[110,0]	0.4	0
机载雷达2	[10,0]	0.4	0
机载雷达3	[0,10]	0.4	90
机载雷达4	[0,150]	0.4	90

下载: 导出CSV

参考文献(34)

[1]	SKOLNIK M I, 左群声, 徐国良, 马林, 等译. 雷达系统导论[M]. 3版. 北京: 电子工业出版社, 2014: 191–199. SKOLNIK M I, ZUO Qunsheng, XU Guoliang, MA Lin, et al. translation. Introduction to Radar Systems[M]. 3rd ed. Beijing: Publishing House of Electronics Industry, 2014: 191–199.
[2]	刘宏伟, 严峻坤, 周生华. 网络化雷达协同探测技术[J]. 现代雷达, 2020, 42(12): 7–12. doi: 10.16592/j.cnki.1004-7859.2020.12.002 LIU Hongwei, YAN Junkun, and ZHOU Shenghua. Collaborative detection technology of netted radar[J]. Modern Radar, 2020, 42(12): 7–12. doi: 10.16592/j.cnki.1004-7859.2020.12.002
[3]	CHENG Ting, LI Shuyi, and ZHANG Jie. Adaptive resource management in multiple targets tracking for co-located multiple input multiple output radar[J]. IET Radar, Sonar & Navigation, 2018, 12(9): 1038–1045. doi: 10.1049/iet-rsn.2018.5153
[4]	张浩为, 谢军伟, 葛佳昂, 等. 基于波形调度的机动目标跟踪算法[J]. 电子学报, 2019, 47(3): 560–567. doi: 10.3969/j.issn.0372-2112.2019.03.007 ZHANG Haowei, XIE Junwei, GE Jiaang, et al. Maneuvering target tracking based on waveform scheduling[J]. Acta Electronica Sinica, 2019, 47(3): 560–567. doi: 10.3969/j.issn.0372-2112.2019.03.007
[5]	SUN Jun, LU Xiujuan, YUAN Ye, et al. Resource allocation for multi-target tracking in multi-static radar systems with imperfect detection performance[C]. 2020 IEEE Radar Conference, Florence, Italy, 2020: 1–6.
[6]	LI Xi, CHENG Ting, SU Yang, et al. Joint time-space resource allocation and waveform selection for the collocated MIMO radar in multiple targets tracking[J]. Signal Processing, 2020, 176: 107650. doi: 10.1016/j.sigpro.2020.107650
[7]	YUAN Ye, YI Wei, HOSEINNEZHAD R, et al. Robust power allocation for resource-aware multi-target tracking with colocated MIMO radars[J]. IEEE Transactions on Signal Processing, 2021, 69: 443–458. doi: 10.1109/TSP.2020.3047519
[8]	NGUYEN N H, DOĞANÇAY K, and DAVIS L M. Joint transmitter waveform and receiver path optimization for target tracking by multistatic radar system[C]. IEEE Workshop on Statistical Signal Processing (SSP), Gold Coast, Australia, 2014: 444–447.
[9]	孟令同. 机载平台相控阵雷达波束和路径资源管理算法研究[D]. [硕士论文], 电子科技大学, 2019. MENG Lingtong. Research on beam and path resource management algorithm of phased array radar on airborne platform[D]. [Master dissertation], University of Electronic Science and Technology of China, 2019.
[10]	DASDEMIR E, KÖKSALAN M, and ÖZTÜRK D T. A flexible reference point-based multi-objective evolutionary algorithm: An application to the UAV route planning problem[J]. Computers & Operations Research, 2020, 114: 104811. doi: 10.1016/j.cor.2019.104811
[11]	张哲, 吴剑, 代冀阳, 等. 基于改进A-Star算法的隐身无人机快速突防航路规划[J]. 航空学报, 2020, 41(7): 323692. doi: 10.7527/S1000-6893.2020.23692 ZHANG Zhe, WU Jian, DAI Jiyang, et al. Fast penetration path planning for stealth UAV based on improved A-Star algorithm[J]. Acta Aeronautica et Astronautica Sinica, 2020, 41(7): 323692. doi: 10.7527/S1000-6893.2020.23692
[12]	LU Xiujuan, YI Wei, and KONG Lingjiang. Joint online route planning and resource optimization for multitarget tracking in airborne radar systems[J]. IEEE Systems Journal, in press.
[13]	魏永超, 邓岚, 李涛, 等. 采用改进细菌觅食优化算法的无人机航迹规划[J]. 电讯技术, 2021, 61(5): 560–566. doi: 10.3969/j.issn.1001-893x.2021.05.006 WEI Yongchao, DENG Lan, LI Tao, et al. UAV track planning with improved bacterial foraging optimization algorithm[J]. Telecommunication Engineering, 2021, 61(5): 560–566. doi: 10.3969/j.issn.1001-893x.2021.05.006
[14]	廖文旭. 复杂环境下无人机航迹规划算法的研究[D]. [硕士论文], 电子科技大学, 2021. LIAO Wenxu. Research on path planning algorithm of unmanned aerial vehicle in complex environment[D]. [Master dissertation], University of Electronic Science and Technology of China, 2021.
[15]	PACE P E, 陈祝明, 江朝抒, 段锐, 译. 低截获概率雷达的检测与分类[M]. 2版. 北京: 国防工业出版社, 2012: 2–23. PACE P E, CHEN Zhuming, JIANG Chaoshu, and DUAN Rui, translation. Detecting and Classifying Low Probability of Intercept Radar[M]. 2nd ed. Beijing: National Defense Industry Press, 2012: 2–23.
[16]	时晨光, 周建江, 汪飞, 等. 机载雷达组网射频隐身技术[M]. 北京: 国防工业出版社, 2019: 1–23. SHI Chenguang, ZHOU Jianjiang, WANG Fei, et al. Radio Frequency Stealth Technology for Airborne Radar Network[M]. Beijing: National Defense Industry Press, 2019: 1–23.
[17]	YAN Junkun, PU Wenqiang, LIU Hongwei, et al. Robust chance constrained power allocation scheme for multiple target localization in colocated MIMO radar system[J]. IEEE Transactions on Signal Processing, 2018, 66(15): 3946–3957. doi: 10.1109/TSP.2018.2841865
[18]	SHI Chenguang, ZHOU Jianjiang, and WANG Fei. Adaptive resource management algorithm for target tracking in radar network based on low probability of intercept[J]. Multidimensional Systems and Signal Processing, 2018, 29(4): 1203–1226. doi: 10.1007/s11045-017-0494-8
[19]	DAI Jinhui, YAN Junkun, WANG Penghui, et al. Optimal resource allocation for multiple target tracking in phased array radar network[C]. 2019 International Conference on Control, Automation and Information Sciences (ICCAIS), Chengdu, China, 2019: 1–4.
[20]	赖作镁, 乔文昇, 古博, 等. 任务性能约束下传感器协同辐射控制策略[J]. 系统工程与电子技术, 2019, 41(8): 1749–1754. doi: 10.3969/j.issn.1001-506X.2019.08.11 LAI Zuomei, QIAO Wensheng, GU Bo, et al. Research on sensor cooperative radiation control strategy under task performance constraints[J]. Systems Engineering and Electronics, 2019, 41(8): 1749–1754. doi: 10.3969/j.issn.1001-506X.2019.08.11
[21]	GHOREISHIAN M J, ANDARGOLI S M H, and PARVARI F. Power allocation in MIMO radars based on LPI optimisation and detection performance fulfilment[J]. IET Radar, Sonar & Navigation, 2020, 14(6): 822–832. doi: 10.1049/iet-rsn.2020.0037
[22]	时晨光, 丁琳涛, 汪飞, 等. 面向射频隐身的组网雷达多目标跟踪下射频辐射资源优化分配算法[J]. 电子与信息学报, 2021, 43(3): 539–546. doi: 10.11999/JEIT200636 SHI Chenguang, DING Lintao, WANG Fei, et al. Radio frequency stealth-based optimal radio frequency resource allocation algorithm for multiple-target tracking in radar network[J]. Journal of Electronics &Information Technology, 2021, 43(3): 539–546. doi: 10.11999/JEIT200636
[23]	KALMAN R E. A new approach to linear filtering and prediction problems[J]. Journal of Basic Engineering, 1960, 82(1): 35–45. doi: 10.1115/1.3662552
[24]	KERSHAW D J and EVANS R J. Optimal waveform selection for tracking systems[J]. IEEE Transactions on Information Theory, 1994, 40(5): 1536–1550. doi: 10.1109/18.333866
[25]	KERSHAW D J and EVANS R J. Waveform selective probabilistic data association[J]. IEEE Transactions on Aerospace and Electronic Systems, 1997, 33(4): 1180–1188. doi: 10.1109/7.625110
[26]	TICHAVSKY P, MURAVCHIK C H, and NEHORAI A. Posterior Cramer-Rao bounds for discrete-time nonlinear filtering[J]. IEEE Transactions on Signal Processing, 1998, 46(5): 1386–1396. doi: 10.1109/78.668800
[27]	VAN TREES H L, BELL K L, and WANG Yige. Bayesian Cramer-Rao bounds for multistatic radar[C]. International Waveform Diversity & Design Conference, Lihue, USA, 2006: 1–4.
[28]	YAN Junkun, LIU Hongwei, PU Wenqiang, et al. Joint beam selection and power allocation for multiple target tracking in netted colocated MIMO radar system[J]. IEEE Transactions on Signal Processing, 2016, 64(24): 6417–6427. doi: 10.1109/TSP.2016.2607147
[29]	刘永坚, 司伟建, 杨承志. 现代电子战支援侦察系统分析与设计[M]. 北京: 国防工业出版社, 2016: 43–47. LIU Yongjian, SI Weijian, and YANG Chengzhi. Analysis and Design of Reconnaissance Systems in Modern ESM[M]. Beijing: National Defense Industry Press, 2016: 43–47.
[30]	陈小龙, 薛永华, 张林, 等. 机载雷达系统与信息处理[M]. 北京: 电子工业出版社, 2021: 150–163. CHEN Xiaolong, XUE Yonghua, ZHANG Lin, et al. Airborne Radar System and Information Processing[M]. Beijing: Publishing House of Electronics Industry, 2021: 150–163.
[31]	温正, 孙华克. MATLAB智能算法[M]. 北京: 清华大学出版社, 2017: 67–79. WEN Zheng and SUN Huake. MATLAB Intelligent Algorithm[M]. Beijing: Tsinghua University Press, 2017: 67–79.
[32]	BOYD S, VANDENBERGHE L, 王书宁, 许鋆, 黄晓霖, 译. 凸优化[M]. 北京: 清华大学出版社, 2013: 1–10. BOYD S, VANDENBERGHE L, WANG Shuning, XU Yun, and HUANG Xiaolin, translation. Convex Optimization[M]. Beijing: Tsinghua University Press, 2013: 1–10.
[33]	刘宏强, 魏贤智, 李飞, 等. 基于射频隐身的雷达跟踪状态下单次辐射能量实时控制方法[J]. 电子学报, 2015, 43(10): 2047–2052. doi: 10.3969/j.issn.0372-2112.2015.10.025 LIU Hongqiang, WEI Xianzhi, LI Fei, et al. The real time control method of radar single radiation power based on RF stealth at the tracking[J]. Acta Electronica Sinica, 2015, 43(10): 2047–2052. doi: 10.3969/j.issn.0372-2112.2015.10.025
[34]	SHI Chenguang, WANG Fei, SALOUS S, et al. Joint transmitter selection and resource management strategy based on low probability of intercept optimization for distributed radar networks[J]. Radio Science, 2018, 53(9): 1108–1134. doi: 10.1029/2018RS006584.

施引文献

期刊类型引用(4)

1.	刘燕，万显荣，易建新. 基于数据失真的雷达通信一体化OFDM波形设计方法. 雷达学报. 2024(01): 160-173 . 本站查看
2.	布锦钶，李鹏飞，周鹏，周志一，曾祥祝，胡城志，孙兴赛，赵青，张文理. 基于杂波知识图谱驱动的空时自适应处理方法. 物联网技术. 2024(11): 122-126 . 百度学术
3.	张云骥，蔡玖良. 基于正负分频信号的测速与测距方法. 电子技术与软件工程. 2023(05): 76-82 . 百度学术
4.	刘柳，梁兴东，李焱磊，曾致远，唐海波. 一种基于分布式孔径的雷达通信一体化波形设计方法. 雷达学报. 2023(02): 297-311 . 本站查看

其他类型引用(8)

资源附件(0)

访问统计

图(10) / 表(4)

计量

文章访问数: 1112
HTML全文浏览量: 677
PDF下载量: 190
被引次数: 12

1. 引言
2. 全极化探地雷达数据融合理论
2.1 主成分分析数据融合
2.2 拉普拉斯金字塔数据融合
2.3 多尺度小波变换数据融合
3. 室内实验和讨论
4. 冰裂缝实验与讨论
5. 结论

面向目标跟踪的机载组网雷达辐射参数与航迹规划联合优化算法

DOI: 10.12000/JR22005

通讯作者:
时晨光 scg_space@163.com

计量

Joint Transmit Resources and Trajectory Planning for Target Tracking in Airborne Radar Networks

Corresponding author: SHI Chenguang, scg_space@163.com

1. 引言

2. 全极化探地雷达数据融合理论

2.1 主成分分析数据融合

2.2 拉普拉斯金字塔数据融合

2.3 多尺度小波变换数据融合

3. 室内实验和讨论

4. 冰裂缝实验与讨论

5. 结论

期刊类型引用(4)

其他类型引用(8)

计量

目录

1. 引言

2. 全极化探地雷达数据融合理论

2.1 主成分分析数据融合

2.2 拉普拉斯金字塔数据融合

2.3 多尺度小波变换数据融合

3. 室内实验和讨论

4. 冰裂缝实验与讨论

5. 结论

期刊介绍

联系我们

面向目标跟踪的机载组网雷达辐射参数与航迹规划联合优化算法

DOI: 10.12000/JR22005

通讯作者: 时晨光 scg_space@163.com

计量

出版历程

Joint Transmit Resources and Trajectory Planning for Target Tracking in Airborne Radar Networks

Corresponding author: SHI Chenguang, scg_space@163.com

1. 引言

2. 全极化探地雷达数据融合理论

2.1 主成分分析数据融合

2.2 拉普拉斯金字塔数据融合

2.3 多尺度小波变换数据融合

3. 室内实验和讨论

4. 冰裂缝实验与讨论

5. 结论

期刊类型引用(4)

其他类型引用(8)

计量

出版历程

目录

1. 引言

2. 全极化探地雷达数据融合理论

2.1 主成分分析数据融合

2.2 拉普拉斯金字塔数据融合

2.3 多尺度小波变换数据融合

3. 室内实验和讨论

4. 冰裂缝实验与讨论

5. 结论

期刊介绍

联系我们

通讯作者:
时晨光 scg_space@163.com