1.   引言

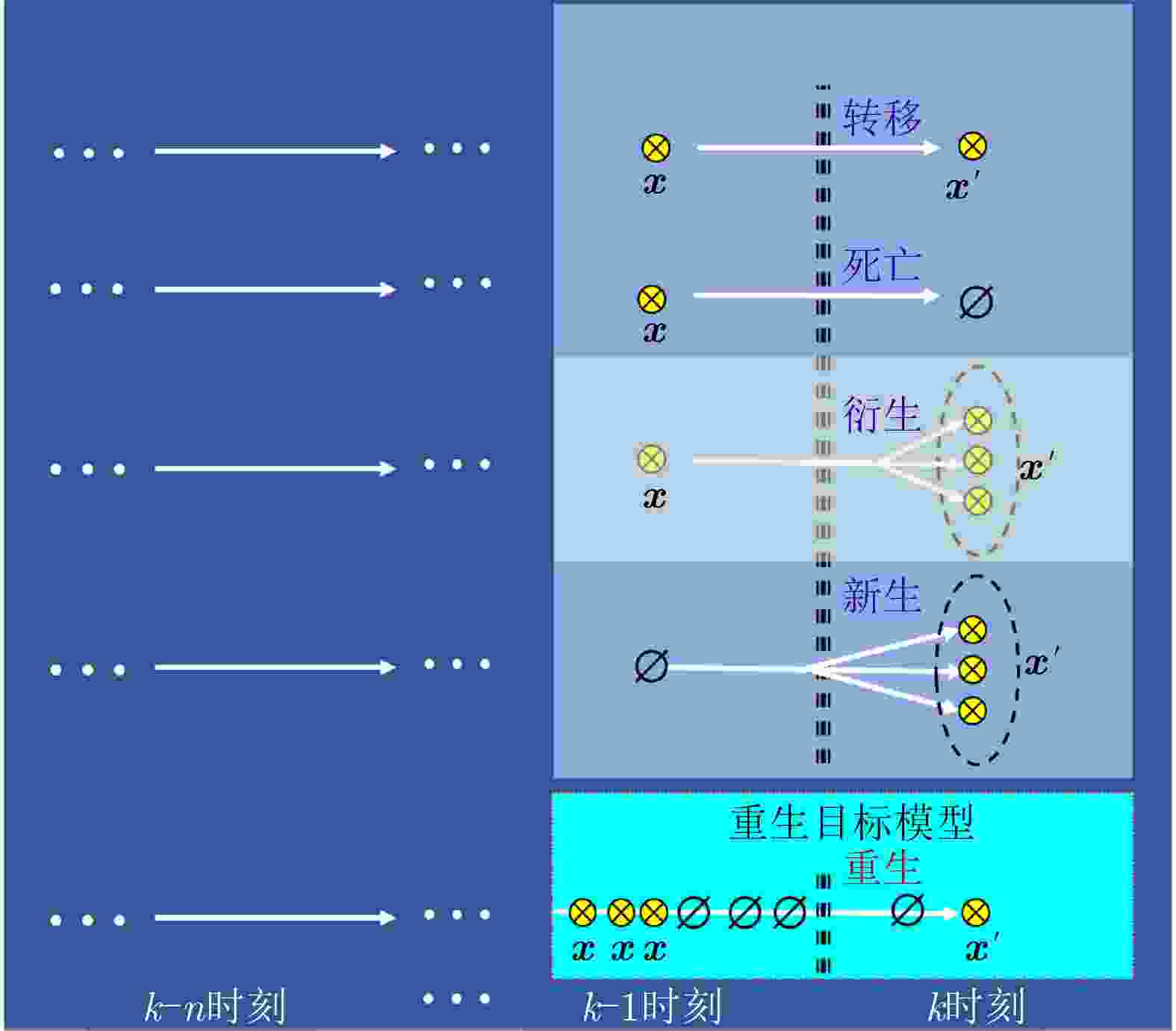
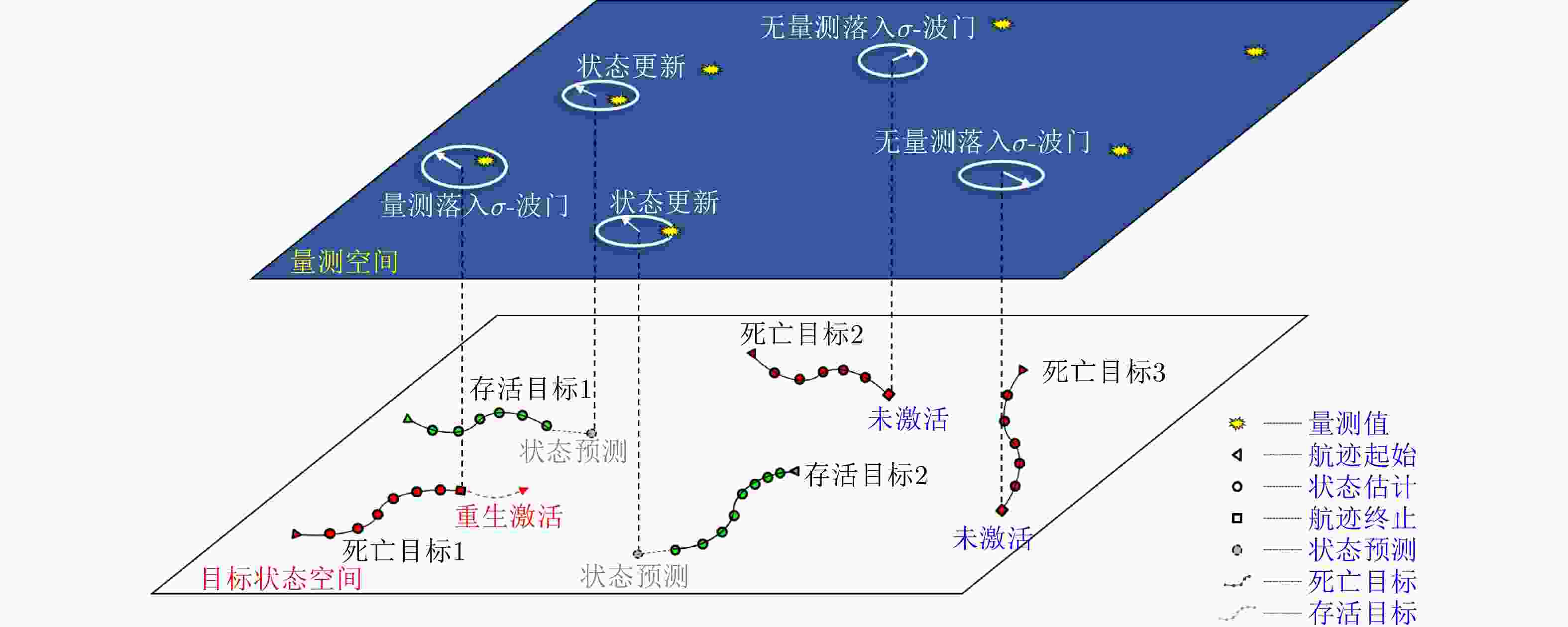
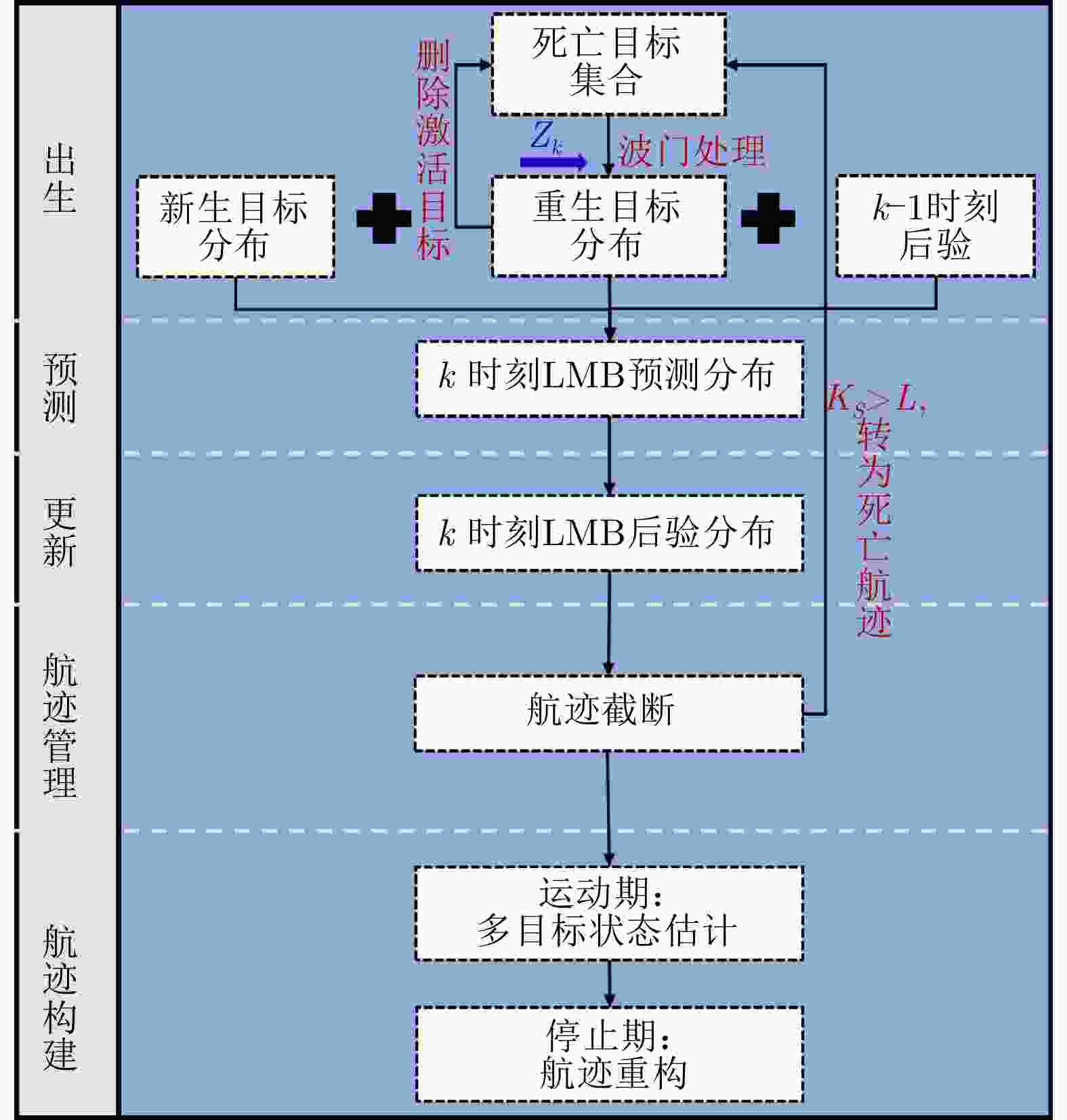
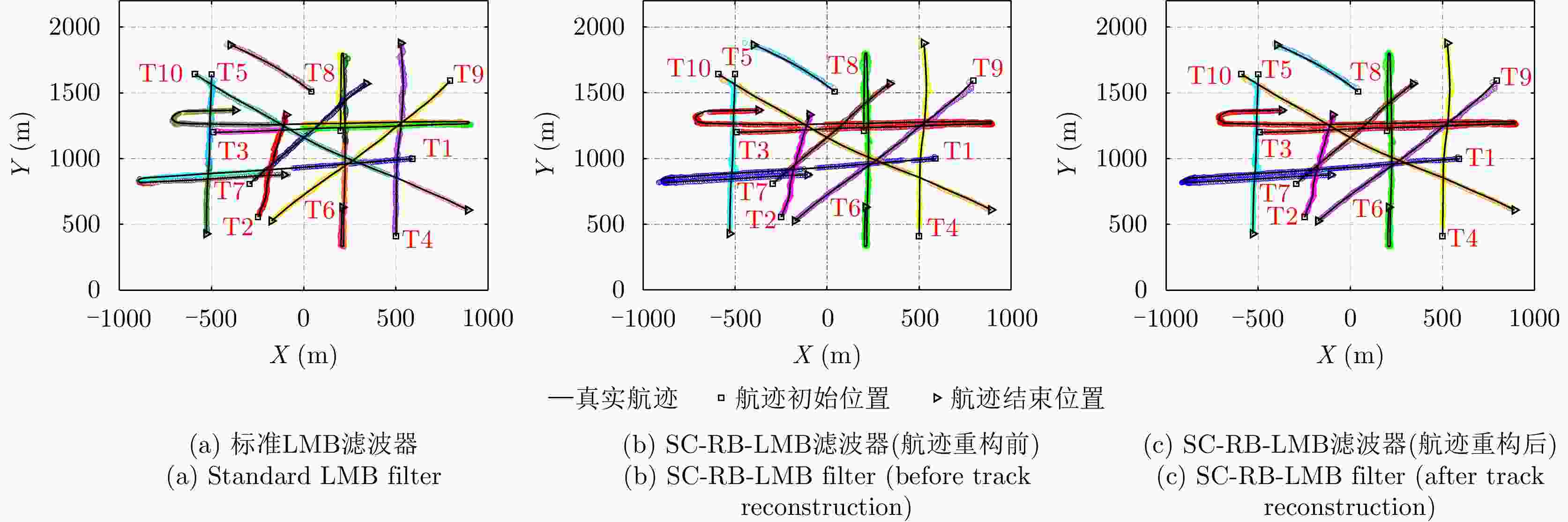
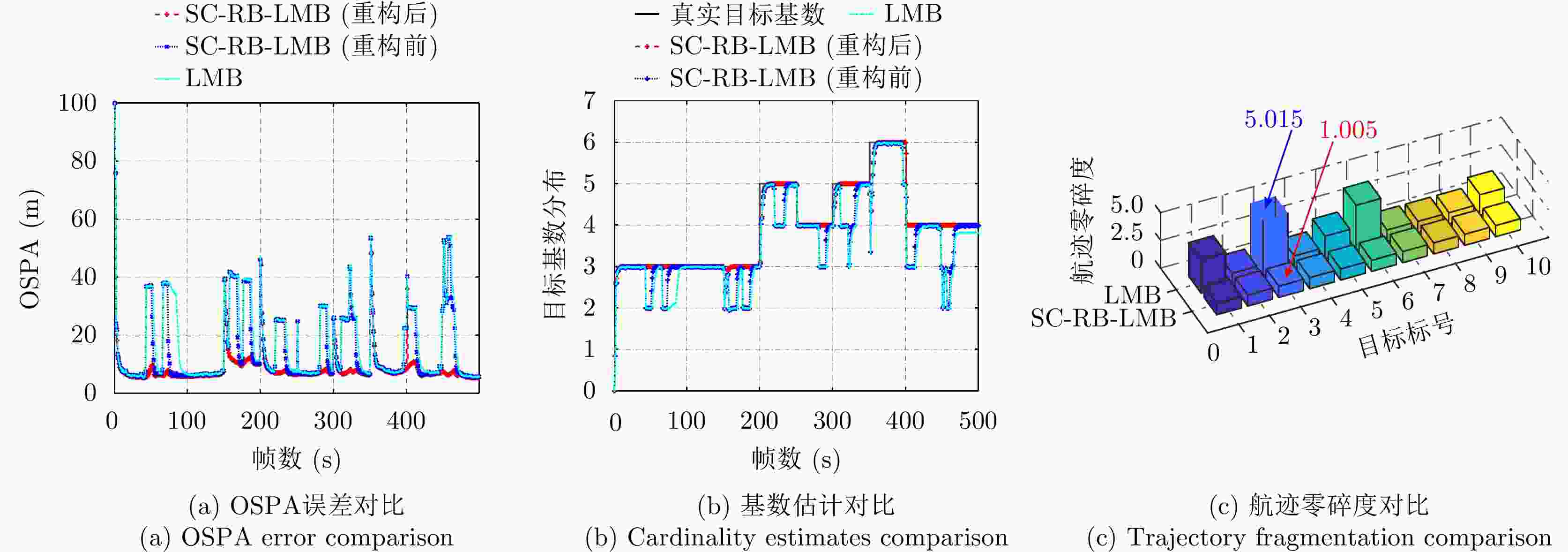
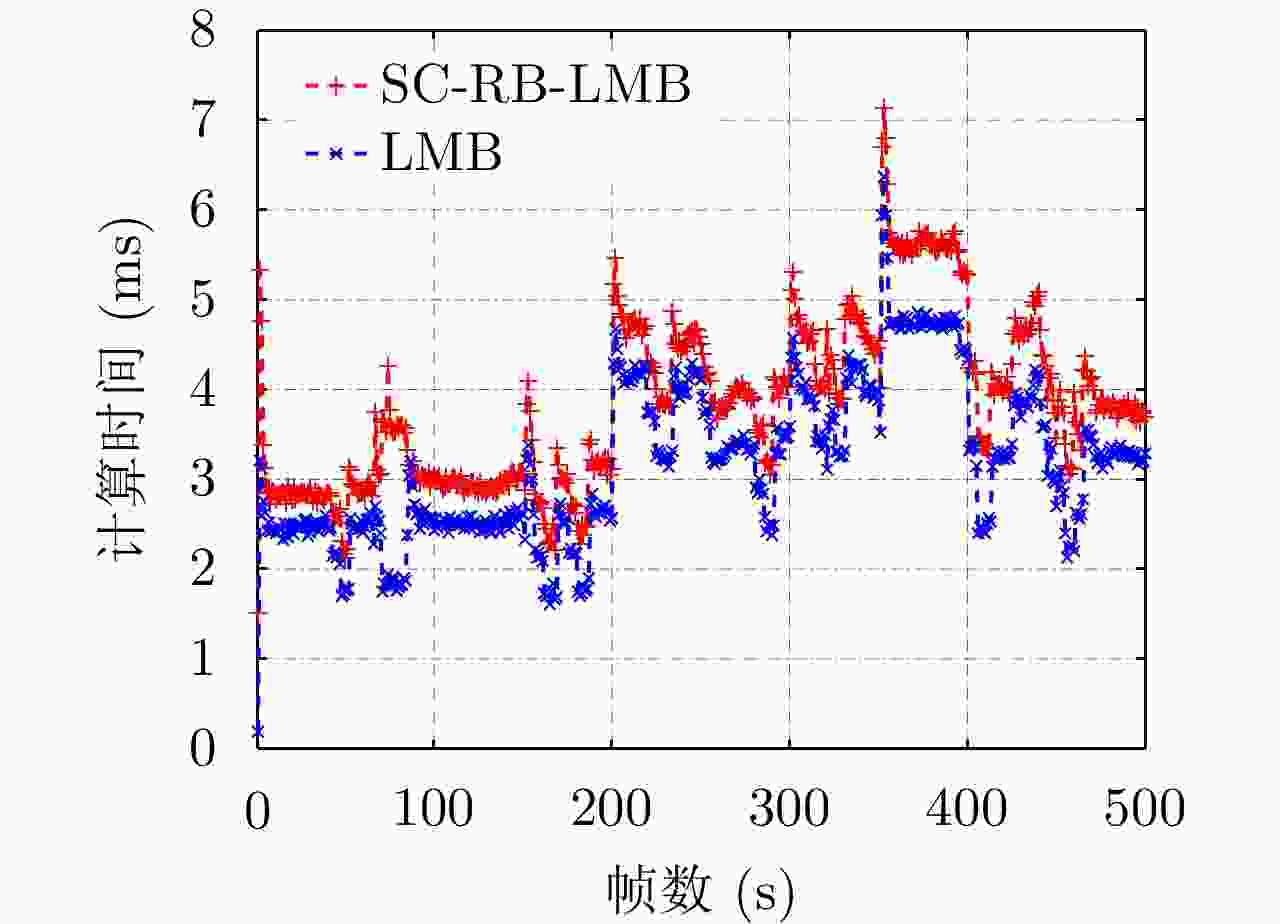
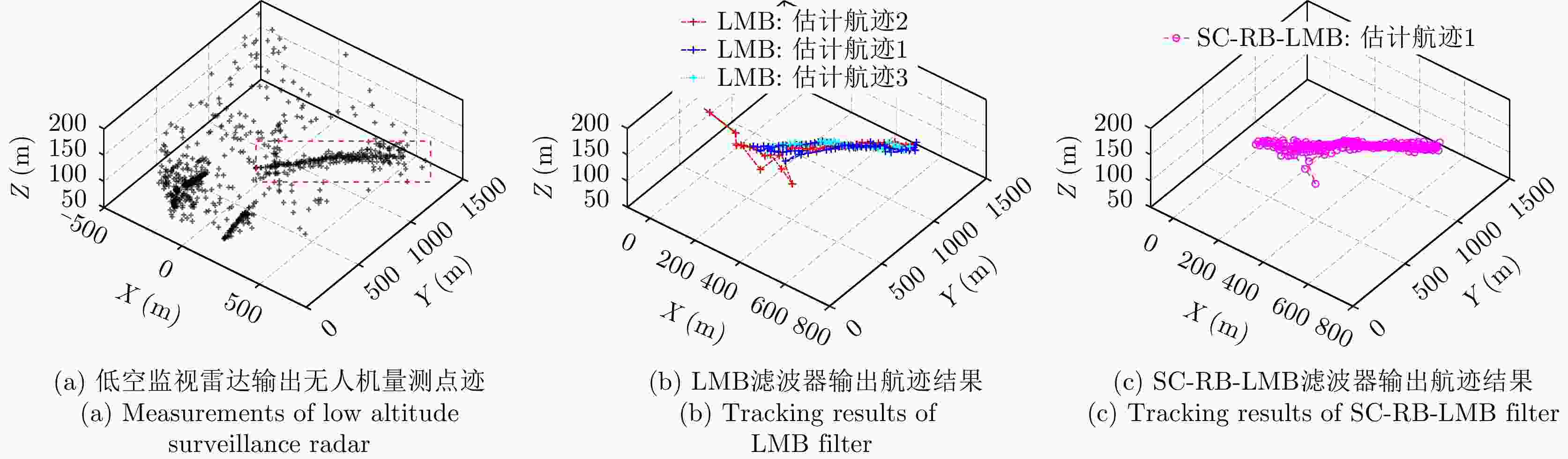
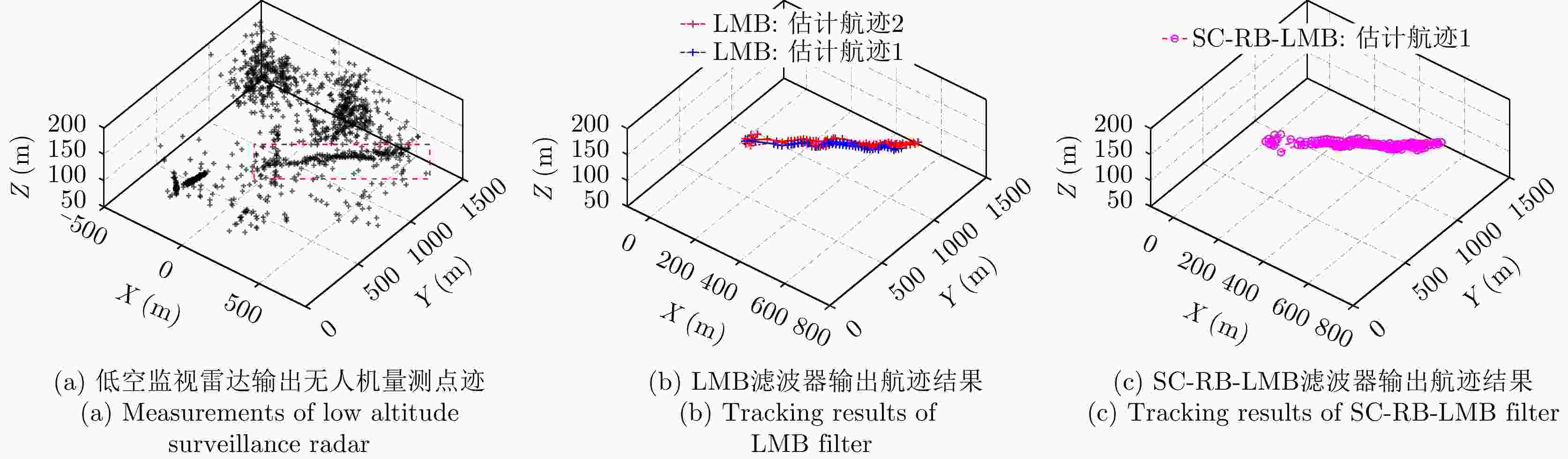
随着低空目标类型的不断增多、性能快速提升和低空作战环境的日益复杂，以二维/三维有源相控阵体制为代表的低空监视雷达^[1,2]在国土防御体系中扮演愈来愈重要的角色。以旋翼无人机为代表的低空小目标常采用低速“走-停”策略或利用障碍物掩护，躲避雷达追踪，对重要信息装备和战略要地进行点穴式打击或干扰。低速“走-停”策略是指目标利用自身的怠速运动，或构造与雷达的特定几何位置关系，使其回波落入雷达多普勒零频区域附近，在强地/海杂波掩护下，暂时消失于雷达视域内。典型低速“走-停”现象有无人机低速掉头、悬停或通过构造目标-雷达几何位置关系，使得径向速度趋于零。另一种情况下，目标可利用地面/海面障碍物，制造物理遮挡，也可短暂的消失于雷达视线当中。因此，这类目标能够多次消失-重返于雷达视域中，称之为“走-停-走”目标。“走-停-走”目标演化特性难以采用传统目标跟踪模型建模和描述，跟踪结果容易出现目标身份不连续、航迹碎片化等问题。碎片化航迹直接影响目标动态监视、意图预测和敌我识别的准确性，进而影响后续拦截打击的效能。因此，“走-停-走”目标连续稳健跟踪是低空监视雷达亟待解决的关键科学问题。

针对“走-停-走”目标跟踪问题，国内外学者已开展相关研究。2003年，加拿大麦克马斯特大学Kirubarajan等人^[3]在地面移动目标指示(Ground Moving Target Indicator, GMTI) 雷达体制下提出一种基于变结构交互多模型的“走-停-走”目标跟踪方法。该方法引入目标停止模型，避免了目标怠速或者停止状态下的航迹中断。2004年，美国康涅狄格大学Lin等人^[4]在文献[3]基础上提出一种基于多维分配的数据关联“走-停-走”目标跟踪方法，在动目标漏检概率${P_D} < 1$情况下，有效提升了该类型目标的正确跟踪率。2011年，美国康涅狄格大学Zhang等人^[5]提出基于状态依赖转移概率模型的目标跟踪方法。该方法将目标运动区分为高速状态与低速状态，在低速状态下引入停止模型，解决停止模型对常速目标的影响。2011年，英国QuinetiQ公司Hernandez等人^[6]提出了一种区分动目标漏检和静目标漏检的性能指标。利用该指标，提出的多假设跟踪(Multiple Hypotheses Tracking, MHT) 方法可实现强杂波环境下“走-停-走”目标的连续跟踪。2019年，国内哈尔滨工业大学Liu等人^[7]提出一种改进的多假设“走-停-走”目标跟踪方法。该方法利用目标动力学统计特性和模型转移概率修正传统MHT似然比，进一步提升MHT跟踪算法性能。2017年，STR (Systems & Technology Research)的Coraluppi等人^[8]提出了一种基于图的“走-停-走”目标轨迹关联分数量化方法，该方法避免了交互多模型方法对马尔科夫链模型的依赖性，降低了多假设跟踪算法的复杂度。上述方法主要集中在传统目标跟踪理论框架下，通过引入停止模态或假设来维持目标怠速或停止状态下航迹的连续性。

低空监视雷达面临时变/空变的强杂波探测环境，雷达量测呈现随机漏检、强杂波干扰等不确定性；且伴随着目标进入或离开监视场景、“走-停-走”目标多次往返雷达视域等随机事件，低空监视雷达探测目标个数具有未知且时变特性。因此，目标和量测信息难以通过传统基于向量随机变量的概率统计工具描述和建模。

随机集理论(Finite Set Statistics, FISST)^[9]的研究始于1994年。与传统向量统计理论不同，随机集理论将量测的不确定性和目标状态维度未知时变特性建模在点过程理论框架下，为多目标跟踪问题提供了统一的最优贝叶斯滤波框架。随后，基于合理近似，各国学者将最优理论解简化为可实现的工程解。现有基于随机集理论的多目标跟踪算法主要分为两类：一类是非标签随机集滤波器，包括概率假设密度(Probability Hypotheses Density, PHD)^[10]/基数均衡化概率假设密度(Cardinality Balanced Probability Hypotheses Density, CPHD)滤波器^[11]、多伯努利(Multi-Bernoulli, MB)滤波器^[12,13]等；另一类是标签随机集滤波器，如广义标签多伯努利(Generalized Labeled Multi-Bernoulli, GLMB)滤波器^[14,15]、标签多伯努利(Labeled Multi-Bernoulli, LMB)滤波器^[16,17]等。

目前，基于随机集理论研究“走-停-走”目标跟踪问题的文献比较有限。2019年，空军预警学院Xie等人^[18]针对多普勒盲区(Doppler Blind Zone, DBZ)下目标跟踪问题，引入最小探测速度(Minimum Detectable Velocity, MDV)模型，提出了基于多模型高斯混合PHD滤波器。2020年，空军预警学院Wu等人^[19]将MDV信息引入多模型GLMB滤波器中，可有效抑制多普勒盲区的遮蔽效应。然而，上述方法主要针对多普勒盲区导致的“走-停-走”问题，对于更普适的“走-停-走”问题(例如，障碍物遮挡导致的目标短暂消失)，该方法存在一定局限性。

与其他随机集滤波器相比，LMB滤波器具有如下优势：

(1) 在建立航迹方面，LMB滤波器不仅计算和递归目标动力学统计特性，还计算和递归目标标签信息，因此具备区别目标身份和建立目标航迹能力。

(2) 在滤波性能和计算量均衡方面，LMB性能逼近最优贝叶斯滤波器的闭合解GLMB滤波器，但其计算量远低于GLMB滤波器。

此外，鉴于LMB的优异性能，该滤波器还广泛应用于传感器网络的分布式融合技术领域^[20-22]。因此，本文在随机集理论框架下，基于LMB滤波器研究“走-停-走”目标跟踪问题。本文的主要贡献如下：

(1) 针对标准多目标转移模型^[11]难以描述“走-停-走”目标重返雷达视域的问题，首次引入第3类目标出生过程，即重生(Re-Birth, RB)过程。利用目标重生前-后的空间位置和动力学参数关系，提出一种基于空域相关(Spatial Correlation, SC)的RB过程。SC-RB过程有效避免了伯努利分量的爆炸式增长，降低了后续迭代滤波算法的复杂度。

(2) 基于SC-RB过程，在贝叶斯滤波框架下，推导了LMB滤波器的迭代递归方程，称之为SC-RB-LMB滤波器算法，可实现“走-停-走”目标连续稳健跟踪，维持航迹标签的一致性；进一步，设计基于前-后向平均的目标状态重构方法，可实现准确重构停止期目标状态，恢复完整航迹。

(3) 在典型低空监视场景下，通过仿真和实测数据验证了提出模型和算法的性能优势。

2.   标签多目标状态和LMB随机集分布

为了便于读者清晰理解本文的符号表征，在随机集合框架下作如下定义：单目标状态用小写字母表示，如$x$, ${\boldsymbol{x}}$；多目标状态用大写字母表示，如$X$, ${\boldsymbol{X}}$；粗体字母${\boldsymbol{x}}$, ${\boldsymbol{X}}$表示标签化变量，例如${\boldsymbol{x}}$由非标签变量$x$和目标标签$\ell$构成，即${\boldsymbol{x}} = (x,\ell )$；$\mathbb{X}$和$\mathbb{L}$分别表示目标状态空间和(离散)标签空间；${\boldsymbol{X}}$表示定义在增广空间$\mathbb{X} \times \mathbb{L}$上的随机有限集。符号${\boldsymbol{\pi }}( \cdot )$表示标签随机集先验或后验概率密度函数，取${\boldsymbol{\pi }}$作为${\boldsymbol{\pi }}( \cdot )$的参数化表征；符号${{f}}( \cdot )$表示状态转移函数；符号$g( \cdot )$表示量测似然函数。

符号$< f( \cdot ),g( \cdot ) > {\mkern 1mu}$表示函数$f(x)$和$g(x)$的内积，定义如下：

多目标指数函数定义为

其中，$h(x)$是实值函数，且${h^\varnothing } \triangleq 1$。符号${\delta _Y}(X)$表示广义Kronecker delta函数，其定义为

符号${1_Y}(X)$表示指示函数，其定义为

2.1   标签多目标状态

为区分目标身份，建立目标航迹，澳洲科廷大学Vo等人^[14]提出标签随机集的概念。首先，将单目标状态扩维，引入目标身份(标签)信息；其次，多目标状态及身份标签被建模为标签随机集合。

令${x^k} \in \mathbb{X}$表示$k$时刻单目标动力学状态，其中$\mathbb{X} = {\mathbb{R}^\nu }$是维度为$\nu$的单目标动力学状态空间。目标的(身份)标签信息用有序整数对${\ell ^k} = ({k_b},i)$表示，其中${k_b}$表示目标出生的时刻，标签$i \in {\mathbb{N}_ + }$用于区分同一时刻出生的目标。$k$时刻新生目标的标签空间为$\{ k\} \times {\mathbb{N}_ + }$，则$k$时刻标签空间${\mathbb{L}_{0:k}}$可迭代地构造，即${\mathbb{L}_{0:k}} = {\mathbb{L}_{0:k - 1}} \cup {\mathbb{L}_k}$。k 时刻，标签单目标状态${{\boldsymbol{x}}^k}$由动力学状态${x^k}$和标签${\ell ^k}$构成，即

标签多目标状态的集合可表示为

其中，$\mathcal{F}(\mathbb{X} \times {\mathbb{L}_{0:k}})$表示状态空间$\mathbb{X} \times {\mathbb{L}_{0:k}}$有限子集全体构成的超空间。

为简化符号表示，在不引起混淆的情况下，后文省略时刻上标$k$，且定义$\mathbb{L} \triangleq {\mathbb{L}_{0:k}}$, ${\mathbb{L}_ + } \triangleq {\mathbb{L}_{0:k + 1}}$。

2.2   LMB随机集分布

本节介绍一种与本文密切相关的随机集分布，即LMB分布。定义在增广空间$\mathbb{X} \times \mathbb{L}$上的LMB随机集服从如下分布，

其中，${\cal L}: \mathbb{X}\times \mathbb{L} \to \mathbb{L}$表示投影$\mathcal{L}((x,\ell )){\mkern 1mu} {\mkern 1mu} = {\mkern 1mu} {\mkern 1mu} \ell$，则$\mathcal{L}({\boldsymbol{X}}){\mkern 1mu} {\mkern 1mu} = {\mkern 1mu} {\mkern 1mu} \{ \mathcal{L}({\boldsymbol{x}}),{\boldsymbol{x}}{\mkern 1mu} {\mkern 1mu} \in {\mkern 1mu} {\mkern 1mu} {\boldsymbol{X}}\}$表示多目标状态${\boldsymbol{X}}$的标签集合。函数$\Delta ({\boldsymbol{X}}){\mkern 1mu} {\mkern 1mu} \triangleq {\mkern 1mu} {\mkern 1mu} {\delta _{|{\boldsymbol{X}}|}}(\mathcal{L}({\boldsymbol{X}}))$为标签互异指示器，

且${r^{(\ell )}}$表示目标$\ell$的存在概率；$p( \cdot ,\ell )$表示目标$\ell$存在条件下的概率密度函数。

式(7)和式(8)表明：LMB随机集可由存在概率${r^{(\ell )}}$和密度函数$p( \cdot ,\ell )$，$\forall \ell \in \mathbb{L}$完全确定。定义LMB参数集合${\boldsymbol{\pi }} \triangleq \{ ({r^{(\ell )}},{p^{(\ell )}}(x)):\ell \in \mathbb{L}\}$，其中

则LMB分布可由LMB参数集合完全表征。

3.   低空监视雷达“走-停-走”目标跟踪模型

3.1   多目标点迹量测模型

多目标点迹量测模型^[9]描述了雷达检测后点迹数据与多目标状态间的似然关系，包括目标随机漏检、杂波分布特性、单目标似然函数等。基于点迹量测模型的目标跟踪算法具有运算速度快、占有内存小等优点，广泛应用于雷达目标跟踪、红外探测和光学图像跟踪领域。

$k$时刻，若单目标${\boldsymbol{x}} \in {\boldsymbol{X}}$以概率$P_D^{}({\boldsymbol{x}})$被检测到，则以似然函数$g(z|{\boldsymbol{x}})$产生一个点迹量测数据$z$；若以概率$1 - P_D^{}( \cdot )$漏检，则不生成量测值。令$\varLambda ({\boldsymbol{x}})$表示单目标状态${\boldsymbol{x}}$的检报集，${Z_c}$表示杂波的检报集，则多目标状态${\boldsymbol{X}}$产生的量测集合$Z$可表示为

杂波检报集合${Z_c}$服从泊松过程^[11]，其密度函数为

$\kappa ( \cdot ) = \lambda c( \cdot )$为杂波强度函数，$\lambda$表示平均杂波个数，又称为杂波率；$c( \cdot )$表示杂波的空间分布函数。

给定多目标状态${\boldsymbol{X}}$，假设不同目标的检报集、杂波检报集相互统计独立，则多目标似然函数可表示为

其中，关联映射函数$\theta :\mathbb{L} \to \{ 0,1, \cdots ,|Z|\}$满足：当且仅当$i = i'$时，$\theta (i) = \theta (i')$；$\varTheta$为所有关联映射函数$\theta$的全体，$\varTheta \left( I \right)$表示定义域为$I$的关联映射函数集合；

其中，${q_D}(x,\ell ) \triangleq 1 - {p_D}(x,\ell )$表示目标的漏检概率；$g(z{\text{| }}x,\ell )$表示单目标似然函数。

3.2   标准多目标状态转移模型

标准多目标转移模型^[9,11,12]包括存活目标运动转移模型、目标新生模型、目标死亡模型和衍生目标模型。本文不涉及衍生目标，故不讨论。

$k$时刻，多目标状态集合${\boldsymbol{X}}$中，对于任意单目标状态${\boldsymbol{x}} \in {\boldsymbol{X}}$，$k + 1$时刻其状态转移有两种可能：

(1) 存活：目标以概率${P_S}\left( {x,\ell } \right)$存活，且以转移概率密度${f_{}}\left( {{x_ + }\left| {x,\ell } \right.} \right){\delta _\ell }\left( {{\ell _ + }} \right)$转移到新状态$\left( {{x_ + },{\ell _ + }} \right)$；

(2) 死亡：目标以概率${q_S}\left( {x,\ell } \right) = 1 - {p_S}\left( {x,\ell } \right)$死亡。死亡描述目标长时间消失于雷达视域的物理现象。

因此，$k + 1$时刻，存活目标状态集合${{\boldsymbol{X}}_S}$的多目标概率密度函数可表示为

其中

新生目标是指首次出现在雷达视域内的目标。令${{\boldsymbol{X}}_B}$表示$k$时刻新生目标集合，其多目标概率密度函数可建模为LMB分布，

因此，标准多目标状态转移模型中，$k$时刻多目标状态集合${{\boldsymbol{X}}_ + }$由存活目标集合${{\boldsymbol{X}}_S}$与新生目标集合${{\boldsymbol{X}}_B}$的并集构成，即

假设多目标演化过程相互独立，且与新生目标相互独立，则$k$时刻标准多目标转移函数可表示为

其中，“–”表示差集运算。

3.3   “走-停-走”多目标状态转移模型

“走-停-走”目标的运动方式为“走-停-走”不断切换，呈现多次往返于雷达视域的运动特性，如图1所示。标准多目标转移模型内嵌假设：目标从出生到死亡一直存活于雷达视线范围内，难以描述“走-停-走”目标多次往返雷达视域的演化特性。若采用标准转移模型，目标重返雷达视域时则以新生目标的身份出生，赋予新的身份标签，导致目标标签不连续，航迹断裂甚至碎片化。

图  1  “走-停-走”目标运动轨迹

Figure  1.  Trajectories of move-stop-move targets

下载: 全尺寸图片 幻灯片

3.3.1   “走-停-走”目标描述

假设监视场景持续总帧数为$K$。首先定义“走-停-走”目标两种运动态势：走动期和停止期。

(1) 走动期：不存在障碍物遮挡时，目标径向速度$v_r^k$大于等于雷达最小可检测速度${v_{r,\min }}$的时段，即

(2) 停止期：目标径向速度$v_r^k$小于雷达最小可检测速度${v_{r,\min }}$的时段，即

或者存在小型障碍物遮挡时段。

实际中，存在以下3种情况可造成目标进入停止期：(1)目标自身怠速或者静止，例如无人机悬停、低速掉头等。(2)目标非怠速，但与雷达位置呈特定几何关系，导致速度径向投影小。情况(1)和情况(2)下目标回波落入零多普勒频率附近，可造成连续多周期漏检，暂时消失于雷达视域中。(3)未知小型障碍物遮挡，导致目标没有被雷达照射，短暂丢失该目标。对于目标跟踪算法而言，连续多帧漏检直接导致该目标的存在概率逐渐削弱，转为死亡目标。

标准多目标状态转移模型包括两大类目标出生过程：新生目标和衍生目标。其中，新生目标描述首次出现在雷达视域的目标状态统计特性；衍生目标则描述了由场景中现存目标分裂出的衍生目标状态统计特性。两者均无法建模和描述死亡目标重返雷达视域的物理现象。为此，本文引入第3大类目标出生过程，即重生(RB)过程，用于描述目标短暂死亡后，重返雷达视域时动力学统计特性和标签身份特性。

重生目标定义：令${x^{{k_{s1}}}}$表示目标在${k_{s1}}$时刻的状态，${x^{{k_{s2}}}}$表示目标在${k_{s2}}$时刻的状态。在任意停止期${K_{{\rm{stop}}}} = {k_{s1}}:{k_{s2}}$，若该目标的空间位移变化量满足如下条件时，

其中

且${p_x}( \cdot )$, ${p_y}( \cdot )$和${p_z}( \cdot )$分别表示目标状态的$x$坐标、$y$坐标和$z$坐标位置，则将停止期后重返视域的目标称为重生目标。

上述定义中，空间位移变化量上限$\Delta {r_{\max }}$与雷达系统参数、监视场景和监视对象特性相关。在情况(1)下，无人机悬停或低速掉头等走-停策略都使目标处于怠速运动状态，属于弱机动性，重返雷达视域前-后空间位移量小；在情况(2)下，虽然目标处于非怠速状态，但是其径向速度受到最小可检测速度范围$[ - {v_{r,\min }},{v_{r,\min }}]$约束，停止帧数有限；在情况(3)下，以海面低空监视场景为例，受到尺寸约束，岛礁等典型遮挡物不会长时间遮挡目标。

3.3.2   多“走-停-走”目标状态转移函数

根据重生目标定义，重生目标起始状态与死亡目标终止状态具有动力学相关性。因此，可利用死亡目标集合构建重生目标集合。

$k + 1$时刻，给定死亡目标集合${{\boldsymbol{X}}_d}$和相应标签空间$\mathbb{D}$。死亡目标$\left( {{x_d},{\ell _d}} \right) \in {{\boldsymbol{X}}_{{d}}}$的演化分为两种情况：

(1) 以概率${P_{{\text{RB}}}}({x_d},{\ell _d})$重生，且以转移概率密度${\delta _{{\ell _d}}}\left( {{\ell _ + }} \right){f_{{\text{RB}}}}\left( {{x_ + }\left| {{x_d},{\ell _d}} \right.} \right)$演化为重生目标状态$\left( {{x_ + },{\ell _ + }} \right)$；

(2) 以概率$1 - {P_{{\text{RB}}}}({x_d},{\ell _d})$保持死亡状态。

${\delta _{{\ell _d}}}(\ell )$描述了死亡目标与重生目标的标签演化关系，保障了死亡目标与重生目标标签的一致性，对维持“走-停-走”目标的航迹连续性具有重要意义；${f_{{\rm{RB}}}}({x_ + }{\mkern 1mu} |{x_d},{\ell _d})$反映了重生目标状态与死亡目标状态的动力学相关性。

不失一般性，假设每个死亡目标的重生过程相互独立。因此，给定死亡集合${{\boldsymbol{X}}_d}$条件下，重生目标集合${{\boldsymbol{X}}_{{\rm{RB}}}}$的多目标密度函数可表示为

其中

根据标签一致性原则，重生目标与死亡目标具有相同的标签空间，即${\mathbb{B}_r} = \mathbb{D}$。

如图2所示，引入重生目标集合后，$k$时刻多目标状态集合${{\boldsymbol{X}}_ + }$不仅包括存活目标集合${{\boldsymbol{X}}_S}$和新生目标集合${{\boldsymbol{X}}_B}$，还包括重生目标集合${{\boldsymbol{X}}_{{\rm{RB}}}}$，即

图  2  多“走-停-走”目标状态转移过程

Figure  2.  Markov transition of multiple move-stop-move targets

下载: 全尺寸图片 幻灯片

假设多目标演化过程相互独立，且与新生目标和重生目标过程相互独立。根据Radon-Nikodym理论^[9]，经推导，$k + 1$时刻多“走-停-走”目标转移函数可表示为

4.   基于空域相关重生目标模型的标签多伯努利滤波器

4.1   基于空域相关的重生过程

“走-停-走”目标在停止期与真正死亡目标具有相似动力学特征，因此可通过死亡目标的演化构建“走-停-走”目标的重生过程。但是，如果将全部死亡目标送入LMB滤波器进行自演化，会导致LMB滤波器更新过程中假设分量随死亡目标个数呈指数增加；另一方面，在“走-停-走”目标死亡时刻，相应存在概率低于截断门限(典型值为${\gamma _t} = {10^{ - 4}}$)且状态协方差发散，难以将死亡目标的后验密度函数直接用于待重生目标先验分布建模。本节首先构建待重生目标先验分布；然后基于预滤波机制计算待重生目标的后验分布，并利用后验存在概率与量测的数学关系，最终提出一种基于空域相关(SC)的重生(RB)过程，简称SC-RB过程。

首先，从死亡目标后验分布中提取动力学状态特征和标签信息，构造待重生目标先验分布${{\boldsymbol{\tilde \pi }}_{{\text{RB}}}}\left( {{{\boldsymbol{X}}_d}} \right)$，其参数化表征如下：

其中，$r_{{\text{RB}}}^{({\ell _d})}$和$p_{{\text{RB}}}^{({\ell _d})}( \cdot )$分别表示死亡目标${\ell _d}$的先验重生概率和先验重生密度函数

其中，$\hat x_d^{({\ell _d})}$为死亡目标${\ell _d}$的动力学状态估计；${\boldsymbol{P}}_d^{({\ell _d})}$表示待重生目标的先验协方差矩阵。

本文采用随机游走模型^[8]描述死亡目标与相应重生目标的动力学演化关系

其中，${{\boldsymbol{F}}_{{\rm{RB}}}}$为单位阵，${{\boldsymbol{P}}_{{\text{RB}}}}$表示死亡到重生的演化协方差矩阵。同时，考虑固定的重生演化概率${P_{{\text{RB}}}} ({x_d},{\ell _d}) = {P_{{\text{RB}}}}$。

基于式(23)给出的待重生目标先验分布和死亡-重生演化模型，依据贝叶斯预测方程^[9,16]，待重生目标的预测分布为LMB分布，其参数化表征为

其中

其中，${\mkern 1mu} {{\boldsymbol{P}}'_{{\rm{RB}}}}$表示待重生目标的预测协方差矩阵，其数学计算公式为${{\boldsymbol{P}}'_{{\text{RB}}}} = {{\boldsymbol{F}}_{{\text{RB}}}}{{\boldsymbol{P}}_d}{\boldsymbol{F}}_{{\text{RB}}}^{\rm{T}} + {{\boldsymbol{P}}_{{\text{RB}}}}$。

经过量测集合$Z$更新，基于一阶矩匹配原则^[16]和最小Kullback Leibler散度准则^[17]，待重生目标后验分布可近似为LMB分布，

具体参数计算方法详见文献[16]。本节主要通过分析$r_{{\rm{RB}}}^{({\ell _{_ + }})}(Z)$特性来研究重生目标激活方法。

令${d_{{\text{MHD}}}}({\hat z^{_{\left( {{\ell _ + }} \right)}}},z)$表示待重生目标${\ell _ + } \in {\mathbb{B}_r}$的伪量测${\hat z^{({\ell _{_ + }})}} = {\boldsymbol{H}}({{\boldsymbol{F}}_{{\text{RB}}}}\hat x_d^{({\ell _ + })})$与量测$z$的马氏距离(MaHalanobis Distance, MHD)，

其中，${\boldsymbol{S}}_{{\ell _ + }}^{}$表示待重生目标${\ell _ + } \in {\mathbb{B}_r}$新息协方差矩阵。

文献[18]指出，当马氏距离满足如下条件时，

其中，$\sqrt \varGamma$表示$\sigma {\text{ - }}$波门^[17]尺寸，待重生目标${\ell _ + }$的后验存在概率由式(36)近似计算，

式(36)的几何解释为，当所有量测$z \in Z$都没有落入${\ell _d} = {\ell _ + } \in \mathbb{D}$的$\sigma {\text{ - }}$波门时，该待重生目标的后验存在概率${\mkern 1mu} r_{{\rm{RB}}, + }^{({\ell _ + })}\left( Z \right) \approx 0$。

根据文献[17], 参数$\varGamma$可在给定波门概率(目标量测落入波门的概率)下，利用逆${\chi ^2}$分布的积累函数计算得出。

综合本节分析表明，对任意死亡目标${\ell _d} \in \mathbb{D}$，若$k$时刻无量测落入相应待重生目标$\sigma {\text{ - }}$波门内，则该死亡目标对应的后验重生概率接近0；相反，若$k$时刻有量测落入其$\sigma {\text{ - }}$波门内，该死亡目标对应的后验重生概率高。

根据$r_{{\rm{RB}}, + }^{({\ell _{_ + }})}(Z)$特征，本文提出SC-RB模型。SC-RB模型中涉及的预测和更新过程是死亡目标的预滤波过程，只有当量测落入死亡目标相应的$\sigma {\text{ - }}$波门时，该目标才会激活重生，不需要全部死亡目标真实参与滤波，如图3所示。该预滤波机制有效避免了LMB更新方程中假设分量随死亡目标个数呈指数增长的问题，降低后续迭代滤波算法的复杂度。

图  3  死亡目标重生激活过程

Figure  3.  The activation process of deaths

下载: 全尺寸图片 幻灯片

综上，利用待重生目标的预测分布构造SC-RB的分布为

其中，$r_{{\text{RB}}, + }^{({\ell _ + })}$和$p_{{\text{RB}}, + }^{({\ell _ + })}( \cdot )$由式(31)和式(32)分别给出；${\mathbb{B}'_r} = {\{ {\ell _ + }|{d_{{\text{MHD}}}}({\hat z^{({\ell _ + })}},z) < \sqrt \varGamma ,\forall z \in Z\} _{{\ell _ + } \in {\mathbb{B}_r}}}$表示激活后重生目标标签集合。由于待重生目标的预测分布是一种概念上的转移过程，在后续滤波实现过程中，可根据实际场景目标的运动特征直接对存在概率$r_{{\text{RB}}, + }^{({\ell _ + })}$和协方差${\mkern 1mu} {{\boldsymbol{P}}'_{{\text{RB}}, + }}$进行数值配置。

基于SC-RB先验分布式(37)，相应的多“走-停-走”目标转移函数构建如下：

后续章节，将本节提出的SC-RB重生过程与贝叶斯滤波器迭代递归方程相结合，具体给出了SC-RB-LMB滤波器的预测过程和更新过程。

4.2   SC-RB-LMB滤波器预测过程

4.2.1   存活目标预测

假设$k$时刻多目标后验${\boldsymbol{\pi }}({\boldsymbol{X}})$服从LMB分布，其参数化表征为

根据文献[18]，基于贝叶斯滤波器预测公式，存活目标预测分布依然服从LMB分布，

其中，目标存活概率$r_{S, + }^{({\ell _ + })}$与状态概率密度函数$p_{S, + }^{({\ell _ + })}(x)$由式(41)—式(43)给出，

其中，${p_S}( \cdot ,{\ell _ + })$表示标签为${\ell _ + }$的目标存活概率； $f(x\mid \cdot ,{\ell _ + })$表示单目标马尔可夫转移密度函数。

4.2.2   SC-RB分布构建

SC-RB目标分布构建基本流程如下：

(1) 死亡目标集合构建：对于任意目标$\ell = ({k_b},i)$，记录该目标死亡时刻${k_d}$。若目标$\ell$航迹维持帧数${K_S} = |{k_d} - {k_b}|$大于$L$帧，则该目标记为死亡目标。记$k$时刻之前死亡目标的标签全体为集合$\mathbb{D}$，且待重生目标集合为${\mathbb{B}_r} = \mathbb{D}$。

(2) 重生目标集合构建：$k$时刻，对于任意待重生目标${\ell _ + } \in {\mathbb{B}_r}$，判断是否有量测$z \in {{Z}}$落入该目标$\sigma {\text{ - }}$波门内，即是否满足条件：${d_{{\text{MHD}}}}({\hat z_{{\ell _ + }}},z) < \sqrt \varGamma$。若满足，则该死亡目标被激活，转为重生目标。重生目标的标签全体记为${\mathbb{B}'_r} = \{ {\ell _ + }|{d_{{\text{MHD}}}}({\hat z_{{\ell _ + }}},z) > \sqrt \varGamma , \forall z \in Z\} _{{\ell _ + } \in {\mathbb{B}_r}}$。SC-RB目标分布则由式(37)构建。

(3) 死亡目标集合更新：从死亡目标标签集合中删除激活重生目标标签，即${\mathbb{D}_ + } = \mathbb{D} - {\mathbb{B}_r}$。

4.2.3   新生目标预测

低空目标监视应用中，新生目标出生位置的先验信息少，因此本文采用基于量测的自适应新生过程^[18]。基于$k - 1$时刻量测信息，构建 k 时刻的出生目标先验分布，

其中

其中，${Z_ - }$表示$k - 1$时刻量测集合；${z_ - } \in {Z_ - }$表示$k - 1$时刻任意量测值；${r_{B,{\rm{max}}}}$表示新生目标最大存在概率；${\lambda _B}$表示$k$时刻新生目标数量期望；${r_U}\left( {{z_ - }} \right)$表示$k - 1$时刻量测${z_ - }$与存活目标的关联概率，计算如下：

依据贝叶斯预测方程，$k$时刻，新生目标预测分布${{\boldsymbol{\pi }}_{B, + }}$同样通过式(41)—式(43)计算得出。

综上，$k + 1$时刻，考虑重生目标出生后，多目标预测分布仍然服从LMB分布，其参数化表征如下：

4.3   SC-RB-LMB滤波器更新过程

$k + 1$时刻，多目标预测分布服从LMB分布，其参数化表征为${{\boldsymbol{\pi }}_ + } = \left\{ {\left( {r_ + ^{(\ell )},p_ + ^{(\ell )}} \right):\ell \in {\mathbb{L}_ + }} \right\}$，其中${\mathbb{L}_ + }$由存活目标、重生目标、新生目标3个部分构成，即${\mathbb{L}_ + } = \mathbb{L} \cup \mathbb{B} \cup {\mathbb{B}'_r}$。假设雷达接收到量测数据集合$Z$，根据LMB更新方程，$k$时刻多目标后验分布依然服从LMB分布，其参数化表征为

其中

其中

4.4   “走-停-走”目标航迹重构

4.4.1   走动期：目标状态估计

“走-停-走”目标走动期，可通过SC-RB-LMB滤波器后验分布进行多目标状态估计。估计方法描述如下：

首先，给定$k$时刻LMB后验参数集合 ${\boldsymbol{\pi }}( \cdot |Z) = \left\{ {\left( {r_{}^{(\ell )}(Z),p_{}^{(\ell )}( \cdot |Z)} \right):\ell \in {\mathbb{L}_ + }} \right\}$，则目标基数估计值计算如下^[8]：

目标基数是多目标状态集合的元素个数，表征随目标出生、重生、死亡等转移过程的目标个数状态^[9]。

其次，从LMB后验参数集合中提取存在概率${r^{(\ell )}}\left( Z \right)$最大的$\hat N$个伯努利分量。根据这$\hat N$个伯努利分量后验概率密度函数$p_{}^{(\ell )}( \cdot |Z)$，基于最大后验概率(Maximum A Posteriori, MAP)准则，估计目标动力学状态如下：

4.4.2   停止期：目标状态重构

“走-停-走”目标停止期，由于连续漏检，目标存在概率逐渐削弱，转为死亡航迹。因此，跟踪算法难以有效输出目标状态估计。通过引入重生过程模型，相应SC-RB-LMB滤波器可维持“走-停-走”过程中标签不变，因此，可利用重返雷达视域前-后的目标状态估计重构停止期目标状态。为此，本文提出一种基于前后向平均(Forwards-Backwards Average, FBA)的目标状态重构方法。具体方法描述如下：

假设停止目标$\ell$终止时刻为${k_d}$，终止时刻目标动力学状态估计为${\hat x^{{k_d}}}$；重生时刻为${k_{rb}}$，重生时刻目标动力学状态为${\hat x^{{k_{rb}}}}$。如3.3节分析，“走-停-走”目标在停止期动力学状态变化量有限，属于弱机动目标，符合近似线性运动模型。因此，本文基于匀速运动模型进行航迹重构。首先，依据重返雷达视域前-后目标动力学状态变化量，估计停止期目标运动速度：

其次，根据停止期目标速度估值，重构停止期目标空间位置状态。

4.5   SC-RB-LMB滤波器算法总体流程

图4给出了SC-RB-LMB滤波器算法总体流程。SC-RB-LMB滤波器算法主要包括目标出生(新生目标、重生目标)、航迹预测、航迹更新、航迹管理和航迹构建等过程。

图  4  SC-RB-LMB滤波器算法总体流程

Figure  4.  The overall flow diagram of the SC-RB-LMB filter algorithm

下载: 全尺寸图片 幻灯片

与标准LMB滤波器算法相比，SC-RB-LMB滤波器算法引入了重生过程模型和航迹重构算法，一方面可解决连续多帧漏检导致的航迹断裂问题，维持“走-停-走”目标重返雷达视域前-后标签不变，在航迹连续性方面具有显著性能优势；另一方面，可准确重构停止期目标状态，恢复“走-停-走”目标完整航迹，在航迹完整度和跟踪精度方面同样具有优势。

5.   雷达“走-停-走”目标跟踪算法性能评估

本节在低空雷达监视无人机目标场景下，通过仿真实验和实测数据，对提出的SC-RB-LMB滤波器算法进行性能评估。算法性能评估以标准LMB滤波器^[16]算法作为性能标杆。

5.1   低空监视雷达与跟踪算法参数设置

5.1.1   低空监视雷达传感器模型

经脉冲压缩、MTI、MTD、到达角估计和恒虚警检测等信号处理过程后，k 时刻，雷达可获得目标的点迹量测数据${{z}} = {\left[ {r,{v_r},\varphi ,\phi } \right]^{\rm{T}}}$，其中$r$表示斜距，${v_r}$表示径向速度，$\varphi$表示方位角，$\phi$表示俯仰角，如图5所示。

图  5  低空监视雷达传感器模型图

Figure  5.  Sensor model of low-altitude surveillance radars

下载: 全尺寸图片 幻灯片

令单目标状态${{x}} \triangleq {\left[ {{p_x},{p_y},{p_z},{{\dot p}_x},{{\dot p}_y},{{\dot p}_z}} \right]^{\rm{T}}}$，雷达量测数据${{z}} \triangleq {\left[ {r,{v_r},\varphi ,\phi } \right]^{\rm{T}}}$与单目标状态$x$的数学关系为

其中，$\left( {{p_{{x_0}}},{p_{{y_0}}},{p_{{z_0}}}} \right)$表示雷达位置坐标，$\arctan \left( \cdot \right)$表示反正切函数，$\arccos \left( \cdot \right)$表示反余弦函数。

式(59)可进一步表示为向量的形式，

其中，${\boldsymbol{H}}( \cdot )$描述了目标状态${{x}}$与量测值${{z}}$的数学关系，$\mathfrak{n}$为高斯白噪声。

5.1.2   量测模型参数设置

由式(60)所构建的量测模型为非线性量测模型。设置每个目标检测概率为${P_D}$，选取${P_D} = \{ 0.80, 0.85, 0.90,0.95,0.99\}$。目标似然函数采用如下非线性高斯模型，

其中，${\boldsymbol{H}}({{x}})$如式(60)所示，量测协方差矩${\boldsymbol{R}}$为

其中，${\sigma _r} = 10{\kern 1pt} {\kern 1pt} {\kern 1pt} {\rm{m}}$, ${\sigma _{{v_r}}} = 0.25\;{\rm{m}}/{\rm{s}}$, ${\sigma _\varphi } = {0.5^ \circ }$和${\sigma _\phi } = {0.5^ \circ }$分别表示斜距、径向速度、方位角和俯仰角的标准差。杂波分布服从泊松过程，其杂波率选取${\lambda _c} = \{ 5,10,15,20\}$。

5.1.3   目标转移模型参数设置

目标状态转移模型如第3节描述。单目标状态转移模型假设为线性高斯模型^[11]，

其中，${\boldsymbol{F}}{\mkern 1mu} {{x}}$表示单目标状态${\mkern 1mu} {{x}}$的一步转移状态；转移矩阵${\boldsymbol{F}}$和过程噪声强度${\boldsymbol{Q}}$分别为

其中，${{\boldsymbol{I}}_n}$和${{{ {\textit{0}}}}_n}$分别表示$n \times n$维度的单位矩阵和零矩阵；${\sigma _v } = 3{\kern 1pt} {\kern 1pt} {\kern 1pt} {\rm{m}}/{{\rm{s}}^2}$表示过程噪声的标准差。目标继续生存概率为${P_S} = 0.98$。SC-RB分布的协方差矩阵${{\boldsymbol{P}}'_{{\text{RB}}}}$设置为${{\boldsymbol{P}}'_{{\text{RB}}}} = {\text{diag}}([400,400,400,100,100,100])$。

5.1.4   SC-RB-LMB滤波器实现参数设置

标准LMB滤波器和提出的SC-RB-LMB滤波器均采用混合高斯(GM)实现方法^[9,16]。各算法GM实现的参数选择如下: 伯努利分量的截断门限为 ${\gamma _t} = {10^{ - 4}}$；GM实现的高斯分量截断与合并门限分别为${\gamma _p} = {10^{ - 5}}$和${\gamma _m} = 4$；高斯分量的最大个数限制为${N_{\max }} = 10$。

5.1.5   算法评价指标

为评估多目标跟踪精度和航迹碎片化程度，主要选取最优子模式分配(Optimal Sub-Patten Assignment, OSPA)^[23]和航迹零碎度^[24]两个性能评价指标。

(1) OSPA误差。OSPA距离是评估跟踪航迹精度和目标数量误差的综合性指标。详细计算过程请参考文献[23]。

(2) 航迹零碎度。航迹零碎度是指一条真实目标航迹在给定观测时间内跟踪算法输出的航迹标签总数^[24]。

假设场景持续总帧数为$K$。对于任意目标$\ell$，$k$时刻，跟踪算法输出的该目标标签估计为${\hat \ell ^k}$，则目标$\ell$的航迹零碎度定义为

其中，${\mkern 1mu} | \cdot |$表示取集合的基数。

航迹零碎度是评价“走-停-走”目标跟踪稳定度的重要指标。航迹零碎度为1时，表示该目标在观测时间内保持一个稳定的标签。航迹零碎度越高，则意味航迹在不同时间段输出的标签越多，航迹碎片化越严重。

所有统计性能结果均是通过200次蒙特卡罗(Monte Carlo, MC)平均得出。

5.2   仿真实验验证

考虑低空监视雷达工作场景。雷达监视区域范围为2000 m×120°×20°(距离-方位-俯仰)，其中距离分辨率设置为1 m、方位分辨率为1°、俯仰分辨率为1°。雷达坐标$\left( {{p_{{x_0}}},{p_{{y_0}}},{p_{{z_0}}}} \right) = \left( {0\; {\rm{m}},0\;{\rm{m}},0\; {\rm{m}}} \right)$。数据周期为$T = 0.5\; {\rm{s}}$，观测数据总帧数为500帧。雷达最小可检测速度为$0.8\; {{\rm{m}}/{\rm{s}}}$。监视场景中包括10个目标，真实运动轨迹如图6所示。目标出生-死亡时刻、起始位置以及平均速度如表1所示。从图6可以看出目标T1, T3, T5, T6轨迹在场景中经过了多次折返，在折返阶段需要采用减速、停止、加速等运动模型刻画。更具体的，根据目标“走-停-走”运动特征设置，目标T1, T3, T5, T6和T10属于“走-停-走”目标。

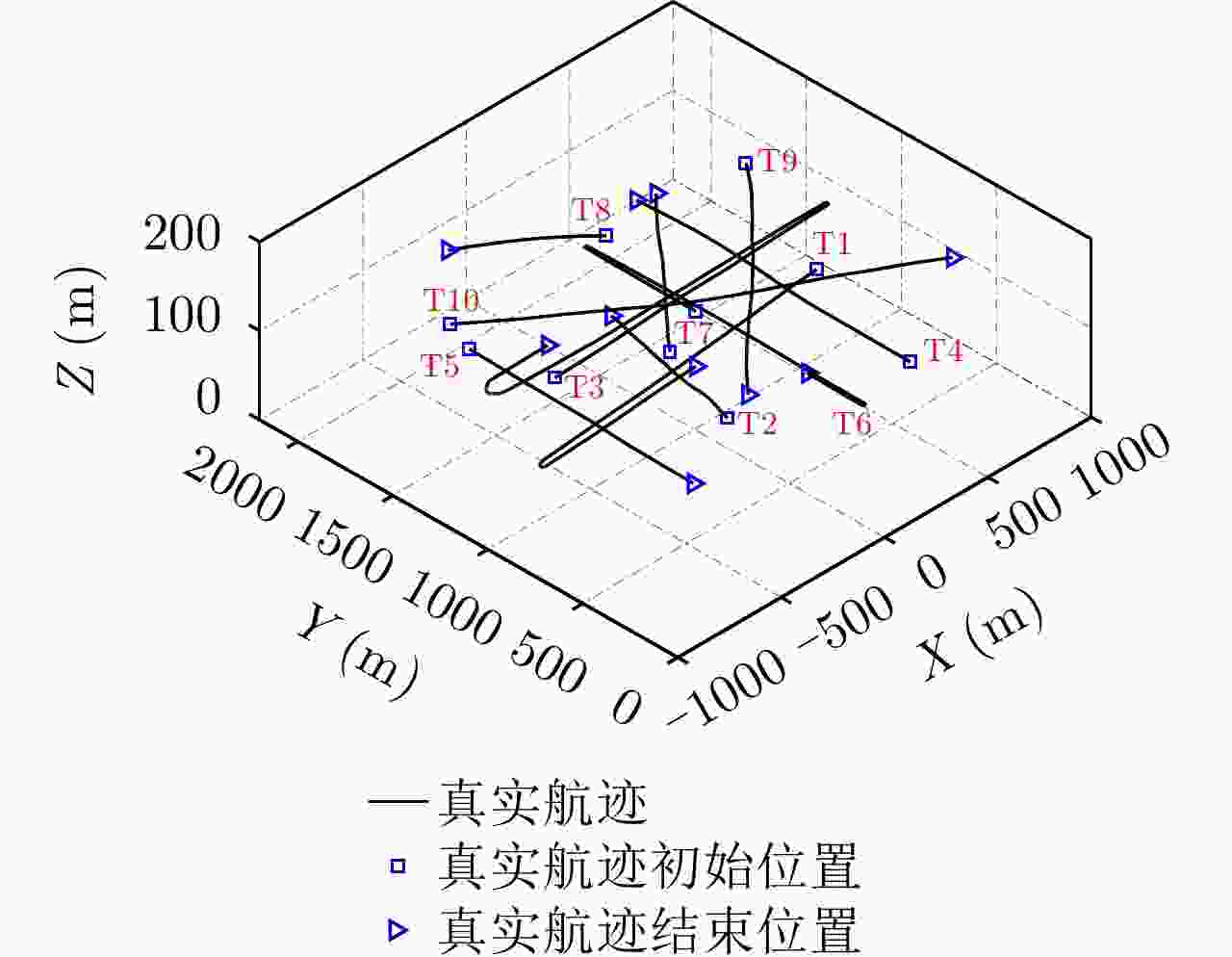
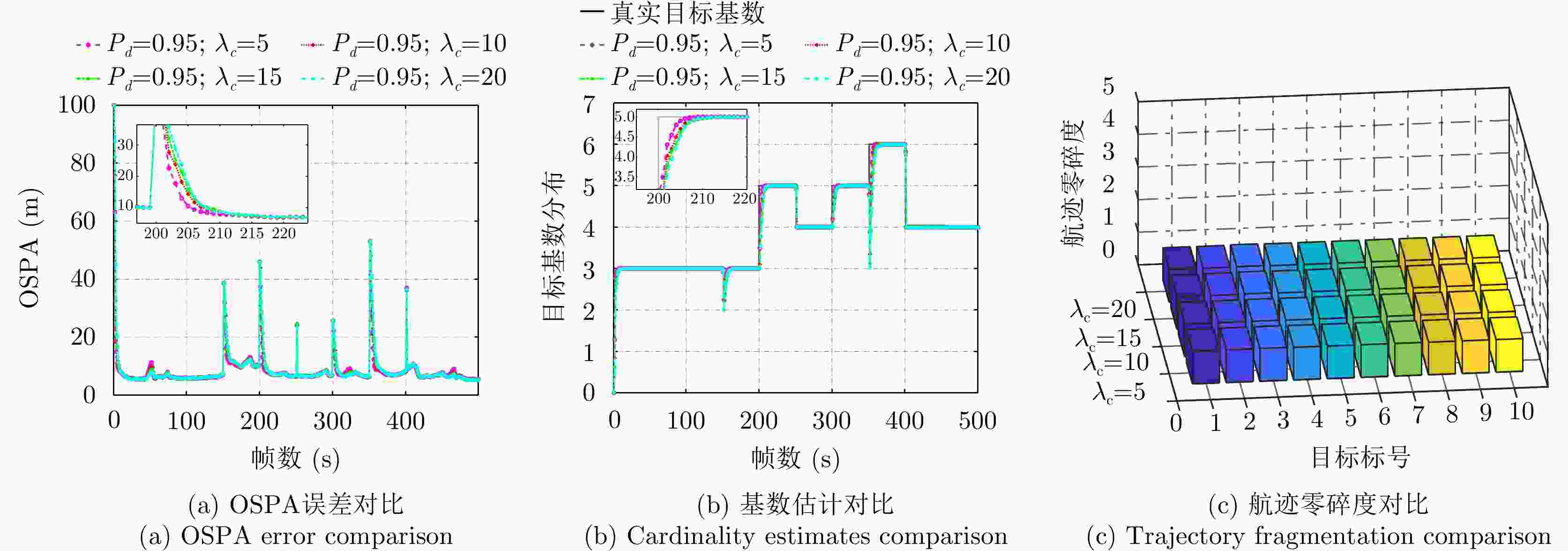
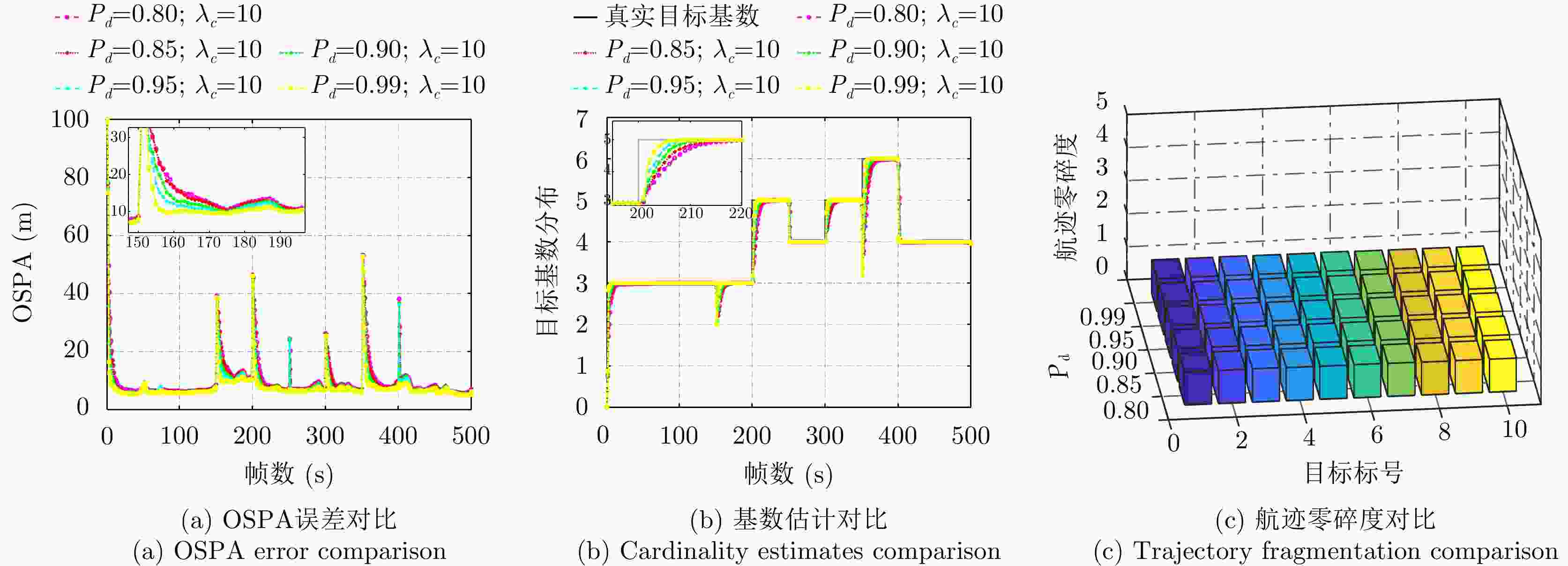
表  1  不同目标的出生时刻和死亡时刻

Table  1.  Time of births and deaths for different targets

目标	出生帧数	死亡帧数	起始位置(m)	结束位置(m)	平均速度(m/s)
T1	1	250	(590,1000)	(–106,877)	(–20,–2)
T2	1	150	(–250,560)	(–95,1333)	(3.5,12)
T3	1	500	(–500,1200)	(–372,1368)	(18,0.5)
T4	200	350	(500,410)	(525,1878)	(0.2,18)
T5	151	500	(–500,1650)	(–530,430)	(–0.2,–18)
T6	200	350	(200,1210)	(208,630)	(0,20)
T7	151	500	(–300,800)	(340,1570)	(12,15)
T8	300	400	(42,1510)	(–400,1865)	(–17,18)
T9	351	500	(800,1600)	(–175,527)	(–12,–16)
T10	351	500	(–600,1650)	(890,610)	(18,–16)

下载: 导出CSV 

| 显示表格

图  6  雷达监视场景-3D视图多目标真实运动轨迹

Figure  6.  The radar surveillance senario: 3D-ground truths

下载: 全尺寸图片 幻灯片

表2给出了目标T1, T3, T5, T6和T10的停止时间，该停止时刻是由目标多普勒盲区、目标怠速等原因导致其径向速度低于最小可检测速度的时间段，雷达暂时看不见该目标。目标T1, T3和T10在横穿场景的过程中，在某些时间段，与雷达存在特殊几何关系，导致径向速度低于雷达最小可检测速度，连续多帧漏检，其停止帧数分别如表2中T1, T3, T10所示。目标T6在两次掉头过程中，运动速度低，直接导致径向速度低于最小可检测速度。目标T5和T6运动过程中，模拟无人机悬停，停止运动了数秒，导致多帧无量测数据，停止帧数分别如表2所示。

表  2  “走-停-走”目标停止期

Table  2.  Stopping period of move-stop-move targets

目标	停止帧数
T1	66～73, 157～168
T3	43～51, 168～176, 310～322, 396～412, 448～450
T5	82～91
T6	70～83, 171～180, 300～309
T10	106～114

下载: 导出CSV 

| 显示表格

实验1：相同杂波率和检测概率下，LMB滤波器和SC-RB-LMB滤波器算法跟踪性能比对。

雷达的目标检测能力一般可达到P_D=0.95以上，不包含“走-停-走”目标停止期漏检情况，虚警能力可达到P_fa=10^–6。为了模拟雷达的目标检测能力，本次实验杂波率设置为${\lambda _c} = 10$和检测概率设置为${P_D} = 0.95$。图7(a)、图7(b)和图7(c)分别给出了单次蒙特卡洛实验标准LMB滤波器、SC-RB-LMB滤波器(航迹重构前)、SC-RB-LMB滤波器(航迹重构后)输出的航迹。不同颜色表示算法输出的航迹标签不同。

图  7  单次蒙特卡洛实验2D目标航迹估计

Figure  7.  2D target track estimation for single Monte-Carlo experiment

下载: 全尺寸图片 幻灯片

由图7(a)可以看出，LMB输出的目标航迹(T1, T3, T5和T6)均出现航迹标签变化的情况，其中T3航迹断裂4次，形成了5条不同标签的航迹。其原因为，在“走-停-走”目标停止期，由于量测漏检帧数过多，标准LMB滤波器无法输出航迹估计；当目标重返雷达视域时，LMB滤波器将其标记为新生目标，航迹标签出现变化。如图7(b)所示，SC-RB-LMB滤波器输出的航迹标签维持不变。进一步，通过航迹重构方法准确实现“走-停-走”目标停止期状态估计，恢复完整航迹，如图7(c)所示。

在杂波率${\lambda _c} = 10$和检测概率${P_D} = 0.95$下，图8(a)和图8(b)给出两种算法的平均OSPA误差和基数估计对比；在“走-停-走”目标停止期，标准LMB滤波器和SC-RB-LMB滤波器都难以有效输出目标状态估计，导致在此时间段OSPA误差持续增大，且基数估计不准确。更具体的，如表2所示，在66~73帧范围，目标T1径向速度小于${v_{r,\max }}$，导致该目标连续漏检。当该目标重返雷达视域时，标准LMB滤波器采用自适应目标出生模型重新起始该目标，然而该目标X轴速度较大，航迹起始阶段需要多帧收敛。与之相比，SC-RB-LMB基于死亡空域位置重生该航迹，航迹重生阶段收敛速度较快。因此，在73～90帧阶段SC-RB-LMB(未重构)的OSPA性能明显优于LMB。 进一步，SC-RB-LMB经过航迹重构后，其OSAP误差可达到走动期的稳定水平，基数估计与真实目标个数相符。

图  8  不同算法跟踪性能对比

Figure  8.  Tracking performance comparison among different algorithms

下载: 全尺寸图片 幻灯片

由于OSPA误差难以完整评估SC-RB-LMB算法较标准LMB的性能得益，本实验进一步采用航迹零碎度指标评价两种算法性能，如图8(c)所示。对于标准LMB算法，目标T1, T3, T5和T6的航迹零碎度均大于1，最高可达5.015；与之相比，本文提出的SC-RB-LMB滤波器算法各目标航迹零碎度最高为1.005。结果表明，SC-RB-LMB滤波器算法可解决“走-停-走”目标停止期量测连续多帧漏检情况导致的航迹断裂问题，输出持续稳定的航迹标签。

上述结果表明，本文所提出SC-RB-LMB滤波器算法在目标跟踪精度和航迹连续性方面具有显著优势。

为了进一步评估SC-RB-LMB滤波器中“走-停-走”目标重生过程计算复杂度，图9给出了SC-RB-LMB滤波器与标准LMB滤波器的平均计算时间对比。从图9可以看出，较标准LMB滤波器，SC-RB-LMB滤波器平均计算时间仅高出23.72%，但是大幅提升了“走-停-走”目标的跟踪精度和航迹连续性。

图  9  计算时间性能对比

Figure  9.  Comparison of execution times

下载: 全尺寸图片 幻灯片

实验2：不同杂波率和检测概率下，SC-RB-LMB滤波器算法跟踪性能评估。

图10(a)、图10(b)和图10(c)给出了不同杂波率下SC-RB-LMB滤波器算法的平均OSPA误差、平均基数估计、平均航迹零碎度3种跟踪性能指标比对。该结果表明，随着杂波率的增大，目标跟踪OSPA误差存在微弱下降，但基数估计与实际目标个数相符；在4种杂波率下，航迹零碎度未存在较大起伏，其数值均接近1，保证了航迹的完整性。另一方面，如图10(a)和图10(b)中子图所示，在航迹出生和死亡阶段，随着杂波率的降低，航迹收敛速度提升。

图  10  不同杂波率下SC-RB-LMB跟踪性能对比

Figure  10.  Tracking performance comparison of SC-RB-LMB filter under different clutter rates

下载: 全尺寸图片 幻灯片

图11(a)、图11(b)和图11(c)分别给出了不同检测概率下SC-RB-LMB滤波器的平均OSPA误差、平均基数估计、平均航迹零碎度3种跟踪性能指标比对。该结果表明，随着检测概率的下降，目标跟踪OSPA误差存在微弱下降，但基数估计与实际目标个数相符， 且航迹零碎度数值均接近1。另一方面，如图11(a)和图11(b)中子图所示，在航迹出生和死亡阶段，随着检测概率的提升，航迹收敛速度提升。

图  11  不同检测概率下SC-RB-LMB跟踪性能对比

Figure  11.  Tracking performance comparison of SC-RB-LMB filter under different detection probabilities

下载: 全尺寸图片 幻灯片

综上，SC-RB-LMB滤波器在不同参数下，均可以准确估计和锁定“走-停-走”目标，OSPA估计误差小，基数估计准确，航迹零碎度低，验证了SC-RB-LMB滤波器算法在复杂探测环境下的鲁棒性。

5.3   实测数据验证

本节采用某所研制的某型号低空监视雷达采集四旋翼无人机数据，进一步验证所提出SC-RB-LMB滤波器的性能优势。

该低空监视雷达采用2D有源相控阵设计，输出点迹量测为低空目标斜距、方位、俯仰、多普勒四维信息，因此，雷达量测模型可采用式(59)或式(60)建模和描述。所监视无人机在200 m高度范围内的低空区域做折返运动。该折返运动可分为“折返”阶段和“巡航”阶段。在折返阶段，无人机做减速运动并掉头，然后加速达到巡航速度；在巡航阶段，无人机做匀速直线运动。总体而言，无人机呈现“走-停-走”目标运动特性。

图12(a)给出了低空监视雷达输出的点迹实测数据，其中红色虚框内主要为无人机点迹量测，红色虚框外为杂波/虚警点迹。通过分析量测随时间变化规律得出，该无人机做了5次折返运动。同时，根据该无人机在折返阶段运动特征，该无人机点迹量测可能存在多帧漏检。

图  12  无人机长时间折返运动场景-跟踪性能对比

Figure  12.  Long palindrome path of the UAV- tracking performance comparison

下载: 全尺寸图片 幻灯片

图12(b)和图12(c)分别给出了标准LMB算法和SC-RB-LMB算法输出的航迹结果。由图12(b)可以看出，LMB滤波器将该无人机多次折返轨迹估计为3条独立航迹。基于雷达视角输出3条目标航迹，可能造成工作人员对监视场景态势的误判；同时，多条航迹会消耗有源相控阵雷达的跟踪波束资源。与之相比，所提出SC-RB-LMB滤波器输出一条完整航迹，如图12(c)所示。此外，由于利用了空域相关重生目标，与LMB滤波器相比，在折返阶段航迹重生收敛速度快，且航迹平滑程度高。

图13给出了无人机短时间折返运动的航迹跟踪结果。与图12 所示结果类似，SC-RB-LMB输出单条完整航迹，而LMB滤波器输出两条断裂目标航迹。

图  13  无人机短时间折返运动场景-跟踪性能对比

Figure  13.  Short palindrome path of the UAV- tracking performance comparison

下载: 全尺寸图片 幻灯片

综上，基于长时间折返和短时间折返两种典型“走-停-走”目标实测场景，充分验证了所提出SC-RB-LMB滤波器算法的鲁棒性和跟踪性能优势。

6.   结论

本文在随机集理论框架下基于标签多伯努利(LMB)滤波器研究低空监视雷达“走-停-走”目标连续跟踪问题。针对“走-停-走”目标多次往返于雷达视域的演化特性，首次引入第3类出生目标模型，即重生(RB)过程模型，并提出一种基于空域相关(SC)的RB过程，简称SC-RB重生过程。利用该重生过程，基于最优贝叶斯滤框架，推导了SC-RB-LMB滤波器的迭代递归方程。SC-RB-LMB滤波器可实现多“走-停-走”目标连续稳健跟踪，维持航迹标签的一致性，同时准确重构停止期目标状态，恢复完整航迹。在典型低空监视场景下，通过仿真和实测数据验证了提出模型和算法的有效性和性能优势。