Multi-emitters Direct Localization Method via Multi-dictionaries and Hierarchical Block Sparse Bayesian Framework
-
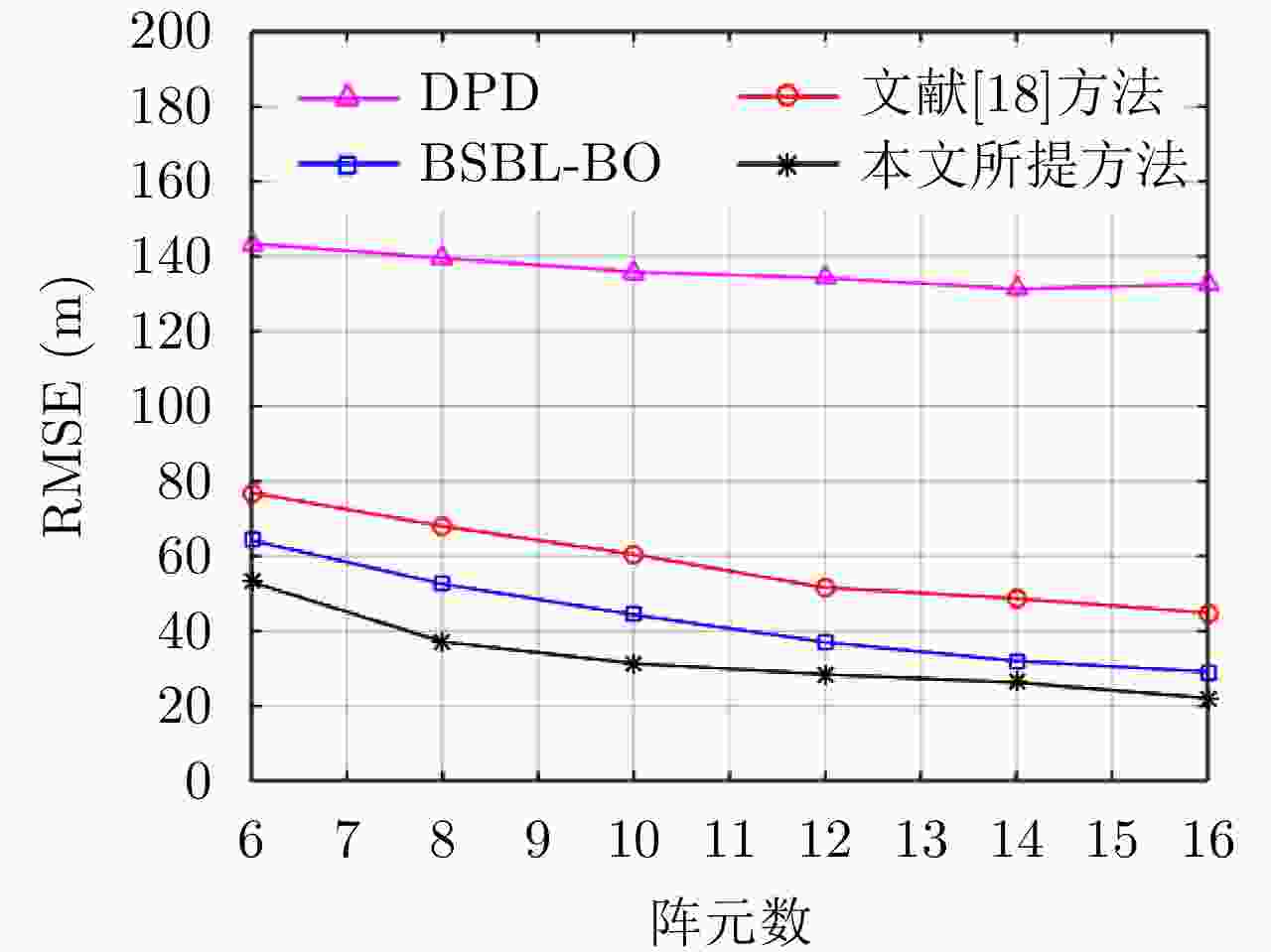
摘要: 基于压缩感知的直接定位方法依赖准确的信号传播模型,当传播模型的参数部分未知时,其定位性能会显著下降。针对这个问题,该文提出了一种基于多字典联合与分层块稀疏贝叶斯框架的多辐射源直接定位方法。该文将辐射源定位问题转化为恢复对应不同字典但具有共享稀疏性的信号,通过多字典联合来解决存在信道衰减的辐射源定位问题。仿真结果表明:所提方法在低信噪比和少快拍条件下,相比稀疏贝叶斯方法和直接定位方法具有更优的定位性能。Abstract: The direct position determination method based on compressed sensing depends on the accurate signal propagation model. With partially unknown propagation model parameters, its location performance will decline significantly. Thus, this study proposed a localization method via multi-dictionaries and hierarchical block sparse Bayesian framework. Herein, the emitter location problem is transformed into recovering signals from different dictionaries but with shared sparsity, and the emitter location with channel attenuation is solved by a multi-dictionary combination. Simulation results revealed that the algorithm has better performance than the traditional Sparse Bayesian Learning (SBL) method and Direct Position Determination (DPD) method under the condition of low signal-to-noise ratio and a few snapshots.
-
表 1 不同定位方法运行时间对比
Table 1. Comparison of run time
定位方法 迭代次数 运行时间(s) 两步法 – 0.099 DPD – 1.115 文献[18] – 1.802 BSBL-BO 23 10.617 本文所提方法 22 10.342 -
[1] 郭英, 冯茗杨, 孙玉曦, 等. 一种基于蓝牙室内指纹定位的贝叶斯改进算法[J]. 测绘通报, 2019(5): 1–6. doi: 10.13474/j.cnki.11-2246.2019.0138GUO Ying, FENG Mingyang, SUN Yuxi, et al. An improved algorithm of Bayesian fingerprint localization based on Bluetooth[J]. Bulletin of Surveying and Mapping, 2019(5): 1–6. doi: 10.13474/j.cnki.11-2246.2019.0138 [2] SUN Sibo, ZHANG Xinyu, ZHENG Ce, et al. Underwater acoustical localization of the black box utilizing single autonomous underwater vehicle based on the second-order time difference of arrival[J]. IEEE Journal of Oceanic Engineering, 2020, 45(4): 1268–1279. doi: 10.1109/JOE.2019.2950954 [3] SUN Sibo, QIN Shasha, HAO Yu, et al. Underwater acoustic localization of the black box based on generalized second-order time difference of arrival (GSTDOA)[J]. IEEE Transactions on Geoscience and Remote Sensing, 2021, 59(9): 7245–7255. doi: 10.1109/TGRS.2020.3032982 [4] WEISS A J. Direct position determination of narrowband radio frequency transmitters[J]. IEEE Signal Processing Letters, 2004, 11(5): 513–516. doi: 10.1109/LSP.2004.826501 [5] MALIOUTOV D, CETIN M, and WILLSKY A S. A sparse signal reconstruction perspective for source localization with sensor arrays[J]. IEEE Transactions on Signal Processing, 2005, 53(8): 3010–3022. doi: 10.1109/TSP.2005.850882 [6] TIBSHIRANI R. Regression shrinkage and selection via the lasso: A retrospective[J]. Journal of the Royal Statistical Society:Series B (Statistical Methodology) , 2011, 73(3): 273–282. doi: 10.1111/j.1467-9868.2011.00771.x [7] TIPPING M E. Sparse Bayesian learning and the relevance vector machine[J]. The Journal of Machine Learning Research, 2001, 1(3): 211–244. doi: 10.1162/15324430152748236 [8] WIPF D P and RAO B D. Sparse Bayesian learning for basis selection[J]. IEEE Transactions on Signal Processing, 2004, 52(8): 2153–2164. doi: 10.1109/TSP.2004.831016 [9] ZHANG Zhilin and RAO B D. Sparse signal recovery with temporally correlated source vectors using sparse Bayesian learning[J]. IEEE Journal of Selected Topics in Signal Processing, 2011, 5(5): 912–926. doi: 10.1109/JSTSP.2011.2159773 [10] ZHANG Zhilin and RAO B D. Extension of SBL algorithms for the recovery of block sparse signals with intra-block correlation[J]. IEEE Transactions on Signal Processing, 2013, 61(8): 2009–2015. doi: 10.1109/TSP.2013.2241055 [11] BABACAN S D, MOLINA R, and KATSAGGELOS A K. Bayesian compressive sensing using Laplace priors[J]. IEEE Transactions on Image Processing, 2010, 19(1): 53–63. doi: 10.1109/TIP.2009.2032894 [12] NANNURU S, GEMBA K L, GERSTOFT P, et al. Sparse Bayesian learning with multiple dictionaries[J]. Signal Processing, 2019, 159: 159–170. doi: 10.1016/j.sigpro.2019.02.003 [13] SUN Baoming, GUO Yan, LI Ning, et al. Multiple target counting and localization using variational Bayesian EM algorithm in wireless sensor networks[J]. IEEE Transactions on Communications, 2017, 65(7): 2985–2998. doi: 10.1109/TCOMM.2017.2695198 [14] 游康勇, 杨立山, 刘玥良, 等. 基于稀疏贝叶斯学习的网格自适应多源定位[J]. 电子与信息学报, 2018, 40(9): 2150–2157. doi: 10.11999/JEIT171238YOU Kangyong, YANG Lishan, LIU Yueliang, et al. Adaptive grid multiple sources localization based on sparse Bayesian learning[J]. Journal of Electronics &Information Technology, 2018, 40(9): 2150–2157. doi: 10.11999/JEIT171238 [15] CHEN Minqiu, MAO Xingpeng, and ZHAO Chunlei. Direct localization of emitters based on sparse Bayesian learning[J]. IEEE Transactions on Vehicular Technology, 2019, 68(6): 5769–5781. doi: 10.1109/TVT.2019.2910831 [16] YOU Kangyong, GUO Wenbin, PENG Tao, et al. Parametric sparse Bayesian dictionary learning for multiple sources localization with propagation parameters uncertainty[J]. IEEE Transactions on Signal Processing, 2020, 68: 4194–4209. doi: 10.1109/TSP.2020.3009875 [17] SCHMITZ J, MATHAR R, and DORSCH D. Compressed time difference of arrival based emitter localization[C]. The 3rd International Workshop on Compressed Sensing Theory and its Applications to Radar, Sonar and Remote Sensing (CoSeRa), Pisa, Italy, 2015. doi: 10.1109/CoSeRa.2015.7330305. [18] HINCAPIE R, GOMEZ C, BETANCUR L, et al. Sparse framework for hybrid TDoA/DoA multiple emitter localization[C]. 2017 IEEE International Symposium on Signal Processing and Information Technology, Bilbao, Spain, 2017. doi: 10.1109/ISSPIT.2017.8388637. [19] CARLIN M, ROCCA P, OLIVERI G, et al. Directions-of-arrival estimation through Bayesian compressive sensing strategies[J]. IEEE Transactions on Antennas and Propagation, 2013, 61(7): 3828–3838. doi: 10.1109/TAP.2013.2256093 [20] 张政超, 童力. 四站时差无源定位精度分析[J]. 中国电子科学研究院学报, 2010, 5(6): 582–585. doi: 10.3969/j.issn.1673-5692.2010.06.007ZHANG Zhengchao and TONG Li. Precision analysis of passive location of 4-stations based on TDOA[J]. Journal of China Acadewy of Electronics and Information Technology, 2010, 5(6): 582–585. doi: 10.3969/j.issn.1673-5692.2010.06.007 [21] TIRER T and WEISS A J. High resolution direct position determination of radio frequency sources[J]. IEEE Signal Processing Letters, 2016, 23(2): 192–196. doi: 10.1109/LSP.2015.2503921 -



 作者中心
作者中心 专家审稿
专家审稿 责编办公
责编办公 编辑办公
编辑办公
 下载:
下载: