作者中心
专家审稿
责编办公
编辑办公
River-Net: A Novel Neural Network Model for Extracting River Channel Based on Refined-Lee Kernel
-
摘要: 高精度提取合成孔径雷达(SAR)图像中的河流边界，对河流水势监测具有重要意义。以检测郑州7·20暴雨后黄河的健康状况为实施例，该文融合精致Lee滤波思想与卷积操作的滤波特性，提出了基于河道几何特性的优化内部权值卷积核Refined-Lee Kernel，进而提出了一种新型河道提取深度神经网络模型，即River-Net。为验证所提模型的有效性，该文获取了郑州7·20暴雨前后两景欧空局Sentinel-1卫星20 m分辨率干涉宽幅(IW)影像数据，利用暴雨前的影像对模型进行训练，用于提取暴雨后的黄河河道，分析黄河在暴雨后的涨势情况。实验结果表明，相比主流语义分割模型，所提模型能够更精确地在SAR图像中提取河道，对洪水灾害的检测与评估有重要应用价值。
-
关键词:
- 合成孔径雷达(SAR) /
- Refined-Lee Kernel /
- 精致Lee滤波 /
- 神经网络 /
- 河道提取
Abstract: High-precision extraction of river boundaries in Synthetic Aperture Radar (SAR) images is of great significance in monitoring rivers. In this paper, the detection of the health of the Yellow River after the rainstorm in 20 July, 2021 in Zhengzhou is the focus of this paper. The refined-Lee filtering concept and the filtering characteristics of the convolution operation are combined, and an optimized internal weight convolution kernel Refined-Lee Kernel is proposed according to the geometric characteristics of the river channel. A novel river extraction deep neural network model, the River-Net, is also proposed. To verify the effectiveness of the proposed model, this article utilized 20 m resolution Interferometric Wideswath (IW) image data obtained from the European Space Agency Sentinel-1 satellite before and after the 20 July rainstorm in Zhengzhou, employing the images before the rainstorm to train the model. The model, after training, was used to extract the Yellow River channel and analyze the rise of the river after the rainstorm. Experimental results show that the proposed model can extract river channels from SAR images more accurately than trendy semantic segmentation models. The model has important application value for flood disaster detection and evaluation. -
1. 引言
高频地波超视距雷达具有探测距离远、范围广、全天候全时段工作等特点，其工作的高频(High Frequency, HF)频段天然具有反隐身的优势[1]，是保障我国领海不可侵犯、实现超视距探测的重要海洋预警雷达。在高频地波雷达中，接收目标信号主要受到电台干扰、电离层杂波、海杂波等的影响。其中，电台干扰来自于各种短波通讯电台，地波雷达的工作频段在短波通信最拥挤的频段之中，空间中的短波电台信号进入到雷达接收机中被当做目标回波处理，污染了雷达的检测背景；海杂波是雷达发射信号由海面的后向散射所形成的杂波，由于海浪的运动是多方向的，因此在多普勒谱中呈现出两个位置对称的Bragg峰，其存在会淹没实际目标引起雷达漏警；高空中的气体分子受太阳辐射影响发生电离，游离的正离子和自由电子构成了一种称为电离层的特殊等离子结构，雷达发射出的信号通过电离层的调制和反射被接收机接收形成了电离层杂波[2,3]。这些干扰与杂波中，尤其以电离层杂波影响最为广泛，其具有全天候存在特点，时刻制约着地波超视距雷达的探测能力[4]，同时，我国独特复杂的电离层结构分布和物理特性，也使得高频地波超视距雷达中电离层杂波干扰影响尤为严重[5]，如何抑制电离层杂波干扰是目前国内外研究的热点内容。
由于电离层是一种时变的、非平稳的、色散和有耗的分层媒质，它可以对高频雷达发射的电磁波产生复杂的相位调制，造成接收到的回波信号在距离上和多普勒域上的展宽，并且可以通过多种传播路径反射到雷达接收机中，这使得电离层杂波成为最难解决的一种雷达杂波[6]。电离层杂波的复杂性进一步体现其时变、非平稳、非均匀以及部分非高斯的特性在多域中均存在，同一积累周期内的电离层杂波，随距离变化其杂波特性千差万别，在实际处理中很难利用一种方法对所有的电离层杂波进行处理，部分残余的电离层杂波依旧会影响目标的检测，这使得电离层杂波的抑制算法存在着普适性差的问题。因此对于电离层杂波的抑制需要分类分情况处理，对不同杂波类型选取有针对性的抑制方法。
针对传统杂波抑制方法对电离层杂波的处理能力单一、普适性差的问题，本文开展了杂波智能分类抑制处理方法的研究，文章结构如下：首先对电离层杂波的成因和特性进行了分析，然后将目前高频地波超视距雷达现有的杂波抑制算法进行了总结，指出若想有效且全面的对电离层杂波进行抑制，需对电离层杂波样本进行分类识别并对不同类杂波采用有针对性的处理，随后给出了基于半监督聚类的电离层杂波抑制方法，最后本文提出了一种电离层杂波的智能分类处理方法框架，以贪婪方法作为算法选取策略为例给出了电离层杂波类型与算法的一种匹配方案，通过对实测数据的处理验证了该电离层杂波抑制方法的有效性。
2. 电离层杂波的成因与特性
电离层是由大气中的气体受到太阳辐射而离子化所产生的等离子体所构成。这些等离子体虽然是由原子失去电子而形成的，但是其整体上却呈中性，其主要特性受电子温度、电子浓度、碰撞频率、离子温度、离子浓度、离子成分及其空间分布情况影响[7,8]。等离子体的不同特性使得电离层对入射到电离层的电磁波产生反射、折射与吸收等不同作用，低频段的电磁波更容易被电离层反射，而高频段的电磁波更容易穿透电离层，仅产生折射现象，随着电离层电子密度的提升，电磁波越难穿透电离层，电离层的反射能力越强[9]。除了反射与折射作用，电离层还对电磁波有吸收作用。当电磁波射入电离层后，受其影响电离层中的自由电子无规则运动加剧，并与其他粒子产生碰撞、结合等效应，这些运动与效应所消耗的能量全部由电磁波所提供，因此电磁波能量被电离层所吸收[10]。
随着形成电离层的电子浓度的不同，其在60～1000 km之间可大致分成3个不同的等离子体。在垂直方向上，从低到高可以依次划分为D层、E层、F层，F层又分为F1层和F2层，由于离子浓度的不同，高频电磁波可以穿透D层电离层，会被E层、F层折射与反射。电离层的分层结构会随着时间而变化，在夜晚D层会消失，E层会变得非常稀薄，F1层和F2层会融合为一层，统称F层。除了这些常规划分之外，还存在一些不均匀的电离层结构，其存在具有一定的偶然性，例如偶发E层(Es层)与扩展F层。这些不均匀结构中Es层较为常见，它主要出现在E层附近，其自由电子浓度往往要高于其附近区域一倍以上，其厚度在0.2～5.0 km间不等。Es层的出现具有偶然性，其水平覆盖范围最大可达到2000 km，维持时间从数十分钟到数小时不等，并且其存在随机运动和定性漂移[11]，当Es层离子浓度足够高时，高频电磁波会被其直接反射。扩展F层是出现在F层附近的电离层不均匀体构成的，常出现在赤道地区附近，在较强流体不稳定性存在时也会在中纬度地区出现，其出现高度在250～1000 km范围内甚至更高处。高频雷达信号经过含有不规则体的电离层传播介质时，随机介质对在其内部传播的电波进行了随机调制，会造成回波信号空时采样样本之间相关性的下降，其中，对信号的空间扰动使得波前相位发生随机波动，引起回波空间谱的展宽。另一方面，受不规则体结构漂移运动和时变特性的影响，对信号的时间扰动使得接收信号脉间相位关系发生随机变化，导致回波多普勒谱展宽[12]。电离层大致分布情况如图1所示。
在高频雷达系统中，由于地球曲率的存在，雷达的发射信号会有部分能量向高仰角方向泄露，电离层杂波是雷达的发射信号在高仰角上的能量泄露经由不同层电离层调制反射被雷达接收机接收所形成。对于固定高度的电离层反射面，不同仰角的回波会导致在距离上产生不同的分布；对于一个固定的仰角，当电离层高度改变时，其杂波距离也会改变。电离层中，E层、Es层、F层均具有反射与散射雷达信号的能力，短波在电离层中的多次反射与散射也会造成多跳的电离层杂波，此外，通过电离层反射到海面的信号也会与目标及海杂波一起沿海水传播进入接收机，成为更为严重的一种干扰杂波。图2给出了电离层杂波可能存在的几种主要路径。
受电离层自身特性影响，电离层杂波在距离上和多普勒分辨单元上是展宽的，且电离层杂波具有时变、非平稳、非均匀以及部分非高斯的性质[5,7,8]。其时变、非平稳性表现在小时间尺度上，且电离层杂波会随着地点、观测方式、观测角度、宇宙环境等不同因素而变化，导致难以分析其统计特征；非均匀性表现在电离层杂波在检测背景中的分布具有同质、异质杂波共存的特点，不同的探测环境和探测条件都可能造成杂波的非均匀，其非均匀导致在样本选取时，很难获得同质的训练样本，这给杂波的参数估计带来了较大的困难，进而削弱了杂波抑制算法的性能，甚至算法失效；由于电离层传播介质物理特性复杂等因素，杂波环境中同质异质分布杂波共存造成了部分杂波非高斯分布，这与传统的检测与抑制算法的基本假设所矛盾，造成模型的失配。这些性质同时体现在不同域中，因此想要对电离层杂波进行研究，需要从不同域、多个角度的不同特性对电离层杂波进行描述。由于电离层具有非平稳、非均匀的特性，对电离层杂波均匀性与平稳性的分析将尤为重要，同时，杂波的功率强弱、方向性指向与图像域的特性直观影响了目标的检测能力，因此以下以功率特征、图像小波尺度特征、方向性特征、空域同质性特征和距离域平稳性特征五个部分为例，对电离层杂波进行分析。
电离层杂波在功率特征上呈现出不同强弱的分布，在文献[13,14]中对电离层杂波功率特性在距离-多普勒(Range-Doppler, RD)域中的分布进行了研究，其将电离层杂波的功率特性分成了聚集型与分散型两种，聚集型杂波具有较强的功率，且在RD谱中呈现出规则的连通形状，占据有限的距离单元；分散型杂波的功率较弱，且在RD谱中占据大量的距离单元与绝大多数的多普勒单元。图3(a)给出了实测数据的RD谱，图3(b)给出了聚集型电离层杂波所在区域。从中可以看出，聚集型电离层杂波具有较强的功率且在RD谱中是“连通”的。
电离层杂波在图像域上呈现出不同小波尺度的特性，在文献[15]中，其将电离层杂波的小波特性划分为与目标尺度相近和与目标尺度不同两种，并提出了以小波空间主角的大小作为参数区分两种不同特性的手段。图3(c)给出了对实测数据计算小波空间主角的结果，小波空间主角越小，电离层杂波的小波尺度越与目标尺度相近。
电离层杂波在空域上呈现不同方向性的特性，在文献[16]中，其利用稀疏分解的方法获取电离层杂波的超分辨空间谱，根据空间谱中非零值的数量将电离层杂波方向性特性划分为集中型与分散型两种表征形式，方向性集中型杂波的空间谱呈现有限个峰值，方向性分散型杂波的空间谱呈现出均匀分布的形式。图3(d)给出了实测数据中第54距离门的稀疏空间谱，该距离单元同时具有集中型与分散型两种杂波特性的杂波。
电离层杂波在空域的统计特征上呈现不同的分布特性，文献[17]对电离层杂波的空域同质性进行研究，文中提出了邻域空间相关性(Neighborhood Spatial Correlation, NSC)系数，用以描述不同分辨单元间电离层杂波在空域分布上的相关性。邻域空间相关性系数越大，电离层杂波的空域同质性越强；反之，则表示电离层杂波的空域异质性越强。图3(e)给出了实测数据的NSC系数，结合专家知识与统计结果，可以通过阈值选取的方式获取到空域同质的电离层杂波与空域异质的电离层杂波。
电离层杂波在距离域上呈现不同的相关特性，在文献[18]中，其使用杂波子空间距离相关性分析的方法，对电离层杂波距离维的相关性进行了研究。其提出距离相关性系数较大的杂波具有距离维相关性，反之则为距离维非相关杂波。图3(f)给出了实测数据的距离相关性系数，与NSC系数相仿，同样可以通过阈值选取的方式获取具有距离维相关性的电离层杂波。
以上这5种电离层杂波特性，每种特性都直接影响着杂波抑制算法的性能与目标的检测能力。杂波的功率特性中，功率聚集型杂波具有较强的功率，往往会将目标淹没在其中，是影响目标检测的主要因素之一；杂波的小波特性中，目标与杂波的小波特性越相近，杂波越易呈现出点状图像特征，目标检测算法中的虚警概率越高；杂波方向性特征中，杂波的方向性特性直接影响着对消算法中杂波协方差矩阵的估计，分散型杂波会造成对消算法自由度过度消耗，降低杂波抑制性能；杂波的空域同质性特性中，空域异质性越强，空域对消算法中协方差矩阵的估计越困难；杂波的距离域相关特性中，相关性越弱，越难获得杂波的统计特性，空时联合算法中杂波协方差矩阵越难估计。对电离层杂波特性的分析有助于杂波抑制算法的开发与改进。
3. 电离层杂波抑制方法综述
电离层杂波的复杂特性使得它在与其他种类杂波抑制方法的研究对比中，既具有相似性也具有特殊性，无法直接套用其他杂波的抑制方法。以机载雷达中的杂波抑制方法研究为例，虽然这两种杂波都具有非均匀性与非平稳性[19]，但二者的产生机理不同，他们的杂波抑制方法也不尽相同。例如，机载非正侧视阵雷达中的非均匀杂波问题[20-22]与电离层杂波的非均匀问题就具有相似性，二者都是由于训练样本的非均匀性导致无法准确估计杂波协方差阵，因此其抑制方法具备一定的共通性，机载雷达杂波抑制算法中对训练样本进行筛选的思想可以直接应用在电离层杂波的处理中[4,23]。而在非平稳性问题的处理上，二者却又截然不同，机载雷达中杂波的非平稳分布是由雷达天线的配置方式导致的，例如：非正侧面阵、圆柱形阵、共形阵、双多基地配置以及分布式雷达等都会引起杂波的距离相关性，导致非平稳杂波的产生。在机载雷达中，非平稳杂波的空时分布特性可以通过系统参数预先估计得到，可以通过补偿的方式抑制[19]；而电离层杂波的非平稳性是由于电离层电子密度的不规则变化所引起，其参数难以获得，无法对其进行估计，因此不可以通过补偿的方法进行抑制。考虑到两种杂波的相似性，对双方抑制方法研究的参考将可以起到相互启发的作用，而电离层杂波的特殊性则使得其难以套用其他杂波的抑制方法，必须针对电离层杂波特性进行算法开发。
在电离层杂波抑制的研究中，学者们根据杂波处理层面的不同，将抑制方法分为雷达系统层面抑制与信号处理层面抑制两种。在雷达系统层面抑制的研究主要集中在雷达的收发天线与雷达发射波形的设计，包括低仰角发射天线、极化接收天线等，文献[24-27]给出了使用二维阵列，依靠阵列自身在方位-俯仰维的分辨能力，利用二维自适应算法抑制高仰角电离层杂波。文献[28]给出了一种L阵列辅助通道构造方法，以获得不含水平方向回波的辅助通道数据，通过对消的方法抑制电离层杂波。考虑到高频地波超视距雷达工作的频段内密集分布着各种短波段干扰，很难找到连续的带宽满足分辨要求，最早由Green等人[29]提出发射频谱截断的非连续谱信号来在频域对抗这一干扰，其后相继发展成非连续谱信号主要包括非连续谱调频信号、非连续脉冲频率编码信号、非连续相位编码信号[30-34]以及综合以上3种信号形式的复杂信号[35,36]；在抗干扰的基础上，文献[37,38]提出一种同时抗频域干扰和抗折叠杂波的波形设计方法，这些波形都在一定程度上提高了系统的抗干扰能力。
在雷达信号处理层面抑制，当前对于电离层杂波的抑制主要依赖于自适应对消信号处理方法，包括自适应阵列信号处理，现代谱估计技术，自适应子空间监测、滤波等。以下将从杂波抑制算法的两个研究趋势角度，分析目前现有的杂波抑制技术。
(1) 电离层杂波的复杂性促使算法研究从单一域处理向多域联合处理方向发展。
在电离层杂波抑制的早期研究中，算法的开发往往是在单一域上的处理，在空域上，Chan等人[2]率先使用相参旁瓣对消算法在空域上对电离层杂波抑制，其研究结果表明对于电离层杂波，同一个距离门内的杂波信号会表现出相对较高的空间相关性，采用逐距离门处理的方法可以获得最优的空域杂波抑制性能。在此基础上，李雷[28]设计了一种单凹口辅助通道对消算法，通过空间陷波器构造理想的辅助通道数据，以获取不含主瓣方向的杂波回波信号，采用对消处理在抑制杂波的同时保护了目标回波。该方法可以有效的对旁瓣电离层杂波进行抑制，但对主瓣杂波无能为力。在频域上，Leong[39]利用电离层对不同频率电磁波的反射特性，设计并提出了基于双频工作模式的雷达系统，使用两种不同工作频率的雷达信号对目标和杂波进行分离。但电离层杂波仍有可能同时覆盖两个工作频率，双频的方法无法彻底解决电离层杂波问题，反而提高了系统的复杂度。在极化域上，毛兴鹏[40,41]在研究中提出了零相移滤波器的方法，主要针对电离层中Es层杂波进行抑制，其利用极化滤波的方法对电离层杂波中椭圆极化的杂波进行滤除，对于沿海面返回的与目标极化特性相近的电离层杂波缺乏抑制能力。
然而电离层杂波是一种时变的复杂杂波，其在单一域内的特征复杂多变，往往在这一距离门中目标和杂波在某一域内区分度较大，下一距离门中二者在同一域内的差异性就变的极小了，单一域的处理始终无法很好的抑制电离层杂波，为弥补单一域处理的不足，多域联合处理的方法逐渐被提出。
在高频地波超视距雷达系统中，多域联合处理主要体现在空时联合与时频联合。Adve和Riddolls的团队[42,43]使用高频雷达中电波的传播理论建立了符合加拿大地区电离层情况的电离层杂波模型，并将机载雷达中的多种空时自适应处理方法(Space Time Adaptive Processing, STAP)引入到高频地波超视距雷达系统中。在时频域联合处理中，熊新农等人[44]提出了一种基于时频分析的电离层杂波抑制方法，利用电离层杂波与目标在时频域上变化速率的不同对目标与杂波进行分离。在进一步的研究中，文献[45]提出了一种基于时频-脊波域滤波的方法，利用目标与杂波在时频域上的不同图像特征，对目标与杂波进行滤波分离。这些多域联合方法，增加了系统自由度，扩大了目标与杂波的区分度，其理论效果往往要优于单一域的一维处理方法，多域联合是当前电离层杂波抑制研究的主要趋势。
(2) 电离层杂波的非均匀、非平稳性促使算法研究从认知处理向智能化杂波抑制算法方向发展。
认知雷达的概念最早是由Haykin[46]于2006年提出，其希望雷达能够通过与环境的不断交互探测，获取战场环境的相关数据，结合专家知识自适应的调整发射与接收端的相关参数，以达到自动探测目标的目的。在高频地波超视距雷达的研究中，认知处理主要体现在对样本的筛选与知识辅助中，以解决电离层杂波的非均匀、非平稳问题。
在电离层杂波的抑制算法初期研究中，算法往往是采用逐距离门处理或滑动窗口处理的方法，缺乏对距离门中样本的筛选[2]。而电离层杂波在检测背景中的分布具有同质、异质杂波共存的特点，不同的探测频率、不同的季节、不同的时间、不同的地理位置、不同的宇宙环境(如太阳黑斑、流行余迹等)都可能造成杂波的非均匀[47]。这种非均匀性使得逐距离门处理的方法很难获取同质的训练样本，为杂波特性的估计带来极大的困难，进而削弱了杂波抑制算法的性能，甚至算法失效。为解决杂波样本的非均匀问题，基于样本筛选的电离层杂波抑制算法逐渐被提出。文献[4]在其研究中率先提出了样本筛选的概念，针对大目标与1阶海杂波过度消耗对消系统自由度的问题，设计了一种基于目标海杂波剔除的预检测对消(Detection Before Cancellation, DBC)方法，通过CFAR检测与海杂波检测剔除大目标和Bragg峰样本，以获取纯电离层杂波训练样本，该方式也被应用在机载雷达的非均匀杂波抑制研究中[23]。但对于电离层杂波只占据部分多普勒单元的情况，该方法同样会将非电离层杂波样本抽选进样本集，无法根据实际杂波环境调整样本集的规模和抽样方式，有效适应电离层杂波分布的多样性。在此方法之上，文献[48]提出了一种基于边缘检测与杂波分段的训练样本筛选方法，该方法采用图像处理中的边缘检测技术对杂波样本实施分段，根据杂波功率变化情况将杂波划分为若干区域，并根据当前数据点所属区间合理选择训练样本集。然而该方法获取的电离层杂波样本中存在同质、异质杂波共存的问题，导致杂波协方差估计困难，电离层杂波抑制性能受限。文献[18]在前两种方法的基础上，设计了一种优化样本选择的多维联合杂波及干扰抑制方法，通过对回波数据的距离相关性分析，将电离层杂波样本分为距离平稳杂波样本(距离域分布同质样本)与距离非平稳杂波样本(距离域分布异质样本)，对不同类型样本采用不同的加权协方差估计方法进行处理。类似的，文献[17]对电离层杂波在空域分布的同质性分析，提出了一种基于杂波分类的电离层杂波抑制方法，其设计了邻域空间相关性系数用以定量的描述电离层杂波在不同分辨单元间的空域同质性，通过门限筛选出空域同分布的电离层杂波，采用变加权方式估计杂波协方差矩阵，使得同质的电离层杂波样本在杂波协方差估计中起到更大的作用，异质的样本起到的作用减弱。
除训练样本的筛选外，另一种认知处理——基于知识辅助的方法概念被提出用以针对时变非平稳的杂波。该方法利用多种异类传感器和先验知识，比如对机载前正视雷达，使用事先测绘的数字地图、实时的载机信息等作为辅助知识，对地波超视距雷达使用长期观测的电离层杂波统计数据辅助杂波估计。然而基于知识辅助的方法对专家知识的依赖性较强，一些不在专家知识库中的突发性杂波数据无法形成有效的应对处理。针对这种感知处理方法的局限性，智能处理的概念被提了出来[49]，它在感知的基础上，具备了性能评估、匹配决策和错误修正的学习能力，可以利用感知到的杂波信息结合专家知识进行分析、评估、判断、决策、修正，自适应的匹配最优杂波抑制算法并调整算法参数，进而得到最优的杂波抑制性能。随着人工智能的发展，智能杂波抑制方法正成为最新的研究热点。
综上，通过以上对目前现有电离层杂波抑制算法的分析，若想有效且全面的对电离层杂波进行抑制，需对电离层杂波样本进行分类识别并对不同类杂波智能的匹配有针对性的处理。例如在杂波抑制处理方法中，对于在某一域中特征明显的杂波，可以使用单一域处理的方法，如在方位、多普勒、小波域或极化域中特征明显的杂波可以使用自适应空域滤波[4,50]、小波斜投影滤波[15]或者极化处理[41]的方法；对于多域联合特征明显的可以采用多域联合处理，如空时STAP处理[51]、时频处理[44,52]、时频-脊波域滤波处理[45]等。
4. 电离层杂波的分类方法
上一节本文剖析了现有电离层杂波抑制算法，在面对复杂多变的电离层杂波时，单一的算法处理显然无法完成对全部距离单元电离层杂波的整体抑制，部分距离-多普勒区域残留的杂波依然会影响目标的检测。由此提出了对电离层杂波进行分类，根据不同类型杂波所表现出来的特性，有针对性的选择相应处理方法，这可以有效的解决复杂电离层杂波抑制问题。如何对电离层杂波进行分类，使得每种杂波类型可区分性强且可匹配到适合处理的杂波抑制算法，是电离层杂波分类的难点。
在杂波分类的研究中，Haykin[53-55]首次提出了杂波分类技术，构建了特征提取-杂波分类-分类器性能评价的一整套较为成熟的分类体系，为后续认知雷达奠定了坚实的基础。后续的杂波分类研究主要围绕着杂波特征提取与不同分类器的应用这两个问题展开，如利用杂波模型的幅相、相关度、熵、高阶累计量等统计特征进行杂波分类，利用支持向量机、人工神经网络、有监督聚类等分类器进行杂波分类[56-59]。在高频地波超视距雷达的杂波分类研究中，李杨[60]以Haykin的研究为基础利用卷积神经网对高频雷达回波数据中的海杂波、电离层杂波、目标进行了分类性能研究。通过建立多维特征库，利用部分有监督的样本进行训练，完成了海杂波与电离层杂波的分类识别。但在其研究中，仅将电离层杂波通过功率大小分为强电离层杂波与弱电离层杂波两种，其分类结果无法对杂波抑制算法起到辅助作用。同样的，在加拿大Chan[61]的研究中将电离层杂波以其所在层和杂波形状进行分类，不同层之间的杂波存在相似性，同一层的杂波也存在差异性，其分类结果依然很难与杂波抑制算法匹配。由于对电离层杂波的分类存在监督样本的难以获取、样本数量不足、分类准则难以选取的问题[12]，导致有监督分类算法产生过拟合，造成分类准确率降低，模型缺乏泛化能力。因此，利用有限的监督样本对电离层杂波进行半监督的聚类，可以有效减少对监督样本数量的依赖，将是解决电离层杂波分类问题的一种合理方法。
4.1 典型电离层杂波特征分析
电离层杂波类别划分的过程是一个典型的半监督聚类过程，即将数据集中的样本按监督信息划分为若干个互不相交的子集，每个子集对应一些潜在的杂波特性，子集所对应的概念语义需由使用者来把握和命名[62]。在电离层杂波分类问题中，典型的杂波样本作为重要的监督信息，其特征须能为杂波抑制算法提供一定辅助。在对电离层杂波实测数据的分析处理中，可以发现电离层杂波在不同域呈现出不同的特性，我们称每种不同的特性组合为一种电离层杂波模式，同一模式的杂波具有相同特征，可以采用相同的杂波抑制算法进行处理。然而，随着杂波特性的增加，杂波模式的数量将成指数倍的增长，为每一种模式的杂波均设计一种抑制算法显然是不可行的。因此，对电离层杂波进行分类，将一些模式相近、可以采用同种抑制算法的杂波进行统一处理是必要且有意义的。
根据文献[4,15-18]的分析，按样本密度最大化原则，结合实测数据，本文提出了5种典型的电离层杂波类型，其杂波特性如表1所示。其中，能量聚集型强方向性杂波往往是由电离层不规则体对雷达发射信号的反射所形成，其功率较强，在RD谱中较为聚集，占据有限个多普勒单元与距离单元，往往具有较为集中的方向性，其空域分布较为同质，距离上相关；点状电离层杂波一般是由扩展E层或F层反射所形成，其功率相对较强，但在RD谱中分布较为集中呈现出点状，覆盖多个距离单元与绝大多数的多普勒单元，没有统一的方向性，且空域分布不统一，距离上相关性较差，是一种主要的电离层杂波干扰；空域同分布杂波一般是由电子浓度变化较快的E层或F层反射所形成，其功率较弱，分散在RD谱中，占据多个距离单元与多普勒单元，且多普勒频率较大，方向性分散但在多普勒域具有相同的空域分布，在距离域上非相关；距离域相关杂波一般是由电子浓度变化较慢的E层或F层反射所形成，其功率较弱，分散在RD谱中，占据多个距离单元与多普勒单元，且分布在零多普频率附近，方向性分散且缺乏统一的空域分布，在距离域上相关；类目标杂波一般没有统一来源，其在RD谱呈点状分布，与点状杂波不同的是这种杂波在RD谱上功率分布较为分散，且具有集中的方向性，其存在会导致空域对消算法的自由度损耗，影响对消算法性能，同时也会造成虚警概率提升。图4给出了这5种典型杂波的示意图。这5种杂波模式的样本密度大，具有不同的处理算法，本文将以其为例对电离层杂波进行进一步分类。
表 1 典型电离层杂波特性Table 1. Characteristics of typical ionospheric clutter杂波类型 功率 小波尺度 方向性 空域同质性 距离域相关性 能量聚集型强方向性 聚集 与目标相异 集中 同质 相关 点状 聚集 与目标相似 分散 异质 非相关 空域同分布 分散 与目标相异 分散 同质 非相关 距离域相关 分散 与目标相异 分散 异质 相关 类目标 分散 与目标相似 集中 异质 非相关 4.2 基于半监督聚类的电离层杂波分类方法
假设在电离层杂波的特征提取阶段获取到的杂波特征数为
$K$ ，每个特征具有${d_k}$ 个表征形式，则可以通过排列组合得出共可将杂波分成$\prod\nolimits_{k = 1}^K {{d_k}}$ 个杂波模式。当提取出的杂波特征数$K$ 较少时，我们可以根据规则直接利用每种杂波模式所对应的杂波特征进行抑制算法的匹配，如图5所示；随着提取出的杂波特征数$K$ 增大，即便每个特征所具有的表征形式数量${d_k}$ 较小，杂波模式依旧会以几何倍数增加，此时继续采用杂波特征与抑制算法的一一对应方式显然不合理也做不到。因此，需要找到一种合理的杂波类别划分方式，满足：每个杂波类型有一定的实际物理意义且至少对应一种杂波抑制算法；每个杂波类型中杂波模式相近(即杂波特征差异最小)。
图 5 传统的电离层杂波分类抑制处理框架流程图Figure 5. Traditional ionospheric clutter classification and suppression processing framework在杂波类别划分的过程中，由于以上约束条件的存在，需要引入了额外的监督信息，故杂波类别划分是一个半监督聚类问题。可用于对电离层杂波聚类的半监督算法有很多种，如K均值算法、基于密度敏感的半监督聚类算法、基于空间条件分布的半监督聚类方法、Bayes 判别法、Fisher 判别函数法、距离函数法和K-近邻法等。本文以约束种子K均值算法(Constrained Seed K-Means, CSKM)为例，给出一种基于半监督聚类的电离层杂波分类方法处理过程。CSKM算法是在K均值算法(K-means)的基础上改进而来，使用监督数据做为初始聚类种子，其可以在标记样本不足的情况下，实现半监督分类，并且具有迭代寻优的特性，可以最大化的实现分类的精确。
给定电离层杂波样本集
$D = \left\{ {{x_1}}\ \ {{x_2}}\ \ ··· \ \ {{x_m}} \right\}$ ，聚类后所得到的簇划分为$\mathbb{C} = \left\{ {{C_1}}\ \ {{C_2}}\ \ ··· \ \ {{C_k}} \right\}$ ，典型杂波类型的样本簇为${\mathbb{C}^*} = \left\{ {C_1^*}\ \ {C_2^*}\ \ ··· \ \ {C_k^*} \right\}$ ，电离层杂波类别划分问题要求每个杂波类型中杂波特征差异最小，即最小化均方误差minCE=k∑i=1∑x∈Ci‖x−μi‖22,s.t. C∗i⊂Ci,i=1,2,···,k (1) 其中
μi=1|Ci|∑x∈Cix (2) 是簇
${C_i}$ 的均值向量。从式(1)和式(2)，均方误差$E$ 描述了簇内样本围绕簇中心点的紧密程度，均方误差越小，簇内样本分布越集中。对于式(1)给出的最优化问题，找到其最优解需要考察样本集$D$ 的所有可能簇划分，这是一个NPC问题，可以采用贪心策略，通过迭代优化的形式来近似求解。考虑到电离层杂波特征属性为离散属性，且样本属性的定义域为一种抽象概念，属于无序属性，在计算样本之间距离
${d_{ij}}$ 时，无法直接使用属性值进行闵可夫斯基距离计算，因此这里引入值差分度量(Value Difference Metric, VDM)[63]用以计算不同样本间的距离。令
${m_{u,a}}$ 表示在属性$u$ 上取值为$a$ 的样本数，${m_{u,a,i}}$ 表示在第$i$ 个样本簇中在属性$u$ 上取值为$a$ 的样本数，$k$ 为样本簇数，则属性$u$ 上的两个离散值$a$ 与$b$ 之间的VDM距离为VDMp(a,b)=k∑i=1|mu,a,imu,a−mu,b,imu,b|p (3) 因此，两个电离层杂波样本
${x_i}$ 与${x_j}$ 之间的距离${d_{ij}}$ 可以表示为dij=(K∑u=1VDMp(xiu,xju))1p (4) 4.3 杂波分类的性能与实验验证
聚类性能度量也可称为有效性指标，一般用其对聚类结果进行性能度量来评估其优劣。聚类性能的度量方式可以分为两种，其一为将聚类结果与某个参考模型进行比较，此种度量方式为外部指标；其二为直接考察聚类结果本身的属性而不依靠任何外部模型，此种度量方式为内部指标。考虑到在电离层杂波的聚类过程中，我们无法得到可靠的真实分组情况，即无法得到确切的监督信息，因此这里考虑采用计算内部指标的形式对电离层杂波分类结果进行评价。
戴维森堡丁指数(Davies-Bouldin Index, DBI)，又称为分类适确性指标，是由Davies和Bouldin[64]提出的一种评估聚类算法优劣的指标。考虑聚类结果的簇划分
$\mathbb{C} = \left\{ {{C_1}}\ \ {{C_2}}\ \ ···\ \ {{C_k}} \right\}$ , DBI指数为DBI(C)=1kk∑i=1maxj≠i(avg(Ci)+avg(Cj)dcen(μi,μj)) (5) 其中
avg(C)=2|C|(|C|−1)∑i≠j∈[1,|C|]dist(xi,xj) (6) dcen(Ci,Cj)=dist(μi,μj) (7) ${\rm{ dist}}\left( \bullet \right)$ 为两个样本之间的距离，可带入式(4)求解。${\rm{avg}}\left( C \right)$ 表示簇内样本的平均距离，${d_{{\rm{cen}}}}\left( {{C_i},{C_j}} \right)$ 表示簇${C_i}$ 与簇${C_j}$ 聚类中心之间的距离。从式(5)中可以看出，DBI指数描述了聚类后类内样本距离之和与类间距离之比，DBI指数越小，聚类性能越好。邓恩指数(Dunn Index, DI)是由Dunn[65]提出的另一种内部指标，用以衡量聚类结果的性能。DI指数为
DI(C)=min1≤i≤k{minj≠i(dmin(Ci,Cj))}max1≤l≤k(diam(Cl)) (8) 其中
dmin(Ci,Cj)=min∀xi∈Ci∀xj∈Cjdist(xi,xj) (9) diam(C)=maxi≠j∈[1,|C|]dist(xi,xj) (10) ${\rm{dist}}\left( \bullet \right)$ 为两个样本之间的距离，可带入式(4)求解。${d_{\min }}\left( {{C_i},{C_j}} \right)$ 表示簇${C_i}$ 与簇${C_j}$ 最近样本间的距离，${\rm{diam}}\left( C \right)$ 表示簇$C$ 内样本间的最远距离。从式(8)中可以看出，DI指数描述了任意两个簇元素间最短距离与任意簇内样本最大距离的比值，DI指数越大，簇间距离越大，簇内距离越小，聚类性能越好。仿真实验设置的样本数为10000个，每个样本的属性均为随机生成，考虑实际情况中典型杂波的样本数量要高于其他模式的杂波样本，因此这里对典型杂波样本进行了10%的数量增强。选取的样本特性个数为5，聚类簇数
$k$ 为6个簇，算法迭代次数为1000次，收敛条件为全部簇中心在迭代前后不变。在CSKM算法中，引入的监督样本为文中所提出的5种典型电离层杂波样本，同时设置了一种不具有这5种特性的杂波作为监督样本，其代表了本文所提5种特性无法描述的电离层杂波类型。这里对比了传统K-means算法与CSKM算法的聚类性能。表2与表3给出了两种聚类算法收敛后各聚类簇样本的特性统计，其数值表示该分类簇中具有对应特性的样本数占该簇总样本数的比例，1代表分类簇所有样本均具有该特性，0代表分类簇所有样本均不具有该特性。表 2 K-means算法聚类后样本的特性统计Table 2. Characteristic statistics after K-means algorithm clustering类型 特性A 特性B 特性C 特性D 特性E A 0 0.26 0.21 0.29 0.25 B 0.44 0.85 0.15 0.41 1.00 C 0.29 0 0.23 1.00 1.00 D 1.00 0.02 0.88 0.04 0.03 E 1.00 0.60 0.09 0.79 0 F 0 0.64 1.00 0.81 0.22 表 3 CSKM算法聚类后样本的特性统计Table 3. Characteristic statistics after CSKM algorithm clustering类型 特性A 特性B 特性C 特性D 特性E A 1.00 0.07 0.90 1.00 0.86 B 0.99 1.00 0.11 0.18 0.14 C 0.15 0 0.11 1.00 0.30 D 0.09 0 0.08 0 1.00 E 0.13 1.00 1.00 0.07 0.06 F 0 0.04 0 0 0 从表2中可以看到，K-means算法由于缺乏专家知识的指导，聚类后的样本簇多数不具有统一的特性，例如在类型B中，有44.2%的样本具有特性A, 41.1%的样本具有特征D，类型B中显然是由多种模式的杂波所构成的，其聚类结果只是数据上的最优解，无法给出每个聚类簇所对应的电离层杂波的实际物理意义，同样也难以给出针对每种类型杂波的抑制算法。而在表3中，由于引入了监督信息，约束杂波样本以典型杂波类型为聚类中心进行聚类，因此其每个聚类簇均拥有较为统一的特性，且每个聚类簇均可与一种典型的电离层杂波类型相对应。表4给出了两种算法的分类性能指标对比，CSKM算法的DBI指数更小且DI指数更大，这说明CSKM算法的类内间距更小，类间间距更大，聚类性能更好。
表 4 聚类结果有效性指标Table 4. Validity index of clustering results算法 DBI DI K-means 0.9916 0.2500 CSKM 0.6336 0.3333 为进一步验证电离层杂波的分类性能，这里同样对实测数据进行分类并计算了其聚类有效性。实测数据采用高频地波超视距雷达的回波数据，天线阵列的分布为均匀线阵，图6给出了实测数据的距离-多普勒谱，波束指向
$\theta = - {9^ \circ }$ 。可以看到部分电离层杂波占据了几乎全部的多普勒单元，在其覆盖范围内很难检测出目标。对该批数据进行特征提取，分析实测数据电离层杂波所具有的特性。实验中，电离层杂波样本个数为24554个，选取的杂波特性个数为5个，聚类簇数$k$ 为6个簇，算法迭代次数为1000次，收敛条件为全部簇中心在迭代前后不变。与仿真实验相同，CSKM算法引入的监督样本为章节3.1中所提5种典型电离层杂波，同时设置了一种不具有这5种特性的杂波作为监督样本，其代表了本文所提5种特性无法描述的电离层杂波类型。这里对比了传统K-means算法与CSKM算法的聚类性能。表5与表6给出了两种聚类算法收敛后各聚类簇样本的特性统计，其数值表示该分类簇中具有对应特性的样本数占该簇总样本数的比例。与仿真相似，K-means算法的聚类结果缺乏统一的杂波特性，很难针对每种类型的杂波进行抑制。对比CSKM算法的聚类结果，可以发现由于引入了监督信息，除类型C与类型F外的聚类结果均具有较为统一的杂波特性，且可以与电离层杂波的实际物理意义相对应，能够找到具有针对性处理的抑制算法。表7给出了两种算法的分类性能指标对比，两种算法的DI指数相同，但CSKM算法的DBI指数更小，这说明CSKM算法的类内间距更小，类间间距更大，聚类性能更好。
表 5 K-means算法聚类后样本的特性统计Table 5. Characteristic statistics after K-means algorithm clustering类型 功率聚集性 小波尺度相似性 方向集中性 空域同质性 距离域相关性 A 0.76 1.00 0.69 0.68 0.79 B 0.78 0.34 0.80 0 0 C 0 0.13 0 0.12 0.16 D 1.00 0 0 0.44 0.87 E 0.50 0 1.00 0.61 0.73 F 0 0.80 0 0.86 0.99 表 6 CSKM算法聚类后样本的特性统计Table 6. Characteristic statistics after CSKM algorithm clustering类型 功率聚集性 小波尺度相似性 方向集中性 空域同质性 距离域相关性 A 0.73 0 0.77 0.87 0.86 B 0.83 1.00 0.10 0.15 0.12 C 0.09 0.55 0.10 1.00 0.78 D 0.12 0 0.13 0 1.00 E 0.14 1.00 0.92 0.18 0.15 F 0.14 0.03 0 0 0.10 表 7 聚类结果有效性指标Table 7. Validity index of clustering results类型 DBI DI K-means 1.3976 0.2500 CSKM 0.8224 0.2500 对于杂波类型C，该种电离层杂波在空域上是同质的，55%的样本在小波尺度上与目标相近，78%的样本在距离域上相关，簇内部特性不统一。对杂波类型C中的样本分布进行分析，可以得到监督样本(空域同分布杂波样本)仅占该簇样本总数的27.7%，占全部样本总数的1.4%。对比聚类结果较为统一的其他类型杂波，如杂波类型D，其监督样本占该簇样本总数的74.8%，占全部样本总数的18.3%。可以发现杂波类型C簇内样本特性不统一的主要原因是其监督样本数量在该批次数据内较少，即该批次数据中空域同分布杂波分布较少。对于杂波类型F，其代表了本文所提出的5种杂波特性无法描述的杂波类型，其样本占总体样本数的18.98%。这类杂波在距离多普勒谱上表现为分散的杂波，在图像上其小波尺度与目标尺度相差较大，且杂波方向性较为分散无明显回波指向，其与周围其他样本在空域上分布不同，在距离域上非相关，是一种完全的时变、非平稳、非均匀且非高斯的杂波。若想对其进行分类，现有的杂波特性不足，需引入新的杂波特性，针对这些杂波样本的研究将在未来的研究工作中展开。
图7给出了实测数据的电离层杂波分类结果的距离多普勒分布，不同颜色区域代表不同的电离层杂波类型，由于电离层往往处于100 km以上，所以分类算法不会对近区进行处理。对比图5与图6，可以看到多数的电离层杂波都能分类到典型的电离层杂波类型中，且每种类型的杂波都是分区域出现的，具有一定的连通性，这说明相邻分辨单元的杂波具有相似性，与实际情况相符。
5. 电离层杂波的智能处理方法
5.1 问题的提出
在电离层杂波的特性分析中，电离层杂波具有时变、非平稳、非均匀的特性且这些特性会同时出现在多个域内，这极大的提升了电离层杂波的复杂性，同一积累周期内的电离层杂波可以分为多种类别，如图4(f)所示。单一种类的电离层杂波抑制方法往往只能处理有限种类型的电离层杂波，残余的电离层杂波依旧会影响目标的检测，这里给出了两种方法的处理对比，如图8(a)、图8(b)所示为雷达回波经过广义旁瓣对消(Generalized Sidelobe Cancellation, GSC)算法处理前后的对比图，圆圈处标记的电离层杂波得到了较好的抑制，可以使用恒虚警检测(Constant False Alarm Rate, CFAR)等目标检测算法将目标检测出来，而其余区域的电离层杂波依旧有较强的残余，在第60个距离单元处的电离层杂波残余几乎覆盖了整个多普勒单元，严重的影响了目标检测。图8(c)和图8(d)所示为雷达回波经过局域联合处理(Joint Domain Localized, JDL)算法处理前后的对比图，圆圈处标记的电离层杂波同样得到了很好的抑制，而其他区域的电离层杂波虽然在一定程度上削弱了，但较强的残留杂波依旧影响着目标的检测。因此对于电离层杂波的抑制需要分类分情况处理，选取的抑制方法也需要对不同杂波类型有针对性。
在常规的杂波分类抑制处理中，往往是人工的利用专家知识对杂波进行分类，并根据杂波类型设计或选取相应的杂波抑制算法，杂波的抑制能力过度依靠操作人员的经验。随着人工智能技术的发展，如何自动的完成对杂波的分类抑制处理，成为了现今的研究热点之一[66]。在高频地波超视距雷达系统中，电离层杂波的智能分类抑制处理可以分为两个部分，其一为电离层杂波的有针对性分类识别，需要分类后的电离层杂波在某一域或某几个域中具有较为统一特性，可以使用同种杂波抑制方法进行抑制处理，这里可以使用第4节提出的半监督聚类的方法对电离层杂波进行分类，利用监督信息完成对杂波特性的约束；其二为电离层杂波抑制方法的选取问题，对已知的电离层杂波类型采用匹配的方法选取对应的杂波抑制方法，对未知的电离层杂波类型采用自适应的方法选取信杂比改善最大的杂波抑制方法，最终完成对电离层杂波的整体最优抑制。
5.2 电离层杂波智能处理方法框架
在电离层杂波智能抑制的研究中，这里给出了一种电离层杂波智能抑制处理流程框架，如图9所示。该方法首先对雷达回波数据进行特征提取构造杂波特征库，并结合专家知识与雷达回波特征向量可以获取到少量典型杂波样本，将这些样本作为监督信息输入给分类器对电离层杂波进行分类，然后利用算法选取器对每种类型的电离层杂波智能的选取出合适的杂波抑制算法，最终得到最优的杂波抑制输出。
在对高频地波雷达的实测数据处理过程中，我们发现由于引入了监督知识，多数的电离层杂波样本可以被分类到前文提出的典型杂波类型中。但由于实测数据中电离层杂波的时变性与复杂性，我们无法保证所有的典型杂波样本都会出现在同一批次雷达回波里，在实际处理中，可能存在部分杂波分类簇无法与典型杂波类型相对应的问题。为解决杂波类型与抑制方法的匹配问题，对于典型的电离层杂波类型，文献[4,15-18]给出了具有针对性处理的电离层杂波抑制算法，当杂波分类簇的信息熵较小时(即簇内样本特性较为统一)，可以直接将杂波类型与算法进行匹配处理；对于无法与典型杂波相对应的杂波类型或杂波分类簇中信息熵较大(即簇内样本特性不统一)的杂波类型，则需要设计算法选取器，智能选取出合适的电离层杂波抑制算法进行处理。
算法选取器的设计可以有多种方法，如基于规则的算法选取器，基于先验知识的算法选取器，基于强化学习的算法选取器[66]等。本文以基于贪心策略的智能电离层杂波抑制方法为例，给出一种电离层杂波算法智能选取器的方案。这里可以将电离层杂波类型与算法匹配问题描述为以下最优化过程：给定电离层杂波的聚类簇划分
$\mathbb{C} = \left\{ {{C_1}}\ \ {{C_2}}\ \ ··· \ \ {{C_k}} \right\}$ ，目前已有的$M$ 个电离层杂波抑制算法集合为$A = \left\{ {{a_1}}\ \ {{a_2}}\ \ ··· \ \ {{a_M}} \right\}$ ,$Q = \left\{ {{q_1}}\ \ {{q_2}}\ \ ··· \ \ {{q_k}} \right\}$ 为簇划分$\mathbb{C}$ 中每个聚类簇所对应使用的电离层杂波抑制算法。电离层杂波类型与杂波抑制算法的匹配问题可以表述为以下最优化问题：寻找一种算法划分$Q$ ，使得雷达回波数据$X$ 经过杂波抑制算法处理后，信杂比改善最大，即maxQk∑i=1∑x∈CiIF(x),s.t.qi∈A,i=1,2,···,k (11) 其中，
${\rm{IF}}\left( x \right)$ 为信杂比改善因子，其定义为算法处理前后的信杂比差值IF(x)=SCRoutput−SCRinput (12) 对于以上最优化问题，找到其最优解需要考察集合
$Q$ 的所有算法组合方式，这是一个NPC问题，可以采用贪心策略利用局部最优解求解整体最优，即通过算法竞争的方式选取局部最优处理方法来获取整体的电离层杂波最优抑制。其算法流程如下：(1) 获取待处理距离单元的雷达回波数据
$X$ 与电离层杂波的聚类簇划分$\mathbb{C}$ 。(2) 利用信息熵公式
H(C)=−N∑i=1pilog2pi (13) 其中
${p_i}$ 为样本集合C中第i类样本所占的比例，计算聚类簇划分$\mathbb{C}$ 中每个聚类簇${C_i}\;,i = 1,2, ···, k$ 的信息熵$H\left( {{C_i}} \right)$ ，将信息熵$H\left( {{C_i}} \right) < \mu $ 且满足$C_j^* \subset {C_i}$ 的聚类簇${C_i}$ 划归为典型的电离层杂波类型，其中${\mathbb{C}^*} = \left\{ {C_1^*}\ \ {C_2^*}\ \ ··· \ \ {C_k^*} \right\}$ 为典型杂波类型的样本簇。对这类杂波直接匹配对应的杂波抑制算法。(3) 对于信息熵
$H\left( {{C_i}} \right) > \mu $ 的聚类簇${C_i}$ ，对其进行算法竞争处理，计算算法集$A$ 处理后的信杂比改善因子${\rm{IF}}\left( x \right)$ ，选取改善因子最大的算法${a_j}$ 作为该类杂波在当前距离门的杂波抑制算法。(4) 对不同算法处理后的数据进行融合。
(5) 重复以上过程。
5.3 实验验证
实测数据采用高频地波超视距雷达的回波数据，雷达工作频率为6.9 MHz，天线阵列的分布为均匀线阵，数据采集时间为中午，图7给出了实测数据的距离-多普勒(RD)谱与杂波分类结果，波束指向
$\theta = - {9^ \circ }$ 。为方便观测算法处理前后目标位置附近的电离层杂波抑制性能，这里给出目标处的局部RD谱放大图和对应位置的电离层杂波分类结果图，如图10所示。从图10(a)中可以看出，电离层杂波功率较强，几乎占据了全部的多普勒分辨单元，目标被电离层杂波所淹没，无法被检测算法所检测，严重影响了雷达探测性能。对比图10(b)可以发现，该区域存在两种类型的电离层杂波，目标处附近以能量聚集型强方向性杂波为主，这种杂波具有较强的功率，一般是由雷达信号经由Es层电离层中的不规则体反射而形成，其具有明显的方向性指向，且在空间上具有相似的分布，适合采用空域杂波抑制的算法进行处理。此区域中另一种电离层杂波为能量分散型点状电离层杂波，这种杂波在小波尺度上呈现出与目标相似的特性，适合采用小波斜投影滤波算法进行处理。对于该区域而言，单一的杂波抑制方法很难做到对两种杂波类型的同时最优抑制，图11给出了不同电离层杂波抑制算法处理后的RD谱。
图 11 不同电离层杂波抑制算法对比Figure 11. Comparison of different ionospheric clutter suppression algorithms对比图11中的5种不同处理算法，基于稀疏重构的自适应波束形成算法(Sparse Space Spectrum Rebuild Beamforming, SSSRB)、小波斜投影滤波算法(Wavelet Oblique Projection Filtering, WOPF)与单凹口辅助通道对消算法(Notch Generalized Sidelobe Cancellation, Notch-GSC)均可对能量聚集型强方向性杂波区域进行抑制，但WOPF算法会造成目标在多普勒展宽且目标本身会被部分对消，其处理性能较另外两种方法较差；而Notch-GSC算法主要针对旁瓣电离层杂波，对于杂波方向与目标方向接近的主瓣杂波处理性能较差，因此其处理后的电离层杂波残余较大；SSSRB算法除了可以抑制旁瓣杂波对主瓣杂波同样拥有一定的抑制能力，因此其处理后的电离层杂波残余更少，在这几种方法中，SSSRB算法对能量聚集型强方向性杂波的抑制效果最好，其处理后的电离层杂波残余最少，目标处的信杂比(Signal to Clutter Ratio, SCR)与原始数据相比改善最大，为18.03 dB，目标可以被检测出来。对于能量分散型点状电离层杂波区域，SSSRB算法、WOPF算法、基于距离相关性分析的变加载JDL算法(Joint Domain Localized processing based on Range Analyzed, RA-JDL)与Notch-GSC算法均具有一定的抑制能力，其中SSSRB算法与Notch-GSC算法均为空域算法，无法处理与波束指向一致的电离层杂波，因此存在部分电离层杂波残余导致虚警概率提升；RA-JDL算法对杂波样本的距离相关性依赖较强，由于能量分散型点状电离层杂波的距离相关性较弱，算法无法准确估计该区域杂波的协方差矩阵，因此算法处理后电离层杂波残留较大；WOPF算法主要针对与目标在小波尺度上相似的点状杂波，其处理后的电离层杂波残余最少且虚警较小，是几种方法中杂波抑制性能最好的方法。本文提出的方法针对不同类型的电离层杂波，智能的选取最优的杂波抑制算法进行抑制，在该批数据区域中，采用SSSRB算法与WOPF算法对不同类型杂波进行抑制，使抑制后的平均电离层杂波功率低于任意单一处理算法，且目标处的信杂比改善最大。
为对比不同算法对不同类型电离层杂波的抑制性能，在实测数据的五种不同杂波类型区域注入相同信杂比的仿真目标，分别使用不同的电离层杂波抑制算法对这5种杂波进行处理，表8给出了处理后不同电离层杂波类型处目标的信杂比。从表8中可以看出，注入的仿真目标信杂比为5 dB，对于每种不同类型的电离层杂波，本文提出的方法均可以得到接近最优的输出信杂比且不会出现漏警的情况，对不同类型电离层杂波处理的平均输出信杂比为17.33 dB，高于任何一种单一算法，比平均处理最好的SSSRB算法高3.77 dB。
表 8 目标在不同类型杂波处各算法处理后的信杂比Table 8. Target SCR after different algorithms processedDBF SSSRB WOPF CS-GSC RA-JDL N-GSC 本文方法 类型A (dB) 5.00 18.03 14.46 5.84 3.51 14.74 18.40 类型B (dB) 5.00 16.46 19.71 4.67 13.20 15.90 19.55 类型C (dB) 5.00 10.12 9.65 16.93 7.30 9.20 16.64 类型D (dB) 5.00 7.31 1.70 10.25 14.10 6.20 14.07 类型E (dB) 5.00 15.90 13.78 12.12 12.41 17.46 18.01 平均SCR (dB) 5.00 13.56 11.86 9.96 10.10 12.70 17.33 6. 结论
本文对高频地波超视距雷达的主要杂波干扰源——电离层杂波的成因与特性进行了详尽而细致的分析，同时对目前电离层杂波的抑制算法进行剖析，从电离层杂波时变、非平稳、非均匀3个特性的角度分析了目前电离层杂波抑制算法的研究趋势与局限性，得出若想有效且全面的对电离层杂波进行抑制，需对电离层杂波样本进行分类识别并对不同类杂波采用有针对性处理的结论。以此结论为基础，本文对杂波分类方法进行了研究，给出了基于半监督聚类的电离层杂波分类方法，并以CSKM算法为例，给出了一种电离层杂波分类的方案，并利用实测数据对该方法的有效性进行了验证。随后本文提出了一种电离层杂波的智能处理方法框架，以贪婪策略为例展示了电离层杂波类型与算法的一种匹配方案，通过对实测数据的处理验证，本文提出的方法均可以得到接近最优的输出信杂比且不会出现漏警的情况，对不同类型电离层杂波处理的平均输出信杂比为17.33 dB，高于任何一种单一算法3.77 dB以上。
-
图 8 不同网络的特征图提取与对比
Figure 8. Feature map extraction and comparison of different networks
图 10 郑州 7·20 暴雨前后部分黄河提取结果
Figure 10. Part extraction results of the Yellow River before and after the Zhengzhou 7·20 rainstorm
表 2 分割结果评价
Table 2. Evaluation of segmentation results
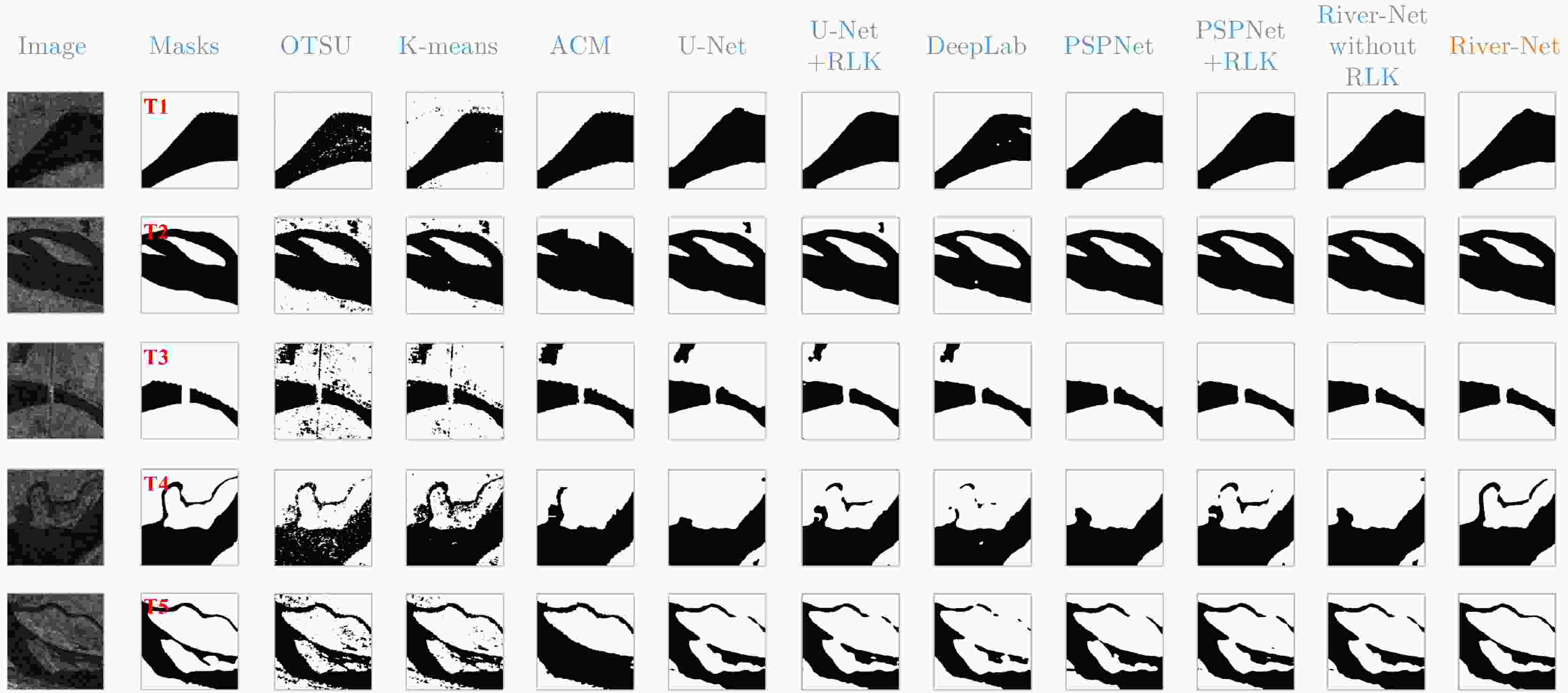
Algorithms/Models Precision (%) Recall (%) IoU (%) F1-score (%) 传统方法 OTSU 93.05 84.74 81.99 88.70 K-means 95.10 87.18 86.67 90.97 ACM 92.08 84.08 81.99 87.90 深度学习 U-Net 95.70 91.03 88.00 93.30 U-Net+RLK 96.22 93.18 91.92 94.68 DeepLab 95.42 91.13 89.40 93.23 PSPNet 96.06 92.73 90.04 94.36 PSPNet+RLK 97.17 93.24 93.36 95.16 River-Net without RLK 96.33 93.36 91.03 94.82 River-Net 97.32 94.40 92.93 95.84 
下载: 导出CSV
-
[1] LI Ning, WANG R, DENG Yunkai, et al. Waterline mapping and change detection of tangjiashan dammed lake after wenchuan earthquake from multitemporal high-resolution airborne SAR imagery[J]. IEEE Journal of Selected Topics in Applied Earth Observations and Remote Sensing, 2014, 7(8): 3200–3209. doi: 10.1109/JSTARS.2014.2345417 [2] 冷英, 李宁. 一种改进的变化检测方法及其在洪水监测中的应用[J]. 雷达学报, 2017, 6(2): 204–212. doi: 10.12000/JR16139LENG Ying and LI Ning. Improved change detection method for flood monitoring[J]. Journal of Radars, 2017, 6(2): 204–212. doi: 10.12000/JR16139 [3] MOREIRA A, PRATS-IRAOLA P, YOUNIS M, et al. A tutorial on synthetic aperture radar[J]. IEEE Geoscience and Remote Sensing Magazine, 2013, 1(1): 6–43. doi: 10.1109/MGRS.2013.2248301 [4] 李宁, 牛世林. 基于局部超分辨重建的高精度SAR图像水域分割方法[J]. 雷达学报, 2020, 9(1): 174–184. doi: 10.12000/JR19096LI Ning and NIU Shilin. High-precision water segmentation from synthetic aperture radar images based on local super-resolution restoration technology[J]. Journal of Radars, 2020, 9(1): 174–184. doi: 10.12000/JR19096 [5] 程江华, 高贵, 库锡树, 等. 高分辨率SAR图像道路交叉口检测与识别新方法[J]. 雷达学报, 2012, 1(1): 100–108. doi: 10.3724/SP.J.1300.2012.20024CHENG Jianghua, GAO Gui, KU Xishu, et al. A novel method for detecting and identifying road junctions from high resolution SAR images[J]. Journal of Radars, 2012, 1(1): 100–108. doi: 10.3724/SP.J.1300.2012.20024 [6] LIU Tao, YANG Ziyuan, MARINO A, et al. PolSAR ship detection based on neighborhood polarimetric covariance matrix[J]. IEEE Transactions on Geoscience and Remote Sensing, 2021, 59(6): 4874–4887. doi: 10.1109/TGRS.2020.3022181 [7] LIU Zhongling, LI Fei, LI Ning, et al. A novel region-merging approach for coastline extraction from sentinel-1A IW Mode SAR imagery[J]. IEEE Geoscience and Remote Sensing Letters, 2016, 13(3): 324–328. doi: 10.1109/LGRS.2015.2510745 [8] LI Wenyu and GONG Peng. Continuous monitoring of coastline dynamics in western Florida with a 30-year time series of Landsat imagery[J]. Remote Sensing of Environment, 2016, 179: 196–209. doi: 10.1016/j.rse.2016.03.031 [9] LI Ning, NIU Shilin, GUO Zhengwei, et al. Dynamic waterline mapping of inland great lakes using time-series SAR data from GF-3 and S-1A satellites: A case study of DJK reservoir, China[J]. IEEE Journal of Selected Topics in Applied Earth Observations and Remote Sensing, 2019, 12(11): 4297–4314. doi: 10.1109/JSTARS.2019.2952902 [10] JIANG Liguang, NIELSEN K, DINARDO S, et al. Evaluation of Sentinel-3 SRAL SAR altimetry over Chinese rivers[J]. Remote Sensing of Environment, 2020, 237: 111546. doi: 10.1016/j.rse.2019.111546.0 [11] 安成锦, 牛照东, 李志军, 等. 典型Otsu算法阈值比较及其SAR图像水域分割性能分析[J]. 电子与信息学报, 2010, 32(9): 2215–2219. doi: 10.3724/SP.J.1146.2009.01426AN Chengjin, NIU Zhaodong, LI Zhijun, et al. Otsu threshold comparison and SAR water segmentation result analysis[J]. Journal of Electronics &Information Technology, 2010, 32(9): 2215–2219. doi: 10.3724/SP.J.1146.2009.01426 [12] BAO Linan, LV Xiaolei, and YAO Jingchuan. Water extraction in SAR Images using features analysis and dual-threshold graph cut model[J]. Remote Sensing, 2021, 13(17): 3465. doi: 10.3390/rs13173465 [13] 冷英, 刘忠玲, 张衡, 等. 一种改进的ACM算法及其在鄱阳湖水域监测中的应用[J]. 电子与信息学报, 2017, 39(5): 1064–1070. doi: 10.11999/JEIT160870LENG Ying, LIU Zhongling, ZHANG Heng, et al. Improved ACM algorithm for poyang lake monitoring[J]. Journal of Electronics &Information Technology, 2017, 39(5): 1064–1070. doi: 10.11999/JEIT160870 [14] LI Ning, WANG R, LIU Yabo, et al. Robust river boundaries extraction of dammed lakes in mountain areas after Wenchuan Earthquake from high resolution SAR images combining local connectivity and ACM[J]. ISPRS Journal of Photogrammetry and Remote Sensing, 2014, 94: 91–101. doi: 10.1016/j.isprsjprs.2014.04.020 [15] JIA Lu, LI Ming, ZHANG Peng, et al. SAR image change detection based on multiple kernel k-means clustering with local-neighborhood information[J]. IEEE Geoscience and Remote Sensing Letters, 2016, 13(6): 856–860. doi: 10.1109/LGRS.2016.2550666 [16] SUN Xian, WANG Bing, WANG Zhirui, et al. Research progress on few-shot learning for remote sensing image interpretation[J]. IEEE Journal of Selected Topics in Applied Earth Observations and Remote Sensing, 2021, 14: 2387–2402. doi: 10.1109/JSTARS.2021.3052869 [17] LIU Wenjie, ZHANG Wenkai, SUN Xian, et al. HECR-Net: Height-embedding context reassembly network for semantic segmentation in aerial images[J]. IEEE Journal of Selected Topics in Applied Earth Observations and Remote Sensing, 2021, 14: 9117–9131. doi: 10.1109/JSTARS.2021.3109439 [18] LATINI D, DEL FRATE F, PALAZZO F, et al. Coastline extraction from SAR COSMO-SkyMed data using a new neural network algorithm[C]. 2012 IEEE International Geoscience and Remote Sensing Symposium, Munich, Germany, 2012: 5975–5977. doi: 10.1109/IGARSS.2012.6352247. [19] LONG J, SHELHAMER E, and DARRELL T. Fully convolutional networks for semantic segmentation[C]. 2015 IEEE Conference on Computer Vision and Pattern Recognition, Boston, USA, 2015: 3431–3440. doi: 10.1109/CVPR.2015.7298965. [20] PAI M M M, MEHROTRA V, AIYAR S, et al. Automatic segmentation of river and land in SAR images: A deep learning approach[C]. 2019 IEEE Second International Conference on Artificial Intelligence and Knowledge Engineering, Sardinia, Italy, 2019: 15–20. doi: 10.1109/AIKE.2019.00011. [21] RONNEBERGER O, FISCHER P, and BROX T. U-Net: Convolutional networks for biomedical image segmentation[C]. The 18th International Conference on Medical Image Computing and Computer-Assisted Intervention, Munich, Germany, 2015: 234–241. doi: 10.1007/978-3-319-24574-4_28. [22] PAI M M M, MEHROTRA V, VERMA U, et al. Improved semantic segmentation of water bodies and land in SAR images using generative adversarial networks[J]. International Journal of Semantic Computing, 2020, 14(1): 55–69. doi: 10.1142/S1793351X20400036 [23] VERMA U, CHAUHAN A, PAI M M M, et al. DeepRivWidth: Deep learning based semantic segmentation approach for river identification and width measurement in SAR images of Coastal Karnataka[J]. Computers & Geosciences, 2021, 154: 104805. doi: 10.1016/j.cageo.2021.104805. [24] 张金松, 邢孟道, 孙光才. 一种基于密集深度分离卷积的SAR图像水域分割算法[J]. 雷达学报, 2019, 8(3): 400–412. doi: 10.12000/JR19008ZHANG Jinsong, XING Mengdao, and SUN Guangcai. A water segmentation algorithm for SAR image based on dense depthwise separable convolution[J]. Journal of Radars, 2019, 8(3): 400–412. doi: 10.12000/JR19008 [25] CHEN L C, PAPANDREOU G, KOKKINOS I, et al. DeepLab: Semantic image segmentation with deep convolutional nets, atrous convolution, and fully connected CRFs[J]. IEEE Transactions on Pattern Analysis and Machine Intelligence, 2018, 40(4): 834–848. doi: 10.1109/TPAMI.2017.2699184 [26] ZHAO Hengshuang, SHI Jianping, QI Xiaojuan, et al. Pyramid scene parsing network[C]. 2017 IEEE Conference on Computer Vision and Pattern Recognition, Honolulu, USA, 2017: 6230–6239. doi: 10.1109/CVPR.2017.660. 期刊类型引用(3)
1. 闫文君，段可欣，凌青，李春雷，黄丽. 数据恶劣条件下的辐射源个体识别方法综述. 海军航空大学学报. 2024(05): 523-534 . 
百度学术2. 王艺卉，闫文君，徐从安，查浩然，桂冠，陈雪梅，葛亮. 面向ADS-B信号辐射源个体识别的轻量化模型设计. 太赫兹科学与电子信息学报. 2023(09): 1100-1108 . 百度学术3. 韦文斌，彭锐晖，孙殿星，张家林，王向伟. 基于频响特性的大起伏密集假目标干扰识别技术. 兵工学报. 2023(10): 3204-3217 . 百度学术其他类型引用(6)
-
下载:
百度学术
计量
- 文章访问数: 1411
- HTML全文浏览量: 788
- PDF下载量: 168
- 被引次数: 9
