作者中心
专家审稿
责编办公
编辑办公
-
摘要: 依据多普勒效应，传统雷达可以实现对运动目标探测，但是在对旋转目标的角向运动趋势感知存在检测盲区。涡旋电磁波的旋转多普勒效应的发现，因有助于解决直视下的旋转目标的角向运动趋势感知问题，引起了国内外研究人员的广泛关注。该文主要介绍了近年来涡旋电磁波旋转多普勒效应的研究进展，特别是微波波段的相关研究成果，包括目标在准轴和非准轴状况下的旋转多普勒效应研究，复杂运动条件下的径向多普勒、微多普勒和旋转多普勒效应的解耦合研究，以及旋转多普勒效应在雷达成像和测速中的应用研究。同时，该文也对该领域亟待解决的问题进行了总结分析，并对未来的研究方向及相关应用进行了展望。Abstract: Traditional radars can detect moving targets using the Doppler effect. However, traditional radars have shadow areas in detecting the angular motion of the rotating targets. The discovery of the rotational Doppler effect based on vortex electromagnetic waves helps solve the problem of detecting the angular motion of the rotating targets under direct vision, which has attracted considerable attention from domestic and foreign scholars. In this study, we discussed the recent research progress on the rotational Doppler effect of vortex electromagnetic waves, particularly for related results in the microwave band, including the rotational Doppler effects on the target under on-axis and off-axis cases; decoupling linear Doppler, micro-Doppler and rotational Doppler effects under complex motion cases; and rotational Doppler effects on the applications of radar imaging and velocity measurement. We summarized and analyzed the existing problems demanding prompt solutions in this field, and proposed future research directions and relative applications.
-
1. 引言
雷达探测不受雾、云和雨的阻挡，具有全天候、全天时的特点，并有一定的穿透能力。因此，它不仅成为军事上必不可少的电子装备，而且广泛应用于社会经济发展 (如气象预报[1]、资源探测[2]、环境监测[3]等) 和科学研究 (天体研究[4]、大气物理[5]、电离层结构[6]等)。传统雷达通过发射固定频率的电磁波对空扫描，如遇到活动目标，会产生多普勒频移，根据频移的大小及信号时间差可测出目标对雷达的径向相对运动速度及目标距离[7]。同时，用频率过滤方法检测目标的多普勒频率谱线，滤除干扰杂波的谱线，可使雷达从强杂波中分辨出目标信号[8]。然而，当目标的速度矢量方向和电磁波的波矢方向垂直时，该分量将难以从回波信号中提取出来，使得传统雷达对目标运动探测存在盲区，因此，需要设计新概念新体制雷达，以提高雷达系统的目标探测性能。
1992年，荷兰物理学家Allen等人[9]发现了拉盖尔-高斯(Laguerre-Gauss, LG) 涡旋光束中的轨道角动量(Orbital Angular Momentum, OAM)，作为电磁波继振幅、相位、频率、极化外的另一种属性，相关学者对涡旋光束的产生和应用进行了大量的研究。在射频波段，OAM电磁波同样受到了研究人员的广泛关注：不同OAM态之间相互正交，互不干扰，可以被应用于无线通信中以提高信道容量和扩展频谱资源[10-13]。相比于普通平面波，其波前相位的多样性也可以提高雷达二维和三维成像的方位向分辨率[14-17]，针对涡旋电磁波在长距离传输中由于发散造成的衰减问题[18]，通过波束整形[19]和优化传输方案[20]等方法可以进行有效解决。此外，当OAM电磁波垂直入射到旋转目标平面时，也会产生类似于径向多普勒频移的效应，称为旋转多普勒效应。1979年，Garetz与Arnold[21]将圆偏振光束通过旋转加速度为ω的半波片时发现其频率偏移量为2ω，这为利用圆偏振光的多普勒效应探测旋转运动目标提供了可能。1996年，Nienhuis[22]利用一个三棱镜系统证明了模式数为m的拉盖尔-高斯光束在通过旋转速度为Ω的棱镜后能形成2mΩ的频率差，从理论上证明了拉盖尔-高斯光束也具有探测旋转运动的潜力。1997年，Bialynicki等人[23]通过类比线性运动产生的多普勒频移引入了旋转频移的概念，并且通过实验测量出该频移与旋转角速度和发射光子的角动量之间成正相关。之后，Courtial等人[24]在毫米波频段也进行了旋转多普勒的测量实验，将分别通过静止和旋转棱镜的两路波束进行干涉，而后对回波的强度进行检测，发现其干涉后的波束强度呈现周期性的变化，并且变化周期与OAM模态数成正相关，上述研究发现了涡旋光束与旋转物体之间存在的相应关系，但是并未给出二者之间的定量关系。2013年，英国格拉斯哥大学Lavery团队[25]根据径向多普勒频移公式推导出旋转多普勒频移公式，得到了涡旋光束、旋转目标与旋转多普勒效应三者之间的定量关系，并在光波段实验验证了理论的正确性，证明了旋转多普勒效应和径向多普勒效应的一致性，为旋转多普勒效应的理论研究打下了坚实的基础。此后，人们对光波段的旋转多普勒效应进行了一系列的研究和应用，包括对旋转多普勒效应的产生机理的解释[26,27]、对旋转目标角速度检测方法的提出[28-31]、对不同情景下旋转目标多普勒效应的研究[32-34]等。
相比于涡旋光波，微波波段的涡旋电磁波的准直性较差，易受电磁干扰，实验现象不易观察[35]。因此，在微波波段的涡旋电磁波的旋转多普勒效应还有待学者们进行更深入的研究。本文对涡旋电磁波的旋转多普勒效应研究进展进行了总结和探讨，内容共分为5个部分，第1部分为引言，概述了涡旋电磁波以及旋转多普勒的起源、发展历程以及应用趋势；第2部分对基于涡旋电磁波的旋转多普勒效应理论基础进行了描述，包括涡旋电磁波的产生原理与方法以及旋转多普勒效应的理论推导；第3部分对光波段的旋转多普勒效应研究进行了简要概括；第4部分重点介绍了微波波段的旋转多普勒效应研究进展，包括准轴、非准轴状况下旋转多普勒效应的研究，径向多普勒、微多普勒和旋转多普勒效应的耦合关系研究以及在涡旋电磁波雷达系统中的应用研究；第5部分对目前的研究进展进行了总结，并为未来的研究以及应用方向进行了展望。
2. 涡旋电磁波旋转多普勒效应理论基础
2.1 涡旋电磁波产生原理与方法
电磁波不仅有能量也具有动量，其中，动量包括线动量和角动量。由麦克斯韦方程可知，电磁波的角动量包括自旋角动量(Spin Angular Momentum, SAM)和轨道角动量(OAM)。一般地，将携带轨道角动量的电磁波称为涡旋电磁波，相比于携带自旋角动量的圆极化电磁波，涡旋电磁波的电场可以表示为
E(r,φ)=E(r)exp(jlφ) (1) 其中，E(r)为电场的幅值，r为电磁波辐射半径，
φ 为空间相位，l为拓扑荷数，也被称为OAM模态数，l可以取任意整数值。可以看到，涡旋电磁波电场存在有相位因子exp(jlφ )，其波前为螺旋结构，如图1所示。在量子理论中，OAM可以被分解成一系列离散的量子本征态[36]，无尽的OAM模态数理论上构成了无穷维的希尔伯特空间，其模态间相互正交。因此，在无线通信当中，基于轨道角动量的模式复用技术可以被认为是除了时间、空间、频率等之外的另一复用技术[37]。OAM模式复用不仅可以提高频谱利用率，在传输信息时，也具有较高的安全性。20世纪90年代，Turnbull等人[38]利用螺旋相位板，首次在毫米波频段产生了涡旋电磁波，之后，研究人员对涡旋电磁波的产生方法进行了较为深入的研究。目前，在射频域产生涡旋电磁波主要有以下几种方法，分别是微带贴片天线、行波天线、阵列天线和超表面天线[39]，如图2所示。微带贴片天线的结构相对简单、尺寸较小且制作成本较低[40,41]；行波天线可以在宽带范围内产生圆极化涡旋电磁波[42-46]；阵列天线可以通过改变馈电相位实现OAM模态的灵活切换[47,48]；超表面天线可以通过改变共振器的形状和大小来实现电磁波振幅或相位上的突变，从而调控涡旋电磁波[49-51]。在今后的应用中，需要能够产生宽带、多OAM模式、高质量的涡旋电磁波，因此，设计符合应用要求，并且制作结构简单、成本低的涡旋电磁波天线，将会是学者们坚持不懈的努力方向。涡旋电磁波相关技术的进步和成熟，将会促进其在无线通信、涡旋雷达成像和目标检测等领域发挥越来越重要的作用。
2.2 旋转多普勒效应检测原理
1842年，奥地利物理学家多普勒提出物体辐射的波长会因为波源和观察者的相对运动而发生变化，即多普勒效应[52]。在运动的波源前面，波被压缩，波长变得较短，频率变得较高；在运动的波源后面，产生相反的效应，波长变得较长，频率变得较低。同时，波源的速度越高，所产生的效应越大。当物体以恒定速度v朝某个方向运动时，电磁波在传播过程中会存在路程差，从而产生的多普勒频移为
Δf=fvcosθc (2) 其中，f为电磁波的频率，θ为速度矢量和波矢的夹角，c为波速。通常所说的多普勒效应主要是指径向多普勒效应，已经被广泛应用于医学诊断、空间速度测量等领域[53,54]。对于旋转目标，散射波也会产生径向多普勒频移。当目标旋转轴不是指向波源和探测器时，该频移可被检测到，然而，当物体的旋转轴和波矢的方向平行时，径向多普勒频移将消失，从而会造成雷达目标检测的“盲区”。
旋转多普勒效应是指当携带轨道角动量的涡旋波束垂直入射到旋转物体表面时，其散射波会产生相应的多普勒频移。一个简单的现象是将手表放在旋转转盘的中心，从上面看，手表的指针比正常情况下旋转得更快[55]。当光波携带有角动量时，其绕传播轴的旋转可以加速或减速电场矢量的旋转，产生与旋转速度相关的频率偏移。2006年，Padgett教授团队[56]使用夏克-哈特曼波前传感器测量了具有螺旋相位波矢的局部倾斜角，发现引起光束轨道角动量的是坡印廷矢量相对于光束轴的倾斜角，并确定了该倾斜角为
α=lkr=lλ2πr (3) 其中，l为拓扑荷数，对应于每个光子l
ℏ 的轨道角动量，k为波数，λ为波长，r为波束半径。2013年，英国格拉斯哥大学Lavery等人[25]利用携带OAM的光束检测旋转物体的速度，通过分析旋转物体散射光的轨道角动量，观察到与物体的旋转速度和光的轨道角动量的乘积成正比的频移。当角动量矢量与观测方向平行时，这种旋转频率偏移仍然存在。如图3所示，在α较小的情况下，根据径向多普勒频移公式得到了旋转多普勒频移公式Δf=αf0vc=lλ2πr(f0Ωrc)=lΩ2π (4) 其中，l为OAM光束的拓扑荷数，Ω为物体旋转速度。此外，从光和物质相互作用中的角动量和能量守恒，也可以解释旋转多普勒效应[26]。对于径向多普勒效应，当光束入射到线速度为v的物体时，反射光的线动量变化了2k
ℏ 并使运动物体受到大小相同、方向相反的冲量，该冲量会将2kℏv 的能量传递给反射光束，使其产生fv/c的频移。同样地，对于携带OAM的涡旋光经过旋转物体反射后，其每光子角动量变化了lℏ ，由角动量守恒可知旋转物体受到一个相反的冲量矩，其大小也为lℏ ，为了对抗该扭矩，物体会向反射光传递Ωlℏ 的能量，从而导致其产生lΩ/2π的频移。可以看出，径向多普勒和旋转多普勒有着密切的联系，目前，对于旋转多普勒效应的理论推导也大多基于径向多普勒效应。所以，旋转多普勒效应是否有明显区别于径向多普勒效应的地方，还是仅仅是径向多普勒效应的一个延伸与推广，还需要相关研究人员对其进行更深入的理论研究和实验验证。微波波段的涡旋电磁波具有和涡旋光波相同的旋转多普勒效应，目标的角向运动会对其回波信号进行调制，从而产生旋转多普勒频移，因此，涡旋电磁波雷达不仅可以探测目标的径向运动，还能获得目标的角向运动信息(角速度、角加速度等)。同时，对于传播方向垂直于目标的旋转平面的涡旋电磁波，其回波信号的旋转多普勒频移与涡旋电磁波的拓扑荷数和目标旋转角速度成正比，采用较大拓扑荷数的涡旋电磁波，可以放大目标微小旋转运动产生的旋转多普勒频移，从而实现涡旋电磁波雷达对目标旋转角速度的精确探测。
3. 光波段旋转多普勒效应研究
旋转多普勒效应首先在光学领域被观察到，因此，相关学者对光波段的旋转多普勒效应进行了大量的研究。基于之前对单光束的研究，2014年，英国格拉斯哥大学Martin课题组又对携带OAM的白光束经旋转物体后向散射后的旋转多普勒频移进行了实验验证[57]，并发现该频移与径向多普勒频移不同，是消色差的。此外，该课题组通过入射拓扑荷数相反的涡旋光并测量回波干涉条纹的调制周期，得到了物体的旋转速度与调制频率成线性关系，如图4(a)所示。同年，该课题组还使用条纹干涉法测量了光阱中一微米大小粒子的角速度[58]，这种基于旋转多普勒效应的检测方法不需要详细了解粒子的形状或散射体的分布，并与粒子的手性、透明度和双折射率无关，仅需要考虑散射光是否为各向异性，时间尺度是否为刚性以及粒子的旋转轴是否容易被定义。
图 4 光波段的旋转多普勒效应研究Figure 4. Researches of the rotational Doppler effect in the optical band此后，研究人员也尝试利用不同的涡旋光束研究旋转多普勒效应，包括拉盖尔-高斯光束(LG)、贝塞尔-高斯光束(Bessel-Gaussian, BG)和完美涡旋光束(Perfect Optical Vortex, POV)。文献[28]利用LG光束探测了旋转物体的角加速度，推导了匀加速旋转目标的旋转多普勒频移并建立了采集非均匀旋转体后向散射LG光束拍频信号的探测系统。文献[29]利用LG光束和开普勒望远镜实现了远距离的旋转目标检测，并发现增加探测距离或许可以减轻由不对准造成的OAM谱展宽效应，实验配置如图4(b)所示。相比于LG光束，BG光束具有无衍射性和自愈性，对于传播路径中存在障碍物的旋转目标仍然能观察到与旋转速度和拓扑荷数成正比的旋转多普勒频移[30]，如图4(c)所示。此外，完美涡旋的光束半径易于改变并且与拓扑荷数的大小无关，相比于LG和BG光束，其在探测不同尺寸目标时会更加灵活。文献[31]提出了一种利用完美涡旋光束来检测旋转物体的方法，实验结果表明，当叠加光束的两个拓扑荷数分量的绝对差值逐渐增大时，POV的信号功率基本保持不变，而LG光束的信号功率会逐渐消失，如图4(d)所示。同时，随着传播距离的增加，完美涡旋的检测精度仍然较高，有利于同时实现微粒操控和转速检测。
上述研究大都是基于涡旋光束准轴状况下的旋转目标检测，文献[32]研究了当涡旋光未对准旋转轴时的旋转多普勒效应，并基于局部散射模型推导出旋转多普勒频移。实验利用氦氖激光器和空间光调制器产生复合涡旋光并入射到旋转圆盘上，改变光束中心和旋转轴的距离并测量不同位置处的多普勒信号，如图4(e)所示。实验结果表明，涡旋光束中心相对于旋转中心的偏移会造成旋转多普勒频谱的展宽，旋转多普勒频移的带宽正比于偏移距离。但是，该结论只适用于偏移距离小于光束内径的情况，即旋转中心仍在光束内。文献[33]讨论了涡旋光束完全偏离旋转中心情况下的旋转多普勒频移。实验结果表明，当旋转中心偏移逐渐增大时，信号峰值逐渐淹没在噪声中，而当旋转中心偏移大于涡旋光束半径时，正确的信号峰值再次出现，如图4(f)所示。因此，对于远距离或非合作的目标，在较难精确对准的情况下，可以利用完全偏离旋转中心的OAM光束实现旋转多普勒频移的精确检测。此外，文献[34]研究了斜入射涡旋光的旋转多普勒效应，并建立了涡旋光的多普勒频移与斜入射角度之间的定量关系。实验结果表明，倾斜入射会同时带来旋转多普勒频移和径向多普勒频移，使用拓扑荷数相反的复合涡旋光，可以消除径向多普勒频移，并从非对称展宽的旋转多普勒频移中得到旋转速度，如图4(g)所示。
目前，在旋转多普勒检测中常用的方法分别为光外差法和条纹法。光外差法使用单模OAM光束入射到旋转目标，将回波和参考光干涉得到拍频信号；条纹法同时产生相反拓扑荷数的复合OAM，入射到旋转目标形成方位角条纹为花瓣状的光束。由于外差法属于相干检测，参考光束和探测光束必须进行严格对准，否则会造成OAM谱的展宽，而条纹法在同一全息图上同时产生两种模式的花瓣状光束，不需要额外的对准，可以减少系统复杂性。文献[59]对这两种检测方法的适用情况进行了分析，外差法对旋转物体的相位敏感，在测量多个旋转粒子时其信噪比(SNR)会有显著的差异。对于随机分布的旋转粒子，在单个粒子存在时条纹法的信噪比最强，随着粒子数的增加，信噪比趋于零；外差法的信噪比随着粒子覆盖面积均匀增加。因此，在设计利用旋转多普勒效应测量旋转目标的光学系统时，旋转目标中的散射体密度是需要考虑的一个重要参数。
4. 微波波段旋转多普勒效应研究
涡旋光束的准直性好，易于制备较大的拓扑荷数，因此，光波段对旋转多普勒效应已经进行了大量的研究，而在微波波段，涡旋电磁波波长较长，其准直性较差，易受电磁波干扰，目标的多普勒效应往往较为复杂，因此，涡旋电磁波的旋转多普勒效应较难观察。然而，相比于光波段，微波波段不需要引入拍频信号，可以直接对回波信号进行分析和处理，从而较为方便就能获取回波的多普勒频移。同时，微波具有覆盖范围广，受天气影响较小的优势，因此，微波波段的涡旋电磁波的旋转多普勒效应正逐渐受到人们的关注与研究。
4.1 准轴旋转多普勒效应研究
当旋转目标的旋转中心与涡旋电磁波的波束中心对准且旋转速度与波束入射方向垂直时(即准轴)，理论上产生的旋转多普勒效应较为明显且易于进行检测和研究。2016年，北京邮电大学黄善国课题组[60]利用相位积累的方法对微波波段的旋转多普勒效应进行了实验验证，如图5(a)所示。在20 GHz采用4阵元的圆形阵列天线产生l=+1的OAM波，垂直入射到50 cm(33倍波长)处涂满了铝粉的旋转金属圆盘，利用矢量网络分析仪得到回波信号的相位。该课题组采用相位积累的方法，增加测量时间t来放大相位差，在误差允许的范围内验证了旋转多普勒效应。实验测得转速为50π rad/s时的旋转多普勒频移为24.83 Hz(最大误差率0.67%)，得到的转速为50.18π rad/s(平均错误率0.36%)。然而，利用相位积累法需要一定的检测时间，天线和目标要保持对准且目标的运动状态需保持稳定，因此，该方法在实际检测中具有一定的局限性。
图 5 准轴情况下的旋转多普勒效应研究Figure 5. Researches of the rotational Doppler effect in on-axis case相比于对回波信号的相位进行检测，利用频谱分析仪可以得到回波信号的瞬时频率，有利于提高检测的时效性。文献[61]在2.47 GHz同样采用4阵元的圆形阵列天线产生l=+1的OAM波并照射4 m(33倍波长)外的旋转金属圆盘，回波信号通过贴片天线单点接收，然后利用频谱仪分析，其检测模型和频谱图如图5(b)所示。由于发射天线和接收天线的直接耦合效应，频谱图的主峰值仍然是发射信号频率，而其旁瓣的频移分别为5.2 Hz和–5.6 Hz，分别对应于转盘的逆时针和顺时针旋转，检测误差均小于3%，该方法不仅能检测出目标瞬时旋转速度的大小，还能根据旁瓣的位置得到目标的旋转方向。
此外，对于匀加速旋转物体的角向加速度检测，其回波信号的形式为线性调频信号，即频率随时间变化，通过FFT得到的频谱图不能反映出目标的加速度大小，因此，可以采用时频分析方法，将信号同时在时域和频域上进行表示。文献[62]利用WVD(Wigner-Ville Distibution)和FRFT (Fractional Fourier Transform)两种时频分析方法研究匀加速目标的旋转多普勒效应，如图5(c)所示。仿真结果表明，加速度的分辨率取决于回波信号时频图的频谱宽度。在加速度较小时，WVD的截断效应会带来较大的检测误差；而当加速度逐渐增大时，其引起的时频图的谱展宽效应也会增大检测误差。
表1给出了一些报道的准轴状况下的旋转多普勒效应检测性能，在准轴状况下，回波信号形式较为理想，目标的旋转多普勒频移能准确地检测出来，因此，对于旋转方向与雷达径向垂直的运动目标，利用涡旋电磁波雷达可以有效获取其垂直径向的运动信息，提升雷达在该特定运动场景下的目标识别能力。
表 1 报道的准轴情况下的旋转多普勒效应检测性能Table 1. Reported performances of detecting the rotational Doppler effect in on-axis case4.2 非准轴旋转多普勒效应研究
对于旋转平面垂直于入射电磁波以及旋转轴和波束轴共轴的理想情况，在实际的旋转目标检测中往往很难满足，因此，研究人员对一般入射即非准轴情况下的目标旋转多普勒效应也进行了一系列的理论研究和实验验证。文献[63]研究了旋转平面偏转以及收发天线非同轴放置对于旋转多普勒频移的影响，通过旋转矩阵推导出散射波的表达式，并在10 GHz进行了实验验证。结果表明，两种情况都会为回波信号带来间隔为Ω/2π的频移，使用高阶OAM有利于区分旋转多普勒频移和平面偏转或收发非同轴带来的频移。但是，当平面偏转过大时，其带来的频移峰值会高于旋转多普勒频移峰值，造成较大的检测误差。如图6(a)所示，对于旋转速度Ω=34.87 rad/s的风扇，其偏转70°带来的5.5 Hz频移峰值大于l=+3的涡旋电磁波产生的16.7 Hz的旋转多普勒频移峰值。文献[64]理论推导了目标在旋转平面偏转和偏轴情况下的角向微多普勒频移，仿真结果表明，两种情况下的角向微多普勒频移分别以2Ω和Ω为周期变化，根据时频图中的最大和最小值，可以推算出散射点的旋转半径、旋转速度等目标信息，如图6(b)所示。文献[65]基于涡旋电磁波雷达研究了任意位置处的旋转物体多普勒效应，并提出了一种旋转目标的参数估计方法。首先利用平面波获得径向多普勒频移，接着利用骨架提取算法从时频信息中分离出旋转多普勒频移，最后通过霍夫变换得到旋转目标的旋转半径、偏转角等参数。仿真实现了对旋转半径为0.499 m，偏转角为30°，旋转速度为10π rad/s的旋转目标参数的成功估计，如图6(c)所示。表2对比了报道的非准轴情况下的旋转多普勒效应检测性能，对于旋转轴方向与涡旋电磁波雷达径向方向存在偏移的运动目标，其会对回波信号产生复杂的旋转多普勒调制，基于涡旋电磁波的多普勒雷达相比于传统多普勒雷达，其多普勒效应更为复杂，有利于提供目标更为丰富的运动信息。
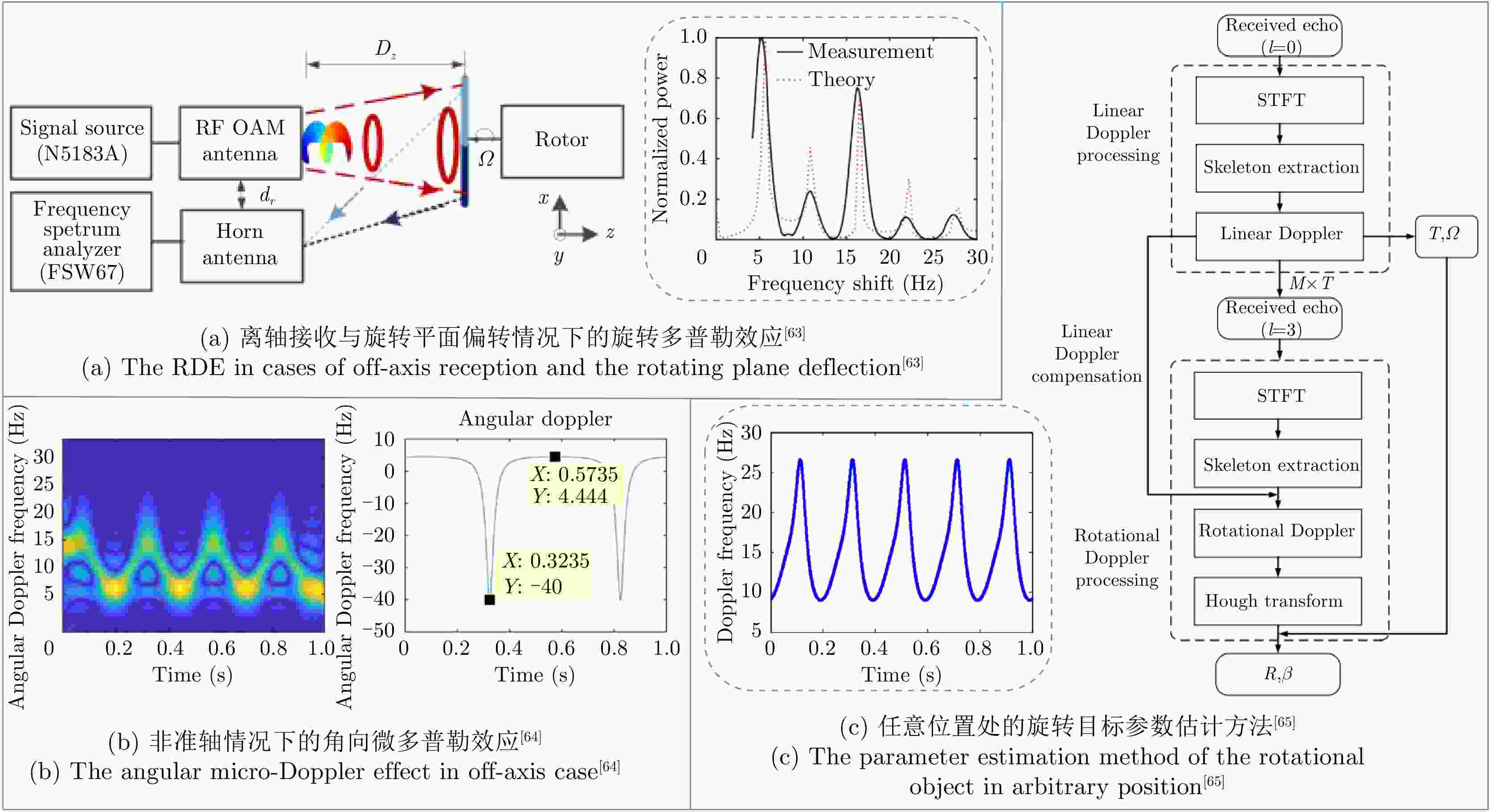
图 6 非准轴情况下的旋转多普勒效应研究Figure 6. Researches of the rotational Doppler effect in off-axis case表 2 报道的非准轴情况下的旋转多普勒效应检测性能Table 2. Reported performances of detecting the rotational Doppler effect in off-axis case4.3 多普勒效应解耦合研究
在实际运动目标检测中，物体存在平动、转动、微动等复杂的运动状态，相应地会产生径向多普勒、旋转多普勒和微多普勒效应，均会对回波信号进行调制，因此，需要分析并寻找将多普勒效应解耦合的方法，从而得到目标的真实运动情况。文献[66]从理论上对旋转多普勒频谱进行分析，理论推导出回波信号频谱为发射谱和离散OAM谱的卷积。仿真在6 GHz用圆形阵列天线产生主模l=3的复合OAM波，根据回波频谱和OAM谱，得到其最高峰值对应于l=3的OAM所产生的旋转多普勒频移，相邻峰值之间的频移均为Ω/2π，而l=0对应的峰值频率即为物体的径向多普勒频移，从而将物体的径向运动和角向运动分离。文献[67]理论推导出回波信号为发射信号、径向多普勒信号和旋转多普勒信号的卷积。实验在9.9 GHz利用圆形阵列天线发射主模l=0的复合OAM波，回波信号的频谱减去l=0的频谱分量，得到主峰值的频移为0 Hz，即物体的径向速度为0 m/s；根据相邻两峰值间隔为20 Hz，得到物体的角向速度为40π rad/s，如图7(a)所示。由于该实验中物体的径向速度为0 m/s，物体实际上仅仅存在角向运动，所以该实验并没有实现径向和角向速度的解耦合。文献[68]在30 GHz利用三叶螺旋桨同时产生了径向和旋转多普勒效应，入射相反拓扑荷的OAM波，求得两次回波信号的频移差，消去了与拓扑荷数无关的径向多普勒频移，从而得到角向速度，完成了对物体角向和径向速度的解耦合。如图7(b)所示，其总频移分别为228.1 Hz, 280.7 Hz和210.5 Hz, 311.4 Hz，计算得到的角向速度分别为52.6π rad/s和50.4π rad/s，检测误差小于2.7%。然而，三叶螺旋桨的径向速度是由推力产生的，该大小很难检测，因此，该实验的径向速度检测精度无法估计。除了目标径向运动带来的径向多普勒效应，当电磁波入射到旋转物体时，由于物体的转动、振动等微运动，其回波会不可避免地产生微多普勒频移，也会干扰基于旋转多普勒效应的旋转目标检测。文献[69]研究了旋转物体检测中的微多普勒频移，分析结果表明，旋转角速度为Ω的物体会带来间隔为Ω/2π的微多普勒频移，并且其峰值功率随频移增大而减小，只需考虑第一和第二峰值的影响时，其带来的频移分别相当于l=+1和+2所产生的旋转多普勒频移，如图7(c)所示。所以，在旋转速度检测中，使用更高阶OAM，有利于区分微动带来的微多普勒频移和旋转多普勒频移，从而减小寄生微多普勒带来的速度检测误差。表3给出了报道的一些多普勒效应解耦方法与参数，基于涡旋电磁波的多普勒雷达，具有比传统多普勒雷达更为丰富的多普勒效应，对多普勒效应解耦合方法的研究，有利于获取目标更为真实的运动信息。
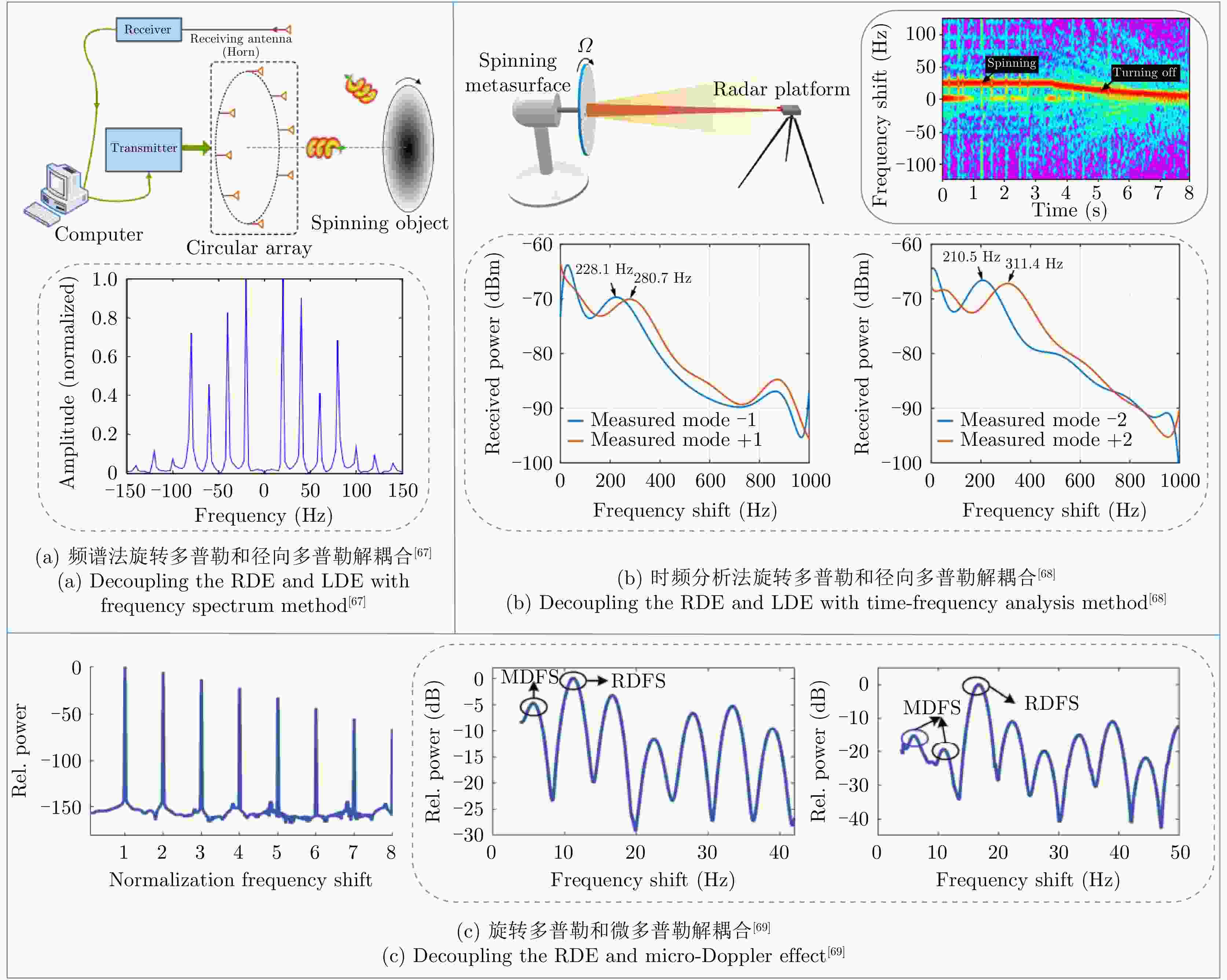
表 3 报道的多普勒效应解耦合方法Table 3. Reported methods of decoupling the Doppler effect4.4 基于旋转多普勒效应的雷达应用系统研究
基于对旋转多普勒效应的理论研究和实验验证，相关研究人员尝试将其应用于测速、成像以及其他雷达系统，以提高系统性能。文献[70]提出了一种旋转物体检测成像方案，利用频率分集原理设计不同OAM模式信号的幅值和频率，使不同OAM电磁波的主瓣聚集于同一方向，之后，根据采集到的旋转多普勒频移对回波信号进行运动补偿和相位校正，最后用FFT或PSD在拓扑荷域对目标进行方位向成像。该课题组在9.9 GHz成功对2.1 m处，旋转速度分别为40π rad/s和50π rad/s的金属圆盘进行了方位向重构，得到和静止目标相同的方位向成像结果，其实验配置和方位向检测结果如图8(a)所示。因此，涡旋电磁波雷达在运动目标成像中有利于提供更精确的多普勒运动补偿，从而提高雷达对于运动目标的成像性能。
图 8 基于旋转多普勒效应的雷达系统研究Figure 8. Researches of radar system based on the rotational Doppler effect在雷达目标检测系统中，对于多个旋转目标，其回波信号在频域会产生波形混叠。因此，有必要研究涡旋电磁波雷达系统对目标的距离和速度分辨能力。文献[71]将传统雷达系统的模糊函数引入到涡旋电磁波雷达系统中，推导出在单脉冲和多脉冲下的目标距离和角速度分辨率。仿真结果表明，涡旋电磁波雷达的距离分辨率和传统雷达一样，而角速度分辨率与脉冲宽度和拓扑荷数成反比，如图8(b)所示。因此，利用脉冲积累的方法可以提高对多普勒频率和角速度的分辨率，使用高阶OAM和宽脉冲有利于实现对微弱旋转目标的精确探测。
此外，由于径向多普勒频移和旋转多普勒频移是线性加减关系，两者可以相互抵消，这将有助于设计一种多普勒斗篷，通过旋转多普勒频移来抵消物体径向运动带来的径向多普勒频移，从而在多普勒雷达上实现“隐身”。文献[72]将多普勒雷达放在线性滑轨上以0.62 m/s的速度向在5.8 GHz产生l=–1的OAM超表面运动，超表面的旋转速度为47.84π rad/s，产生的径向多普勒和旋转多普勒频移分别为±24 Hz，得到的多普勒雷达的输出速度为0 m/s，如图8(c)所示，实现目标的多普勒“隐身”。
表4对上述几种基于旋转多普勒效应的雷达系统性能指标进行了总结，利用涡旋电磁波雷达的旋转多普勒效应，可以提高其系统性能，在运动目标探测、目标成像与雷达体系对抗等领域都有着重要的应用前景。
表 4 报道的旋转多普勒效应雷达系统Table 4. Reported rotational Doppler effect radar systems可以看出，对于微波波段的旋转多普勒效应研究，目前的检测方法有相位测量法、频谱分析法以及时频分析法，其中，相位测量的检测精度相对较高，但受限于较长的检测时间；频谱分析法可以得到信号的瞬时频移，便于提取出目标的瞬时速度；时频分析法可用于分析频率时变信号，适用于检测非匀速目标。对于旋转目标的选择，在实验研究中，金属圆盘以及金属螺旋叶片因较好的反射性能被广泛使用，而为了不失一般性，在理论模型中通常使用理想散射点。此外，目前的实验研究均利用涡旋电磁波的全相位面照射目标，然而，涡旋电磁波在未经过波束调控的情况下具有较大的发散角，以均匀圆形阵列(Uniform Circular Array, UCA)为例，其产生的涡旋电磁波的发散角与贝塞尔幅度项Jl(·)有关。图9对不同OAM模式数的涡旋电磁波在传输过程中的发散情况进行了分析，工作频率f=9 GHz，阵列半径a=5λ。从图中可以看出，在相同传输距离下，涡旋电磁波的发散半径随着OAM模式数的增大而增大，即使采用l=1的涡旋电磁波进行探测，在传输1 km时其发散半径也有60 m，难以满足全相位面照射目标的条件，因此，目前实验的探测距离一般小于100倍波长，以便较好地观察到回波信号。无论基于何种研究条件，在目标旋转速度较小的情况下(Ω≤50π rad/s)，利用OAM模式数较小(|l|≤3)的涡旋电磁波也能获得较高的精度，其实验检测误差均小于5%，这也证明利用涡旋电磁波的旋转多普勒效应能高效地检测旋转目标以及复杂运动目标的角向速度，有利于提高雷达探测系统的性能。
图 9 阵列半径a=5λ时，不同OAM模式数的涡旋电磁波在传输过程中的发散情况Figure 9. Divergence situation of transmitting vortex electromagnetic waves with different OAM modes generated by the UCA with radius of a=5λ5. 总结与展望
目前，在光学领域，相关学者对于涡旋光束的旋转多普勒效应已经进行了较多研究，而在微波波段的研究还相对较少，本文对基于涡旋电磁波的旋转多普勒效应研究进展进行了总结和探讨，简要概述了涡旋电磁波以及旋转多普勒效应的起源、发展历程以及应用趋势；对旋转多普勒效应的理论基础进行了描述并简要概括了光波段的旋转多普勒效应研究；接着，重点介绍了微波波段的旋转多普勒效应研究进展，包括准轴、非准轴状况下旋转多普勒效应的研究，对径向多普勒、旋转多普勒和微多普勒效应的耦合研究以及旋转多普勒效应在雷达系统中的应用；最后，对今后的研究和发展方向进行了展望。
相比于传统多普勒雷达对角向运动目标存在探测“盲区”，涡旋电磁波雷达的旋转多普勒效应使其具有探测旋转运动目标的能力，对于复杂运动目标能获取更为丰富的运动信息，可以有效探测目标的旋转速度、加速度，这些将能够有效提高雷达成像中的运动补偿能力。基于旋转多普勒效应的涡旋电磁波雷达，在探测与预警龙卷风、涡流等自然灾害中将可能发挥出重要作用，在导弹真假弹头预测、战时环境态势感知、雷达对抗等军事领域也具有广泛的应用前景。对于微波波段的旋转多普勒效应，要想进行更为充分的研究并应用到实际中，研究人员还需要解决以下几点问题：(1)在微波波段产生能应用于实验和实际应用中的涡旋电磁波。要进一步提高旋转速度的检测精度，需要更大的OAM模式数，以放大目标微弱运动所产生的旋转多普勒频移。然而，目前在微波波段所设计的各种天线实际能产生的OAM模式数一般不大于5，利用圆形阵列天线所产生的模式数也不超过8。此外，随着模式数的增大，其发散程度也随之增加，例如，对于发散角为0.1 rad的涡旋电磁波，其传输100 km后的主瓣直径达到10 km，难以有效照射到截面积较小的飞行器、导弹等目标以产生可探测的多普勒频移；同时，由于发散问题，回波信号能量可能会衰减到接收机灵敏度以下，从而影响对长距离目标的有效探测。因此，设计新型涡旋电磁波天线，优化天线结构来产生高纯度、较大模式数和较小发散角的涡旋电磁波，以及采用波束整形等波束调控方法来实现涡旋电磁波的可控波束传输，仍然是相关研究人员需要努力的方向。(2)研究一般性运动目标的旋转多普勒效应。现如今的研究都集中于较为理想的准直入射情况，且研究目标大都为金属圆盘，对于复杂运动和多散射点目标，如空中的飞机、导弹，其回波信号会经历更为复杂的多普勒调制，需要研究人员通过数学建模、理论分析和实验验证对目标的复合多普勒效应进行有效解耦合，从而精确获取目标信息。(3)优化涡旋电磁波雷达探测模型和方法。目前的探测模型和方法都较为单一，探测距离近、探测效率低是亟待解决的问题，此外，复杂电磁环境以及障碍物也会对运动目标回波产生较为严重的干扰，这需要我们进一步优化物理模型和信号处理算法。相信未来随着研究人员对涡旋电磁波旋转多普勒效应研究的日益深入和成熟，其在雷达目标检测、雷达成像等领域将发挥更加重要的作用和价值。
-
图 4 光波段的旋转多普勒效应研究
Figure 4. Researches of the rotational Doppler effect in the optical band
图 5 准轴情况下的旋转多普勒效应研究
Figure 5. Researches of the rotational Doppler effect in on-axis case
图 6 非准轴情况下的旋转多普勒效应研究
Figure 6. Researches of the rotational Doppler effect in off-axis case
图 8 基于旋转多普勒效应的雷达系统研究
Figure 8. Researches of radar system based on the rotational Doppler effect
图 9 阵列半径a=5λ时，不同OAM模式数的涡旋电磁波在传输过程中的发散情况
Figure 9. Divergence situation of transmitting vortex electromagnetic waves with different OAM modes generated by the UCA with radius of a=5λ
表 1 报道的准轴情况下的旋转多普勒效应检测性能
Table 1. Reported performances of detecting the rotational Doppler effect in on-axis case
下载: 导出CSV
表 2 报道的非准轴情况下的旋转多普勒效应检测性能
Table 2. Reported performances of detecting the rotational Doppler effect in off-axis case
下载: 导出CSV
-
[1] KRAJEWSKI W F and SMITH J A. Radar hydrology: Rainfall estimation[J]. Advances in Water Resources, 2002, 25(8/12): 1387–1394. doi: 10.1016/S0309-1708(02)00062-3 [2] 李晓峰, 张彪, 杨晓峰. 星载合成孔径雷达遥感海洋风场波浪场[J]. 雷达学报, 2020, 9(3): 425–443. doi: 10.12000/JR20079LI Xiaofeng, ZHANG Biao, and YANG Xiaofeng. Remote sensing of sea surface wind and wave from spaceborne synthetic aperture radar[J]. Journal of Radars, 2020, 9(3): 425–443. doi: 10.12000/JR20079 [3] FIORANI L, COLAO F, and PALUCCI A. Environmental monitoring by laser radar[J]. Romanian Journal of Physics, 2011, 56(3/4): 448–459. [4] NEAL A. Ground-penetrating radar and its use in sedimentology: Principles, problems and progress[J]. Earth-Science Reviews, 2004, 66(3/4): 261–330. doi: 10.1016/j.earscirev.2004.01.004 [5] KUSTAS W P, FRENCH A N, HATFIELD J L, et al. Remote sensing research in hydrometeorology[J]. Photogrammetric Engineering & Remote Sensing, 2003, 69(6): 631–646. doi: 10.14358/PERS.69.6.631 [6] NIELSEN E and GREENWALD R A. Electron flow and visual aurora at the Harang discontinuity[J]. Journal of Geophysical Research: Space Physics, 1979, 84(A8): 4189–4200. doi: 10.1029/JA084iA08p04189 [7] 赵耀东, 吕晓德, 李纪传, 等. 无源雷达多普勒谱分析实现动目标检测的方法[J]. 雷达学报, 2013, 2(2): 247–256. doi: 10.3724/SP.J.1300.2012.20081ZHAO Yaodong, LÜ Xiaode, LI Jichuan, et al. Detection of moving targets based on Doppler spectrum analysis technique for passive coherent radar[J]. Journal of Radars, 2013, 2(2): 247–256. doi: 10.3724/SP.J.1300.2012.20081 [8] 陈世超, 罗丰, 胡冲, 等. 基于多普勒谱非广延熵的海面目标检测方法[J]. 雷达学报, 2019, 8(3): 344–354. doi: 10.12000/JR19012CHEN Shichao, LUO Feng, HU Chong, et al. Small target detection in sea clutter background based on Tsallis entropy of Doppler spectrum[J]. Journal of Radars, 2019, 8(3): 344–354. doi: 10.12000/JR19012 [9] ALLEN L, BEIJERSBERGEN M W, SPREEUW R J C, et al. Orbital angular momentum of light and the transformation of Laguerre-Gaussian laser modes[J]. Physical Review A, 1992, 45(11): 8185–8189. doi: 10.1103/PhysRevA.45.8185 [10] TAMBURINI F, MARI E, PARISI G, et al. Ripling the capacity of a point-to-point radio link by using electromagnetic vortices[J]. Radio Science, 2015, 50(6): 501–508. doi: 10.1002/2015RS005662 [11] PARK W, WANG Lei, BRÜNS H D, et al. Introducing a mixed-mode matrix for investigation of wireless communication related to orbital angular momentum[J]. IEEE Transactions on Antennas and Propagation, 2019, 67(3): 1719–1728. doi: 10.1109/TAP.2018.2889033 [12] ZHANG Yiming and LI Jialin. An orbital angular momentum-based array for in-band full-duplex communications[J]. IEEE Antennas and Wireless Propagation Letters, 2019, 18(3): 417–421. doi: 10.1109/LAWP.2019.2893035 [13] LEI Yi, YANG Yang, WANG Yanzhe, et al. Throughput performance of wireless multiple-input multiple-output systems using OAM antennas[J]. IEEE Wireless Communications Letters, 2021, 10(2): 261–265. doi: 10.1109/LWC.2020.3027006 [14] 郭桂蓉, 胡卫东, 杜小勇. 基于电磁涡旋的雷达目标成像[J]. 国防科技大学学报, 2013, 35(6): 71–76. doi: 10.3969/j.issn.1001-2486.2013.06.013GUO Guirong, HU Weidong, and DU Xiaoyong. Electromagnetic vortex based radar target imaging[J]. Journal of National University of Defense Technology, 2013, 35(6): 71–76. doi: 10.3969/j.issn.1001-2486.2013.06.013 [15] YUAN Tiezhu, WANG Hongqiang, CHENG Yongqiang, et al. Electromagnetic vortex-based radar imaging using a single receiving antenna: Theory and experimental results[J]. Sensors, 2017, 17(3): 630. doi: 10.3390/s17030630 [16] LIU Kang, LI Xiang, GAO Yue, et al. High-resolution electromagnetic vortex imaging based on sparse Bayesian learning[J]. IEEE Sensors Journal, 2017, 17(21): 6918–6927. doi: 10.1109/JSEN.2017.2754554 [17] WANG Jianqiu, LIU Kang, CHENG Yongqiang, et al. Three-dimensional target imaging based on vortex stripmap SAR[J]. IEEE Sensors Journal, 2019, 19(4): 1338–1345. doi: 10.1109/JSEN.2018.2879814 [18] NGUYEN D K, PASCAL O, SOKOLOFF J, et al. Antenna gain and link budget for waves carrying orbital angular momentum[J]. Radio Science, 2015, 50(11): 1165–1175. doi: 10.1002/2015RS005772 [19] YAO Yu, LIANG Xianling, ZHU Weiren, et al. Experiments of orbital angular momentum phase properties for long-distance transmission[J]. IEEE Access, 2019, 7: 62689–62694. doi: 10.1109/ACCESS.2019.2916029 [20] ZHANG Chao and ZHAO Yufei. Orbital angular momentum nondegenerate index mapping for long distance transmission[J]. IEEE Transactions on Wireless Communications, 2019, 18(11): 5027–5036. doi: 10.1109/TWC.2019.2927672 [21] GARETZ B A and ARNOLD S. Variable frequency shifting of circularly polarized laser radiation via a rotating half-wave retardation plate[J]. Optics Communications, 1979, 31(1): 1–3. doi: 10.1016/0030-4018(79)90230-X [22] NIENHUIS G. Doppler effect induced by rotating lenses[J]. Optics Communications, 1996, 132(1/2): 8–14. doi: 10.1016/0030-4018(96)00295-7 [23] BIALYNICKI-BIRULA I and BIALYNICKA-BIRULA Z. Rotational frequency shift[J]. Physical Review Letters, 1997, 78(13): 2539–2542. doi: 10.1103/PhysRevLett.78.2539 [24] COURTIAL J, DHOLAKIA K, ROBERTSON D A, et al. Measurement of the rotational frequency shift imparted to a rotating light beam possessing orbital angular momentum[J]. Physical Review Letters, 1998, 80(15): 3217–3219. doi: 10.1103/PhysRevLett.80.3217 [25] LAVERY M P J, SPEIRITS F C, BARNETT S M, et al. Detection of a spinning object using light’s orbital angular momentum[J]. Science, 2013, 341(6145): 537–540. doi: 10.1126/science.1239936 [26] FANG Liang, PADGETT M J, and WANG Jian. Sharing a common origin between the rotational and linear Doppler effects[J]. Laser & Photonics Reviews, 2017, 11(6): 1700183. doi: 10.1002/lpor.201700183 [27] ZHOU Hailong, FU Dongzhi, DONG Jianji, et al. Theoretical analysis and experimental verification on optical rotational Doppler effect[J]. Optics Express, 2016, 24(9): 10050–10056. doi: 10.1364/OE.24.010050 [28] ZHAI Yanwang, FU Shiyao, YIN Ci, et al. Detection of angular acceleration based on optical rotational Doppler effect[J]. Optics Express, 2019, 27(11): 15518–15527. doi: 10.1364/OE.27.015518 [29] ZHAI Yanwang, FU Shiyao, ZHANG Jianqiang, et al. Remote detection of a rotator based on rotational Doppler effect[J]. Applied Physics Express, 2020, 13(2): 022012. doi: 10.35848/1882-0786/ab6e0c [30] FU Shiyao, WANG Tonglu, ZHANG Zheyuan, et al. Non-diffractive Bessel-Gauss beams for the detection of rotating object free of obstructions[J]. Optics Express, 2017, 25(17): 20098–20108. doi: 10.1364/OE.25.020098 [31] QIU Song, REN Yuan, LIU Tong, et al. Spinning object detection based on perfect optical vortex[J]. Optics and Lasers in Engineering, 2020, 124: 105842. doi: 10.1016/j.optlaseng.2019.105842 [32] QIU Song, LIU Tong, LI Zhimeng, et al. Influence of lateral misalignment on the optical rotational Doppler effect[J]. Applied Optics, 2019, 58(10): 2650–2655. doi: 10.1364/AO.58.002650 [33] ZHANG Zijing, CEN Longzhu, ZHANG Jiandong, et al. Rotation velocity detection with orbital angular momentum light spot completely deviated out of the rotation center[J]. Optics Express, 2020, 28(5): 6859–6867. doi: 10.1364/OE.380324 [34] QIU Song, LIU Tong, REN Yuan, et al. Detection of spinning objects at oblique light incidence using the optical rotational Doppler effect[J]. Optics Express, 2019, 27(17): 24781–24792. doi: 10.1364/OE.27.024781 [35] PADGETT M J, MIATTO F M, LAVERY M P J, et al. Divergence of an orbital-angular-momentum-carrying beam upon propagation[J]. New Journal of Physics, 2015, 17(2): 023011. doi: 10.1088/1367-2630/17/2/023011 [36] LEACH J, PADGETT M J, BARNETT S M, et al. Measuring the orbital angular momentum of a single photon[J]. Physical Review Letters, 2002, 88(25): 257901. doi: 10.1103/PhysRevLett.88.257901 [37] TAMBURINI F, MARI E, SPONSELLI A, et al. Encoding many channels on the same frequency through radio vorticity: First experimental test[J]. New Journal of Physics, 2012, 14(3): 033001. doi: 10.1088/1367-2630/14/3/033001 [38] TURNBULL G A, ROBERTSON D A, SMITH G M, et al. The generation of free-space Laguerre-Gaussian modes at millimetre-wave frequencies by use of a spiral phaseplate[J]. Optics Communications, 1996, 127(4/6): 183–188. doi: 10.1016/0030-4018(96)00070-3 [39] 郭忠义, 汪彦哲, 郑群, 等. 涡旋电磁波天线技术研究进展[J]. 雷达学报, 2019, 8(5): 631–655. doi: 10.12000/JR19091GUO Zhongyi, WANG Yanzhe, ZHENG Qun, et al. Advances of research on antenna technology of vortex electromagnetic waves[J]. Journal of Radars, 2019, 8(5): 631–655. doi: 10.12000/JR19091 [40] XU Jianchun, ZHAO Mingyang, ZHANG Ru, et al. A wideband F-shaped microstrip antenna[J]. IEEE Antennas and Wireless Propagation Letters, 2017, 16: 829–832. doi: 10.1109/LAWP.2016.2606118 [41] SHEN Fei, MU Jiangnan, GUO Kai, et al. Generating circularly polarized vortex electromagnetic waves by the conical conformal patch antenna[J]. IEEE Transactions on Antennas and Propagation, 2019, 67(9): 5763–5771. doi: 10.1109/TAP.2019.2922545 [42] ZHENG Shilie, HUI Xiaonan, JIN Xiaofeng, et al. Transmission characteristics of a twisted radio wave based on circular traveling-wave antenna[J]. IEEE Transactions on Antennas and Propagation, 2015, 63(4): 1530–1536. doi: 10.1109/TAP.2015.2393885 [43] WANG Lulu, CHEN Huiyong, GUO Kai, et al. An inner-and outer-fed dual-arm Archimedean spiral antenna for generating multiple orbital angular momentum modes[J]. Electronics, 2019, 8(2): 251. doi: 10.3390/electronics8020251 [44] SHEN Fei, MU Jiangnan, GUO Kai, et al. Generation of continuously variable-mode vortex electromagnetic waves with three-dimensional helical antenna[J]. IEEE Antennas and Wireless Propagation Letters, 2019, 18(6): 1091–1095. doi: 10.1109/LAWP.2019.2907931 [45] YANG Yang, GUO Kai, SHEN Fei, et al. Generating multiple OAM based on a nested dual-arm spiral antenna[J]. IEEE Access, 2019, 7: 138541–138547. doi: 10.1109/ACCESS.2019.2942601 [46] YANG Yang, GONG Yubin, GUO Kai, et al. Broad-band multiple OAMs’ generation with eight-arm Archimedean spiral antenna (ASA)[J]. IEEE Access, 2020, 8: 53232–53239. doi: 10.1109/ACCESS.2020.2980751 [47] THIDÉB, THEN H, SJÖHOLM J, et al. Utilization of photon orbital angular momentum in the low-frequency radio domain[J]. Physical Review Letters, 2007, 99(8): 087701. doi: 10.1103/PhysRevLett.99.087701 [48] MOHAMMADI S M, DALDORFF L K S, BERGMAN J E S, et al. Orbital angular momentum in radio—A system study[J]. IEEE Transactions on Antennas and Propagation, 2010, 58(2): 565–572. doi: 10.1109/TAP.2009.2037701 [49] YU Nanfang, GENEVET P, KATS M A, et al. Light propagation with phase discontinuities: Generalized laws of reflection and refraction[J]. Science, 2011, 334(6054): 333–337. doi: 10.1126/science.1210713 [50] YIN Zhiping, ZHENG Qun, GUO Kai, et al. Tunable beam steering, focusing and generating of orbital angular momentum vortex beams using high-order patch array[J]. Applied Sciences, 2019, 9(15): 2949. doi: 10.3390/app9152949 [51] GUO Kai, ZHENG Qun, YIN Zhiping, et al. Generation of mode-reconfigurable and frequency-adjustable OAM beams using dynamic reflective metasurface[J]. IEEE Access, 2020, 8: 75523–75529. doi: 10.1109/ACCESS.2020.2988914 [52] CENSOR D. Theory of the Doppler effect: Fact, fiction and approximation[J]. Radio Science, 1984, 19(4): 1027–1040. doi: 10.1029/RS019i004p01027 [53] MO L Y L and COBBOLD R S C. "Speckle" in continuous wave Doppler ultrasound spectra: A simulation study[J]. IEEE Transactions on Ultrasonics, Ferroelectrics, and Frequency Control, 1986, 33(6): 747–753. doi: 10.1109/T-UFFC.1986.26891 [54] BARLOW E J. Doppler radar[J]. Proceedings of the IRE, 1949, 37(4): 340–355. doi: 10.1109/JRPROC.1949.231638 [55] PADGETT M. Like a speeding watch[J]. Nature, 2006, 443(7114): 924–925. doi: 10.1038/443924a [56] LEACH J, KEEN S, PADGETT M J, et al. Direct measurement of the skew angle of the Poynting vector in a helically phased beam[J]. Optics Express, 2006, 14(25): 11919–11924. doi: 10.1364/OE.14.011919 [57] LAVERY M P J, BARNETT S M, SPEIRITS F C, et al. Observation of the rotational Doppler shift of a white-light, orbital-angular-momentum-carrying beam backscattered from a rotating body[J]. Optica, 2014, 1(1): 1–4. doi: 10.1364/OPTICA.1.000001 [58] PHILLIPS D B, LEE M P, SPEIRITS F C, et al. Rotational Doppler velocimetry to probe the angular velocity of spinning microparticles[J]. Physical Review A, 2014, 90(1): 011801(R). doi: 10.1103/PhysRevA.90.011801 [59] ANDERSON A Q, STRONG E F, HEFFERNAN B M, et al. Detection technique effect on rotational Doppler measurements[J]. Optics Letters, 2020, 45(9): 2636–2639. doi: 10.1364/OL.390425 [60] ZHAO Mingyang, GAO Xinlu, XIE Mutong, et al. Measurement of the rotational Doppler frequency shift of a spinning object using a radio frequency orbital angular momentum beam[J]. Optics Letters, 2016, 41(11): 2549–2552. doi: 10.1364/OL.41.002549 [61] BROUSSEAU C, MAHDJOUBI K, and EMILE O. Measurement of the rotational sense and velocity of an object using OAM wave in the radio-frequency band[J]. Electronics Letters, 2019, 55(12): 709–711. doi: 10.1049/el.2019.0942 [62] ZHOU Zhenglong, CHENG Yongqiang, LIU Kang, et al. Detection of uniformly accelerated spinning target based on OAM beams[C]. 2018 International conference On Microwave and Millimeter Wave Technology, Chengdu, China, 2018: 1–3. doi: 10.1109/ICMMT.2018.8563538. [63] ZHENG Jiayu, ZHENG Shilie, SHAO Zhenlei, et al. Analysis of rotational Doppler effect based on radio waves carrying orbital angular momentum[J]. Journal of Applied Physics, 2018, 124(16): 164907. doi: 10.1063/1.5050448 [64] LUO Ying, CHEN Yijun, ZHU Yongzhong, et al. Doppler effect and micro-Doppler effect of vortex-electromagnetic-wave-based radar[J]. IET Radar, Sonar & Navigation, 2020, 14(1): 2–9. doi: 10.1049/iet-rsn.2019.0124 [65] WANG Yu, LIU Kang, LIU Hongyan, et al. Detection of rotational object in arbitrary position using vortex electromagnetic waves[J]. IEEE Sensors Journal, 2021, 21(4): 4989–4994. doi: 10.1109/JSEN.2020.3032665 [66] YANG Tao and WANG Gang. Rotational Doppler shift for electromagnetic waves carrying orbital angular momentum based on spectrum analysis[J]. AIP Conference Proceedings, 2017, 1820(1): 090024. doi: 10.1063/1.4977408 [67] GONG Ting, CHENG Yongqiang, LI Xiang, et al. Micromotion detection of moving and spinning object based on rotational Doppler shift[J]. IEEE Microwave and Wireless Components Letters, 2018, 28(9): 843–845. doi: 10.1109/LMWC.2018.2858552 [68] LIU Baiyang, CHU Hongchen, GIDDENS H, et al. Experimental observation of linear and rotational Doppler shifts from several designer surfaces[J]. Scientific Reports, 2019, 9(1): 8971. doi: 10.1038/s41598-019-45516-1 [69] ZHENG Jiayu, ZHENG Shilie, SHAO Zhenlei, et al. Rotational Doppler effect based on the radio orbital angular momentum wave[C]. 2017 IEEE Asia Pacific Microwave Conference (APMC), Kuala Lumpur, Malaysia, 2017: 1298–1301. doi: 10.1109/APMC.2017.8251700. [70] LIU Kang, LI Xiang, GAO Yue, et al. Microwave imaging of spinning object using orbital angular momentum[J]. Journal of Applied Physics, 2017, 122(12): 124903. doi: 10.1063/1.4991655 [71] ZHOU Zhenglong, CHENG Yongqiang, LIU Kang, et al. Rotational Doppler resolution of spinning target detection based on OAM beams[J]. IEEE Sensors Letters, 2019, 3(3): 5500404. doi: 10.1109/LSENS.2019.2900227 [72] LIU Baiyang, GIDDENS H, LI Yin, et al. Design and experimental demonstration of Doppler cloak from spatiotemporally modulated metamaterials based on rotational Doppler effect[J]. Optics Express, 2020, 28(3): 3745–3755. doi: 10.1364/OE.382700 期刊类型引用(4)
1. 周涵楚，朱永忠，张玲玲，王志伟，徐军伟，谢文宣. 旋翼无人机目标雷达探测技术研究进展. 电讯技术. 2024(08): 1335-1345 . 
百度学术2. 马晖，胡敦法，师竹雨，刘宏伟. 基于涡旋电磁波的雷达应用研究进展. 现代雷达. 2023(05): 27-41 . 百度学术3. 罗迎，袁航，袁延鑫. 单频涡旋电磁波雷达旋转目标微动参数提取方法. 信号处理. 2023(09): 1587-1595 . 百度学术4. 袁航，何其芳，罗迎，王志浩，张群. 涡旋电磁波雷达平动旋转目标三维微动参数提取方法. 雷达学报. 2023(04): 804-816 . 
本站查看其他类型引用(2)
-
下载:
百度学术
计量
- 文章访问数: 2715
- HTML全文浏览量: 1758
- PDF下载量: 417
- 被引次数: 6
