基于扰动的结合Off-grid目标的层析SAR三维成像方法

杜邦; 仇晓兰; 张柘; 雷斌; 丁赤飚

doi:10.12000/JR21093

基于扰动的结合Off-grid目标的层析SAR三维成像方法

DOI: 10.12000/JR21093

杜邦^{1, 2, 3},
仇晓兰^{1, 2, 4, ,},
张柘^{1, 4},
雷斌^{1, 2},
丁赤飚^{1, 2, 3}

1.
中国科学院空间信息处理与应用系统技术重点实验室北京 100190
2.
中国科学院空天信息创新研究院北京 100190
3.
中国科学院大学北京 100049
4.
苏州空天信息研究院苏州 215123

基金项目: 国家自然科学基金(61991421, 61991420)

详细信息

作者简介:
杜　邦(1995–)，男，中国科学院空天信息创新研究院在读博士，研究方向为阵列信号处理、SAR三维成像

仇晓兰(1982–)，女，中国科学院空天信息创新研究院研究员，博士生导师，IEEE高级会员、IEEE地球科学与遥感快报副主编、雷达学报青年编委。主要研究方向为SAR成像处理、SAR图像理解

张　柘(1988–)，男，博士，中国科学院空天信息研究院、苏州空天信息研究院副研究员，硕士生导师，研究方向为稀疏信号处理与合成孔径雷达成像

雷　斌(1978–)，男，中国科学院空天信息创新研究院研究员，博士生导师，主要研究方向为合成孔径雷达及多源遥感信息处理与应用系统等

丁赤飚(1969–)，男，研究员，博士生导师，中国科学院院士，先后主持多项国家重点项目和国家级遥感卫星地面系统工程建设等项目，曾获国家科技进步奖一等奖、二等奖，国家技术发明二等奖等奖励。研究方向为合成孔径雷达、遥感信息处理和应用系统等领域

通讯作者:
仇晓兰 xlqiu@mail.ie.ac.cn

责任主编：廖明生 Corresponding Editor: LIAO Mingsheng
中图分类号: TN957.52
计量
- 文章访问数: 1666
- HTML全文浏览量: 835
- PDF下载量: 265
- 被引次数: 1
出版历程
- 收稿日期: 2021-07-01
- 修回日期: 2021-09-17
- 网络出版日期: 2021-10-15
- 刊出日期: 2022-02-28

L₁ Minimization with Perturbation for Off-grid Tomographic SAR Imaging

DU Bang^{1, 2, 3},
QIU Xiaolan^{1, 2, 4
, ,},
ZHANG Zhe^{1, 4},
LEI Bin^{1, 2},
DING Chibiao^{1, 2, 3}

1.
Key Laboratory of Technology in Geospatial Information Processing and Application System, Chinese Academy of Sciences, Beijing 100190, China
2.
Aerospace Information Research Institute, Chinese Academy of Sciences, Beijing 100190, China
3.
University of Chinese Academy of Sciences, Beijing 100049, China
4.
Suzhou Aerospace Information Research Institute, Suzhou 215123, China

Funds: The National Natural Science Foundation of China (61991421, 61991420)

More Information

Corresponding author: QIU Xiaolan, xlqiu@mail.ie.ac.cn

摘要

摘要: 层析合成孔径雷达(TomoSAR)通过组合在不同高度上获取的多基线二维SAR数据，实现合成孔径雷达的三维成像。TomoSAR的求解本质是一维谱估计问题，基于压缩感知的方法可以在非均匀分布的少量基线观测下实现求解，逐渐成为了主流的成像方式。在经典的压缩感知算法流程中，需要将连续的高程向划分成固定的网格，并且假定目标正好位于所划分的网格上。然而该假设通常难以成立，从而引起“基失配”问题，目前该问题在TomoSAR中很少被讨论。该文首先讨论了目标不在网格(Off-grid)上的TomoSAR观测模型，提出了采用加性扰动项来修正目标偏离网格所带来影响的求解模型。在此基础之上，引入局部优化算法与 ${L}_{1}$ 范数最小化结合的方法，求解所提出的Off-grid TomoSAR模型。最后，利用仿真数据和机载阵列干涉SAR实际飞行数据进行了验证，结果表明，对于Off-grid目标，该方法能够得到比基于 ${L}_{1}$ 范数最小化的经典方法更准确的位置、幅度和相位求解结果，证明了方法的优越性。
- 压缩感知 /
- 层析合成孔径雷达 /
- 离网格 /
- 扰动 /
- 局部阈值
Abstract: Synthetic Aperture Radar (SAR) Tomography (TomoSAR) is a novel technique that enables three-Dimensional (3-D) imaging using multi-baseline two-Dimensional (2-D) data. The essence of TomoSAR is actually to solve a one-dimensional spectral estimation problem. Compressed Sensing-based (CS) algorithm can retrieve solutions with only a few non-uniform acquisitions and has gradually become the main imaging method. In the conventional processing flow of CS algorithms, the continuous elevation direction is divided into a pre-set grid, and the targets are assumed to be exactly on the grid. ${{L}}_{1}$ minimization has been proven to be effective in TomoSAR imaging. In the conventional processing flow, the continuous elevation axis is divided into fixed grids, and scatters are assumed to be exactly on the pre-set grid. However, this hypothesis is generally untenable, and will lead to a problem called “Basis Mismatch”, which is rarely discussed in TomoSAR. In this letter, we first discuss the model of Off-grid TomoSAR, and then propose an addictive perturbation model to compensate for the errors caused by the grid effect. We utilize the local optimization thresholding algorithm to solve the complex-valued ${{L}}_{1}$ minimization problem of TomoSAR. We conducted experiments both on simulation data and actual airborne flight data. Our simulation results indicate that the proposed method can estimate a more accurate position of scatters, which leads to better original signal recovery. The reconstruction results of actual data verify that the impact of grid mismatch can be mostly eliminated.
- Compressive Sensing (CS) /
- Synthetic Aperture Radar Tomography (TomoSAR) /
- Off-grid /
- Perturbation /
- Locally optimization thresholding

HTML全文

1. 引言

机载雷达前视成像在态势感知、自主导航、地形跟踪和地形跟随等方面有着广泛的应用^[1−3]。由于扫描雷达具有连续和广域观测的优势，因此常用于前视成像。然而与其他成像技术如双基前视合成孔径雷达成像方法相比，扫描雷达前视成像存在角度分辨率低的问题^[4−7]。

近年来，研究学者提出了多种超分辨方法来获得高角度分辨率^[8,9]。在超分辨方法中，扫描雷达回波信号可以看作天线方向图与目标散射系数之间的卷积。目标散射系数可以通过反卷积的方式得到，但是因为天线方向图的低通特性，直接进行反卷积是一个病态问题^[10]。在矩阵分析中，天线方向图矩阵中小的奇异值求逆会提高噪声的幅值。根据这个特点，文献[]提出了截断奇异值分解(Truncated Singular Value Decomposition, TSVD)方法，通过舍弃小的奇异值来抑制噪声。正则化方法也是一个很好地解决病态问题的方法，其核心是选择合适的正则化项^[12−14]。在文献[]中，作者提出了Tikhonov正则化，其引入 ${L_2}$ 范数项来抑制噪声。除此之外，谱估计方法也可以用来提高角度分辨率^[16−18]。电子科技大学张永超等人^[19−21]将迭代自适应方法(Iterative Adaptive Approach, IAA)用于前视超分辨成像，并证明了IAA方法可以抑制噪声并提高角度分辨率。与整个成像场景相比，感兴趣成像目标是稀疏的，因此稀疏成像被引入到机载雷达前视超分辨成像中^[22−25]。在文献[]中，作者提出了一个贝叶斯稀疏前视成像方法，该方法利用拉普拉斯分布来描述目标的稀疏特性。成像结果显示拉普拉斯分布可以很好地拟合目标，提高前视成像的角度分辨率。当飞机在船舶上自主着陆时，船舶的轮廓信息尤为重要。文献[]将全变差(Total Variation, TV)和 ${L_1}$ 范数作为正则化约束项来实现前视成像。该方法在提高雷达前视成像角度分辨率的同时，很好地保留了目标的轮廓信息。

相比于提高前视成像的角度分辨率，如何降低前视成像的计算复杂度也是当前研究的一个热点^[28−30]。文献[31]提出将雷达回波信号从时域转换到频域，利用特普利茨矩阵的低位移秩特点，采用Gohberg-Semencul分解实现了矩阵的快速求逆。因为矩阵的维度影响前视成像的实时性，文献[32]采用低秩近似思想对回波信号降维，并采用低秩迭代自适应方法(Low Rank Iterative Adaptive Approach, LRIAA)实现快速前视成像。文献[33]提出了一个二维前视成像处理方法，通过对整体的回波信号进行处理，避免了逐距离单元进行前视成像带来的计算负担，提高了前视成像的实时性。

在前视成像中，雷达回波可能会受到电磁脉冲干扰，或者受设备性能不稳定影响，导致雷达回波数据出现异常^[34,35]。传统的成像方法假设噪声的统计分布服从高斯分布。在面对异常值时，异常值可能会被重构为虚假目标，影响前视成像的准确性。在之前的工作中，我们提出采用学生t分布来拟合雷达回波数据异常时的噪声^[35]。相比于高斯混合模型，基于学生t分布的超分辨方法避免了估计过多的系统参数。但是在估计过程中基于学生t分布的方法依然面临高计算复杂度问题。

本文提出了一种机载雷达超分辨方法实现回波数据异常时的快速前视成像。首先，为了更好地拟合噪声和异常值，我们引入对异常值更加鲁棒的学生t分布。为了更好地重构目标，引入拉普拉斯分层先验来模拟目标的稀疏特征。然后基于期望最大化方法对成像参数进行估计。受TSVD方法的启发，将截断酉矩阵引入目标散射系数的估计公式中。通过矩阵变换降低了求逆矩阵的尺寸从而降低了参数估计的计算复杂度。仿真结果表明本文提出的快速方法可以通过更短的时间实现回波数据异常情况下的前视超分辨成像。

2. 机载雷达前视成像回波模型

为扫描雷达前视成像的几何示意图。图中机载平台距离地面高度为H，搭载着雷达以速度v向前飞行，天线以扫描速度 $\omega$ 逆时针扫描成像区域。初始时刻，载机位于点A所在位置。此时雷达与目标 ${P_1}$ 之间的初始距离记为 ${R_0}$ ，目标 ${P_1}$ 的方位角记为 ${\theta _0}$ ，俯仰角记为 ${\varphi _0}$ 。经过t时刻，载机飞行至B，此时雷达与目标 ${P_1}$ 的方位角为 $\theta \left( t \right)$ ，雷达与目标 ${P_1}$ 之间的瞬时距离记为 $R\left( t \right)$ 。

图 1 扫描雷达几何示意图

Figure 1. Geometric model of scanning radar

下载: 全尺寸图片幻灯片

假设雷达发射线性调频信号

$s\left( \tau \right) = {{\mathrm{rect}}} \left( {\tau /T} \right)\exp \left( {{\mathrm{j}}\pi \mu {\tau ^2}} \right)\exp \left( {{\mathrm{j}}2\pi {f_{\text{c}}}\tau } \right)$

(1)

其中， $\tau$ 为快时间，T为脉冲持续时间， $\mu$ 为脉冲调制频率， ${f_{\text{c}}}$ 为脉冲载波频率， ${\text{rect}}\left( \cdot \right)$ 为窗函数。

对于目标 ${P_1}$ ，经过脉冲压缩和运动补偿后的回波信号可写为

$\begin{split} s\left( {\tau ,t} \right) =\,& \sigma h\left( {t - {t_0}} \right){\text{sinc}}\left[ {{B_{\text{r}}}\left( {\tau - \frac{{2{R_0}}}{{\mathrm{c}}}} \right)} \right]\\ & \cdot \exp \left( { - {\mathrm{j}}\frac{{4\pi }}{\lambda }R\left( t \right)} \right) \end{split}$

(2)

其中， $\sigma$ 表示目标 ${P_1}$ 的散射系数。 $h\left( \cdot \right)$ 表示天线方向图调制函数。 ${B_{\text{r}}}$ 为信号带宽。 $\lambda$ 为信号波长。式(2)中指数项 $\exp \left( - {\mathrm{j}}{{4\pi }R(t)}/{\lambda }\right)$ 为多普勒频移项。瞬时距离 $R\left( t \right)$ 可写为

$\begin{split} R\left( t \right) = \,&\sqrt {R_0^2 + {{\left( {vt} \right)}^2} - 2{R_0}vt\cos {\theta _0}\cos {\varphi _0}} \\ \approx \,&{R_0} - vt\cos {\theta _0}\cos {\varphi _0} \end{split}$

(3)

在某一距离单元，回波信号可写为

${\boldsymbol{y}} = \left( {{\boldsymbol{F}} \odot {\boldsymbol{H}}} \right){\boldsymbol{\sigma}} + {\boldsymbol{n}}$

(4)

其中， ${\boldsymbol{y}} = {\left[ {{y_1},{y_2}, \cdots ,{y_M}} \right]^{\text{T}}}$ 为该距离单元上的回波向量。M为回波信号的长度。 ${\boldsymbol{\sigma}} = {\left[ {{\sigma _1},{\sigma _2}, \cdots ,{\sigma _M}} \right]^{\text{T}}}$ 为目标散射向量。 ${\boldsymbol{n}} = {\left[ {{n_1},{n_2}, \cdots ,{n_M}} \right]^{\text{T}}}$ 为成像噪声。F为多普勒相位矩阵。H为由天线方向图向量 ${\boldsymbol{h}} = {[{h_1},{h_2}, \cdots ,{h_L}]^{\text{T}}}$ 组成的方向图矩阵。L为天线方向图长度。

${\boldsymbol{F}} = {\left[ {\begin{array}{*{20}{c}} 1 & 1 & \cdots & 1 \\ {{{\mathrm{e}}^{{\mathrm{j}}2\pi {\textstyle\frac{{{f_{\text{d}}}\left( {{\theta _1}} \right)}}{{{\text{PRF}}}}}}}} & {{{\mathrm{e}}^{{\mathrm{j}}2\pi {\textstyle\frac{{{f_{\text{d}}}\left( {{\theta _2}} \right)}}{{{\text{PRF}}}}}}}} & \cdots & {{{\mathrm{e}}^{{\mathrm{j}}2\pi{\textstyle \frac{{{f_{\text{d}}}\left( {{\theta _M}} \right)}}{{{\text{PRF}}}}}}}} \\ \vdots & \vdots & \ddots & \vdots \\ {{{\mathrm{e}}^{{\mathrm{j}}2\pi {f_{\text{d}}}\left( {{\theta _1}} \right){\textstyle\frac{{M - 1}}{{{\text{PRF}}}}}}}} & {{{\mathrm{e}}^{{\mathrm{j}}2\pi {f_{\text{d}}}\left( {{\theta _2}} \right){\textstyle\frac{{M - 1}}{{{\text{PRF}}}}}}}} & \cdots & {{{\mathrm{e}}^{{\mathrm{j}}2\pi {f_{\text{d}}}\left( {{\theta _M}} \right){\textstyle\frac{{M - 1}}{{{\text{PRF}}}}}}}} \end{array}} \right]_{ M \times M}}$

(5)

${\boldsymbol{H}} = {\left[ {\begin{array}{*{20}{c}} {{h_{\left\lceil {L/2} \right\rceil \;}}}&{{h_{\left\lceil {L/2} \right\rceil - 1\;}}}& \cdots &{{h_1}}&{}&{}&{} \\ {{h_{\left\lceil {L/2} \right\rceil + 1\;}}}&{{h_{\left\lceil {L/2} \right\rceil \;}}}&{}& \ddots &{{h_1}}&{}&{} \\ \vdots & \vdots & \ddots &{}& \ddots & \ddots &{} \\ {{h_L}}& \vdots &{}& \ddots &{}& \ddots &{{h_1}} \\ {}&{{h_L}}& \ddots &{}& \ddots &{}&{{h_2}} \\ {}&{}& \ddots & \ddots &{}& \ddots & \vdots \\ {}&{}&{}&{{h_L}}&{{h_{L - 1}}}& \cdots &{{h_{\left\lceil {L/2} \right\rceil \;}}} \end{array}} \right]_{M \times M}}$

(6)

${f_{\text{d}}}\left( {{\theta _m}} \right)$ 为多普勒中心频率。PRF为脉冲重复频率。 $\left\lceil \cdot \right\rceil$ 为向上取整操作。

${f_{\text{d}}}\left( {{\theta _m}} \right) = \frac{{2v\cos {\theta _m}\cos \varphi }}{\lambda }$

(7)

$\varphi$ 为此距离单元上的俯仰角。为了获取目标散射向量的幅值和位置信息，本文仅考虑式(4)中的幅值信息，即

$\left| {\boldsymbol{y}} \right| = \left| {\left( {{\boldsymbol{F}} \odot {\boldsymbol{H}}} \right){\boldsymbol{\sigma}} } \right| + \left| {\boldsymbol{n}} \right|$

(8)

方便起见，将式(8)写为

${\boldsymbol{s}} = {\boldsymbol{Hx}} + {\boldsymbol{n}}$

(9)

其中， ${\boldsymbol{s}} = {\left[ {{s_1},{s_2}, \cdots ,{s_M}} \right]^{\text{T}}}$ 为回波幅值向量， ${\boldsymbol{x}} = {\left[ {{x_1},{x_2}, \cdots ,{x_M}} \right]^{\text{T}}}$ 为目标散射幅值向量。

3. 回波数据异常时的快速前视超分辨方法

本节提出了快速超分辨方法实现回波数据异常时的前视成像。首先，采用学生t分布来拟合回波数据异常时的噪声。接着引入拉普拉斯分层分布模拟目标的稀疏分布。然后采用期望最大化方法实现对成像参数的估计。最后将截断的酉矩阵引入到目标散射系数的估计公式中，并通过矩阵变换对目标估计公式进行重写，降低估计过程中的计算复杂度。

3.1 贝叶斯模型

在前视成像过程中，雷达边发射波束边扫描前方场景，通过接收目标的扫描信号对前视场景进行成像。然而在成像场景中可能存在无意的窄带电磁干扰，如非合作脉冲雷达发射的信号。在这种情况下，回波信号的某些方位角上将会出现异常值。此外，雷达受设备性能的影响，如应答器性能、通信链路性能、信号时间戳抖动/量化等多种因素。在这种情况下，整个回波信号中会在不同的方位向距离向随机出现异常值。

受异常值影响，成像噪声变为系统固有高斯白噪声和异常值的组合。文献[36]指出，与高斯分布相比，学生t分布可以容忍回波信号中少数异常值的存在

$\begin{split} p\left( {{\boldsymbol{n}}\left| {{\boldsymbol{\mu}} ,\eta ,v} \right.} \right) =\,& \frac{{\Gamma \left( {\dfrac{{M + \nu }}{2}} \right)}}{{\Gamma \left( {\dfrac{\nu }{2}} \right)}}{\left( {\frac{\eta }{{\pi \nu }}} \right)^{\textstyle\frac{M}{2}}}\\ & \cdot {\left[ {1 + \frac{{{{\left( {{{\boldsymbol{n}}} - {\boldsymbol{\mu}} } \right)}^{\mathrm{T}}}\eta \left( {{\boldsymbol{n}} - {\boldsymbol{\mu}} } \right)}}{\nu }} \right]^{ - \textstyle\frac{{M + \nu }}{2}}}\\[-1pt] \end{split}$

(10)

其中， ${\boldsymbol{\mu}}$ 为学生t分布的均值， $\eta$ 为学生t分布的精度。 $\nu$ 为自由度，当 $\nu = 1$ ，学生t分布变为柯西分布，当 $\nu \to \infty$ ，学生t分布变为高斯分布。 $\Gamma \left( \cdot \right)$ 为Gamma函数。

图2给出了高斯分布和学生t分布的概率密度图比较。图中高斯分布的均值为0、方差为1.13，学生t分布的均值为0、精度为1、自由度为2。从图中可以看出，虽然高斯分布与学生t分布的峰值近似，但学生t分布拥有更高的拖尾，更高的拖尾意味着学生t分布可以容忍回波信号中少量的异常值存在，对异常值更加鲁棒。为了直观地展示学生t分布对异常值的鲁棒性，我们分别拟合了高斯数据和混合少量异常值的高斯数据。直方图拟合曲线如图3所示，其中图3(a)为高斯分布和学生t分布对高斯数据的直方图拟合曲线，图3(b)为高斯分布和学生t分布对混合少量异常值数据的直方图拟合曲线。相比于图3(a)中的拟合曲线，图3(b)中高斯分布的拟合曲线受异常值的影响变化较大，学生t分布的拟合曲线变化较小，说明学生t分布比高斯分布对异常值的鲁棒性更好。

图 2 高斯分布和学生t分布的比较

Figure 2. Comparison of Gaussian distribution and student-t distribution

下载: 全尺寸图片幻灯片

图 3 直方图拟合曲线

Figure 3. Fitting curve of histogram distribution

下载: 全尺寸图片幻灯片

同时，学生t分布也可由高斯分布和Gamma分布得到

$p\left( {{\boldsymbol{n}}\left| {{\boldsymbol{\mu}} ,\eta ,v} \right.} \right) = \int_0^\infty {\mathcal{N} \left( {{\boldsymbol{n}}\left| {{\boldsymbol{\mu}} ,{{\left( {\eta {{\boldsymbol{\varSigma}} }} \right)}^{ - 1}}} \right.} \right)} \mathcal{G} \left( {{{\boldsymbol{\varSigma}} }\left| {\frac{\nu }{2},\frac{\nu }{2}} \right.} \right){\mathrm{d}}{{\boldsymbol{\varSigma}} }$

(11)

其中， $\eta$ 和 ${{\boldsymbol{\varSigma}} } = {\text{diag}}\left( {{\varepsilon _1},{\varepsilon _2}, \cdots ,{\varepsilon _M}} \right)$ 共同表示高斯分布的逆协方差矩阵。 $\mathcal{N}\left( \cdot \right)$ 为高斯分布， $\mathcal{G}\left( \cdot \right)$ 为Gamma分布。从式(11)可以看出，学生t分布由有限个均值相同、方差不同的高斯分布叠加组成。脉冲压缩后的回波信号已经实现了距离向高分辨，在超分辨过程中通过逐距离单元对方位向回波信号进行处理来提高分辨率。异常值不管出现在某些角度上或随机出现在整个回波信号中，在固定距离单元上异常值的形式是相同的。因此本文引入学生t分布来模拟成像噪声的统计特征。为了简化学生t分布，成像噪声服从

$p\left( {{{\boldsymbol{n}}}\left| {\eta ,{{\boldsymbol{\varSigma}} }} \right.} \right) = \mathcal{N}\left( {{\boldsymbol{n}}\left| {{\mathbf{0}},{{\left( {\eta {\boldsymbol{\varSigma}} } \right)}^{ - 1}}} \right.} \right)$

(12)

在式(12)中，假设成像噪声的均值为零。回波信号s服从

$p\left( {{\boldsymbol{s}}\left| {{\boldsymbol{x}},\eta ,{\boldsymbol{\varSigma}} } \right.} \right) = \mathcal{N}\left( {{\boldsymbol{s}}\left| {{\boldsymbol{Hx}},{{\left( {\eta {\boldsymbol{\varSigma}} } \right)}^{ - 1}}} \right.} \right)$

(13)

参数 $\eta$ 服从Gamma分布

$p\left( \eta \right) = \mathcal{G}\left( {\eta \left| {{a_\eta },{b_\eta }} \right.} \right)$

(14)

其中， ${a_\eta }$ 和 ${b_\eta }$ 为超参数，共同控制 $\eta$ 的分布。

同时，参数矩阵 ${{\boldsymbol{\varSigma}} }$ 服从

$p\left( {{\boldsymbol{\varSigma}} \left| \nu \right.} \right) = \prod\limits_{m = 1}^M {\mathcal{G}\left( {{\varepsilon _m}\left| {\frac{\nu }{2},\frac{\nu }{2}} \right.} \right)}$

(15)

自由度 $\nu$ 服从Gamma分布

$p\left( \nu \right) = \mathcal{G}\left( {\nu \left| {{a_\nu },{b_\nu }} \right.} \right)$

(16)

其中，超参数 ${a_\nu }$ 和 ${b_\nu }$ 共同控制 $\nu$ 的分布。

前视成像中感兴趣目标相对于成像场景是稀疏的，因此本文引入拉普拉斯分层先验分布模拟目标的稀疏特征

$p\left( {{\boldsymbol{x}}\left| {\boldsymbol{\lambda}} \right.} \right) = \prod\limits_{m = 1}^M {\frac{{\lambda _m^{}}}{2}\exp \left( { - \lambda _m^{}\left| {{x_m}} \right|} \right)}$

(17)

然后， ${\boldsymbol{\lambda}} = {\left[ {{\lambda _1},{\lambda _2}, \cdots ,{\lambda _M}} \right]^{\text{T}}}$ 服从

$\begin{split} p\left( {\boldsymbol{\lambda}} \right) =\,& \prod\limits_{m = 1}^M {p\left( {{\lambda _m}} \right)} \\ =\,& \prod\limits_{m = 1}^M {\mathcal{G}\left( {{\lambda _m}\left| {{a_{\boldsymbol{\lambda}} },{b_{\boldsymbol{\lambda}} }} \right.} \right)} \end{split}$

(18)

其中，超参数 ${a_{\boldsymbol{\lambda}} }$ 和 ${b_{\boldsymbol{\lambda}} }$ 共同控制 ${\boldsymbol{\lambda}}$ 的分布。

上述成像参数的概率模型如图4所示，图中每个结点表示一个变量，链接表示变量之间存在概率关系，箭头表示生成方向，如图中噪声n和目标x共同作用于回波信号s。

图 4 概率图模型

Figure 4. Probabilistic graphical model

下载: 全尺寸图片幻灯片

3.2 参数估计

3.1节给出了数据异常情况时机载前视成像中噪声和目标的概率模型，本节引入期望最大化方法对成像参数进行估计。期望最大化方法主要分为两步，E步骤和M步骤。E步骤的主要任务是确定目标散射系数x的Q函数。M步骤是通过最大化Q函数来估计目标散射系数x。

E步骤：定义Q函数

$\begin{split} Q\left( {{\boldsymbol{\zeta}} ;{{\boldsymbol{\zeta}} ^{\left( q \right)}}} \right) =\,& {E_{{\phi }\left| {{\boldsymbol{s}},{{\boldsymbol{\zeta}} ^{\left( q \right)}}} \right.}}\left[ {\ln p\left( {{\boldsymbol{s}},{\boldsymbol{\zeta}} ,\phi } \right)} \right] \\ =\,& {E_{\eta ,{{\boldsymbol{\lambda}} },\nu \left| {{\boldsymbol{s}},{{\boldsymbol{x}}^{\left( q \right)}},{{{\boldsymbol{\varSigma}} }^{\left( q \right)}}} \right.}}\left[ {\ln p\left( {{\boldsymbol{x}},\eta ,{{\boldsymbol{\varSigma}} },{{\boldsymbol{\lambda}} },\nu ,{\boldsymbol{s}}} \right)} \right] \end{split}$

(19)

其中， $\phi$ 表示隐藏变量， $\phi = \left\{ {\eta ,{\boldsymbol{\lambda}} ,\nu } \right\}$ 。 ${\boldsymbol{\zeta}}$ 表示模型参数， ${\boldsymbol{\zeta}} = \left\{ {{\boldsymbol{x}},{\boldsymbol{\varSigma}} } \right\}$ 。 ${E_{\phi \left| {{\boldsymbol{s}},{{\boldsymbol{\zeta}} ^{\left( q \right)}}} \right.}}\left[ \cdot \right]$ 表示关于 $p\left( {\phi \left| {{\boldsymbol{s}},{{\boldsymbol{\zeta}} ^{\left( q \right)}}} \right.} \right)$ 的期望。 ${{\boldsymbol{\zeta}} ^{\left( q \right)}}$ 表示第q次迭代中模型参数的值。

M步骤：通过最大化E步骤中Q函数获得模型参数 ${\boldsymbol{\zeta}}$

${{\boldsymbol{\zeta}} ^{\left( {q + 1} \right)}} = \mathop {{\text{arg max}}}\limits_{\boldsymbol{\zeta}} {\mkern 1mu} \left[ {Q\left( {{\text{ }}{\boldsymbol{\zeta}} ;{{\boldsymbol{\zeta}} ^{\left( q \right)}}} \right)} \right]$

(20)

通过E步骤，可以得到 $\nu$ 的期望为

$\left\langle \nu \right\rangle = \frac{{2{a_\nu } + M}}{{2{b_\nu } - \displaystyle\sum\limits_{m = 1}^M {\left( {\ln {\varepsilon _m} - {\varepsilon _m}} \right) - M} }}$

(21)

$\eta$ 的期望为

$\left\langle \eta \right\rangle = \frac{{M + 2{a_\eta }}}{{{{\left( {{\boldsymbol{s}} - {\boldsymbol{Hx}}} \right)}^{\text{T}}}\varSigma \left( {{\boldsymbol{s}} - {\boldsymbol{Hx}}} \right) + 2{b_\eta }}}$

(22)

${\lambda _m}$ 的期望为

$\left\langle {{\lambda _m}} \right\rangle = \frac{{{a_{\boldsymbol{\lambda}} } + 1}}{{\left| {{x_m}} \right| + {b_{\boldsymbol{\lambda}} }}}$

(23)

将式(21)、式(22)和式(23)代入式(19)，Q函数可写为

$\begin{split} Q\left( {{{\boldsymbol{\zeta}} };{{{\boldsymbol{\zeta}} }^{\left( q \right)}}} \right) =\,& {E_{{\phi }\left| {{{\boldsymbol{s}}},{{{\boldsymbol{\zeta}} }^{\left( q \right)}}} \right.}}\left[ {\ln p\left( {{{\boldsymbol{s}}},{{\boldsymbol{\zeta}} },{\phi }} \right)} \right] \\ =\,& \frac{1}{2}\ln {{\boldsymbol{\varSigma}} } - \frac{{\left\langle \eta \right\rangle }}{2}{\left( {{{\boldsymbol{s}}} - {{\boldsymbol{Hx}}}} \right)^{\text{T}}}{{\boldsymbol{\varSigma}} }\left( {{{\boldsymbol{s}}} - {{\boldsymbol{Hx}}}} \right) \\ & + \left( {\frac{{\left\langle \nu \right\rangle }}{2} - 1} \right)\ln {{\boldsymbol{\varSigma}} } - \frac{{\left\langle \nu \right\rangle }}{2}{{\boldsymbol{\varSigma}} } \\ & - {\left\| {{{\boldsymbol{\varLambda}} }{{\boldsymbol{x}}}} \right\|_1} + {\text{const}} \\[-1pt] \end{split}$

(24)

其中， ${\boldsymbol{\varLambda}} = {\text{diag}}\left\{ {\left\langle {{\lambda _1}} \right\rangle ,\left\langle {{\lambda _2}} \right\rangle , \cdots ,\left\langle {{\lambda _M}} \right\rangle } \right\}$ 。

在M步骤中，通过求解 ${\nabla _{\boldsymbol{\zeta}} }Q\left( {{\boldsymbol{\zeta}} ;{{\boldsymbol{\zeta}} ^{\left( q \right)}}} \right) = 0$ 找到最优模型参数 ${\boldsymbol{\zeta}}$ ，可以得到

$\quad\;\; {\varepsilon _m} = \frac{{1 + \left\langle \nu \right\rangle }}{{\left\langle \eta \right\rangle {{\left( {{s_m} - {{\boldsymbol{H}}_m}{\boldsymbol{x}}} \right)}^2} + \left\langle \nu \right\rangle }}$

(25)

${\boldsymbol{x}} = \left\langle \eta \right\rangle {\left( {\left\langle \eta \right\rangle {{\boldsymbol{H}}^{\text{T}}}{\boldsymbol{\varSigma}} {\boldsymbol{H}} + {\boldsymbol{W}}} \right)^{ - 1}}{{\boldsymbol{H}}^{\text{T}}}{\boldsymbol{\varSigma }}{\boldsymbol{s}}$

(26)

其中， ${{\boldsymbol{H}}_m}$ 为天线方向图矩阵的第m行， ${\boldsymbol{W}} =$ diag $\left\{ \left\langle {{\lambda _1}} \right\rangle {{\left( {|{x_1}{|^2} + \delta } \right)}^{ - {\textstyle\frac{1}{2}}}},\;\left\langle {{\lambda _2}} \right\rangle {{\left( {|{x_2}{|^2} + \delta } \right)}^{ - {\textstyle\frac{1}{2}}}},\; \cdots ,\;\left\langle {{\lambda _M}} \right\rangle \cdot{{\left( {|{x_M}{|^2} + \delta } \right)}^{ - \textstyle\frac{1}{2}}} \right\}$ ， $\delta$ 为避免 ${L_1}$ 范数不可微引入的辅助参数。

3.3 快速参数估计

在目标散射系数x的估计过程中，需要计算矩阵 $\left( {\left\langle \eta \right\rangle {{\boldsymbol{H}}^{\text{T}}}{\boldsymbol{\varSigma}} {\boldsymbol{H}} + {\boldsymbol{W}}} \right)$ 的逆，其计算复杂度为 $\mathcal{O}\left( {{M^3}} \right)$ ，本节引入辅助矩阵并通过矩阵变换对目标散射估计公式进行重写，降低了估计过程的计算复杂度。

方向图矩阵H可以通过奇异值分解写为

${\boldsymbol{H}} = {\boldsymbol{UA}}{{\boldsymbol{V}}^{\text{T}}}$

(27)

其中， ${\boldsymbol{U}} = \left[ {{{\boldsymbol{u}}_1},{{\boldsymbol{u}}_2}, \cdots ,{{\boldsymbol{u}}_M}} \right]$ ， ${\boldsymbol{V}} = \left[ {{{\boldsymbol{v}}_1},{{\boldsymbol{v}}_2}, \cdots ,{{\boldsymbol{v}}_M}} \right]$ 为酉矩阵， ${\boldsymbol{A}} = {\text{diag}}\left\{ {{\alpha _1},{\alpha _2}, \cdots ,{\alpha _M}} \right\}$ 为H的奇异值矩阵。

在TSVD方法中，目标散射系数x的估计方式为

$\begin{split} {\boldsymbol{x}} =\,& {{\boldsymbol{H}}_r}^{ - 1}{\boldsymbol{s}} \\ =\,& {{\boldsymbol{V}}_r}{\boldsymbol{A}}_r^{ - 1}{\boldsymbol{U}}_r^{\text{T}}{\boldsymbol{s}} \\ =\,& {{\boldsymbol{V}}_r}{\boldsymbol{V}}_r^{\text{T}}{\boldsymbol{x}} + \sum\limits_{i = 1}^r {{{\boldsymbol{v}}_i}} \alpha _i^{ - 1}{\boldsymbol{u}}_i^{\text{H}}{\boldsymbol{n}} \end{split}$

(28)

其中， ${{\boldsymbol{H}}_r} = {{\boldsymbol{U}}_r}{{\boldsymbol{A}}_r}{\boldsymbol{V}}_r^{\text{T}}$ 是截断的方向图矩阵，r为截断参数。 ${{\boldsymbol{U}}_r} = \left[ {{{\boldsymbol{u}}_1},{{\boldsymbol{u}}_2}, \cdots ,{{\boldsymbol{u}}_r}} \right]$ , ${{\boldsymbol{V}}_r} = \left[ {{{\boldsymbol{v}}_1},{{\boldsymbol{v}}_2}, \cdots ,{{\boldsymbol{v}}_r}} \right]$ 为截断的酉矩阵。 ${{\boldsymbol{A}}_r} = {\text{diag}}\left\{ {{\alpha _1},{\alpha _2}, \cdots ,{\alpha _r}} \right\}$ 为截断的奇异值矩阵。

不考虑噪声的情况下，式(28)可以写为

${\boldsymbol{x}} = {{\boldsymbol{V}}_r}{\boldsymbol{V}}_r^{\text{T}}{\boldsymbol{x}}$

(29)

从式(29)近似得到

${{\boldsymbol{V}}_r}{\boldsymbol{V}}_r^{\text{T}} \approx {\boldsymbol{I}}$

(30)

利用式(30)的性质，可以将式(26)重写为

$\begin{split} {\boldsymbol{x}} = \,&\left\langle \eta \right\rangle {\left[ {\left\langle \eta \right\rangle {{\boldsymbol H}^{\text{T}}}{\boldsymbol{\varSigma}} {\boldsymbol{H}} + {\boldsymbol{W}}} \right]^{ - 1}}{{\boldsymbol H}^{\text{T}}}{\boldsymbol{\varSigma}} {\boldsymbol{s}} \\ =\,& {\left( {{{\boldsymbol H}^{\text{T}}}{{\boldsymbol V}_r}{\boldsymbol V}_r^{\text{T}}{{\boldsymbol{\varSigma}}^{\textstyle\frac{1}{2}}}{{\boldsymbol{\varSigma}}^{\textstyle\frac{1}{2}}}{{\boldsymbol V}_r}{\boldsymbol V}_r^{\text{T}}{\boldsymbol{H}} + {\boldsymbol{W}}{{\left\langle \eta \right\rangle }^{ - 1}}} \right)^{ - 1}} {{\boldsymbol H}^{\text{T}}}{{\boldsymbol V}_r}{\boldsymbol V}_r^{\text{T}}{{\boldsymbol{\varSigma}} ^{\textstyle\frac{1}{2}}}{{\boldsymbol{\varSigma}} ^{\textstyle\frac{1}{2}}}{{\boldsymbol{V}}_r}{\boldsymbol{V}}_r^{\text{T}}{\boldsymbol{s}} \\ =\,& {\left( {{{\boldsymbol H}^{\text{T}}}{{\boldsymbol V}_r}{\boldsymbol V}_r^{\text{T}}{{\boldsymbol{\varSigma}} ^{\textstyle\frac{1}{2}}}{{\boldsymbol{\varSigma}} ^{\textstyle\frac{1}{2}}}{{\boldsymbol V}_r}{\boldsymbol V}_r^{\text{T}}{\boldsymbol{H}} + {\boldsymbol{W}}{{\left\langle \eta \right\rangle }^{ - 1}}} \right)^{ - 1}} {{\boldsymbol H}^{\text{T}}}{{\boldsymbol V}_r}{\boldsymbol V}_r^{\text{T}}{{\boldsymbol{\varSigma}} ^{\textstyle\frac{1}{2}}}\left( {{\boldsymbol{\varSigma}} ^{\textstyle\frac{1}{2}}}{{\boldsymbol V}_r}{\boldsymbol V}_r^{\text{T}}{\boldsymbol{H}}{{\boldsymbol W}^{ - 1}}{{\boldsymbol H}^{\text{T}}}{{\boldsymbol V}_r}{\boldsymbol V}_r^{\text{T}}{{\boldsymbol{\varSigma}} ^{\textstyle\frac{1}{2}}} + {{\left\langle \eta \right\rangle }^{ - 1}}{\boldsymbol{I}} \right)\\ & \times \left( {{\boldsymbol{\varSigma}} ^{\textstyle\frac{1}{2}}}{{\boldsymbol V}_r}{\boldsymbol V}_r^{\text{T}}{\boldsymbol{H}}{{\boldsymbol W}^{ - 1}}{{\boldsymbol H}^{\text{T}}}{{\boldsymbol{V}}_r}{\boldsymbol{V}}_r^{\text{T}}{{\boldsymbol{\varSigma}} ^{\textstyle\frac{1}{2}}} + {{\left\langle \eta \right\rangle }^{ - 1}}{\boldsymbol{I}} \right)^{ - 1}{{\boldsymbol{\varSigma}} ^{\textstyle\frac{1}{2}}}{{\boldsymbol V}_r}{\boldsymbol V}_r^{\text{T}}{\boldsymbol{s}} \\ =\,& {{\boldsymbol W}^{ - 1}}{{\boldsymbol H}^{\text{T}}}{{\boldsymbol V}_r}{\boldsymbol V}_r^{\text{T}}{{\boldsymbol{\varSigma}} ^{\textstyle\frac{1}{2}}}{\left( {{\boldsymbol{\varSigma}} ^{\textstyle\frac{1}{2}}}{{\boldsymbol V}_r}{\boldsymbol V}_r^{\text{T}}{\boldsymbol{H}}{{\boldsymbol W}^{ - 1}}{{\boldsymbol H}^{\text{T}}}{{\boldsymbol{V}}_r}{\boldsymbol{V}}_r^{\text{T}} {{\boldsymbol{\varSigma}} ^{\textstyle\frac{1}{2}}} + {{\left\langle \eta \right\rangle }^{ - 1}}{\boldsymbol{I}} \right)^{ - 1}}{{\boldsymbol{\varSigma}} ^{\textstyle\frac{1}{2}}}{{\boldsymbol V}_r}{\boldsymbol V}_r^{\text{T}}{\boldsymbol{s}} \\ = \,&{{\boldsymbol W}^{ - 1}}{{\boldsymbol H}^{\text{T}}}{{\boldsymbol V}_r}{\left( {\boldsymbol V}_r^{\text{T}}{\boldsymbol{H}}{{\boldsymbol W}^{ - 1}}{{\boldsymbol H}^{\text{T}}}{{\boldsymbol{V}}_r} + {{\left\langle \eta \right\rangle }^{ - 1}}{\boldsymbol V}_r^{\text{T}}{{\boldsymbol{\varSigma}} ^{ - 1}}{{\boldsymbol V}_r} \right)^{ - 1}}{\boldsymbol V}_r^{\text{T}}{\boldsymbol{s}} \\ = \,&{{\boldsymbol W}^{ - 1}}{{\tilde {\boldsymbol H}}^{\text{T}}}{\left( {\tilde {\boldsymbol H}{{\boldsymbol W}^{ - 1}}{{\tilde {\boldsymbol H}}^{\text{T}}} + {{\left\langle \eta \right\rangle }^{ - 1}}{\boldsymbol V}_r^{\text{T}}{{\boldsymbol{\varSigma}} ^{ - 1}}{{\boldsymbol V}_r}} \right)^{ - 1}}\tilde {\boldsymbol{s}} \end{split}$

(31)

其中

$\tilde {\boldsymbol{H}} = {\boldsymbol{V}}_r^{\text{T}}{\boldsymbol{H}}$

(32)

$\tilde {\boldsymbol{s}} = {\boldsymbol{V}}_r^{\text{T}}{\boldsymbol{s}}\quad$

(33)

在原始基于学生t分布的方法中需要计算式(26)矩阵 $\left( {\left\langle \eta \right\rangle {{\boldsymbol{H}}^{\text{T}}}{\boldsymbol{\varSigma}} {\boldsymbol{H}} + {\boldsymbol{W}}} \right)$ 的逆，矩阵的尺寸为 $M \times M$ ，其计算复杂度为 $\mathcal{O}\left( {{M^3}} \right)$ 。在经过引入截断酉矩阵并通过矩阵变换后，式(31)中矩阵 $\left( \tilde {\boldsymbol{H}}{{\boldsymbol{W}}^{ - 1}}{{\tilde {\boldsymbol{H}}}^{\mathrm{T}}} + {{\left\langle \eta \right\rangle }^{ - 1}}{\boldsymbol{V}}_r^{\text{T}}{{\boldsymbol{\varSigma}} ^{ - 1}}{\boldsymbol{V}}_r \right)$ 的尺寸为 $r \times r$ ，计算矩阵逆的计算复杂度变为 $\mathcal{O}\left( {{r^3}} \right)$ 。

截断参数r的选择可以参考TSVD方法的思想。按照表1的雷达系统参数，图5给出了方向图矩阵(尺寸400×400)的奇异值曲线，从图中可以看出大奇异值数量为40左右。因为大的奇异值包含了更多的信息，因此本论文中在选择截断参数r时，可以根据奇异值曲线选择拐角处的截断参数，在尽可能保留大奇异值的同时，平衡加速方法的时间性能。

表 1 仿真系统参数

Table 1. System parameters of simulation

参数	数值	参数	数值
扫描速度 $\left( {{{^ \circ } \mathord{\left/ {\vphantom {{^ \circ } {\text{s}}}} \right. } {\text{s}}}} \right)$	$50$	载波频率 $\left( {{\text{GHz}}} \right)$	$9.5$
扫描范围 $\left( {^ \circ } \right)$	$\pm 10$	信号带宽 $\left( {{\text{MHz}}} \right)$	$40$
脉冲重复频率 $\left( {{\text{Hz}}} \right)$	$1000$	平台速度 $\left( {{{\text{m}} \mathord{\left/ {\vphantom {{\text{m}} {\text{s}}}} \right. } {\text{s}}}} \right)$	$30$
主瓣波束宽度 $\left( {^ \circ } \right)$	3

下载: 导出CSV

| 显示表格

图 5 奇异值曲线

Figure 5. Singular value curve

下载: 全尺寸图片幻灯片

最后，所提方法的成像参数可以通过式(34)得到

$\begin{split} & \left\langle \eta \right\rangle = \frac{{M + 2{a_\eta }}}{{{{\left( {{\boldsymbol{s}} - {\boldsymbol{Hx}}} \right)}^{\text{T}}}{\boldsymbol{\varSigma}} \left( {{\boldsymbol{s}} - {\boldsymbol{Hx}}} \right) + 2{b_\eta }}} \\ & \left\langle {{\lambda _m}} \right\rangle = \frac{{{a_{\boldsymbol{\lambda}} } + 1}}{{\left| {{x_m}} \right| + {b_{\boldsymbol{\lambda}} }}} \\ & \left\langle \nu \right\rangle = \frac{{2{a_\nu } + M}}{{2{b_\nu } - \displaystyle\sum\limits_{m = 1}^M {\left( {\ln {\varepsilon _m} - {\varepsilon _m}} \right) - M} }} \\ & {\varepsilon _m} = \frac{{1 + \left\langle \nu \right\rangle }}{{\left\langle \eta \right\rangle {{\left( {{s_m} - {{\boldsymbol{H}}_m}{\boldsymbol{x}}} \right)}^2} + \left\langle \nu \right\rangle }} \\ & {\boldsymbol{x}} = {{\boldsymbol{W}}^{ - 1}}{{\tilde {\boldsymbol{H}}}^{\mathrm{T}}}{\left( {\tilde {\boldsymbol{H}}{{\boldsymbol{W}}^{ - 1}}{{\tilde {\boldsymbol{H}}}^{\text{T}}} + {{\left\langle \eta \right\rangle }^{ - 1}}{\boldsymbol{V}}_r^{\text{T}}{{\boldsymbol{\varSigma}} ^{ - 1}}{\boldsymbol{V}}_r^{}} \right)^{ - 1}}\tilde {\boldsymbol{s}} \end{split}$

(34)

在初始化参数中，本文将待估参数初始化为 ${x_m} = {{{\boldsymbol{H}}_m^{\text{T}}{\boldsymbol{s}}}}/({{{\boldsymbol{H}}_m^{\mathrm{T}}{{\boldsymbol{H}}_m})}}$ ， ${\boldsymbol{\varSigma}}$ 设置为单位矩阵。超参数如 ${a_\eta }$ , ${b_\eta }$ , ${a_{\boldsymbol{\lambda}} }$ , ${b_{\boldsymbol{\lambda}} }$ , ${a_\nu }$ , ${b_\nu }$ 设置为较小的值，如 ${10^{ - 4}}$ 。手动选择合适的截断参数r，在保留大奇异值的同时兼顾算法的加速性能。

3.4 计算复杂度分析

本节对基于学生t分布的方法和其加速方法的计算复杂度进行了分析。假设固定距离单元上回波信号s的尺寸为 $M \times 1$ ，迭代次数为q。在分析中，因为基于学生t分布的方法和加速方法中均对 $\eta$ , ${\boldsymbol{\lambda}}$ , $\nu$ , ${\boldsymbol{\varSigma}}$ 进行了估计，因此本文忽略了这些参数的计算复杂度，仅考虑计算目标散射系数的计算复杂度。

在基于学生t分布的方法中，计算矩阵 ${{\boldsymbol{H}}^{\text{T}}}{\boldsymbol{\varSigma}} {\boldsymbol{H}}$ 的复杂度为 $\mathcal{O}\left( {q{M^3}} \right)$ 。计算矩阵 $\left( {\left\langle \eta \right\rangle {{\boldsymbol{H}}^{\text{T}}}{\boldsymbol{\varSigma}} {\boldsymbol{H}} + {\boldsymbol{W}}} \right)$ 逆的复杂度为 $\mathcal{O}\left( {q{M^3}} \right)$ 。计算 $\left\langle \eta \right\rangle \left( \left\langle \eta \right\rangle {{\boldsymbol{H}}^{\text{T}}}{\boldsymbol{\varSigma}} {\boldsymbol{H}} + {\boldsymbol{W}} \right)^{ - 1}{{\boldsymbol{H}}^{\text{T}}}{\boldsymbol{\varSigma}} {\boldsymbol{s}}$ 的复杂度为 $\mathcal{O}\left( {q{M^3}} \right)$ 。因此总的计算复杂度为 $\mathcal{O}\left( {3q{M^3}} \right)$ 。

在其加速方法中，需要对方向图矩阵H进行奇异值分解，其计算复杂度为 $\mathcal{O}\left( {{M^3}} \right)$ 。计算 $\tilde {\boldsymbol{H}}$ 的复杂度为 $\mathcal{O}\left( {r{M^2}} \right)$ ，计算 ${{\tilde {\boldsymbol{s}}}}$ 的复杂度为 $\mathcal{O}\left( {rM} \right)$ ，计算矩阵 $\tilde {\boldsymbol{H}}{{\boldsymbol{W}}^{ - 1}}{\tilde {\boldsymbol{H}}^{\text{T}}}$ 的复杂度为 $\mathcal{O}\left( {qM{r^2}} \right)$ ，计算 ${\boldsymbol{V}}_r^{\text{T}}{{\boldsymbol{\varSigma}} ^{ - 1}}{\boldsymbol{V}}_r^{}$ 的复杂度为 $\mathcal{O}\left( {qM{r^2}} \right)$ 。计算矩阵 $( \tilde {\boldsymbol{H}}{{\boldsymbol{W}}^{ - 1}}{{\tilde {\boldsymbol{H}}}^{\text{T}}} + {{\left\langle \eta \right\rangle }^{ - 1}}{\boldsymbol{V}}_r^{\text{T}}{{\boldsymbol{\varSigma}} ^{ - 1}}{\boldsymbol{V}}_r^{} )$ 逆的复杂度为 $\mathcal{O} \left( {q{r^3}} \right)$ 。计算 ${{\boldsymbol{W}}^{ - 1}}{\tilde {\boldsymbol{H}}^{\text{T}}} \cdot{( {\tilde {\boldsymbol{H}}{{\boldsymbol{W}}^{ - 1}}{{\tilde {\boldsymbol{H}}}^{\text{T}}} + {{\left\langle \eta \right\rangle }^{ - 1}}{\boldsymbol{V}}_r^{\text{T}}{{\boldsymbol{\varSigma}} ^{ - 1}}{\boldsymbol{V}}_r^{}} )^{ - 1}}\tilde {\boldsymbol{s}}$ 的复杂度为 $\mathcal{O}\left( {qM{r^2}} \right)$ 。加速方法总的计算复杂度为 $\mathcal{O}\left( 3qM{r^2} + q{r^3} + {M^3} + r{M^2} + rM \right)$ 。

加速方法相比于未加速方法需要进行奇异值分解以及其他附加运算，如计算 ${\boldsymbol{V}}_r^{\text{T}}{{\boldsymbol{\varSigma}} ^{ - 1}}{\boldsymbol{V}}_r^{}$ , $\tilde {\boldsymbol{H}}$ , $\tilde {\boldsymbol{s}}$ 。当截断参数与回波信号长度接近时，加速方法的计算复杂度会比未加速方法的计算复杂度高。根据前面截断参数的选择， $r \ll M$ ，因此加速方法的计算复杂度低于基于学生t分布的计算复杂度。

4. 仿真结果

本节将采用仿真数据和半实测数据验证所提方法的有效性。本文将所提加速的基于学生t分布方法与Tikhonov正则化(Tikhonov regularization, REGU)方法，LRIAA方法，基于学生t分布的方法进行了比较。为方便起见，将基于学生t分布的方法简写为MBSD (Method Based on Student-t Distribution)，加速的基于学生t分布的方法简写为AMBSD (Accelerated Method Based on Student-t Distribution)。在仿真中，假设信噪比(Signal-to-Noise Ratio, SNR)为信号与高斯白噪声的比值。仿真中的异常值为生成回波信号后随机加入。

4.1 点目标仿真

为原始点目标场景，其中两个目标分别位于 $- {0.5^ \circ }$ 和 ${0.5^ \circ }$ ，雷达仿真系统参数如表1所示。

图 6 点目标仿真结果

Figure 6. Point target simulation results

下载: 全尺寸图片幻灯片

图6(b)为信噪比为15 dB的雷达回波信号，回波信号的尺寸为400×1。在回波信号中，我们加入了5个幅值随机的异常值。从图中可以看出，经过雷达波束的调制，两个目标被混合在一起无法分辨，并且有异常值融合在了两个目标之间。图6(c)—图6(f)分别为不同方法的处理结果。在图6(c)中，REGU方法可以将两个目标大致区分开，但两目标之间的谷值还是较高。而且受异常值影响，很难判断目标的真实位置。图6中LRIAA方法可以很好地区分目标，但是同REGU方法一样，因为没有考虑异常值对前视成像的影响，一部分的异常值被重构为虚假目标。图6(e)和图6(f)分别为MBSD方法以及AMBSD方法的处理结果，其中截断参数设为50。从图中可以看出，MBSD方法和AMBSD方法均可以将两相邻目标进行区分并且可以抑制回波中的异常值。

4.2 MSE和计算时间对比

为了评估所提方法的优越性，本文引入均方误差(Mean Square Error, MSE)来定量地观察不同方法的性能。MSE可以通过式(35)得到

${\text{MSE}} = \frac{1}{{{M_{\text{c}}}}}\left( {\frac{1}{M}\left\| {{\boldsymbol{x}} - \hat {\boldsymbol{x}}} \right\|_2^2} \right)$

(35)

其中，x是真实的目标值， ${{\hat {\boldsymbol{x}}}}$ 是x的估计值， ${M_{\text{c}}}$ 是蒙特卡罗实验的次数。仿真分别在信噪比为 ${\text{30 dB}}$ , ${\text{25 dB}}$ , ${\text{20 dB}}$ , ${\text{15 dB}}$ 和 ${\text{10 dB}}$ 的环境下进行500次蒙特卡罗实验。MSE曲线如图7所示，可以观察到随着信噪比的提升，不同方法的性能均得到提升。相对于其他方法，MBSD方法和AMBSD方法可以获得更好的MSE结果。

图 7 不同信噪比情况下的MSE曲线

Figure 7. MSE curves under different SNRs

下载: 全尺寸图片幻灯片

然后我们对不同方法的计算时间进行了对比。仿真时的CPU为 Intel Core i5-12500H 3.10 GHz，RAM为16 GB。仿真软件为MATLAB 2021a。计算时间对比结果如所示。从图中可以看出REGU方法的计算时间相对于其他方法更低，但其角度分辨率较低。LRIAA方法的运行时间低于MBSD方法，但其MSE结果不如MBSD方法。反观AMBSD方法 $\left( {r = 50} \right)$ 在重构目标准确性和运算时间上都拥有一个良好的性能。

图 8 不同方位维度情况下的运行时间曲线

Figure 8. Time curves under different azimuth dimensions

下载: 全尺寸图片幻灯片

4.3 截断参数对性能的影响

基于点目标仿真，本节仿真了 ${\text{20 dB}}$ 信噪比时不同截断参数情况下MSE和计算时间。截断参数对MSE影响的仿真结果如图9所示。从图中可以看出，随着截断参数r取值的逐渐增大，AMBSD方法的MSE逐渐下降并趋于MBSD方法的MSE。并且可以看出MSE曲线的趋势与图5中奇异值曲线的趋势类似，说明大奇异值保留了大部分的原始信息，对目标参数的重构误差影响较大。截断参数对计算时间的影响情况如图10所示。从图中可以看出当截断参数较大时，因为存在附加运算，因此加速方法的运行时间比未加速方法的运行时间长。当截断参数较小时，AMBSD方法的计算时间比MBSD方法的计算时间更短，并且截断参数与方位向回波尺寸的比值越小，AMBSD方法相比于MBSD方法的加速效果更加明显。

图 9 截断参数对MSE影响

Figure 9. Influence of truncated parameter on MSE

下载: 全尺寸图片幻灯片

图 10 截断参数对运行时间影响

Figure 10. Influence of truncated parameter on running time

下载: 全尺寸图片幻灯片

4.4 面目标仿真结果

本节我们通过面目标仿真验证所提方法的有效性。图11为原始目标场景，尺寸为300×400(距离向×方位向)，图中8个合成目标分别分布于不同位置。AMBSD方法的截断参数设为50。表2给出了面目标仿真的雷达系统参数。受到电磁干扰或雷达设备性能影响，异常值可能会出现在回波中的某个方位角上或者随机出现在整个回波上，因此我们将面目标仿真分为两部分。

图 11 原始目标场景

Figure 11. Original target scene

下载: 全尺寸图片幻灯片

表 2 面目标仿真系统参数

Table 2. System parameters of area target simulation

参数	数值	参数	数值
扫描速度 $\left( {{{^ \circ } \mathord{\left/ {\vphantom {{^ \circ } {\text{s}}}} \right. } {\text{s}}}} \right)$	$50$	载波频率 $\left( {{\text{GHz}}} \right)$	$9.5$
扫描范围 $\left( {^ \circ } \right)$	$\pm 10$	信号带宽 $\left( {{\text{MHz}}} \right)$	$40$
脉冲重复频率 $\left( {{\text{Hz}}} \right)$	$1000$	平台速度 $\left( {{{\text{m}} \mathord{\left/ {\vphantom {{\text{m}} {\text{s}}}} \right. } {\text{s}}}} \right)$	$30$
主瓣波束宽度 $\left( {^ \circ } \right)$	5

下载: 导出CSV

| 显示表格

(1) 受电磁干扰时前视成像：为雷达回波信号，此时的信噪比为 ${\text{10 dB}}$ ，有8个随机幅值的异常值随机分布在某些方位角上。从回波信号中可以看出目标被混合在一起，无法分辨。图12(b)为LRIAA方法的处理结果，因为没有考虑异常值，LRIAA方法受到异常值的影响，2500 m附近的重构目标被干扰严重。在图12(c)和图12(d)中，MBSD方法和AMBSD方法可以很好地抑制异常值并且区分目标。为了更好地量化重构结果，表3给出了MSE结果对比和运行时间对比。从表中可以看出，所提AMBSD方法可以用更短的运行时间获得更好的重构结果。

图 12 受电磁干扰时面目标仿真结果

Figure 12. Area target simulation results with electromagnetic interference

下载: 全尺寸图片幻灯片

表 3 受电磁干扰时面目标仿真的MSE和运行时间

Table 3. MSE and running time of area target simulation with electromagnetic interference

方法	MSE	运行时间(s)
LRIAA方法	6.15×10^–3	4.90
MBSD方法	0.65×10^–3	23.14
AMBSD方法	0.70×10^–3	3.82

下载: 导出CSV

| 显示表格

(2) 设备性能异常时前视成像：从的运行时间可以看出，所提AMBSD方法具有更快的运行时间。为雷达回波信号，此时的信噪比为 ${\text{10 dB}}$ ，异常值被随机地添加到回波信号中。图13(b)为LRIAA方法处理结果，图中目标可以被分开，但是异常值依旧零散地分布于整个重构场景中。相比于LRIAA方法的处理结果，MBSD方法和AMBSD方法获得了更好的重构结果。

表 4 设备性能异常时面目标仿真的MSE和运行时间

Table 4. MSE and running time of area target simulation with abnormal equipment performance

方法	MSE	运行时间(s)
LRIAA方法	1.09×10^–3	4.80
MBSD方法	0.80×10^–3	23.03
AMBSD方法	0.81×10^–3	3.90

下载: 导出CSV

| 显示表格

图 13 设备性能异常时面目标仿真结果

Figure 13. Area target simulation results with abnormal equipment performance

下载: 全尺寸图片幻灯片

4.5 半实测数据处理结果

前面的仿真实验证明了所提AMBSD方法可以用更快的速度抑制回波信号中的异常值，提高前视成像的角度分辨率。本节采用半实测数据进一步验证所提方法的性能。图14(a)为机载雷达实测回波信号，其中红色矩形框内存在两个混合在一起的目标，回波信号尺寸为513×208(距离向×方位向)。AMBSD方法的截断参数设为50。图14(b)和图14(c)为MBSD方法和AMBSD方法的处理结果。从处理结果中可以看出，各方法可以对红色矩形框中的目标进行分辨，提高前视成像的角度分辨率，证明了MBSD方法和AMBSD方法对实测数据的有效性。

图 14 实测数据结果

Figure 14. Processed results of real data

下载: 全尺寸图片幻灯片

(1) 受电磁干扰时前视成像：图15(a)为半实测回波信号，我们将异常值随机添加到不同的方位角上。图15(b)—图15(d)为不同方法的处理结果。从图15(b)中可以看出，LRIAA方法对异常值的抑制能力较差，并且红色矩形框中的目标没有被区分开。相比于LRIAA方法，MBSD方法和AMBSD方法均可以抑制异常值，并且红色矩形框中的目标也可以被区分出来。表5给出了不同方法的运行时间对比，可以看出AMBSD方法具有更短的运行时间。

图 15 受电磁干扰时半实测数据仿真结果

Figure 15. Processed results of semi-real data with electromagnetic interference

下载: 全尺寸图片幻灯片

表 5 半实测数据运行时间(s)

Table 5. Running time of semi-real data (s)

方法	受电磁干扰时运行时间	设备性能异常时运行时间
LRIAA方法	1.98	1.89
MBSD方法	4.57	4.58
AMBSD方法	1.18	1.19

下载: 导出CSV

| 显示表格

(2) 设备性能异常时前视成像：图16(a)为回波信号，此时异常值随机分布于回波信号中。图16(b)—图16(d)为不同方法的处理结果。从图16(c)和图16(d)中可以看出MBSD方法和AMBSD方法可以抑制异常值并且区分红色矩形框中的目标。并且表5说明AMBSD方法可以用更短的运行时间获得与MBSD方法近似的分辨性能。相比于表3和表4中AMBSD方法与MBSD方法的加速比值，因为在半实测仿真中截断参数与方位向尺寸的比值增大，因此表5中的加速比值更小。

图 16 设备性能异常时半实测数据仿真结果

Figure 16. Processed results of semi-real data with abnormal equipment performance

下载: 全尺寸图片幻灯片

5. 结语

本文提出了一种机载雷达超分辨方法实现回波数据异常时快速前视成像。该方法通过利用学生t分布对异常值的鲁棒性，使噪声模型对存在异常值时的回波信号更加灵活。为了更好地重构目标，引入拉普拉斯分层先验来模拟目标的稀疏特征。然后基于期望最大化方法对成像参数进行估计。为了降低参数估计过程的运算量，本文将截断后的酉矩阵引入到目标散射系数的估计公式中，并通过矩阵变换的方法将原方法中需要对 $M \times M$ 维矩阵求逆转变为对 $r \times r$ 维矩阵求逆。从仿真数据和半实测数据中可以看出，本文所提出的快速方法可以用更短的时间实现在回波数据异常情况下的前视超分辨成像。

图 1 TomoSAR成像几何关系

Figure 1. The geometry of TomoSAR imaging

下载: 全尺寸图片幻灯片

图 2 高程向目标重建结果的简单示意图

Figure 2. Sketch map of the reconstruct results in the elevation direction

下载: 全尺寸图片幻灯片

图 3 点目标仿真结果

Figure 3. Point target simulation results

下载: 全尺寸图片幻灯片

图 4 散射点位置估计值与真值距离的统计平均值

Figure 4. The average distance between the estimated scattering point position and the true value

下载: 全尺寸图片幻灯片

图 5 本文方法优于传统方法的概率与SNR的关系

Figure 5. Probability of the proposed algorithm providing better estimation versus SNR

下载: 全尺寸图片幻灯片

图 6 获得更精确估计的概率与观测数量的关系

Figure 6. Probability of the proposed algorithm providing better estimation versus number of acquisitions

下载: 全尺寸图片幻灯片

图 7 RMSE的计算结果

Figure 7. RMSE results

下载: 全尺寸图片幻灯片

图 8 从谷歌地球获取的实验地区于2015年的光学影像和对应的SAR图像

Figure 8. Optical image of the experiment area obtained from Google Earth in 2015 and SAR image of the corresponding area

下载: 全尺寸图片幻灯片

图 9 图8(a)中最后一排建筑光学影像

Figure 9. Optical image of the last row of buildings Fig. 8(a)

下载: 全尺寸图片幻灯片

图 10 图9中红框建筑的三维重建结果

Figure 10. TomoSAR results of the building marked in Fig. 9

下载: 全尺寸图片幻灯片

图 11 本文方法与传统L₁范数最小化的方法对图8中红线标记的方位向切片的成像结果比较

Figure 11. Comparison of our method and the conventional process of ${L}_{1}$ minimization in the slant range plane for the azimuth-bin marked in Fig. 8

下载: 全尺寸图片幻灯片

图 12 图11中区域的放大图

Figure 12. Zoom in of the circled area in Fig. 11

下载: 全尺寸图片幻灯片

表 1 BPLOT的流程

Table 1. The process of BPLOT

　算法 : BPLOT

　(1) 输入:

$\boldsymbol{A},{\boldsymbol{A} }',\boldsymbol{g},\Delta s{\text{，}}\mathrm{稀}\mathrm{疏}\mathrm{度}K$
　(2)

${L}_{1}$ 范数求解:
　　　

$\mathrm{argmin} \left\{ {\left|\left|{ { {\boldsymbol{g} } } }-{{ {\boldsymbol{A} } } }_{\mathit{g} }{\boldsymbol\varGamma }\right|\right|}_{2}^{2}+\mu {\left|\left|{\boldsymbol\varGamma }\right|\right|}_{1}\right\}$
　　　

$\boldsymbol{\varGamma }={\left[\boldsymbol{\gamma }\;\;{\boldsymbol{\gamma } }'\right]}^{t},{\boldsymbol{A} }_{\mathit{g} }=\left[\begin{array}{cc}\boldsymbol{A}& {\boldsymbol{A} '} \end{array}\right]$
　(3) For count t=1: K,
　(4)

${\alpha }_{t}$ =

${\mathrm{a}\mathrm{r}\mathrm{g}\mathrm{m}\mathrm{a}\mathrm{x} }_{p}\{\left|{\mathit{\gamma } }_{p}\right|+\left|{\mathit{\gamma } }_{p}\right|/|2\pi {\Delta }s\left|\right\}$ ,

$p\notin \left({S}^{t-1}\right)$
　(5)

${S}^{t}={S}^{t-1}\cup \left\{{\alpha }_{t}\right\}$
　(6) 计算网格偏差

$\Delta k\Delta s=\mathfrak{R}e({{\boldsymbol{\gamma}} }'/({\rm{j} }2\pi {\boldsymbol{\gamma}} \left)\right)$
　(7) 计算散射值
　　　

${\hat{\boldsymbol{A} } }_{f}={{\boldsymbol{A}}}(S+\Delta k\Delta s)$
　　　

${\hat{\gamma } }_{f}={\left({ {\hat{ \boldsymbol{A} } }_{f} }^{\rm{H} }{\hat{ \boldsymbol{A} } }_{f}\right)}^{-1}{ {\hat{ \boldsymbol{A} } }_{f} }^{\rm{H} }\boldsymbol{g}$
　(8) 输出：

${\hat{\gamma } }_{f},S,\Delta k$

下载: 导出CSV

表 2 仿真参数

Table 2. Simulation parameters

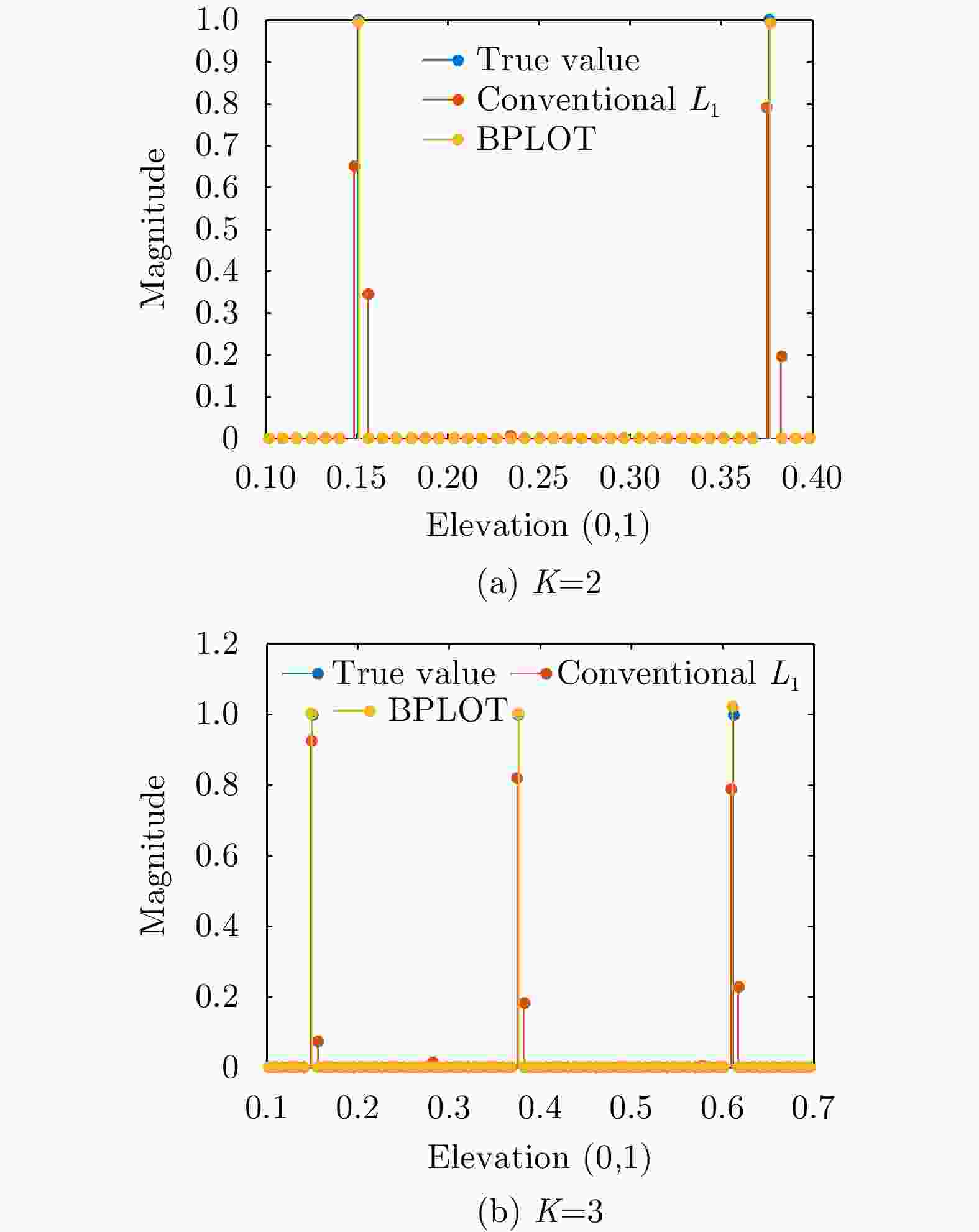
参数	参数值
载波频率(GHz)	14.5
信号带宽(MHz)	500
通道数N	8
基线宽度(m)	0.084
脉冲重复频率(Hz)	480
平台高度(m)	1200
平台速度(m/s)	70
下视角(°)	45

下载: 导出CSV

表 3 图3对应的位置计算结果

Table 3. Point calculation results corresponding to Fig. 3

参数	真值	${L}_{1}$	BPLOT
K=2	[0.1506, 0.3764]	[0.1400, 0.3750]	[0.1506, 0.3764]
K=3	[0.1501, 0.3764, 0.6120]	[0.1484, 0.3750, 0.6094]	[0.1501 0.3765 0.6119]

下载: 导出CSV

参考文献(31)

[1]	FORNARO G, SERAFINO F, and SOLDOVIERI F. Three-dimensional focusing with multipass SAR data[J]. IEEE Transactions on Geoscience and Remote Sensing, 2003, 41(3): 507–517. doi: 10.1109/TGRS.2003.809934
[2]	REIGBER A and MOREIRA A. First demonstration of airborne SAR tomography using multibaseline L-band data[J]. IEEE Transactions on Geoscience and Remote Sensing, 2000, 38(5): 2142–2152. doi: 10.1109/36.868873
[3]	ZHU Xiaoxiang and BAMLER R. Very high resolution spaceborne SAR tomography in urban environment[J]. IEEE Transactions on Geoscience and Remote Sensing, 2010, 48(12): 4296–4308. doi: 10.1109/TGRS.2010.2050487
[4]	FORNARO G, REALE D, and SERAFINO F. Four-dimensional SAR imaging for height estimation and monitoring of single and double scatterers[J]. IEEE Transactions on Geoscience and Remote Sensing, 2009, 47(1): 224–237. doi: 10.1109/TGRS.2008.2000837
[5]	CHAI Huiming, LV Xiaolei, YAO Jingchuan, et al. Off-grid differential tomographic SAR and its application to railway monitoring[J]. IEEE Journal of Selected Topics in Applied Earth Observations and Remote Sensing, 2019, 12(10): 3999–4013. doi: 10.1109/JSTARS.2019.2940730
[6]	AUSTIN C D, ERTIN E, and MOSES R L. Sparse signal methods for 3-D radar imaging[J]. IEEE Journal of Selected Topics in Signal Processing, 2011, 5(3): 408–423. doi: 10.1109/JSTSP.2010.2090128
[7]	FERRARA M, JACKSON J A, and AUSTIN C. Enhancement of multi-pass 3D circular SAR images using sparse reconstruction techniques[C]. Proceedings of SPIE 7337, Algorithms for Synthetic Aperture Radar Imagery XVI, Orlando, United States, 2009. doi: 10.1117/12.820256.
[8]	ZHU Xiaoxiang and BAMLER R. Super-resolution power and robustness of compressive sensing for spectral estimation with application to spaceborne tomographic SAR[J]. IEEE Transactions on Geoscience and Remote Sensing, 2012, 50(1): 247–258. doi: 10.1109/TGRS.2011.2160183
[9]	ZHU Xiaoxiang and BAMLER R. Tomographic SAR inversion by L₁-norm regularization—The compressive sensing approach[J]. IEEE transactions on Geoscience and Remote Sensing, 2010, 48(10): 3839–3846. doi: 10.1109/TGRS.2010.2048117
[10]	李杭, 梁兴东, 张福博, 等. 一种基于组稀疏的阵列干涉SAR三维重建方法[J]. 中国科学:信息科学, 2018, 48(8): 1051–1064. doi: 10.1360/N112017-00023 LI Hang, LIANG Xingdong, ZHANG Fubo, et al. A novel 3-D reconstruction approach based on group sparsity of array InSAR[J]. Science in China Information, 2018, 48(8): 1051–1064. doi: 10.1360/N112017-00023
[11]	JIAO Zekun, DING Chibiao, QIU Xiaolan, et al. Urban 3D imaging using airborne TomoSAR: Contextual information-based approach in the statistical way[J]. ISPRS Journal of Photogrammetry and Remote Sensing, 2020, 170: 127–141. doi: 10.1016/j.isprsjprs.2020.10.013
[12]	MA Peifeng, LIN Hui, LAN Hengxing, et al. On the performance of reweighted L₁ minimization for tomographic SAR imaging[J]. IEEE Geoscience and Remote Sensing Letters, 2015, 12(4): 895–899. doi: 10.1109/LGRS.2014.2365613
[13]	廖明生, 魏恋欢, 汪紫芸, 等. 压缩感知在城区高分辨率SAR层析成像中的应用[J]. 雷达学报, 2015, 4(2): 123–129. doi: 10.12000/JR15031 LIAO Mingsheng, WEI Lianhuan, WANG Ziyun, et al. Compressive sensing in high-resolution 3D SAR tomography of urban scenarios[J]. Journal of Radars, 2015, 4(2): 123–129. doi: 10.12000/JR15031
[14]	王爱春, 向茂生. 基于块压缩感知的SAR层析成像方法[J]. 雷达学报, 2016, 5(1): 57–64. doi: 10.12000/JR16006 WANG Aichun and XIANG Maosheng. SAR tomography based on block compressive sensing[J]. Journal of Radars, 2016, 5(1): 57–64. doi: 10.12000/JR16006
[15]	CHI Yuejie, SCHARF L L, PEZESHKI A, et al. Sensitivity to basis mismatch in compressed sensing[J]. IEEE Transactions on Signal Processing, 2011, 59(5): 2182–2195. doi: 10.1109/TSP.2011.2112650
[16]	HERMAN M A and NEEDELL D. Mixed operators in compressed sensing[C]. The 44th Annual Conference on Information Sciences and Systems (CISS), Princeton, USA, 2010. doi: 10.1109/CISS.2010.5464909.
[17]	CANDÈS E and ROMBERG J. Sparsity and incoherence in compressive sampling[J]. Inverse Problems, 2007, 23(3): 969–985. doi: 10.1088/0266-5611/23/3/008
[18]	STOICA P and BABU P. Sparse estimation of spectral lines: Grid selection problems and their solutions[J]. IEEE Transactions on Signal Processing, 2012, 60(2): 962–967. doi: 10.1109/TSP.2011.2175222
[19]	TANG Gongguo, BHASKAR B N, SHAH P, et al. Compressed sensing off the grid[J]. IEEE Transactions on Information Theory, 2013, 59(11): 7465–7490. doi: 10.1109/TIT.2013.2277451
[20]	YANG Zai and XIE Lihua. Enhancing sparsity and resolution via reweighted atomic norm minimization[J]. IEEE Transactions on Signal Processing, 2016, 64(4): 995–1006. doi: 10.1109/TSP.2015.2493987
[21]	陈栩杉, 张雄伟, 杨吉斌, 等. 如何解决基不匹配问题: 从原子范数到无网格压缩感知[J]. 自动化学报, 2016, 42(3): 335–346. doi: 10.16383/j.aas.2016.c150539 CHEN Xushan, ZHANG Xiongwei, YANG Jibin, et al. How to overcome basis mismatch: from atomic norm to gridless compressive sensing[J]. Acta Automatica Sinica, 2016, 42(3): 335–346. doi: 10.16383/j.aas.2016.c150539
[22]	FANNJIANG A and LIAO Wenjing. Super-resolution by compressive sensing algorithms[C]. 2012 Conference Record of the Forty Sixth Asilomar Conference on Signals, Systems and Computers (ASILOMAR), Pacific Grove, USA, 2012. doi: 10.1109/ACSSC.2012.6489036.
[23]	HERMAN M A and STROHMER T. General deviants: An analysis of perturbations in compressed sensing[J]. IEEE Journal of Selected Topics in Signal Processing, 2010, 4(2): 342–349. doi: 10.1109/JSTSP.2009.2039170
[24]	YANG Zai, XIE Lihua, and ZHANG Cishen. Off-grid direction of arrival estimation using sparse Bayesian inference[J]. IEEE Transactions on Signal Processing, 2013, 61(1): 38–43. doi: 10.1109/TSP.2012.2222378
[25]	FANNJIANG A and TSENG H C. Compressive radar with off-grid targets: A perturbation approach[J]. Inverse Problems, 2013, 29(5): 054008. doi: 10.1088/0266-5611/29/5/054008
[26]	CHEN S S, DONOHO D L, and SAUNDERS M A. Atomic decomposition by basis pursuit[J]. SIAM Review, 2001, 43(1): 129–159. doi: 10.1137/S003614450037906X
[27]	仇晓兰, 焦泽坤, 彭凌霄, 等. SARMV3D-1.0: SAR微波视觉三维成像数据集[J]. 雷达学报, 2021, 10(4): 485–498. doi: 10.12000/JR21112 QIU Xiaolan, JIAO Zekun, PENG Lingxiao, et al. SARMV3D-1.0: Synthetic aperture radar microwave vision 3D imaging dataset[J]. Journal of Radars, 2021, 10(4): 485–498. doi: 10.12000/JR21112
[28]	FANNJIANG A and LIAO Wenjing. Coherence pattern-guided compressive sensing with unresolved grids[J]. SIAM Journal on Imaging Sciences, 2012, 5(1): 179–202. doi: 10.1137/110838509
[29]	SCHMITT M. Reconstruction of urban surface models from multi-aspect and multi-baseline interferometric SAR[D]. [Ph. D. dissertation], Technische Universität München, 2014.
[30]	ZHU Xiaoxiang. Spectral estimation for synthetic aperture radar tomography[D]. [Master dissertation], Technische Universität München, 2008.
[31]	李杭. 阵列干涉SAR高精度三维成像算法研究[D]. [博士论文], 中国科学院大学, 2017. LI Hang. Research on high-precision 3-D imaging algorithm of array interferometric synthetic aperture radar[D]. [Ph. D. dissertation], University of Chinese Academy of Sciences, 2017.

施引文献

期刊类型引用(1)
1. 毛德庆，杨建宇，杨明杰，张永超，张寅，黄钰林. IAA-Net：一种实孔径扫描雷达迭代自适应角超分辨成像方法. 雷达学报. 2024(05): 1073-1091 . 本站查看
其他类型引用(0)

资源附件(0)

访问统计

图(12) / 表(3)

计量

文章访问数: 1666
HTML全文浏览量: 835
PDF下载量: 265
被引次数: 1

1. 引言
2. 机载雷达前视成像回波模型
3. 回波数据异常时的快速前视超分辨方法
3.1 贝叶斯模型
3.2 参数估计
3.3 快速参数估计
3.4 计算复杂度分析
4. 仿真结果
4.1 点目标仿真
4.2 MSE和计算时间对比
4.3 截断参数对性能的影响
4.4 面目标仿真结果
4.5 半实测数据处理结果
5. 结语

1. 引言
2. 机载雷达前视成像回波模型
3. 回波数据异常时的快速前视超分辨方法
3.1 贝叶斯模型
3.2 参数估计
3.3 快速参数估计
3.4 计算复杂度分析
4. 仿真结果
4.1 点目标仿真
4.2 MSE和计算时间对比
4.3 截断参数对性能的影响
4.4 面目标仿真结果
4.5 半实测数据处理结果
5. 结语

参考文献(31)

施引文献

资源附件(0)

访问统计

基于扰动的结合Off-grid目标的层析SAR三维成像方法

DOI: 10.12000/JR21093

通讯作者:
仇晓兰 xlqiu@mail.ie.ac.cn

计量

L₁ Minimization with Perturbation for Off-grid Tomographic SAR Imaging

Corresponding author: QIU Xiaolan, xlqiu@mail.ie.ac.cn

1. 引言

2. 机载雷达前视成像回波模型

3. 回波数据异常时的快速前视超分辨方法

3.1 贝叶斯模型

3.2 参数估计

3.3 快速参数估计

3.4 计算复杂度分析

4. 仿真结果

4.1 点目标仿真

4.2 MSE和计算时间对比

4.3 截断参数对性能的影响

4.4 面目标仿真结果

4.5 半实测数据处理结果

5. 结语

期刊类型引用(1)

其他类型引用(0)

计量

目录

1. 引言

2. 机载雷达前视成像回波模型

3. 回波数据异常时的快速前视超分辨方法

3.1 贝叶斯模型

3.2 参数估计

3.3 快速参数估计

3.4 计算复杂度分析

4. 仿真结果

4.1 点目标仿真

4.2 MSE和计算时间对比

4.3 截断参数对性能的影响

4.4 面目标仿真结果

4.5 半实测数据处理结果

5. 结语

期刊介绍

联系我们

基于扰动的结合Off-grid目标的层析SAR三维成像方法

DOI: 10.12000/JR21093

通讯作者: 仇晓兰 xlqiu@mail.ie.ac.cn

计量

出版历程

L1 Minimization with Perturbation for Off-grid Tomographic SAR Imaging

Corresponding author: QIU Xiaolan, xlqiu@mail.ie.ac.cn

1. 引言

2. 机载雷达前视成像回波模型

3. 回波数据异常时的快速前视超分辨方法

3.1 贝叶斯模型

3.2 参数估计

3.3 快速参数估计

3.4 计算复杂度分析

4. 仿真结果

4.1 点目标仿真

4.2 MSE和计算时间对比

4.3 截断参数对性能的影响

4.4 面目标仿真结果

4.5 半实测数据处理结果

5. 结语

期刊类型引用(1)

其他类型引用(0)

计量

出版历程

目录

1. 引言

2. 机载雷达前视成像回波模型

3. 回波数据异常时的快速前视超分辨方法

3.1 贝叶斯模型

3.2 参数估计

3.3 快速参数估计

3.4 计算复杂度分析

4. 仿真结果

4.1 点目标仿真

4.2 MSE和计算时间对比

4.3 截断参数对性能的影响

4.4 面目标仿真结果

4.5 半实测数据处理结果

5. 结语

期刊介绍

联系我们

通讯作者:
仇晓兰 xlqiu@mail.ie.ac.cn

L₁ Minimization with Perturbation for Off-grid Tomographic SAR Imaging